1 Introduction

Recently, scientific interest in solid-state terahertz (THz) devices (operating at frequencies between 300 GHz and 3 THz) has increased significantly [1,2,3,4,5]. The main idea, based on the shallow-water analogy put forward by Dyakonov and Shur [6,7,8], is to use field-effect transistors with high-mobility channels as nonlinear elements for the resonant detection of incident THz radiation. Moreover, the possibility of plasma instabilities leading to the emission of THz radiation by planar field-effect transistors, as pointed out by Dyakonov and Shur, has resulted in investigations by many groups (e.g., [9,10,11,12,13]). The question arises whether similar plasma instabilities could occur in nanowire or nanotube transistors. Although the methods developed previously for planar transistors could be applied to nanowire transistors, it is not clear whether the assumptions on which these models are based hold in the case of quasi-ballistic transport, which is a prerequisite for plasma instabilities [14]. Therefore, we discuss in addition to the drift-diffusion (DD) model, which is similar to the transport model used by Dyakonov and Shur, also the Boltzmann transport equation (BE) from which the DD model can be derived under rather stringent approximations [15].

Since the stabilization scheme based on the H-transformation for the BE fails for quasi-ballistic transport, a scheme based on the phase-space trajectories of the electrons is presented [16]. Furthermore, in the case of quasi-ballistic transport the stationary drain current of a MOSFET is limited by the finite injection velocity of the electrons from the source into the channel (e.g., [17, 18]). This leads to a much more complex behavior of the source contact at high frequencies that can be described by the simple approximation made by Dyakonov and Shur and that the small-signal electron density must satisfy a Dirichlet boundary condition (D-BC) at the source side of the channel [6]. In order to describe the quasi-ballistic transport in such devices, it is not only necessary to go beyond the drift-diffusion approximation but to also include a more realistic contact model.

In the semiclassical framework, the BE provides the most precise information about the distribution of the charge carriers in the multidimensional phase space [19]. The most frequently applied method to solve the BE is the Monte-Carlo method [19], but there are no Monte-Carlo methods known to the authors that can perform small-signal simulations at complex frequencies required by the Dyakonov–Shur approach to plasma instabilities. On the other hand, deterministic solvers for the BE have been successfully used in the case of nanowire transistors (e.g., [20]), even including small-signal calculations [21]. In these cases, a transformation from the wavenumber to energy is used, which causes trouble in the case of a 1D k-space, because the density of states diverges at zero energy. This exacerbates the problems of small-signal calculations already encountered in the case of a 2D k-space [22]. Furthermore, in the ballistic limit the distribution function can be strongly asymmetric and discontinuous w.r.t. the wavenumber. This leads to further problems with the usual stabilization schemes based on the maximum entropy dissipation scheme [23] and the H-transformation [24]. These deficiencies are fatal in the numerical analysis of plasma resonances, where a numerically robust solver for the BE is required for handling the ballistic limit. In order to solve the above-mentioned problems, the BE is discretized directly in the phase space [16] and the quasi-ballistic limit of a nanowire transistor is investigated. The particular focus is on demonstrating a stabilization method, which is based on the method of characteristic curves and matrix exponentials. Thermal bath BCs, with the assumption of thermal equilibrium only for the electrons entering the device, give a more realistic description of the contacts [25]. The results are compared to the results of the DD equations.

The paper is organized as follows. Section 2 provides a description of the numerical framework used to evaluate the DC and small-signal behavior extending to the ballistic limit. In Sect. 3, the device structure is presented and the simulation results concentrating, in particular, on the small-signal drain self-admittance are discussed. Finally, in Sect. 4 the conclusions are drawn.

2 Theory

The numerical models are mostly constructed with the usual methods [16, 26,27,28,29,30], and only the new aspects are discussed. Since it is difficult to include the Pauli exclusion principle properly in moments-based transport models and it was neglected by Dyakonov and Shur, we will also neglect it in this investigation.

The device model for the silicon nanowire transistor consists of three partial differential equations, the Poisson, Schrödinger, and Boltzmann equations [20]. The Poisson equation is formulated for the 3D real space

$$\begin{aligned} \nabla \cdot \left( \kappa \nabla \varphi \right) = q\left( n -N_{\text{D}} \right) , \end{aligned}$$
(1)

where \(\kappa ({\vec {r}})\) is the permittivity at position \({\vec {r}}\) in real space, \(\varphi ({\vec {r}},t)\) the quasi-stationary potential at time t, q the positive electron charge, \(n({\vec {r}},t)\) the electron density and \(N_{\text{D}}({\vec {r}})\) the donor concentration. The quasi-stationary approach is sufficient in this case, because even at 1 THz the wave length of light in silicon is about \(100\,\upmu \hbox{m}\) and thus much larger than the device dimensions.

The device is sliced into \(N_{\text{sec}}\) sections perpendicular to the transport direction (z-direction), and the quasi-stationary Schrödinger equation is solved for 2D cross sections parallel to the xy-plane at fixed positions for z

$$\begin{aligned} \dfrac{-\hbar ^2}{2}\left( \dfrac{1}{m_{xx}^\nu }\dfrac{\partial ^2}{\partial x^2} + \dfrac{1}{m_{yy}^\nu }\dfrac{\partial ^2}{\partial y^2} \right) \psi ^\nu -q\varphi \psi ^\nu = \varepsilon _{\text{sub}}^\nu \psi ^\nu \end{aligned}$$
(2)

under the assumption that the wave functions vanish outside of the silicon region. \(\hbar\) is the reduced Planck constant, \(m_{xx}^\nu\), \(m_{yy}^\nu\) the electron masses in x and y direction assuming a \(\langle 100 \rangle\) orientation of the silicon nanowire and parabolic bands, \(\psi ^\nu ({\vec {r}},t)\) the envelope function and \(\varepsilon _{\text{sub}}^\nu (z,t)\) the subband energy. The superscript \(\nu =(v,s)\) contains the valley index v of the minima of the conduction band and the subband index s. Again, the quasi-stationary approximation is used, because the largest part of the confining potential, which results in the boundary conditions, does not depend on time and due to the high symmetry of the device, which suppresses acoustic-wave-like plasma oscillations perpendicular to the transport direction.

The multi-subband 1D Boltzmann equation along the transport direction (z-axis) is given by

$$\begin{aligned} \dfrac{\partial f^\nu }{\partial t} + v^\nu \dfrac{\partial f^\nu }{\partial z} - \dfrac{1}{\hbar }\dfrac{\partial \varepsilon _{{\text{sub}}}^\nu }{\partial z} \dfrac{\partial f^\nu }{\partial k} + S^\nu \{f\} = 0 , \end{aligned}$$
(3)

where \(f^\nu (z,k,t)\) is the electron distribution function at wavenumber k, \(v^\nu (k)\) the group velocity and \(S\{f\}\) the scattering integral for single electron interactions [20]

$$\begin{aligned} S\{f\}&= \frac{L_{{\text{sys}}}}{2\pi } \sum _{\nu '}\int W^{\nu ,\nu '}(z,k,k',t)f^{\nu '}(z,k',t) \\&\quad - W^{\nu ',\nu }(z,k',k,t)f^{\nu }(z,k,t) {\mathrm {d}}k'. \end{aligned}$$
(4)

\(L_{{\text{sys}}}\) is the 1D system volume and \(W^{\nu ,\nu '}(z,k,k',t)\) the rate of a transition from state \((k',\nu ')\) into \((k,\nu )\) calculated by Fermi’s golden rule [31]. Unless otherwise stated, we use the macroscopic relaxation time approximation (RTA) to improve the consistency of the BE and the moments-based models

$$\begin{aligned} S\{f\} \approx \frac{\sum _{\nu '}\int f^{\nu '}(z,k',t) \dfrac{{\mathrm {d}}k'}{\pi } p^\nu _{{\text{eq}}}(k)-f^{\nu }(z,k,t)}{\tau _{{\text{RTA}}}} , \end{aligned}$$
(5)

where \(\tau _{{\text{RTA}}}\) is the macroscopic relaxation time and \(p^\nu _{{\text{eq}}}(k)\) the one-particle Maxwell–Boltzmann distribution. The electron density is evaluated by

$$\begin{aligned} n = \dfrac{2}{2\pi } \sum _\nu \int f^\nu {\mathrm {d}}k \, \vert \psi ^\nu \vert ^2 \;. \end{aligned}$$
(6)

The Poisson and Schrödinger equations are discretized with the standard methods (finite volume method, dimensional splitting, finite differences etc. [26]). The resultant linear systems of equations are solved with PARDISO [32] and the eigenvalue problems with FEAST [33].

The BE is directly discretized in the phase space, which is the Cartesian product of the position along the channel axis z and the axial wavevector k. An equidistant spatial grid \(z_i = i\Delta z\) with \(i = 1, \ldots , N_z\) is introduced. In the k-space, a nonuniform grid with constant \(\Delta k\) near \(k=0\) and a \(\Delta k\) at higher energies corresponding to a constant step in energy is chosen. The number of grid nodes for negative wavenumbers is \(N_k\) and the same for positive ones. For the sake of legibility, the time arguments are dropped from now on.

We start our formulation by considering the ballistic limit (\(W^{\nu ,\nu '}(z,k,k')=0\)), because this is the most critical case w.r.t. stability. Assuming a linear approximation for the subband energy \(\varepsilon _{{\text{sub}}}^\nu (z)\) between the adjacent grid nodes \(z_i\) and \(z_{i+1}\), the force \(F_i^\nu = - (\varepsilon _{\text{sub},i+1}^\nu - \varepsilon _{\text{sub},i}^\nu ) / (z_{i+1}-z_i)\) is constant and the characteristic curves (ballistic electron path in the phase space) are parabolas. If the force is positive, the electrons are accelerated into the positive z-direction, and for \(k>0\), an electron can move from \(z_i\) to \(z_{i+1}\) (blue trajectories in Fig. 1). The wavenumber of an electron in state \(\nu\) starting at \(z_i\) with \(k\left( z_i\right)\) is at position \(z_{i+1}\)

$$\begin{aligned} k\left( z_{i+1}\right) = \sqrt{ k\left( z_i\right) ^2 + \left( K_{i+\nicefrac {1}{2}}^\nu \right) ^2 } \end{aligned}$$
(7)

with

$$\begin{aligned} K_{i+\nicefrac {1}{2}}^\nu = \sqrt{ \left| \frac{2 m_{zz}^\nu (\varepsilon _{\text{sub},i+1}^\nu - \varepsilon _{\text{sub},i}^\nu )}{\hbar ^2} \right| } . \end{aligned}$$
(8)

\(m_{zz}^\nu\) is the electron mass in transport direction. Thus, \(k\left( z_{i+1}\right) \ge K_{i+\nicefrac {1}{2}}^\nu\) holds. For electrons starting at \(z_{i+1}\) and moving into the negative direction, we get

$$\begin{aligned} k\left( z_i\right) = - \sqrt{ k\left( z_{i+1}\right) ^2 - \left( K_{i+\nicefrac {1}{2}}^\nu \right) ^2 } . \end{aligned}$$
(9)

The electrons can pass the barrier only, if their kinetic energy is larger than \(\varepsilon _{\text{sub},i}^\nu - \varepsilon _{\text{sub},i+1}^\nu\) and thus \(k\left( z_{i+1}\right) \le -K_{i+\nicefrac {1}{2}}^\nu\) (red trajectories in Fig. 1). If this is not the case (\(-K_{i+\nicefrac {1}{2}}^\nu \le k\left( z_{i+1}\right) \le 0\)), the electron returns to position \(z_{i+1}\), where its wavenumber has reversed sign (black trajectories in Fig. 1).

Fig. 1
figure 1

Schematic representation of the characteristic curves for the case \(\varepsilon _{\text{sub},i}^\nu > \varepsilon _{\text{sub},i+1}^\nu\)

Full size image

The change in the wavenumber depends only on the difference in the subband energy and not on the exact force profile between both grid nodes. We can therefore assume that the subband energy is piecewise constant and changes abruptly at position \(z_{i+\nicefrac {1}{2}}=(z_{i+1}+z_i)/2\). Due to the Liouville theorem, the electron flux at position \(z_{i+\nicefrac {1}{2}}\) on the left-hand side of the step must equal the one on the right-hand side. For \(k_{{\text{L}}}>0\), where the superscript L indicates quantities on the LHS and R the ones on the RHS, we get

$$\begin{aligned} v^\nu (k_{{\text{R}}}) f^\nu _{{\text{R}}}(z_{i+\nicefrac {1}{2}},k_{{\text{R}}}) {\mathrm {d}}k_{{\text{R}}}= v^\nu (k_{{\text{L}}}) f^\nu _{\text{L}}(z_{i+\nicefrac {1}{2}},k_{{\text{L}}}) {\mathrm {d}}k_{{\text{L}}} \end{aligned}$$
(10)

with

$$\begin{aligned} k_{{\text{R}}}= \sqrt{ k_{{\text{L}}}^2 + \left( K_{i+\nicefrac {1}{2}}^\nu \right) ^2}. \end{aligned}$$
(11)

Thus, for the piecewise constant subband energy profile the characteristic curves are no longer continuous at \(z_{i+\nicefrac {1}{2}}\) and the values of the distribution function on the left and right sides of the step have to be distinguished. For \(k_{{\text{R}}}< -K_{i+\nicefrac {1}{2}}^\nu\), the electrons can pass the barrier from right to left resulting in the negative root for the wavenumber

$$\begin{aligned} k_{{\text{L}}}= - \sqrt{ k_{{\text{R}}}^2 - \left( K_{i+\nicefrac {1}{2}}^\nu \right) ^2} . \end{aligned}$$
(12)

together with (10). For \(|k_{{\text{R}}}| < K_{i+\nicefrac {1}{2}}^\nu\), we get reflection

$$\begin{aligned} f^\nu _{{\text{R}}}(z_{i+\nicefrac {1}{2}},k_{{\text{R}}}) = f^\nu _{{\text{R}}}(z_{i+\nicefrac {1}{2}},-k_{{\text{R}}}) . \end{aligned}$$
(13)

Discrete equations are obtained by box integration in the k-space. The k-grid has \(2N_k\) grid nodes, which are symmetrically distributed around zero and the value zero itself is excluded from the grid. The jth box is given by \(k^-_j< k < k^+_j\) with its boundaries \(k^\pm _j = (k_j+k_{j\pm 1})/2\) and \(j=1,\ldots ,2N_k\). The interpolation function for the jth box is one inside the jth box and zero outside

$$\begin{aligned} \Omega _j(k) = \Theta \left( \frac{k^+_j-k^-_j}{2} - \left| k-\frac{k^+_j+k^-_j}{2} \right| \right) , \end{aligned}$$
(14)

where \(\Theta (x)\) is the Heaviside function. The distribution functions are assumed to be piecewise constant with the value \(f^{\nu ,j}(z)\) for the jth box

$$\begin{aligned} f^\nu (z,k) \approx \sum _{j=1}^{2N_k} f^{\nu ,j}(z) \Omega _j(k) . \end{aligned}$$
(15)

On the LHS/RHS of the step in subband energy, we have

$$\begin{aligned} f^{\nu ,j}_{\text{L},i+\nicefrac {1}{2}} = f_{{\text{L}}}^{\nu ,j}(z_{i+\nicefrac {1}{2}}), \quad f^{\nu ,j}_{\text{R},i+\nicefrac {1}{2}} = f_{{\text{R}}}^{\nu ,j}(z_{i+\nicefrac {1}{2}}). \end{aligned}$$
(16)

Particle flux conservation is mapped onto the discrete k-grid by box integration. This allows to discretize (10) together with (13) for \(j>N_k\) (positive wavenumbers)

$$\begin{aligned}&f^{\nu ,j}_{\text{R},i+\nicefrac {1}{2}} \int _{k^-_j}^{k^+_j} v^\nu (k_{{\text{R}}}) {\mathrm {d}}k_{{\text{R}}} \\ &\quad =\sum _{j'=N_k+1}^{2N_k} f^{\nu ,j'}_{\text{L},i+\nicefrac {1}{2}} \int _{\text{K}_{{\text{min}}}^{\nu ,j}}^{\text{K}_{{\text{max}}}^{\nu ,j}} v^\nu (k_{{\text{L}}}) \Omega _{j'}(k_{{\text{L}}}) {\mathrm {d}}k_{{\text{L}}} \\ &\qquad + f^{\nu ,2N_k-j+1}_{\text{R},i+\nicefrac {1}{2}} \int _{k^-_j}^{k^+_j} v^\nu (k_{{\text{R}}}) \Theta \left( K_{i+\nicefrac {1}{2}}^\nu - k_{{\text{R}}}\right) {\mathrm {d}}k_{{\text{R}}}\,. \end{aligned}$$
(17)

The first term on the RHS describes the flux of electrons from the left to the right and the second term electrons reflected at the step. The integration limits are defined as

$$\begin{aligned}&\text{K}_{{\text{min}}}^{\nu ,j} = \sqrt{ \max \left\{ k_{j-\nicefrac {1}{2}}^2 - (K_{i+\nicefrac {1}{2}}^\nu )^2,0\right\} } \,, \end{aligned}$$
(18)
$$\begin{aligned}&\text{K}_{{\text{max}}}^{\nu ,j} = \sqrt{ \max \left\{ k_{j+\nicefrac {1}{2}}^2 - (K_{i+\nicefrac {1}{2}}^\nu )^2,0\right\} } \,. \end{aligned}$$
(19)

If we assemble the \(N_k\) values of the distribution function for positive wavenumbers into a vector on the LHS of the step \({\vec {f}}^\nu _{{\text{Lp,i}}+\nicefrac {1}{2}}\), on the RHS \({\vec {f}}^\nu _{{\text{Rp,i}}+\nicefrac {1}{2}}\) and for negative wavenumbers \({\vec {f}}^\nu _{{\text{Ln,i}}+\nicefrac {1}{2}}\), \({\vec {f}}^\nu _{{\text{Rn,i}}+\nicefrac {1}{2}}\), we can formulate (17) with matrices

$$\begin{aligned} \hat{D}^\nu _{{\text{p}}} {\vec {f}}^\nu _{{\text{Rp,i+}\nicefrac {1}{2}}} = \hat{RL}^\nu _{i+\nicefrac {1}{2}} {\vec {f}}^\nu _{{\text{Lp,i}+\nicefrac {1}{2}}}+ \hat{RR}^\nu _{i+\nicefrac {1}{2}} {\vec {f}}^\nu _{{\text{Rn,i}+\nicefrac {1}{2}}}, \end{aligned}$$
(20)

where the diagonal \(N_k \times N_k\) matrix \(\hat{D}^\nu _{{\text{p}}}\) is invertible and does not depend on the position in real space

$$\begin{aligned} \left[ \hat{D}^\nu _{{\text{p}}} \right] _{jj'} = \int _{k^-_{j+N_k}}^{k^+_{j+N_k}} v^\nu (k) {\mathrm {d}}k \delta _{j,j'} \end{aligned}$$
(21)

for \(j,j'=1,\ldots ,N_k\). The other two matrices are

$$\begin{aligned} \left[ \hat{RL}^\nu _{i+\nicefrac {1}{2}} \right] _{jj'} = \int _{{\text{K}}_{{\text{min}}}^{\nu ,j+N_k}}^{\text{K}_{{\text{max}}}^{\nu ,j+N_k}} v^\nu (k) \Omega _{j'+N_k}(k) {\mathrm {d}}k \end{aligned}$$
(22)

and

$$\begin{aligned} \left[ \hat{RR}^\nu _{i+\nicefrac {1}{2}} \right] _{jj'} = \int _{k^-_{j+N_k}}^{k^+_{j+N_k}} v^\nu (k) \Theta \left( K_{i+\nicefrac {1}{2}}^\nu - k \right) {\mathrm {d}}k \delta _{j', N_k-j+1} . \end{aligned}$$
(23)

Flux conservation for particles moving from right to left results with (10) and (12) in

$$\begin{aligned} \hat{D}^\nu _\text{n} {\vec {f}}^\nu _{\text{Ln},i+\nicefrac {1}{2}} = \hat{LR}^\nu _{i+\nicefrac {1}{2}} {\vec {f}}^\nu _{\text{Rn},i+\nicefrac {1}{2}}+ \hat{LL}^\nu _{i+\nicefrac {1}{2}} {\vec {f}}^\nu _{\text{Lp},i+\nicefrac {1}{2}}. \end{aligned}$$
(24)

The second term on the RHS is due to the assumption of a maximal positive wavenumber \(k^+_{2N_k}\), and all particles, which were to exceed this value while moving from left to right \(\left( \sqrt{k_{{\text{L}}}^2+\left( K_{i+\nicefrac {1}{2}}^\nu \right) ^2}>k^+_{2N_k}\right)\), are instead reflected to ensure flux conservation (dashed black line in Fig. 1). Furthermore, a similar set of equations can be formulated for a positive step in energy.

Under stationary conditions, the ballistic distribution function does not depend on position for a constant subband energy and within a box of the real space grid \(z_{i-\nicefrac {1}{2}}< z < z_{i+\nicefrac {1}{2}}\) we get

$$\begin{aligned} {\vec {f}}^\nu _\text{Lp}(z_{i+\nicefrac {1}{2}})=\, & {} {\vec {f}}^\nu _\text{Rp}(z_{i-\nicefrac {1}{2}}) = {\vec {f}}^\nu _{\text{p},i} \end{aligned}$$
(25)
$$\begin{aligned} {\vec {f}}^\nu _\text{Ln}(z_{i+\nicefrac {1}{2}})=\, & {} {\vec {f}}^\nu _\text{Rn}(z_{i-\nicefrac {1}{2}}) = {\vec {f}}^\nu _{\text{n},i} . \end{aligned}$$
(26)

Due to the TB-BCs, the distribution function of the incoming particles is given by the equilibrium one \({\vec {f}}^\nu _\text{eq}\) [25]

$$\begin{aligned} {\vec {f}}^\nu _{\text{p},1 }=\, & {} {\vec {f}}^\nu _{\text{p},\text{eq},\text{SRC}} \end{aligned}$$
(27)
$$\begin{aligned} {\vec {f}}^\nu _{\text{n},N_z}=\, & {} {\vec {f}}^\nu _{\text{n},\text{eq},\text{DRN}} . \end{aligned}$$
(28)

The Fermi energies of the contacts are chosen such that the space charge densities are zero within the contacts at equilibrium. This closes the system of equations, and in most cases, a unique solution can be obtained for \({\vec {f}}^\nu _{\text{p},i}\), \({\vec {f}}^\nu _{\text{n},i}\).Footnote 1 Since the Pauli exclusion principle occurs in the BE only in the scattering integral, it can be included in the ballistic case by using Fermi functions instead of Boltzmann distributions in the boundary conditions.

The solution becomes unique for arbitrary subband profiles, if scattering is taken into account, because scattering couples all states for a given position [20]. Since scattering couples different subbands and valleys, the index \(\nu\) is dropped and the vector of the distribution function contains from now on the distribution functions for all values of \(\nu\). Due to the assumption of a piecewise constant subband energy, the force is zero within a box of the real space. Integration of the BE over a box in k-space yields

$$\begin{aligned} \underbrace{ \begin{pmatrix} \hat{D}_{{\text{p}}} &{} \\ &{}\hat{D}_\text{n} \end{pmatrix} }_{=\hat{D}_v} \frac{\partial }{\partial z} \underbrace{ \begin{pmatrix} {\vec {f}}_{\text{p}}(z) \\ {\vec {f}}_{\text{n}}(z) \end{pmatrix}}_{={\vec {f}}(z)} +\underbrace{\begin{pmatrix} \hat{S}_\text{pp} &{} \hat{S}_\text{pn} \\ \hat{S}_\text{np} &{} \hat{S}_\text{nn} \end{pmatrix} }_{=\hat{S}(z)} \begin{pmatrix} {\vec {f}}_{\text{p}}(z) \\ {\vec {f}}_{\text{n}}(z) \end{pmatrix} = \vec {0} \end{aligned}$$
(29)

with the scattering integral

$$\begin{aligned} \left[ \hat{S}(z)\right] _{jj'}^{\nu ,\nu '}&= \frac{L_\text{sys}}{2\pi } \int \limits _{k_j^-}^{k_j^+} \left( \int \limits _{k_{j'}^-}^{k_{j'}^+} W^{\nu ,\nu '}(z,k,k') {\mathrm {d}}k' \right. \\&\left. - \sum _{\nu ''} \int \limits _\infty ^\infty W^{\nu '',\nu }(z,k'',k) {\mathrm {d}}k'' \delta _{\nu ,\nu '} \delta _{j,j'} \right) {\mathrm {d}}k. \end{aligned}$$
(30)

Due to scattering, the solution depends on the z-coordinate within a box of the real space, even if we assume that the transition rate itself does not depend on position within the box. With \({\vec {f}}_i = {\vec {f}}(z_i)\), \(\hat{S}_i=\hat{S}(z_i)\) and the matrix exponential [35], the solution is within the ith box of the real space grid

$$\begin{aligned} {\vec {f}}(z) = \exp \left( (z_i-z) \hat{D}_v^{-1}\hat{S}_i\right) {\vec {f}}_i . \end{aligned}$$
(31)

With the abbreviation \(\hat{C}_i(z)=(z_i-z) \hat{D}_v^{-1}\hat{S}_i\), the solution at the boundaries of the ith box in real space is

$$\begin{aligned} {\vec {f}}_{\text{L},i+\nicefrac {1}{2}}= & {} \exp \left( \hat{C}_i(z_{i+\nicefrac {1}{2}})\right) {\vec {f}}_i \end{aligned}$$
(32)
$$\begin{aligned} {\vec {f}}_{\text{R},i-\nicefrac {1}{2}}= & {} \exp \left( \hat{C}_i(z_{i-\nicefrac {1}{2}})\right) {\vec {f}}_i . \end{aligned}$$
(33)

These equations replace (25), (26) of the ballistic case. Thus, it is possible to calculate the distribution function on the left- and right-hand side of the steps based on the distribution function on the ith grid node and a complete set of equations can again be assembled. The matrix exponential can be calculated with the methods described in Ref. [35], but for large matrices the numerical accuracy might not be sufficient. In this case, Expokit together with an iterative solver, which requires only multiplications of the matrix exponential with a vector, yields results with a higher precision and is more CPU efficient [36]. If the Pauli exclusion principle were included in the scattering integral, (29) would become nonlinear and could be integrated by ODE-solvers.

For small-signal analysis, we assume a time dependence for the solution quantities given by \(x(t) = x + \mathfrak {R}\{\delta x \exp (s t)\}\), where x is the large-signal stationary solution, \(\delta x\) the complex phasor of the small-signal solution and \(s = \sigma + \text{i}\omega\) the complex frequency, where \(\sigma\) is the real part describing a damped (\(\sigma < 0\)) or growing (\(\sigma > 0\)) solution and \(\omega =2\pi f\) the imaginary part corresponding to a harmonic oscillation with the frequency f. The time derivative in the BE can therefore be replaced by s, and within a box of the spatial grid, the linearized BE has two additional terms compared to the stationary case (29)

$$\begin{aligned} s\hat{D}_k \delta {\vec {f}}(z) + \hat{D}_v\dfrac{\partial \delta {\vec {f}}(z)}{\partial z} + \hat{S} \delta {\vec {f}}(z) = - \delta \hat{S} {\vec {f}}(z) . \end{aligned}$$
(34)

\(\hat{D}_k\) is a diagonal matrix, which is due to box integration in k-space and contains the k-space box volumes

$$\begin{aligned} \left[ \hat{D}_k \right] _{jj'}^{\nu \nu '} = (k_j^+ - k_j^-)\delta _{\nu ,\nu '}\delta _{j,j'} . \end{aligned}$$
(35)

Since the scattering integral depends on the subband energies and wave functions, linearization of the scattering integral yields the term on the RHS of (34). The corresponding derivatives are calculated by the chain rule and stationary perturbation theory for the SE [30]. With the abbreviation \(\hat{C}'_i(z)=(z_i-z) \hat{D}_v^{-1}\left( \hat{S}_i+s\hat{D}_k \right)\), the solution of the small-signal BE is obtained

$$\begin{aligned} \delta {\vec {f}}(z)&= \exp \left( \hat{C}'_i(z) \right) \delta {\vec {f}}_i \\ &\quad +\int _0^1 \exp \left( \hat{C}'_i(z)(1-\alpha )\right) \delta \hat{C}_i(z) \exp \left( \hat{C}_i(z)\alpha \right) {\mathrm {d}}\alpha {\vec {f}}_i . \end{aligned}$$
(36)

With this result, the values of the small-signal distribution function at the boundaries of the real-space box can be calculated by numerical means. Linearization of (20) yields

$$\begin{aligned} \hat{D}^\nu _{{\text{p}}} \delta {\vec {f}}^\nu _{{\text{Rp,i}}+\nicefrac {1}{2}}&= \hat{RL}^\nu _{i+\nicefrac {1}{2}} \delta {\vec {f}}^\nu _{{\text{Lp,i}}+\nicefrac {1}{2}} +\delta \hat{RL}^\nu _{i+\nicefrac {1}{2}} {\vec {f}}^\nu _{{\text{Lp,i}}+\nicefrac {1}{2}}\\ &\quad +\hat{RR}^\nu _{i+\nicefrac {1}{2}} \delta {\vec {f}}^\nu _{{\text{Rn,i}}+\nicefrac {1}{2}} +\delta \hat{RR}^\nu _{i+\nicefrac {1}{2}} {\vec {f}}^\nu _{{\text{Rn,i}}+\nicefrac {1}{2}} \end{aligned}$$
(37)

and (24) similarly. These equations together with the small-signal PE and the small-signal version of the boundary conditions (27), (28)

$$\begin{aligned} \delta {\vec {f}}^\nu _{\text{p},1 } = \vec {0}, \quad \delta {\vec {f}}^\nu _{\text{n},N_z} = \vec {0} \end{aligned}$$
(38)

can be used to assemble a linear system of equations for the complete system. For the calculation of the small-signal terminal currents, a formulation of the Ramo–Shockley theorem is used that is consistent with the presented numerical framework [21, 37]. Thus, admittance parameters can be calculated as a function of the complex frequency s, as required by the analysis of plasma instabilities.

3 Results and discussion

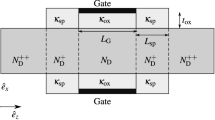
The test structure with a gate all-around architecture is shown in Fig. 2. The rectangular channel cross section is \(5\,\hbox{nm}\times 4\,\hbox{nm}\) with a gate oxide thickness of 1 nm (further details are given in Table 1).

Fig. 2
figure 2

Schematic representation of the nanowire NMOSFET. The carriers are confined in the \(x-y\) plane and the transport happens along the z-axis from source to drain

Full size image
Table 1 Parameters of the nanowire NMOSFET
Full size table

First, simulation of the ballistic case is demonstrated, because this is the numerically most challenging case. Since scattering is neglected, particles cannot transfer between valleys and subbands, and only a single parabolic subband with \(m_{xx}=m_{zz}=0.19m_{{\text{e}}}\), \(m_{yy}=0.98m_{{\text{e}}}\) is simulated (\(m_{{\text{e}}}\) is the electron rest mass). The k-space grid has a constant spacing of \(\Delta k=0.0225\,\hbox{nm}^{-1}\) at low energies and at higher ones a spacing corresponding to an energy of 2.5 meV. The maximal energy is 1.01 eV. The structure described in Table 1 is simulated with a grid spacing in real space of 0.5 nm, and the doping profile is shown in Fig. 3. To demonstrate the stability of the approach, the electron density in the device is shown for different gate and drain voltages under ballistic conditions (Fig. 3). The electron density can vary by more than 10 orders of magnitude without any problems. In Fig. 4, distribution functions in the k-space are shown near the drain and the source/channel barrier (top of the subband energy). The distribution function is positive in the whole phase space and shows no spurious oscillations. Due to the larger number of electrons moving from the left to the right than into the other direction, the distribution function is strongly asymmetric. Since the electrons do not loose energy by scattering when moving from source to drain, they gain \(q V_{\mathrm{DS}}= 100\,\hbox{meV}\) in energy and a second maximum occurs in the distribution function near the drain at positive wavenumbers. Although the cutoff by the source/channel barrier is abrupt, the left flank of the second maximum near the drain is not as abrupt as at the top of the barrier. This is due to the finite k-space grid, which leads to artificial diffusion in the k-space, because a k-space box on the LHS of a step of the subband energy in real space is connected to multiple boxes on the RHS and vice versa (see (17)). This is a fundamental problem of tensor-product grids in phase space and occurs regardless of the treatment of the derivative in k-space, because any formulation of the derivative in k-space involves multiple grid nodes. In principle, a finer grid in k-space could reduce the diffusion, but a finer k-space grid requires a finer real space grid to prevent numerical problems and a certain level of diffusion cannot be avoided. On the other hand, the impact of the artificial diffusion is weak, the phase-space solver based on the tensor-product grid is stable in the ballistic case, and the problems due to the H-transformation in the case of the small-signal parameters are avoided.

Fig. 3
figure 3

Doping profile (dotted blue curve) and electron density at \(V_{\mathrm{DS}} = 0.1\,\hbox{V}\) (solid curves) and \(V_{{\text{DS}}}= 0.5\,\hbox{V}\) (dashed curves) and room temperature (Color figure online)

Full size image
Fig. 4
figure 4

Distribution functions near the drain contact and top of the barrier for the ballistic case at \(V_{\mathrm{GS}}=0.5\,\hbox{V}\), \(V_{\mathrm{DS}}= 0.1\,\hbox{V}\) and room temperature

Full size image

In silicon nanowires, the mobility is rather low due to strong scattering resulting in diffusive transport [34], and it is not clear whether the numerical methods developed for the ballistic case will work. To investigate this, a silicon nanowire is simulated. The electron bandstructure in silicon is modeled in the conventional way accounting for six ellipsoidal and parabolic valleys, and five subbands are considered in each valley. As for the scattering mechanisms, various inter-valley and intra-valley electron–phonon interactions are included according to [38] and the deformation potential of elastic phonon scattering is adjusted in high-doped regions to reproduce the results of [20]. The simulations are performed at room temperature, assuming a \(\langle 100\rangle\) orientation in transport direction. The calculated \(I_{{\text{DS}}}-V_{{\text{DS}}}\) curves are presented in Fig. 5 (red curves), and the results are smooth.

Fig. 5
figure 5

Calculated \(I_{\mathrm{DS}}-V_{\mathrm{DS}}\) curves of the silicon \(\hbox{N}^{+}\hbox{NN}^{+}\) transistor at different gate voltages. The results are obtained from simulation of the BE under H-transformation, simulation of the BE in phase space, and tenth-order moments-based equations (TM)

Full size image

This shows that also strongly diffusive transport can be simulated. In order to validate the model, the results are compared to consistent simulations by other means. The BE is solved in addition based on the H-transformation [21] and by projection onto the first 10 Hermitian polynomials (TM) [14], and the results are almost identical. At \(V_{{\text{DS}}}=0.2\,\hbox{V}\), the calculations by the H-transformed BE and moments equations differ by \(\approx 1.5\%\) for \(V_{{\text{GS}}}=0.6\,\hbox{V}\) and \(\approx 0.8\%\) for \(V_{{\text{GS}}}=0.5\,\hbox{V}\), where an energy grid with a uniform spacing of approximately \(2.6\,\text{meV}\) has been used for the H-transformed BE. Figure 6 shows the \(I_{{\text{DS}}}-V_{{\mathrm{GS}}}\) characteristics of the device for \(V_{{\text{DS}}}=0.1\,\hbox{V}\) and different discretization parameters. The artificial diffusion in phase space translates to artificial carrier heating and increases the subthreshold slope of the device. This effect, however, is not very significant, and our simulations show that even for a coarse k-grid (\(\Delta k = 0.055\,\hbox{nm}^{-1}\)), the subthreshold slope changes from \(\text{SS}=60.5\,\hbox{mV}/\hbox{dec}\) to \(\text{SS}=66.5\,\hbox{mV}/\hbox{dec}\) as we move from a very coarse spatial grid (\(\Delta z=2\,\hbox{nm}\)) to a very fine one (\(\Delta z=0.2\,\hbox{nm}\)). Refining the k-grid alleviates this problem and we have \(\text{SS}=62.5\,\hbox{mV}/\hbox{dec}\) for \(\Delta k = 0.0225\,\hbox{nm}^{-1}\). Although \(\Delta k\) cannot be reduced below a certain value for a given \(\Delta z\), the spurious increase in the subthreshold slope can be reduced to such a level that it is negligible (at least at room temperature). Keeping this in mind, our results confirm the validity of all three approaches for the simulation of conventional devices with relatively low mobilities.

Fig. 6
figure 6

Calculated \(I_{{\text{DS}}}-V_{{\text{GS}}}\) curves of the silicon \(\hbox{N}^{+}\hbox{NN}^{+}\) transistor, obtained from simulation of the BE in phase space. \(\Delta z=2\,\hbox{nm}\) and \(\Delta k = 0.055\,\hbox{nm}^{-1}\) were chosen for these simulations

Full size image

Next, we investigate the quasi-ballistic limit of the nanowire transistor. In the rest of this paper, single-subband and single-valley transport together with the RTA for the scattering integral is assumed for the sake of CPU efficiency and consistency of the BE and the moments-based models. In the case of high mobilities, the impact of scattering is weak anyway and the error due to the RTA is small for small \(V_{{\text{DS}}}\). In order to check the accuracy of our BE solver, the ballistic small-signal drain self-admittance \(\underline{Y}_{{\text{DD}}}\) is calculated for different grid refinement factors and the relative error w.r.t. the finest grid is shown in Fig. 7. It is important to note that the refinements of the z- and k-grids have contrary impacts on the numerical stability of the discretized equations, which leads to a Courant–Friedrich–Lewy-like condition for \(\Delta z\) and \(\Delta k\). While the k-grid should be fine enough to capture discontinuities, the z-grid must be refined accordingly to prevent numerical instabilities. Hence, Fig. 7 presents the relative error with simultaneous refinement of both z- and k-grids. The error decreases for finer grids and the method converges.

Fig. 7
figure 7

Convergence of \(\underline{Y}_{\text{DD}}\) at zero frequency. Ballistic simulations for \(L_{{\text{G}}}=20\,\text{nm}\). \(V_{{\text{GS}}}=0.6\,\hbox{V}\), \(V_{{\text{DS}}}=0\,\hbox{V}\)

Full size image

We investigate the drain self-admittance as a function of the frequency, because it is an important quantity to determine the impact of plasma waves on the device behavior. For example, a negative real part of the drain self-admittance corresponds to an instability and could enable the generation of THz waves [7, 39]. Results of the BE are compared to the ones calculated with projections onto different numbers of Hermitian polynomials and boundary conditions, where the first two Hermitian polynomials result in the DD model. In order to obtain a plasma instability, specific bias conditions have to be applied to the contacts of the device. The gate/source port should be short-circuited and the drain/source port open (i.e., the drain self-admittance should be zero). These bias conditions should not be confused with the boundary conditions of the transport models at the contacts inside the device, which are determined by the contact model.

Results are presented for mobilities of \(\mu =q\tau ^\nu _{{\text{RTA}}}/m^{\nu }_{zz}=100\,\hbox{cm}^{2}/\hbox{Vs}\) in Fig. 8 (strong damping of plasma waves) and \(\mu ={10}^{6}\,\hbox{cm}^{2}/\hbox{Vs}\) (quasi-ballistic case) in Fig. 9 for TB-BCs and 10 for D-BCs. For lower mobilities, good agreement between the two methods is observed over the entire frequency range and the details of the source and drain boundary conditions do not play an important role, i.e., even the drift-diffusion (DD) model with D-BCs can give reasonably accurate predictions in the diffusive regime for frequencies \(f<3\,\hbox{THz}\). Although the DD model deviates from the results of the BE solver at higher frequencies (e.g., it has an error of \(\approx 8\%\) at \(f=8\,\hbox{THz}\)), it performs well in predicting the overall behavior of the real part. Truncation of the Hermite polynomial expansion at higher orders and TB-BCs improve the accuracy of the results.

Fig. 8
figure 8

\(\mathfrak {R}\{\underline{Y}_{{\text{DD}}}(\text{i}2\pi f)\}\) versus frequency at \(V_{{\text{GS}}}=0.5\,\text{V}\) and \(V_{{\text{DS}}}=0\,\hbox{V}\). Simulations are performed for the mobility of \(\mu =100\,\hbox{cm}^{2}/\hbox{Vs}\)

Full size image

However, when the mobility is increased to \(\mu =10^{6}\,\hbox{cm}^{2}/\hbox{Vs}\), moments of the BE fail to even provide a qualitative description of the device’s small-signal behavior (Fig. 9). Although the model with ten moments (TM) does a better job than the DD model, the overall error below 5 THz is rather large. The DD model not only shows an artificial peak at about 5 THz, it also yields a far too large admittance at zero frequency. This is a well-known deficiency of the DD model [40, 41]. The situation becomes worse, if we change the boundary conditions of the moments-based models from TB-BCs to D-BC, which were used by Dyakonov and Shur (Fig. 10). The unrealistically large values of \(\mathfrak {R}\{\underline{Y}\}\) at zero frequency increase by another 2–3 orders of magnitude. In addition, the peaks of the real part of the admittance become much sharper and higher and the minima smaller. The latter result is important, because the Dyakonov–Shur instability corresponds to a zero of the drain self-admittance (pole of the drain self-impedance for a short-circuited input). In Fig. 11, the absolute value of the drain self-admittance is shown for the DD model with different BCs, where the maxima and minima correspond to the poles and zeros, respectively. For D-BCs, the poles and zeros are lined up at \(\sigma =-1/2\tau _\text{RTA}\) [6], which is very small for \(\mu =10^{6}\,\hbox{cm}^{2}/\hbox{Vs}\) and results in sharp peaks on the imaginary axis. The three poles with an imaginary part between 4 and 10 THz correspond to the three peaks of the DD model in Fig. 10 in that frequency range. On the other hand, TB-BCs shift these poles (and zeros) to the left and the plasma resonances are strongly damped. This reduces their impact on the self-admittance at \(\sigma =0\) which is why the results in Fig. 9 are much smoother than in Fig. 10. For a plasma instability poles or zeros with \(\sigma > 0\) are required. Unfortunately, the more realistic TB-BCs move the poles and zeros far to the left making plasma instabilities even more improbable. Since the DD model fails for quasi-ballistic transport anyway, the absolute values of the drain self-admittance calculated by the BE are shown in Fig. 12. The poles and zeros of the BE also occur at large negative real parts of s, and even a nonzero drain/source bias does not result in a significant shift to the right.

Fig. 9
figure 9

\(\mathfrak {R}\{\underline{Y}_\text{DD}\}\) versus frequency at \(V_{{\text{GS}}}=0.5\,\hbox{V}\) and \(V_{{\text{DS}}}=0\,\hbox{V}\). Simulations are performed for a mobility of \(\mu =10^{6}\,\hbox{cm}^{2}/\hbox{Vs}\) and TB-BCs are applied

Full size image
Fig. 10
figure 10

\(\mathfrak {R}\{\underline{Y}_{{\text{DD}}}\}\) versus frequency at \(V_{{\text{GS}}}=0.5\,\hbox{V}\) and \(V_{{\text{DS}}}=0\,\hbox{V}\). Simulations are performed for a mobility of \(\mu =10^{6}\,\hbox{cm}^{2}/\hbox{Vs}\) and D-BCs are applied (BE with TB-BCs)

Full size image
Fig. 11
figure 11

Logarithm of the absolute value of the drain self-admittance for \(V_{{\text{GS}}}=0.5\,\hbox{V}\) and \(V_{{\text{DS}}}=0\,\hbox{V}\) (i.e., equilibrium) for \(\mu = 10^{6}\,\hbox{cm}^{2}/\hbox{Vs}\). The results are calculated by the DD model with D-BCs (upper figure) and TB-BCs (lower figure)

Full size image
Fig. 12
figure 12

Logarithm of the absolute value of the drain self-admittance for \(V_{{\text{GS}}}=0.5\,\hbox{V}\) and the ballistic case. The results are calculated by the BE for \(V_{{\text{DS}}}=0\,\hbox{V}\) (upper figure) and \(V_{{\text{DS}}}=0.1\,\hbox{V}\) (lower figure)

Full size image

In Fig. 13, the nonequilibrium behavior of \(\mathfrak {R}\{\underline{Y}_{{\text{DD}}}(\text{i}2\pi f)\}\) is shown for various drain/source voltages as a function of frequency. The BE results are compared to the tenth-order model. As it is evident at zero frequency, the transistor operates in the saturation regime for \(V_{{\text{DS}}}> 0.2\,\hbox{V}\) (\(Y_\text{DD}(0) \rightarrow 0\)). Increasing the drain bias shifts the peak at \(f=8\,\hbox{TH}_{\mathrm{z}}\) to higher frequencies (see Fig. 12). The moments-based model follows this behavior up to \(V_{{\text{DS}}}=0.1\,\hbox{V}\), whereas for higher biases it becomes unstable and cannot produce meaningful results. The BE, on the other hand, can be solved without problems for larger voltages and its results do not show any active behavior (i.e., \(\mathfrak {R}\{\underline{Y}_\text{DD}\}<0\)) for drain voltages larger than zero. The above results clearly show that the internal contact BCs of the transport model play an important role and that the more realistic TB-BCs strongly damp plasma resonances.

Fig. 13
figure 13

\(\mathfrak {R}\{\underline{Y}_\text{DD}\}\) versus frequency at \(V_{{\text{GS}}}= 0.5\,\hbox{V}\) using the BE and tenth-order moments-based model. Simulations are performed for the mobility of \(\mu =10^{6}\,\hbox{cm}^{2}/\hbox{V}_{\mathrm{s}}\) and TB-BCs. The arrow denotes the increase in \(V_{{\text{DS}}}\)

Full size image

Since the damping of the plasma resonances depends on the type of the BCs, it would be interesting to investigate the impact of the D-BCs onto the BE results. The D-BCs are applied in the case of the moments-based models to the even moments (density, energy density (temperature), etc.). In the case of the BE, this would correspond to the application of D-BCs to the even parts of the distribution functions. Without scattering, such a boundary condition violates the Liouville theorem, because the ratio of the even part of the distribution function at the source and drain at energies above the top of the barrier is fixed by transport for an inversion symmetric bandstructure and cannot be imposed by the BCs. Thus, D-BCs for the even part of the distribution function and the ballistic BE are incompatible.

4 Conclusion

In this paper, a numerically stable approach for phase space discretization of the BE was proposed, which is applicable to the diffusive as well as ballistic regime. The presented BE solver was used to calculate the small-signal self-admittance of an \(\hbox{N}^{+}\hbox{NN}^{+}\) nanowire transistor up to THz frequencies, and the results were compared to the ones by moments-based models. D-BCs were shown to result in spurious plasma resonances for weak scattering, and moments-based models fail at describing the small-signal behavior of quasi-ballistic devices. This calls into question the credibility of DD or higher-order models for the investigation of high-mobility phenomena in electronic devices.