Abstract
We present a method for the automatic generation of netlists describing general three-dimensional electrothermal and electromagnetic field problems. Using a pair of structured orthogonal grids as spatial discretisation, a one-to-one correspondence between grid objects and circuit elements is obtained by employing the finite integration technique. The resulting circuit can then be solved with any standard available circuit simulator, circumventing the need for the implementation of a custom time integrator and dealing with non-linearities. Additionally, the approach straightforwardly allows for field-circuit coupling simulations by appropriately stamping the circuit description of lumped devices. As the computational domain in wave propagation problems must be finite, stamps representing absorbing boundary conditions are developed as well. Representative numerical examples are used to verify the approach. The results obtained by circuit simulation on the generated netlists are compared with appropriate reference solutions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In order to analyse complex electromagnetic (EM) problems, two main routes can be identified. First, a numerical approach for solving the full set of Maxwell ’s field equations offers the advantage of capturing all relevant effects but can be very demanding in terms of computational resources. One of the first methods for EM analysis was the finite difference time domain (FDTD) scheme proposed by Yee [1] in the 1960s. This method became popular and is still a standard approach for high-frequency EM simulations [2]. About ten years later, in the 1970s, Weiland [3] introduced the finite integration technique (FIT) as an extension to the FDTD scheme using integral unknowns and allowing for non-Cartesian and unstructured grids [4]. Additionally, later developments of the method led to the usage of integral unknowns to obtain an exact implementation of Maxwell ’s equations [5]. The method proved to be more efficient in terms of memory requirements and computing time. While the finite element (FE) method was mainly used in structural mechanics for many years, the introduction of edge elements made it applicable for EM problems as well [6]. Secondly, one may use compact models to obtain an efficient representation of a complex system. For example, electrical engineers employ circuits to model and describe the behaviour of complex devices. One of the first works concerned with equivalent circuits was presented by Kron [7]. Nevertheless, the generation of such compact models can be a tedious task requiring empirical knowledge to apply the appropriate approximations. To generate such circuit models, different techniques are available. For instance, mathematical analysis and physical insight allow to construct circuits representing the problem at hand as is presented by Choi et al. [8]. A circuit’s topology and the required component values can also be obtained from experimental results as done by Moumouni and Baker [9] and other groups. Another approach, e.g. followed by Codecasa et al. [10], Eller [11] and Wittig et al. [12], is to apply model order reduction (MOR) techniques directly to the field formulation of the problem from which a circuit description can be found more easily [10]. However, the resulting elements may have non-physical values. Now, if one is able to represent an EM problem by means of an electric circuit, one can use any circuit simulator to obtain the solution. The most popular representatives are SPICE programs that were introduced in the 1970s [13] and are still used as a synonym for circuit solvers. Later, extensions to deal with electrothermal (ET) simulations using circuits were developed within the SPICE framework [14, 15]. The mathematical tool employed by most SPICE-like programs is still the modified nodal analysis (MNA) presented by Ho et al. [16] in the 1970s.
First approaches to combine numerical field simulation with circuit elements were proposed in the 1990s. These were based on the FDTD scheme [17,18,19,20] because of the topological similarities between the finite difference scheme and circuits. Later, the insertion of lumped elements into FE schemes in time or frequency domain was developed by Guillouard et al. [21, 22]. These approaches became known as field-circuit coupling and have evolved into an important research topic [23,24,25,26]. For example, a possible field-circuit coupling method consists of the direct insertion of lumped circuit elements into the field model by applying these to edges of the discretisation grid [27].
To extract compact EM circuits from a given 3D field problem in a generic way, numerous approaches can be found in the literature. In the partial element equivalent circuit (PEEC) method presented by Ruehli [28, 29], equivalent circuits are derived from integral equations, allowing for a combined EM circuit solution both in frequency and time domains. However, PEEC requires empirical approximations in addition to the applied discretisation. For quasistatic approximations, automated circuit generation based on the boundary element method was presented by Milsom [30]. The method presented therein yields circuits whose size depends on the electrical dimensions of the problem. Many methods for application-specific circuit extraction based on the device or system response are also available [31,32,33]. A methodology for the generation of equivalent circuits based on the semi-discrete Maxwell ’s field equations was also proposed by Ramachadran et al. [34]. Therein, Yee ’s discretisation scheme is employed to cast Maxwell ’s curl equations as the concatenation of interacting fundamental circuits in which voltages and currents model the sought electric and magnetic fields. In this manner, circuit stamps are required for both primal and dual edges. Their interaction is organised by voltage-controlled voltage sources (VCVSs) and current-controlled current sources (CCCSs), respectively.
In the design of electronic devices, enhancing their functionalities is always of high interest. The according volume shrinking may give rise to high power densities that can lead to thermal issues. As an example, the introduction of stacked 3D chips intensifies the heat issue since the heat can be trapped between the stacked layers. Therefore, ET modelling is of great importance for device engineers. To handle the ET coupling in a circuit simulation framework, two general approaches are mainly available: the relaxation method which consists of the iterative coupling of an electric circuit with an external thermal-only field simulator [35,36,37], and the monolithic approach which consists of the direct coupling of the electric circuit with a thermal circuit [38]. The latter allows to run the simulation directly on the full ET circuit without any software package and thereby avoids the weak coupling between solvers. To extract compact ET circuits from a given 3D field problem in a generic way, various methods were proposed. Some of them were based on existing EM simulation methods and have been extended in functionality to also cover the ET case, as for instance done by Lombardi et al [39] for the PEEC. Generating compact models from the calculated or measured response function is another popular approach and has been followed by Evans et al. and Bernardoni et al [40, 41]. For thermal problems, methods that derive an equivalent circuit directly from the mesh can also be found [42, 43], but none of them accounts for the ET coupling. Karagol and Bikdash [44] presented an approximate representation obtained from a graph-partitioning algorithm of an FE mesh resulting in a medium-sized ET circuit. Another approach for ET simulations consists of a lumped-element representation of every element in the mesh and has been proposed by Hsu and Vu-Quoc [45]. For an exact representation of a semi-discretised 3D ET field problem, Casper et al [46] developed an automatic netlist generation method based on the FIT.
In this paper, we present a method to automatically generate netlists representing general 3D ET and EM coupled field problems. In our approach, neighbouring cells in the primal grid interact via the parallel connection of circuit elements as illustrated in Fig. 1. Thus, the size of the resulting circuit depends on the geometrical size of the problem and the fineness of the discretisation grid. This allows to use any available circuit simulator. Hence, the need for a dedicated field solver with a custom time integrator is alleviated. To accomplish this, we employ the FIT for discretising the relevant continuous field equations. In contrast to Yee ’s finite difference scheme employed by Ramachandran et al. [34], FIT is a structure-preserving discretisation strategy which does not require further approximations in dealing with the field and material quantities. Moreover, the concept of integral quantities used in the FIT translates naturally into the framework of circuit descriptions. In this manner, we obtain an exact grid representation of the field equations that we map transparently into circuit stamps. The values of the lumped elements making up a stamp are directly taken from the entries of the material matrices. These entries are properly integrated constitutive parameters. Fig. 2 summarises this approach. In addition to previous work on ET problems [46], we also present a more elaborated description and implementation of boundary conditions and excitations. We also point out that the methodology presented herein allows for straightforward field-circuit coupling and is especially useful for an accurate representation of small devices in a larger circuit. In order to simulate wave propagation problems on a finite computational domain by means of circuit simulation, we present absorbing boundary conditions (ABCs) [47, 48].
The outline of this paper is as follows. In Sect. 3, we provide the required basics of the FIT. The fundamentals of the MNA are summarised in Sect. 4. Then, the main part of the paper starts with the circuit representation of ET field problems in Sect. 5. How to extract circuit stamps for EM field problems is presented in Sect. 6. Finally, we show numerical examples in Sect. 7 and conclude the paper in Sect. 8.
2 Continuous thermal and electromagnetic formulations
Let us consider a domain \(\mathcal {D}\) with boundary \(\partial \mathcal {D}\) and characterised by the constitutive parameters \(\lbrace \varepsilon ,\nu ,\sigma \rbrace \), where \(\varepsilon \) is the electric permittivity, \(\nu \) is the magnetic reluctivity and \(\sigma \) is the electric conductivity. For every facet \(A\), every volume \(V\) and with impressed electric sources \(\mathbf {J}_{\mathrm {i}}\), the EM field \(\lbrace \mathbf {E},\mathbf {H}\rbrace \) in \(\mathcal {D}\) is given by Maxwell ’s equations
We call henceforth (1) the E–H formulation for conciseness. Above, \(\mathbf {D}\) and \(\mathbf {B}\) are the electric and magnetic flux density, respectively, \(\mathbf {J}_{\mathrm {c}}\) is the electric conduction current and \(\varrho \) is the electric charge density. To guarantee the uniqueness of the solution, Maxwell ’s equations are supplemented with the constitutive relations, viz.
with suitable initial and boundary conditions (BCs) on \(\partial \mathcal {D}\).
We also deem it convenient to obtain Maxwell ’s equations involving the auxiliary magnetic vector potential \(\mathbf {A}\). To this end, we recall that \(\mathbf {E}=-\nabla \varphi -\partial \mathbf {A}/\partial t\) and \({\nabla \cdot (\sigma _{\text{ g }}\mathbf {A})=f}\), with an auxiliary scalar potential \(\varphi \), a gauging material parameter \(\sigma _{\text {g}}\) and an arbitrary scalar gauging function f. Substitution of these definitions in (1) and applying Stokes ’ theorem yields
which we refer to as the E–A formulation.
Whenever conducting materials are involved, electric currents result in Joule losses \(Q_{\text {J}}=\sigma \left( \nabla \varphi \right) ^{2}\) that enter as source term into the heat equation which is given by
where \(\rho c\) is the volumetric heat capacity, T is the temperature, \(\lambda \) is the thermal conductivity and \(\mathbf {q}_{\mathrm {i}}\) represent any impressed thermal flux density. In general, when thermal effects are considered, all constitutive parameters are also a function of the temperature. To perform circuit extraction, we shall consider the above ET and EM formulations separately as described in Sects. 5 and 6, respectively.
3 Discretising the thermal and electromagnetic formulations
We discretise the domain \(\mathcal {D}\) into a pair of orthogonal grids given by the primal grid G and its dual \(\widetilde{G}\). The grid G consists of primal points \(P_{i},\,i=1,\dots ,N_{\text {P}}\), primal edges (lines) \(L_{n}, n=1,\ldots ,N_{\text {E}}\), primal facets (areas) \(A_{n},\,n=1,\ldots ,N_{\text {F}}\), and primal volumes \(V_{i},\,i=1,\ldots ,N_{\text {V}}\). Similarly, the grid \(\widetilde{G}\) consists of dual points \(\widetilde{P}_{i},\,i=1,\dots ,\widetilde{N}_{\text {P}}\), dual edges \(\widetilde{L}_{n},\,n=1,\ldots ,\widetilde{N}_{\text {E}}\), dual facets \(\widetilde{A}_{n}, n=1,\ldots ,\widetilde{N}_{\text {F}}\), and dual volumes \(\widetilde{V}_{i},\,i=1,\ldots ,\widetilde{N}_{\text {V}}\). The grids G and \(\widetilde{G}\) are dual to each other in the sense that a primal edge \(L_{n}\) intersects a dual facet \(\widetilde{A}_{n}\) and a primal point \(P_{i}\) is located inside a dual volume \(\widetilde{V}_{i}\) and vice versa. For a regular hexahedral grid, the grid staggering is depicted in Fig. 3. Due to this duality, the number of primal and dual grid objects fulfils
As mentioned above, we write \(L_{n}\) for the n-th edge of the primal grid and we emphasise the duality of edges and facets by using the same index. Thus, \(\widetilde{A}_{n}\) is the dual facet corresponding to the primal edge \(L_{n}\) and \(\widetilde{L}_{n}\) is the dual edge corresponding to the primal facet \(A_{n}\). Let us further introduce a short (index) notation for geometric objects. If \(L_{n}\) or \(A_{n}\) are used as an index, we simply write n instead. Whether n refers to an edge or a facet should become clear from the context. For the dual objects, we use \(\tilde{n}\) instead of \(\widetilde{L}_{n}\) or \(\widetilde{A}_{n}\). The notation for points and volumes and their duals is done accordingly. In Table 1, we summarise this notation.
The grid counterparts of the field quantities are allocated to points, edges, facets or volumes and collected in column vectors. Typical examples from electromagnetics (EM) are the discrete electric potentials \(\varvec{\varphi }\), fields  , currents
, currents  and charges
and charges  that are allocated to primal points, edges, facets and volumes, respectively. The number of bows indicates the dimension of the corresponding geometric object. Nevertheless, we typically write \({\mathbf {q}}\) instead of
that are allocated to primal points, edges, facets and volumes, respectively. The number of bows indicates the dimension of the corresponding geometric object. Nevertheless, we typically write \({\mathbf {q}}\) instead of  for conciseness. Defining all other grid quantities accordingly, their allocation used in this paper is shown in Fig. 3. Furthermore, if we want to indicate a grid quantity, e.g. an electric field, to be allocated to an edge \(L_{n}\) that is part of the boundary of a facet \(A_{k}\) (\(L_{n}\cap \partial A_{k}=L_{n}\)), we use the indexed notation
for conciseness. Defining all other grid quantities accordingly, their allocation used in this paper is shown in Fig. 3. Furthermore, if we want to indicate a grid quantity, e.g. an electric field, to be allocated to an edge \(L_{n}\) that is part of the boundary of a facet \(A_{k}\) (\(L_{n}\cap \partial A_{k}=L_{n}\)), we use the indexed notation  . To relate grid quantities on either the primal or dual mesh, topological matrices, corresponding to the continuous topological operators, have to be defined. The incidence between grid points and edges is given by the discrete gradient matrix \(\mathbf {G} \). For an oriented edge \(L_{n}\), \(G_{ni}=-1\) if \(P_{i}\) is the starting point of the edge, \(G_{ni}=1\) if \(P_{i}\) is the ending point of the edge and \(G_{ni}=0\) if \(P_{i}\) is neither starting nor ending point of the edge (\(P_{i}\cap \partial L_{n}=\emptyset \)). To express the incidence between grid edges and facets, we use the discrete curl matrix \(\mathbf {C} \). Given a primal facet \(A_{k}\) and its oriented boundary \(\partial A_{k}\), \(C_{kn}=-1\) if edge \(L_{n}\) is oriented in opposite direction than \(\partial A_{k}\), \(C_{kn}=1\) if edge \(L_{n}\) is oriented in the same way as \(\partial A_{k}\) and \(C_{kn}=0\) if \(L_{n}\) does not touch \(A_{k}\) (\(L_{n}\cap \partial A_{k}=\emptyset \)). Finally, the discrete divergence matrix \(\mathbf {S} \) denotes the incidence between grid facets and volumes. For a primal volume \(V_{i}\) and its oriented boundary \(\partial V_{k}\), the entries of \(\mathbf {S} \) are defined in analogy to those of \(\mathbf {G} \) and \(\mathbf {C} \). Additionally, we have the dual gradient, curl and divergence matrices \(\widetilde{\mathbf {G}}\), \(\widetilde{\mathbf {C}}\) and \(\widetilde{\mathbf {S}}\), respectively, defined accordingly. Useful relations between the topological matrices on the primal and dual grids are given by \(\mathbf {G} =-\widetilde{\mathbf {S}}^\top \), \(\widetilde{\mathbf {G}} =-\mathbf {S} ^{\top }\) and \(\mathbf {C} =\widetilde{\mathbf {C}} ^{\top }\) [49].
. To relate grid quantities on either the primal or dual mesh, topological matrices, corresponding to the continuous topological operators, have to be defined. The incidence between grid points and edges is given by the discrete gradient matrix \(\mathbf {G} \). For an oriented edge \(L_{n}\), \(G_{ni}=-1\) if \(P_{i}\) is the starting point of the edge, \(G_{ni}=1\) if \(P_{i}\) is the ending point of the edge and \(G_{ni}=0\) if \(P_{i}\) is neither starting nor ending point of the edge (\(P_{i}\cap \partial L_{n}=\emptyset \)). To express the incidence between grid edges and facets, we use the discrete curl matrix \(\mathbf {C} \). Given a primal facet \(A_{k}\) and its oriented boundary \(\partial A_{k}\), \(C_{kn}=-1\) if edge \(L_{n}\) is oriented in opposite direction than \(\partial A_{k}\), \(C_{kn}=1\) if edge \(L_{n}\) is oriented in the same way as \(\partial A_{k}\) and \(C_{kn}=0\) if \(L_{n}\) does not touch \(A_{k}\) (\(L_{n}\cap \partial A_{k}=\emptyset \)). Finally, the discrete divergence matrix \(\mathbf {S} \) denotes the incidence between grid facets and volumes. For a primal volume \(V_{i}\) and its oriented boundary \(\partial V_{k}\), the entries of \(\mathbf {S} \) are defined in analogy to those of \(\mathbf {G} \) and \(\mathbf {C} \). Additionally, we have the dual gradient, curl and divergence matrices \(\widetilde{\mathbf {G}}\), \(\widetilde{\mathbf {C}}\) and \(\widetilde{\mathbf {S}}\), respectively, defined accordingly. Useful relations between the topological matrices on the primal and dual grids are given by \(\mathbf {G} =-\widetilde{\mathbf {S}}^\top \), \(\widetilde{\mathbf {G}} =-\mathbf {S} ^{\top }\) and \(\mathbf {C} =\widetilde{\mathbf {C}} ^{\top }\) [49].
To relate quantities on the primal grid to quantities on the dual grid and vice versa, material relations are employed. For the problem formulated in Sect. 2, the following three different kinds of relations can be identified:
Quantities allocated to primal facets must be related to quantities allocated to dual edges.
Quantities allocated to primal edges must be related to quantities allocated to dual facets.
Quantities allocated to primal points must be related to quantities allocated to dual volumes.
As representatives for the above listed constitutive relations, we formulate three discrete material laws as

where \(\mathbf {M}_{\nu } \) is the magnetic reluctance matrix mapping the discrete magnetic flux  allocated to primal facets to the discrete magnetic field
allocated to primal facets to the discrete magnetic field  allocated to dual edges, \(\mathbf {M}_{\varepsilon } \) is the electric capacitance matrix mapping the discrete electric field
allocated to dual edges, \(\mathbf {M}_{\varepsilon } \) is the electric capacitance matrix mapping the discrete electric field  allocated to primal edges to the discrete electric flux density
allocated to primal edges to the discrete electric flux density  allocated to dual facets, and \(\mathbf {M}_{\rho c} \) is the thermal capacitance matrix mapping the time derivative of the grid temperature \(\dot{\mathbf {T}}\) allocated to primal points to the discrete heat power \( \mathbf {Q} \) allocated to dual volumes. For other constitutive parameters, the material matrices are defined following these three cases.
allocated to dual facets, and \(\mathbf {M}_{\rho c} \) is the thermal capacitance matrix mapping the time derivative of the grid temperature \(\dot{\mathbf {T}}\) allocated to primal points to the discrete heat power \( \mathbf {Q} \) allocated to dual volumes. For other constitutive parameters, the material matrices are defined following these three cases.
Having established the grid constructs G and \(\widetilde{G}\) and the corresponding topological and material matrices, the E–H formulation (1) of Maxwell ’s equations upon such a grid pair can be written as [5]




where \(\mathbf {M}_{\sigma }\) is the electric conductance matrix,  is the discrete magnetic flux density,
is the discrete magnetic flux density,  is the discrete impressed electric current density and \({\mathbf {q}}\) is the discrete electric charge. Similarly, with the discrete vector potential
is the discrete impressed electric current density and \({\mathbf {q}}\) is the discrete electric charge. Similarly, with the discrete vector potential  , the discrete E–A formulation is given by
, the discrete E–A formulation is given by


together with the discrete form of the gauging

where \( \mathbf {F} \) is the discrete counterpart of the gauging function f and \(\mathbf {M}_{\text {G}}\) is a gauging matrix. Since \(\mathbf {M}_{\text {G}}\) maps from quantities on primal edges to dual facets, it shares properties with the material matrices (e.g. \(\mathbf {M}_{\varepsilon } \)) and thus can be interpreted as a material matrix with a material value equal to \(\sigma _{\text {g}}\).
Casting also the heat equation (3) into a spatially discrete form, we obtain

where \(\mathbf {M}_{\lambda } \) is the thermal conductance matrix and \(\mathbf {Q}_{\text {J}}\) is the discrete vector of the Joule losses. For details on the computation of \(\mathbf {Q}_{\text {J}}\), we refer the reader to the work by Casper et al. [46]. The impressed thermal fluxes are given by their discrete representative  .
.
3.1 Finite integration technique and its relation to other discretisation schemes
For the circuit extraction from 3D field models as presented in this paper, we require diagonal, symmetric and positive definite material matrices. To fulfil this requirement, we choose to use the FIT and assume the material to coincide with the primal grid cells, see Fig. 3. While the FIT has also been formulated for anisotropic materials [50], diagonal material matrices are obtained only in the isotropic case or in the case when the principal axes of anisotropy coincide with the coordinate axes. Then, the entries of the different material matrices are given by
where \(\varepsilon _{\tilde{n} n}\), \(\sigma _{\tilde{n} n}\), \(\lambda _{\tilde{n} n}\), \(\nu _{\tilde{n} n}\), and \(\rho c_{\tilde{i} i}\) are obtained by a suitable averaging scheme [49, 51] and \(|\cdot |\) represents the measure (i.e. area, length or volume) of the corresponding geometrical object.
When using the FIT as the discretisation scheme with a canonical numbering of the grid nodes, the curl and material matrices exhibit the block structure
where \(\mathbf {P} _{\xi }\in \{0,\pm 1\}^{N_{\text {E}}\times N_{\text {P}}}\), \(\xi \in \{x,y,z\}\) are the grid differential operators for the different coordinate directions. Here, \(\mathbf {M}_{\varepsilon }\) was used as an example whereas an equivalent block structure applies for all other material matrices. Within the theory of the FIT, the discrete quantities \(\varvec{{\varphi }}\),  ,
,  , \({\mathbf {q}}\) that were introduced in Sect. 3 are defined by means of integration with respect to their corresponding geometrical object, such that
, \({\mathbf {q}}\) that were introduced in Sect. 3 are defined by means of integration with respect to their corresponding geometrical object, such that

where an analogous definition applies for  ,
,  ,
,  and
and  . Due to the applied integration, one speaks of grid voltages instead of discrete fields, of grid currents (fluxes) instead of discrete current (flux) densities and of grid charges instead of discrete charge densities.
. Due to the applied integration, one speaks of grid voltages instead of discrete fields, of grid currents (fluxes) instead of discrete current (flux) densities and of grid charges instead of discrete charge densities.
As an alternative to the FIT, equivalent approaches such as the cell method [52] or FE methods can be used as long as the orthogonality and one-to-one relation between primal and dual grid objects is guaranteed. When using FE methods, linear basis functions together with an appropriate mass lumping for the material matrices must be used to obtain an equivalent scheme [53].
4 A primer on circuit theory and the modified nodal analysis
In this section, we briefly review some fundamentals about circuit theory and the MNA [16, 54]. Kirchhoff ’s current and voltage laws are derived and form the basics for circuit analysis.
Any circuit can be understood as a directed graph consisting of interconnected nodes and branches. Let \(v_{i}\) be one of the \(N_{\text {n}}\) nodal potentials in a circuit and \(b_{n}\) one of \(N_{\text {b}}\) directed branches. With the incidence matrix \( \mathbf {A} \in \{-1,0,1\}^{N_{\text {n}}\times N_{\text {b}}}\) linking nodes and branches, the voltage-potential relation is given by
The entries of \( \mathbf {A} \) are defined such that \(a_{in}=+1\) if the branch \(b_{n}\) is directed away from node \(n_{i}\) and \(a_{in}=-1\) if \(b_{n}\) is directed towards \(n_{i}\). If \(n_{i}\) is neither starting nor ending point of \(b_{n}\), then \(a_{in}=0\). With this definition, the exemplary voltage \(V_{n}\) on the branch \(b_{n}\) directed from \(n_{i}\) to \(n_{j}\) is given by \(V_{n}=v_{i}-v_{j}\).
For time invariant geometries, the current continuity equation reads
for an arbitrary volume V. By considering a volume \(\widetilde{V}_{i}\) around an arbitrary circuit node \(n_{i}\) and assuming that capacitive charges are located either fully inside or outside of \(\widetilde{V}_{i}\), the total charge and also the charge’s change rate in \(\widetilde{V}_{i}\) is zero. Therefore, (8) becomes
If \(\partial \widetilde{V}_{i}\) is composed by a finite number s of conductors with cross-sectional areas \(\widetilde{A}_{n}\), Kirchhoff’s current law (KCL) is obtained as
where \(I_{n}\) is the total current through the facet \(\widetilde{A}_{n}\). This relation is also depicted in Fig. 4a. To express (9) for all nodes in the circuit (cf. Fig. 4b), the incidence matrix \( \mathbf {A} \) can be used such that
where \( \mathbf {I} \in \mathbb {R}^{N_{\text {b}}}\) is a vector of all currents allocated to the branches and \(\mathbf {0}\) is a vector of zeros of suitable dimension.
In a circuit, the basic branch elements are conductors, capacitors, inductors as well as voltage and current sources. As these elements are allocated to branches, sets of \(N_{\text {G}}\), \(N_{\text {C}}\), \(N_{\text {L}}\), \(N_{\text {V}}\) and \(N_{\text {I}}\) branches are defined. Hence, \( \mathbf {A} \) can be arranged into a block matrix with sub-blocks for these elements [54], viz.
A circuit example consisting of a current source, two resistors and two capacitors together with the corresponding block structure of \(\mathbf {A}\) is shown in Fig. 5. A similar subdivision is done for the current and voltage vectors,
With these definitions, the voltages are given by
and (10) becomes
The relation between voltages and currents for the different branches is established by constitutive diagonal matrices that contain the element-wise material parameters. These are the conductance, capacitance, and inductance matrices \(\mathbf {G}\), \(\mathbf {C}\) and \(\mathbf {L}\), respectively. Expressing the corresponding source branches by means of the source voltages \(\mathbf {V}_\text {s}\) and source currents \(\mathbf {I}_\text {s}\), this relation becomes
Combining (11), (12) and (13), we obtain the MNA formulation
Note that in contrast to the standard MNA theory, (14) still requires regularisation, typically done by the introduction of a reference (ground) node.
5 Circuit representation of electrothermal field problems
In this section, we neglect inductive effects and derive the circuit representation of transient ET field problems. We apply the electroquasistatic (EQS) approximation [55] to Maxwell ’s equations given by (1) and consider the coupling with the transient heat equation given by (3). Then, the bi-directionally coupled system in differential form reads
with suitable initial and boundary conditions. The coupling is manifested by the Joule heating given by \(Q_{\text {J}}=\sigma (\nabla \varphi )^{2}\) in one way and by the temperature-dependent conductivity \(\sigma (T)\) in the opposite way. Due to the EQS approximation, this formulation does not account for inductive effects but does consider resistive and capacitive effects. For simplicity, we neglect the temperature dependency of the permittivity \(\varepsilon \) and of the volumetric heat capacity \(\rho c\). Applying FIT upon the ET system of (15), the semi-discrete formulation reads


with initial and boundary conditions yet to be applied. Note that the electric part of the problem requires a regularisation which is typically done by choosing a reference (ground) node \(\varphi _{\text {gnd}}=0\), where \(\varphi _{\text {gnd}}\) is one of the entries of \(\varvec{{\varphi }}\).
To generate the netlist corresponding to (16), the electric and thermal sub-problems are considered separately. The connection is subsequently established by the Joule losses and the temperature-dependent electric conductivity. Next, in Sects. 5.1 and 5.2, the netlist generation for the EQS case and the thermal case is presented, respectively. Temperature-dependent materials are discussed in Sect. 5.3 and finally, the implementation of initial and boundary conditions is described in Sect. 5.4. This allows us to formulate an algorithm for the ET netlist generation as presented in Sect. 5.5.
5.1 Electroquasistatic circuit representation
Let us now concentrate on the EQS sub-problem given by (15a). Since inductances are neglected in the EQS case, the MNA formulation (14) simplifies to
Then, by inspection of (16a) and (17), we are led to the following equivalences:
The incidence matrices \(\mathbf {A}_\text {C}\) and \(\mathbf {A}_\text {G}\) coincide with the FIT divergence matrix \(\widetilde{\mathbf {S}} \).
The capacitance matrix \(\mathbf {C}\) coincides with the FIT capacitance matrix \(\mathbf {M}_{\varepsilon } \).
The incidence matrices \(\mathbf {A}_\text {V}\) and \(\mathbf {A}_\text {I}\) coincide with the identity matrix.
The conductance matrix \(\mathbf {G}\) coincides with the FIT conductance matrix \(\mathbf {M}_{\sigma } \).
The nodal voltages \(\mathbf {v}\) correspond to the FIT degrees of freedom \(\varvec{{\varphi }}\).
The source currents \(\mathbf {I}_\text {s}\) are given by the divergence of the impressed currents
 .
.The source voltages \(\mathbf {V}_\text {s}\) correspond to the Dirichlet potentials \(\varvec{{\varphi }}_{\text {Dir}}\), which are related to the reference node \(\varphi _{\text {gnd}}\).
These equivalences also prevail themselves in the physical units.
Summarised, the field-circuit relations for EQS read

where \(\mathbb {I}\) is the identity matrix of corresponding size and \(\varvec{{\varphi }}_{\text {Dir}}\) represents the potentials on the Dirichlet boundary nodes. To find the circuit stamp of each edge in the grid upon which (16a) holds, we employ the equivalences of (18) from which the circuit topology is derived. From (18a), conductors and capacitors are placed along the branches of the circuit. According to (18b), the values of the conductors and capacitors are directly taken from the corresponding FIT material matrices. Current and voltage sources are connected between a circuit node and ground as indicated by (18c). Furthermore, (18d) shows that the circuit’s nodal potentials are equal to the potentials at the grid points. According to (18e), the current sources in the circuit represent the divergence of the FIT impressed currents. Finally, if Dirichlet BCs are imposed, voltage sources in the circuit represent FIT Dirichlet potentials as given by (18f). We further discuss BCs in Sect. 5.4. To summarise, if we consider an exemplary grid point \(P_i\) and a grid edge \(L_{m}\) connecting \(P_i\) to another grid point \(P_j\), we obtain a representative EQS circuit stamp as shown in Fig. 6. To this end, the temperature dependence of the materials is neglected for now and will be discussed in Sect. 5.3
5.2 Thermal circuit representation
In this section, we describe the circuit representation of the sub-problem described by (15b). By comparing the discrete counterpart (16b) to the discrete EQS formulation (16a), the equation structure is very similar. Nevertheless, thermal capacities are not subject to spatial differences and thus do not link to neighbouring nodes. Instead, they influence the change rate of the absolute temperature of a node. Thus, thermal capacitors are placed along branches connecting each node to a reference node at zero temperature. This reference node is an additional non-physical node that is introduced to obtain a consistent circuit representation. In the literature, this approach is also referred to as the Cauer model representing a discretised image of the heat flow [56, 57]. An equivalent approach is the Foster model, in which the capacitances are placed between the circuit nodes and the parameters are adjusted accordingly. In the Foster model, the heat propagation is instantaneous and does not account for the fact that an object requires some delay before changing its temperature.
The MNA formulation of (14) must be extended by this additional reference ground node such that
where
where \(\mathbb {1}\) is a column vector of ones of appropriate size and \(v_{\text {gnd}}=T_{\text {gnd}}=0\). With these definitions, the equivalences between the MNA formulation of (19) and the thermal formulation of (16b) are readily obtained as

where \(\mathbf {T}_{\text {Dir}}\) represents the temperatures at Dirichlet boundary points. To derive the circuit stamp for each point and edge in the grid upon which which (16b) holds, we employ the equivalences in (20) from which the circuit topology is derived. From (20a), we infer that capacitances, as well as voltage and current sources are directly connected between a circuit node and the thermal ground. As in the EQS case, conductors connect two neighbouring nodes in the circuit as seen from (20b). According to (20c), the values of the conductors and capacitors are taken directly from the FIT material matrices. As seen from (20d), the nodal potentials represent the sought temperatures. The current source is the sum of the divergence of the impressed heat fluxes and the negative Joule losses, see (20e). Finally, if Dirichlet BCs are given, these are modelled by voltage sources in the circuit as stated in (20f). We further comment on BCs in Sect. 5.4. To summarise, if we consider an exemplary grid point \(P_i\) and grid edge \(L_{m}\), we obtain a representative thermal circuit stamp as shown in Fig. 7. To this end, the temperature dependence of the materials is neglected and will be discussed in Sect. 5.3.
To further highlight the equivalences between electric and thermal circuits, we would like to briefly comment on these relationships. Many quantities in electrical circuits can find their equivalent in thermal circuits. For example, electric potentials are equivalent to temperatures while electric currents are equivalent to heat fluxes. Table 2 summarises some of these equivalences.
5.3 Temperature-dependent circuit components
Most materials exhibit temperature-dependent behaviour. For the kind of considered materials, the temperature mainly influences the electric and thermal conductivity of the involved materials. In this section, we describe an approach to account for a temperature-dependent electric conductivity when generating the corresponding SPICE netlist. Nevertheless, for the temperature dependence of other materials such as the thermal conductivity or the volumetric mass density, the presented approach can be applied accordingly.
Since the SPICE elements that represent the electric conductivities are conductors placed in circuit branches (cf. Sect. 5.1), we first need to define the temperature of a branch \(b_{m}\). To this end, we take the average temperature \(\overline{T}_{m}\) of the nodes interconnected by the branch \(b_{m}\). Assuming that the temperature dependence of the electric conductivity is known, the temperature-dependent electric conductance of branch \(b_{m}\) is given by
As described in Sect. 5.5, we implement (21) by means of behavioural sources in the SPICE language.
5.4 Circuit implementation of initial and boundary conditions
When a coupled problem of more than one transient differential equation is considered, each sub-problem requires its own initial conditions and BCs. Therefore, we impose these conditions on the EQS and thermal sub-problems separately. However, certain equivalences allow to follow the same procedure for both sub-problems. For any kind of transient problem, initial conditions are required. Since every SPICE dialect supports directives to specify initial conditions, we impose these conditions directly in the netlist. For electric problems, different types of BCs are of interest. In low-frequency problems as the EQS case, Dirichlet or Neumann conditions are typically used. Dirichlet BCs conditions correspond to a fixed potential enforced at the boundary, while Neumann conditions prescribe the electric current through the boundary. Similarly, in thermal problems, Dirichlet BCs correspond to a prescribed temperature at the boundary, while Neumann BCs prescribe thermal fluxes through the boundary. Additionally, thermal problems commonly also involve Robin BCs that describe convective and radiative boundaries.
Dirichlet BCs are represented in the circuit by voltage sources between the Dirichlet nodes and the ground node. Homogeneous Neumann conditions are automatically fulfilled since no edge or branch leaves the domain. For simplicity, we do not consider inhomogeneous Neumann conditions in this paper. A Robin BC can be understood as the conduction between a boundary node and an external node \(n_{\infty }\) at the fixed ambient temperature \(T_{\infty } \). Therefore, Robin BCs are represented in the circuit by conductors connected between the boundary nodes and \(n_{\infty }\) as shown in Fig. 8. We collect the relevant BCs in Table 3.
5.5 Electrothermal netlist generation
Now, we possess all the required ingredients to formulate Algorithm 1 for the automated generation of ET SPICE netlists from field problems discretised by FIT. For every grid edge \(L_{m}\) that connects grid points \(P_{i}\) and \(P_{j}\), where \(i<j\), the temperature-dependent electric conductance, the electric capacitance, and the thermal conductance are written to the netlist to connect the nodes \(n_{i}\) and \(n_{j}\) of the circuit (lines 2–4). Due to the possible nonlinearity of the electric conductivity (cf. Sect. 5.3), a behavioural source is used, where \(V_{ij}\) is the voltage between node \(n_{i}\) and \(n_{j}\). Initial conditions (ic) for the electric part can be included using the corresponding syntax for the capacitors. Here, we use zero initial conditions as an example. Additionally, for every grid point \(P_{i}\), the thermal capacitance and the current-controlled current source (CCCS) representing the Joule losses are added to the netlist to connect node \(n_{i}\) and the ground node (gnd) of the circuit (lines 7 and 8).Footnote 1 Initial conditions (ic) for the thermal part are stated by specifying the initial temperature \(T_{0}\) as the pre-charging of the thermal capacitors. To specify a CCCS in the SPICE language, a behavioural source is used. If \(P_{i}\) is specified as an electric (thermal) Dirichlet node, an additional voltage source connecting node \(n_{i}\) and the ground node of the circuit is inserted (lines 9–14). Furthermore, if an impressed current (heat flux) flows out of the dual volume surrounding \(P_{i}\), an additional current source is added to the netlist connecting node \(n_{i}\) and the ground node of the circuit (lines 15–20).

6 Circuit representation of electromagnetic field problems
In this section, we neglect thermal effects and derive the circuit representation of general 3D EM field problems as given by (1)–(2). However, the thermo-EM coupling can be established analogously. First, in Sect. 6.1, we introduce an auxiliary set notion to collect specific edges and facets of the grid. In Sect. 6.2, the E–H formulation (4) and the E–A formulation (5)–(6) of the Maxwell grid equations (MGEs) are transparently mapped into an electric circuit that fully describes the problem at hand. Finally, in Sect. 6.3, we extend our analysis in order to realise ABCs as circuit stamps. These are typically needed to limit the computational domain while minimising unphysical reflections caused by the domain truncation.
6.1 Auxiliary sets of edges and facets
In the following sections, we will take sums over specific edges or facets of the grid. Since the edges and facets in the neighbourhood of a specific edge \(L_{m}\) are of interest, we introduce sets containing collections of these edges and facets and label them with the superscript \(^{m}\). Let \(\mathcal {A}^{m}\) be the set of all facets in which \(L_{m}\) is embedded. For a regular hexahedral grid, these facets are shown in Fig. 9. All edges that are embedded in the facets contained in \(\mathcal {A}^{m}\) are collected in the set \(\mathcal {L}^{m}\), where this definition also implies \(L_{m}\in \mathcal {L}^{m}\). We denote by \(\mathcal {L}^{m,0}\) the resulting set after extracting the very edge \(L_{m}\) from \(\mathcal {L}^{m}\), that is \(\mathcal {L}^{m,0}:=\mathcal {L}^{m}{\setminus }\{L_{m}\}\). Additionally, we denote the edges that are embedded in facet \(A_{k}\in \mathcal {A}^{m}\) by the sets \(\mathcal {L}_{k}^{m}\) and \(\mathcal {L}_{k}^{m,0}\), respectively. The definitions of the sets \(\mathcal {L}^{m}\), \(\mathcal {L}^{m,0}\), \(\mathcal {L}_{k}^{m}\) and \(\mathcal {L}_{k}^{m,0}\) are visualised in Fig. 9 for the case of a regular hexahedral grid. For such a grid, \(\mathcal {L}^{m}\), \(\mathcal {L}^{m,0}\), \(\mathcal {L}_{k}^{m}\) and \(\mathcal {L}_{k}^{m,0}\) contain 13, 12, 4 and 3 edges, respectively. In Sect. 6.2.2, an additional tree and cotree splitting is introduced. Thereby, edges can either belong to the tree or the cotree. This motivates the introduction of the subscripts \(_{t}\) and \(_{c}\) to denote tree and cotree, respectively. The additional auxiliary sets that are used due to this splitting are denoted by \(\mathcal {L}_{k;\text {t}}^{m}\), \(\mathcal {L}_{k;\text {c}}^{m}\), \(\mathcal {L}_{k;\text {t}}^{m,0}\) and \(\mathcal {L}_{k;\text {c}}^{m,0}\). Lastly, the dual edges that are embedded in the dual facet \(\widetilde{A}_{m}\) are collected in the set \(\widetilde{\mathcal {L}}_{\tilde{m}}^{m}\).
6.2 Circuit representation of the Maxwell grid equations
In this section, circuit representations of the MGEs given by (4)–(6) are derived. First, we start with the E–H formulation of (4) to find a corresponding circuit description which is presented in Sect. 6.2.1. Subsequently, in Sect. 6.2.2 a circuit description based on the E–A formulation of (5)–(6) is presented. For this formulation, a tree-cotree decomposition is used.
A pair of interlocked primal and dual facet \(A_{k}\) and \(\widetilde{A}_{m}\) for the case of a regular hexahedral grid, respectively. The values of \(C_{kn}\) and \(\widetilde{C}_{\tilde{m}\tilde{k}}\) for the edges \(L_{n}\) of \(A_{k}\) and the edges \(\widetilde{L}_{k}\) of \(\widetilde{A}_{m}\) are annotated
6.2.1 Circuit representation based on the E–H formulation
A first electric circuit representing the MGEs is realised from the E–H formulation of (4). The goal is to find an expression for the electric voltage on one primal edge such that a circuit stamp for each edge is obtained. Let \(L_{m}\) be the edge of interest with its corresponding dual facet \(\widetilde{A}_{m}\). We collect all relevant quantities on the grid objects in the neighbourhood of \(L_{m}\) by using the notation introduced in Sect. 6.1. To find the voltage  on \(L_{m}\), let us consider the pair of interlocked facets \(A_{k}\) and \(\widetilde{A}_{m}\) as illustrated in Fig. 10. For this part of the grid, it suffices to consider only the k-th row of (4a) and the \(\tilde{m}\)-th row of (4b) giving
on \(L_{m}\), let us consider the pair of interlocked facets \(A_{k}\) and \(\widetilde{A}_{m}\) as illustrated in Fig. 10. For this part of the grid, it suffices to consider only the k-th row of (4a) and the \(\tilde{m}\)-th row of (4b) giving


From (22a), the magnetic grid voltage  allocated to edge \(\widetilde{L}_{k}\) (which happens to be also embedded in facet \(\widetilde{A}_{m}\)) reads
allocated to edge \(\widetilde{L}_{k}\) (which happens to be also embedded in facet \(\widetilde{A}_{m}\)) reads

By inserting (23) in (22b) for all  , the voltage
, the voltage  on edge \(L_{m}\) is implicitly given by
on edge \(L_{m}\) is implicitly given by

Since \(L_{m}\) is contained in \(\mathcal {L}_{k}^{m}\), we can extract the contribution of \(L_{m}\) from the sum on the left hand side such that

We further define

Thanks to the properties \(\mathbf {C} =\widetilde{\mathbf {C}} ^{\top }\), \(\widetilde{C}_{\tilde{m}\tilde{k}}\in \{-1,1\}\), and \(C_{km}\in \{-1,1\}\), we have that \(\widetilde{C}_{\tilde{m}\tilde{k}}=C_{km}\) and thus, their product equals to unity. However, the product \(\widetilde{C}_{\tilde{m}\tilde{k}}C_{kn}\) can be either \(-1\) or 1 as illustrated in Fig. 10. Therefore, we write (24) with the help of (25) compactly as

Equation (26) is the Kirchhoff ’s current law (KCL) associated with the primal edge \(L_{m}\) with  representing the voltage drop along the edge. In fact, according to the definitions of the field quantities in (26), it is easy to realise that
representing the voltage drop along the edge. In fact, according to the definitions of the field quantities in (26), it is easy to realise that
 has unit of voltage (V),
has unit of voltage (V), has unit of current (A),
has unit of current (A),\(M_{\varepsilon ;\tilde{m} m}\) is positive and has unit of capacitance (F),
\(M_{\sigma ;\tilde{m} m}\) is positive and has unit of conductance (S),
\(M_{\nu ;\tilde{m} m}^{\varSigma }\) is positive and has unit of reluctance (\(\hbox {H}^{-1}\)),
 has unit of current (A).
has unit of current (A).
Thus, by using voltage-controlled current sources (VCCSs) to model  accounting for the contributions from neighbouring edges, we can directly represent (26) with the circuit stamp depicted in Fig. 11, which preserves the voltage drop between the terminals of \(L_{m}\). There are as many of these stamps as primal edges in the 3D grid G, and all of them interact via VCCSs. The concatenation of these elementary stamps constitutes the electric circuit representing the electromagnetic problem at hand.
accounting for the contributions from neighbouring edges, we can directly represent (26) with the circuit stamp depicted in Fig. 11, which preserves the voltage drop between the terminals of \(L_{m}\). There are as many of these stamps as primal edges in the 3D grid G, and all of them interact via VCCSs. The concatenation of these elementary stamps constitutes the electric circuit representing the electromagnetic problem at hand.
Circuit stamp of a primal edge \(L_{m}\) with material matrices mapped into RLC lumped elements as stated by (26). VCCSs account for the interaction with neighbouring edges
In Algorithm 2, the steps to generate the netlist corresponding to the EM circuit representation for the entire grid are listed. A circuit stamp, as shown in Fig. 11, needs to be created for every edge \(L_{m}\) in the grid, and is realised by a loop in the algorithm. In each iteration, a resistor, inductor, and capacitor with the values taken from the material matrices is added (lines 2–4). If an impressed current source shall be placed along \(L_{m}\), an independent current sourcewith a predefined value  is used (lines 5–7). Finally, an inner double loop is required to insert the controlled current sources that model the influence of the edges in the neighbourhood. For this purpose, we choose to insert CCCSsFootnote 2 being controlled by the current
is used (lines 5–7). Finally, an inner double loop is required to insert the controlled current sources that model the influence of the edges in the neighbourhood. For this purpose, we choose to insert CCCSsFootnote 2 being controlled by the current  with a gain of \(g_{\tilde{m}\tilde{k} n}^{\text {I}}:=\widetilde{C}_{\tilde{m}\tilde{k}}M_{\nu ;\tilde{k} k}C_{kn}(M_{\nu ;\tilde{n} n}^{\varSigma })^{-1}\) (lines 8–12). By abuse of notation, we denote the controlling device by
with a gain of \(g_{\tilde{m}\tilde{k} n}^{\text {I}}:=\widetilde{C}_{\tilde{m}\tilde{k}}M_{\nu ;\tilde{k} k}C_{kn}(M_{\nu ;\tilde{n} n}^{\varSigma })^{-1}\) (lines 8–12). By abuse of notation, we denote the controlling device by  .
.

We remark that a similar analysis on (4) in which magnetic conductivities and sources are considered instead of electric ones can be carried out.Footnote 3 This approach would lead to a circuit stamp that is dual to the one in Fig. 11. Namely, in this dual stamp, the Kirchhoff’s voltage law (KVL) is guaranteed for each dual edge and  represents the electric current in the circuit. Furthermore, the resulting lumped elements, stemming from the material matrices, are placed in series with the discrete impressed magnetic current
represents the electric current in the circuit. Furthermore, the resulting lumped elements, stemming from the material matrices, are placed in series with the discrete impressed magnetic current  that plays the role of an independent voltage source exciting the circuit. The interaction between the dual stamps is mediated via current-controlled voltage sources (CCVSs). In the general case, when both electric and magnetic sources are present, the electric circuit will consist of both the primal and dual stamps, which interact via CCCSs and VCVSs, accordingly.
that plays the role of an independent voltage source exciting the circuit. The interaction between the dual stamps is mediated via current-controlled voltage sources (CCVSs). In the general case, when both electric and magnetic sources are present, the electric circuit will consist of both the primal and dual stamps, which interact via CCCSs and VCVSs, accordingly.
6.2.2 Circuit representation based on the E–A formulation
In this section, we describe a circuit representation based on the E–A formulation of (5)–(6). To guarantee uniqueness of the solution, the magnetic potential  is gauged by means of a tree-cotree decomposition [60]. Therefore, although the inferred circuit stamps are gauge dependent, the solution obtained for
is gauged by means of a tree-cotree decomposition [60]. Therefore, although the inferred circuit stamps are gauge dependent, the solution obtained for  is unique. We start by considering one primal facet \(A_{k}\in \mathcal {A}^{m}\) (cf. Fig. 10). For this facet, it suffices to consider the k-th row of (5a) and the \(\tilde{m}\)-th row of (5b) such that the E–A formulation of the MGEs for a generic edge \(L_{m}\) reads
is unique. We start by considering one primal facet \(A_{k}\in \mathcal {A}^{m}\) (cf. Fig. 10). For this facet, it suffices to consider the k-th row of (5a) and the \(\tilde{m}\)-th row of (5b) such that the E–A formulation of the MGEs for a generic edge \(L_{m}\) reads


As in Sect. 6.2.1, we aim at finding a unique circuit representation of edge \(L_{m}\). We start by observing that the system matrix \(\widetilde{\mathbf {C}} \mathbf {M}_{\nu } \mathbf {C} \) of (5) is singular.Footnote 4 This singularity manifests itself in the non-uniqueness of  . In fact, only the curl of
. In fact, only the curl of  is uniquely defined. As a remedy, we must explicitly impose the gauging (6) upon (5). To this end, let us assume that we have constructed a suitable tree\(G_{\text {t}}\) and a cotree\(G_{\text {c}}\) out of the primal grid G, as exemplified in Fig. 12. Then, we symbolically introduce the orthogonal permutation matrix \(\mathbf {P}_{\text {G}}\) to partition
is uniquely defined. As a remedy, we must explicitly impose the gauging (6) upon (5). To this end, let us assume that we have constructed a suitable tree\(G_{\text {t}}\) and a cotree\(G_{\text {c}}\) out of the primal grid G, as exemplified in Fig. 12. Then, we symbolically introduce the orthogonal permutation matrix \(\mathbf {P}_{\text {G}}\) to partition  into its tree
into its tree and cotree
and cotree components with \(N_{\text {t}}\) and \(N_{\text {c}}\) entries, respectively. Symbolically, this reads
components with \(N_{\text {t}}\) and \(N_{\text {c}}\) entries, respectively. Symbolically, this reads

Similarly, we also divide \(\mathbf {M}_{\text {G}}\) and \(\widetilde{\mathbf {S}} \) into their tree and cotree components by applying the \(\mathbf {P}_{\text {G}}\) matrix accordingly, viz.
The identities of (28) and (29) together with the orthogonality property of \(\mathbf {P}_{\text {G}}\) enable us to rewrite the gauging of (6) as

Additionally, since \(\widetilde{\mathbf {S}} _{\mathbb {1}\text {t}}\mathbf {M}_{\text {G}_{\text {t}}}\) is a square and invertible matrix,Footnote 5 we may finally express the tree component  as
as

The column vector \( \mathbf {F} \), which represents the grid counterpart of the scalar function f quantifying the divergence of \(\mathbf {A}\), is of free choice. Therefore, we conveniently choose \( \mathbf {F} \,{=}\,\mathbf {0}\) impressing the Coulomb gauge [61] to straightforwardly arrive at

The matrix \(\mathbf {E}_{\text {tc}}\in \mathbb {R}^{N_{\text {t}}\times N_{\text {c}}}\) is known as the essential incidence matrix [60] and establishes a direct relation between the tree and cotree components  and
and  , respectively.Footnote 6 By inspection and expansion of (31), we express the m-th component of the column vector
, respectively.Footnote 6 By inspection and expansion of (31), we express the m-th component of the column vector  as
as

with
and i spanning over the nodes in G. In this manner, (32) removes the redundancy associated with  and guarantees a unique solution of (27).
and guarantees a unique solution of (27).
Let us now get back to the generic primal edge \(L_{m}\) once again. As introduced in Sect. 6.1, we use specific sets to refer to edges in the tree and cotree denoted by \(\mathcal {L}_{k;\text {t}}^{m}\), \(\mathcal {L}_{k;\text {t}}^{m,0}\) and \(\mathcal {L}_{k;\text {c}}^{m}\), \(\mathcal {L}_{k;\text {c}}^{m,0}\), respectively. Isolating the voltage  along edge \(L_{m}\) embedded in facet \(A_{k}\) from (27a), we arrive at
along edge \(L_{m}\) embedded in facet \(A_{k}\) from (27a), we arrive at

We may then take the sum over all facets \(A_{k}\in \mathcal {A}^{m}\) (cf. Fig. 13). Then, by splitting  into tree and cotree components, we arrive at
into tree and cotree components, we arrive at

where \(N_{\text {F};m}\) is the number of facets in G containing the edge \(L_{m}\). Note that \(N_{\text {F};m}=4\) for a regular hexahedral grid. Let us now introduce the auxiliary definitions
where

which allow to express (33) as

Similarly, we expand the left-hand side of (27b) as

which, upon substitution in (27b) and by splitting  into tree and cotree components, yields
into tree and cotree components, yields

where
since \(\widetilde{C}_{\tilde{m}\tilde{k}}=C_{km}\). By means of the auxiliary definitions

where

we express (35) as

We observe that (34) and (36) can be interpreted as the KVL and KCL of an arbitrary primal edge \(L_{m}\) provided that  and
and  represent the sought voltage and current, respectively. As a matter of fact, we observe that
represent the sought voltage and current, respectively. As a matter of fact, we observe that
 has unit of V and represents the voltage drop along \(L_{m}\) that is either in the tree or cotree set.
has unit of V and represents the voltage drop along \(L_{m}\) that is either in the tree or cotree set. has unit of Weber (Wb) and represents the current along \(L_{m}\). If \(L_{m}\in G_{\text {c}}\), this current is a degree of freedom. Otherwise, it is modelled by a CCCS as stated in (32). For compact notation, we label this CCCS as \({I_{\varSigma ;m}:=\sum _{n\in G_{\text {c}}}I_{\varSigma ;mn}}\), where
has unit of Weber (Wb) and represents the current along \(L_{m}\). If \(L_{m}\in G_{\text {c}}\), this current is a degree of freedom. Otherwise, it is modelled by a CCCS as stated in (32). For compact notation, we label this CCCS as \({I_{\varSigma ;m}:=\sum _{n\in G_{\text {c}}}I_{\varSigma ;mn}}\), where  .
.\(M_{\nu ;\tilde{m} m}^{\varSigma }\) has unit of \(\hbox {H}^{-1}\) and is expected to be positive since \(M_{\nu ;\tilde{k} k}>0\) for all materials. This term scales the displacement, conduction and impressed current as seen in (35).
With these observations, we may depict (33) and (35) by means of the circuit stamps of Fig. 14a, b for a cotree and tree edge, respectively. As we can see therein,  is regarded as the electric current along the primal edge \(L_{m}\), while the voltage drop between its terminals is established by the VCVS \(V_{e;m}\) and the CCVSs \(V_{\text {c};m}\) and \(V_{\text {t};m}\) that mediate the interaction with neighbouring edges. When the edge \(L_{m}\) belongs to the tree \(G_{\text {t}}\), then the current
is regarded as the electric current along the primal edge \(L_{m}\), while the voltage drop between its terminals is established by the VCVS \(V_{e;m}\) and the CCVSs \(V_{\text {c};m}\) and \(V_{\text {t};m}\) that mediate the interaction with neighbouring edges. When the edge \(L_{m}\) belongs to the tree \(G_{\text {t}}\), then the current  is modelled by the CCCS \(I_{\varSigma ;m}\) as demanded by (32). Otherwise, for cotree edges,
is modelled by the CCCS \(I_{\varSigma ;m}\) as demanded by (32). Otherwise, for cotree edges,  is a degree of freedom. The current
is a degree of freedom. The current  is then split into several branches where a resistance, capacitance, the impressed current source, and CCCSs are connected. The concatenation of these fundamental stamps forms the electric circuit representing the magnetic vector potential formulation of the electromagnetic problem.
is then split into several branches where a resistance, capacitance, the impressed current source, and CCCSs are connected. The concatenation of these fundamental stamps forms the electric circuit representing the magnetic vector potential formulation of the electromagnetic problem.
In Algorithm 3, we show the pseudocode to generate the netlist of the circuit stamps depicted in Fig. 14. The iteration over all edges \(L_{m}\) in the grid is done in the outermost loop. In each iteration, one resistor and capacitor connecting the node \(n_{m}\) to ground (gnd) must be added to the netlist (lines 2 and 3). If an impressed current is present at \(L_{m}\), an independent current source with value \(I_{\text {i};m}\) is added between \(n_{m}\) and gnd (lines 4–6). For every tree edge, the currents \(I_{\varSigma ;mn}\) from the cotree edges in the neighbourhood are modelled by a parallel connection of CCCSs between \(n_{e;m}\) and \(n_{m}\) (lines 7–11). Using a double loop, the inductive currents \(I_{\text {t};m\tilde{k} n}\) and \(I_{\text {c};m\tilde{k} n}\) from the tree and cotree branches, respectively, are added as a parallel connection of CCCSs between \(n_{m}\) and gnd (lines 12–19). The controlling current is given by the current through device FIcn11 and the gain is \({g_{m\tilde{k} n}^{\text {I}}=\widetilde{C}_{\tilde{m}\tilde{k}}M_{\nu ;\tilde{k} k}C_{kn}(M_{\nu ;\tilde{m} m}^{\varSigma })^{-1}}\). Finally, the voltages \(V_{e;mkn}\), \(V_{\text {c};mkn}\) and \(V_{\text {t};mkn}\) are added as a series connection between \(n_{e;m}\) and gnd with intermediate nodes indexed by k, n and \(\hat{n}=n+1\) (lines 20–30). For the voltage \(V_{e;mkn}\), the voltage between node nn and gnd controls a VCVS with a gain of \(g_{mkn}^{\text {V}}=N_{\text {F};m}^{-1}C_{kn}C_{km}^{-1}\) On the other hand, the voltages \(V_{\text {c};mkn}\) and \(V_{\text {t};mkn}\) are added as behavioural sources using DDT as the SPICE syntax for time derivatives and a gain of \(g_{mkn}^{\text {I}}=N_{\text {F};m}^{-1}C_{kn}C_{km}^{-1}\). Note that for a cotree edge, the node \(n_{e;m}\) coincides with the node \(n_{m}\).

We remark that a similar analysis on (1) by considering only magnetic conductivities and sources instead of electric ones is also possible. Thus, with the auxiliary electric potential \(\mathbf {D}=\nabla \times \mathbf {F}\) and \(\nabla \cdot \mathbf {F}=a\), where a is an arbitrary gauging function, circuit stamps which are dual to those shown in Fig. 14 can be found. In these dual stamps,  represents an electric current while
represents an electric current while  , namely the grid counterpart of \(\mathbf {F}\), would be regarded as a voltage drop. Finally, if both electric and magnetic sources were present, then the entire circuit would consist of the aggregate of interacting primal and dual stamps.
, namely the grid counterpart of \(\mathbf {F}\), would be regarded as a voltage drop. Finally, if both electric and magnetic sources were present, then the entire circuit would consist of the aggregate of interacting primal and dual stamps.
6.3 Absorbing boundary conditions
In many electromagnetic field simulation setups, the computational domain must be bounded. To simulate free wave propagation, one must impose according conditions for the fields at the boundaries of the domain. These conditions are known as ABCs [47] and aim at minimising (ideally cancelling) unphysical incoming reflections. At the boundary of the domain, a distinction is made between normal and tangential components and between longitudinal and transverse derivatives.Footnote 7
For starters, let \(\partial _{r}\), \(\nabla _{\text {t}}\) and \(\partial _{t}\) denote the longitudinal, transversal and temporal derivative operators, respectively. Furthermore, within the context of this analysis, we define \(\nabla :=\left( \partial ^{2}_{r}+\nabla _{\text {t}}^{2}\right) ^{1/2}\). We start the realisation of circuit stamps for ABCs by considering the time-domain wave equation for the electric field \(\mathbf {E}\) in a homogeneous and isotropic medium,Footnote 8 viz.
Equation (37) can be expanded in terms of the so-called travelling wave operators as
Above, we observe that in an arbitrary point in space, the field \(\mathbf {E}\) can in general be considered as the superposition of an inward and outward travelling wave \(\mathbf {E}^{+}\) and \(\mathbf {E}^{-}\), respectively, viz.
which upon substitution in (38) straightforwardly leads to the following set of travelling wave equations,
inasmuch as both wave components \(\mathbf {E}^{\pm }\) are linearly independent. Owing to their definition, the wave components \(\mathbf {E}^{\pm }\) satisfy independently and simultaneously the following,Footnote 9
which tells us explicitly that the outward (inward) travelling wave operator cancels out the inward (outward) travelling wave at any point of interest.
Now, let us get back to (38) to further expand the operators therein to obtain
As we can see, the above wave operators entail the calculation of the inverse of \(\sqrt{1+\nabla _{\text {t}}^{2}/\partial _{r}^{2}}\), which generally translates into a global integral operator [62]. In principle, the expansion of this integral operator around the observation point yields the exact explicit representation of the travelling wave operators in (40). However, this approach is contrary to the idea of realising simple and efficient ABCs for circuit simulations.
As a remedy, we may expand \(1/\sqrt{1+\nabla _{\text {t}}^{2}/\partial _{r}^{2}}\) as in a Taylor series to yield
The above equation holds for any component of \(\mathbf {E}\). Furthermore, if the field \(\mathbf {E}\) propagates in free space, we may assume that the operation \(\nabla ^{2}_{\text {t}}\) is negligible in the neighbourhood of an observation point within the spherical wavefront. Hence, we may rewrite (41) in terms of simplified inward and outward travelling wave propagators as
since the general expression of \(\mathbf {E}\) in (42) admits the superposition of inward and outward travelling waves \(\mathbf {E}^{+}\) and \(\mathbf {E}^{-}\). Then, to minimise unwanted incoming reflections at a certain boundary given by \(r=r_{\text {B}}\), we may impose on \(\mathbf {E}\) the condition
in agreement with (39). The condition given by (43) is a first-order ABC known as Engquist-Majda condition [47]. It is a local condition because it is evaluated pointwise taking only into account the wave component propagating perpendicularly to the boundary. Thereby, the condition in (43) states that a practical transparent boundary at \(r=r_{\text {B}}\) can be realised if it is guaranteed that the phase-amplitude of the field on the boundary at a certain time \(t_{\text {B}}\) is equal to that one the field had at some previous instant \(t_{\text {B}}-\varDelta t\) at a point \(r=r_{\text {B}}-\varDelta t/\sqrt{\mu \varepsilon }\). The practical relevance of (43) comes from its simplicity.
Let us now interpret (43) within the context of the Maxwell grid equations in order to realise circuit stamps associated with the ABCs of (43). To this end, let us consider the grid wave equation for the electric grid voltage  , which for time-independent constitutive parameters and non-conducting source-free regions can be obtained from the grid curl equations of (4), viz.
, which for time-independent constitutive parameters and non-conducting source-free regions can be obtained from the grid curl equations of (4), viz.

With the structure of the matrices \(\mathbf {C}\), \(\mathbf {M}_{\varepsilon }\) and \(\mathbf {M}_{\nu }\) given by (7) and the subdivision  , the expression
, the expression

for the component  is obtained. Similar expressions can be also obtained for the other two components
is obtained. Similar expressions can be also obtained for the other two components  and
and  .
.
The grid counterpart of the ABC in (43) is obtained from (44) by extracting the grid wave equation associated with a generic primal edge \(L_{x;m}\in G\) oriented along the x-direction. This yields

with n and \(\tilde{k}\) spanning over the corresponding primal and dual edges oriented along the indicated directions. We make the following observations upon the above grid wave equation.
Two main grid wave components contribute to the time variation of
 along \(L_{x;m}\). The first of these grid wave components propagates along the z-direction and stems from the spatial variation of
along \(L_{x;m}\). The first of these grid wave components propagates along the z-direction and stems from the spatial variation of  along this direction as stated by the grid derivatives in
along this direction as stated by the grid derivatives in 
 . The second one propagates along the y-direction and stems from the spatial variation of
. The second one propagates along the y-direction and stems from the spatial variation of  along this direction as stated by
along this direction as stated by  .
.Two secondary grid wave components contribute to the time variation of
 along \(L_{x;m}\). The first one propagates along the y-direction and stems from the spatial variation of
along \(L_{x;m}\). The first one propagates along the y-direction and stems from the spatial variation of  along the x-direction as stated by
along the x-direction as stated by  . The second one propagates along the z-direction and stems from the spatial variation of
. The second one propagates along the z-direction and stems from the spatial variation of  along the x-direction as stated by
along the x-direction as stated by  .
.Owing to both the structure of (45) and the grid-like embedding where the propagation takes place, we may apply superposition to treat each propagation direction separately. Therefore, each grid wave component satisfies its own one-dimensional grid wave equation.
We construct the grid counterpart of (43) by adhering to the same principle that led to it. Namely, we take only into account grid wave propagation perpendicular to the boundary of interest. Thereby, let us assume that our boundary is located for example at \(z=z_{\text {B}}\). Thus, by invoking the superposition principle, we may write the grid wave equation associated with the component  that propagates along the z-direction as
that propagates along the z-direction as

where we have used the labels \(^{(z)}\) and \(^{(x)}\) to explicitly indicate directions of propagation. By considering that for sufficiently well-refined grids G and \(\widetilde{G}\) we may expect \(M_{\nu ;y;\tilde{k} k}\) to not vary significantly for the two relevant facets \(A_{y;k}\) (cf. Fig. 15), we may define an average value \(\overline{M}_{\nu ;y;k\tilde{k}}\) that enables us to write the leftmost term on the left-hand side of (46) as

with a similar result for the rightmost term on the left-hand side of (46). Thus, together with the property \(P^{\top }_{\xi ;nk}=-\widetilde{P}_{\xi ;nk}\), we may proceed to write (46) as

Above, the term  is the grid counterpart of the continuous operator in the wave equation of (37). Analogously, we may assume that in the vicinity of \(L_{x;m}\) at the boundary \(z=z_{\text {B}}\), the wavefront of the impinging grid wave is plane. Therefore, we may neglect transverse variations and we arrive at
is the grid counterpart of the continuous operator in the wave equation of (37). Analogously, we may assume that in the vicinity of \(L_{x;m}\) at the boundary \(z=z_{\text {B}}\), the wavefront of the impinging grid wave is plane. Therefore, we may neglect transverse variations and we arrive at

We observe that  is formally the second-order grid derivative of the scalar field
is formally the second-order grid derivative of the scalar field  along the z-direction. This directly leads us to the grid counterpart of (37) in the vicinity of \(L_{x;m}\), viz.
along the z-direction. This directly leads us to the grid counterpart of (37) in the vicinity of \(L_{x;m}\), viz.

Again, this equation can be factorised in terms of grid wave propagators similar to (42) to yield the grid version of (43), viz.

which can be easily extended to other field components and to other boundary orientations. It also states that the grid wave impinging perpendicularly to the boundary \(z=z_{\text {B}}\) at the edge \(L_{x;m}\) propagates at a speed \(\nu =(\overline{M}_{\nu ;y;\tilde{k} k}^{-1}M_{\varepsilon ;x;\tilde{m} m})^{-\frac{1}{2}}\). A similar result can be obtained if we had used the grid wave equation of the magnetic field  . Having said this, we can think of the space between edge \(L_{x;m}\) and \(L_{x;m-M_{z}}\), namely the preceding x-edge in z-direction, as a homogeneous transmission line with characteristic impedance
. Having said this, we can think of the space between edge \(L_{x;m}\) and \(L_{x;m-M_{z}}\), namely the preceding x-edge in z-direction, as a homogeneous transmission line with characteristic impedance
and length \(|L_{z;m-M_{z}}|\), see Fig. 16. The voltage that excites the line is given by the voltage on edge \(L_{x;m-M_z}\), namely  . Therefore, if one wants to implement the ABC at edge \(L_{m}\), an impedance \(Z_{0;m}\) must be assigned to \(L_{m}\). A subsequent circuit extraction can be carried out by implementing either Algorithm 2 or 3.
. Therefore, if one wants to implement the ABC at edge \(L_{m}\), an impedance \(Z_{0;m}\) must be assigned to \(L_{m}\). A subsequent circuit extraction can be carried out by implementing either Algorithm 2 or 3.
7 Numerical examples
In this section, the presented methodology to generate circuit stamps representing 3D field problems is applied to several representative numerical examples. In Sect. 7.1, we use the netlist extraction method as described in Sect. 5 on an ET model problem consisting of a 3D field problem corresponding to the series connection of a capacitor and a resistor. Applying an external voltage, the transient heating due to the resulting current is simulated using SPICE, and then compared to a field solver reference solution. To quantify the scalability of state-of-the-art circuit simulators, a convergence study with up to \(80\,024\) unknowns is presented. Additionally, a circuit representation for the ET field problem of a microelectronic chip package is obtained and used for circuit simulation. In Sect. 7.2, we apply the method of circuit extraction for EM field problems as described in Sect. 6 to compute the resonant frequencies of a rectangular cavity with perfect electric conducting (PEC) boundaries. This example is quite illustrative and easy to implement because of the required BCs on the cavity walls. It simply suffices not to print the circuit stamp associated with those edges on the wall, meaning that the associated stamps are short-circuited. Furthermore, the availability of an analytic formula for the resonant frequencies permits a direct error assessment. Finally, in Sect. 7.3, the implementation of ABCs as discussed in Sect. 6.3 is carried out to investigate reflections at the end of a rectangular coaxial waveguide. For all presented examples, the Matlab\(^{\circledR }\) code to generate the corresponding netlists from the discretised 3D field problem is freely available [63].
7.1 Electrothermal circuit validation
To verify our netlist extraction method for an ET problem, we consider the Joule heating in a 3D field model problem represented by a series connection of a resistor and a capacitor. The temperature dependence of the electric conductivity is manifested via the temperature coefficient \(\alpha =3.9\times 10^{-3}1/\hbox {K}\). The relevant configuration is realised by a brick of two different materials as shown in Fig. 17. The brick is of dimension \(0.4\times 0.1\times 0.1 \,{\upmu }\hbox {m}^{3}\), with the resistive part having a length of \(\ell =0.3\,{\upmu }\hbox {m}\), and the capacitive part having a length of \(d={0.1}\,{\upmu }\hbox {m}\). At \(x=0\) and \(x=\ell +d\), PEC electrodes are used. Table 4 summarises all material properties for a reference temperature of \(T_{0}={293}\,\hbox {K}\).
A spatial grid with \(9\times 9\times 9\) cells is employed and the field problem is solved by using an in-house implementation of the FIT method with a first-order implicit Euler scheme as time integrator. The simulation time amounts to \(t_{\text {end}}={13}\,{\upmu }\hbox {s}\). For the simulation of the extracted electric circuit, we use the freely available LTspice software.Footnote 10 LTspice uses adaptive refinement in time for which an initial time step of \(\varDelta t_{\text {init}}={0.13}\,\mu \hbox {s}\) is used. The resulting non-equidistant time axis is refined by a factor of three and then used for the FIT solver. A voltage \(V_{\text {app}}={1}\,\hbox {kV}(1-\exp (-t/\tau ))\) with \(\tau =0.1 t_{\text {end}}\) is applied at the electrodes as shown in Fig. 17. Using this setting, two simulations are run. The first run neglects the temperature dependence of the conductivities and thus a linear setting ensues. The second run neglects only the temperature dependence of the thermal conductivity but accounts for the one of the electric conductivity via the temperature coefficient \(\alpha \) entailing a nonlinear setting. To observe the transient behaviour, we select the resistor–capacitor interface point \(\mathbf {x}_{0}=(\ell ,0,0)\) as observation point and plot the results in Fig. 18.
For a quantitative error assessment of the solution, we define the measures
where \(\varvec{{\varphi }}^{\text {cir}}\), \(\varvec{{\varphi }}^{\text {FIT}}\), \(\mathbf {T}^{\text {cir}}\) and \(\mathbf {T}^{\text {FIT}}\) are the potential and temperature solution vectors obtained via circuit and FIT simulation, respectively. To calculate these errors appropriately, the circuit solution is interpolated to the time axis employed by the FIT solution using cubic spline interpolation. Let us remark that the quantities in (48) are not errors in the classical sense since none of the solutions is exact. The computed differences amount to \(\varDelta _{\varvec{{\varphi }}}^{\text {lin}}\approx 0.36\%\) and \(\varDelta _{\mathbf {T}}^{\text {lin}}\approx 0.48\%\) for the linear case and \(\varDelta _{\varvec{{\varphi }}}^{\text {nlin}}\approx 0.42\%\) and \(\varDelta _{\mathbf {T}}^{\text {nlin}}\approx 0.44\%\) for the nonlinear case. The remaining error is mainly attributed to the different time integrators.
To analyse the convergence of the solution obtained by circuit simulation, we consider a 1D stationary electrothermal example with available analytical solution. We use the example from Fig. 17, which exhibits 1D behaviour for a symmetric excitation. In particular, we neglect the transient and impressed terms in (16), generate the corresponding netlist using Algorithm 1, and solve the problem using a circuit simulator. While using only one element in y- and z-direction, the number of elements in x-direction is varied. Figure 19 shows the convergence of the relative \(L_{2}\)-error with respect to the analytical solution, giving the expected second-order convergence. For the finest resolution of \(80\,024\) unknowns, an error of \(5.652 \times 10^{-9}\) is achieved. This error is obtained by an LTspice simulation which requires about \({410}\,\hbox {s}\) on an Intel Core i7-3820 with \({16}\,{\hbox {GB}}\) of memory. However, more optimised circuit simulators for large circuits are available. Using Xyce [64] to solve the problem on the same machine demonstrates this benefit by requiring only about \({40}\,{\hbox {s}}\). Pushing the capabilities of Xyce to a limit, the simulation of a refinement with 1 000 028 devices and 400 024 unknowns finished after about 14 minutes with an error of \(4.351 \times 10^{-9}\).
For an industry-relevant example, the proposed method is applied to the 3D microelectronic chip package [46] as shown in Fig. 20a. The field problem is discretised as described in Sect. 3 and Algorithm 1 is used to generate the corresponding netlist. This netlist uses 101 147 circuit elements to describe a field problem that has been discretised using a grid with 9660 nodes. Running a transient analysis on this netlist, an error of \(\varDelta _{\varvec{{\varphi }}}\approx 0.23\%\) and \(\varDelta _{\mathbf {T}}\approx 0.17\%\) compared to the field simulation is achieved. Figure 20b shows the temperature of the hottest point in the chip package obtained by FIT and circuit simulation. The temperature distribution in the chip package resulting from circuit simulation is shown in Fig. 20c. Thus, a good agreement of circuit simulation results for a 3D ET problem is achieved when compared to the corresponding field solver results.
7.2 Electromagnetic circuit validation
In this section, we verify the method presented in Sect. 6 for the circuit representation of EM field problems. To this end, a lossless rectangular resonant cavity with PEC boundaries and outer dimensions of \(a\times b\times d=0.1\times 0.2\times 0.2\,\hbox {m}^{3}\) is simulated and its resonant frequencies are computed. The homogeneous material within the cavity is specified by the relative permittivity \(\varepsilon _{\mathrm {r}}={2}\) and the relative permeability \(\mu _{\mathrm {r}}={1}\). The resonant frequencies can be calculated by means of the formula [65]
where \(c_{0}\) is the speed of light and \(\left\{ m,n,p\right\} \) are the indices of the resonant modes, given by the natural numbers including zero. For these resonant frequencies, the longitudinal transverse electric (TE) and transverse magnetic (TM) field components are given by
respectively, where \(H_{0}^{mnp}\) and \(E_{0}^{mnp}\) are the corresponding field amplitudes. For a TE (TM) mode mnp to exist, \(H_{z}\) (\(E_{z}\)) must not become zero.
To simulate the excitation of modes within the cavity, we discretise the interior of the cavity using an equidistant regular grid of 10 cells in each direction and apply PECs upon all cavity walls. Then, we obtain the resonant frequencies by solving the generalised eigenvalue problem given by

where a resonant frequency is denoted by \(f_{\text {r};\text {E}}^{\text {FIT}}\). Alternatively, we can use appropriate excitations to analyse the resulting field at a set of given frequencies. For example, TM modes are excited by using an electric current source allocated at a primal edge that is oriented along the positive z-direction and attached to the central grid point. In a similar manner, TE modes are excited by means of a looping electric current source located in the cavity centre. We then solve the discretised problem given by

for a set of angular frequencies \(\omega \), where  is the current source vector whose entries are all zero except at the corresponding source edges. The frequency axis from 0.5 to \({3}\,{\hbox {GHz}}\) is discretised using 2000 points for the TM excitation and 3000 points for the TE excitation. The results are evaluated on one edge for each excitation type. For the TM case, an edge in positive z-direction connected to the central grid point is used while for the TE case, an edge in positive x-direction connected to the point (5,6,10)cm is used. In Fig. 21, the voltages
is the current source vector whose entries are all zero except at the corresponding source edges. The frequency axis from 0.5 to \({3}\,{\hbox {GHz}}\) is discretised using 2000 points for the TM excitation and 3000 points for the TE excitation. The results are evaluated on one edge for each excitation type. For the TM case, an edge in positive z-direction connected to the central grid point is used while for the TE case, an edge in positive x-direction connected to the point (5,6,10)cm is used. In Fig. 21, the voltages  and
and  along these edges are plotted. From the peaks in the plots, the corresponding resonant frequencies \(f_{\text {r;TE}}^{\text {FIT}}\) and \(f_{\text {r;TM}}^{\text {FIT}}\) are identified.Footnote 11
along these edges are plotted. From the peaks in the plots, the corresponding resonant frequencies \(f_{\text {r;TE}}^{\text {FIT}}\) and \(f_{\text {r;TM}}^{\text {FIT}}\) are identified.Footnote 11
To verify our circuit extraction method for EM problems, we generate the netlist of the resonant cavity according to Algorithm 2 and simulate the resulting circuit in LTspice by performing an AC analysis in the same frequency range as before. We then identify the circuit voltages corresponding to  and
and  and plot them directly in Fig. 21 for a comparison. The circuit resonant frequencies \(f_{\text {r;TE}}^{\text {Cir}}\) and \(f_{\text {r;TM}}^{\text {Cir}}\) are again identified by means of the peaks, and we collect the computed resonant frequencies for the first few modes in Table 5. Note that, according to (49), the TM-mode does not exist for \(m=0\). Additionally, the errors
and plot them directly in Fig. 21 for a comparison. The circuit resonant frequencies \(f_{\text {r;TE}}^{\text {Cir}}\) and \(f_{\text {r;TM}}^{\text {Cir}}\) are again identified by means of the peaks, and we collect the computed resonant frequencies for the first few modes in Table 5. Note that, according to (49), the TM-mode does not exist for \(m=0\). Additionally, the errors
are presented. For all modes, these errors are smaller than \(0.1\%\).
Geometry of a coaxial transmission line oriented along the z-axis and excited at port 1 by a Gaussian current pulse. A propagating wave is thus generated arriving at port 2 that is connected to an external impedance. For reasons of visibility, the annotations of the inner conductor’s dimensions are not shown
7.3 Signal transmission using absorbing boundary conditions
In this section, based on the method described in Sect. 6.3, we present a simple validation example for ABCs in the context of circuit simulation. To this end, let us consider a coaxial transmission line of rectangular cross section oriented along the z-direction as depicted in Fig. 22. For the simulation of an infinitely long line using a finite computational domain, the implementation of ABCs is required to counteract unwanted incoming reflections. We use an excitation signal at port 1 and simulate its propagation in time until it has reached port 2. Thus, we generate two simulation results in time domain. The first one corresponds to the case when port 2 is terminated with a perfect magnetic wall, that is an open port (\(Z_{2}\,{\rightarrow }\,\infty \)). The second one corresponds to the case when port 2 is terminated with the characteristic line impedance (\(Z_{2}\,{=}\,Z_{0}\)). For both cases, a perfect magnetic conducting (PMC) (\(Z_{1}\rightarrow \infty \)) at port 1 is applied.Footnote 12
The length of the coaxial line is \(l=150\,{\hbox {cm}}\), the width and height of the outer conductor are \(w_{\text {o}}=h_{\text {o}}={3}\,{\hbox {cm}}\) and of the inner conductor \(w_{\text {i}}=h_{\text {i}}={1}\,{\hbox {cm}}\). While the conductors are modelled as PEC, the material between them is vacuum. Due to the expected propagation in z-direction, the longitudinal direction requires a finer discretisation compared to the transversal direction. Thus, we choose a grid of \(3\times 3\times 150\) cells. According to (47) for such a discretisation grid, the characteristic impedance for the edges connecting the inner and outer conductor along the plane of port 2 should amount toFootnote 13\(Z_{0;m}=(\overline{M}_{\nu ;y;k\tilde{k}}M_{\varepsilon ;x;\tilde{m} m})^{-1/2}\approx 376.7\,\Omega \). For the given grid, there are eight such edges giving eight parallel conductances such that the total resistance at port 2 equals \(Z_{2}=Z_{0}=8Z_{0;m}\approx 47.09\,\Omega \), which is also the characteristic impedance of the line. To excite the signal at port 1, the edges connecting the inner and outer conductors along the plane of port 1 are impressed with a current such that the total current from inner to outer conductor is
with \(\hat{I}=1\,{\hbox {A}}\), which is a Gauss pulse with a maximal frequencyFootnote 14 component of \(f_{\text {max}}={1}\,{\hbox {GHz}}\). The used constants are given by \({\sigma _{\text {G}}=\sqrt{\ln (10)}/(\pi f_{\text {max}})}\) and by \({t_{0}=\sqrt{6\sigma _{\text {G}}^2\ln (10)}}\). The simulation time \(t_{\text {end}}={10}\,{\hbox {ns}}\) is chosen such that the excited pulse can reach port 2. Having defined the geometry, the excitation and the simulation time, we also generate the corresponding netlist using Algorithm 2.
Snapshots of the wave propagating along the z-axis at times \(t_{1}={3}\,{\hbox {ns}}\), \(t_{2}={5}\,{\hbox {ns}}\), \(t_{3}= {7}\,{\hbox {ns}}\) and \(t_{4}={8}\,{\hbox {ns}}\) computed by FIT and circuit simulation. a shows the case \(Z_{2}\rightarrow \infty \) to realise total reflection. b shows the case \(Z_{2}=Z_{0}\) to realise ABCs
The generated netlist is simulated by means of a transient analysis in LTspice. On the other hand, the Leapfrog scheme is used as a time integrator within the FIT framework to carry out the simulation directly on the 3D grid. In both cases, we use the time axis generated by the adaptive time stepping algorithm provided by LTspice, which satisfies the Courant-Friedrichs-Levy (CFL)-condition being a stability requirement for the explicit Leapfrog scheme [1]. In the following, we compare the voltage \(V_{\text {oi}}(z,t)\) between outer and inner conductor and the voltage \(V_{2}(t)=V_{\text {oi}}(l,t)\) at port 2. For \(Z_{2}\rightarrow \infty \) and \(Z_{2}=Z_{0}\), Fig. 23 shows \(V_{\text {oi}}(z,t)\) at different times computed by means of FIT and circuit simulation. Figure 23a shows the case in which port 2 is terminated by a perfect magnetic boundary (standard homogeneous Neumann) condition while Fig. 23b shows the case when a matching impedance \(Z_{2}=Z_{0}\) according to (47) is applied at port 2. As predicted by the theory in Sect. 6.3, we observe that the matching impedance at port 2 counteracts incoming reflections effectively. In Fig. 24, we show \(V_{2}(t)\) computed by means of FIT and circuit simulation for the two already considered cases. We observe therein that incoming reflections at port 2 result in an undesired overshooting of the voltage. For a quantitative comparison, we define the relative error of \(V_{2}(t)\) between FIT and circuit results as
and obtain \(\varDelta _{V_{2}}^{Z_{0}}\approx 1.046 \%\) and \(\varDelta _{V_{2}}^{\infty }\approx 1.136 \%\).
8 Conclusion and future work
A method for the automatic netlist generation of general 3D ET and EM problems has been presented. The topology of each circuit stamp associated with edges in the regular primal grid has been derived by using FIT for spatial discretisation. Using the MNA, the FIT-discretised ET formulation has been mapped into a circuit that can be solved by any SPICE-like program. It has been shown that initial conditions can be easily prescribed as initial potentials for the lumped capacitances in the SPICE language. Furthermore, the implementation of mixed boundary conditions of Dirichlet, homogeneous Neumann and Robin type has been discussed. We have also shown that temperature-dependent material models result in nonlinearities in the lumped resistances requiring the implementation of behavioural VCCSs in SPICE.
From the standard E–H formulation and the E–A formulation, we have derived circuit stamps representing general EM problems. In both circuit representations, the integrated electric field models the voltage between the stamp terminals while the integrated magnetic vector potential models the electric current in the E–A formulation. To guarantee uniqueness of the solution in the latter, we have employed Coulomb ’s gauge on the magnetic vector potential, that has been implemented by means of a tree-cotree decomposition of the primal discretisation grid. Thereby, the electric current along edges in the cotree are degrees of freedom whereas those along edges in the tree are modelled by CCCSs being controlled by currents in the cotree. For both representations, a dual circuit formulation exists if magnetic sources instead of electrical sources are considered. In the dual case, an auxiliary electric potential would be used instead of the magnetic vector potential. To demonstrate the correctness of our formulations, several numerical examples have been shown for the primal circuits involving electric sources only.
The formulation of inhomogeneous Neumann BCs could be a further extension to the presented approach. Furthermore, the method can also be applied to extract circuits from FE models. To account for thermal effects in EM problems, the methods for the extraction of ET and EM circuit stamps can be combined to generate a thermo-EM circuit stamp. Methods to account for nonlinear material characteristics in the EM case are still to be developed. However, in principle one can follow similar ideas to those presented in the ET case. For large field models, the resulting circuit can become very large. Therefore, to efficiently simulate such circuits, dedicated MOR techniques for circuits can be applied. The first of these techniques is known as the asymptotic waveform evaluation (AWE) proposed by Pillage and Rohrer [66] and extensions developed afterwards. The most prominent ones are the matrix Padé via a Lanczos-type process (MPVL) by Feldmann and Freund [67] and the passive reduced-order interconnect macromodeling algorithm (PRIMA) [68]. More recent approaches are based on the proper orthogonal decomposition [69] and other well-known general MOR techniques.
Notes
For a straightforward implementation, we use behavioural sources instead of CCCSs.
Due to the integral term in the expression for
 , a direct translation into VCCSs is not possible. Instead, behavioural sources or CCCSs can be used.
, a direct translation into VCCSs is not possible. Instead, behavioural sources or CCCSs can be used.Note that this is also true for the corresponding continuous operator.
These two properties come from two facts: the squareness is a consequence of removing the row associated with the ground node required in circuit analysis. The invertibility is due to removing the non-null kernel space of the matrix \(\widetilde{\mathbf {C}} \mathbf {M}_{\nu } \mathbf {C} \) by means of the tree-cotree decomposition.
Owing to this property, we identify in the rows of \(\mathbf {E}_{\text {tc}}\in \mathbb {R}^{N_{\text {t}}\times N_{\text {c}}}\) the collection of all fundamental cut-sets associated with the selected tree and cotree. We recall that a fundamental cut-set is a set formed by the union of a single tree edge and the unique set of adjoining cotree edges. In this manner, the fundamental cut-sets are used to express Kirchhoff ’s current law in the general form of (31).
In this regard, the longitudinal (transverse) derivative coincides with the normal (tangent) derivative at the boundary.
Although we restrict ourselves to homogeneous and isotropic media, the analysis can also be extended to more general cases.
This property can be easily visualised if we consider, for a moment, one-dimensional wave propagation along the x-axis. In this circumstance, we have that \(\nabla \equiv \partial _{x}\) and \(e^{\phi \left( x\pm \nu t\right) }\) representing backward and forward travelling waves at speed \(\nu =1/\sqrt{\mu \varepsilon }\) with \(\phi \) an arbitrary function.
All circuit simulations in this paper have been done using LTspice in its version 4.22x with default settings.
We have used the function findpeaks of Matlab\(^{\circledR }\) R2017a to identify the peaks in the plot.
According to image theory, the perfect magnetic wall at port 1 serves as a mirror which reflects uprightly the otherwise backward travelling wave.
Note that in the calculation of \(Z_{0;m}\), the value employed for \(M_{\varepsilon ;x;\tilde{m} m}\) is taken directly from the parallel edge just in front of the boundary edge in accordance with the impinging grid wave front speed.
Confining the excitation to this maximal frequency component, we assure that the TEM mode is the only propagating mode on the line.
References
Yee, Kane S.: Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antenn. Propag. 14(3), 302–307 (1966)
Taflove, A.: Advances in Computational Electrodynamics: The Finite-Difference Time-Domain-Method. Artech House, Dedham, MA (1998)
Weiland, T.: A discretization method for the solution of Maxwell’s equations for six-component fields. AEÜ 31, 116–120 (1977)
van Rienen, U., Weiland, T.: Triangular discretization method for the evaluation of RF-fields in cylindrically symmetric cavities. IEEE Trans. Magn. 21(6), 2317–2320 (1985)
Weiland, T.: Time domain electromagnetic field computation with finite difference methods. Int. J. Numer. Model. Electron. Netw. Dev. Field 9(4), 295–319 (1996)
Bossavit, A.: A rationale for “edge-elements” in 3-D fields computations. IEEE Trans. Magn. 24(1), 74–79 (1988)
Kron, G.: Numerical solution of ordinary and partial differential equations by means of equivalent circuits. JAP 16(3), 172–186 (1945)
Choi, M.J., Hwang, K.-P., Cangellaris, N.: Direct generation of SPICE compatible passive reduced order models of ground/power planes. In: Reynolds, T.G., Slota, P., McShane, M., Howell, W.J. (eds.) Proceedings of the 50th Electronic Components and Technology Conference, pp. 775–780. IEEE (2000)
Moumouni, Y., Baker, R.J.: Concise thermal to electrical parameters extraction of thermoelectric generator for SPICE modeling. In: Chen, T., Baker, R.J. (eds.) IEEE 58th International Midwest Symposium on Circuits and Systems (MWSCAS), pp. 1–4. IEEE (2015)
Codecasa, L., d’Alessandro, V., Magnani, A., Irace, A.: Circuit-based electrothermal simulation of power devices by an ultrafast nonlinear MOR approach. IEEE Trans. Power Electron. 31(8), 5906–5916 (2016)
Eller, M.: A Low-Frequency Stable Maxwell Formulation in Frequency Domain and Industrial Applications. Dissertation, Technische Universität Darmstadt, Darmstadt (2017)
Wittig, T., Munteanu, I., Schuhmann, R., Weiland, T.: Model order reduction and equivalent circuit extraction for FIT discretized electromagnetic systems. Int. J. Numer. Model. Electron. Netw. Dev. Field 15(5–6), 517–533 (2002)
Nagel, L.W., Pederson, D.O.: Simulation program with integrated circuit emphasis. Technical Report UCB/ERL M382, EECS Department, University of California, Berkeley (1973)
Vogelsong, R.S., Brzezinski, C.: Extending SPICE for electro-thermal simulation. In: Milano, R., Hartranft, M., Brown, D. (eds.) Proceedings of the IEEE 1989 Custom Integrated Circuits Conference, pp. 21.4/1–21.4/4 (1989)
Hefner, A.R., Blackburn, D.L.: Simulating the dynamic electrothermal behavior of power electronic circuits and systems. IEEE Trans. Power Electron. 8(4), 376–385 (1993)
Ho, C.-W., Ruehli, A.E., Brennan, P.A.: The modified nodal approach to network analysis. IEEE Trans. Circ. Syst. 22(6), 504–509 (1975)
Sui, W., Christensen, D.A., Durney, C.H.: Extending the two-dimensional FDTD method to hybrid electromagnetic systems with active and passive lumped elements. IEEE Trans. Microw. Theor. Tech. 40(4), 724–730 (1992)
Tsuei, Y.-S., Cangellaris, A.C., Prince, J.L.: Rigorous electromagnetic modeling of chip-to-package (first-level) interconnections. IEEE Trans. Comp. Hybrids Manuf. Technol. 16(8), 876–883 (1993)
Piket-May, M., Taflove, A., Baron, J.: FD-TD modeling of digital signal propagation in 3-D circuits with passive and active loads. IEEE Trans. Microw. Theor. Tech. 42(8), 1514–1523 (1994)
Thomas, V.A., Jones, M.E., Piket-May, M., Taflove, A., Harrigan, E.: The use of SPICE lumped circuits as sub-grid models for FDTD analysis. IEEE Microw. Guided Wave Lett. 4(5), 141–143 (1994)
Guillouard, K., Wong, M.F., Hanna, V.F., Citerne, J.: A new global finite element analysis of microwave circuits including lumped elements. IEEE Trans. Microw. Theor. Tech. 44(12), 2587–2594 (1996)
Guillouard, K., Wong, M.F., Hanna, V.F., Citerne, J.: A new global time-domain electromagnetic simulator of microwave circuits including lumped elements based on finite-element method. IEEE Trans. Microw. Theor. Tech. 47(10), 2045–2049 (1999)
Kettunen, L.: Fields and circuits in computational electromagnetism. IEEE Trans. Magn. 37(5), 3393–3396 (2001)
Benderskaya, G., De Gersem, H., Weiland, T., Clemens, M.: Transient field-circuit coupled formulation based on the finite integration technique and a mixed circuit formulation. COMPEL 23(4), 968–976 (2004)
Schöps, S., De Gersem, H., Weiland, T.: Winding functions in transient magnetoquasistatic field-circuit coupled simulations. COMPEL 32(6), 2063–2083 (2013)
Schöps, S: Multiscale Modeling and Multirate Time-Integration of Field/Circuit Coupled Problems. Dissertation, Bergische Universität Wuppertal & Katholieke Universiteit Leuven, Düsseldorf. VDI Verlag. Fortschritt-Berichte VDI, Reihe 21 (2011)
Witting, M.: Simulation elektrischer Netzwerke unter Berücksichtigung ihrer elektromagnetischen Umgebung. Dissertation, Technische Universität Darmstadt, Darmstadt (1997)
Ruehli, A.E.: Equivalent circuit models for three-dimensional multiconductor systems. IEEE Trans. Microw. Theor. Tech. 22(3), 216–221 (1974)
Ruehli, A.E., Antonini, G., Jiang, L.: The Partial Element Equivalent Circuit Method for Electro-Magnetic and Circuit Problems. Wiley, Hoboken, NJ (2015)
Milsom, R.F.: Efficient SPICE-compatible electromagnetic model of arbitrarily shaped integrated passive structure. IEEE Trans. Microw. Theor. Tech. 47(7), 1033–1044 (1999)
Antonini, G.: SPICE equivalent circuits of frequency–domain responses. IEEE Trans. EMC 45(3), 502–512 (2003)
Russer, P., Righi, M., Eswarappa, C., Hoefer, W.J.R.: Lumped element equivalent circuit parameter extraction of distributed microwave circuits via TLM simulation. In: IEEE MTT-S International Microwave Symposium Digest, pp. 887–890. IEEE (1994)
Choi, M.J., Cangellaris, A.C.: A quasi three-dimensional distributed electromagnetic model for complex power distribution networks. IEEE Trans. Adv. Packag. 25(1), 28–34 (2002)
Ramachandran, A., Ramachandran, A., Cangellaris, A.C.: SPICE-compatible stamps for semi-discrete approximations of Maxwell’s equations. Int. J. Numer. Model. Electron. Netw. Dev. Field 21(4), 265–277 (2008)
Chvala, A., Donoval, D., Marek, J., Pribytny, P., Molnar, M., Mikolasek, M.: Fast 3-D electrothermal device/circuit simulation of power superjunction MOSFET based on SDevice and HSPICE interaction. IEEE Trans. Electron. Dev. 61(4), 1116–1122 (2014)
Wünsche, S., Clauss, C., Schwarz, P., Winkler, F.: Electro-thermal circuit simulation using simulator coupling. IEEE Trans. Very Large Scale Integr. Syst. 5(3), 277–282 (1997)
van Petegem, W., Geeraerts, B., Sansen, W., Graindourze, B.: Electrothermal simulation and design of integrated circuits. IEEE J. Solid State Circ. 29(2), 143–146 (1994)
Simpson, N., Wrobel, R., Mellor, P.H.: An accurate mesh-based equivalent circuit approach to thermal modeling. IEEE Trans. Magn. 50(2), 269–272 (2014)
Lombardi, L., Raimondo, R., Antonini, G.: Electrothermal formulation of the partial element equivalent circuit method. Int. J. Numer. Model. Electron. Netw. Dev. Field 31(4), e2253 (2018)
Evans, P.L., Castellazzi, A., Johnson, C.M.: Automated fast extraction of compact thermal models for power electronic modules. IEEE Trans. Power Electron. 28(10), 4791–4802 (2013)
Bernardoni, M., Delmonte, N., Chiozzi, D., Cova, P.: Non-linear thermal simulation at system level: compact modelling and experimental validation. Microelectron. Reliab. 80, 223–229 (2018)
Culpo, M., de Falco, C., Denk, G., Voigtmann, S.: Automatic thermal network extraction and multiscale electro-thermal simulation. In: Roos, J., Costa, L.R.J. (eds.) Scientific Computing in Electrical Engineering SCEE 2008, Volume 14 of Mathematics in Industry, pp. 281–288. Springer, Berlin (2010)
Wilkerson, P., Raman, A., Turowski, M.: Fast, automated thermal simulation of three-dimensional integrated circuits. In: Ramakrishna, K. (ed.) The Ninth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, ITHERM’04, vol. 1, pp. 706–713. IEEE (2004)
Karagol, S., Bikdash, M.: Generation of equivalent-circuit models from simulation data of a thermal system. IEEE Trans. Power Electron. 25(4), 820–828 (2010)
Hsu, J.T., Vu-Quoc, L.: A rational formulation of thermal circuit models for electrothermal simulation. I. Finite element method [power electronic systems]. IEEE Trans. Circ. Syst. Fund. Theor. Appl. 43(9), 721–732 (1996)
Casper, T., De Gersem, H., Schöps, S.: Automatic generation of equivalent electrothermal SPICE netlists from 3D electrothermal field models. In: van Driel, W., Rodgers, P. (eds.) 17th International Conference on Thermal, Mechanical and Multi-physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE 2016) (2016)
Engquist, B., Majda, A.: Absorbing boundary conditions for the numerical simulation of waves. Math. Comput. 31(139), 629–651 (1977)
Mur, G.: Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations. IEEE Trans. EMC 4, 377–382 (1981)
Clemens, M., Weiland, T.: Discrete electromagnetism with the finite integration technique. PIER 32, 65–87 (2001)
Krüger, H., Spachmann, H., Weiland, T.: Time domain modeling of gyromagnetic materials using the finite integration technique. IEEE Trans. Magn. 37(5), 3269–3272 (2001)
Casper, T., De Gersem, H., Gillon, R., Götthans, T., Kratochvíl, T., Meuris, P., Schöps, S.: Electrothermal simulation of bonding wire degradation under uncertain geometries. In: Fanucci, L., Teich, J. (eds.) Proceedings of the 2016 Design, Automation & Test in Europe Conference & Exhibition (DATE), pp. 1297–1302. IEEE (2016)
Alotto, P., De Cian, A., Molinari, G.: A time-domain 3-D full-Maxwell solver based on the cell method. IEEE Trans. Magn. 42(4), 799–802 (2006)
Bondeson, A., Rylander, T., Ingelström, P.: Computational Electromagnetics. Texts in Applied Mathematics. Springer, New York (2005)
Günther, M., Feldmann, U., Jan, E., ter Maten, W.: Modelling and Discretization of Circuit Problems, Volume 13 of Handbook of Numerical Analysis. Elsevier, Amsterdam (2005)
Clemens, M., Wilke, M., Benderskaya, G., De Gersem, H., Koch, W., Weiland, T.: Transient electro-quasistatic adaptive simulation schemes. IEEE Trans. Magn. 40(2), 1294–1297 (2004)
Gerstenmaier, Y.C., Kiffe, W., Wachutka, G.: Combination of thermal subsystems modeled by rapid circuit transformation. In: Courtois, B., Rencz, M., Lasance, W., Székely, V. (eds.) 13th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC 2007). IEEE (2007)
Bechtold, T., Rudnyi, E.B., Korvink, J.G.: Fast Simulation of Electro-Thermal MEMS: Efficient Dynamic Compact Models. MEMS and Microtechnology. Springer, Heidelberg (2006)
Wait, J.R.: Letter to the editor: the “magnetic conductivity” and wave propagation. IEEE Trans. EMC 34(2), 139 (1992)
Kharzeev, D.E., Warringa, H.J.: Chiral magnetic conductivity. Phys. Rev. D 80(3), 034028 (2009)
Munteanu, I.: Tree-cotree condensation properties. ICS Newsl. (International Compumag Society) 9, 10–14 (2002)
Balanis, C.A.: Advanced Engineering Electromagnetics. Course Smart Series. Wiley, New York (2012)
Zhukovsky, K.: Solution of some types of differential equations: operational calculus and inverse differential operators. Sci. World J. 2014, 1–8 (2014)
Casper, T., Duque, D., Heinz, V., Moiz, A., De Gersem, H., Schöps, S.: ANTHEM-Automatic Netlist generator for THermo-EM field problems (2018)
Keiter, E.R., Aadithya, K.V., Mei, T., Russo, T.V., Schiek, R.L., Sholander, P.E., Thornquist, H.K., Verley, J.C.: Xyce Parallel Electronic Simulation: User’s Guide, Version 6.10. Technical report sand2018-12373, Sandia National Laboratories, Albuquerque, NM (2018)
Griffiths, D.F.: Introduction to Electrodynamics. Prentice-Hall, Upper Saddle River, NJ (1999)
Pillage, L.T., Rohrer, R.A.: Asymptotic waveform evaluation for timing analysis. IEEE Trans. Comput. Aided Des. Integr. Circ. Syst. 9(4), 352–366 (1990)
Feldmann, P., Freund, R.W.: Reduced-order modeling of large linear subcircuits via a block Lanczos algorithm. In: Preas, B.T., Pennino, T.P., Yoffa, E.J. (eds) Proceedings of the 32nd annual ACM/IEEE Design Automation Conference, pp. 474–479. ACM (1995)
Odabasioglu, A., Celik, M., Pileggi, L.T.: PRIMA: passive reduced-order interconnect macromodeling algorithm. IEEE Trans. Comput. Aided Des. Integr. Circ. Syst. 17(8), 645–654 (1998)
Hinze, M., Kunkel, M., Matthes, U.: POD model order reduction of electrical networks with semiconductors modeled by the transient drift–diffusion equations. In: Günther, M., Bartel, A., Brunk, M., Schöps, S., Striebel, M. (eds.) Progress in Industrial Mathematics at ECMI 2010, Volume 17 of Mathematics in Industry. Springer, Berlin (2012)
Acknowledgements
The authors thank Abdul Moiz and Victoria Heinz for their passionate work on implementing the automated electrothermal netlist generation. The work is supported by the European Union within FP7-ICT-2013 in the context of the Nano-electronic COupled Problems Solutions (nanoCOPS) project (Grant No. 619166), by the Excellence Initiative of the German Federal and State Governments and the Graduate School of Computational Engineering at Technische Universität Darmstadt
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Casper, T., Duque, D., Schöps, S. et al. Automated netlist generation for 3D electrothermal and electromagnetic field problems. J Comput Electron 18, 1306–1332 (2019). https://doi.org/10.1007/s10825-019-01368-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10825-019-01368-6



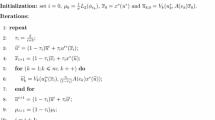





 .
.




 has unit of voltage (V),
has unit of voltage (V), has unit of current (A),
has unit of current (A), has unit of current (A).
has unit of current (A).




 has unit of V and represents the voltage drop along
has unit of V and represents the voltage drop along  has unit of Weber (Wb) and represents the current along
has unit of Weber (Wb) and represents the current along  .
. along
along  along this direction as stated by the grid derivatives in
along this direction as stated by the grid derivatives in 
 . The second one propagates along the y-direction and stems from the spatial variation of
. The second one propagates along the y-direction and stems from the spatial variation of  along this direction as stated by
along this direction as stated by  .
. along
along  along the x-direction as stated by
along the x-direction as stated by  . The second one propagates along the z-direction and stems from the spatial variation of
. The second one propagates along the z-direction and stems from the spatial variation of  along the x-direction as stated by
along the x-direction as stated by  .
.






 and
and  are evaluated at the edges connected to the central grid point
are evaluated at the edges connected to the central grid point


 , a direct translation into VCCSs is not possible. Instead, behavioural sources or CCCSs can be used.
, a direct translation into VCCSs is not possible. Instead, behavioural sources or CCCSs can be used.