Introduction

In many protein engineering applications one seeks to optimize or control the physical chemical properties of a protein under a given set of conditions. For protein therapeutics, often site directed mutagenesis studies are done to find mutants that have similar activity but have enhanced solubility or solution stability. To a crystallographer, creating mutant series can help optimize protein crystallization conditions thereby eliminating conditions or mutations that do not lead to optimal crystal growth. Often this work is carried out empirically and can lead to unexpected results. A more rational approach, however simple, would immensely help guide the researcher toward their goal.

Bioanalytical laboratories routinely quantitate basic parameters such as size, zeta potential, isoelectric point, the second osmotic virial (B 22) and dipole moment. These key parameters aid the understanding of the behavior of colloidal suspensions and proteins. For certain formulations such as injectable drugs one may want to maximize the repulsive forces between particles. This ensures that the suspension does not settle or lead to caking. Alternatively one may want to separate a protein from the mother liquor by minimizing the repulsive forces between particles allowing for efficient flocculation.

The electrostatic properties of a protein play a large role in solution solubility. These properties are governed both by the protein charge distribution and by the nature of the solvent in the formation of the electric double layer. The double layer arises from the presence of surface charges on the protein and its influence on ions at the protein-solvent interface. This results in an increased concentration of ions of opposite charge (counter-ions) near charged surface regions. As one moves further away from the surface, the ion distribution eventually becomes homogeneous as in the bulk solvent. The layer of counter-ions also acts to screen or attenuate surface charges felt further out in solution. Because of these effects, the inner layer of solvent molecules and counter ions surrounding the protein are tightly bound and move in concert. Furthermore there exists an equilibrium distance at which there is a balance between ions that are held by electrostatic forces and those that sheared away due to Brownian motion. This characteristic distance is known as the Debye screening length [1]. This length, κ−1, is typically on the order of tens of Ångstroms and depends on the concentration and properties of dissolved salts in solution. At the Debye length these forces may be quantified as measurable electric potential. Theoretically the zeta potential is the average potential, \( \varphi ({\mathbf{r}}) \) at the solvation boundary. In the laboratory the zeta potential is determined either by optical means [2] or through electrophoretic band velocity measurements. In its simplest form, the zeta potential, ζ, is related to the electrophoretic velocity, U through the following equation:

$$ {\mathbf{U}} = {\frac{\varepsilon \zeta }{\eta }}{\mathbf{E}} $$
(1)

where η is the solution viscosity, ε is the dielectric constant and E is the strength of the applied field. A variety of techniques also exist for estimating ζ from a molecular simulation. Typically these involve the use of the Poisson–Boltzmann (PB) equation [1]. For proteins, boundary integral approaches [3] to solving the PB equation or non-equilibrium molecular dynamics [4] may be used. As practical a rule of thumb, if the measured zeta potential lies within +30 mV to −30 mV this would be indicative of colloidal instability. In this range surface charges on the protein are simply not strong enough for effective protein–protein repulsion.

The second osmotic virial coefficient is also routinely measured electro-optically in the laboratory. This thermodynamic property arises as a higher order term in the equation governing osmotic pressure,

$$ \Uppi = RTc_{P} \left( {{\frac{1}{{M_{W} }}} + B_{22} c_{P} + \ldots } \right) $$
(2)

where Π is the osmotic pressure, c P is the protein concentration, R is the gas constant, T is the absolute temperature and M W is the protein molecular weight. The second virial coefficient B 22 indicates the magnitude and direction of the deviations from solution ideality and may be thought of as the effective volume of the protein. This should not be interpreted as a hard sphere volume but one that is influenced by protein–protein electrostatic interactions. By measuring B 22 at various solution conditions one can gain insight about the underlying effective pair interactions between proteins. A positive value may be interpreted to reflect repulsive interactions whereas a negative value would indicate the presence of attractive forces. Statistical mechanics also provides a mathematical relationship between the B 22 and the potential of mean force, U, in an average solvent environment [5]

$$ B_{22} = {\frac{1}{{2M_{W} \rho V}}}\int\limits_{{\Upomega_{1} }} {\int\limits_{{\Upomega_{2} }} {\int\limits_{0}^{\infty } {(1 - e^{ - U/kT} )r_{12}^{2} dr_{12} } d\Upomega_{1} d\Upomega_{2} } } $$
(3)

where ρ is the density of the protein, V is its volume, k is the Boltzmann constant and r 12 is the intermolecular center-to-center distance. For an isotropic sphere, the integral may be interpreted as a Boltzmann weighted volume. However where there is non-uniform charge distribution, it may be more appropriate to think of this as a Boltzmann average over all protein–protein configurations (Ω1, Ω2). The portion of the integral corresponding to an overlap where U → ∞ leads to the excluded volume contribution of the virial coefficient [6].

When estimating B 22, often an idealized protein geometry is assumed. Protein molecules are typically treated as uniform spheres with a fixed charge. Although these simplistic models can provide some insight, they may not be reliable near the protein’s isoelectric point i.e. when z, the net charge, is zero. If classical DLVO theory [7, 8] were to serve as the electrostatic potential energy function, then the potential U, and thus B 22, would be zero. However if charge anisotropy were taken into account, then configurations that lead to energetically favorable interactions between proteins would bias the Boltzmann weighting term in Eq. 3 toward a negative B 22. This would indicate protein that would have a higher tendency to agglomerate than what would otherwise be predicted by an isotropic model.

A number of years ago it was shown by George and Wilson that there is a strong correlation between the measured B 22 and the range of solution conditions that favor protein crystallization [9, 10]. The crystallization success rate was highest if B 22 falls within a well defined range of −1 × 10−4 to −8 × 10−4 mol mL g−2. If B 22 is too large, crystallization rates are slowed due to the dominating repulsive interactions. Conversely if B 22 is too small, amorphous aggregation can result. It was pointed out that this “crystallization window” corresponds closely to the necessary conditions for the presence of a liquid–liquid immiscibility region in a phase diagram [11, 12]. Further, this region may indicate nucleation via a liquid–liquid phase separation as a first step is a favorable mechanism for crystal growth [12, 13].

Other research efforts have focused on finding a relation between B 22 and protein solubility in aqueous solutions [13–16]. Finding such a trend is not unexpected as both solubility and the second virial coefficient are governed to a large degree by interactions between protein molecules. However the relationship between the two is not trivial as solubility is a function of the protein–protein binding energy at specific orientation in the crystal whereas B 22 is a statistical quantity relating protein–protein interactions in solution over all distance and orientations [13]. The theoretical relation developed by Haas and Wilson has been shown to be in excellent agreement with experimental data for lysozyme and holds over a range solvent pHs, temperature and salt concentrations where the second virial coefficient would be expected to apply [13]. However other studies have shown non-monotonic variation of B 22 with salt concentration [14]. At high salt concentrations, so called “salting-in” and “salting-out” effects are poorly modeled within the standard DLVO or non-linear Poisson Boltzmann framework.

In this study, our goal is to explore the use of calibrative models of protein solubility at a fixed salt concentration. Such models may prove to be of high value to biochemists who seek insight into which point mutations and pH conditions optimize solubility. In this work we use a crystal structure to provide the necessary information about a protein’s three dimensional charge distribution, although a homology model could be used. Additionally we will explore the possibility of employing a modified DVLO theory that can account for non-isotropic charge distribution in a protein. These ideas will be tested on a series of mutants of Ribonuclease Sa, a well characterized protein for which published solubility data exists [17, 18].

Methods

A protein properties calculator has recently been developed in the Molecular Operating Environment (MOE) [19]. This tool allows one to process one or more proteins, create mutations, and compute a series of protein-specific descriptors. The user can specify the working temperature, pH, solvent dielectric and viscosity and the concentration and nature of the dissolved binary salt. A series of 19 descriptors are output. These range from basic size, eccentricity, volume, and surface area descriptors to electrostatic and transport properties. Most of these properties may be quantified in an analytical laboratory using light scattering, ultracentrifugation and electrophoretic techniques. Although all descriptors were computed only the critical ones actually used in the models are discussed in detail below.

Protein preparation and charge model

Prior to computing the protein descriptors, partial charges were first assigned to all atoms using the AMBER 99 forcefield. If one or more point mutations needed to be made, the appropriate residues sidechains were exchanged and minimized keeping atom coordinates of all other residues fixed.

For the purposes of determining the protein’s isoelectric point (pI), routines were used that identify titratable groups within the structure and estimate their pKa values based on the PROPKA method [20]. Given pKa estimates for each titratible residue, the Sillero and Ribeiro method was then used to estimate the pI of the protein [21]. As this pI estimate is based on pKa values determined from local 3D residue geometries, it will be referred to as pI3D. For comparison, estimates of pI were also made using fixed group pKa values. This pI estimate will be referred to as pIseq. The group pKa values used originate from a recent review [22] of 78 folded proteins (His: 6.6, Lys: 10.5, Arg: 12.3, Asp: 3.5, Glu: 4.2, Cys: 6.8, Tyr: 10.3).

Charges on individual residues were set with the use of the Henderson-Hasselbalch equation [23] given their estimated pKa values. This ensured a zero net charge at the isoelectric point and allowed for smooth transitions as the pH is varied. It is recognized that charges set in this manner are only appropriate for relative comparisons of similar proteins and are not suitable for molecular mechanical minimizations.

It should also be noted out that in a study of conformational stability of these same proteins [17], the pH of maximum stability for each protein lies near pH 5. The conformational stability measured as a free energy dropped by approximately 50% from its peak value by either raising or lowering the solution pH by 3 units. In light of this, care must be taken when interpreting the physical significance of the descriptors under conditions that may denature or affect the ionization state of the protein.

Zeta potential estimates

From the Gouy-Chapman-Stern model the ζ potential of a charged particle may be determined by estimating the electrostatic potential at the slipping plane in the diffuse layer. It is recognized that although the position of this plane somewhat dependent on the mathematical model and on particle size [24], in this study we are primarily considered with relative changes in ζ potential. We therefore simply assume that this surface is situated at one Debye length, κ−1 away from the protein. This characteristic distance is typically on the order of tens of Ångstroms and depends on the ionic strength of dissolved salts in solution, the permittivity of free space, ε0, and the dielectric constant εr as well as the absolute temperature, T:

$$ \kappa^{ - 1} = \sqrt {{\frac{{\varepsilon_{0} \varepsilon_{r} kT}}{{2N_{A} e^{2} I}}}} . $$
(4)

The other constants in Eq. 4 are Avogadro’s number, N A, the Boltzmann constant, k, and the charge on the electron, e. Additionally the ionic strength, I, is defined as

$$ I = \frac{1}{2}\sum\limits_{i} {z_{i}^{2} m_{i} } $$
(5)

where m is the mass concentration of the ith ionic species and z its valency. For a protein with an inhomogeneous distribution of charges, the electrostatic potential field, \( \varphi ({\mathbf{r}}) \) was estimated from a numerical solution of the linearized Poisson–Boltzmann equation. In this study the interior and exterior dielectric constants were fixed at 4 and 78 respectively. The Poisson–Boltzmann equation was solved numerically with the multi-grid preconditioned conjugate residual algorithm in MOE on a (129)3 grid. The grid was constructed so that it encompassed the entire protein and extended one Debye length plus and additional buffer in each Cartesian direction away from the protein’s extremities. This ensured a convergent solution over a wide range of solution conditions. The ζ potential was then computed by integrating the potential, \( \varphi ({\mathbf{r}}) \) over the solvation boundary:

$$ \left\langle \zeta \right\rangle = {\frac{1}{{A_{\kappa } }}}\int\limits_{{V_{\kappa } }} {\varphi ({\mathbf{r}})dA} $$
(6)

where V κ defines a set of points encompassing the protein and solvation layer and A κ is its surface area.

Dipole moment

The dipole moment of the protein was computed from Eq. 6 at a given pH-appropriate protonation state:

$$ {\varvec{\upmu}} = 4.802\sum\limits_{i}^{N} {q{}_{i}{\mathbf{r}}_{i} } $$
(7)

where q i is the partial charge of ith atom and r i is the distance in Å from the center of mass. The multiplicative factor was used to convert the dipole moment to units of Debye. AMBER 99 charges calculated in MOE were used as the charge model.

Second virial coefficient, B22

The interaction energies between two proteins were sampled using a 5-axis z-x–z Eulerian gimbal system. This allows one to test any relative configuration. Each protein may be separated by a distance, r 12, rotated by an arbitrary longitudinal and azimuthal angle (α, β for protein 1 and θ, φ for protein 2), and rotated by a relative twist angle, γ). As for the potential model used to compute the interaction energies, a variety of forms are typically used and is still the subject of much discussion [6, 13, 14, 16, 25]. However in a study comparing square-well to Yukawa potentials it was concluded that the relation between the solubility and the second virial coefficient depended very little on the shape of the interaction potential [13]. In light of this, we developed a potential model that was easy to compute using the existing machinery in MOE. Toward this end, the electrostatic component of the interaction energy was computed using the following formula,

$$ U_{el} = {\frac{{e^{2} }}{{4\pi \varepsilon_{ 0} \varepsilon_{r} }}}\sum\limits_{i} {\sum\limits_{j} {{\frac{{q_{i} q_{j} }}{{r_{ij} }}}} } $$
(8)

where i and j are atom indices for proteins 1 and 2 respectively, q is the partial charge on a given atom and r ij is the relative distance between atoms i and j. Unfortunately Eq. 8 does not account for inter-particle charge screening effects due the presence of dissolved salts in the medium. In order to account for this, numerical solutions of the Poisson Boltzmann equation would be normally be required for all configurations. However such an approach would simply be too time prohibitive. There exists however a linearized solution to the Poisson Boltzmann equation for two spheres of radius α with uniform surface change z 0 placed in a dielectric medium separated by a distance r 12. This approximation is the framework of Derjaguin, Landau, Verwey and Overbeek (DLVO) theory [7, 8]. The electrostatic component of this classical theory is,

$$ U_{\text{DLVO}} (r_{12} ) = {\frac{{(z_{0} e)^{2} }}{{4\pi \varepsilon_{0} \varepsilon_{r} }}}\,{\frac{{{ \exp }(2\kappa \alpha )}}{{(1 + \kappa \alpha )^{2} }}}\,{\frac{{{ \exp }( - \kappa r_{12} )}}{{r_{12} }}} . $$
(9)

If a system of two particles both having a charge z 0 are considered, then by inspection it may be seen that Eq. 9 closely resembles Eq. 8 multiplied by a scaling factor that accounts for dielectric screening. For large separation distances, r 12, Eq. 8 may be modified to:

$$ U(r_{12} ) \approx {\frac{{e^{2} }}{{4\pi \varepsilon_{0} \varepsilon_{r} }}}\,{\frac{{{ \exp }(2\kappa \alpha )\;{ \exp }( - \kappa r_{12} )}}{{(1 + \kappa \alpha )^{2} }}}\sum\limits_{i} {\sum\limits_{j} {{\frac{{q_{i} q_{j} }}{{r_{ij} }}}} } $$
(10)

This approximation will serve as the electrostatic model. For small distances (r 12 ≤ α) inside the exclusion volume, a hard sphere potential will be used.

Additionally there exists several forms of the multiplicative constant outside of the configuration integral in Eq. 3 [6, 13, 14]. In general this factor depends on protein molecular weight, density and volume and a normalization constant. Since we will employ a calibrative approach to estimating the solubility from B 22, we are less concerned this factor and allow it to be a free parameter, a, in our model. We leave the divisor 2M WρV in place to account for the units and to ensure proper scaling. The Boltzmann volumetric weighting factor in Eq. 3 also presents a challenge when one encounters either a very favorable (quasi-docked) protein–protein configuration or a low energy sample not in the training set. Because of this we employ a modified potential \( b\left[ {U\left( r \right) - c\left\langle {U_{0} } \right\rangle } \right] \, \) where \( \left\langle {U_{0} } \right\rangle \) is an estimate of the average minimum interaction energy over all samples under consideration and b and c are free scaling factors. The minimum interaction energy \( \left\langle {U_{0} } \right\rangle \) is needed especially when dealing with protein solutions that are not infinitely dilute or when solving Eq. 3 numerically. At a typical working protein concentrations for crystallization (~15 mg mL−1), the average maximum protein–protein separation distance is on the order of 115 Å and gives a rough indication of the required upper limit of integration along r 12. Although interaction energies beyond this point may be non-zero, they will not contribute significantly to the Boltzmann average. We therefore choose \( c\left\langle {U_{0} } \right\rangle \) as our reference point. For our modified potential, the scaling factors b and c can be seen to account for discrepancies between the theoretical and actual exclusion volume, solution conditions and choice of energy scale. The functional form of B 22 becomes:

$$ B_{22} = {\frac{a}{{2M_{W} \rho V}}}\int\limits_{{\Upomega_{1} }} {\int\limits_{{\Upomega_{2} }} {\int\limits_{0}^{\infty } {(1 - e^{{ - b(U - cU_{0} )/kT}} )r_{12}^{2} dr_{12} } d\Upomega_{1} d\Upomega_{2} } } . $$
(11)

Continuing toward our ultimate goal of relating the second virial to solubility a survey of the literature has revealed a few thermodynamical and empirical forms [13, 15, 16]. An equation developed by Haas et al. provides us with a mathematically stable functional form for the fitting procedure [12]. Writing the solubility in terms of B 22 we use the following equation:

$$ S = 55.55\,M_{W} \left( {{\frac{{1 - \rho M_{W} B_{22} /4}}{d}} + 1} \right)^{ - N/2} $$
(12)

where d is a parameter which depends on the anisotropy, N is the coordination number and S is the solubility in mg mL−1. Typically N is between 3 and 6 and d is on the order of 0.001. The coordination number is reported to be related to be number of nearest neighbor protein molecules in the crystal.

Finally given a set of experimental solubilities, conditions and a crystal structure for the training compounds, and an estimate of \( \left\langle {U_{0} } \right\rangle \), we fit the optimal parameters in Eqs. 11 and 12 that minimize \( ({ \log }\,S - { \log }\,\hat{S})^{2} \) where \( \hat{S} \) is the estimated solubility. Non-linear optimization functions in MOE based on the steepest decent method were used to perform the fitting.

Reduced protein representation

With a fully atomistic representation of the protein, the time required to evaluate a large number interaction energies makes the above computation of B 22 impractical. Although there are many ways to reduce computation times, a convenient solution was found by replacing the atoms of each amino acid residue with two that preserve the net residue charge and the residue dipole moment. In this reduced representation, two “atoms” were placed at the centers of negative and positive charge respectively. The radius α, of this reduced representation was taken to be that of a sphere that minimally encompassed the reduced set of atoms plus a small buffer. With this approach, the protein’s net charge and higher moments are retained. Additionally the potential energy machinery in MOE could be employed without modification.

Modeling

The crystal structure of Ribonuclease Sa (PDB code: 1RGG) was submitted to the protein properties calculator. Descriptors were computed at the pH values shown in Fig. 1 for the wild type, 3K (D17K + E41K + D1K), and 5K (D17K + E41K + D1K + D25K + E74K) mutants. The dielectric medium was specified to be a 10 mM NaCl solution at 298 K. The solvent viscosity was set to that of water, 0.89 cP. For the intermediate calculations required to estimate B 22, a total of 351,000 protein–protein configurations were sampled. This is comprised of 26 separation distances from 0 to 104 Å, and 30 evenly sampled sets of azimuthal and longitudinal angles for each protein and 15 twist angles. A total computation time of 14 h was required for the 24 samples on a 1.8 GHz Intel dual core system.

Fig. 1
figure 1

Measured solubilities as a function of pH for RNase Sa (circles), 3K (squares) and 5K variants (triangles). The lines are meant as a guide only. This figure is reconstructed from Ref. [13]

Full size image

After the descriptor calculation was complete, a fitting procedure using experimental solubilities from the training set allowed for the completion of the descriptor table with estimates of B 22 and log \( \hat{S} \) for all samples. For these calculations, we assumed a density of 1.36 g cm−3 for the protein.

Additional pI values were estimated for the 2K (D17K + E41K) and 4K (D17K + E41K + D1K + D25K) variants for comparison with experimental values.

Results and discussion

A set of protein descriptors was computed using the protein properties calculator for Ribonuclease Sa and four lysine mutants at solution pHs where published pI and solubility data exists [17]. The wild type protein contains 96 residues, has a pI of 3.5 and contains no Lys residues. A set of variants was created by replacing highly exposed surface Asp and Glu residues with Lys. This is of interest given that the natural substrate for the ribonucleases is negatively charged, the net charge on the enzyme might influence its steady-state kinetics [17]. As shown in Table 1, the isoelectric points for the 2K, 3K, 4K and 5K variants show an increasing shift toward higher pH. The estimated isoelectric points, pIseq and pI3D, are based respectively on fixed group pKas and those determined from local 3D residue geometries. With this small sample, the average error between the estimated and experimental values is 0.66 pH units for pIseq and 0.45 pH units for pI3D. In this set, the pI estimate of the 5K variant appears to have the largest error of approximately 1 pH unit. This may be due to the fact that RNase Sa has eight Tyr that are largely buried having experimental pKa values greater than 11. This is much higher than the pKa of 10 that is assumed in the calculation of pIseq. However with most theoretical determinations of pI, is it a given that the results are accurate to within ±1 pH unit of the experimental value [17, 26]. Although these estimates based on pI3D look very encouraging for this set, we have not yet performed any larger scale studies validating the method and have used these estimates simply to set the point of zero change for charge based descriptors.

Table 1 Isoelectric points of RNase Sa and the 2K, 3K, 4K and 5K variants
Full size table

The protein properties calculator also returns pKa estimates of the individual ionizable amino acids given their relative 3D environment in a protein using the PROKPA method. Estimates for RNase Sa and its 5K variant are listed in Table 2 along with of their respective measured values [27]. For this system the pKas may be estimated to within ± 1 pH unit of the measured value. It is interesting to note that that the pKa estimates for each ionizable group are almost identical between the wild type and the modeled 5K variant. Only the pKa of Glu78 was found to decrease by 0.1 pH unit. However a different picture emerged when the group pKa estimates were made on the known crystal structure of the 5K variant (PDB code 3A5E). In this case the estimated pKas of eight residues were different.

Table 2 pKa values for RNase Sa and its 5K mutant
Full size table

In order to understand the difference between these modeled 5K variant and its known crystal structure, two types of alignments were performed. The first was an alignment on the backbone alpha carbons. Since there was only a the 0.37 Å RMSD between the two structures, it may be concluded that the surface mutations do not influence the overall protein structure. When the second alignment was done using the heavy atoms of the five lysine sidechains, the RMSD was found to be 1.9 Å. Given that the level of variation, the scoring function employed in PROPKA used to shift the pKa from its baseline value seems quite sensitive to sidechain configuration. This scoring function attempts to account for desolvation, hydrogen bonding and buried charge–charge interactions [20]. Since there is such a difference in the predicted shift in pKa between the modeled 5K mutant and the known crystal structure, this would indicate that the surface lysines in the model are not forming as many hydrogen bonds with nearby residues. This is in fact observed by inspection. In light of this result, it may be better to first perform a short molecular dynamics run on the sidechain atoms in order to generate an ensemble of conformers then compute a Boltzmann-weighted average of the predicted group pKas. The only drawback to this approach is the lengthy computation time.

Solubility modeling with simple electrostatic descriptors

For an initial model, data from the wild type and 3K variant served as the training set. The remainder from the 5K variant served as the test set used for model assessment. This calibration set was chosen to cover the entire dynamic range of solubilities. An initial study was done to determine which of the 19 descriptors were correlated with the experimentally available solubility values in the training set. For the charge based descriptors z (net charge) and ζ (zeta potential), their square values were used. This was done because, to a first approximation, the solubility of a protein is known to be proportional to the square of the net change on the protein [28]. The characteristic parabolic shape shown in the solubility profiles in Fig. 1 clearly demonstrates this trend: proteins are usually least soluble near their isoelectric points and their solubility increases when either the pH is raised or lowered. Furthermore the descriptor values were autoscaled to avoid biasing and the log of the solubility (log S) was used throughout.

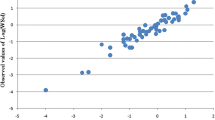
Working with the 17 data points in the training set, a stepwise multi-linear regression procedure was used for variable selection [29]. With this procedure candidate variables are included in the model one by one. This process continues until successive models are deemed not to be statistically by means of an F-test at the 95% confidence level. Using this method it was found that ζ 2 and μ (dipole moment) were most correlated to log S. It is interesting to note that although z 2 is also correlated to log S (r 2 = 0.77), it was not selected with the stepwise procedure given that ζ 2 is slightly more correlated (r 2 = 0.83). It was also found that after removing two of the 3K samples (at pH 5.4 and 5.7) the standard error of prediction for the training set decreased significantly from 0.24 to 0.15. We therefore constructed our models without them. This leads to a simple relation which will be referred to a Model 1: log S = 2.50 + 0.00274ζ 2 − 0.00266μ (r 2 = 0.968, R 2 = 0.937). As shown in Fig. 2, a plot of experimental log S versus estimated log S for the calibration set demonstrates that the residues are homoscedastically distributed about the line of identity.

Fig. 2
figure 2

Plot of the measured versus estimated log S on the training set. A line of identity is plotted along the diagonal

Full size image

A more informative view of the results demonstrating the accuracy of the model is shown in Fig. 3. Here the estimated and experimental solubilities are plotted as a function of pH. The standard error of prediction on the test set (seven 5K samples) was 0.393. Results indicate that the model reproduces the characteristic parabolic trend in solubility about the pI in the wild type and shows a minimum point with the 3K and 5K variants. The model also reproduces the non-linear progression in solubility as the number of positively charged Lys groups is increased. However the point of minimum solubility for the 3K variant predicted by the model is shifted 0.5 pH units lower than what appears experimentally but remains close to the observed pI. From the reported experimental conditions [17] it should be noted that the buffer composition is varied according to the pH which may lead to some uncertainty as where the true minimum solubility actually lies. The conclusions that may drawn however are clear: the 3K variant is predicted to be less soluble than the wild type and the 5K slightly more soluble that the wild type at their respective isoelectric points. In spite of these results there exists a fundamental problem as the chemist would need training data that is likely to cover the full dynamic range of solubilities ensuring the model be used in an interpolative manner. This calibrative procedure has little utility since the chemist might only have solubility data of the wild type and wants to know in advance if it is worth expressing and testing a given mutant!

Fig. 3
figure 3

Plot of the measured and estimated log S as a function of pH. Estimated values were determined from Model 1. Training data from the wild type and 3K variant is shown as crosses. Experimental solubilities in the test set (5K variant) are shown as triangles. Estimated values are shown with lines

Full size image

A more realistic approach to solubility modeling would be to train the model using data from a single protein and employ it in an extrapolative sense to estimate solubilities of similar proteins at a desired pH. Toward this goal, the above process was repeated using five calibration points from the wild type. A two parameter model based on ζ 2 and μ lead to the following regression equation (Model 2): log S = 2.68 + 0.00246ζ 2 − 0.002805μ (r 2 = 0.9985, R 2 = 0.9971, SEP = 0.33). The solubilities of the wild type are estimated very well as is shown in Fig. 4, however for the 3K and 5K variants, only the broad trends are captured. It is interesting to note that even with much fewer training points, the calibration coefficients for Model 1 and Model 2 are similar. This type of model is more error prone but more realistic in how it would be used. In this case, the chemist would get a semi-quantitative picture that around their respective isoelectric points, the 3K is less soluble than the wild type and the 5K is slightly more soluble.

Fig. 4
figure 4

Plot of the measured and estimated log S as a function of pH. Estimated values were determined from Model 2. Training set data is shown as crosses. Experimental solubilities belonging to the test set are shown as either circles (wild type), squares (3K variant) or triangles (5K variant). Estimated values are shown with lines

Full size image

Physical interpretation of solubility models based on simple electrostatic descriptors

Plots of the estimated zeta potential and dipole moments as a function of pH are shown in Figs. 5 and 6 respectively. The zeta potential plot is a type protein titration curve with ζ playing the role of an indicator. This may be used to approximate the isoelectric point (pI)—the point where the electrophoretic mobility is zero. If the protein were an isotropic charged sphere of radius a, then at the pI both the net charge and ζ would be zero. This condition arises naturally from the solution of the Poisson Boltzmann equation for an isotropic sphere as \( z = 4\pi \varepsilon_{0} a(1 + \kappa a)\zeta /e \). If this relation holds more generally, then one can make comparisons between protein solutions over a range of pHs at same ionic strength. With this in mind, it may be seen from Fig. 5 that pI of the mutant series generally increases with the number of Lys groups. Additionally, the slopes of the linear regions near the pI for the wild type and 3K variants protein give an indication of the steepness of their corresponding parabolic shaped solubility curves in Fig. 1. This is because the protein’s relative solubility is typically proportional to square of the net charge. However for the 5K variant, at 2 pH units lower than the pI there is a gradual download slope in ζ whereas the wlope is more pronounced at 2 pH units higher than the pI. In this case one would expect a non-symmetric trend in solubility about the pI which is indeed observed.

Fig. 5
figure 5

Plot of the estimated zeta potential as a function of pH for the wild type, 3K and 5K variants

Full size image
Fig. 6
figure 6

Plot of the estimated dipole moment as a function of pH for the wild type, 3K and 5K variants

Full size image

A plot of the estimated protein dipole moments as a function of pH shown in Fig. 6 demonstrates a different set of trends. In this case the curve shapes of the wild type and variants are similar but the magnitude of the dipole moment mirrors the trend in solubility at their respective pIs. It should be mentioned that since we are concerned with relative changes in dipole moment for a mutant ladder series, the use AMBER 99 charges is sufficient. For absolute measures of dipole moment other charge models may be more appropriate [30]. Generally a larger dipole moment represents greater separation of charge resulting in a more polarized system. This may lead to increased protein–protein interactions by attraction of oppositely charged regions. When this occurs solubility may decrease due to flocculation.

Solubility modeling with the second osmotic virial

A solubility model based on the expression for the second osmotic virial (Eq. 11) together with a functional form relating it to solubility (Eq. 12) was also developed. A reduced protein configuration was used in the sampling 351,000 interaction energies needed for the configurational integral at the heart of the B 22 estimate.

Model training was also made using samples from the wild type. One of the issues encountered when allowing each parameter a, b, c, d and N to vary is that more training data was required. Even using all available samples, it was found that the d and N parameters were too interdependent to allow for rapid convergence. In studies with lysozyme, it is reported [13] that a good fit between experimental data and Eq. 12 was obtained for d = 0.01 and N = 4. In the absence of any a priori B 22 data to suggest otherwise, we held d and N fixed at these values. Therefore Eq. 12 simply serves as a generic mapping function relating B 22 to the solubility. The fitting process was done with the same five calibration points from the wild type as used previously.

The best fit parameters a, b and c values were found to be −0.166, 0.23 and 0.136 respectively and the standard error of prediction was 0.201. The results for Model 3 shown in Fig. 7 demonstrate that the model captures the broad trends in solubility in the test set. The solubilities of the wild type are again determined quite well, and the overall trends in solubility for the 3K and 5K are as good as those predicted in Model 2. Using the best fit a, b and c values, one may estimate which proteins/conditions fall into crystallization window i.e. the range where B 22 is between −1 × 10−4 and −8 × 10−4 mol mL g−2. It is recognized however that since we employed a fixed, generic mapping function relating B 22 to the solubility, the corresponding “solubility window” is rather approximate. The use of experimental B 22 data however may be used to set more appropriate values for d and N. The solubility window shown in Fig. 7 suggests that the wild type and 5K variants might have a greatest chance of being crystallized at ±1 pH units on either side of their respective isoelectric points. However the 3K variant appears to be too insoluble under the current solution conditions.

Fig. 7
figure 7

Plot of the measured and estimated log S as a function of pH. Estimated values were determined from Model 3. Training set data is shown as crosses. Experimental solubilities belonging to the test set are shown as either circles (wild type), squares (3K variant) or triangles (5K variant). Estimated values are shown with lines

Full size image

Additionally, preliminary tests were performed by allowing d vary between 0.01 and 0.035 and N from 3 to 4. As no significant change in the error of prediction was found in this range, the values of the fitting parameters a, b and c adjusted to compensate for imprecise knowledge of d and N. This indicates that one might not need to explicitly include d and N in the fitting procedure as they are relatively insensitive. From a practical standpoint this may be advantageous as fewer calibration samples would be required leaving only the need to pick from amongst a small set of pre-determined generic mapping functions that best suits a given protein family.

Conclusions

In this study we have developed simple calibrative approaches to estimating protein solubility as a function of pH using a set of descriptors calculated from its 3D structure. The models are purely electrostatics-based and other factors that may affect solubility such as hydrophobic interactions and salting out at high salt concentration are not accounted for. However even with this limitation, solubility models may be still be constructed when estimates for a mutant series are sought. A solubility model of Ribonuclease Sa based on zeta potential and dipole moment trained on wild type data only demonstrate this. Additionally the approach allows one to rationalize solubility trends. Another solubility model based on the second virial coefficient also provides information of interest to crystallographers who wish to determine whether a given mutant may likely have a chance of being crystallized. These results are encouraging given that the models are extrapolative, based on a range of different theories and trained on experimental data that is not highly accurate by its nature. The protein descriptors employed in this work may be computed very efficiently and can provide the analyst with estimates of critical parameters that take much longer to determine experimentally. In the future we wish to extent the methods to non-globular proteins and investigate the effect of amino acid side chain conformation on model stability.