Abstract
The recent literature is replete with papers evaluating computational tools (often those operating on 3D structures) for their performance in a certain set of tasks. Most commonly these papers compare a number of docking tools for their performance in cognate re-docking (pose prediction) and/or virtual screening. Related papers have been published on ligand-based tools: pose prediction by conformer generators and virtual screening using a variety of ligand-based approaches. The reliability of these comparisons is critically affected by a number of factors usually ignored by the authors, including bias in the datasets used in virtual screening, the metrics used to assess performance in virtual screening and pose prediction and errors in crystal structures used.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Based on the large number of papers recently published, it has become obvious that a large proportion of the computational chemistry community, both in academia and in industry, is very interested in evaluating and comparing software for a number of different purposes. A large number of publications have appeared over the last 5 years or so that are focused on the evaluation of docking tools for pose prediction [1], virtual screening [2] and affinity prediction [3]. There have also been a number of recent publications examining the performance of ligand-based tools in similar tasks. The ligand-based tools have also been evaluated in the areas of pose reproduction (by conformer generators [4–6]), virtual screening [7] and affinity prediction [8]. In the following sections some issues with studies on pose prediction and virtual screening will be discussed.
Pose prediction
A common method of evaluating a docking program is to gauge its performance in cognate re-docking or self-docking. In this process a ligand is extracted from a co-crystal structure with its target protein and the program is challenged to pose the ligand as closely as possible to its experimentally identified structure. It may be argued that cognate re-docking is not a task commonly faced in the normal use of docking tools, since cross-docking (docking of a ligand into a structure with which it was not crystallised) is the actual application of a docking tool [9]. However, the exercise remains popular, doubtless in part due to the relative ease of execution of a self-docking study and partly for comparison with previous studies. As has been pointed out previously [10], comparing docking programs for their ability to predict the bioactive pose of a ligand is difficult for a number of reasons, some of which are obvious while others are subtler. However, the operational difficulties in comparing programs in a robust way should not cause other sources of error to be ignored. It is a truism that it is meaningless to compute a property with greater precision than the accuracy of the experiment that measures that property. Unfortunately, as will be seen in subsequent sections, this is often ignored by authors of papers in the area of pose prediction.
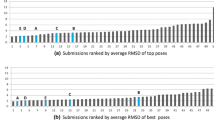
When comparing tools for pose prediction, the heavy atom root mean square deviation (RMSD) between the computed and experimental poses is the de facto standard. A regrettably common method to compare docking tools for pose prediction success––illustrated, for example, in the papers presenting results from the MolDock program [11] or the Glide XP evaluation [8]––is to compare the average RMSDs across a set of structures. The use of the average RMSD admits of many possible problems of interpretation, not least of which is the biasing of the average by a few very large or very small numbers. In the case of the MolDock results, the mean RMSD across a set of structures was used to suggest that the performance of MolDock was comparable to that of GLIDE and superior to that of Surflex (see Table 1). However, the use of the median RMSD, which is far less biased by a few extrema, suggests a different conclusion—that MolDock is in fact somewhat superior to Surflex, but not as good as GLIDE. For a similar analysis on the drawbacks of using average RMSD as a comparator, see Cole et al. [10]. A number that is noticeably absent from this, and all other comparisons of docking tools using RMSD, is an error bar on the average RMSD (which can be calculated by bootstrapping). Without such an error bar it is impossible to assert that any tool compared in this study is actually better than any other.
A separate issue with these two experiments involves contamination of the dataset used to evaluate the performance of the tools. In the case of the Glide results the RMSD’s given are not to the deposited crystallographic pose but rather to one that results from a pre-processing step, as noted by the authors of the MolDock paper [11]. As such this is not an “apples to apples” comparison, since the Glide pre-processing step optimizes protein and ligand coordinates using the force-field component of the Glide scoring function, which necessarily introduces bias in the structure. In the MolDock case the authors have essentially trained the MolDock fitness function on the 77 complexes that they use to evaluate its performance. As such the reported results give no indication of the likelihood of success in predicting a pose for a system upon which MolDock was not trained.
The RMSD between two poses is a geometric measure, comparing the atomic positions between the experimental structure and the docked or predicted structure. Other metrics based on comparing the geometry of the experimental and the computed pose have been developed, such as relative displacement error (RDE) [12]. These, and all other atom-based metrics, suffer from the drawbacks pointed out by Cole et al. [10]. A more serious problem for metrics like RMSD and RDE is that they attempt to indicate the quality of reproduction of a model for the data, not the crystallographic data itself, i.e., the electron density. This disconnection between RMSD as a metric of quality for pose prediction and the original crystallographic data has been a cause for concern. Some attempts have been made to arrive at metrics that better reflect the reproduction of the actual crystallographic data, in particular real-space refinement (RSR) [13]. Unfortunately, RSR has not been widely used, possibly because it is more difficult to calculate than atom-based metrics like RMSD or RDE. Other metrics that are not based purely on atom position, such as interaction-based accuracy classification (IBAC) [14], try to reflect the ultimate use of the predicted pose, i.e., determining the nature of the interactions that the ligand makes with the protein. While the IBAC approach has value in that it assesses a computed pose by its interactions with the protein, it is not amenable to automation; it is therefore tedious to assemble sufficient data to make statistically robust comparisons between tools based on IBAC.
However, the problem of choosing which metric to use to compare pose prediction studies is dwarfed by the difficulty in choosing a dataset of protein–ligand co-complexes upon which to perform the comparison. A widespread tendency in conformer reproduction and pose prediction studies is to ignore even the possibility of error in the crystal structures that are being reproduced. Crystal structures are often treated as perfect, infinitely precise and accurate representations of the atomic details of a protein–ligand complex. There are a number of reasons why this is not so; a few will be discussed in the following paragraphs.
Crystal structures are models
This statement makes up the warp and weft of crystallography, yet in the transition of crystallographic data from crystallographer to computational chemist the distinction between the actual data and a model for that data is often lost. The actual data in crystallography is, of course, diffraction data leading to electron density. The atom positions that make up a crystal structure are a model that attempts to explain this data in as complete a fashion as possible. This is illustrated in Fig. 1.
The process of fitting or modeling the atoms (of a ligand or of a protein) into the electron density is not always straightforward, and the problems are often more serious when the fitting of a ligand into density is being carried out. The sources of these problems include:
-
(i)
Incomplete or fragmentary density;
-
(ii)
The electron density not defining the positions of all atoms unambiguously;
-
(iii)
Poor structural parameters are used for the fitting process, which can give inappropriate conformations (particularly of ligands);
-
(iv)
Errors by the users, arising from careless treatment of the data or lack of expertise with small molecules.
A variety of metrics can be calculated for a given crystal structure that attempts to give an indication of the quality of the model. While no single number can encompass the quality of a structure, some of the metrics of quality are more useful than others. The most commonly used is the nominal resolution. This is a measure only of the quantity (of data collected) and not of the quality of the data nor, most especially, of the quality of the model fitted to that data. (For a discussion on the problems with resolution, see Ref. [15]) It is therefore unfortunate that nominal resolution is often the only criterion used to select a protein structure, and that its meaning is often misconstrued. For example, in a paper [16] by Nissink et al. the following incorrect statement is made: “The resolution of a protein structure is directly related to the accuracy of the data.” Not only is this statement not entirely true, it also confuses what the nominal resolution means (quantity of data collected) with the accuracy of a model, which are two very different things. A metric that does attempt to assess the quality of the fit of the crystallographic model to the source data is the so-called R free, introduced by Brunger [17]. R free is an indication of how well an atomic model explains a small percentage of the density data that was omitted during the fitting process, and is thus an unbiased metric that can be reliably used to distinguish a well fitted model from a poorly fitted model. Unfortunately, R free is infrequently used as a metric of quality when selecting crystal structures for docking studies or other purposes (see Ref. [18] for the use of R free as a criterion for selection of structures). More frequent use of R free as one of a set of metrics for selection of crystal structures could help to avoid the selection of poorly fitted models for pose reproduction.
Crystal structures have unavoidable imprecision
As already discussed, nominal resolution is not a metric of quality for a structure and although R free indicates the quality of the fit of the model to the original data it can provide no estimate of the uncertainty in the atomic positions within that model. It is often assumed that the experimental uncertainty in the atomic positions in a crystallographic model can be estimated by use of the isotropic B-factor, which is supposedly a measure of the thermally driven fluctuation in atomic positions. However B-factors are a refined parameter and so they cannot be compared between structures without detailed knowledge of the restraints used [19]. It is therefore impermissible to use low B-factors as a sure indication of low positional uncertainty. Nor is it possible that there exists a uniform cut-off for B-factors that indicates low positional uncertainty in all structures, though such an assumption is frequently made [20]. Another potential problem with B-factors is that they can be over-refined in the pursuit of better quality metrics for a structure. An example is given in Fig. 2, which shows the ligand (leucinol) from the structure 5ER1 from the RCSB [21] annotated with its B-factors. The B-factors for every atom in the ligand are <1. In contrast, B-factors even for well-located atoms in high quality models, are generally not <5 [22]. In this instance the crystallographer has over-refined the B-factors of the ligand atoms in order to improve the quality of the overall model. In this model the B-factors are unphysically low only as a consequence of a pathology of the refinement process. Accordingly, B-factors as an indication of local mobility in a protein structure should be treated with caution, as they are not simply an experimentally derived quantity but are free parameters in the refinement process.
An alternative to using the average B-factor for estimating the uncertainty of the position of atoms an atom in a structure is the average coordinate precision (or diffraction-component precision index, DPI). The DPI expresses the average precision for the atomic coordinates in a protein structure [23] and as such can be used as a measure of the experimental precision of the atomic positions in that structure. The original formulation of DPI was very complex and has recently been recast in a more easily calculable way by Blow [24]. The use of DPI as a metric of quality for crystal structures used for docking studies was introduced to the computational community by Goto et al. [18], and their formula is given in Eq. 1 Footnote 1.
In this treatment the standard error of position, σ(r), is related to the number of atoms in the unit cell, N atoms, the volume of the unit cell, V a, the number of crystallographic observations, n obs and the R free. It should be noted that the formula presented by Goto et al. is not precisely the same formula that Blow derives in his paper. In Eq. 1 the prefactor is given as 2.2, while in the original work by Blow the prefactor is given as 1.28. This is because Blow is calculating coordinate error for a particular axis, σ(x, y, or z), while Goto et al. are calculating the error in the distance, σ(r), giving rise to the √3 difference between the two prefactors. As such it is appropriate to consider the error in the coordinates, σ(x, y, z) as a measure of the uncertainty in the atomic positions, and the error in inter-atomic distances, σ(r), when comparing a computed and an experimental structure.
The resolution of a crystallographic model, as has been mentioned, is often used to select protein structures for pose prediction by docking or conformer generation studies, on the assumption that resolution imparts some information on the quality and precision of the model. The DPI is a much more direct estimate of the reliability of crystallographic models when it comes to comparing experimental and computed atom positions (as is done in conformer reproduction or pose prediction). It is therefore of interest to compare the nominal resolution for a large number of “good quality” crystal structures with the DPI (σ(r)) for the same structures. A good dataset for this comparison is provided by the extensive investigations performed by Kirchmair et al. [4]. Here 776 co-crystal structures were used to provide experimental ligand structures that were then compared to sets of computed conformations from conformer generation applications. For 556 of these crystal structures there exists sufficient data to allow the DPI to be calculated and the relationship between the nominal resolution for these structures and their DPI is shown in Fig. 3. It is obvious from Fig. 3 that the statement by Kirchmair that “0.5 Å approximately represents the accuracy of protein X-ray crystallography” is not supported by the actual properties of the crystal structures they studied. In fact, in those cases where the DPI can be calculated, almost 56% of the structures from their paper have DPIs > 0.5 Å.
Coordinate error for 556 structures from the paper by Kirchmair et al. [4]
Figure 3 illustrates a number of other interesting points. While the expectation that greater coordinate precision will arise from structures with better nominal resolution is generally borne out by the data, there are many exceptions. Table 2 shows some examples of structures where the nominal resolution gives an unexpected estimation of coordinate precision. In the top half of the table are structures with good nominal resolution but unexpectedly high DPI, while the lower half of the table shows some structures with low nominal resolution and either unexpectedly low or unexpectedly high DPIs. Accordingly, simply using nominal resolution as a metric of quality for structures to be used in a pose prediction or conformer generation study is insufficient to guarantee that structures of appropriate quality will be used.
With the DPI for a structure in hand one can set a lower limit on the precision with which a computed conformation can reproduce an experimental one—the RMSD between the two conformations cannot be less than the DPI for the experimental structure. It can be seen that over half (55.6%) of the structures in this set has DPIs > 0.5 Å, while Kirchmair et al. report pose reproduction statistics both at <0.1 Å and at <0.5 Å RMSD. Since in over half of the structures in this dataset the DPI is >0.5 Å, Kirchmair et al. report pose reproductions at <0.5 Å RMSD that are more precise than the accuracy of the source data allows. This analysis is made on the conservative assumption that the error in the atomic positions in the computed pose is zero. In the Goto et al. paper [18] the assumption is made that the errors in the computed pose are the same as for the experimental pose. In this analysis a computed and experimental pose must be different by an RMSD of √2 × DPI for the difference to be significant, which would mean that an even higher proportion of the poses in the Kirchmair set have been reproduced with a greater precision than the experimental accuracy.
The same tendency to reproduce experimental data with a precision greater than the experimental accuracy is seen frequently in pose prediction experiments with docking engines. In Fig. 4 nominal resolution is plotted against the DPI for crystal structures from two well known docking validation sets, those for GOLD [25] and GLIDE [3]. The two graphs are plotted on the same scale to allow direct comparison. On each graph is also plotted an estimate of the theoretical lower limit for the atomic precision (the pink line). A formula describing the relationship between nominal resolution and DPI is given in Eq. 2 Footnote 2 below, based on a derivation by Blow [24].
The variables found in Eq. 2 are as follows: s is the percent solvent present in the crystal, V m is the asymmetric unit volume to molecular weight ratio, C is the completeness of the data, and d min is the nominal resolution of the structure. The ideal lines shown in Fig. 4 were calculated using Eq. 2 and assuming an s of 0.0, a V m of 2.5, a C of 100%, and that R free is equal to the resolution/10.
Inspection of Fig. 4 shows that the GOLD set contains one structure (1YEE) whose calculated DPI lies below the theoretical lower limit. This is probably due to a mistranscription error in the PDB file. The PDB file for the 1YEE structure gives the number of reflections as 77209, while the number of unique reflections is 21342—a disparity that cannot be reconciled by reference to the data redundancy for this structure. Accordingly the calculated DPI for 1YEE is too low because the reported number of reflections is erroneously high. In the GLIDE set all structures have DPIs higher than our predicted theoretical minimum. In fact, in this set 52% of the structures have a DPI > 0.5 Å, and in 31% of the cases the reported RMSD for redocking is less than the DPI (so that the prediction is more precise than experimental accuracy allows). This is only one example of a publication in which protein structures are assumed to be free of uncertainty in their atomic positions; the literature abounds with others.
The combination of R free and the DPI for a structure can give a good overall picture of the quality of a model and the reliability of the atom positions within that model. In spite of the availability of these and other measures of quality, there are a number of test sets of protein co-crystal structures used for evaluating docking engines that appear to have been selected by other criteria that do not relate in any way to their quality [26]. Accordingly, the results from these studies should be treated with some caution.
Crystal structures have avoidable errors
The R free and the DPI are global measures of quality; other, local, measures of quality are also useful. For example, if a small portion of the atoms in a structure have been poorly fitted to the density, this will not be revealed by any global measure of fit. Only a local measure would reveal the error. A relatively common problem in co-crystal structures in the PDB is poor fitting of small molecules to the density, giving unrealistic ligand structures. These poorly fitted ligand structures are then used as a “standard” to judge the quality of a docking program’s or conformer generator’s performance. While the poor quality of some ligand structures in PDB models has been known for some time [27], these reports have been anecdotal and few systematic attempts to avoid such poorly solved structures (other than visual inspection) appear to have been undertaken. If appropriate attention is not paid to selecting good quality ligand structures, then a dataset could be constructed that contains ligand structures that have significant errors. For pose prediction studies, poorly solved ligand structures in the dataset must be avoided. It is senseless to try to computationally reproduce an “experimental” ligand structure that has been incorrectly fitted to the electron density. Examples of some possible errors in ligand structures that should result in structures that are not computationally reproducible are shown in Figs. 5 and 6.
In the case of the 1A8T structure (Fig. 5), the deposited ligand coordinates contain two serious atom–atom clashes that give the resulting conformation very high energy (28.4 kcal/mol above a refitted structure by the MMFF94 forcefield [28]). The deposited coordinates are clearly in error in this case and no docking engine or conformer generator should be expected to reproduce such a structure.
The error shown in Fig. 6 for the 1A4k structure is of a more subtle nature. Here the crystallographer has fitted a highly strained cis-amide into the electron density with no compelling reason from the electron density to do so. The amide group is packing against a tyrosine residue from a symmetry mate in the unit cell, and makes no polar interaction with it. The corresponding trans-amide, which fits the experimental density just as well, is 15.5 kcal/mol lower in energy (using the MMFF94 force-field). Also this trans amide is able to make a hydrogen bond (with a backbone carbonyl group) that is not available to the cis conformation. Once again, this model should not be reproduced by a docking engine or conformer generator, as it is obviously not the correct solution.
One of the only studies that bears on the issue of ligand strain was published by Perola and Charifson in 2004 [29]. The authors examined ligand strain in a number of public structures from the RCSB database and proprietary structures from Vertex internal collection and found that 10% of the ligand structures examined had high strain (10 kcal/mol or greater above the global minimum). The two examples discussed above, 1A8T and 1A4K, are both part of the Perola dataset. Clearly these two ligand structures have high strain energies due to errors in fitting and not due to a fundamental property of the ligand’s conformation in complex with the protein. Close examination of the rest of the models for the ligands (where structure factors are available) showed that a number of them are incorrect, and re-solving them provided lower energy structures in about 85% of the cases [30]. Recent re-examination of the Perola dataset by the Snyder group has provided further insights into the large strain energies originally reported [31]. It is therefore most likely that the vast majority of ligand conformations in complex with a protein show strain energies less than 6 kcal/mol, unless the ligand is rather large [32]. Those ligand conformations with strain energies higher than 10 kcal/mol are almost certainly incorrect. As such low ligand strain should be among the criteria for selection of structures for pose prediction, as structures with high strain are very likely to arise from errors in the fitting process.
It is clear from the foregoing discussion that, while crystal structures are an invaluable source of information on protein–ligand binding, these structures are not without many sources of confounding errors. These errors, those inherent to the data and the process of fitting, as well as those introduced by human error or the insufficiencies of the fitting program, should be borne in mind before using crystal structure data. The selection of a reliable set of structures for pose prediction is a therefore not a trivial task. An excellent study considering these issues can be found in Hartshorn et al. [33].
Virtual screening
Virtual screening can be defined as any method that ranks a set of compounds by some score. Successful virtual screening relies on having a scoring method that assigns good scores to interesting molecules (usually defined as active against a target protein of interest) and worse scores to uninteresting (inactive) molecules. Accordingly a successful virtual screen will provide, from the top of this ranked list, a set of compounds for experimental screening that is highly enriched in active molecules. This topic has been of great interest both in academia and in the pharmaceutical industry in recent years, and a large number of publications have appeared on the subject. While a few of the publications have investigated virtual screening conducted prospectively [34–36], the vast majority have been concentrated in the area of retrospective virtual screening. In the rest of this article we shall concern ourselves solely with the retrospective experiments. The goal of such experiments is often to identify an application that performs well on a given target, or across a wide range of targets, with a view to utilizing this application in prospective virtual screens.
There are a number of approaches to quantitating the success of a particular tool for virtual screening. The most often used, and simplest to calculate, is enrichment at a given percentage of the database screened. Enrichment (EF) is defined according to Eq. 3 Footnote 3 (Hits x%sampled = number of hits found at x% of the database screened, N x%sampled = number of compounds screened at x% of the database, Hitstotal = number of actives in entire database, Ntotal = number of compounds in entire database).
Enrichment appears to measure the quantity of most interest to those performing virtual screening: the ability of a tool to place a large proportion of the active compounds at the top of the ranked list. Enrichment is also simple to calculate and understand, so it seems the ideal metric with which to compare tools for their virtual screening performance. However, enrichment suffers from a number of significant drawbacks, especially when comparing results between studies or using enrichment to predict future performance:
-
(i)
It is dependent on the structure of the dataset, in that datasets with larger proportions of actives will have a narrower range of possible enrichments.
-
(ii)
It penalizes ranking one active compound above another.
-
(iii)
It exhibits pernicious behaviour at the cut-off at which the enrichment is calculated.
-
(iv)
It gives no weight to where in the ranked list a known active compound appears. Thus to calculate enrichment at 1% in a virtual screen of 10,000 compounds, the number of actives (N) in the top ranked 100 compounds is needed. However the enrichment at 1% is the same whether the N active compounds are ranked at the very top of the list or at the very bottom of the top ranked 100.
-
(v)
It is difficult to calculate analytically errors in enrichment, and there is no available literature for such a calculation.
With regard to point (i), experiments performed on different datasets cannot be compared when using enrichment, as the dynamic range of enrichment will be different for different datasets, but there are several cases where this has been done [37]. Early enrichment can also suggest overly impressive performance for tools that rank a small fraction of the active molecules very early in the list, but fail to give good ranks to the majority of the actives [37]. It has been shown by Seifert [38] that enrichment does not detect significant pathologies in the ranking function. Other metrics have been developed by some groups specifically to address some of these problems: RIE by Merck [39], cumulative probability by Molsoft [40] and average number of outranking decoys by Schrodinger [3]. These metrics have, historically, only been used by the groups that invented them and are thus not useful for comparison to studies conducted by other groups. This lack of direct comparability across studies is compounded by the fact that these metrics cannot be converted into a more commonly used metric that could be used to compare results. Also, as with enrichment, it is unknown how to estimate analytically errors in any of these metrics.
A metric used to determine success in detecting a signal in a background of noise is the receiver operator characteristic (ROC). The ROC curve is derived by plotting noise (fraction of false positives) on the x-axis versus signal (fraction of true positives) on the y-axis. The area under the ROC curve (AUC) is a widely used measure in a variety of fields including medical statistics, criminology and bioinformatics [41, 42]. When applied to virtual screening the ROC illustrates success in ranking actives (signal) above decoys (noise). The AUC for the ROC curve shows performance of a given tool when screening across the entire database is examined, not just at fixed, early points in the screen as enrichment does. The theoretically perfect performance of a virtual screening application gives the maximum area under a ROC curve (1.0), while random performance of a tool gives an AUC of 0.5. Areas under the curve of less than 0.5 imply a systematic ranking of decoys higher than known actives. For recent applications of the ROC curve in virtual screening, see [2, 43]. The AUC for the ROC curve is also known as the ‘discrimination’. Discrimination is defined as the fraction of occurrences that a randomly chosen true positive (active) is given a better score than a randomly chosen true negative (decoy). This number then allows prediction of the likely effectiveness of a tool in experiments that have not yet been conducted. This predictive ability is not provided by metrics such as enrichment, cumulative probability and average number of outranking decoys, because while the ROC describes a property of the application studied, the other metrics essentially describe a property of the experiment. The AUC assesses virtual screening performance across the entire database and many practitioners of virtual screening are, rightly, most concerned about early performance of the tools they use. This is one reason why enrichment is so commonly used to measure success. The metric of early performance based on the ROC curve is the true positive rate at fixed false positive rates. The true positive rate at a false positive rate of, for example, 1% is a much more robust measure than the enrichment at 1% and provides similar information about the early performance of a tool.
The AUC also offers the advantage that a statistically robust estimate of its errors can be estimated analytically from the AUC itself, using a method developed by Hanley [41]. This is not a property possessed by enrichment, average number of outranking decoys etc. For these metrics errors can only be estimated (by bootstrapping or other approaches) from the raw data, which is rarely provided. The error in the AUC, as with other metrics, is reduced by increasing the number of positives (active compounds) and by increasing the number of negatives (inactives). The Hanley treatment shows that the error in the AUC is most significantly reduced by increasing the number of actives, while increasing the number of decoys has a much smaller impact on the error. Therefore virtual screening datasets with high proportions of active compounds will provide results with lower error bars for the AUC. With the error for an AUC available, meaningful comparisons can be made between two or more different tools. However the other metrics used for virtual screening mentioned above do not allow an analytical estimation of their errors. Comparisons designed to determine which tool is superior for a given purpose, that are based on metrics assumed to be free of errors, are fraught with difficulty.
While the choice of metric may affect the relative ranking of tools compared on the same datasets, the composition of those datasets has a very profound effect on the results generated. Until very recently it has been common practice to assemble a dataset for virtual screening by seeding a set of active molecules against a target of interest into a background of compounds (decoys) chosen essentially at random. These decoys compounds were often drawn from public sources such as vendor catalogues. An example of this approach is the seminal paper on virtual screening by docking from the Rognan lab where decoy compounds were selected at random from the publicly available compounds [44]. This set of decoys, or a subset thereof, has been used extensively since its publication in 2000 [2 and references therein] so that this same set of decoy compounds has been used in more than 45 different published virtual screening experiments on a wide variety of target systems. Given the huge variety in the types of active molecules camouflaged in this same set of decoys it seems intuitively obvious that in some cases the active compounds for a given target will be very easily discriminated from these decoys. As such a number of the virtual screening experiments performed using this set of decoy compounds have given good results purely due to differences in simple properties between the actives and the decoys (vide infra). In the Rognan dataset there were 10 active compounds for each of the targets studied and 990 randomly selected decoys. There are two problems arising from constructing a dataset in this way. The first is that the small number of active compounds means that the errors can be very high (vide supra). The second is that trivial property differences between the active compounds and the decoys can result in undeservedly good performance. The first issue, low prevalence, is still widespread in retrospective virtual screening studies. Although low prevalence reduces the reliability of the results, many virtual screening experiments are still conducted using very low numbers of active compounds. Reasons for this could include a desire to mimic “real” HTS experiments, where hit rates are often on the order of 0.01–0.1% [45] or to allow enrichment, the most commonly used metric for success in these studies, the maximal dynamic range. Tribelleau et al. [43] show that the dynamic range of enrichment, the difference between random and maximal performance, decreases as the proportion of active molecules in a dataset rises. For a recent example of a retrospective virtual screening study with deliberately large numbers of actives, providing high statistical power and small error bars, see Ref. [37].
The second issue, systematic differences in simple properties between decoys and actives in retrospective virtual screening experiments, is much more serious. As has been pointed out in a number of publications, scoring functions in docking programs, which are almost always additive, are sensitive to molecular size or heavy atom count, the number of hydrogen bonds that the molecule can make etc. Accordingly, systematic differences in these simple molecular properties between actives and decoys will cause systematic differences in ranking. For example, active compounds with higher average heavy atom counts will tend to rank better than the decoys when scored by a function that is sensitive to heavy atom count. For a fuller discussion of this issue see Verdonk et al. [46]. An example of the influence of the selection methods for decoys on virtual screening performance is shown in Fig. 7. In this figure, two retrospective virtual screening studies against CDK-2 using the docking tool FRED [47] are compared using ROC curves. In both cases the same actives were docked against the same co-crystal structure, while different decoy compounds were used. In one case (the green line), the decoys were chosen at random from the Maybridge compound collection [48], in the other (the red line), decoys were chosen to match the properties of the actives based on simple 1D properties. The striking difference, especially in early performance, is obvious. Clearly the performance of FRED is heavily affected by the nature of the decoy compounds, and to obtain a predictive indication of the utility of FRED in virtual screening decoy sets similar to those giving the red line should be used. It is worthy of note that the AUC’s for the two experiments shown are different by more than their respective 95% confidence intervals, so that this difference is indeed statistically significant.
Another example of how much of the signal that separates active from inactive compounds arises from systematic differences between their properties is shown in Fig. 8. In these eight examples, drawn from the Surflex-Dock dataset [2], the performance of three 3D virtual screening methods––Surflex-Dock, ROCS [49] and FRED––is compared to a simple 1D method. In this 1D approach [46, 50], compounds are ranked by distance in an Euclidean property space to the centre of the space defined by the active compounds. The Euclidean space is defined by five simple molecular properties: number of donors, number of acceptors, number of rotatable bonds, XlogP and 0.01 × molecular weight. This concept of ranking compounds by distance in a high dimensional Euclidean property space has recently been published as a virtual screening method, known as DACCS [51].
It is clear from Fig. 8 that in four of the eight cases (OPPA, HIV-PR, TK and PARP) the active compounds are very dissimilar from the background set, as the 1D ranking method gives very good virtual screening performance. In a fifth case (TS) the performance of 1D method is as good as any of the 3D methods, although none of the tools perform particularly well. Accordingly, judging virtual screening performance for any tool using such datasets is unlikely to be productive as most of the “signal” separating actives from decoys lies purely in differences in simple molecular properties. A further confounding issue with these datasets is that a large number of the active compounds in these sets are close structural analogues of one another. For ligand-based methods this high structural similarity amongst the actives can cause the actives to be very easily discriminated from the decoys, while a structure-based method may have more difficulty. Accordingly, while property bias is an important consideration in constructing decoy sets, analogue bias should be carefully considered when selecting sets of active compounds.
A recent effort to avoid some pathologies arising from poorly selected decoy sets has come from the work of Huang et al. [52] with the Database of Useful Decoys, or DUD. In this work decoys were selected to match the same simple molecular properties of the active compounds using a similar approach to that mentioned earlier, so that the decoys are not trivially separable from the actives. DUD represents a very wide-ranging dataset (actives against 40 target proteins) that has been designed to evaluate the underlying performance of docking tools, and not the sensitivity of that tool’s scoring metric to differences in simple molecular properties. Note that the DUD decoy selection approach uses a discontinuous representation of the molecular properties, while the approach mentioned above uses a continuous representation. The similarity between these two approaches for decoy selection and the DACCS approach for active selection is striking. It is a topic of further investigation whether much of the reported success of the DACCS method is due to over-training/poor active compound selection.
The work of Huang et al. with the DUD dataset showed that, at least for DOCK, this approach of specifically matching the properties of the decoys to those of the actives can produce more difficult decoy sets than those chosen purely for drug-likeness in a number of cases. It should be noted that the differences in performance reported in the DUD paper are essentially anecdotal, since no error bars are reported. With that caveat in mind inspection of Fig. 4 of the DUD paper, in which comparisons of performance of DOCK between the DUD “own” decoy sets and some commonly available agnostic decoys are shown, is instructive. In 10 of the 12 cases presented the DUD “own” decoy set is the most challenging of the four decoy sets compared, implying that a property-matched decoy set can provide a more difficult background set than an “agnostic” or general decoy set. For a drug-like decoy set chosen without specific reference to the active compounds being screened for, which is therefore to be expected to be less challenging than decoy sets designed with specific reference to the actives being searched for, see Ref [53]. The DUD datasets also have relatively high prevalence (the design goal was to achieve a prevalence close to 3%, though this varies slightly from target to target), giving the results generated with DUD reasonably low errors (except for those cases where the number of actives is small). This is not to say that DUD is perfectly constructed––there are still some large differences between the properties of the actives and the decoys in some cases and in some cases there are so few active molecules that statistically robust results cannot be generated. An important property not considered in the selection of the DUD decoys is formal charge. As such, there are some sets of the DUD actives that are easily discriminated from the decoys based on formal charge. For example, the mean formal charge on the neuraminidase ligands is +1.76, while the mean charge on the decoys is +0.76. For acetylcholinesterase, the mean charge on the actives is −1.68, while the mean charge on the decoys is −0.76. As with the datasets illustrated in Fig. 8, the DUD active sets were not chosen with a view to structural diversity and some of the active sets consist entirely of closely analogous compounds. Very recently the original DUD dataset has been extended by adding more active compounds and by clustering the actives to remove trivially graph similar actives from the set [54]. This makes “DUD 2.0” a suitable dataset not only for docking approaches but also ligand-based techniques. It should be noted that there is a limit to the acceptable level of similarity between actives and presumptive decoys. When the decoys are too similar to the actives the assumption that the decoys are inactive becomes increasingly untenable, giving rise to large numbers of “false false positives”. Accordingly the problem of decoy selection is not yet completely solved, and may not admit of a single solution for all problems or tools. However, since in retrospective work the point is purely to gain a measure of the expectation of performance in as yet unperformed studies, the use of carefully designed decoy sets is mandatory.
It is unfortunate that the docking targets in DUD (39 crystal structures and 1 homology model) were not selected with as much care as the small molecule datasets. In 6 of the 38 co-crystal structures in DUD (there is one apo structure in the set), the DPIs are 1.5 Å or more, resulting in significant uncertainty in the positioning of any atom in these structures. These structures are ALR2 (1AH3), COX-2 (1CX2), EGFR (1M17), GR (1M2XZ), InhA (1P44) and p38 (1KV2). Accordingly docking results from these structures should be interpreted with great care.
Conclusions
Large numbers of evaluations and comparisons of tools for pose prediction and virtual screening have been published in recent years, an indication of significant interest in identifying tools that will have robust performance in one or both of these areas. Unfortunately the vast majority of these studies have been invalidated by poor choice of datasets, lack of consideration of error in source data and use of metrics that do not permit robust comparisons. For those papers using crystal structure data, too little account is taken both of the unavoidable imprecision in these structures and of the errors of fitting that are regrettably frequently seen in structures in the RCSB. In many cases nominal resolution, a measure of the quantity of data gathered, is confused with a measure of quality for the structure and other metrics indicating quality and reliability (DPI and R free) are ignored. When performing pose prediction geometric measures such as RMSD are almost always used to compare the experimental and predicted pose. These measures are uniformly used without taking into account either the inevitable imprecision in the atomic positions in crystal structures or the fact that using geometric measures necessarily implies comparing a model for the source data with a computed pose. In almost no cases are crystal structures inspected for errors in fitting. Without taking all these sources of error into account the results of any publication that uses crystal structure data will be suspect and of little use in deciding what tools are the most suitable for the task at hand. In papers concerned with virtual screening there has been, until recently, too little focus on eliminating trivial reasons for good performance from a given tool. The DUD dataset [52] has illustrated ways in which challenging virtual screening datasets can be constructed and, since it is publicly available, DUD offers the opportunity for a common benchmark upon which a wide variety of tools can be compared. The plethora of metrics used to judge and compare virtual screening performance serves merely to confuse the field rather then to clarify it. The lack of confidence intervals on metrics for success makes meaningful comparisons between tools almost impossible to interpret. The AUC for ROC offers great promise as a metric for virtual screening, as it offers the possibility of predictive value along with robust errors. For an exemplary use of ROC in virtual screening tests see a recent paper by Jain [55]. It is hoped that the field will soon converge to a single metric of virtual screening performance, such as the ROC, that will allow robust and direct comparisons between tools and between studies.
Notes
Goto et al.’s formula to calculate DPI.
Blow’s derivation for the relationship between nominal resolution and atomic precision using the Goto et al. [18] coefficient.
Enrichment calculation.
Abbreviations
- AUC:
-
Area under the curve
- DPI:
-
Diffraction-coordinate precision index
- RMSD:
-
Root mean square deviation
- ROC:
-
Receiver operator characteristic
References
Warren G, Webster Andrews C, Capelli A-M, Clarke B, LaLonde J, Lambert MH, Lindvall M, Nevins N, Semus S, Senger S, Tedesco G, Wall ID, Woolven JM, Peishoff CE, Head MSJ (2006) Med Chem 49:5912
Pham TA, Jain AN (2006) J Med Chem 49:5856
Freisner RA, Murphy RB, Repasky MP, Frye LL, Greenwood JR, Halgren TA, Sanschagrin PC, Mainz DT (2007) J Med Chem 47:1564
Kirchmair J, Wolber G, Laggner C, Langer TJ (2006) Chem Inf Model 46:1848
Bostrom J, Greenwood JR, Gottfries J (2003) J Mol Graphics Model 21:449
Bohme-Leite T, Gomes D, Miteva MA, Chomilier J, Villoutreix BO, Tuffery P (2007) Nucleic Acids Res 35:W568
Hawkins PCD, Skillman AG, Nicholls A (2007) J Med Chem 50:74
Evans DA, Doman TN, Thorner DA, Bodkin MJ (2007) J Chem Inf Model 47:1248
Erickson JA, Jalaie M, Robertson DH, Lewis RA, Vieth M (2004) J Med Chem 47:45
Cole JC, Murray CW, Nissink JWM, Taylor RD, Taylor R (2005) Proteins: Struct Funct Bioinformat 60:325
Thomsen R, Christensen MK (2006) J Med Chem 49:3315
Abagyan RA, Totrov MM (1997) J Mol Biol 268:678
http://www.eyesopen.com/about/events/cup7/schmitt/060308_present4CUP7_SS.pdf
Kroemer RT, Vulpetti A, McDonald JJ, Rohrer DC, Trosset J-Y, Giordanetto F, Cotesta S, McMartin C, Kihlen M, Stouten PFW (2004) J Chem Inf Comput Sci 44:871
Kleywegt GJ (2000) Acta Cryst D56:249
Nissink JMW, Murray C, Hartshorn M, Verdonk ML, Cole JC, Taylor R (2002) Proteins: Struct Funct Genetics 49:457
Brünger AT (1993) Nature 355:527
Goto J, Kataoka R, Hirayama N (2004) J Med Chem 47:6804
Tronrud DE (1996) J Appl Cryst 29:100
Bostrom J (2002) J Comput-Aided Mol Design 15:1137
Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IH, Bourne PE (2000) Nucleic Acids Res 28:235 http://www.rcsb.org
Hooft RWW, Vriend G, Sander C, Abola EE (1996) Nature 381:272
Cruickshank DW (1999) Acta Cryst D55:583
Blow DM (2002) Acta Cryst D58:792
http://www.ccdc.cam.ac.uk/products/life_sciences/validate/astex/pdb_entries
Bursulaya BD, Totrov M, Abagyan R, Brooks CL III (2003) J Comput-Aided Mol Design 17:1
Jones G, Willett P, Glen RC, Leach AR, Taylor R (1997) J Mol Biol 267:727
Halgren TA (1996) J Comput Chem 17:490
Perola E, Charifson PS (2004) J Med Chem 47:2499
http://www.eyesopen.com/about/events/cup7/stahl/Stahl_cup7_pdb_mistakes.pdf
http://www.farma.ku.dk/index.php/Computational-Chemistry-Ligan/4613/0/
Bostrom J, Grant A (2007) In: Mannhold R (ed) Drug properties: measurement and computation, Chapter 8. Wiley-VCH, Weinheim, Germany
Hartshorn MJ, Verdonk ML, Chessari G, Brewerton SC, Mooij WTM, Mortenson PN, Murray CW (2007) J Med Chem 50:726
Perola E, Xu K, Kollmeyer TM, Kaufmann SH, Prendergast FG, Pang Y-P (2000) J Med Chem 43:401
Jenkins JL, Kao RYT, Shapiro R (2003) Proteins: Struct Funct Genet 50:81
Forino M, Jung D, Easton JB, Houghton PJ, Pellechia M (2005) J Med Chem 48:2278
McGaughey GB, Sheridan RP, Bayly CI, Culberson JC, Kreatsoulas C, Lindsley S, Maiorov V, Truchon J-F, Cornell WD (2007) J Chem Inf Model 47:1504
Seifert M (2006) J Chem Inf Model 46:1456
Sheridan RP, Singh SB, Fluder EM, Kearsley SK (2001) J Chem Inf Comput Sci 41:1395
Bursulaya BD, Totrov M, Abagyan R, Brooks CL III (2003) J Comput Aided Mol Des 17:1
Hanley JA, McNeil BJ (1982) Radiology 143:29
Baldi P (2000) Bioinformatics 16:412
Tribelleau N, Acher F, Brabet I, Pin J-P, Bertrand H-O (2005) J Med Chem 48:2534
Bissantz C, Folkers G, Rognan D (2000) J Med Chem 43:4759
Sills MA, Weiss D, Pham Q, Schweitzer R, Wu Y, Wu JJ (2002) J Biomol Screening 7:191
Verdonk ML, Berdini V, Hartshorn MJ, Mooij WTM, Murray CW, Taylor RD, Watson P (2004) J Chem Inf Comput Sci 44:793
FRED version 2.1—http://www.eyesopen.com
http://www.maybridge.com. Accessed November 2005
ROCS version 2.1—http://www.eyesopen.com
http://www.eyesopen.com/about/events/cup7/hawkins/Hawkins_UKqsar_06_ph.png
Godden JW, Bajorath J (2006) J Chem Inf Model 46:1094
Huang N, Shiochet BK, Irwin JJ (2006) J Med Chem 49:6789
Freisner RA, Banks JL, Murphy RB, Halgren TA, Klicic JJ, Mainz DT, Repasky MP, Knoll EH, Shelly M, Perry JK, Shaw DE, Francis P, Shenkin PS (2004) J Med Chem 47:1739
http://dud.docking.org. Accessed 5th November 2007
Jain AJ (2007) J Comput-Aided Mol Des 21:281
Acknowledgement
The authors wish to thank Annie Lux, MFA for editing and proof-reading of the manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article can be found at http://dx.doi.org/10.1007/s10822-008-9201-z
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Hawkins, P.C.D., Warren, G.L., Skillman, A.G. et al. How to do an evaluation: pitfalls and traps. J Comput Aided Mol Des 22, 179–190 (2008). https://doi.org/10.1007/s10822-007-9166-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10822-007-9166-3