Abstract
A laboratory experiment where human subjects play a repeated public goods game with high-powered punishment technology (50:1). Results on three attributes are similar to lower-powered punishment settings (e.g., 3:1): Subjects contribute almost 100 % to the public good, punishment rates are low (under 10 % of maximum), and punishment is directed more toward low contributors. In contrast to lower-powered punishment settings, however, subjects earn less money than they would have in the same setting without punishment. These results contribute to the debate about the origins and maintenance of cooperation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cooperation is an important issue for economics, other social sciences, and evolutionary biology. Punishment has been shown to increase cooperation under some conditions (Yamagishi 1986; Fehr and Gachter 2002). There is a considerable literature on the role of punishment in sustaining cooperation (Trivers 1971; Clutton-Brock and Parker 1995; Fehr and Gachter 2000; Fowler 2005; Sigmund 2007).
Cooperation, punishment, and reciprocity are important to a wide-range of species including apes (Brosnan et al. 2005; Silk et al. 2005; Jensen et al. 2006, 2007a, b; Vonk et al. 2008; Brosnan et al. 2009; Leeuwen et al. 2011; Riedl et al. 2012; Proctor et al. 2013), monkeys (Brosnan and Waal 2003; Cronin et al. 2010; Talbot et al. 2011), and rodents (Rutte and Taborsky 2007) . The implications of reciprocity include cooperation itself as well as the impact on hierarchy and health (Sapolsky 2005; Yee et al. 2008).
Three main findings regarding the role of punishment and cooperation are salient for this study. First, punishment can sustain cooperation at higher levels than observed in the same settings without punishment (Yamagishi 1986; Fehr and Gachter 2002). Second, in some societies, which may be unusual (Henrich et al. 2010), punishment supports cooperation as it is preferentially imposed upon relatively low cooperators. However, in some settings, and with some populations, ‘anti-social’ punishment is directed toward high cooperators (Shinada et al. 2004; Herrmann et al. 2008). Third, punishment can increase efficiency (in situations where the cost of punishment is lower than the benefits created by increased cooperation), although not in all settings (Rand and Nowak 2011).
This paper contributes to the literature on punishment and cooperation in two ways. First, it investigates punishment technology that may be more similar to non-laboratory punishment. Second, and relatedly, it contributes to an important debate about the evolutionary origin of cooperation.
The first motivation is that non-laboratory punishment is often much more extreme than that used in many experiments. Commonly, the laboratory ratio used is 3 units of money taken from the punished for every 1 unit taken from the punisher (3:1 hereafter). In some studies the punishment technology is as high as 4:1 (Cinyabuguma et al. 2006; Nikiforakis and Normann 2008). Within the range studied, cooperation increases as the punishment power is increased (Nikiforakis and Normann 2008).
These experiments may be unrealistic as outside the laboratory punishment technology is often much higher-powered. Sanctions in the criminal justice system impose severe punishments often far in excess of the crime’s impact. For example, “three strikes” laws in states such as California frequently result in life imprisonment for relatively minor crimes. Criminal convictions have long-term impacts on the ability to obtain employment, and as such constitute very costly punishments.
In social settings, punishments for norm violations can also be severe. These costs can range from exclusion from networks (including access to jobs) to outright violence. In the US in 2012, for example, 27 % of identified homicides were committed in face-to-face conflict between strangers (FBI 2013). Conflicts between strangers commonly result from extremely minor infractions such as failure to yield in traffic situations, or perceived insults in social settings such as bars. Violence has tremendously high costs to both parties. Furthermore, such high-powered punishment has been a persistent feature of human society that predates industrialization; current rates of violence are argued to be much lower than those for our ancestors (Pinker 2011).
There is a line of research that argues that punishment is not part of cooperation (Dreber et al. 2008; Rand et al. 2009). However, among human foragers, there is evidence that punishment is both important and higher-powered than the standard 3:1 in laboratory experiments. One study documents 235 incidents of peer-to-peer punishment linked to norm enforcement among the Ju/’hoansi Bushmen (Wiessner 2005). This paper summarizes its results by saying that costs to the punisher are “relatively low,” p. 135 and impose “very real material consequences on the target” p. 122.
The extent of costly punishment among hunter-gatherers is debated. One article looks across several societies and argues that punishment is not costly among hunter-gatherers (Guala 2012). In discussing the Bushmen data in Wiessner (2005), however, this article emphasizes that those who punish do not suffer high costs writing, “material cost for the punishers is close or equal to zero” Guala (2002), p. 10. The low cost to punisher and “material consequences” to punished (noted by Wiessner) is precisely the asymmetry between costs and punishment that a 50:1 technology is designed to investigate.
Thus, to understand punishment and cooperation outside the laboratory, it may be useful to look at higher-powered punishment than the typical 3:1 ratio used in economic experiments.
The second, and related, motivation for this study is the ongoing debate about the origin of human cooperation. A leading group of scholars sees a particular form of group selection, so-called strong reciprocity, as an important source of cooperation; a view that is sharply contested by others.
Beginning in 1964, various types of cooperation that were once considered puzzles have been reconciled with evolutionary theory via kin selection (Hamilton 1964), reciprocal altruism (Trivers 1971), group selection (Wilson 1975), and costly signaling (Zahavi 1975), and indirect reciprocity (Nowak and Sigmund 1998).
In all these cases, the apparent puzzle of cooperation is resolved when the costly behavior is revealed to increase the fitness of the genes of the cooperator. In some cases, the individual organism receives future benefits that compensate for the cost of cooperation (reciprocal altruism, indirect reciprocity, costly signaling), and in the other cases, the organism is not repaid, but its genes’ are repaid via impact on other organisms (kin selection, group selection).
While there has been significant progress in understanding cooperation, one area remains controversial: Costly cooperation in situations where the behaviors cannot redound to the benefit of the cooperators’ genes. Experimental investigations that produce such behavior are final and anonymous interactions among people who are neither kin nor members of evolutionarily relevant groups.
In these anonymous and final interactions, costly cooperation cannot redound to the benefit of the gene via any of the five theories listed above.
-
1.
If the players are not kin, then costly acts cannot redound to the benefit of genes in kin via kin selection.
-
2.
If the players are not part of evolutionarily relevant groups, then costly acts cannot redound to the benefit of genes via group selection.
-
3.
If there are no future interactions, then costly acts cannot be repaid via reciprocal altruism.
-
4.
If no reputation can be formed, then costly acts cannot be repaid via indirect reciprocity.
-
5.
If behavior is anonymous then costly acts cannot be repaid via signaling.
The remaining ‘puzzle of cooperation’ is the human propensity to cooperate even in final and anonymous interactions played among people who are neither kin nor members of evolutionarily relevant groups.
There are two main explanations for this ‘puzzling’ cooperation. The first is ‘strong reciprocity’, a form of group selection (Gintis 2000; Fehr et al. 2002). Note that strong reciprocity is group selection, but it is not standard group selection as the individuals in laboratory experiments are not part of evolutionarily relevant groups (Burnham and Johnson 2005). Thus, strong reciprocity is a new aspect of human nature where the altruistic behavior is directed toward transient, anonymous strangers in laboratories.
The second set of explanations for the puzzling cooperation is diverse, but united in that they do not rely upon group selection (Price et al. 2002; Johnson et al. 2003; Trivers 2004; Burnham and Johnson 2005; Binmore 2006; Dreber et al. 2008; West et al. 2011; Burton-Chellew and West 2013; Kurzban and DeScioli 2013). One common theme in these views is that the cooperation is produced by psychological mechanisms in particular settings. The behavioral outcome may benefit others in the transient, experimental groups, but group selection is not required for the evolutionary origin of the mechanisms that produce cooperation in these settings.
The proponents of strong reciprocity focus on the fact that in some settings costly acts increase efficiency. In particular, proponents write, “Everyone in the group will be better off if free riding is deterred”, and “the act of punishment, although costly for the punisher, provides a benefit to other members of the population ... For this reason, the act of punishment is an altruistic act.” (Fehr and Gachter 2002) pp. 137, 139
Table 1 is a representation of the strong reciprocity view that cooperation is fostered by costly acts that cannot be repaid.
The proponents of strong reciprocity do not propose any empirical test of the idea that punishment in this setting is grounded in group selection. However, one form of test is to examine the robustness of the “bad for the individual, good for the group” outcome.
The robustness of this “bad for the individual, good for the group” outcome with respect to punishment technology has an important history. In 1986, Yamagishi et al. reported that cooperation increases towards 100 % with a punishment technology of 3:1. They also report, however, that with a punishment technology of 1:1 cooperation rates decline. More recent work (Nikiforakis and Normann 2008), examines punishment technology ranging from 1:1 and 4:1. In their introduction, the authors write, “Despite the large number of experiments, little is known about the robustness of the punishment schemes and the requirements on them to lead to higher cooperation and welfare improvement” p. 359.
Thus, the goal of this study is to study cooperation with higher-powered punishment technology. To accomplish this goal, a public goods game based on Fehr and Gachter (2002) was played where punishers could pay 1 monetary unit to reduce another player’s payoff by 50 units (50:1 hereafter). Four aspects of behavior are relevant to the motivation for this study.
-
Q1: What is the cooperation level under 50:1?
-
Q2: What is the punishment level under 50:1?
-
Q3: Who gets punished under 50:1—low or high contributors?
-
Q4: Is efficiency increased by 50:1 punishment?
2 Methods
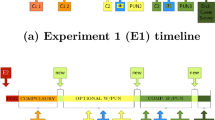
A total of 96 undergraduate students from Chapman University voluntarily participated in the experiments. Four experimental sessions with 24 subjects took place. Each of the 24 subjects played a six-period public goods game with a punishment stage. Within this experimental session, subjects in two of the four sessions first played a similar public goods game with rank order payoffs (reported elsewhere).
In each period of a session, the 24 subjects were allocated to six groups of four subjects. The allocation of subjects to the groups ensured that, within a given treatment, no one ever met the same person more than once. In each round, players were identified with a transient identifier to ensure no reputations could be formed. At the end of each period, subjects were informed about their own decisions, the decisions of the other group members, and their payoff in current period.
Subjects were given written instructions that explained the structure of the game, the composition of groups in each period, the inability to form reputations because of anonymity. After the instructions, and before the experiment, subjects were given a test of knowledge on several hypothetical examples. In order to participate, each subject was required to get all the payoff examples correct. All experimental decisions were made on a computer screen using z-tree software.
The subjects sat in four rows with six individuals per row. All decisions were made via computers, and each subject had his or her own computer. Three-sided opaque screens separated each computer and subject. Subjects were instructed not to look at anyone else’s screen and not to speak to each other.
Subjects each received $7 in advance for participation, and were paid according to behavior in the game. In each round, each player was given 20 Experimental Currency Units (ECU) to allocate between a public and a private account. ECUs in the private account remained with the player, while those allocated to the group account were multiplied by 1.6 and divided equally among 4 players in a group. ECUs were converted to cash at a rate of 100 tokens to $1. Subjects were paid in cash and privately at the end of the session.
The punishment phase came after each round of the public good. Group members were identified by a transient number and their contribution to the public good. Each player could allocate up to 10 units of punishment to each of the three other group members. A unit of punishment cost the punisher 1 ECU and reduced the punished player’s payoff by 50 ECU.
The 50:1 punishment technology allows for large negative payouts. The maximum punishment possible in a round is 30 points (Ten from each of the three other players in the group), which would result in a loss of 1,500 ECU. Players with negative balances would no longer suffer the costs of punishment, and might behavior differently. Accordingly, two changes were made. First, endowments were large relative to the public goods game payoffs; endowments in three sessions were 2,000 ECU and in one session the endowment was 1,500 ECU. Second, the game would be stopped if any player’s cumulative balance turned negative. (However, none of the sessions needed to be terminated early.)
Subjects were recruited by email via Chapman University’s Economics Science Institute (ESI) email list. Subjects were restricted to not having participated in previous ESI public goods experiments. Each session had equal numbers of men and women for a total of 48 woman and 48 men. All sessions were conducted in May 2012, beginning at the same time (4pm) on a Tuesday, Wednesday, or Thursday.
No deception was used in the experiment.
3 Results
Four main findings are reported. First, cooperation was high, approaching 100 % in later rounds. Second, punishment rates were low. Third, punishment was directed more towards low contributors. Fourth, earnings for most players in most periods were negative. In addition, there is considerable heterogeneity across the four sessions, but the main findings are found in each session.
3.1 Contributions are high
Contributions to the public good are high, and in later rounds the average contribution approaches 100 % (Table 2; Fig. 1). The average amount contributed is 14.05/20 in round one and rises to over 19 in rounds five and six. The median contribution is 20 in rounds 2–6, and the percentage of contributions that are half the possible or lower falls to just 2 % by round six.
3.2 Punishment is low
Punishment is low. Table 3 and Fig. 2 contain average punishment received (in points before being multiplied by 50). Each player can receive a maximum of 30 units of punishment (10 units from each of the three other players in the group). The average punishment per player in a round ranges from 1.47 in round one to 2.99 in round six. The highest level is just below 10 % of the maximum punishment.
Not only is punishment low, it is relatively rare. 71.5 % of the punishment amounts are zero. As with other aspects of these results, this is similar to that exhibited in prior experiments using 3:1 punishment technology. For example, Fehr and Gachter (2002) report punishment (more than zero) occurred “a total of 1,270 times,” which equates to no punishment in 70.6 % of the cases.
3.3 Punishment is directed more toward low contributors
Punishment is directed more toward low contributors. Table 4 and Fig. 3 contain the average punishment received as a function of contribution and round.
In round 1, for example, subjects who contributed the full 20 ECUs to the public good received an average of 0.51 units of punishment. In contrast, in round 1, subjects who contributed 10 or fewer ECUs to the public good received an average of 2.45 units of punishment.
In every round, punishment is greater for subjects who contributed less to the public good. The final column of Table 4 displays the ratio of punishment received by low contributors (10 or fewer ECUs) to punishment received by subjects who contributed the full 20 ECU. This ratio varies by round between 2.4 and 9.2, and shows no clear trend over the rounds.
Table 5 counts the number of subjects contributing in three ranges (20, 19–11, and 10 or fewer). Subjects who contribute little are punished, and the number of low contributors decreases rapidly toward zero. In round 1, for example, more than one third of subjects contribute 10 or fewer ECU. This behavior is almost completely absent in round 3 and beyond.
3.4 Total earnings are lower than without punishment
Earnings are lower in this game with punishment than they could be in the same public good game without punishment. In a public goods game with these parameters without punishment, the lowest average payoff occurs when nothing is contributed to the public good. In this case, each player earns 20 ECUs in each round for a total of 120 ECU.
In this game with punishment, the average earnings are negative 460 ECU. Contribution rates are very high, and this increases the total earnings, but with powerful punishment technology, the cost of punishment (51 ECU per unit of punishment) overwhelms the gains from contribution (Table 6; Fig. 4).
3.5 There is considerable variability between sessions, but not in the main results
The experiment consisted of four sessions; each with 24 subjects. All of the sessions were created via the same process, drawn from the same population and run at the same time of day. In addition, subjects in session one and three played a different public goods game with punishment before this game. The four sessions show some considerable variation in both contribution and punishment. Table 7 and Fig. 5 contain the contribution to the public good by round and group.
There is considerable variation between sessions in the initial level of contribution. Session three starts with nearly maximal contributions. The other three sessions (1, 2, and 4) start with lower contributions, and increase toward maximal.
Table 8 and Fig. 6 contain the punishment received by round and session. In later rounds, subjects in session one punish more than subjects in any of the other three sessions.
It is not clear why there is so much variability between sessions. Session 1 has the highest punishment and it averages 4.8 out of a maximum of 30. Cooperation is high in all sessions, punishment is low in all sessions, and earnings are lower than the lowest possible earnings in same game without punishment in all four sessions (although only fractionally lower in session 4).
In particular, it would good to investigate the impact of heterogeneity in the procedures and subjects on behavior. As noted earlier, subjects in session 1 and 3 played a different public goods game with punishment before this game, and endowments in three sessions were 2,000 ECU and in one session the endowment was 1,500 ECU.
Formal analysis of the relationship between these variations and behavior is challenging because after the first round, each session has its own path dependency. We can, however, examine punishment in the first round. There is no statistically significant difference in first-round contributions related to these variations. In particular, average first-round punishment in sessions 1 and 3 was 1.63 units versus 1.31 in sessions 2 and 4 (p value > 0.10). Similarly, average first-round punishment in the three sessions with an endowment of 2,000 ECU was 1.21 versus 2.25 in the one session with an endowment of 1,500 ECU (p value > 0.10).
4 Discussion
This study was motivated by two questions. First, how would subjects behave in a public goods game with punishment technology more similar to that found outside the laboratory? Second, what are the implications for the debate on the role of group selection in cooperation?
In answer to the first question, 50:1 punishment technology induces very high contributions to the public good. Punishment is low and promotes cooperation as it is preferentially directed toward those who contribute less to the public good. However, because the punishment is so powerful, the outcome is inefficient. Indeed, the average payoff is lower than the lowest possible payoff in the same game without punishment.
To the extent that 50:1 more closely approximates non-laboratory conditions, many other experiments are suggested.
First, this is a study on humans. Related studies on non-humans would be insightful. In particular, as noted in the introduction, there is a rich literature on these issues using apes and monkeys (Brosnan and Waal 2003; Jensen et al. 2007b; Leeuwen et al. 2011).
Second, this study uses US college students. It would be informative to run this experiment with other subjects, particularly those who been shown to exhibit anti-social punishment of cooperators (Shinada et al. 2004; Herrmann et al. 2008).
Third, ‘counter punishment’ studies allow multiple rounds of punishment that can be used to counter punishments received, or to punish others who fail to punish (Denant-Boemont et al. 2007; Nikiforakis 2008). In some cases, counter punishment makes punishment inefficient. These investigations could be repeated with 50:1 technology.
Fourth, the decrease in efficiency may be caused because the minimum punishment is a full unit. This suggests allowing fractional punishmentFootnote 1.
Fifth, a comparative statics experiment could be done across a range of high-powered punishment technologies similar to that done for low-powered punishment (Nikiforakis and Normann 2008). Based on such an experiment, a standard high punishment technology could be suggested for use in a broad range of experiments.
Sixth, this study replicates the six-period design of Fehr and Gachter (2002). More recent papers argue long-term cooperation, with many more than six periods, is more important (Gachter et al. 2008; Frey and Rusch 2012). This line of work suggests experiments using 50:1 technology with more periods. The finding that efficiency decreases in this experiment may be importantly driven by the 6-period structure. Therefore, the generalizability of the decrease in efficiency based on this current study is limited.
The second motivation for this study is the claim that group selection is the origin of ‘altruistic punishment’ in public goods games. The label altruistic was applied because punishment in this institution (anonymous and final interactions) is costly for the punisher and, at least in the original Fehr and Gachter (2002) study, increases efficiency. Thus, punishment is good for the group, bad for the individual as shown in Table 1 in the introduction.
In this experiment, however, average payoffs were lower than the lowest possible for a public goods game with no punishment. This result combines with two other results to suggest that the good for the group outcome is not robust. Punishment is bad for the group (e.g., inefficient) in societies that exhibit high levels of anti-social punishment (Herrmann et al. 2008). Punishment is also bad for the group in the presence of some counter-punishment institutions (Denant-Boemont et al. 2007; Nikiforakis 2008).
Table 9 updates Table 1 with some of the other studies on public goods games with punishment.
The ‘altruistic’ label was applied because, in one particular setting, punishment in anonymous and final interactions is bad for the individual and good for the group (Fehr and Gachter 2002). The three additional studies in Table 9 are among the most obvious tests for robustness of the ‘good for group’ aspect. Change the subject pool, change the structure to allow another counter-punishment, change the payoffs to punishment. Each of these three changes leads to inefficient outcomes.
In conclusion, cooperation in public goods games with punishment is very sensitive to the rules. Slight changes in game structure lead to inefficiency. These findings suggest that the maintenance of cooperation via punishment requires careful crafting and monitoring of institutions.
Notes
The idea of fractional punishment units was suggested to the author by Nikos Nikiforakis.
References
Binmore, K. (2006). Why do people cooperate. Politics, Philosophy and Economics, 5(1), 81–96.
Brosnan, S. F., & de Waal, F. B. M. (2003). Monkeys reject unequal pay. Nature, 425(18 September), 297–299.
Brosnan, S. F., Schiff, H. C., & De Waal, F. B. (2005). Tolerance for inequity may increase with social closeness in chimpanzees. Proceedings of the Royal Society B: Biological Sciences, 272(1560), 253–258.
Brosnan, S. F., Silk, J. B., Henrich, J., Mareno, M. C., Lambeth, S. P., & Schapiro, S. J. (2009). Chimpanzees (Pan troglodytes) do not develop contingent reciprocity in an experimental task. Animal Cognition, 12(4), 587–597.
Burnham, T. C., & Johnson, D. (2005). The biological and evolutionary logic of human cooperation. Analyse & Kritik, 27, 113–135.
Burton-Chellew, M. N., & West, S. A. (2013). Prosocial preferences do not explain human cooperation in public-goods games. Proceedings of the National Academy of Sciences, 110(1), 216–221.
Cinyabuguma, M., Page, T., & Putterman, L. (2006). Can second-order punishment deter perverse punishment? Experimental Economics, 9(3), 265–279.
Clutton-Brock, T. H., & Parker, G. A. (1995). Punishment in animal societies. Nature, 373, 209–216.
Cronin, K. A., Schroeder, K. K., & Snowdon, C. T. (2010). Prosocial behaviour emerges independent of reciprocity in cottontop tamarins. Proceedings of the Royal Society B: Biological Sciences, 277(1701), 3845–3851.
Denant-Boemont, L., Masclet, D., & Noussair, C. N. (2007). Punishment, counterpunishment and sanction enforcement in a social dilemma experiment. Economic Theory, 33, 154–167.
Dreber, A., Rand, D., Fudenberg, D., & Nowak, M. (2008). Winners don’t punish. Nature, 452(20 March 2008), 348–351.
FBI, U. D. o. J. (2013). Crime in the United States 2012. http://www.fbi.gov/about-us/cjis/ucr/crime-in-the-u.s/2012/crime-in-the-u.s.-2012.
Fehr, E., Fischbacher, U., & Gachter, S. (2002). Strong reciprocity, human cooperation and the enforcement of social norms. Human Nature, 13, 1–25.
Fehr, E., & Gachter, S. (2000). Cooperation and punishment in public goods experiments. American Economic Review, 90, 980–994.
Fehr, E., & Gachter, S. (2002). Altruistic punishment in humans. Nature, 415, 137–140.
Fowler, J. H. (2005). Altruistic punishment and the origin of cooperation. PNAS, 102(19), 7047–7049.
Frey, U. J., & Rusch, H. (2012). An evolutionary perspective on the long-term efficiency of costly punishment. Biology & Philosophy, 27(6), 811–831.
Gachter, S., Renner, E., & Sefton, M. (2008). The long-run benefits of punishment. Science, 322(5907), 1510.
Gintis, H. (2000). Strong reciprocity and human sociality. Journal of Theoretical Biology, 206, 169–179.
Guala, F. (2012). Reciprocity: Weak or strong? What punishment experiments do (and do not) demonstrate. Behavioral and Brain Sciences, 35(01), 1–15.
Hamilton, W. D. (1964). The genetical evolution of social behavior I and II. Journal of Theoretical Biology, 7(1): 1–16, 17–52.
Henrich, J., Heine, S. J., & Norenzayan, A. (2010). The weirdest people in the world? Behavioral and Brain Sciences, 33, 61–135.
Herrmann, B., Thöni, C., & Gächter, S. (2008). Antisocial punishment across societies. Science, 319(5868), 1362–1367.
Jensen, K., Call, J., & Tomasello, M. (2007). Chimpanzees are rational in an ultimatum game. Science, 318(5 October), 107–109.
Jensen, K., Call, J., & Tomasello, M. (2007). Chimpanzees are vengeful but not spiteful. Proceedings of the National Academy of Sciences, 104(32), 13046–13050.
Jensen, K., Hare, B., Call, J., & Tomasello, M. (2006). What’s in it for me? Self-regard precludes altruism and spite in chimpanzees. Proceedings of the Royal Society B: Biological Sciences, 273(1589), 1013–1021.
Johnson, D., Stopka, P., & Knights, S. (2003). The puzzle of human co-operation. Nature, 421(27 February), 911–912.
Kurzban, R., & DeScioli, P. (2013). Adaptationist punishment in humans. Journal of Bioeconomics: 1–11.
Nikiforakis, N. (2008). Punishment and counter-punishment in public good games: Can we really govern ourselves? Journal of Public Economics, 92, 91–112.
Nikiforakis, N., & Normann, H.-T. (2008). A comparative statics analysis of punishment in public-good experiments. Experimental Economics, 11(4), 358–369.
Nowak, M., & Sigmund, K. (1998). Evolution of indirect reciprocity by image scoring. Nature, 393, 573–577.
Pinker, S. (2011). The better angels of our nature: why violence has declined. New York: Viking.
Price, M., Cosmides, L., & Tooby, J. (2002). Punitive sentiment as an anti-free rider psychological device. Evolution and Human Behavior, 23, 203–231.
Proctor, D., Williamson, R. A., de Waal, F. B. M., & Brosnan, S. F. (2013). Chimpanzees play the ultimatum game. Proceedings of the National Academy of Sciences, 110(6), 2070–2075.
Rand, D. G., Dreber, A., Ellingsen, T., Fudenberg, D., & Nowak, M. A. (2009). Positive interactions promote public cooperation. Science, 325(5945), 1272–1275.
Rand, D. G., & Nowak, M. A. (2011). The evolution of antisocial punishment in optional public goods games. Nature Communications, 2, 434.
Riedl, K., Jensen, K., Call, J., & Tomasello, M. (2012). No third-party punishment in chimpanzees. Proceedings of the National Academy of Sciences, 109(37), 14824–14829.
Rutte, C., & Taborsky, M. (2007). Generalized reciprocity in rats. PLoS Biology, 5(7), e196.
Sapolsky, R. M. (2005). The influence of social hierarchy on primate health. Science, 308(5722), 648–652.
Shinada, M., Yamagishi, T., & Ohmura, Y. (2004). False friends are worse than bitter enemies: “altruistic” punishment of in-group members. Evolution and Human Behavior, 25, 379–393.
Sigmund, K. (2007). Punish or perish? Retaliation and collaboration among humans. Trends in Ecology & Evolution, 22(11), 593–600.
Silk, J. B., Brosnan, S. F., Vonk, J., Henrich, J., Povinelli, D. J., Richardson, A. F., et al. (2005). Chimpanzees are indifferent to the welfare of other group members. Nature, 435, 1357–1359.
Talbot, C. F., Freeman, H. D., Williams, L. E., & Brosnan, S. F. (2011). Squirrel monkeys’ response to inequitable outcomes indicates a behavioural convergence within the primates. Biology Letters, 7(5), 680–682.
Trivers, R. L. (1971). The evolution of reciprocal altruism. Quarterly Review of Biology, 46(1), 35–57.
Trivers, R. L. (2004). Mutual benefit at all levels of life. Science, 304(14 May 2004), 964.
Van Leeuwen, E. J., Zimmermann, E., & Ross, M. D. (2011). Responding to inequities: Gorillas try to maintain their competitive advantage during play fights. Biology Letters, 7(1), 39–42.
Vonk, J., Brosnan, S. F., Silk, J. B., Henrich, J., Richardson, A. S., Lambeth, S. P., et al. (2008). Chimpanzees do not take advantage of very low cost opportunities to deliver food to unrelated group members. Animal Behaviour, 75(5), 1757–1770.
West, S. A., Mouden, C. E., & Gardner, A. (2011). Sixteen common misconceptions about the evolution of cooperation in humans. Evolution and Human Behavior, 32, 231–262.
Wiessner, P. (2005). Norm enforcement among the Ju/’hoansi Bushmen. Human Nature, 16(2), 115–145.
Wilson, D. S. (1975). A theory of group selection. Proceedings of the National Academy of Sciences, 72(1), 143–146.
Yamagishi, T. (1986). The provision of a sanctioning system as a public good. Journal of Personality and Social Psychology, 51(1), 110–116.
Yee, J. R., Cavigelli, S. A., Delgado, B., & McClintock, M. K. (2008). Reciprocal affiliation among adolescent rats during a mild group stressor predicts mammary tumors and lifespan. Psychosomatic Medicine, 70(9), 1050–1059.
Zahavi, A. (1975). Mate selection-A selection for a handicap. Journal of Theoretical Biology, 53, 205–214.
Acknowledgments
Helpful comments on experimental design were provided by Dominic Johnson, Robert Kurzban, Nikos Nikiforakis, and Toshio Yamagishi. The z-tree code and the experimental instructions for this experiment were modified versions of those received from Nikos Nikiforakis and Hans-Theo Normann from their 2008 paper ‘A Comparative Statics Analysis of Punishment in Public-Good Experiments’. Dominic Donato wrote the new z-tree code, and ran the software during the experiments. The experiments were run in Chapman University’s ESI laboratory, under the guidance of Jennifer Cunningham and Jennifer Brady. The final experimental design and manuscript text remains the responsibility of the author.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Burnham, T.C. Public goods with high-powered punishment: high cooperation and low efficiency. J Bioecon 17, 173–187 (2015). https://doi.org/10.1007/s10818-014-9191-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10818-014-9191-y