Abstract
Fish stocks around the world are heavily overexploited in spite of fishing policies in several parts of the world designed to limit overfishing. Recent studies have found that the complexity of ecological systems and the diversity of species, as well as negative impact of fishing activities on environmental carrying capacity of fish stocks—all contribute to the problem. A number of biologists, managers, and practitioners strongly support the use of marine reserves as a management strategy for marine conservation. This paper contributes to this line of research by seeking an optimum reserve size and fishing effort for situations where species diversity decrease at fishing grounds and fishing activities impact carrying capacity. We found that a reserve size which maximizes economic rents could ruin a fish stock if fishing impacts are not accounted for. On the other hand, the reserve serves as a bifurcation term which could improve the resilience of a marine ecosystem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fishery resources in many parts of the world are heavily overexploited, with some stocks completely collapsed or on the verge of doing so (see e.g., Myers and Worm 2003; Sumaila and Cheung 2009). This phenomenon has also been acknowledged in a Food and Agriculture Organization (FAO) publication, which notes that 69 % of the world’s marine stocks are either fully to heavily exploited, overexploited, or depleted (Lauck et al. 1998). It is estimated that between the mid-1970s and 2005, more than 75 % of the world’s fisheries were underperforming or were subject to economic overfishing (FAO 2006). In a bid to control the over-fishing problem, countries have advanced policies including moratoriums and restrictions on fishing methods (Sterner 2007; NOAA Fisheries 2007). Unfortunately, in spite of seemingly good policies, some fisheries such as the North Sea cod have collapsed (European Environmental Agency 2003; Sterner 2007). A number of emerging studies have attributed the unanticipated overexploitation and collapse to inadequate accounting for species diversity (Sterner 2007; Akpalu 2009; Akpalu and Bitew 2011) and fishing impact on habitats and production of planktons (Armstrong 2007; Armstrong and Falk-Petersen 2008; Akpalu and Bitew 2011). As noted by Arnason et al. (2009), the uncertain dynamics of marine ecosystems could result in the failure of certain stocks, such as Canadian cod stocks, to readily rebuild, despite a reduction in fishing effort.
In recent years, there has been a strong campaign by biologists, economists, managers, and practitioners for the use of marine reserves as a management strategy for marine conservation (Man et al. 1995; Allison et al. 1998; Boersma and Parrish 1999; Pezzey et al. 2000; Sanchirico and Wilen 2001; Armstrong and Skonhoft 2006). This involves protection of critical areas from some or all human activities (Bergen and Carr 2003), in order to conserve species and communities (Allison et al. 1998). Some economists and fishery managers believe reserves are less effective or beneficial than other traditional tools, especially if populations are not overexploited (Holland and Brazee 1996; Bergen and Carr 2003). However, scientists present the contrary argument that reserves generate ecosystem benefits within and outside their boundaries (see e.g., Gell and Roberts 2003) and improve the resilience of ecosystems (see e.g., Apostolaki et al. 2002; Grafton et al. 2009). Worm et al. (2006) noted that large proportions of overfished stocks impact biodiversity and alter ecosystem functioning. An important question which has not been addressed adequately in the bio-economics literature is whether reserves could guarantee resilient ecosystems if fishing alters species diversity, and the fishing impact on habitat is accounted for in calculating catch potentials. This paper seeks to address these important questions.
The current study highlights the use of a marine reserve as a management tool for dampening the negative effect of fishing on carrying capacity, when species are biologically diverse.Footnote 1 To the best of our knowledge this is the first paper that seeks an optimum marine reserve size which simultaneously addresses the issue of species diversity and fishing impact on carrying capacity. Like Akpalu (2009) and Akpalu and Bitew (2011), this paper employs a bioeconomic model that incorporates species diversity. In addition, similar to Akpalu and Bitew (2011), the study accounts for fishing externality on habitat or environmental carrying capacity in fisheries management.
We found that (1) if the reserve-size is large enough and surpasses a certain threshold, the fisheries ecosystem is resilient and the stock may not collapse even if an effort-limiting policy does not account for the negative impacts of fishing activities. Conversely, if the reserve is below the threshold, the fishery could collapse if the negative fishing impact is not accounted for; (2) if fishing impacts habitat, all else equal, the equilibrium reserve size and fishing effort that maximize economic surplus have to be set lower than otherwise; (3) if species diversity is decreasing in the fishing area, all other things being equal, the equilibrium reserve size must increase, but equilibrium fishing effort must be reduced in order to maximize economic surplus; and (4) if future benefits and costs are discounted at a positive rate, 1 through 3 applies but in each case the equilibrium effort and reserve size are set lower than in a zero discount or static scenario.
The remainder of the paper is organized as follows: Section 2 introduces the model. Sect. 3 presents the static model and presents numerical results. Section 4 contains the dynamic version of the model. The final section concludes the paper.
2 The theoretical model
In the following sections (i.e., Sects. 3, 4) static and dynamic models are presented and conditions for optimal reserve sizes and fishing effort have been derived. For each case, three scenarios are discussed: a basic situation where the impact of fishing on the environmental carrying capacity of the stock and phenotypic diversity of the stock are ignored; a second situation where fishing impact on environmental carrying capacity is considered but its effect on phenotypic diversity is not accounted for; and the third scenario where both effects are considered. As noted by Armstrong and Skonhoft (2006), ecological conditions outside a reserve naturally differ from those within the reserve, due to fishing pressure. For example, fishing gears could plane off structures and upset the nutrient content and organisms in sediments if the ocean bottom is soft (Akpalu and Bitew 2011). In addition, fishing equipment may damage corals, boulders, and other bottom-dwelling organisms, thereby reducing the plankton production capacity of the ecosystem. For each of these scenarios, the analytical model assumes that a reserve creation does not affect the intrinsic growth rate of the stock. We begin with the static model followed by the dynamic analysis.
3 Optimum reserve size in a timeless (static) framework
As a first step, consider an analytical model that assumes a marine reserve area has the same ecological condition as the fishing area (see e.g., Levin 1974, 1976; Hastings 1982, 1983; Holt 1985; Sanchirico and Wilen 1998). Following Sanchirico and Wilen (1998), if we assume a sink-source relationship between a fishing area and a reserve area where fish flow from the reserve to the fishing area, the equations of motion defining the stock of fish outside and within a marine reserve are given byFootnote 2
where \(m\in ({0,1})\) is the proportion of the carrying capacity that is set aside as a reserve,Footnote 3 \(x=\frac{X}{K}\) and \(y=\frac{Y}{K}\) are the stocks of fish in the fishing and reserve areas (i.e., \(X\) and \(Y\) respectively) scaled down by the total environmental carrying capacity \((K); h=\frac{H}{K}\) is harvest; \(\mathrm{dot} (\cdot )\) is time derivative; \(d\) is dispersion rate; and \(d\frac{y}{m}\) is the biomass of fish that flows from the reserve to the fishing ground. Like Sanchirico and Wilen (2001) and Conrad (1999), we have assumed symmetric density-dependent stocks. Suppose the growth functions in the fishing and reserve area, \(f\) and \(g\), are logistic (i.e., \(f(y,m)=ry\left( {1-\frac{y}{m}} \right) \), and \(g(x,1-m)=rx\left( {1-\frac{x}{1-m}} \right) \), where \(r\) is the intrinsic growth rate) and the harvest function is of the Schaefer-type (i.e., \(h=\sigma Ex\), where \(E\) is fishing effort and \(\sigma \) is catchability coefficient, a measure of gear effectiveness).
In steady state \(\dot{y}=\dot{x}=0\) implying, from Eq. (2), \(y=m\left( {1-d({mr})^{-1}} \right) \). In addition, from Eq. (1), we haveFootnote 4:
The corresponding yield is
Recall that the instantaneous profit function is\(\pi \left( {E,m} \right) =p\sigma Ex-cE\), and \(Z^{*}\left( {E,m} \right) =\sigma Ex^{*}\left( {E,m} \right) \). Substituting the yield into the instantaneous profit function gives
Figure 1, which is sketched using Mathematica 6.0, presents the plot of the first and second terms on the right hand side of the profit function. The thick and broken concave functions are the revenue function for relatively low and high values of the reserve size, which were arbitrarily chosen. The straight upward sloping line is the cost function. Any vertical gap between the concave and the straight line curves measure the instantaneous profit. Consequently, the largest gap between the two functions determines the level of effort that maximizes profit. From the two concave functions, an increase in the reserve size must be accompanied by lowering the optimum effort level in order to obtain maximum economic surplus from the fishery (i.e., \(E_1 >E_2\)). It is noteworthy that the reserve size cannot be chosen arbitrarily but optimally, and derived from Eq. (5).
The first order condition of Eq. (5) with respect to E and m are as follows:
Equation (6) stipulates that, in equilibrium, the value of the marginal productivity of effort (i.e., \(pZ_E^*\left( {E,m} \right) )\) must equal the marginal cost of effort (i.e., c). According to Eq. (7), in order to maximize economic surplus from the fishery, the social planner must set the reserve size to a level that equates the marginal net benefit from the chosen reserve size to zero. We assume the optimum reserve size lies between zero and one, which eliminates the possibility of zero or infinite yield as per Eq. (4).Footnote 5
3.1 Fishing negatively impacts carrying capacity
To extend the model a step further, let fishing negatively impact carrying capacity, but its impact on phenotypic diversity be ignored. As noted earlier, fishing pressure could impact the nutrient content and organisms in sediments as well as reduce the plankton production capacity of the ecosystem. For ease of exposition, we assume that the impact increases linearly with fishing effort; i.e., \(\varepsilon E\), where \(\varepsilon \in (0,1)\) is a constant. A restriction is imposed on the constant, to ensure that \(\left( {1-m-\varepsilon E} \right) >0\).Footnote 6 The stock evolution within the fishing area is re-specified as
If the negative externality does not extend to the reserve area, following the routine prior calculations, the corresponding steady state stock level similar to Eq. (3) is
The profit function corresponding to Eq. (5) is
where \(Z^{**} \left( {E,m} \right) =\sigma Ex^{**}(E,m)\) is the yield function.
Figure 2 compares the plots of the preceding situation (where fishing does not impact carrying capacity and phenotypic diversity; i.e., \(pZ^*\left( {E,m} \right) )\) to a situation where fishing impacts only carrying capacity (i.e., \(pZ^{**} \left( {E,m}\right) )\). The broken concave functions represent the latter case. Due to the fact that fishing negatively impact the carrying capacity, the results show that, for any given \(m\), the optimum effort must be lower. In addition, in each of the two cases, higher values of \(m\) result in lower equilibrium effort, indicating that all else equal, lower levels of fishing effort must be encouraged if a relatively larger area is devoted to a reserve.
3.2 Fishing negatively impacts carrying capacity and phenotypic diversity
Empirical studies have found that marine reserves significantly improve species diversity (see e.g., Halpern 2003; Russ and Alcala 2011). Conversely, overfishing can have detrimental effects on marine biodiversity and the structure of marine ecosystems (Russ and Alcala 2011). To align our model with realism, consider a situation where in equilibrium there is no significant gain in diversity within the marine reserve, but fishing alters the diversity within the fishing area. To account for the biodiversity, following Norberg et al. (2001), Akpalu (2009), and Akpalu and Bitew (2011), let the per capita growth function of the stock within the fishing area be re-specified as \(f\left( {x,E,m,s} \right) =r\left( {1-\frac{x}{1-m-\varepsilon E}} \right) -\frac{\alpha }{s}\), where \(s\) is average phenotype and \(\alpha \left( {\ge 0} \right) \) is a constant. For tractability, we set \(\alpha =0\) in the reserve area where diversity is at its peak. Furthermore, suppose \(v\) denote phenotypic variance, which represents the spread of individual species phenotypes around the mean, hence a measure of diversity (Akpalu 2009). Thus, since the extra term \(\frac{\alpha }{s}\) in the growth function is non-negative, the stock buildup within the fishing area is slower if diversity is accounted for. Following Akpalu and Bitew (2011), the equation of motion is specified as:
where \(f_{ss} \left( {x,E,m,s} \right) \) is the second order partial derivative of the per capita instantaneous growth rate with respect to \(s\). Note that\(f_{ss} \left( {x,E,m,s} \right) <0\) and a high \(v\) indicates large varieties of species, of which some could be underperforming. As a result, \(vf_{ss} \left( {x,E,m,s} \right) \!<\!0\) implies the average growth rate of the total biomass will be low for relatively large values of \(v\). Using the specific growth function, and assuming the stock in the reserve is in steady state, so that \(y=m\left( {1-\frac{d}{mr}} \right) \), Eq. (11) becomes:
The model uses moment-approximation methods to capture the dynamics of the macroscopic or aggregate characteristics of a functional group of species in terms of total biomass, average phenotype, and phenotypic variance. In addition, since we have assumed the growth function is logistic, it has a global maximum. Also if there are large varieties of species of which some underperform (i.e., if \(v\) is high), the average growth rate of the total biomass will be low. Following Akpalu (2009) and Akpalu and Bitew (2011), we define the equation of motion of the average phenotype as
where \(f_s \left( {x,E,m,s} \right) \) is the first order partial derivative of the per capita instantaneous growth rate with respect to \(s\).
In Eq. (13), the growth in average phenotype increases in the biomass of fish and increases in phenotypic variance, since\(vf_s \left( {x,E,m,s} \right) >0\). Thus, having more diverse species has a direct negative impact on total biomass growth and indirect positive impact through the growth in the average phenotype (Akpalu 2009). In steady state, \(\dot{x}=\dot{s}=0\) and \(s=\left( {vx} \right) ^{1/3}\), we have
where \(x^{\prime }=x^{\prime }\left( {E,m} \right) \) is obtained by solving for the optimum stock from Eq. (14). The related profit function is
where \(Z^{\prime }\left( {E,m} \right) =\sigma Ex^{\prime }(E,m)\) is the yield function.
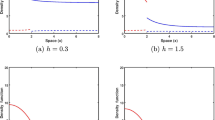
A plot of the two terms in Eq. (15) is presented as Fig. 3. From the figure, relatively low values of the reserve size generate critical depensation in the yield function, implying effort levels beyond a given threshold will collapse the stock (the threshold is the point on the curve \(pZ^{\prime }\left( {E,m_\mathbf{1} } \right) \) where the thick and the dash lines meet). This function is represented by the function with the combination of thick and broken lines (i.e., \(pZ^{\prime }\left( {E,m_\mathbf{1} } \right) )\). However, the yield function indicates noncritical depensation if \(m\) is large enough; meaning the stock within the fishing area is resilient to high effort levels (i.e., \(pZ^{\prime }\left( {E,m_2 } \right) )\). Thus the reserve size is a bifurcation term that could preserve or collapse the stock.
Comparing the three profit functions, it is evident that optimum effort levels could be set higher if we ignore the effects of fishing impacts on carrying capacity and phenotypic diversity within the fishing area. The plots of the three cases are presented in Fig. 4. The compensated yield function (i.e., \(pZ^*\left( {E,m_1 } \right) )\) is the baseline situation which yields the highest optimum effort for any given \(m\). On the other hand, the critical depensation function (i.e., \(pZ^{\prime } ({E,m_1}))\) generates the lowest optimum effort. If the reserve is relatively small, an effort limiting policy may collapse the stock. However if the reserve size is set high enough (i.e., say \(m_2 \)so that the corresponding function is \(pZ^{\prime } \left( {E,m_2 } \right) )\), the equilibrium effort may generate lower economic surplus but will not collapse the stock.
Due to the complicated nature of the functional forms, explicit parametric solutions are long, complicated, and devoid of any direct economics intuition. As a result, the optimal values for the three scenarios are calculated and presented in Appendix Table 3 in the Appendix based on some chosen parameter values in Appendix Table 2, which are derived mostly from studies on anchovies fishing in Ghana.
The results reveal the following:
-
1.
For any given level of phenotypic diversity (i.e., for any given \(v>0\)), the optimum reserve size and fishing effort must be set lower if the impact of fishing on carrying capacity becomes more intense or severe.
-
2.
For any given impact of fishing on carrying capacity (i.e., for a given \(\varepsilon >0\)) and given that diversity is positive (i.e., \(v>0\)) – a lower diversity must be accompanied by bigger reserve size but lower fishing effort and harvest in order to maximize economic surplus.
-
3.
If the negative impact of fishing on habitat is increasing and phenotypic diversity is not accounted for (i.e., \(\nu =0)\), the equilibrium fishing effort and reserve size that maximize economic surplus have to be set lower.
The first result is consistent with the fact that by reducing fishing pressure on the carrying capacity of the fishing ground, all else equal, the reserve size necessary to guarantee maximum economic surplus should be higher. The second result, which is expected, confirms that if the negative fishing impact on carrying capacity is fixed, but biodiversity is decreasing in the fishing area, all else equal, it is better to set a bigger portion of the management area aside as a reserve. This result is also consistent with findings in the literature, which confirm that reserves should be established to improve marine ecosystems (see e.g., Allison et al. 1998). The third result, which builds on the first one, implies that if the diversity in the fishing area remains constant and is equal to zero (i.e., \(\nu =0\); there is no diversity), a higher impact of fishing on the carrying capacity must be accompanied by lower reserve size and lower fishing effort in order to maximize economic surplus. The relative values from the empirical simulations show that the reduction in fishing effort must exceed the reduction in the reserve size. Clearly, ignoring the negative fishing impact on carrying capacity and diversity could result in over-fishing and a possible stock collapse.
4 A dynamic model of optimum reserve size
This section provides a dynamic version of the problem discussed earlier since society exists in perpetuity. Moreover, the dynamic version makes it possible to include discounting in the analysis. Suppose the catch is sold in a competitive market, with a unit price of \(p\) and the cost of harvest \(cE\). The instantaneous profit function is \(p\sigma Ex-cE\). If all future costs and benefits are discounted at a positive social discount rate of \(\delta \), the social planner’s optimization problem can be stated as:
subject to Eqs. (17) and (18). That is,
The corresponding current-value Hamiltonian of the program is specified as:
where \(\lambda \) and \(\mu \) are the shadow or scarcity values of the stock within the fishing area, and the average phenotype respectively. From the maximum principle, the first-order conditions with respect to the flow variables (i.e., fishing effort and reserve size) are denoted by:
The corresponding costate equations areFootnote 7:
Since the fish stock is a renewable resource, the steady state solutions are explored. In steady state \(\dot{s}=\dot{\mu }=\dot{\lambda }=\dot{x}=0\) implying the following:
Like the static case, the preceding results can also be compared to the situations where (1) both fishing impacts on carrying capacity and diversity are ignored, \(\varepsilon =0=\nu \); and (2) fishing impacts carrying capacity, \(\varepsilon >0\), but phenotypic diversity is not accounted for, \(\nu =0\).
The parametric solutions are very complicated and difficult to compute and compare; hence we resort to numerical solutions using the parameter values in Table 2 in the Appendix. The results reported in Table 3 in the Appendix show lower optimum reserve sizes, compared to the static scenario in the preceding section. For example, for the benchmark case where the impact of fishing on carrying capacity and phenotypic diversity are ignored, the 5 % discount rate lowers the optimum effort and reserve size by 39 and 24 % respectively. Generally, the trend holds for all levels of fishing impact on carrying capacity and phenotypic diversity. Moreover, the impact of intensified fishing on carrying capacity requires lowering the reserve size and reducing fishing effort levels. Also, as found in the static case, declining species diversity requires bigger reserve size but lower fishing effort. Most importantly, by extending the model to a dynamic setting, and discounting future costs and benefits at a positive rate of 5 %, optimum effort and reserve size become lower, relative to the static case. In addition the density of the stock in the fishing ground is higher. Intuitively, renewable natural resources are better conserved if long-term views on management are taken into account.
5 Conclusion
Recent studies have found that fishing activities impact species diversity as well as environmental carrying capacity of stocks within fishing areas, which are both negative externalities. These phenomena have been linked to stock depletion and collapse in some parts of the world. On the other hand, marine reserves or protected areas have been found to improve and restore the health of ecological systems. Since setting aside a reserve has an opportunity cost of taking up a portion of a fishing ground, the planner faces a dilemma of deciding how large the reserve should be in order to internalize the externalities and avoid catastrophic collapse. Our study, which sought to address this issue, has found that ignoring the externalities results in overestimating catch potentials and the optimum marine reserve size.
Conversely, if the reserve size is high enough, net economic surplus levels will be low but the stock will not collapse if the fishing impacts are not accounted for. Thus, a reserve size is a bifurcation term that could potentially guarantee the resilience of a fishery. It is imperative that fisheries managers consider a reserve not only as a tool for addressing an overharvesting problem but also as an instrument which could inherently generate multiple dividends.
Furthermore, the results show that, in order to maximize economic surplus from the fishery, fishing efforts and reserve size must be reduced if the impact of fishing on carrying capacity intensifies. This finding has an intuitive appeal: If fishing activities quicken the depletion of a fish stock within a fishing ground, then less fishing effort should be permitted. Moreover, if the effort level is relatively low, then a lower reserve size is necessary to guarantee a maximum economic surplus.
Also, the fisheries manager may have to increase the reserve size and lower the fishing effort if species diversity in the fishing ground is decreasing. This finding supports the claim that marine reserves preserve or improve biodiversity. In situations where fishing impacts are difficult to ascertain, reserve sizes could be set high enough to prevent stock collapse.
Finally, in a dynamic setting where society discounts future costs and benefits at a positive rate, the results show that optimum fishing effort and the reserve size must be set lower, but density of fish within the fishing ground must be kept higher than the static case. Thus, from a sustainability point of view, it is important for fisheries managers to limit current harvest levels in order to maximize the perpetual stream of net benefits from the fishery.
The results from this study provide some general policy directions, but the study is limited due to lack of better empirical data for the analysis. In order to generate the optimal values necessary for policy making in specific situations, it would be very helpful to have further empirical analysis of other specific cases.
Notes
Carrying capacity and habitat are used interchangeably since destruction of habitat reduces primary food production for the fish stock.
An alternative specification of the link between the reserve and the fishing area is to assume a density-dependent dispersion or diffusion model (see, e.g., Hannesson 1998; Kramer and Chapman 1999; Neubert 2003; Reithe 2006). Under sink-source flows, the level of dispersal is dependent on the size of the protected area but not the relative densities of the reserve and the fishing area. As a result, if a sink-source is assumed, a minimum size of a protected area is necessary to guarantee that benefits of having a reserve offset the effects of reduced fishing area. We surmise a sink-source relationship for convenience and also because human predation within the fishing area lowers the density in the source and makes the net flow unidirectional (from the source to the sink).
The proportion of the carrying capacity set aside as reserve could be specified as \(m=\frac{M}{K}\), where \(M\) is the absolute part of the carrying capacity found inside the reserve, and \(K\) is the environmental carrying capacity.
Note that if \(m\rightarrow 1, x^{*}\rightarrow 0\) and \(h^{*}\rightarrow 0\) implying there will be no human predation.
This assumption is confirmed by the numerical illustrations presented in the Appendix.
As discussed in Armstrong and Falk-Petersen (2008), fishing gears negatively impact habitats hence the carrying capacity of the stock. Thusly, the difference in carrying capacity between any two periods depends on the fishing effort within that period. An alternative specification is to make a time derivative of the carrying capacity a function of effort but this may yield results similar to what is obtained from our specification if the time derivative is zero in the absence of any fishing effort.
Since the problem does not have a terminal condition, the following limit conditions satisfy the sufficient optimality condition: \(\frac{\lim }{t\rightarrow \infty }\lambda (t).\left( {x_t -x^{*}} \right) \ge 0\) and \(\frac{\lim }{t\rightarrow \infty }\mu (t).\left( {s_t -s^{*}} \right) \ge 0\).
Although there are multiple equilibrium values of the variables of interest for each set of parameter values, only one of them has all positive values for all the variables in the model, hence it is considered admissible. This situation applies to the dynamic model presented in the next section as well.
References
Akpalu, W. (2009). Economics of Biodiversity and Sustainable Fisheries Management. Ecological Economics, 68, 2729–2733.
Akpalu, W., & Bitew, W. T. (2011). Species diversity, fishing induced change in carrying capacity and sustainable fisheries management. Ecological Economics, 70(7), 1336–1343.
Allison, G. W., Lubchenco, J., & Carr, M. H. (1998). Marine reserves are necessary but not sufficient for marine conservation. Ecological Applications, 8(Suppl 1), S79–S92.
Apostolaki, P., Milner-Gulland, E. J., McAllister, M. K., & Kirkwood, G. P. (2002). Modeling the effects of establishing a marine reserve for mobile fish species. Canadian Journal of Fisheries and Aquatic Sciences, 59, 405–415.
Armstrong, C. W. (2007). A note on the ecological-economic modeling of marine reserves. Ecological Economics, 62, 242–250.
Armstrong, C. W., & Falk-Petersen, J. (2008). Habitat-fisheries interactions: a missing link? ICES Journal of Marine Science, 65, 817–821.
Armstrong, C. W., & Skonhoft, A. (2006). Marine reserves: A bio-economic model with asymmetric density dependent migration. Ecological Economics, 57, 466–476.
Arnason, R., Killeher, K., & Willman, R. (2009). The Sunken Billions - The Economic Justification for Fisheries Reform. Washington, Rome: The World Bank and FAO.
Bergen, L. K., & Carr, M. H. (2003). Establishing Marine Reserves: How Can Science Best Inform Policy. Environment, 45(2), 8–19.
Boersma, D. P., & Parrish, J. K. (1999). Limiting abuse: marine protected areas, a limiting solution. Ecological Economics, 31, 287–304.
Conrad, J. M. (1999). Resource economics. New York: Cambridge University Press.
European Environmental Agency. (2003). Fishery indicators. Copenhagen: EEA.
FAO. (2006). The state of world highly migratory, straddling and other high seas fishery resources and associated species. FAO Fisheries Technical Papers, 495.
Gell, F. R., & Roberts, C. M. (2003). Benefits beyond boundaries: The fishery effects of marine reserves and fishery closures. Trends in Ecology and Evolution, 18, 448–455.
Grafton, R. Q., Kompas, T., & Van Ha, P. (2009). Cod today and none tomorrow: The economic value of a marine reserve. Land Economics, 85(3), 454–469.
Halpern, B. S. (2003). The impact of marine reserves: Do reserves work and does reserve size matter? Ecological Applications, 13(1), S117–S137.
Hannesson, R. (1998). Marine reserves: What would they accomplish? Marine Resource Economics, 13, 159–170.
Hastings, A. (1982). Dynamics of a single species in a spatially varying environment: The stabilizing role of high dispersal rates. Journal of Mathematical Biology, 16, 49–55.
Hastings, A. (1983). Can spatial variation alone lead to selection for dispersal? Theoretical Population Biology, 24, 244–251.
Holland, D. S., & Brazee, R. J. (1996). Marine reserves for fisheries management. Marine Resource Economics, 11, 157–171.
Holt, R. D. (1985). Population dynamics in two-patch environments: Some anomalous consequences of an optimal habitat distribution. Theoretical Population Biology, 28, 181–208.
Koranteng, K. A. (1993). Size at first maturity of the anchovy (Engraulis encrasicolus) in Ghanaian waters and suggestions for appropriate mesh size in its fishery. NAGA, the ICLARM Quarterly, CEOS Contribution No. 19.
Kramer, D. L., & Chapman, M. R. (1999). Implications of fish home range size and relocation for marine reserve function. Environmental Biology of Fishes, 55, 65–79.
Lauck, T., Clark, C. W., Mangel, M., & Munro, G. R. (1998). Implementing the precautionary principle in fisheries management through marine reserves. Ecological Applications, 8, S72–S78.
Levin, S. A. (1974). Dispersion and population interactions. The American Naturalist, 108(960), 207–227.
Levin, S. A. (1976). Population dynamic models in heterogeneous environments. Annual Review of Ecological Systems, 7, 287–310.
Man, A., Law, R., & Polunin, N. V. C. (1995). Role of marine reserves in recruiting to reef fisheries: A metapopulation model. Biological Conservation, 71, 197–204.
Myers, R. A., & Worm, B. (2003). Rapid worldwide depletion of predatory fish communities. Nature, 423, 280–283.
NOAA Fisheries. (2007). Status of fisheries 2005.
Norberg, J., Swaney, D. P., Dushoff, J., Lin, J., Casagrandi, R., & Levin, S. A. (2001). Phenotypic diversity and ecosystem functioning in changing environments: A theoretical framework. Proceedings of the National Academy of Sciences of the United States of America, 98(20), 11376–11381.
Neubert, M. G. (2003). Marine reserves and optimal harvesting. Ecology Letters, 6, 843–849.
Pezzey, J. C. V., Roberts, C. M., & Urdal, B. T. (2000). A simple bioeconomic model of a marine reserve. Ecological Economics, 33, 77–91.
Reithe, S. (2006). Marine reserves as a measure to control bycatch problems: The importance of multispecies interactions. Natural Resource Modeling, 19, 221–242.
Rowse, J. (2004). Using the wrong discount rate to allocate a marine resource. Marine Resource Economics, 19, 243–264.
Russ, G. R., & Alcala, A. C. (2011). Enhanced biodiversity beyond marine reserve boundaries: The cup spillith over. Ecological Applications, 21, 241–250.
Sanchirico, J. N., & Wilen, J. E. (1998). Marine reserves: Is there a free lunch? Resources for the Future, Discussion Paper, No. 99–02, Washington DC.
Sanchirico, J. N., & Wilen, J. E. (2001). Bioeconomics of marine reserve creation. Journal of Environmental Economics and Management, 42(3), 257–276.
Silva, G., Horne, J. B., & Castilho, R. (2014). Anchovies go north and west without losing diversity: Post-glacial range expansions in a small pelagic fish. Journal of Biogeography. doi:10.1111/jbi.12275.
Sterner, T. (2007). Unobserved diversity, depletion and irreversibility: The importance of subpopulations for management of cod stocks. Ecological Economics, 16(2–3), 566–574.
Sumaila, U. R., & Cheung, W. W. L. (2009). Vulnerability and sustainability of marine fish stocks worldwide: With emphasis on fish stocks of the commonwealth of nations. In R. Bourne, & M. Collins (Eds.), From hook to plate: The state of marine fisheries: A Commonwealth perspective (pp. 195–210).
Worm, B., Barbier, E. B., Beaumont, N., Duffy, J. E., Folke, C., Halpern, B. S., Jackson, J. B. C., Lotze, H. K., Micheli, F., Palumbi, S. R., Sala, E., Selkoe, K. A., Stachowicz, J. J., & Watson, R. (2006). Impacts of biodiversity loss on ocean ecosystem services. Science, 314, 787–790.
Acknowledgments
The authors are indebted to two anonymous reviewers and the editor of this journal for their insightful comments. We are also grateful to the participants at the Applied Economics and Mathematics seminar at SUNY-Farmingdale for their comments. We would like to acknowledge the Center for Environmental Economics Research & Consultancy (CEERAC) for supporting this research.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Numerical illustration
Our numerical illustration is largely based on data from anchovies fishing in Ghana. The marine fish resources of Ghana include small pelagic, demersal, mollusc and crustaceans, and large pelagic species. The small pelagic species are mainly sardinellas, mackerels and anchovies. The anchovies in the eastern Atlantic Ocean bordering Ghana are known as European anchovies (Engraulis encrasicolus). It is considered one of the most important marine fish species in Ghana contributing up to 25 % of total fish landings (Koranteng 1993; also confirmed by data on current landings). In addition to contributing directly to the protein requirement of Ghanaians, the anchovies are used as fish meal and live baits by boats mainly fishing tuna for export. Studies have found that two mitochondrial clades were present in samples taken from the eastern Atlantic (from Ghana to Norway), with the frequency of each clade varying by latitude (Silva et al. 2014). In recent times, fishing pressure resulting from overcapitalization and the use of very small mesh sizes, is leading to a general decline of the stock.
To obtain some reasonable parameter values, data on catch of anchovies and fishing effort (i.e., number of fishing trips) covering the period of January 2000 to December 2009 (with data for 2007 missing) were used to estimate a simple Gordon-Schaefer type yield function. The function is of the form \(Y_t =aE_t +bE_t^2 +\mu _t \), where \(a=\sigma K\) and \(b=-\frac{\sigma ^{2}K}{r}\) are parameters to be estimated; and \(\mu _t \sim N\left( {0,\sigma _\mu } \right) \). The average monthly catch is about 40 tons, with a corresponding monthly average fishing effort of 20,600 trips. The standard deviations for catch and effort are 1.49 and 0.19, respectively, which are quite low. The regression results reported in Appendix Table 1 indicate that the line is a good fit, with an adjusted \(R^{2}=0.94\). Furthermore, both coefficients estimated were statistically significant at 1 % level. Since we estimated only two parameters, a and b, it is impossible to recover the three parameters (i.e., \(\sigma , K\), and \(r\)), hence we borrowed the intrinsic growth rate for anchovies \((r=0.4)\) from Rowse (2004) and then computed the remainder (i.e., \(\sigma , K\)). Using these and other parameter values from Appendix Table 2, the corresponding results are computed and reported in Appendix Table 3.Footnote 8
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Akpalu, W., Bitew, W.T. Optimum reserve size, fishing induced change in carrying capacity, and phenotypic diversity. J Bioecon 16, 289–304 (2014). https://doi.org/10.1007/s10818-014-9178-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10818-014-9178-8