Abstract
We address the challenges of scaling verification efforts to match the increasing complexity and size of systems. We propose a research agenda aimed at building a performant proof engine by studying the asymptotic performance of proof engines and redesigning their building blocks. As a case study, we explore equational rewriting and introduce a novel prototype proof engine building block for rewriting in Coq, utilizing proof by reflection for enhanced performance. Our prototype implementation can significantly improve the development of verified compilers, as demonstrated in a case study with the Fiat Cryptography toolchain. The resulting extracted command-line compiler is about 1000\(\times \) faster while featuring simpler compiler-specific proofs. This work lays some foundation for scaling verification efforts and contributes to the broader goal of developing a proof engine with good asymptotic performance, ultimately aimed at enabling the verification of larger and more complex systems.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This paper is about verification at scale. We investigated and worked on scalable verification concretely via improving Fiat Cryptography [16] which generates code for big-integer modular arithmetic at the heart of elliptic-curve-cryptography algorithms. Routines generated (with proof) with Fiat Cryptography now ship with all major Web browsers and all major mobile operating systems. However, a paper about scaling would be lacking if limited to the scale of current projects instead of the scale of possible projects.
1.1 Blue Sky
Let us ask an ambitious question: What would it take for verification to keep pace with the scale of the largest computations being run?
Any less ambitious performance goal for automated proof tooling can be expended to fall short of real-world use cases where rigorous verification would be appreciated. Across projects, verification typically involves a 10\(\times \) – 100\(\times \) overhead in lines of verification over lines of code being verified [22]. The largest of current verification projects are a little more than \(10^6\) lines of verification code. This overhead, of course, is limiting the applicability of formal verification, so it makes sense to look at use cases that have not yet been tackled.
The standard list of software bug disasters cited in verification papers includes Intel Pentium’s $475 M chip recall over a floating point division bug [17, 25, 45], the crashing of NASA’s $235 M Mars Climate Orbiter [32, 35, 39], Therac-25 radiation overdoses [3, p. 434] [34, 38], the loss of the $370 M Ariane 5 rocket [15, 28, 40], and Knight Capital’s loss of $460 M in 45 min due to a configuration bug [37]. Scaling verification to similar systems to prevent future mishaps will require qualitatively improving the peformance characteristics of verification tools.
But one may wish to aim even higher: Large Language Models (LLMs) are part of a young and vibrant field, and gaining correctness guarantees about them is both obviously desirable and an open, nebulous problem. These “programs” consist of a small handful of relatively simple matrix operations arranged in standard ways, operating on truly massive matrices. The size of these programs is measured by the number of parameters of the model; each entry in a matrix is a single parameter. LLM size has grown at a rate of approximately \(10\times \) per year, increasing from around 94 million parameters in 2018 to over 500 billion in 2021 [50]. Wildly extrapolating from current projects, verifying an LLM would take \(10^{12}\)–\(10^{13}\) lines of verification code. This would require increasing our largest efforts thus far by at least 6 orders of magnitude!
Of course, there are a number of challenges in understanding, let alone verifying, machine-learning-derived artifacts—but this does not appear to be an issue for practical deployment and subsequent consequences, so it would be dissatisfying to just give up! So far, the reported consequences of occasional incorrect operation of these systems have been indirect and thus hard to compare, but they already cover a wide range from suicide [55] to slander [53] to corporate embarrassment [26, 31] and $100B valuation impact [13]. Even if we leave aside fuzzy specifications like “never encourages harming anyone” or “provides only helpful and truthful responses, except when doing so would encourage harm” and just seek to verify basic properties of LLMs that would be feasibly ascertainable about a conventional program, the sheer size of LLMs is a non-starter by itself. For example, we can still seek to prove that “basic arithmetic expressions of 20 characters or fewer are always accurately completed”,Footnote 1 or, more ambitiously, “every response to any query contains an ‘end-of-sequence’ delimiter within the first 32k tokens” or “for any response \({\mathcal {R}}\) ever given by the model, the completion of the query ‘Answer with a single word, either Yes or No: Is the following text hate-speech? \({\mathcal {R}}\)’ will always be ‘No.’” But for goals of this kind, trustworthy and efficient formal analysis of comparably large programs appears to be a strict prerequisite.
When looking to scale computer-checked proofs, there are two basic approaches available to us: we can produce a machine-checkable proof, or we can write a computational validator that we trust or prove correct. The latter approach shines when the domain of reasoning is well-delimited: SMT solvers, for example, are great on domains that they naturally support. But when the domain of reasoning is open and unbounded—as in any evolving, real-world product such as compilers, microkernels, file systems, hardware designs—we need machine-checkable proofs, likely relying on proven-correct or proof-producing domain-specific validators whenever appropriate.
While hand-written machine-checkable proofs may suffice for some of the applications currently targeted by verification, we cannot hope to scale such effort as we aim ourselves at larger and larger applications. We need automation to generate the proofs for us.
The framework atop which we build automatic generation of machine-checkable proofs is a proof engine. A proof engine consists of proven correct or trusted building blocks that can be modularly combined to form proofs, and this set of building blocks must be powerful or complete enough to prove any property we might want to validate.
Naively, automated approaches should scale linearly with input size. The trouble is that proof engine performance often scales exponentially in the size of programs being verified [22]. For example, as we’ll see in Sect. 2, exponential scaling means that proof automation that succeeds in seconds on toy examples would not complete within the lifetime of the universe on real-world examples! Then the grand target is A proof engine with good asymptotic performance.
1.2 Performant Rewriting
We see two sets of research priorities for building a performant proof engine:
-
Studying proof engines: What is the asymptotic performance of proof engines? What’s fast, what’s slow, and why? What algorithms would get around the slowness?
-
Redesigning proof engine building blocks: Once we have algorithms that are asymptotically faster than existing proof engines, what do we need to close the gap between “having a performant algorithm” and getting an actually usable proof engine building block?
We took a stab at this research for equational rewriting, an essential technique for simplifying expressions, proving equivalence between programs, and streamlining the development of verified systems. Among the 70 or so developments tested in the Continuous Integration of Coq, our target proof assistant, the rewrite tactic occurs over 350,000 times, being surpassed only by apply.
Unfortunately, it appears that building blocks provided by current proof engines do not allow for a performant direct implementation of rewriting on their data structures. In this paper, we study the underpinnings of the asymptotic performance inadequacies of equational rewriting built atop existing proof engines, and demonstrate how to use proof by reflection to integrate an efficient implementation of a rewriting proof engine building block.
Proof by reflection is a well-known strategy for performance, enabling leveraging the efficiency of writing dedicated computational verifiers within general purpose proof assistants. Once we write and prove correct an efficient computation that checks a given property holds, we can combine the correctness proof with the primitives for fast full reduction shipped in Coq’s kernel, via a virtual machine [19] or compilation to native code [6].
We presented our prototype implementation of a rewrite building block in Accelerating Verified-Compiler Development with a Verified Rewriting Engine [21], where we described our design, implementation, and performance evaluation. In that paper we introduced our framework as a novel and powerful tool for formally verified rewriting in Coq, demonstrating its potential to improve the development of verified compilers, like CompCert [33] and CakeML [30], through a case study with Fiat Cryptography. In this extended version, we explore our prototype implementation in context of building performant proof engines. In Sects. 2 and 3 we investigate the inadequacy of the status quo for rewriting and provide explanations for contributing factors. In Sect. 4 we lay out a desiderata for adequate proof engine building block for rewriting, against which we evaluate our prototype in Sect. 5. Then we reprise the content of Accelerating Verified-Compiler Development with a Verified Rewriting Engine [21] in Sects. 6 to 8. Finally, we lay out a research agenda in Sect. 9 for developing our prototype into an adequately performant, modular, and complete proof engine building block.
The paper focuses primarily on dependently typed proof assistants like Coq. Where our limited expertise allows, we make some comparisons with Isabelle/HOL. A more thorough evaluation of performant proof engine building blocks in other proof assistants might be useful.
2 Where is the Status Quo on Rewriting?
Many proof assistants, Coq included, ship with equational rewriting tactics. Let us start by evaluating the rewriting tactics on Fiat Cryptography, a real-world project that generates 10–100 s lines of code per function.
Fiat Cryptography uses rewriting and partial evaluation to specialize generic templates for performing big-integer modular arithmetic to specific primes and machine architectures. The generic templates are written as functional programs which can be both implemented and proven correct with just a handful of lines of code and proof. The code output is straightline C (or Go, Rust, Zig, etc.), avoiding loops, branching constructs, and memory allocation; these demands are used to meet the requirement that code used to implement internet security be efficient and timing-side-channel-free.
The relevant parameter for performance scaling evaluation in Fiat Cryptography is the number of limbs: modular arithmetic of big integers is performed by carving each big integer up into multiple 32- or 64-bit machine words. The number of machine words used to represent a single big integer is the number of limbs. For any given arithmetic template, the total number of lines of code in the output of the Fiat Cryptography compiler is determined almost entirely by the number of limbs used. The smallest of toy examples might use one or two limbs; widely-used Curve25519 implementations use 5 limbs on 64-bit machines (10 limbs on 32-bit machines) to represent numbers up to \(2^{255}-19\); P-256 uses 4 limbs (or 8 limbs) for numbers up to around \(2^{256}\); P-384 uses 6 limbs (or 12 limbs) for numbers up to around \(2^{384}\). Our largest example, P-521, uses 9 limbs (or 18 limbs) to represent numbers up to around \(2^{521}\).
When attempting to use
 for partial evaluation and rewriting on unsaturated Solinas on a prime requiring 4 limbs, we ran into an out-of-memory error after using over 60 GB RAM! See Coq bug #13576 for more details and for updates. Then we painstakingly optimized typeclass instances and rewriting lemmas so that we could use rewrite_strat instead, which does not require duplicating the entire goal at each rewriting step. We arrived at invocation involving sixteen consecutive calls to rewrite_strat with varying arguments and strategies. While we were able to get up to 4 limb examples, extrapolating from the exponential asymptotics of the fastest growing subcall to rewrite_strat indicates that our smallest real-world example of 5 limbs would take 11 h, and our largest real-world example of 17 limbs would take over 1000\(\times \) the age of the universe. See Fig. 1 and see Coq bug #13708 for more details and updates.
for partial evaluation and rewriting on unsaturated Solinas on a prime requiring 4 limbs, we ran into an out-of-memory error after using over 60 GB RAM! See Coq bug #13576 for more details and for updates. Then we painstakingly optimized typeclass instances and rewriting lemmas so that we could use rewrite_strat instead, which does not require duplicating the entire goal at each rewriting step. We arrived at invocation involving sixteen consecutive calls to rewrite_strat with varying arguments and strategies. While we were able to get up to 4 limb examples, extrapolating from the exponential asymptotics of the fastest growing subcall to rewrite_strat indicates that our smallest real-world example of 5 limbs would take 11 h, and our largest real-world example of 17 limbs would take over 1000\(\times \) the age of the universe. See Fig. 1 and see Coq bug #13708 for more details and updates.
We also tried rewriting in Lean in the hopes that a proof assistant specifically optimized for performance would be up to the challenge. Although Lean performed about 30% better than Coq’s
 on the 1-limb example, taking a bit under a minute, it did not complete on the two-limb example even after four hours (after which we stopped trying), and a five-limb example was still going after 40 h.
on the 1-limb example, taking a bit under a minute, it did not complete on the two-limb example even after four hours (after which we stopped trying), and a five-limb example was still going after 40 h.
In Fig. 7e we will see that using our rewriting prototype for Fiat Cryptography results in a tool that can synthesize code for 32-bit P-521 in under four minutes.
3 Why is the Status Quo so Slow?
In Fiat Cryptography, we ease proving correctness of the arithmetic templates by using a shallowly embedded representation, implementing cryptographic primitives as functions in Coq’s functional programming language Gallina. This shallow embedding forces us to encode subterm sharing using
 binders, one binder for each variable assignment. All of the rewriting performance bottlenecks we encountered that scale superlinearly in the number lines of code result from underlying superlinear scaling of rewriting in the number of binders.
binders, one binder for each variable assignment. All of the rewriting performance bottlenecks we encountered that scale superlinearly in the number lines of code result from underlying superlinear scaling of rewriting in the number of binders.
Detailed debugging reveals six performance bottlenecks in the existing rewriting tactics (\({\texttt {rewrite}}\),
 ) in Coq. These bottlenecks contribute to the scaling we see in the microbenchmark of Fig. 7b, which is explained in more detail in Sect. 8.2 and in complete detail in Appendix C.2, “Rewriting Under Binders: UnderLetsPlus0”, in the arXiv version of our ITP submission [21].
) in Coq. These bottlenecks contribute to the scaling we see in the microbenchmark of Fig. 7b, which is explained in more detail in Sect. 8.2 and in complete detail in Appendix C.2, “Rewriting Under Binders: UnderLetsPlus0”, in the arXiv version of our ITP submission [21].
3.1 Inefficient Matching Representations Involving Existential-Variable Contexts
We found that even when there are no occurrences fully matching a given rewrite rule,
 can still be cubic in the number of binders (or, more accurately, quadratic in the number of binders with an additional multiplicative linear factor of the number of head-symbol matches). It is easy to end up in a situation where the majority of time in
can still be cubic in the number of binders (or, more accurately, quadratic in the number of binders with an additional multiplicative linear factor of the number of head-symbol matches). It is easy to end up in a situation where the majority of time in
 is spent dealing with partial matches that ultimately fail to match.
is spent dealing with partial matches that ultimately fail to match.
We posit that the overhead in this microbenchmark comes from
 looking for head-symbol matches and then creating evars (existential variables) to instantiate the arguments of the lemmas for each head-symbol-match location. Even if there are no matches of the rule as a whole, there may still be head-symbol matches!
looking for head-symbol matches and then creating evars (existential variables) to instantiate the arguments of the lemmas for each head-symbol-match location. Even if there are no matches of the rule as a whole, there may still be head-symbol matches!
Coq uses a locally nameless representation [2] for its terms, so evar contexts are necessarily represented as named contexts. Representing a substitution between named contexts takes linear space, even when the substitution is trivial, resulting in each evar incurring linear overhead in the number of binders above it. Furthermore, fresh-name generation in Coq is quadratic in the size of the context, and since evar-context creation uses fresh-name generation, the additional multiplicative factor likely comes from fresh-name generation [23].
To eliminate the overhead in the microbenchmark, Coq would likely have to represent identity evar contexts using a compact representation, which is only naturally available for de Bruijn representations.Footnote 2 Any rewriting system that uses unification variables with a locally nameless (or named) context will incur at least quadratic overhead on this benchmark!
Note that rewrite_strat uses exactly the same rewriting engine as
 , just with a different strategy. We found that
, just with a different strategy. We found that
 and
and have identical performance when there are no matches and generate identical proof terms when there are matches. Hence we conclude that the difference in performance between rewrite_strat and
have identical performance when there are no matches and generate identical proof terms when there are matches. Hence we conclude that the difference in performance between rewrite_strat and
 is entirely due to an increased number of failed rewrite attempts.
is entirely due to an increased number of failed rewrite attempts.
3.2 Proof-Term Size
Setting aside the performance bottleneck in constructing the matches in the first place, we can ask the question: how much cost is associated to the proof terms? One way to ask this question in Coq is to see how long it takes to run \(\texttt {Qed}\). While \(\texttt {Qed}\) time is asymptotically better than proof construction time, it is still quadratic in the number of binders. This outcome is unsurprising, because the proof-term size is quadratic in the number of binders. On this microbenchmark, we found that \(\texttt {Qed}\) time hits one second at about 250 binders, and using the best-fit quadratic line suggests that it would hit 10 s at about 800 binders and 100 s at about 2 500 binders. While this may be reasonable for our microbenchmarks, which only contain as many rewrite occurrences as there are binders, it would become unwieldy to try to build and typecheck such a proof with a rule for every primitive reduction step, which would be required if we want to avoid manually converting the code in Fiat Cryptography to continuation-passing style.
The quadratic factor in the proof term comes because we repeat subterms of the goal linearly in the number of rewrites. For example, if we want to rewrite
 into
into
 by the equation \(\mathtt {\forall }\)
by the equation \(\mathtt {\forall }\) , then we will first rewrite
, then we will first rewrite
 into
into
 , and then rewrite
, and then rewrite
 into
into
 . Note that
. Note that
 occurs three times (and will continue to occur in every subsequent step). Also note that the duplication appears already in the statements of the intermediate theorems being proven, so it would be a consideration regardless of the representation of the proofs themselves.
occurs three times (and will continue to occur in every subsequent step). Also note that the duplication appears already in the statements of the intermediate theorems being proven, so it would be a consideration regardless of the representation of the proofs themselves.
Although the rewrite_strat tactic makes some effort to avoid duplication in the proof term, doing much better than any of the other tactics shipped with Coq, it still produces proof terms that are far from optimal. While multiple rewrites can be chained on subterms without having to duplicate the surrounding context, no effort is made to avoid duplicating subterms at different depths in the AST.
3.3 Poor Subterm Sharing
How easy is it to share subterms and create a linearly sized proof? While it is relatively straightforward to share subterms using \(\texttt {let}\) binders when the rewrite locations are not under any binders, it is not at all obvious how to share subterms when the terms occur under different binders. Hence any rewriting algorithm that does not find a way to share subterms across different contexts will incur a quadratic factor in proof-building and proof-checking time, and we expect this factor will be significant enough to make applications to projects as large as Fiat Crypto infeasible.
3.4 Asymptotic Performance Challenges in Rewriting
Even setting aside the sharing and typechecking problems of proof-term checking, there is still an asymptotic bottleneck in generating such a proof term, or implementing the rewriting in an incremental manner at all. We specifically consider here a rewriting tactic which is built from smaller correct and modular primitives. A good proof engine allows combining its primitive building blocks efficiently while still getting local error messages about mistakes; proving would be quite tricky if there was no feedback on incorrect proofs until \(\texttt {Qed}\)-time!
Rather than considering a concrete microbenchmark in this subsection, we analyze asymptotic performance of the pseudocode of Figs. 2 and 3.
Consider the dataflow-directed rewriter
 , parametrized by a local rewriting function
, parametrized by a local rewriting function
 (“rewrite head”). Both
(“rewrite head”). Both
 and
and
 and take as input a expression
and take as input a expression
 in which rewriting will be performed, and return either “nothing to rewrite” or an expression
in which rewriting will be performed, and return either “nothing to rewrite” or an expression
 and the theorem e’ = e. The analysis here will only assume that the representation of a theorem allows its statement to be read out, allowing for instantions with explicit proof terms or LCF-style abstract types. A simple rewrite-head function would match its input against the left-hand side of a quantified equality theorem, and return (an instantiated version of) the right-hand side and the theorem in case of success.
and the theorem e’ = e. The analysis here will only assume that the representation of a theorem allows its statement to be read out, allowing for instantions with explicit proof terms or LCF-style abstract types. A simple rewrite-head function would match its input against the left-hand side of a quantified equality theorem, and return (an instantiated version of) the right-hand side and the theorem in case of success.
 simply recurses over the structure of the expression, applying
simply recurses over the structure of the expression, applying
 at each node after rewriting it recursively. The application case appears in Fig. 2 on the facing page.
at each node after rewriting it recursively. The application case appears in Fig. 2 on the facing page.
The intent of the code is clear as far as to which expressions and theorems it manipulates (returning
 and
and
 ), but to understand the performance we also need to pay attention to how these objects are represented. As each theorem must at least include its statement, we have eight occurrences of the function argument if both matches succeed: in the input expression (
), but to understand the performance we also need to pay attention to how these objects are represented. As each theorem must at least include its statement, we have eight occurrences of the function argument if both matches succeed: in the input expression (
 ), the expression after recursive rewriting (
), the expression after recursive rewriting (
 ), the theorem that relates the two (
), the theorem that relates the two (
 ), the
), the
 applied to the same expressions and its equality proof (
applied to the same expressions and its equality proof (
 and
and
 ), the expression after rewriting in mid the head position (
), the expression after rewriting in mid the head position (
 ) and its equality proof (
) and its equality proof (
 ), and the combined equality proof for the two rewriting steps (rw (f x)). In this example, straightforward sharing of syntactic subexpressions using aliasing pointers can completely avoid storing multiple copies of the expression, relying on run-time automatic memory management as one would expect given the ML-like syntax in the example. Both Coq and Lean implement this optimization.
), and the combined equality proof for the two rewriting steps (rw (f x)). In this example, straightforward sharing of syntactic subexpressions using aliasing pointers can completely avoid storing multiple copies of the expression, relying on run-time automatic memory management as one would expect given the ML-like syntax in the example. Both Coq and Lean implement this optimization.
However, maintaining sharing in memory is only the beginning: it is also important to avoid duplicate computation on the implicitly shared subexpressions. The strategy in Lean is centered around memoizing functions commonly applied to terms where loss of sharing would result in dramatic slowdown, whereas Coq developers seek to minimize the use of functions that would be slow on expressions whose form without sharing is large. In both cases, developments using the proof engine have come to rely on the speedups.
We will return to deduplication of computation shortly, but first, let’s analyze how the general strategy so far fares in expressions that contain binders in the expression itself. The \(\lambda \) abstraction case is shown in Fig. 3.
The challenge in this case is the representation of the two components of the return value: the expression and the theorem. Unlike the function application case, the theorem is no longer constructed directly from the new expression, rather both are the result of beta-reducing different applications of the lambda under which the recursive rewriting is performed. Depending on the underlying term representation, the two copies of the resulting expression may even not be represented using identical meta-language objects. Further, the notation these examples elides “lifting”—extracting a well-typed term in an initial context and then using it in a strictly extended context—which is non-trivial in representations involving de Brujin indices. Implementing this pseudocode using the Coq ML API would likely result the expression being copied 5 times: lifting
 over
over
 , lifting
, lifting
 over
over
 , substituting
, substituting
 into
into
 , lifting
, lifting
 over
over
 , and substituting
, and substituting
 into
into
 . It is possible to generate the same proof term in linear time, but we are not aware of any existing term representation where this can be achieved using a small set of generic primitive operations supporting dependent types whose soundness can be checked incrementally.
. It is possible to generate the same proof term in linear time, but we are not aware of any existing term representation where this can be achieved using a small set of generic primitive operations supporting dependent types whose soundness can be checked incrementally.
Note that if we drop the requirement for dependent type support, we could implement such an algorithm in Isabelle/HOL. Although rewriting suffers from a similar quadratic asymptotic blowup in the standard kernel, this blowup can be avoided when using a kernel based on nominal binders. In Isabelle’s nominal kernel, closing an open term over a binder is \({\mathcal {O}}(1)\): an open nominal term can be closed without walking the term, and if variable references are scoped by type, no additional typechecking is needed either. This approach does not scale to dependently typed proof assistants, where types can include variables and where checking equality of types can be arbitrarily expensive. In theory, the quadratic blowup arising in the standard kernel could be avoided if there were a primitive for simultaneously closing an open term over a collection of binders, walking the term only once. Even this solution is not entirely satisfying, as the delaying of term closure ought to be an optimization performed by the tactic language, not by the implementer of \({\texttt {rewrite}}\) and similar tactics. Furthermore, without appropriate support for tracking the provenance of open terms, delaying the closing would result in non-local errors.
3.5 Empirical Cost of Incrementality
In line with out analysis, the performance results reported by Aehlig et al. [1] suggest that even if all of the superlinear bottlenecks were fixed—no small undertaking—rewriting and partial evaluation via reflection might still be orders of magnitude faster than any tactic that constructs theorems for intermediate results. Aehlig et al. [1] reported a \(10\times \)–\(100\times \) speed-up of their rewriting tactic over the simp tactic in Isabelle, which performs all of the intermediate rewriting steps via the kernel API. Their rewriting tactic follows an approach relatively similar to ours (see Sect. 4), although they avoid producing proofs by stepping outside of Isabelle/HOL’s TCB.
3.6 Overhead from the let Typing Rule
Returning to concrete issues in Coq, suppose we had a proof-producing rewriting algorithm that shared subterms even under binders. Would it be enough? It turns out that even when the proof size is linear in the number of binders, the cost to typecheck it in Coq is still quadratic! The reason is that when checking that f: T in a context x:= v, to check that let x:= v in f has type T (assuming that x does not occur in T), Coq will substitute v for x in T. So if a proof term has n let binders (e.g., used for sharing subterms), Coq will perform n substitutions on the type of the proof term, even if none of the \(\texttt {let}\) binders are used. If the number of \(\texttt {let}\) binders is linear in the size of the type, there is quadratic overhead in proof-checking time, even when the proof-term size is linear.
We performed a microbenchmark on a rewriting goal with no binders (because there is an obvious algorithm for sharing subterms in that case) and found that the proof-checking time reached about one second at about 2000 binders and reached 10 s at about 7000 binders. While these results might seem good enough for Fiat Cryptography, we expect that there are hundreds of thousands of primitive reduction/rewriting steps even when there are only a few hundred binders in the output term, and we would need \(\texttt {let}\) binders for each of them. Furthermore, we expect that getting such an algorithm correct would be quite tricky.
Fixing this quadratic bottleneck would, as far as we can tell, require deep changes in how Coq is implemented; it would either require reworking all of Coq to operate on some efficient representation of delayed substitutions paired with unsubstituted terms, or else it would require changing the typing rules of the type theory itself to remove this substitution from the typing rule for \(\texttt {let}\). Note that there is a similar issue that crops up for function application and abstraction.
4 Desiderata for a New Rewriting Building Block
Existing built-in rewriting tactics fall short in addressing real-world project requirements. Naturally, the field must look towards building a new rewriting building block that would be adequate for real-world projects.
There are two strategies for ensuring correctness of such a rewriting building block. Proof-producing \({\texttt {rewrite}}\) tactics build proofs out of smaller, trusted or proven-correct building blocks. Proven correct \({\texttt {rewrite}}\) tactics implement a procedure for computing the final term, and have an associated proof that whatever rewritten term they output will be equal to the initial term.
Hickey and Nogin [27] discuss at length how to build compilers around proof-producing rewrite rules. “All program transformations, from parsing to code generation, are cleanly isolated and specified as term rewrites.” While they note that the correctness of the compiler is thus reduced to the correctness of the rewrite rules, they did not prove correctness mechanically. More importantly, it is not clear that they manage to avoid the asymptotic blow-up associated with proof-producing rewriting of deeply nested let-binders. Since they give no performance numbers, it is hard to say whether or not their compiler performs at the scale necessary for Fiat Cryptography.
So, we turn towards the style of using a proven-correct computational procedure within a larger proof engine, known as proof by reflection [8]. Proof by reflection is a well-known strategy for improving performance, and tactics in this style are called reflective. Reflective tactics shine on fixed, well-circumscribed domains. Coq ships with a number of reflective tactics in the standard library, including solvers for linear and non-linear integer, real, and rational arithmetic [5, 10]; for polynomial positivity over the real field \({\mathbb {R}}\) [44], for systems of equations over a ring [8]; for polynomial equality over integral domains [20, 46].
In contrast, rewriting does not naturally have a fixed domain, such as the structure of rings, fields, integral domains, etc. Braibant et al. [9] develop a reflective tactic for rewriting modulo associativity and commutativity. However, the reflective part of the tactic is restricted to just the equations
 and
and
 . \({\mathcal {R}}_{tac }\) [41] is a general framework for verified proof tactics in Coq, including an experimental reflective version of rewrite_strat supporting arbitrary setoid relations, unification variables, and arbitrary semidecidable side conditions solvable by other verified tactics, using de Bruijn indexing to manage binders.
. \({\mathcal {R}}_{tac }\) [41] is a general framework for verified proof tactics in Coq, including an experimental reflective version of rewrite_strat supporting arbitrary setoid relations, unification variables, and arbitrary semidecidable side conditions solvable by other verified tactics, using de Bruijn indexing to manage binders.
However, \({\mathcal {R}}_{tac }\) is missing a critical feature for compiling large programs: subterm sharing. As a result, our experiments with Fiat Cryptography yielded clear asymptotic slowdown. Furthermore, unlike the convenience of single invocation proof-producing rewriting tactics, \({\mathcal {R}}_{tac }\) is fairly heavyweight to use! For instance, \({\mathcal {R}}_{tac }\) requires that theorems be restated manually in a deep embedding to bring them into automation procedures. This makes it effort-intensive to adapt \({\mathcal {R}}_{tac }\) as a rewriting building block to a new project..
Aehlig et al. [1] come close to a fitting approach, using normalization by evaluation (NbE) [4] to bootstrap reduction of open terms on top of full reduction, as built into a proof assistant. However, they expand the proof-assistant trusted code base in ways specific to their technique. They also do not report any experiments actually using the tool for partial evaluation (just traditional full reduction), potentially hiding performance-scaling challenges or other practical issues. They also do not preserve subterm sharing explicitly, representing variable references as unary natural numbers (de Bruijn-style). Finally, they require that rewrite rules be embodied in ML code, rather than stated as natural “native” lemmas of the proof assistant.
Thus we find that an adequate proof engine rewriting building block might be built with the following features:
-
Correct: does not extend the trusted code base
-
Complete: handles rewriting on any goal phrasable in the proof assistant
-
Performant: has good asymptotic scaling with input size
-
Convenient: as easy to use as proof-producing rewrite tactics
-
Modular: supports side conditions
5 How Well Does Our Prototype Do?
The standard of correctness we hold ourselves to in developing this building block is not extending Coq’s trusted code base (TCB). By not extending the TCB in any way, our rewriting engine guarantees that building proofs on top of it maintains Coq’s rigorous standards for correctness and reliability. Weaker standards may have use in some applications, but we manage to live up to this exacting standard without too much difficulty.
Our rewriting framework is adequately performant into the 100 s and 1000 s of binders; while still a long way from the gigabytes of code required to tackle blue sky projects, this is adequate to handle the real-world demands of Fiat Cryptography.
Much like \({\mathcal {R}}_{tac }\), our framework is built around a type of expressions parameterized over an arbitrary enumeration of types and constants. Extending this modular convenience further, we demonstrate how to achieve easy plug-and-play modularity by fully automating the enumerating of type codes, constant codes, and the specialization of our rewriter to these parameters. Partial evaluation of the reflective rewriting procedure itself nets us additional performance gains.
Similar to \({\mathcal {R}}_{tac }\) we provide support for decidable side conditions. However, neither our framework nor \({\mathcal {R}}_{tac }\) interoperate with the rest of the proof engine as well as necessary for modularity. Similarly, neither our framework nor \({\mathcal {R}}_{tac }\) adequately support dependenttypes for completeness.
In the context of Fiat Cryptography, there are several critical design criteria and performance bottlenecks that need to be addressed for effective rewriting and partial evaluation, most of which were not provided natively by \({\mathcal {R}}_{tac }\).
-
Sharing of common subterms: It is essential to represent output programs with shared common subterms for large-scale partial-evaluation problems. Inlining shared subterms redundantly can lead to an exponential increase in space requirements. The importance of maintaining shared subterms is highlighted in the Fiat Cryptography example of generating a 64-bit implementation of field arithmetic for the P-256 elliptic curve, described in Sect. 7.2.
-
Proper handling of variable binders: Fiat Cryptography implements the generic arithmetic templates as functional Gallina programs. Subterm sharing is achieved with let binders. The number of nested variable binders in output terms can be so large that we expect it to be performance-prohibitive to perform bookkeeping operations on first-order-encoded terms (e.g., with de Bruijn indices, as is done in \({\mathcal {R}}_{tac }\) by Malecha and Bengtson [41]). Fiat Cryptography may generate a single routine with nearly a thousand nested binders, emphasizing the need for an efficient rewriting mechanism.
-
Rules with side conditions: Unconditional rewrite rules are generally insufficient, and we require rules with side conditions. For instance, Fiat Cryptography depends on checking lack-of-overflow conditions.
-
Integration with abstract interpretation: It is not feasible to expect a general engine to discharge all side conditions on the spot. We need integration with abstract interpretation that can analyze whole programs to support reduction.
-
Reduction-ordering of rewriting: Existing rewriting tactics order rewrites either in a topdown (starting from the root of the syntax tree) or bottomup (starting from the leaves) manner. However, when rewriting is used for doing computation in higher-order functional language, functions play a much more central role than concepts like “root” or “leaves” of an abstract syntax tree. It’s much more important to decide whether to evaluate function arguments before or after transforming the body of the function. We want to order our rewrites according to something more like call-by-value or call-by-need than topdown or bottomup.
Table 1 summarizes the comparison of our approach with existing approaches to rewriting.
Much of the rest of this paper is spent reprising the material from Accelerating Verified-Compiler Development with a Verified Rewriting Engine [21], diving into the details of the design, implementation, and performance evaluation of our rewriting framework. Readers primarily interested in the high-level insights may wish to skip straight to Sect. 9, Future Work.
6 Building a Rewriter
We are mostly guided by Aehlig et al. [1] but made a number of crucial changes. Let us review the basic idea of the approach of Aehlig et al. First, their supporting library contains:
-
1.
Within the logic of the proof assistant (Isabelle/HOL, in their case), a type of syntax trees for ML programs is defined, with an associated (trusted) operational semantics.
-
2.
They also wrote a reduction function in (deeply embedded) ML, parameterized on a function to choose the next rewrite, and proved it sound once-and-for-all.
Given a set of rewrite rules and a term to simplify, their main tactic must:
-
1.
Generate a (deeply embedded) ML program that decides which rewrite rule, if any, to apply at the top node of a syntax tree, along with a proof of its soundness.
-
2.
Generate a (deeply embedded) ML term standing for the term we set out to simplify, with a proof that it means the same as the original.
-
3.
Combining the general proof of the rewrite engine with proofs generated by reification (the prior two steps), conclude that an application of the reduction function to the reified rules and term is indeed an ML term that generates correct answers.
-
4.
“Throw the ML term over the wall,” using a general code-generation framework for Isabelle/HOL [24]. Trusted code compiles the ML code into the concrete syntax of Standard ML, and compiles it, and runs it, asserting an axiom about the outcome.
Here is where our approach differs at that level of detail:
-
Our reduction engine is written as a normal Gallina functional program, rather than within a deeply embedded language. As a result, we are able to prove its type-correctness and termination, and we are able to run it within Coq’s kernel.
-
We do compile-time specialization of the reduction engine to sets of rewrite rules, removing overheads of generality.
6.1 Our Approach in Ten Steps
Here is a bit more detail on the steps that go into applying our Coq plugin, many of which we expand on in the following sections. Our plugin introduces a new command
 for precomputing rewriters from a set of rewrite rules. For example, we might write:
for precomputing rewriters from a set of rewrite rules. For example, we might write:

This command automates the following steps:
-
1.
The given lemma statements are scraped for which named identifiers to encode.
-
2.
Inductive types enumerating all available primitive types and functions are emitted. This allows us to achieve the performance gains attributed in Boespflug [7] to having native metalanguage constructors for all constants, without manual coding.
-
3.
Tactics generate all of the necessary definitions and prove all of the necessary lemmas for dealing with this particular set of inductive codes. Definitions include operations like Boolean equality on type codes and lemmas like “all types have decidable equality.”
-
4.
The statements of rewrite rules are reified and soundness and syntactic-well-formedness lemmas are proven about each of them.
-
5.
Definitions and lemmas needed to prove correctness are assembled into a single package.
Then, to rewrite in a goal, which merely requires invoking a tactic such as
 or
or
 , the following steps are performed automatically:
, the following steps are performed automatically:
-
1.
Rearrange the goal into a single quantifier-free logical formula.
-
2.
Reify a selected subterm and replace it with a call to our denotation function.
-
3.
Rewrite with a theorem, into a form calling our rewriter.
-
4.
Call Coq’s built-in full reduction (
 ) to reduce this application.
) to reduce this application. -
5.
Run standard call-by-value reduction to simplify away use of the denotation function.
The object language of our rewriter is nearly simply typed, with limited support for calling polymorphic functions.
The Ident case is for identifiers, which are described by an enumeration specific to a use of our library. For example, the identifiers might be codes for \(+\), \(\cdot \), and literal constants. We write \(\llbracket e \rrbracket \) for a standard denotational semantics.
6.2 Pattern-Matching Compilation and Evaluation
Aehlig et al. [1] feed a specific set of user-provided rewrite rules to their engine by generating code for an ML function, which takes in deeply embedded term syntax (actually doubly deeply embedded, within the syntax of the deeply embedded ML!) and uses ML pattern matching to decide which rule to apply at the top level. Thus, they delegate efficient implementation of pattern matching to the underlying ML implementation. As we instead build our rewriter in Coq’s logic, we have no such option to defer to ML.
We could follow a naive strategy of repeatedly matching each subterm against a pattern for every rewrite rule, as in the rewriter of Malecha and Bengtson [41], but in that case we do a lot of duplicate work when rewrite rules use overlapping function symbols. Instead, we adopted the approach of Maranget [43], who describes compilation of pattern matches in OCaml to decision trees that eliminate needless repeated work (for example, decomposing an expression into \(x + y + z\) only once even if two different rules match on that pattern).
There are three steps to turn a set of rewrite rules into a functional program that takes in an expression and reduces according to the rules. The first step is pattern-matching compilation: we must compile the left-hand sides of the rewrite rules to a decision tree that describes how and in what order to decompose the expression, as well as describing which rewrite rules to try at which steps of decomposition. Because the decision tree is merely a decomposition hint, we require no proofs about it to ensure soundness of our rewriter. The second step is decision-tree evaluation, during which we decompose the expression as per the decision tree, selecting which rewrite rules to attempt. The only correctness lemma needed for this stage is that any result it returns is equivalent to picking some rewrite rule and rewriting with it. The third and final step is to actually rewrite with the chosen rule. Here the correctness condition is that we must not change the semantics of the expression.
While pattern matching begins with comparing one pattern against one expression, Maranget’s approach works with intermediate goals that check multiple patterns against multiple expressions. A decision tree describes how to match a vector (or list) of patterns against a vector of expressions. It is built from these constructors:
-
TryLeaf k onfailure: Try the \(k\text {th}\) rewrite rule; if it fails, keep going with onfailure.
-
Failure: Abort; nothing left to try.
-
Switch icases app_case default: With the first element of the vector, match on its kind; if it is an identifier matching something in icases, which is a list of pairs of identifiers and decision trees, remove the first element of the vector and run that decision tree; if it is an application and app_case is not None, try the app_case decision tree, replacing the first element of each vector with the two elements of the function and the argument it is applied to; otherwise, do not modify the vectors and use the default.
-
Swap i cont: Swap the first element of the vector with the \(i\texttt {th}\) element (0-indexed) and keep going with cont.
Consider the encoding of two simple example rewrite rules, where we follow Coq’s \({\mathcal {L}}_{tac }\) language in prefacing pattern variables with question marks.
We embed them in an AST type for patterns, which largely follows our ASTs for expressions.

The decision tree produced is

where every nonswap node implicitly has a “default” case arrow to Failure and circles represent Switch nodes.
We implement, in Coq’s logic, an evaluator for these trees against terms. Note that we use Coq’s normal partial evaluation to turn our general decision-tree evaluator into a specialized matcher to get reasonable efficiency. Although this partial evaluation of our partial evaluator is subject to the same performance challenges we highlighted in the introduction, it only has to be done once for each set of rewrite rules, and we are targeting cases where the time of per-goal reduction dominates this time of metacompilation.
For our running example of two rules, specializing gives us this match expression.

6.3 Adding Higher-Order Features
Fast rewriting at the top level of a term is the key ingredient for supporting customized algebraic simplification. However, not only do we want to rewrite throughout the structure of a term, but we also want to integrate with simplification of higher-order terms, in a way where we can prove to Coq that our syntax-simplification function always terminates. Normalization by evaluation (NbE) [4] is an elegant technique for adding the latter aspect, in a way where we avoid needing to implement our own \(\lambda \)-term reducer or prove it terminating.
To orient expectations: we would like to enable the following reduction
using the rewrite rule
We begin by reviewing NbE’s most classic variant, for performing full \(\beta \)-reduction in a simply typed term in a guaranteed-terminating way. Our simply typed \(\lambda \)-calculus syntax is:
with v for variables, c for constants, and b for base types.
We can now define normalization by evaluation. First, we choose a “semantic” representation for each syntactic type, which serves as an interpreter’s result type.
Function types are handled as in a simple denotational semantics, while base types receive the perhaps-counterintuitive treatment that the result of “executing” one is a syntactic expression of the same type. We write \(\texttt {expr}(b)\) for the metalanguage type of object-language syntax trees of type b, relying on a type family \(\texttt {expr}\).
Now the core of NbE, shown in Fig. 4, is a pair of dual functions reify and reflect, for converting back and forth between syntax and semantics of the object language, defined by primitive recursion on type syntax. We split out analysis of term syntax in a separate function reduce, defined by primitive recursion on term syntax. Usually this functionality would be mixed in with reflect, which typically does not need to be recursive over type syntax when constants c can be listed explicitly. The reason for this choice will become clear when we extend NbE to perform rewriting only on fully-applied constants whose \(\eta \)-long forms do require recursion over type syntax.
We write v for object-language variables and x for metalanguage (Coq) variables, and we overload \(\lambda \) notation using the metavariable kind to signal whether we are building a host \(\lambda \) or a \(\lambda \) syntax tree for the embedded language. The crucial first clause for reduce replaces object-language variable v with fresh metalanguage variable x, and then we are somehow tracking that all free variables in an argument to reduce must have been replaced with metalanguage variables by the time we reach them. We reveal in Sect. 7.1 the encoding decisions that make all the above legitimate, but first let us see how to integrate use of the rewriting operation from the previous section. To fuse NbE with rewriting, we only modify the constant case of reduce. First, we bind our specialized decision-tree engine (which rewrites at the root of an AST only) under the name rewrite-head.
In the constant case, we still reflect the constant, but underneath the binders introduced by full \(\eta \)-expansion, we perform one instance of rewriting. In other words, we replace the call to \(\text {reflect}(c)\) in the constant case \(\text {reduce}(c)\) with a variant of reflect where we change the one function-definition clause of \(\text {reflect}_{b}(e)\) to:
It is important to note that a constant of function type will be \(\eta \)-expanded only once for each syntactic occurrence in the starting term, though the expanded function is effectively a thunk, waiting to perform rewriting again each time it is called. From first principles, it is not clear why such a strategy terminates on all possible input terms.
The details so far are essentially the same as in the approach of Aehlig et al. [1]. Recall that their rewriter was implemented in a deeply embedded ML, while ours is implemented in Coq’s logic, which enforces termination of all functions. Aehlig et al. did not prove termination, which indeed does not hold for their rewriter in general, which works with untyped terms, not to mention the possibility of divergent rule-specific ML functions. In contrast, we need to convince Coq up-front that our interleaved \(\lambda \)-term normalization and algebraic simplification always terminate. Additionally, we must prove that rewriting preserves term denotations, which can easily devolve into tedious binder bookkeeping.
The next section introduces the techniques we use to avoid explicit termination proof or binder bookkeeping, in the context of a more general analysis of scaling challenges.
7 Scaling Challenges
Aehlig et al. [1] only evaluated their implementation against closed programs. What happens when we try to apply the approach to partial-evaluation problems that should generate thousands of lines of low-level code?
7.1 Variable Environments will be Large
We should think carefully about representation of ASTs, since many primitive operations on variables will run in the course of a single partial evaluation. For instance, Aehlig et al. [1] reported a significant performance improvement changing variable nodes from using strings to using de Bruijn indices [14]. However, de Bruijn indices and other first-order representations remain painful to work with. We often need to fix up indices in a term being substituted in a new context. Even looking up a variable in an environment tends to incur linear time overhead, thanks to traversal of a list. Perhaps we can do better with some kind of balanced-tree data structure, but there is a fundamental performance gap versus the arrays that can be used in imperative implementations. Unfortunately, it is difficult to integrate arrays soundly in a logic. Also, even ignoring performance overheads, tedious binder bookkeeping complicates proofs.
Our strategy is to use a variable encoding that pushes all first-order bookkeeping off on Coq’s kernel or the implementation of the language we extract to, which are themselves performance-tuned with some crucial pieces of imperative code. Parametric higher-order abstract syntax (PHOAS) [11] is a dependently typed encoding of syntax where binders are managed by the enclosing type system. It allows for relatively easy implementation and proof for NbE, so we adopted it for our framework.
Here is the actual inductive definition of term syntax for our object language, PHOAS-style. The characteristic oddity is that the core syntax type expr is parameterized on a dependent type family for representing variables. However, the final representation type Expr uses first-class polymorphism over choices of variable type, bootstrapping on the metalanguage’s parametricity to ensure that a syntax tree is agnostic to variable type.

The type of base codes
 is constructed automatically based on the types in the specific lemmas the user requests, and might, for example, be
is constructed automatically based on the types in the specific lemmas the user requests, and might, for example, be

A good example of encoding adequacy is assigning a simple denotational semantics. First, a simple recursive function assigns meanings to types.

Next we see the convenience of being able to use an expression by choosing how it should represent variables. Specifically, it is natural to choose the type-denotation function itself as variable representation. Especially note how this choice makes rigorous last section’s convention (e.g., in the suspicious function-abstraction clause of reduce), where a recursive function enforces that values have always been substituted for variables early enough.

It is now easy to follow the same script in making our rewriting-enabled NbE fully formal, in Fig. 5. Note especially the first clause of reduce, where we avoid variable substitution precisely because we have chosen to represent variables with normalized semantic values. The subtlety there is that base-type semantic values are themselves expression syntax trees, which depend on a nested choice of variable representation, which we retain as a parameter throughout these recursive functions. The final definition \(\lambda \)-quantifies over that choice. The rewrite_head function is automatically generated; the match statement in Sect. 6.2 on page 18 is an example of what it might compute.
One subtlety hidden in Fig. 5 in implicit arguments is in the final clause of reduce, where the two applications of the Ident constructor use different variable representations. With all those details hashed out, we can prove a pleasingly simple correctness theorem, with a lemma for each main definition, with inductive structure mirroring recursive structure of the definition, also appealing to correctness of last section’s pattern-compilation operations. (We now use syntax \(\llbracket \cdot \rrbracket \) for calls to DenoteE.)

To understand how we now apply the soundness theorem in a tactic, it is important to note how the Coq kernel builds in reduction strategies. These strategies have, to an extent, been tuned to work well to show equivalence between a simple denotational-semantics application and the semantic value it produces. In contrast, it is rather difficult to code up one reduction strategy that works well for all partial-evaluation tasks. Therefore, we should restrict ourselves to (1) running full reduction in the style of functional-language interpreters and (2) running normal reduction on “known-good” goals like correctness of evaluation of a denotational semantics on a concrete input.
Operationally, then, we apply our tactic in a goal containing a term e that we want to partially evaluate. In standard proof-by-reflection style, we reify e into some E where \(\llbracket E \rrbracket = e\), replacing e accordingly, asking Coq’s kernel to validate the equivalence via standard reduction. Now we use the \({\texttt {rewrite}}\) correctness theorem to replace \(\llbracket E \rrbracket \) with  . Next we ask the Coq kernel to simplify
. Next we ask the Coq kernel to simplify  by full reduction via native compilation. Finally, where \(E'\) is the result of that reduction, we simplify \(\llbracket E' \rrbracket \) with standard reduction.
by full reduction via native compilation. Finally, where \(E'\) is the result of that reduction, we simplify \(\llbracket E' \rrbracket \) with standard reduction.
We have been discussing representation of bound variables. Also important is representation of constants (e.g., library functions mentioned in rewrite rules). They could also be given some explicit first-order encoding, but dispatching on, say, strings or numbers for constants would be rather inefficient in our generated code. Instead, we chose to have our Coq plugin generate a custom inductive type of constant codes, for each rewriter that we ask it to build with Make. As a result, dispatching on a constant can happen in constant time, based on whatever pattern-matching is built into the execution language (either the Coq kernel or the target language of extraction). To our knowledge, no past verified reduction tool in a proof assistant has employed that optimization.
7.2 Subterm Sharing is Crucial
For some large-scale partial-evaluation problems, it is important to represent output programs with sharing of common subterms. Redundantly inlining shared subterms can lead to exponential increase in space requirements. Consider the Fiat Cryptography [16] example of generating a 64-bit implementation of field arithmetic for the P-256 elliptic curve. The library has been converted manually to continuation-passing style, allowing proper generation of \(\texttt {let}\) binders, whose variables are often mentioned multiple times. We ran that old code generator (actually just a subset of its functionality, but optimized by us a bit further, as explained in Sect. 8.3) on the P-256 example and found it took about 15 s to finish. Then we modified reduction to inline \(\texttt {let}\) binders instead of preserving them, at which point the job terminated with an out-of-memory error, on a machine with 64 GB of RAM.
We see a tension here between performance and niceness of library implementation. When we built the original Fiat Cryptography, we found it necessary to CPS-convert the code to coax Coq into adequate reduction performance. Then all of our correctness theorems were complicated by reasoning about continuations. In fact, the CPS reasoning was so painful that at one point most algorithms in the template library were defined twice, once in continuation-passing style and once in direct-style code, because it was easier to prove the two equivalent and work with the non-CPS version than to reason about the CPS version directly. It feels like a slippery slope on the path to implementing a domain-specific compiler, rather than taking advantage of the pleasing simplicity of partial evaluation on natural functional programs. Our reduction engine takes shared-subterm preservation seriously while applying to libraries in direct style.
Our approach is \(\texttt {let}\)-lifting: we lift \(\texttt {let}\) s to top level, so that applications of functions to \(\texttt {let}\) s are available for rewriting. For example, we can perform the rewriting

using the rules
We define a telescope-style type family called
 :
:

A value of type
 is a series of let binders (where each expression
is a series of let binders (where each expression
 may mention earlier-bound variables) ending in a value of type
may mention earlier-bound variables) ending in a value of type
 .
.
Recall that the NbE type interpretation mapped base types to expression syntax trees. We add flexibility, parameterizing by a Boolean declaring whether to introduce telescopes.

There are cases where naive preservation of let binders blocks later rewrites from triggering and leads to suboptimal performance, so we include some heuristics. For instance, when the expression being bound is a constant, we always inline. When the expression being bound is a series of list “cons” operations, we introduce a name for each individual list element, since such a list might be traversed multiple times in different ways.
7.3 Rules Need Side Conditions
Many useful algebraic simplifications require side conditions. For example, bit-shifting operations are faster than divisions, so we might want a rule such as
The trouble is how to support predictable solving of side conditions during partial evaluation, where we may be rewriting in open terms. We decided to sidestep this problem by allowing side conditions only as executable Boolean functions, to be applied only to variables that are confirmed as compile-time constants, unlike Malecha and Bengtson [41] who support general unification variables. We added a variant of pattern variable that only matches constants. Semantically, this variable style has no additional meaning, and in fact we implement it as a special identity function (notated as an apostrophe) that should be called in the right places within Coq lemma statements. Rather, use of this identity function triggers the right behavior in our tactic code that reifies lemma statements.
Our reification inspects the hypotheses of lemma statements, using type classes to find decidable realizations of the predicates that are used, thereby synthesizing one Boolean expression of our deeply embedded term language, which stands for a decision procedure for the hypotheses. The Make command fails if any such expression contains pattern variables not marked as constants.
Hence, we encode the above rule as \(\forall n, m. \; 2^{\lfloor \log _2(\texttt {'}m)\rfloor } = \texttt {'}m \rightarrow n / \texttt {'}m = n \gg \texttt {'}(\log _2 m)\).
7.4 Side Conditions Need Abstract Interpretation
With our limitation that side conditions are decided by executable Boolean procedures, we cannot yet handle directly some of the rewrites needed for realistic compilation. For instance, Fiat Cryptography reduces high-level functional to low-level code that only uses integer types available on the target hardware. The starting library code works with arbitrary-precision integers, while the generated low-level code should be careful to avoid unintended integer overflow. As a result, the setup may be too naive for our running example rule \({?n} + 0 \rightarrow n\). When we get to reducing fixed-precision-integer terms, we must be legalistic:
We developed a design pattern to handle this kind of rule.
First, we introduce a family of functions \(\texttt {clip}_{l,u}\), each of which forces its integer argument to respect lower bound l and upper bound u. Partial evaluation is proved with respect to unknown realizations of these functions, only requiring that \(\texttt {clip}_{l, u}(n) = n\) when \(l \le n < u\). Now, before we begin partial evaluation, we can run a verified abstract interpreter to find conservative bounds for each program variable. When bounds l and u are found for variable x, it is sound to replace x with \(\texttt {clip}_{l,u}(x)\). Therefore, at the end of this phase, we assume all variable occurrences have been rewritten in this manner to record their proved bounds.
Second, we proceed with our example rule refactored:
If the abstract interpreter did its job, then all lower and upper bounds are constants, and we can execute side conditions straightforwardly during pattern matching.
See Appendix F, “Limitations and Preprocessing”, in the arXiv version of our ITP submission [21] for discussion of some further twists in the implementation.
7.5 Fusing Compiler Passes
When we moved the constant-folding rules from before abstract interpretation to after it, to discharge obligations that we could only prove by bounds analysis, the performance of our compiler on Word-by-Word Montgomery code synthesis decreased significantly. (The generated code did not change.) We discovered that the number of variable assignments in our intermediate code was quartic in the number of bits in the prime, while the number of variable assignments in the generated code is only quadratic. The performance numbers we measured supported this theory: the overall running time of synthesizing code for a prime near \(2^{k}\) jumped from \(\Theta (k^{2})\) to \(\Theta (k^{4})\) when we made this change. We believe that fusing abstract interpretation with rewriting and partial evaluation would allow us to fix this asymptotic-complexity issue.
To make this situation more concrete, consider the following example: Fiat Cryptography uses abstract interpretation to perform bounds analysis; each expression is associated with a range that describes the lower and upper bounds of values that expression might take on. Abstract interpretation on addition works as follows: if we have that \(x_\ell \le x \le x_u\) and \(y_\ell \le y \le y_u\), then we have that \(x_\ell + y_\ell \le x + y \le x_u + y_u\). Performing bounds analysis on \(+\) requires two additions. We might have an arithmetic simplification that says that \(x + y = x\) whenever we know that \(0 \le y \le 0\). If we perform the abstract interpretation and then the arithmetic simplification, we perform two additions (for the bounds analysis) and then two comparisons (to test the lower and upper bounds of y for equality with 0). We cannot perform the arithmetic simplification before abstract interpretation, because we will not know the bounds of y. However, if we perform the arithmetic simplification for each expression after performing bounds analysis on its subexpressions and only after this perform abstract interpretation on the resulting expression, then we need not use any additions to compute the bounds of \(x + y\) when \(0 \le y \le 0\), since the expression will just become x.
Another essential pass to fuse with rewriting and partial evaluation is let-lifting. Unless all of the code is CPS-converted ahead of time, attempting to do let-lifting via rewriting, as must be done when using
 , rewrite_strat, or \({\mathcal {R}}_{tac }\), results in slower asymptotics. This pattern is already apparent in the example of Fig. 7c on page 29. Consider the code of Fig. 6. We achieve linear performance in \(n\cdot m\) when ignoring the final
, rewrite_strat, or \({\mathcal {R}}_{tac }\), results in slower asymptotics. This pattern is already apparent in the example of Fig. 7c on page 29. Consider the code of Fig. 6. We achieve linear performance in \(n\cdot m\) when ignoring the final
 ,Footnote 3 while
,Footnote 3 while
 and rewrite_strat are both cubic. The rewriter in \({\mathcal {R}}_{tac }\) cannot possibly achieve better than \({\mathcal {O}}\left( n\cdot m^2\right) \) unless it can be sublinear in the number of rewrites, because our rewriter gets away with a constant number of rewrites (four), plus evaluating recursion principles for a total amount of work \({\mathcal {O}}(n\cdot m)\). But without primitive support for let-lifting, it is instead necessary to lift the lets by rewrite rules, which requires \({\mathcal {O}}\left( n\cdot m^2\right) \) rewrites just to lift the lets. The analysis is thus: running make simply gives us m nested applications of map_dbl to a length-n list. To reduce a given call to map_dbl, all existing let-binders must first be lifted (there are \(n\cdot k\) of them on the k-innermost-call) across map_dbl, one-at-a-time. Then the map_dbl adds another n let binders, so we end up doing \(\sum _{k=0}^{m} n\cdot k\) lifts, i.e., \(n\cdot m(m+1)/2\) rewrites just to lift the lets.
and rewrite_strat are both cubic. The rewriter in \({\mathcal {R}}_{tac }\) cannot possibly achieve better than \({\mathcal {O}}\left( n\cdot m^2\right) \) unless it can be sublinear in the number of rewrites, because our rewriter gets away with a constant number of rewrites (four), plus evaluating recursion principles for a total amount of work \({\mathcal {O}}(n\cdot m)\). But without primitive support for let-lifting, it is instead necessary to lift the lets by rewrite rules, which requires \({\mathcal {O}}\left( n\cdot m^2\right) \) rewrites just to lift the lets. The analysis is thus: running make simply gives us m nested applications of map_dbl to a length-n list. To reduce a given call to map_dbl, all existing let-binders must first be lifted (there are \(n\cdot k\) of them on the k-innermost-call) across map_dbl, one-at-a-time. Then the map_dbl adds another n let binders, so we end up doing \(\sum _{k=0}^{m} n\cdot k\) lifts, i.e., \(n\cdot m(m+1)/2\) rewrites just to lift the lets.
8 Evaluation
Our implementation, available on GitHub at \(\texttt {mit-plv/rewriter@ITP-2022-perf-}\)\(\texttt {data}\) and with a roadmap in Appendix G, “Reading the Code Supplement”, in the arXiv version of our ITP submission [21], includes a mix of Coq code for the proved core of rewriting, tactic code for setting up proper use of that core, and OCaml plugin code for the manipulations beyond the tactic language’s current capabilities. We report here on evidence that the tool is effective, first in terms of productivity by users and then in terms of compile-time performance.
8.1 Iteration on the Fiat Cryptography Compiler
We ported Fiat Cryptography’s core compiler functionality to use our framework. The result is now used in production by a number of open-source projects. We were glad to retire the CPS versions of verified arithmetic functions, which had been present only to support predictable reduction with subterm sharing. More importantly, it became easy to experiment with new transformations via proving new rewrite theorems, directly in normal Coq syntax, including the following, all justified by demand from real users:
-
Reassociating arithmetic to minimize the bitwidths of intermediate results
-
Multiplication primitives that separately return high halves and low halves
-
Strings and a “comment” function of type \(\forall A. \; \texttt {string} \rightarrow A \rightarrow A\)
-
Support for bitwise exclusive-or
-
A special marker to block C compilers from introducing conditional jumps in code that should be constant-time
-
Eliding bitmask-with-constant operations that can be proved as no-ops
-
Rules to introduce conditional moves (on supported platforms)
-
New hardware backend, via rules that invoke special instructions of a cryptographic accelerator
-
New hardware backend, with a requirement that all intermediate integers have the same bitwidth, via rules to break wider operations down into several narrower operations
8.2 Microbenchmarks
Now we turn to evaluating performance of generated compilers. We start with microbenchmarks focusing attention on particular aspects of reduction and rewriting, with Appendix C, “Additional Information on Microbenchmarks”, in the arXiv version of our ITP submission [21] going into more detail, including on a few more benchmarks.
Our first example family, nested binders, has two integer parameters n and m. An expression tree is built with \(2^n\) copies of an expression, which is itself a free variable with m “useless” additions of zero. We want to see all copies of this expression reduced to just the variable. Figure 7a on the facing page shows the results for \(n = 3\) as we scale m. The comparison points are Coq’s rewrite!, setoid_rewrite, and rewrite_strat. The first two perform one rewrite at a time, taking minimal advantage of commonalities across them and thus generating quite large, redundant proof terms for large, redundant statements. The third makes top-down or bottom-up passes with combined generation of proof terms and claims. For our own approach, we list both the total time and the time taken for core execution of a verified rewrite engine, without counting reification (converting goals to ASTs) or its inverse (interpreting results back to normal-looking goals). The comparison here is very favorable for our approach so long as \(m > 2\). (See Appendix B.1, “Rewriting Without Binders”, in the arXiv version of our ITP submission [21] for more detailed plots.)
Now consider what happens when we use let binders to share subterms within repeated addition of zero, incorporating exponentially many additions with linearly sized terms. Figure 7b shows the results. The comparison here is again very favorable for our approach. The competing tactics spike upward toward timeouts at just a few hundred generated binders, while our engine is only taking about 10 s for examples with 5000 nested binders.
When recursive functions are mixed with let binders, we must lift the let binders across the functions to avoid blocking reduction and expose more rewriting opportunities. We may either lift let binders with additional equations passed to
 or rewrite_strat, build in support for let-lifting (our approach), or manually rewrite the code in continuation passing style and module-opacify the constants which are not to be unfolded (to take advantage of Coq’s built-in VM reduction without our rewriter). Note that this last option is available for this example because it only involves partial reduction and not equational rewriting. Figure 7c shows the results of our evaluation on the code in Fig. 6 on page 27. The prior state of the art—writing code in CPS—suitably tweaked by using module opacity to allow
or rewrite_strat, build in support for let-lifting (our approach), or manually rewrite the code in continuation passing style and module-opacify the constants which are not to be unfolded (to take advantage of Coq’s built-in VM reduction without our rewriter). Note that this last option is available for this example because it only involves partial reduction and not equational rewriting. Figure 7c shows the results of our evaluation on the code in Fig. 6 on page 27. The prior state of the art—writing code in CPS—suitably tweaked by using module opacity to allow
 , remains the best performer here, though the cost of rewriting everything is CPS may be prohibitive. Our method soundly beats rewrite_strat. When we collected the data for Fig. 7, we were additionally bottlenecked on
, remains the best performer here, though the cost of rewriting everything is CPS may be prohibitive. Our method soundly beats rewrite_strat. When we collected the data for Fig. 7, we were additionally bottlenecked on
 , which is used to unfold the goal post-rewriting and cost about a minute on the largest of terms; about 99% of the difference between the full time of our method and just the rewriting is spent in the final
, which is used to unfold the goal post-rewriting and cost about a minute on the largest of terms; about 99% of the difference between the full time of our method and just the rewriting is spent in the final
 at the end, used to denote our output term from reified syntax. This performance bottleneck is an artifact of the unfortunate fact that reduction in Coq was quadratic in the number of nested binders present when we collected our performance data; see Coq bug #11151. This bug has since been fixed, as of Coq 8.14; see Coq PR #13537.
at the end, used to denote our output term from reified syntax. This performance bottleneck is an artifact of the unfortunate fact that reduction in Coq was quadratic in the number of nested binders present when we collected our performance data; see Coq bug #11151. This bug has since been fixed, as of Coq 8.14; see Coq PR #13537.
Although we have made our comparison against the built-in tactics
 and rewrite_strat, by analyzing the performance in detail, we can argue that these performance bottlenecks are likely to hold for any proof assistant designed like Coq. Detailed debugging reveals six performance bottlenecks in the existing tactics, already discussed in Sect. 3.
and rewrite_strat, by analyzing the performance in detail, we can argue that these performance bottlenecks are likely to hold for any proof assistant designed like Coq. Detailed debugging reveals six performance bottlenecks in the existing tactics, already discussed in Sect. 3.
8.3 Macrobenchmark: Fiat Cryptography
Finally, we consider an experiment (described in more detail in Appendix B.2, “Additional Information on the Fiat Cryptography Benchmark”, in the arXiv version of our ITP submission [21]) replicating the generation of performance-competitive finite-field-arithmetic code for all popular elliptic curves by Erbsen et al. [16]. In all cases, we generate essentially the same code as they did, so we only measure performance of the code-generation process. We stage partial evaluation with three different reduction engines (i.e., three Make invocations), respectively applying 85, 56, and 44 rewrite rules (with only 2 rules shared across engines), taking total time of about 5 min to generate all three engines. These engines support 95 distinct function symbols.
Figure 7d on the preceding page graphs running time of three different partial-evaluation and rewriting methods for Fiat Cryptography, as the prime modulus of arithmetic scales up. Times are normalized to the performance of the original method of Erbsen et al. [16], which relied on standard Coq reduction to evaluate code that had been manually written in CPS, followed by reification and a custom ad-hoc simplification and rewriting engine.
As the figure shows, our approach gives about a 10\(\times \)–1000\(\times \) speed-up over the original Fiat Cryptography pipeline. Inspection of the timing profiles of the original pipeline reveals that reification dominates the timing profile; since partial evaluation is performed by Coq’s kernel, reification must happen after partial evaluation, and hence the size of the term being reified grows with the size of the output code. Also recall that the old approach required rewriting Fiat Cryptography’s library of arithmetic functions in continuation-passing style, enduring this complexity in library correctness proofs, while our new approach applies to a direct-style library. Finally, the old approach included a custom reflection-based arithmetic simplifier for term syntax, run after traditional reduction, whereas now we are able to apply a generic engine that combines both, without requiring more than proving traditional rewrites.
The figure also confirms a clear performance advantage of running reduction in code extracted to OCaml, which is possible because our plugin produces verified code in Coq’s functional language. The extracted version is about 10\(\times \) faster than running in Coq’s kernel.
Figure 7e on page 29 graphs running time of the same three partial-evaluation and rewriting methods for Fiat Cryptography, in addition to the impractical rewrite_strat-based method, as the prime modulus of arithmetic scales up.
9 Future Work
By far the biggest next step for our engine is to integrate abstract interpretation with rewriting and partial evaluation. We expect this would net us asymptotic performance gains as described in Sect. 7.5. Additionally, it would allow us to simplify the phrasing of many of our post-abstract-interpretation rewrite rules, by relegating bounds information to side conditions rather than requiring that they appear in the syntactic form of the rule.
There are also a number of natural extensions to our engine. For instance, we do not yet allow pattern variables marked as “constants only” to apply to container datatypes; we limit the mixing of higher-order and polymorphic types, as well as limiting use of first-class polymorphism; we do not support rewriting with equalities of nonfully-applied functions; we only support decidable predicates as rule side conditions, and the predicates may only mention pattern variables restricted to matching constants; we have hardcoded support for a small set of container types and their eliminators; we support rewriting with equality and no other relations; and we require decidable equality for all types mentioned in rules.
9.1 What Would it Take for Our Prototype to be a Full-Fledged Proof Engine Building Block?
We return now to the context of our introduction: having a rewriting proof engine building block that performs adequately at scale.
9.1.1 Performance
While we achieve adequate performance on the real-world demands of Fiat Cryptography, there is much work left to be done. While we can handle 100 s–1 000 s of lines of code in a single function, easily accomodating even the largest of commonly-used primes in ECC, other uses of finite field arithmetic use much larger primes. For example, the uses for Bitcoin involve primes such as \(2^{3072} - 1103717\). At over 3000 bits and 48 limbs, we’d need to be able to handle generating nearly 42,000 lines of code. (In fact the situation is worse: unless we fuse rewriting with abstract interpretation, our intermediate code will be nearly 11.5 million lines long.Footnote 4) At this rate, it would take approximately somewhere between a week and a month to generate the code for this prime.Footnote 5
Achieving adequate performance on code that is gigabytes or terabytes in size is an open research question!
9.1.2 Modularity in Side Conditions
As discussed at the end of Related & Future Work in Extensible and Efficient Automation Through Reflective Tactics [41], reflective procedures cannot invoke unverified tactic automation. Malecha and Bengtson [41] suggest “native support for invoking external procedures and reconstructing the results in Coq a la Claret’s work [12].” Another possibility might be to make Coq’s efficient computation routines reentrant: when an existential variable or other special marker shows up during reduction, the reduction tactic might be able to pop back into interactive tactic mode, allowing the user to partially fill the existential variable with other tactics before resuming efficient computation.
9.1.3 Scaling Up the Scope
The final deficiency of our prototype rewriting tactic is a lack of support for the full scope of Coq’s mathematical language. We cannot handle most dependent types, bare (co)fixpoint constructs, primitive integers and floats, etc.
Hence we conclude this paper by laying out a research agenda for scaling up our prototype rewriting tactic to be a fully adequate replacement for the built-in rewriting tactics.
The first step is to upgrade the term representation to something like MetaCoq’s [42, 51, 52] AST, which can faithfully represent all terms accepted by the Coq kernel.
Five obstacles remain to writing a denotation function, which is essential for making use of reflective automation. We posit that all five obstacles can be overcome with the same kind of automatic specialization automation we use in our prototype to allow easy rewriting on supported domains.
The Gödelian Obstacle
Gödel’s incompleteness theorem [18] says that no consistent system can prove its own consistency. Even more directly, Löb’s theorem [36] tells us that any total denotation function—a necessary part of reflective automation—gives rise to a proof of False.Footnote 6Footnote 7
Folklore has it that strong normalization of the theory of Coq with n universes can be proven in Coq with \(n+k\) universes for some \(0 < k \le 4\) [47, 54].
By parameterizing the rewriter over an arbitrary universe graph and autospecializing to a desired universe graph on-the-fly, we could in theory handle any number of universes, thus bypassing the Gödelian obstacle.
Named Constants and Inductives
Just as in our prototype, the denotation function will need to be paraterized over a mapping of named constants, (co)inductive types, constructors, and eliminators. The same sort of autospecialization that our prototype uses should handle the full scope of types and constants available in Coq without any problem. For performance, the term representation should perhaps be parameterized over named constants and (co)inductives, though, rather than using strings as is currently done in MetaCoq.
(Co)Fixpoints, Case Analysis, and the Guard Condition
Unlike Lean, Coq has primitive constructs for general case analysis and guarded (co)recursion. We cannot translate these constructs directly, because the fix, cofix, and match constructs are not first-class terms in Coq. However, autospecialization can rescue us again, by generating on-the-fly the set of anonymous recursive functions and case analyses that are present in the term we are rewriting in and the lemmas we use for rewriting.
Judgmental Equality and Reduction: The Semisimplicial Obstacle
Even if we manage to automatically generate strong normalization proofs for our rewriting building block, there remains one final (forseeable) obstacle to writing a total denotation function in an intensional type theory: judgmental equality. This problem can be most easily seen by considering the semisimplicial types. This is an infinite telescope of types which require only one universe to write, but for which nobody knows how to write a denotation function [49]. We can write a function SST: \(\mathbb {N} \rightarrow \) syntax, and we can even write a function \(\mathtt{{\forall }}\) n: \(\mathbb {N}\), (SST n) is well-typed, but nobody knows if it is possible to write a function \(\mathbb {N} \; \rightarrow \; \texttt {Type}\) interpreting this sequence of type syntax [29]. Since semisimplicial types capture the essential idea of “arbitrary many levels of type dependency,” folklore conjectures that the problem of writing an interpreter for raw syntax with one universe, without assuming UIP (uniqueness of identity proofs) is equivalent to the problem of internalizing semisimplicial types into a function \(\mathbb {N} \; \rightarrow \; \texttt {Type}\).
While future results may allow us to bypass this obstacle entirely, autospecialization can again rescue us by determining how many levels of dependent judgmental equality are required, internalizing semisimplicial types on-the-fly up to this bound automatically—for example by unquoting the general syntax for semisimplicial types—and having the entire denotation function be parameterized on a “partial semisimplicial gadget”.
Supplementary Information Our code and data is available on GitHub:
-
Our rewriting framework: \(\texttt {mit-plv/rewriter}\) archived at swh:1:rev:f3f6bc1f48e4ff7475e0bba53c679e7a774114db
-
Fiat Cryptography: \(\texttt {mit-plv/fiat-crypto}\) archived at swh:1:rev:8377bca1f8e2bdc7997480fd33b1492291f87c8c
-
Experiments with Lean: \(\texttt {mit-plv/fiat-crypto@lean}\) archived at swh:1:dir:a5c9b1b2c700e061832d1cb87e9348bd2815c5e2
-
Experiments mixing Fiat Cryptography with
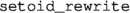 and rewrite_strat: \(\texttt {coq-community/coq-performance-tests}\) (in src/fiat_crypto_via_setoid_rewrite_standalone.v) archived at swh:1:cnt:9135903b92751770505441d8b011cdae01da3e7d
and rewrite_strat: \(\texttt {coq-community/coq-performance-tests}\) (in src/fiat_crypto_via_setoid_rewrite_standalone.v) archived at swh:1:cnt:9135903b92751770505441d8b011cdae01da3e7d -
Microbenchmarks performance evaluation: \(\texttt {mit-plv/rewriter@ITP-2022-perf-data}\) archived at swh:1:rev:1787ab401a7e71afc9937010e2e155e4b1594ab5
-
Fiat Cryptography performance evaluation: \(\texttt {mit-plv/fiat-crypto@perf-}\)\(\texttt {testing-data-ITP-2022-rewriting}\) archived at swh:1:rev:72fe0dddee5e6dceeab0b8a2e6a745abf5287d3e
More detail on the particular performance experiments we ran, as well as instructions for reading the version of the code supplement included with our ITP paper are available in the appendices of the arXiv version of our ITP submission [21].
Notes
More formally, any query consisting of 19 or fewer characters from the string 0123456789+-()*/ followed by =, is completed with its correct evaluation whenever the query is a valid arithmetic expression that computes to an integer.
See Coq bug #12526 for updates.
The final
 reduces away the denotation function on the AST that results from rewriting. As discussed in Sect. 8.2 on page 30, the necessity of ignoring this final reduction step to achieve linear performance is an artifact of measuring performance on a version of Coq prior to 8.14.
reduces away the denotation function on the AST that results from rewriting. As discussed in Sect. 8.2 on page 30, the necessity of ignoring this final reduction step to achieve linear performance is an artifact of measuring performance on a version of Coq prior to 8.14.See Fiat Crypto Issue #851: Support for large finite fields for more details.
Plotting the time of code generation for our extracted tool on WBW Montgomery on x32 and x64 as a function of computed intermediate lines of code \(\ell \) (for n limbs, \(\ell \approx 3.57+10n+2.57n^2+8.26n^3+1.98n^4\)) shows a definite superlinear trend. The best-fit quadratic (\(R^2 > 0.995\)) is \(\# \text { seconds} = 0.803 + 1.94\cdot 10^{-4}\ell + 4.28\cdot 10^{-9}\ell ^2\) for x32 and \(\# \text { seconds} = 3.42\cdot 10^{-5} + 2.84\cdot 10^{-4}\ell + 1.6\cdot 10^{-8}\ell ^2\) for x64. For 48 limbs, this comes out to 2 093 768 s (\(\approx \) 6.5 days) or 561 433 s (\(\approx \) 24 days), respectively.
Löb’s theorem says \((\square P \rightarrow P) \rightarrow P\) for any proposition P. 7 We may interpret \(\square P\) as “a proof of P” or, by Curry-Howard, “an abstract syntax tree for a term of type P”. Functions of type \(\square P \rightarrow P\) are just total denotation functions from syntax to semantics: they consume abstract syntax trees well-typed at P and produce inhabitants of P. Instantiating P with False completes the claim.
Other variants include \(\square (\square P \rightarrow P) \rightarrow \square P\), \(\square (\square (\square P \rightarrow P) \rightarrow \square P)\), and \((\vdash (\square P \rightarrow P)) \Longrightarrow (\vdash P)\). The assumptions used to prove each variant differ only slightly, and we elide them in this footnote.
References
Aehlig, K., Haftmann, F., Nipkow, T.: A compiled implementation of normalization by evaluation. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) Theorem Proving in Higher Order Logics, pp. 39–54. Springer, Berlin, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_8
Aydemir, B., Charguéraud, A., Pierce, B.C., Pollack, R., Weirich, S.: Engineering formal metatheory. In: Proc. POPL, pp. 3–15 (2008). https://www.cis.upenn.edu/~bcpierce/papers/binders.pdf
Baase, S., Henry, T.: A Gift of Fire: Social, Legal, and Ethical Issues for Computing Technology, 5th edn. Pearson, London (2012)
Berger, U., Schwichtenberg, H.: An inverse of the evaluation functional for typed \(\lambda \)-calculus. In: Proceedings Sixth Annual IEEE Symposium on Logic in Computer Science, pp. 203–211 (1991). https://doi.org/10.1109/LICS.1991.151645
Besson, F.: Fast reflexive arithmetic tactics the linear case and beyond. In: Altenkirch, T., McBride, C. (eds.) Types for Proofs and Programs, pp. 48–62. Springer, Berlin (2007). https://doi.org/10.1007/978-3-540-74464-1_4
Boespflug, M., Dénès, M., Grégoire, B.: Full reduction at full throttle. In: Proceedings of the First International Conference on Certified Programs and Proofs. CPP’11, pp. 362–377. Springer, Berlin, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25379-9_26
Boespflug, M.: Efficient normalization by evaluation. In: Danvy, O. (ed.) Workshop on Normalization by Evaluation, Los Angeles, USA (2009). https://hal.inria.fr/inria-00434283
Boutin, S.: Using reflection to build efficient and certified decision procedures. In: Abadi, M., Ito, T. (eds.) Theoretical Aspects of Computer Software, pp. 515–529. Springer, New York. https://doi.org/10.1007/BFb0014565
Braibant, T., Pous, D.: Tactics for reasoning modulo AC in Coq. In: Jouannaud, J.-P., Shao, Z. (eds.) Certified Programs and Proofs, pp. 167–182. Springer, Berlin (2011). https://doi.org/10.1007/978-3-642-25379-9_14
Chaieb, A., Nipkow, T.: Verifying and reflecting quantifier elimination for presburger arithmetic. In: Sutcliffe, G., Voronkov, A. (eds.) Logic for Programming, Artificial Intelligence, and Reasoning, pp. 367–380. Springer, Berlin (2005). https://doi.org/10.1007/11591191_26
Chlipala, A.: Parametric higher-order abstract syntax for mechanized semantics. In: ICFP’08: Proceedings of the 13th ACM SIGPLAN International Conference on Functional Programming, Victoria, British Columbia, Canada (2008). http://adam.chlipala.net/papers/PhoasICFP08/
Claret, G., del Carmen González Huesca, L., Régis-Gianas, Y., Ziliani, B.: Lightweight proof by reflection using a posteriori simulation of effectful computation. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) Interactive Theorem Proving, pp. 67–83. Springer, Berlin (2013). https://doi.org/10.1007/978-3-642-39634-2_8
Coulter, M., Bensinger, G.: Alphabet shares dive after google AI Chatbot Bard Flubs Answer in ad, Reuters (2023). Accessed 24 Apr 2023. https://www.reuters.com/technology/google-ai-chatbot-bard-offers-inaccurate-information-company-ad-2023-02-08/
De Bruijn, N.G.: Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with application to the Church-Rosser theorem. In: Indagationes Mathematicae (Proceedings), vol. 75, pp. 381–392. Elsevier, Amsterdam (1972). https://doi.org/10.1016/1385-7258(72)90034-0
Dowson, M.: The Ariane 5 software failure. ACM SIGSOFT Softw Eng Notes 22(2), 84 (1997). https://doi.org/10.1145/251880.251992
Erbsen, A., Philipoom, J., Gross, J., Sloan, R., Chlipala, A.: Simple high-level code for cryptographic arithmetic—with proofs, without compromises. In: 2019 IEEE Symposium on Security and Privacy (SP), pp. 1202–1219. San Francisco, CA, USA (2019). https://doi.org/10.1109/SP.2019.00005. http://adam.chlipala.net/papers/FiatCryptoSP19/
Gawron, N.: Infamous Software Bugs: FDIV Bug. https://www.olenick.com/blog/articles/infamous-software-bugs-fdiv-bug
Gödel, K.: On formally undecidable propositions of Principia Mathematica and related systems I. Monatshefte für Mathematik 38(1), 173–198 (1931). https://doi.org/10.1007/BF01700692
Grégoire, B., Leroy, X.: A compiled implementation of strong reduction. In: Proceedings of the Seventh ACM SIGPLAN International Conference on Functional Programming. ICFP ’02, pp. 235–246. Association for Computing Machinery, New York, NY, USA (2002). https://doi.org/10.1145/581478.581501
Grégoire, B., Pottier, L., Théry, L.: Proof certificates for algebra and their application to automatic geometry theorem proving. In: Sturm, T., Zengler, C. (eds.) Automated Deduction in Geometry, pp. 42–59. Springer, Berlin (2011). https://doi.org/10.1007/978-3-642-21046-4_3
Gross, J., Erbsen, A., Philipoom, J., Agrawal, R., Chlipala, A.: Accelerating verified-compiler development with a verified rewriting engine. In: Andronick, J., de Moura, L. (eds.) Proceedings of the 13th International Conference on Interactive Theorem Proving (ITP 2022). Leibniz International Proceedings in Informatics (LIPIcs), vol. 237, pp. 17–11718. Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Dagstuhl, Germany (2022). https://doi.org/10.4230/LIPIcs.ITP.2022.17. arXiv:2205.00862
Gross, J.S.: Performance engineering of proof-based software systems at scale. PhD thesis, Massachusetts Institute of Technology (February 2021). https://dspace.mit.edu/handle/1721.1/130763
Gross, J.: setoid_rewrite and rewrite_strat Are Cubic in the Number of Binders Even When There Are No Matches \(\bullet \) Issue #12524 \(\bullet \) Coq/coq, GitHub issue (2020). Accessed 25 Apr 2023. https://github.com/coq/coq/issues/12524
Haftmann, F., Nipkow, T.: A code generator framework for Isabelle/HOL. In: Proc. TPHOLs (2007)
Halfhill, T.R.: The Truth Behind the Pentium Bug. https://web.archive.org/web/20060209005434, http://www.byte.com/art/9503/sec13/art1.htm
Hern, A.: Microsoft scrambles to limit PR damage over abusive AI Bot Tay, The Guardian (2016). Accessed 24 Apr 2023. https://www.theguardian.com/technology/2016/mar/24/microsoft-scrambles-limit-pr-damage-over-abusive-ai-bot-tay
Hickey, J., Nogin, A.: Formal compiler construction in a logical framework. Higher-Order Symb. Comput. 19(2), 197–230 (2006). https://doi.org/10.1007/s10990-006-8746-6
Jézéquel, J.-M., Meyer, B.: Design by contract: the lessons of Ariane. Computer 30(1), 129–130 (1997). https://doi.org/10.1109/2.562936
Kolomatskaia, A., Shulman, M.: Semi-simplicial types, GitHub repository (2022). Accessed 25 Apr 2023. https://github.com/FrozenWinters/SSTs
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: A verified implementation of ML. In: POPL ’14: Proceedings of the 41st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. POPL ’14, pp. 179–191. ACM Press, New York, NY, USA (2014). https://doi.org/10.1145/2535838.2535841
Lee, P.: Learning from Tay’s Introduction, Official Microsoft Blog (2016). Microsoft. Accessed 24 Apr 2023. https://blogs.microsoft.com/blog/2016/03/25/learning-tays-introduction/
Leech, J.P., Klaes, L., Wiener, M., Yamada, Y.: Space FAQ 08/13—planetary probe history. http://www.faqs.org/faqs/space/probe/
Leroy, X.: A formally verified compiler back-end. J. Autom. Reason. 43(4), 363–446 (2009). https://doi.org/10.1007/s10817-009-9155-4
Leveson, N.G., Turner, C.S.: An investigation of the Therac-25 accidents. Computer 26(7), 18–41 (1993). https://doi.org/10.1109/MC.1993.274940
Lloyd, R.: Metric mishap caused loss of NASA orbiter. http://www.cnn.com/TECH/space/9909/30/mars.metric.02/index.html
Löb, M.H.: Solution of a problem of Leon Henkin. J. Symb. Logic 20(2), 115–118 (1955). https://doi.org/10.2307/2266895
Lynch, J.: The worst computer bugs in history: losing \$460m in 45 minutes. BugSnag Blog. Accessed 25 Apr 2023 (2017). https://www.bugsnag.com/blog/bug-day-460m-loss
Lynch, J.: The worst computer bugs in history: race conditions in Therac-25. BugSnag Blog. Accessed 25 Apr 2023 (2017). https://www.bugsnag.com/blog/bug-day-race-condition-therac-25
Lynch, J.: The worst computer bugs in history: rapid unanticipated disassembly of the Mars Climate Orbiter. BugSnag Blog. Accessed 25 Apr 2023 (2017). https://www.bugsnag.com/blog/bug-day-mars-climate-orbiter
Lynch, J.: The worst computer bugs in history: the Ariane 5 disaster. BugSnag Blog. Accessed 25 Apr 2023 (2017). https://www.bugsnag.com/blog/bug-day-ariane-5-disaster
Malecha, G., Bengtson, J.: Extensible and efficient automation through reflective tactics. In: Thiemann, P. (ed.) Programming Languages and Systems: 25th European Symposium on Programming, ESOP 2016, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2016, Eindhoven, The Netherlands, April 2–8, 2016, Proceedings, pp. 532–559. Springer, Berlin (2016). https://doi.org/10.1007/978-3-662-49498-1_21
Malecha, G.M.: Extensible proof engineering in intensional type theory. PhD thesis, Harvard University (November 2014). http://gmalecha.github.io/publication/2015/02/01/extensible-proof-engineering-in-intensional-type-theory.html
Maranget, L.: Compiling pattern matching to good decision trees. In: Proceedings of the 2008 ACM SIGPLAN Workshop on ML, pp. 35–46 (2008). ACM. http://moscova.inria.fr/~maranget/papers/ml05e-maranget.pdf
Martin-Dorel, É., Roux, P.: A reflexive tactic for polynomial positivity using numerical solvers and floating-point computations. In: Proceedings of the 6th ACM SIGPLAN Conference on Certified Programs and Proofs. CPP 2017, pp. 90–99. Association for Computing Machinery, New York, NY, USA (2017). https://doi.org/10.1145/3018610.3018622
Nicely, T.R.: Pentium FDIV Flaw FAQ. https://web.archive.org/web/20190618044444, http://www.trnicely.net/pentbug/pentbug.html
Pottier, L.: Connecting Gröbner bases programs with Coq to do proofs in algebra, geometry and arithmetics (2010) arXiv:1007.3615
Pujet, L.: A logical relation for MLTT using indexed inductive types, GitHub repository (2022). Accessed 25 Apr 2023. https://github.com/loic-p/logrel-mltt/
Schropp, A., Popescu, A.: Nonfree datatypes in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) Certified Programs and Proofs, pp. 114–130. Springer, New York. https://doi.org/10.1007/978-3-319-03545-1_8
Shulman, M.: Homotopy type theory should eat itself (but so Far, It’s Too Big to Swallow), Homotopy Type Theory Blog (2014). Accessed 24 Apr 2023. https://homotopytypetheory.org/2014/03/03/hott-should-eat-itself/
Smith, S., Patwary, M., Norick, B., LeGresley, P., Rajbhandari, S., Casper, J., Liu, Z., Prabhumoye, S., Zerveas, G., Korthikanti, V., Zhang, E., Child, R., Aminabadi, R.Y., Bernauer, J., Song, X., Shoeybi, M., He, Y., Houston, M., Tiwary, S., Catanzaro, B.: Using DeepSpeed and Megatron to train Megatron-Turing NLG 530B, a large-scale generative language model (2022) arXiv:2201.11990
Sozeau, M., Boulier, S., Forster, Y., Tabareau, N., Winterhalter, T.: Coq Coq correct! verification of type checking and erasure for Coq. In: Coq. Proc. ACM Program. Lang. 4(POPL) (2019). https://doi.org/10.1145/3371076
Sozeau, M., Anand, A., Boulier, S., Cohen, C., Forster, Y., Kunze, F., Malecha, G., Tabareau, N., Winterhalter, T.: The MetaCoq project. J. Autom. Reason. 64(5), 947–999 (2020). https://doi.org/10.1007/s10817-019-09540-0
Turley, J.: ChatGPT falsely accused me of sexually harassing my students. Can we really trust AI? USA Today. Accessed 1 May 2023 (2023). https://www.usatoday.com/story/opinion/columnist/2023/04/03/chatgpt-misinformation-bias-flaws-ai-chatbot/11571830002/
Westbrook, E.: Uniform logical relations. Technical Report TR11-01, Rice University (2011). April 1, 2011. https://hdl.handle.net/1911/96394
Xiang, C.: ‘He Would Still Be Here’: man dies by suicide after talking with AI Chatbot, Widow Says, Vice (2023). Accessed 24 Apr 2024. https://www.vice.com/en/article/pkadgm/man-dies-by-suicide-after-talking-with-ai-chatbot-widow-says
Funding
’Open Access funding provided by the MIT Libraries’ This work was supported in part by a Google Research Award, National Science Foundation grants CCF-1253229, CCF-1512611, and CCF-1521584, and the National Science Foundation Graduate Research Fellowship under Grant Nos. 1122374 and 1745302. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Contributions
Jason Gross wrote the bulk of the code of the rewriting framework—building on a proof-of-concept prototype Andres Erbsen wrote for Fiat Cryptography—performed the performance evaluations, and did some work on Fiat Cryptography. Jason Gross, Andres Erbsen, Jade Philipoom, and Adam Chlipala contributed to the design of the rewriting framework. Andres Erbsen, Jason Gross, and Jade Philipoom contributed to the integration of the rewriting framework with Fiat Cryptography and did non-performance evaluation and testing. Jason Gross prepared all performance plots, wrote the technical explanations of the rewriting framework. Jason Gross, Andres Erbsen, and Adam Chlipala wrote the technical content already present in the ITP submission. All authors reviewed the original text of the ITP submission. Jason Gross and Rajashree Agrawal, with input from and in conversation with Andres Erbsen, developed the new context of the rewriting framework as a prototype for a performant proof engine building block. Jason Gross and Rajashree Agrawal wrote most of the new text of the article, with the section on the theoretical asymptotic analysis of incremental rewriting based on a draft by Andres Erbsen.
Corresponding author
Ethics declarations
Competing interests
Financial interests None. Non-financial interests Jason Gross is a member of the Coq development team.
Ethical Approval
Not applicable.
Consent to Participate
Not applicable.
Consent for Publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported in part by a Google Research Award, National Science Foundation grants CCF-1253229, CCF-1512611, and CCF-1521584, and the National Science Foundation Graduate Research Fellowship under Grant Nos. 1122374 and 1745302. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gross, J., Erbsen, A., Philipoom, J. et al. Towards a Scalable Proof Engine: A Performant Prototype Rewriting Primitive for Coq. J Autom Reasoning 68, 19 (2024). https://doi.org/10.1007/s10817-024-09705-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10817-024-09705-6






 and
and


 ) to reduce this application.
) to reduce this application.



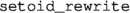 and
and  reduces away the denotation function on the AST that results from rewriting. As discussed in Sect.
reduces away the denotation function on the AST that results from rewriting. As discussed in Sect.