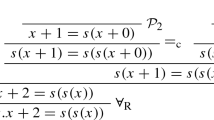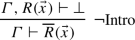Skip to main content
SpringerLink
Log in

Theorem Proving as Constraint Solving with Coherent Logic

  • Published:
Journal of Automated Reasoning Aims and scope Submit manuscript

Abstract

In contrast to common automated theorem proving approaches, in which the search space is a set of some formulae and what is sought is again a (goal) formula, we propose an approach based on searching for a proof (of a given length) as a whole. Namely, a proof of a formula in a fixed logical setting can be encoded as a sequence of natural numbers meeting some conditions and a suitable constraint solver can find such a sequence. The sequence can then be decoded giving a proof in the original theory language. This approach leads to several unique features, for instance, it can provide shortest proofs. In this paper, we focus on proofs in coherent logic, an expressive fragment of first-order logic, and on SAT and SMT solvers for solving sets of constraints, but the approach could be tried in other contexts as well. We implemented the proposed method and we present its features, perspectives and performances. One of the features of the implemented prover is that it can generate human understandable proofs in natural language and also machine-verifiable proofs for the interactive prover Coq.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. A coherent formula is also known as a “special coherent implication”, “geometric formula”, “basic geometric sequent” [27]. A coherent theory is sometimes called a “geometric theory” [49]. However, the much more widely used notion of “geometric formula” allows infinitary disjunctions (but only over finitely many variables) [76]. Coherent formulae involve only finitary disjunctions, so coherent logic can be seen as a special case of geometric logic, or as a first-order fragment of geometric logic.

  2. Notice the hidden link between the formulae \(B_i(\vec {a},\vec {b})\) from the rule \(\mathrm {MP}\) and the formula ax: the formulae \(B_i(\vec {a},\vec {b})\) from the rule are instances of the formulae \(B_i(\vec {x},\vec {y})\) from ax.

  3. The rule \(\mathrm {\lnot Intro}\):

    could be added to the given set of inference rules. In the intuitionistic setting, it can be more suitable (i.e. weaker) than the axiom \(\forall \vec {x} (R(\vec {x}) \vee {\overline{R}}(\vec {x}))\) (for concrete R).

  4. https://github.com/janicicpredrag/URSA.

  5. Transformation to CL2 differs for axioms and for conjectures, because they have different polarity in the proving context: \( axioms \vdash conjecture \).

  6. Transformation based on binary cuts of sets of formula would lead to a smaller set of new short-hands and additional axioms—of size \(O(\log k)\) instead of O(k). However, the size of disjunctions in real-world examples is usually not too large, so we keep the simple version and will experiment with the second one in the future.

  7. The given content, i.e., a proof represented by numbers, was created automatically by our prover. The shown proof representation does not include all variables that were considered during the proving/solving process. Also, some of the given values are redundant (but are still kept for convenience in this representation).

  8. The way we represent this condition is described in Sect. 4.

  9. For the very first proof step following the given assumptions, there should be also a constraint corresponding to a posibility that the goal has been met by some of the given assumptions.

  10. Even if there are broadly available SAT and SMT solvers which have been tested on a large amount of problems by a large amount of users and even some integrated in interactive proof assistant using either a reflexive approach or one based on checking certificates, we think it is simpler to use the final reconstructed proof for the original statement as a certificate.

  11. This optimisation may be useless when the underlying SAT or SMT prover uses a common sub-expression elimination pre-processing optimisation.

  12. Larus is Latin for seagull. A symbolic meaning sometimes attached to seagull is: looking at the problem at hand from a different angle. That may be appropriate for a prover based on a new proving paradigm: looking for a proof as a whole.

  13. The source code of the system and the benchmarks are publicly available from here: https://github.com/janicicpredrag/Larus. For running the system, one needs also one of the tools URSA [38] or z3 [51].

  14. There are some small differences between the description of proof step FirstCase (Sect. 3.7) and the implementation. It can be shown that the condition StepKind \((s-1)=\) MP is redundant (since the previous step has to be branching), so it was omitted in the implementation. The constraint nNesting[nProofStep-1] \(<=\) nMaxNesting is not given in the description of proof step FirstCase. Indeed, this constraint is optional. Limiting the maximal nesting simplifies the problem and cuts-off some parts of the search space. If there are no branching axioms, by using this constraint it can be easily stated that there is no nesting at all.

  15. https://vprover.github.io/.

  16. https://wwwlehre.dhbw-stuttgart.de/~sschulz/E/E.html.

  17. http://www.cs.man.ac.uk/~korovink/iprover/.

  18. http://www.leancop.de/.

  19. http://leancop.de/nanocop/.

  20. http://www.ii.uni.wroc.pl/~nivelle/software/geo/index.html.

  21. https://github.com/erimcg/ChewTPTP.

  22. http://zenon.inria.fr/.

  23. https://github.com/lukaszcz/coqhammer.

  24. https://isabelle.in.tum.de/.

  25. https://github.com/lukaszcz/tptp2coq.

  26. https://code.google.com/archive/p/clp/source.

  27. https://geocoq.github.io/GeoCoq/.

  28. Note that in the Coq files generated from TPTP files, the statements are not curryfied. We noticed that this reduces the efficiency of the Coq tactics.

  29. For this corpus, Larus is used with options: no case splits, start by looking for a proof of at most 2 steps, do not use negation elimination. Proof verification using Coq is not used for this corpus (only for this corpus the time needed for proof verification is not negligible).

  30. https://mathcs.clarku.edu/~djoyce/java/elements/bookI/propI5.html.

  31. https://github.com/GeoCoq/GeoCoq/blob/master/Elements/OriginalProofs/proposition_43.v.

References

  1. Alrabbaa, C., Baader, F., Borgwardt, S., Koopmann, P., Kovtunova, A.: Finding small proofs for description logic entailments: theory and practice. In LPAR23. LPAR-23: 23rd International Conference on Logic for Programming, Artificial Intelligence and Reasoning, pp. 32–5 (2020)

  2. Atserias, A., Müller, M.: Automating resolution is NP-hard. In: Zuckerman, D. (ed.) 60th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2019, Baltimore, Maryland, USA, November 9–12, 2019, pp. 498–509. IEEE Computer Society (2019)

  3. Avigad, J.: Automated reasoning for the working mathematician. In Frontiers of Combining Systems (FroCoS), London (2019). Invited Talk

  4. Avigad, J., Dean, E., Mumma, J.: A formal system for Euclid’s elements. Rev. Symb. Logic 2, 700–768 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  5. Beeson, M., Narboux, J., Wiedijk, F.: Proof-checking Euclid. Ann. Math. Artif. Intell. 85(2–4), 213–257 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bezem, M., Coquand, T.: Newman’s Lemma—a case study in proof automation and geometric logic. Curr. Trends Theor. Comput. Sci. 2, 267–282 (2004)

    Article  MATH  Google Scholar 

  7. Bezem, M., Coquand, T.: Automating coherent logic. In: Sutcliffe, G., Voronkov, A., (eds.) 12th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning—LPAR 2005, volume 3835 of Lecture Notes in Computer Science, pp. 246–260. Springer (2005)

  8. Bezem, M., Hendriks, D.: On the mechanization of the proof of Hessenberg’s theorem in coherent logic. J. Autom. Reason. 40(1), 61–85 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  9. Biere, A., Heule, M., van Maaren, H., Walsh, T. (eds.): Handbook of Satisfiability, Volume 185 of Frontiers in Artificial Intelligence and Applications. IOS Press, Amsterdam (2009)

    Google Scholar 

  10. Blanchette, J.C., Kaliszyk, C., Paulson, L.C., Urban, J.: Hammering towards QED. J. Formal. Reason. 9, 101–148 (2016)

    MathSciNet  MATH  Google Scholar 

  11. Blanchette, J.C., Bulwahn, L., Nipkow, T.: Automatic proof and disproof in Isabelle/HOL. In: Tinelli, C., Sofronie-Stokkermans, V. (eds.) Frontiers of Combining Systems, 8th International Symposium, Proceedings, volume 6989 of Lecture Notes in Computer Science, pp. 12–27. Springer (2011)

  12. Blanchette, J.C., Böhme, S., Fleury, M., Smolka, S.J., Steckermeier, A.: Semi-intelligible Isar proofs from machine-generated proofs. J. Autom. Reason. 56(2), 155–200 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  13. Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. J. Autom. Reason. 51(1), 109–128 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  14. Blanchette, J.C., Popescu, A., Wand, D., Weidenbach, C.: More SPASS with Isabelle. In: International Conference on Interactive Theorem Proving, pp. 345–360. Springer (2012)

  15. Bongio, J., Katrak, C., Lin, H., Lynch, C., McGregor, R.E.: Encoding first order proofs in SMT. Electron. Notes Theor. Comput. Sci. 198(2), 71–84 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Bonichon, R., Delahaye, D., Doligez, D.: Zenon: An extensible automated theorem prover producing checkable proofs. In: Dershowitz, N., Voronkov, A. (eds.) Logic for Programming, Artificial Intelligence, and Reasoning, vol. 4790, pp. 151–165. Springer, Berlin/Heidelberg (2007). Series Title: Lecture Notes in Computer Science

  17. Boutry, P., Gries, C., Narboux, J., Schreck, P.: Parallel postulates and continuity axioms: a mechanized study in intuitionistic logic using Coq. J. Autom. Reason. 62, 1–68 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  18. Boutry, P., Narboux, J., Schreck, P.: A reflexive tactic for automated generation of proofs of incidence to an affine variety (2015)

  19. Böhme, S., Weber, T.: Fast LCF-style proof reconstruction for Z3. In: Kaufmann, M., Paulson, L.C. (eds.) Interactive Theorem Proving, First International Conference, ITP 2010, Edinburgh, UK, July 11–14, 2010. Proceedings, volume 6172 of Lecture Notes in Computer Science, pp. 179–194. Springer (2010)

  20. Brown, C.E.: Reducing higher-order theorem proving to a sequence of SAT problems. J. Autom. Reason. 51(1), 57–77 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Contejean, E., Corbineau, P.: Reflecting proofs in first-order logic with equality. In Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Rangan, C.P., Steffen, B., Sudan, M., Terzopoulos, D., Tygar, D., Vardi, M.Y., Weikum, G., Nieuwenhuis, R. (eds,) Automated Deduction—CADE-20, vol. 3632, pp. 7–22. Springer, Berlin/Heidelberg (2005). Series Title: Lecture Notes in Computer Science

  22. Cropper, A., Dumancic, S., Evans, R., Muggleton, S.H.: Inductive logic programming at 30. Mach. Learn. 111(1), 147–172 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Czajka, Ł.: Practical proof search for coq by type inhabitation. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020, Automated Reasoning, vol. 12167, pp. 28–57. Springer, Cham (2020). Series Title: Lecture Notes in Computer Science

  24. Czajka, Ł, Kaliszyk, C.: Hammer for Coq: automation for dependent type theory. J. Autom. Reason. 61(1–4), 423–453 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  25. Deshane, T., Hu, W., Jablonski, P., Lin, H., Lynch, C., McGregor, R.E.: Encoding first order proofs in SAT. In: Pfenning, F. (ed.) Automated Deduction—CADE-21, 21st International Conference on Automated Deduction, Bremen, Germany, July 17-20, 2007, Proceedings, vol. 4603 of Lecture Notes in Computer Science, pp. 476–491. Springer (2007)

  26. Dowek, G., Thiré, F.: Logipedia: a multi-system encyclopedia of formal proofs. In Workshop on Large Mathematical Libraries, Prague (2019)

  27. Dyckhoff, R., Negri, S.: Geometrization of first-order logic. Bull. Symb. Log. 21, 123–163 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  28. Dyckhoff, R., Pinto, L.: Permutability of proofs in intuitionistic sequent calculi. Theoret. Comput. Sci. 212(1–2), 141–155 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  29. Font, L., Cyr, S., Richard, P.R., Gagnon, M.: Automating the generation of high school geometry proofs using prolog in an educational context. In: Proceedings 8th International Workshop on Theorem Proving Components for Educational Software, ThEdu@CADE, Natal, Brazil (2019)

  30. Ganesalingam, M., Gowers, W.T.: A fully automatic problem solver with human-style output. CoRR, arXiV:1309.4501 (2013)

  31. Gebser, M., Kaufmann, B., Neumann, A., Schaub, T.: clasp : a conflict-driven answer set solver. In: Baral, C., Brewka, G., Schlipf, J.S. (eds.) Logic Programming and Nonmonotonic Reasoning, 9th International Conference, LPNMR 2007, Tempe, AZ, USA, May 15–17, 2007, Proceedings, volume 4483 of Lecture Notes in Computer Science, pp. 260–265. Springer (2007)

  32. Gentzen, G.: Untersuchungen über das logische Schliessen, I, II. Mathematische Zeitschrift, 39:176–210, 405–431, 1935. English translation in "The Collected Papers of Gerhard Gentzen", North-Holland Publ. Co. (1969)

  33. Guenot, N.: Concurrency and permutability in the sequent calculus. In Parigot, M., Straßburger, L. (eds.) Structures and deduction (ESSLLI’09 workshop), pp. 39–52 (2009)

  34. Hales, T.: An argument for controlled natural languages in mathematics (2019)

  35. Harrison, J.: Meta theory and reflection in theorem proving: a survey and critique. Technical Report CRC-053, SRI International Cambridge Computer Science Research Center (1995)

  36. Holen, B., Hovland, D., Giese, M.: Efficient rule-matching for automated coherent logic. In NIK-2013 proceedings (2012)

  37. Imbert, J.-L.: Fourier’s elimination: which to choose? In: Principles and Practice of Constraint Programming, pp. 117–129 (1993)

  38. Janičić, P.: URSA: a system for uniform reduction to SAT. Logic. Methods Comput. Sci. 8(3), 30 (2012)

    MathSciNet  MATH  Google Scholar 

  39. Janičić, P., Kordić, S.: EUCLID—the geometry theorem prover. FILOMAT 9(3), 723–732 (1995)

    MathSciNet  MATH  Google Scholar 

  40. Janičić, P., Narboux, J., Quaresma, P.: The area method : a recapitulation. J. Autom. Reason. 48(4), 489–532 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  41. Jiang, J., Zhang, J.: A review and prospect of readable machine proofs for geometry theorems. J. Syst. Sci. Complexity 25(4), 802–820 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  42. Kaliszyk, C., Urban, J.: HOL (y) hammer: online ATP service for HOL light. Math. Comput. Sci. 9(1), 5–22 (2015)

    Article  MATH  Google Scholar 

  43. Kinyon, M.: Proof simplification and automated theorem proving. Philos. Trans. R. Soc. A 377(2140), 20180034 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  44. Kleene, S.C.: Permutability of inferences in Gentzen’s calculi LK and LJ. Mem. Am. Math. Soc. 10, 1–26 (1952)

    MathSciNet  MATH  Google Scholar 

  45. Korovin, K.: iProver—an instantiation-based theorem prover for first-order logic (system description). In: Armando, A., Baumgartner, P. Dowek, G. (eds.) Automated Reasoning, volume 5195, pp. 292–298. Springer, Berlin/ Heidelberg (2008). ISSN: 0302-9743, 1611–3349 Series Title: Lecture Notes in Computer Science

  46. Kovács, L., Voronkov, A.: First-order theorem proving and vampire. In Sharygina, N., Veith, H. (eds.) Computer Aided Verification—25th International Conference, CAV 2013, Saint Petersburg, Russia, July 13–19, 2013. Proceedings, volume 8044 of Lecture Notes in Computer Science, pp. 1–35. Springer (2013)

  47. Lagniez, J.-M., Marquis, P.: On preprocessing techniques and their impact on propositional model counting. J. Autom. Reason. 58(4), 413–481 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  48. Lutovac, T., Harland, J.: A contribution to automated-oriented reasoning about permutability of sequent calculi rules. Comput. Sci. Inf. Syst. 10(3), 1185–1210 (2013)

    Article  Google Scholar 

  49. MacLane, S., Moerdijk, I.: Sheaves in Geometry and Logic: A First Introduction to Topos Theory. Springer, Berlin (1992)

    Google Scholar 

  50. McGregor, R.E.: Automated theorem proving using SAT. PhD Thesis, Clarkson University (2011). Publication Title: Electron. Notes Theor. Comput. Sci

  51. Mendonça de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In Ramakrishnan, C.R., Rehof, J. (eds.) Tools and Algorithms for the Construction and Analysis of Systems, 14th International Conference, TACAS 2008, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2008, Budapest, Hungary, March 29–April 6, 2008. Proceedings, volume 4963 of Lecture Notes in Computer Science, pp. 337–340. Springer (2008)

  52. Mertz, I., Pitassi, T., Wei, Y.: Short proofs are hard to find. In: Baier, C., Chatzigiannakis, I., Flocchini, P., Leonardi, S. (eds.) 46th International Colloquium on Automata, Languages, and Programming, ICALP 2019, July 9–12, 2019, Patras, Greece, volume 132 of LIPIcs, pp. 84:1–84:16. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, (2019)

  53. Nguyen, H.D., Nguyen, D., Pham, V.T.: Design an intelligent problem solver in solid geometry based on knowledge model about relations. In 2016 Eighth International Conference on Knowledge and Systems Engineering (KSE), pp. 150–155 (2016)

  54. Nikolić, M., Janičić, P.: CDCL-based abstract state transition system for coherent logic. In Jeuring, J., Campbell, J.A., Carette, J., Dos Reis, G., Sojka, P., Wenzel, M., Sorge, V. (eds.) Intelligent Computer Mathematics - 11th International Conference, AISC 2012, 19th Symposium, Calculemus 2012, 5th International Workshop, DML 2012, 11th International Conference, MKM 2012, Systems and Projects, Held as Part of CICM 2012, Bremen, Germany, July 8–13, 2012. Proceedings, volume 7362 of Lecture Notes in Computer Science, pp. 264–279. Springer (2012)

  55. Nikolić, M., Marić, F., Janičić, P.: Simple algorithm portfolio for SAT. Artif. Intell. Rev. (2012). to appear

  56. Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle HOL: a proof assistant for higher-order logic, volume 2283 of Lecture Notes in Computer Science. Springer (2002)

  57. de Nivelle, H.: Subsumption algorithms for three-valued geometric resolution. In: Olivetti, N. Tiwari, A. (eds.) Automated Reasoning - 8th International Joint Conference, IJCAR 2016, Coimbra, Portugal, June 27–July 2, 2016, Proceedings, volume 9706 of Lecture Notes in Computer Science, pp. 257–272. Springer (2016)

  58. de Nivelle, H., Meng, J.: Geometric resolution: a proof procedure based on finite model search. In: Furbach, U., Shankar, N. (eds.) Automated Reasoning, Third International Joint Conference, IJCAR 2006, Seattle, WA, USA, August 17–20, 2006, Proceedings, volume 4130 of Lecture Notes in Computer Science, pp. 303–317. Springer (2006)

  59. Otten, J.: nanoCoP: natural non-clausal theorem proving. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, pp. 4924–4928, Melbourne, Australia (2017). International Joint Conferences on Artificial Intelligence Organization

  60. Otten, J., Bibel, W.: leanCoP: lean connection-based theorem proving. J. Symb. Comput. 36(1–2), 139–161 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  61. Paulson, L.C.: Isabelle: a generic theorem prover, volume 828 of Lecture Notes in Computer Science. Springer (1994)

  62. Paulson, L.C.: Three years of experience with sledgehammer, a practical link between automatic and interactive theorem provers. In: Schmidt, R.A., Schulz, S., Konev, B. (eds.) Proceedings of the 2nd Workshop on Practical Aspects of Automated Reasoning, PAAR-2010, Edinburgh, Scotland, UK, July 14, 2010, volume 9 of EPiC Series in Computing, pp. 1–10. EasyChair (2010)

  63. Polonsky, A.: Proofs, types and lambda calculus. PhD thesis, University of Bergen (2011)

  64. Prestwich, S.D., Lynce, I.: Local search for unsatisfiability. In: Biere, A., Gomes, C.P. (eds.) Theory and Applications of Satisfiability Testing - SAT 2006, 9th International Conference, Seattle, WA, USA, August 12-015, 2006, Proceedings, volume 4121 of Lecture Notes in Computer Science, pp. 283–296. Springer (2006)

  65. Reynolds, A., Tinelli, C.: Sygus techniques in the core of an SMT solver. In: Fisman, D., Jacobs, S. (eds.) Proceedings Sixth Workshop on Synthesis, SYNT@CAV 2017, Heidelberg, Germany, 22nd July 2017, volume 260 of EPTCS, pp. 81–96 (2017)

  66. Schulz, S.: Light-weight integration of SAT solving into first-order reasoners–first experiments. Vampire 2017—Proceedings of the 4th Vampire Workshop, vol. 53, pp. 9–19 (2017)

  67. Schurr, H., Fleury, M., Desharnais, M.: Reliable reconstruction of fine-grained proofs in a proof assistant. In: Platzer, A., Sutcliffe, G. (eds.) Automated Deduction - CADE 28 - 28th International Conference on Automated Deduction, Virtual Event, July 12–15, 2021, Proceedings, volume 12699 of Lecture Notes in Computer Science, pp. 450–467. Springer (2021)

  68. Smith, P.: An introduction to Gödel’s theorems. Cambridge University Press (2013)

  69. Stojanović, S., Narboux, J., Bezem, M., Janičić, P.: A Vernacular for Coherent Logic. In: Watt, S.M., Davenport, J.H., Sexton, A.P., Sojka, P., Urban, J. (eds.) Intelligent Computer Mathematics, volume 8543 of Lecture Notes in Computer Science, pp. 388–403. Springer International Publishing (2014)

  70. Stojanović, S., Pavlović, V., Janičić, P.: A coherent logic based geometry theorem prover capable of producing formal and readable proofs. In: Automated Deduction in Geometry, volume 6877 of Lecture Notes in Computer Science, pp. 201–220. Springer (2011)

  71. Sutcliffe, G.: The TPTP World—infrastructure for automated reasoning. In Clarke, E.M., Voronkov, A. (eds.) 16th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning – LPAR-16, volume 6355 of Lecture Notes in Computer Science, pp. 1–12. Springer (2010)

  72. The Coq development team. The Coq proof assistant. (2020)

  73. Thiele, R., Wos, L.: Hilbert’s twenty-fourth problem. J. Autom. Reason. 29(1), 67–89 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  74. Urban, J., Rudnicki, P., Sutcliffe, G.: ATP and presentation service for Mizar formalizations. J. Autom. Reason. 50(2), 229–241 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  75. Veroff, R.: Finding shortest proofs: an application of linked inference rules. J. Autom. Reason. 27(2), 123–139 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  76. Vickers, S.: Geometric logic in computer science. In: Theory and Formal Methods, Workshops in Computing, pp. 37–54. Springer (1993)

  77. Voronkov, A.: AVATAR: the architecture for first-order theorem provers. In: Computer Aided Verification, pp. 696–710. Springer, Cham (2014)

  78. Wiedijk, F.: Formal proof sketches. In: International Workshop on Types for Proofs and Programs, pp. 378–393. Springer (2003)

  79. Wos, L.: Automating the search for elegant proofs. J. Autom. Reason. 21(2), 135–175 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  80. Xu, L., Hutter, F., Hoos, H.H., Leyton-Brown, K.: SATzilla: portfolio-based algorithm selection for SAT. J. Artif. Intell. Res. 32, 565–606 (2008)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

We are grateful to the anonymous reviewers who gave us a very useful feedback and number of suggestions that significantly improved the earlier version of this paper. For useful feedback we are also grateful to Petar Vukmirović.

Author information

Authors and Affiliations

  1. Department for Computer Science, Faculty of Mathematics, University of Belgrade, Studentski trg 16, 11000, Belgrade, Serbia

    Predrag Janičić

  2. UMR 7357 CNRS, University of Strasbourg, Pôle API, Bd Sébastien Brant, BP 10413, 67412, Illkirch, France

    Julien Narboux

Authors
  1. Predrag Janičić
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Julien Narboux
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Predrag Janičić.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Example Proofs of Proposition 5

Appendix: Example Proofs of Proposition 5

In this section, we list the proofs of Euclid Book 1, Proposition 5 [Example 10], generated by different theorem provers.

1.1 A.1 Larus

Non-minimal proof (Coq output):

figure s

Minimal CL proof found (Coq output):

figure t

Proof with inline lemmas (Coq output):

figure u

1.2 A.2 Leancop

figure v

1.3 A.3 Nanocop

figure w

1.4 A.4 Vampire

figure x
figure y

1.5 A.5 iProver

figure z

1.6 A.6 Zenon

figure aa
figure ab

1.7 A.7 Isabelle

Isabelle 2016 generated several proof using Sledgehammer. The first proof is the most informative but we can still feel that the proof has been converted from resolution proof. Moreover, the generated proof is not accepted by Isabelle. The second proof is accepted but not very informative. The third proof is a one-liner calling the meeson tactic.

figure ac
figure ad
figure ae

1.8 A.8 Manual Formal Proof in Coq

For comparison, we provide the original Coq proof:

figure af

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Janičić, P., Narboux, J. Theorem Proving as Constraint Solving with Coherent Logic. J Autom Reasoning 66, 689–746 (2022). https://doi.org/10.1007/s10817-022-09629-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10817-022-09629-z

Keywords

Search

Navigation