The Resolution of Keller’s Conjecture

Abstract

We consider three graphs, $G_{7,3}$, $G_{7,4}$, and $G_{7,6}$, related to Keller’s conjecture in dimension 7. The conjecture is false for this dimension if and only if at least one of the graphs contains a clique of size $2^7 = 128$. We present an automated method to solve this conjecture by encoding the existence of such a clique as a propositional formula. We apply satisfiability solving combined with symmetry-breaking techniques to determine that no such clique exists. This result implies that every unit cube tiling of $\mathbb {R}^7$ contains a facesharing pair of cubes. Since a faceshare-free unit cube tiling of $\mathbb {R}^8$ exists (which we also verify), this completely resolves Keller’s conjecture.

A Appendix

In this Appendix, we formalize the connection between Keller graphs and Keller’s original conjecture on cube tilings. In particular, we give an overview of the various results since the mid-twentieth century which have contributed toward understanding Keller’s conjecture. For similar discussions and surveys on Keller’s conjecture, see for example [29, 31]. In addition, the survey of Zong [33] situates Keller’s conjecture in the broader context of research on unit cubes. An additional motivation for this appendix is to give insight to the steps needed in order to fully, formally verify the proof of Keller’s conjecture in dimension 7.

1.1 A.1 Cube Tilings

Let $d \ge 1$ be the dimension–the case $d=7$ is of the most interest in this paper. A unit cube (or just cube) is a translation of $[0, 1)^d$. In particular, for any $x \in \mathbb R^d$, we define $[0, 1)^d + x$ to be the translated cube $[x_1, x_1+1) \times \cdots [x_d, x_d+1)$. We call x the corner of the cube $[0, 1)^d + x$. For brevity, we denote $C^d(x) := [0, 1)^d + x$. We say that two cubes are disjoint if they do not intersect. Disjointness is equivalent to the cube corners being “far apart” in some coordinate.

Proposition 1

For all $x, y \in \mathbb R^d$, the cubes $C^d(x)$ and $C^d(y)$ are disjoint if and only if there exists a coordinate $i \in [d]$ such that $|x_i - y_i| \ge 1$.

Proof

If for some i, $|x_i - y_i| \ge 1$, then $[x_i, x_i+1)$ and $[y_i, y_i+1)$ cannot intersect. Therefore, $C^d(x)$ and $C^d(y)$ are disjoint.

We prove the contrapositive to show the reverse implication. Assume that for all i, $|x_i - y_i| < 1$. In this case, $[x_i, x_i+1)$ and $[y_i, y_i+1)$ intersect non-trivially for all i. Therefore, $C^d(x)$ and $C^d(y)$ intersect non-trivially. $\square$

We say that disjoint cubes $C^d(x)$ and $C^d(y)$ are facesharing if there exists exactly one coordinate $i \in [d]$ such that $|x_i - y_i| = 1$ and for all $j \in [d]$ such that $j \ne i$, $x_j = y_j$. This is equivalent to saying that $x = y \pm e_i$, where $e_1, \ldots , e_d$ are the standard unit basis vectors.

Let $T \subset \mathbb R^d$ be a set of cube corners. T is a cube tiling of $\mathbb {R}^d$ if $[0,1)^d + T = \{C^d(t) : t \in T\}$ is a family of pairwise disjoint cubes such that $\bigcup _{t\in T} C^d(t) = \mathbb {R}^d$. Note that $T = \mathbb Z^d$ produces the standard lattice cube tiling of $\mathbb R^d$.

We say that a cube tiling is faceshare-free if no pair of distinct cubes in the tiling shares a face. For example, $[0, 1)^d + \mathbb Z^d$ is not faceshare-free since, e.g., $[0, 1)^d$ and $[0, 1)^d+e_1$ faceshare. Keller conjectured that all tilings have a facesharing pair of cubes.

Conjecture 1

(Keller’s conjecture [14]) For all integers $d \ge 1$, there does not exist a faceshare-free tiling of $\mathbb R^d$ .

Perron [26, 27] was able to resolve the conjecture in dimensions $d \le 6$ using combinatorial casework. Lagarias and Shor [20] and Mackey [23] showed the conjecture to be false for dimensions $d \ge 8$. This paper resolves the final case of $d=7$ in the affirmative.

We shall explain in the remainder of this Appendix the key structural results in the literature that led to the full resolution of Keller’s conjecture.

1.2 A.2 Structure of Tilings

Let $T \subset \mathbb R^d$ be any set of cube corners such that $[0, 1)^d + T$ is a cube tiling. By the definition of cube tiling, we know that for any $x \in \mathbb Z^d$, there exists a unique $t \in T$ such that $x \in C^d(t)$.

Likewise, for any $t \in T$, there exists a unique $x \in \mathbb Z^d$ such that $x \in C^d(t)$. This is the point $x := (\lceil t_1\rceil , \lceil t_2 \rceil , \ldots , \lceil t_n\rceil )$, where $\lceil r \rceil$ represents the least integer that r does not exceed. Thus, we can refer to each cube by the integral point it contains. For all $x \in \mathbb Z^d$, we let $t(x) \in T$ be the unique corner such that $x \in C^d(t(x))$.

For all $x \in \mathbb R^d$ and $i \in [d]$, let $\ell _i(x)$ the be line through x parallel to the ith coordinate. Formally,

$$\begin{aligned} \ell _i(x) = \{y \in \mathbb R^d : \forall j \in [d] \setminus \{i\}, y_j = x_j \}. \end{aligned}$$

We use the term line to refer to these axis-parallel lines. We also define

$$\begin{aligned} T_i(x) = \{t \in T : C^d(t) \cap \ell _i(x) \ne \emptyset \} \end{aligned}$$

We say that $T_i(x)$ is an i-lattice if there exists $a \in \mathbb R$ such that for all $t \in T_i(x)$, $t_i \equiv a \mod 1$ and for all $y \in \mathbb Z$, there exists exactly one $t \in T_i(x)$ such that $t_i = a + y$. In other words, the ith coordinates of $T_i(x)$ are a “shift” of $\mathbb Z$.

To illustrate this definition, consider the tiling $T = \{(a+ 0.5 b,b) + [0,1)^2 : a,b \in \mathbb Z\}.$ That is a tiling of cubes in $\mathbb R^2$ where the cubes line up in horizontal rows, but each row is shifted by 0.5 from the next row. For all $x \in \mathbb R^2$, $T_1(x)$ is one of these rows of cubes. However, $T_2(x)$ is a “zig-zag” column of cubes, where each successive cube moves back/forth by 1/2 across the vertical line through x.

Proposition 3

Let $T \subset \mathbb R^d$ be a collection of cube corners. Fix $i \in [d]$. $[0, 1)^d + T$ is a tiling if and only if for all $x \in \mathbb R^d$, $T_i(x)$ is an i-lattice.

Proof

First, assume $[0, 1)^d + T$ is a tiling. Note that the intersection of any unit cube with any line is either the empty set or a half-open interval of length 1. Furthermore, the half-open intervals must partition the line, so the starting points of the intervals are integrally spaced. Thus, $T_i(x)$ is an i-lattice.

Likewise, if $T_i(x)$ is an i-lattice for all $x \in \mathbb R^d$, then every point on each line is in exactly one cube. Thus, every point is in exactly one cube, so $[0, 1)^d + T$ is a tiling. $\square$

The following structural result also follows.

Proposition 4

Let $T \subset \mathbb R^d$ be such that $[0, 1)^d + T$ is a cube tiling. For all $x \in \mathbb Z^d$ and $i \in [d]$,

$$\begin{aligned} t(x)_i + 1 = t(x + e_i)_i. \end{aligned}$$

Proof

Consider the line $\ell _i(x)$. The intervals $C^d(t(x)) \cap \ell _i(x)$ and $C^d(t(x+e_i)) \cap \ell _i(x)$ must be adjacent since they contain adjacent integral points. Therefore, by Proposition 3, $t(x)_i + 1 = t(x+e_i)_i$. $\square$

The t(x) notation also gives a straightforward condition for checking whether the corresponding tiling is faceshare-free.

Proposition 5

Let $[0, 1)^d+T$ be a tiling. If for all $x\in \mathbb R^d$ and all $i \in [d]$ we have that $C^d(t(x))$ and $C^d(t(x + e_i))$ do not faceshare, then $[0, 1)^d+T$ is faceshare-free.

Proof

Assume for sake of contradiction some pair of cubes $C^d(t(x))$ and $C^d(t(y))$ faceshare. This implies that $t(x) = t(y) \pm e_i$ for some i. Since x is each coordinate of t(x) rounded up, and y is each coordinate of t(y) rounded up, $x = y \pm e_i$. This is a contradiction. $\square$

The specific values of the coordinates in a tiling are somewhat artificial. That is, the values of the coordinates can be changed while preserving the tiling, as long as the following rule is observed:

lemequation0

Lemma 1

(“Replacement Lemma”) Let $[0, 1)^d + T$ be a tiling. Fix $a, b \in \mathbb R$ and $i \in [d]$. Define

$$\begin{aligned} T' := \{t \mid t \in T \wedge t_i \not \equiv a\!\mod 1\} \cup \{t + b e_i \mid t \in T \wedge t_i \equiv a\!\mod 1\}. \end{aligned}$$

Then, $[0, 1)^d + T'$ is a tiling. Furthermore, if $[0, 1)^d + T$ is faceshare-free, and there exists no $t \in T$ such that $t_i \equiv a + b\mod 1$, then $[0, 1)^d + T'$ is faceshare-free.

To partially illustrate the lemma, recall the tiling $T = \{(a+ 0.5 b,b) + [0,1)^2 : a,b \in \mathbb Z\}.$ By the replacement lemma, if we shift every other row so that it is offset by 1/3 instead of 1/2, then no new facesharing is introduced.

Proof

For all $x \in \mathbb R^d$, consider the i-lattice $T_i(x)$. Either every ith coordinate in this lattice is $\not \equiv a \mod 1$, in which case nothing changes. Otherwise, every ith coordinate is $\equiv a \mod 1$, in which case adding b to every ith coordinate preserves it as an i-lattice. Thus, by Proposition 3, $[0, 1)^d + T'$ is a tiling.

Now assume $[0, 1)^d + T$ is faceshare-free, and there exists no $t \in T$ such that $t_i \equiv a + b\mod 1$. If $[0, 1)^d + T'$ has facesharing, there are $t^1, t^2 \in T'$ such that $t^1 = t^2 \pm e_j$ for some $j \in [d]$. In particular, $t^1_k \equiv t^2_k \mod 1$ for all $k\in [d]$.

If $t^1_i \not \equiv a+b\mod 1$, then $t^1$ and $t^2$ were not shifted when transforming T to $T'$. Thus, $t^1$ and $t^2$ are a facesharing pair in T, which is a contradiction.

Otherwise, if $t^1_i \equiv a+b\mod 1$, then we know that $t^1$ and $t^2$ were shifted by $be_i$ when going from T to $T'$ (this uses the condition that $t_i \not \equiv a + b\mod 1$ for all $t \in T$). Thus, $t^1-be_i$ and $t^2-be_i$ faceshare in T, again a contradiction. $\square$

1.3 A.3 Reduction to Periodic Tilings

In this subsection, we show it suffices to look at periodic tilings. We say that $T \subset \mathbb R^d$ and its cube tiling $[0, 1)^d + T$ are periodic if for all $t \in T$ and , we also have $t + 2x \in T$. For instance, $T = \mathbb Z^d$ is periodic, as well as the tiling $T = \{(a+ 0.5 b,b) + [0,1)^2 : a,b \in \mathbb Z\}.$ mentioned earlier. In the t(x) notation (see Section A.2), we have that for all $x, y \in \mathbb Z^d$,

$$\begin{aligned} t(x + 2y) = t(x) + 2y. \end{aligned}$$

For a given dimension d, if Keller’s conjecture is true for all tilings, then it is also true for the periodic tilings. The work of Hajós [6, 7] shows that the reverse implication is also true.

Theorem 2

(Hajós [6, 7]) For all $d \ge 1$, if Keller’s conjecture is true for all periodic tilings, then Keller’s conjecture is true in dimension d.

Proof

We prove this by contradiction. Assume there exists $T \in \mathbb R^d$, not necessarily periodic, such that $[0, 1)^d + T$ is faceshare-free.

Let $\hat{T} \subset T$ be the corners whose corresponding cubes contain the points $\{0, 1\}^d$. In the t(x) notation, we have

$$\begin{aligned}\hat{T} := \{t(x) : x \in \{0, 1\}^d\}.\end{aligned}$$

Note that $\hat{T}$ has exactly $2^d$ cubes (which is ultimately why the maximum clique size of the Keller graph is $2^d$).

We extend $\hat{T}$ to a new periodic set $T'$ as follows

$$\begin{aligned} T' := \{t' = t + 2x \mid t \in \hat{T}, x \in \mathbb Z^d\}. \end{aligned}$$

Observe that each point $y \in \mathbb Z^d$ is in exactly one cube of $[0, 1)^d + T'$. Call this cube $t'(y)$.

We claim that $[0, 1)^d + T'$ is a periodic faceshare-free tiling of $\mathbb R^d$. This follows from the following three facts:

• 1. Every point of $[0, 1]^d$ is in exactly one cube of $[0, 1)^d + T'$. Since $[0, 1)^d + T$ is a tiling, every point of $[0, 1]^d$ is in exactly one cube of T. Furthermore, any cube which covers a point of $[0, 1]^d$ must cover one of the corners. Since the cubes which cover $\{0, 1\}^d$ are the same for T and $T'$ (by definition), every point of $[0, 1]^d$ must also be in exactly one cube of $[0, 1)^d + T'$.

• 2. $[0, 1)^d + T'$ is a tiling. We seek to show that for all $i \in [d]$, every point of the closed cube $[0, 1]^d + e_i$ is in exactly one point of the tiling $[0, 1)^d + T'$. Fix $x \in [0, 1]^d + e_i$. Let $x^{i\rightarrow 0}$ be the point identical to x except the ith coordinate is replaced with 0. Define $x^{i\rightarrow 1}$ and $x^{i\rightarrow 2}$ similarly. Let $\ell _1$ be the closed line segment from $x^{i\rightarrow 0}$ to $x^{i\rightarrow 1}$ and $\ell _2$ be the closed line segment from $x^{i\rightarrow 1}$ to $x^{i\rightarrow 2}$. Since every point of $[0, 1]^d$ is in exactly one cube of $T'$, there must exist $y, z \in \{0, 1\}^d$ such that $x^{i\rightarrow 0} \in C^d(t'(y))$ and $x^{i\rightarrow 1} \in C^d(t'(z))$. By an argument similar to that of Proposition 4, this implies that $\ell _1$ is covered by the union of $C^d(t'(y))$ and $C^d(t'(z))$ and that $t'(y)_i+1 = t'(z)_i$. Now, consider $y' = y + 2e_i$, observe that since $x^{i\rightarrow 0} \in C^d(t'(y))$, $x^{i\rightarrow 0} +2e_2 = x^{i\rightarrow 2} \in C^d(t'(y'))$. Also, $t'(z)_i + 1 = t'(y')_i$. Therefore, $C^d(t'(z))$ and $C^d(t'(y'))$ disjointly cover $\ell _2$ and thus exactly one of them contains x. To see that no other cube can cover x, assume that a third cube $C^d(t'(w))$ covers $\ell _2$. Then, either a portion of $C^d(t'(w))$ intersects $\ell _1$ or a portion of $C^d(t'(w-2e_i))$ intersects $\ell _1$. In either case, since every point of $\ell _1$ is covered by exactly one cube, we deduce that $w = z$ or $w = y + 2e_i$. Thus, x is covered by exactly one cube. By a similar argument, every point of $[0, 1]^d - e_i$ is covered by exactly one point of $[0, 1)^d + T'$. By a suitable induction, every closed cube $[0, 1]^d + y$ for some $y \in \mathbb Z^d$ has every point covered by exactly one cube of $[0, 1)^d + T'$. Thus, every point of $\mathbb R^d$ is covered by exactly one cube of $[0, 1)^d + T'$, and thus $[0, 1)^d + T'$ is a tiling.

• 3. $[0, 1)^d + T'$ is faceshare-free. If not, then by Proposition 5, we must have that $t'(x) +e_i= t'(x+e_i)$ for some $x \in \mathbb Z^d$ and $i \in [d]$. Note there exist $x' \in \{0, 1\}^d$ and $y \in \mathbb Z^d$ such that $x = x' + 2y$. Then,

  $$\begin{aligned} t'(x') + e_i&= t'(x'+2y)-2y + e_i\\&= t'(x)+e_i - 2y\\&= t'(x+e_i) - 2y\\&= t'(x'+e_i). \end{aligned}$$

  If $x'_i = 0$, then $x'+e_i \in \{0, 1\}^n$ as well. Thus, $C^d(t'(x')), C^d(t'(x'+e_i))$ faceshare in $[0,1)^d+\hat{T}$ (and thus $[0, 1)^d+T$), which is a contradiction. If $x'_i=1$, then, $x'-e_i \in \{0, 1\}^n$. And a similar calculation shows that $t'(x' - e_i) + e_i = t'(x')$. Therefore, $C^d(t'(x')), C^d(t'(x'-e_i))$ faceshare in $\hat{T}$ (and T), which is a contradiction.

$\square$

1.4 A.4 Reduction to Keller graphs

In the previous section, we showed that Keller’s conjecture for $\mathbb R^d$ is equivalent to showing that there is no faceshare-free periodic tiling of $\mathbb R^d$. Now we show faceshare-free periodic tilings correspond to cliques in the Keller graph.

We say that a periodic tiling is s-discrete if every coordinate has at most s distinct values modulo 1 in the tiling. A key observation is that s is bounded by the a function of the dimension.⁴

Proposition 2

( [30]) Every periodic tiling in dimension d is $2^{d-1}$-discrete.

Proof

For a given periodic tiling T, every cube is an integral translate of one of the $2^d$ cubes t(x) for $x \in \{0, 1\}^d$. By Proposition 4, we know that for all $i \in [d]$, $t(x)_i$ and $t(x \oplus e_i)_i$ are the same modulo 1. Pairing up the elements of $\{0, 1\}^d$, we see that there can be at most $2^{d-1}$ distinct values modulo 1 in the ith coordinate. $\square$

Lemma 3

$G_{d,s}$ has a clique of size $2^d$ if and only if there exists a faceshare-free s-discrete periodic tiling $[0, 1)^d+T$ in dimension d.

Proof

First, let $[0, 1)^d + T$ be an s-discrete periodic tiling. By repeatedly applying the Replacement Lemma, we can replace each coordinate of the entries of T with elements of $\left\{ 0, \dfrac{1}{s}, \ldots , \dfrac{s-1}{s}\right\}$ modulo 1. In other words, we may assume without loss of generality that $T \subset (\frac{1}{s}\mathbb Z)^d$.

Note that each $t(x) \in T$ $(x \in \mathbb Z^d)$ corresponds to a vertex in $G_{d, s}$. To see why, note that $st(x) \in \mathbb Z^d$. Thus, there is a unique $u(x) \in \{0, 1, \ldots , 2s-1\}^d$ (the vertices of $G_{d, s}$) such that $st(x) \equiv u(x) \mod 2s$.

We claim that $K = \{u(x) : x \in \{0, 1\}^d\}$ is a clique of $G_{d,s}$. Assume for sake of contradiction that for some $x, y \in \{0, 1\}^d$, u(x) and u(y) are not connected by an edge. We have two cases to consider

• 1. $u(x)_i \ne u(y)_i+s$ for all $i \in [d]$. Thus, $t(x)_i \not \equiv t(y)_i + 1 \mod 2$ for all $i \in [d]$. Then for all $i \in [d]$, there exists a positive integer $z_i \in \mathbb Z$ such that $[t(x)_i + 2z, t(x_i) + 2z+1)$ intersects $[t(y)_i, t(y)_i+1)$. In other words, $t(x+2z)$ and t(y) intersect non-trivially. This is a contradiction.

• 2. $u(x)_i = u(y)_i+s$ for some $i \in [d]$ and $u(x)_j = u(y)_j$ for all $j \ne i$. Then, $t(x) = t(y)+e_i$. This contradicts that T is faceshare-free.

Thus, K is indeed a clique of size $2^d$ in $G_{n, s}$ (note that case 1 above rules out repeated vertices).

For the reverse implication, let $K \subset \{0, 1, \ldots , 2s-1\}^d$ be a clique of size $2^d$. Define a periodic set of cube corners T as follows

$$\begin{aligned} T := \left\{ \frac{u}{s} + 2x : u \in K, x \in \mathbb Z^d\right\} . \end{aligned}$$

Note that T is s-discrete because modulo 1 each coordinate must be in the set $\{0, \frac{1}{s}, \ldots , \frac{s-1}{s}\}$.

Next we show every pair of cubes in $[0, 1)^d + T$ is disjoint. If not, by the definition of T, there exist $u, v \in K$ and $x, y \in \mathbb Z^d$ such that $C^d(u/s + 2x)$ and $C^d(v/s+ 2y)$ intersect. By Proposition 1, this means for all $i \in [d]$,

$$\begin{aligned} \left| \frac{u_i - v_i}{s} + 2x - 2y\right| < 1. \end{aligned}$$

If $u = v$, then we must have $x = y$, so the cubes are identical. Otherwise, the above inequality implies that $u_i \ne v_i \pm s$ for all $i \in [d]$, which means that u and v cannot be in the same clique, which is a contradiction.

To show that $[0, 1)^d + T$ is a tiling, it suffices to show that every point $x \in \mathbb R^d$ is in some cube of the tiling. We partition $\mathbb R^d$ into cubelets: $[0, 1/s)^d + (\frac{1}{s}\mathbb R)^d$. It suffices to show that each cubelet is in some cube of the tiling. In fact, each cube of T contains $s^d$ cubelets. Call two cubelets equivalent if their corners differ by an even integer vector. For each coordinate, there are 2s non-equivalent starting coordinates $\{0, \frac{1}{s}, \ldots , \frac{2s-1}{s}\}$ so there are a total of $(2s)^d$ inequivalent cubelets.

Observe that for all $u \in K$ and $x, y \in \mathbb Z^d$, $C^d(\frac{u}{s} + x)$ and $C^d(\frac{u}{s}+2y)$ cover equivalent cubelets. Another observation is that if $u, v \in K$ are distinct, then $C^d(\frac{u}{s})$ and $C^d(\frac{v}{s})$ cover inequivalent cubelets. Otherwise, by the equivalence, we could shift one of the cubes by an even integer vector to make them overlap, which contradicts the assumption that the cubes are disjoint. Since K has size $2^d$, this means $[0, 1)^d + T$ covers at least $2^ds^d = (2s)^d$ inequivalent cubelets. This means that all cubelets are covered; therefore, all of $\mathbb R^d$ is covered.

Next, we show that $[0, 1)^d + T$ is faceshare-free. Otherwise, there exists, $u, v\in K$ and $x, y \in \mathbb Z^d$ and $i \in [d]$ such that

$$\begin{aligned} \frac{u}{s} + 2x = \frac{v}{s} + 2y + e_i. \end{aligned}$$

This would imply that $u_i = v_i \pm s$ and $u_j = v_j$ for all $j \ne i$, which is a contradiction. $\square$

As a corollary, we deduce that Keller’s conjecture is equivalent to the maxclique problem for a suitable Keller graph.

Theorem 3

( [3]) A faceshare-free periodic tiling exists in dimension d if and only if there exists a clique of size $2^d$ in $G_{d,s}$ where $s = 2^{d-1}$. Therefore, Keller’s conjecture in dimension 7 is equivalent to the lack of a clique of size 128 in $G_{7,64}$.

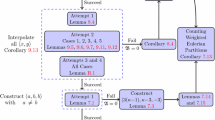
The relatively recent line of papers by Kisielewicz and Łysakowska improved on the above theorem in dimension 7 by showing that any potential faceshare-free tilings must be s-discrete for a small value of s (in comparison to 64). These results are stated as follows.

Theorem 5

( [15]) Every periodic faceshare-free tiling in 7 dimensions is 6-discrete. Therefore, Keller’s conjecture in dimension 7 is equivalent to the lack of a clique of size 128 in $G_{7,6}$.

Theorem 6

( [17]) Every periodic faceshare-free tiling in 7 dimensions is 4-discrete. Therefore, Keller’s conjecture in dimension 7 is equivalent to the lack of a clique of size 128 in $G_{7,4}$.

Theorem 7

(Corollary 1.3 of [16]) Every periodic faceshare-free tiling in 7 dimensions is 3-discrete. Therefore, Keller’s conjecture in dimension 7 is equivalent to the lack of a clique of size 128 in $G_{7,3}$.