Skip to main content
SpringerLink
Log in

Craig Interpolation with Clausal First-Order Tableaux

  • Published:
Journal of Automated Reasoning Aims and scope Submit manuscript

Abstract

We develop foundations for computing Craig-Lyndon interpolants of two given formulas with first-order theorem provers that construct clausal tableaux. Provers that can be understood in this way include efficient machine-oriented systems based on calculi of two families: goal-oriented such as model elimination and the connection method, and bottom-up such as the hypertableau calculus. We present the first interpolation method for first-order proofs represented by closed tableaux that proceeds in two stages, similar to known interpolation methods for resolution proofs. The first stage is an induction on the tableau structure, which is sufficient to compute propositional interpolants. We show that this can linearly simulate different prominent propositional interpolation methods that operate by an induction on a resolution deduction tree. In the second stage, interpolant lifting, quantified variables that replace certain terms (constants and compound terms) by variables are introduced. We justify the correctness of interpolant lifting (for the case without built-in equality) abstractly on the basis of Herbrand’s theorem and for a different characterization of the formulas to be lifted than in the literature. In addition, we discuss various subtle aspects that are relevant for the investigation and practical realization of first-order interpolation based on clausal tableaux.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. The development of Craig’s interpolation theorem is described in [25].

  2. This does not preclude to represent equality as a predicate with axioms that express reflexivity, symmetry, transitivity and substitutivity.

  3. Symbols that appear only in F or \(G\) are called F -colored and \(G\) -colored, respectively, or colored in general (also local has been used synonymously to colored), while the other symbols are called transparent (or grey). It appears that the association with occurrences is in particular necessary to take account of predicate polarity required by Craig-Lyndon (in contrast to just Craig) interpolants. Another reason for the occurrence-based labeling is that the possibility that some clause C is an instance of a clause in F as well as an instance of a clause in \(G\) should be retained. An occurrence of C then can be associated with either side label. A perhaps confusing aspect of the color-based terminology is that the term colored on the one hand indicates for a symbol that it appears only in one of F or \(G\), a property called isolated in [24], while, on the other hand, the colored property for compound structures, that is, terms and formulas, permits occurrences of transparent symbols. We apply the color-based terminology in Sect. 5 and discuss it further in the context of first-order interpolation at the end of Sect. 7. Limitations of the color-based approaches are also discussed in [14, Sect. 3].

  4. The \({\mathsf {ipol}}\) function is also defined on non-ground tableaux, as it is independent of occurrences of variables. However, the association with properties relevant for interpolation is simplified if we assume a ground tableau, which is without loss of generality: A calculus may construct as proof a closed free-variable tableau with occurrences of free rigid variables. Any ground instantiation of these variables yields a ground tableau that provides a proof of the same formula. In particular, an instantiation of each variable by a dedicated constant. For the considered properties, tableaux with variables can be represented by ground tableaux with such constants. The restriction that the tableau is for ground formulas provides another simplification that, however, does not restrict the applicability of the lemma in a first-order context: A ground tableau that provides a proof of a clausal first-order formula also provides a proof of a clausal ground formula, the conjunction of the tableau clauses. In the setting of two-sided tableaux this can be stated more precisely as: A leaf-closed two-sided ground tableau for two clausal first-order formulas is also a leaf-closed two-sided ground tableau for two clausal ground formulas, the conjunction of the tableau clauses with side \({\mathsf {F}}\) and the conjunction of the tableau clauses with side \({\mathsf {G}}\).

  5. Exhaustively rewriting with \(F \wedge \bot \equiv \bot \), \(F \vee \top \equiv \top \), \(F \wedge \top \equiv F\), \(F \vee \bot \equiv F\), modulo commutativity.

  6. An argument for this is that even clausal tableaux with atomic cut, which can polynomially simulate tree resolution, cannot polynomially simulate unrestricted resolution where proofs may have the form of dags [49].

  7. That semantic trees and tree resolution can simulate each other polynomially has been shown already in [69], where also relationships to many other propositional systems are investigated.

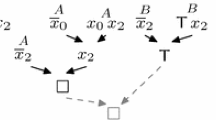
  8. To take account of merging duplicate literals, the method as presented in [8] has to be supplemented by the explicit consideration of factoring steps with the dedicated assignment of partial interpolants from [14, Def. 15], or, alternatively, it must be possible to label an occurrence with both provenance values at the same time, as noted in [36], and retaining Huang’s original definition for case (iii).(c) for the subcase where the resolution step is upon two literals which each have both provenances. As an example where merging is necessary consider \(F = (p \vee q) \wedge (\lnot p \vee r)\) and \(G= (p \vee \lnot q) \wedge (\lnot p \vee \lnot r)\).

  9. The argument in the proof of Theorem 12 to show that in case (i) for any leaf with label \(L_i\) there exists a target with the same side \({\mathsf {F}}\) can also be applied here, but the analogy for case (ii) has to be shown differently. It follows since in case (ii) a leaf with label \(L_i\) must have an ancestor with complementary literal that was introduced by the encoding of a resolution step upon \(L_i\) and its complement. If the label of the involved occurrence of the complement is \({\mathsf {F}}\), then the encoding of the resolution step would result in two successive nodes with the complement of \(L_i\), one with side \({\mathsf {F}}\) and one with side \({\mathsf {G}}\).

  10. The symbol \(\lhd \) is an adaptation of \(t \unrhd s\) for s is a subterm of t, common in the literature on term rewriting [27]. We use it in the strict version and in flipped direction because it is then in direct correspondence with ordering constraints on terms that determine the order of quantifications in our Theorem 21.

  11. \(C_1, \ldots , C_n\) can be arbitrary quantifier-free formulas, with clauses as a special case.

  12. In the case where \(F'\) and \(G'\) are clausal formulas, there also may exist smaller formulas \(F_{\textsc {exp}}\) and \(G_{\textsc {exp}}\) obtained as conjunction of variants of clauses of \(F'\) and by negating a conjunction of variants of clauses of \(G'\), respectively.

  13. This contrast to approaches like [21], where instantiation is performed specifically for interpolation.

  14. Inspired by the Prolog Technology Theorem Prover [74] and SETHEO [51], CMProver was originally written in 1993 but had been revived in 1996 [26] and in 2016. It was evaluated in 2018 on all suitable TPTP problems, that is, problems that have a distinguished theorem, are not classified as satisfiable and are in clausal or quantified first-order form: Of these, it can solve about 76% of the 2143 problems without equality (in 9 configurations) and about 26% of the 11321 problems with equality (in 4 configurations). The timeout was 600s, the TPTP version was 7.1.0. See http://cs.christophwernhard.com/pie/cmprover/ for details.

References

  1. Baaz, M., Leitsch, A.: Methods of Cut-Elimination. Springer, Berlin (2011)

    MATH  Google Scholar 

  2. Bachmair, L., Ganzinger, H., Voronkov, A.: Elimination of equality via transformation with ordering constraints. In: CADE-15, LNCS (LNAI), vol. 1421, pp. 175–190. Springer (1998)

  3. Baumgartner, P., Furbach, U., Niemelä, I.: Hyper tableaux. In: JELIA’96, LNCS (LNAI), vol. 1126, pp. 1–17. Springer (1996)

  4. Baumgartner, P., Schmidt, R.A.: Blocking and other enhancements for bottom-up model generation methods. J. Autom. Reason. 64, 197–251 (2020)

    Article  MathSciNet  Google Scholar 

  5. Baumgartner, P., Thorstensen, E.: Instance based methods – a brief overview. KI 24(1), 35–42 (2010)

    Google Scholar 

  6. Bender, M., Pelzer, B., Schon, C.: System description: E-KRHyper 1.4. In: CADE-24, LNCS (LNAI), vol. 7898, pp. 126–134. Springer (2013)

  7. Benedikt, M., ten Cate, B., Tsamoura, E.: Generating low-cost plans from proofs. In: PODS’14, pp. 200–211. ACM (2014)

  8. Benedikt, M., Kostylev, E.V., Mogavero, F., Tsamoura, E.: Reformulating queries: theory and practice. In: IJCAI 2017, pp. 837–843 (2017)

  9. Benedikt, M., Leblay, J., ten Cate, B., Tsamoura, E.: Generating Plans from Proofs: The Interpolation-based Approach to Query Reformulation. Morgan & Claypool, New York (2016)

    Book  Google Scholar 

  10. Bibel, W.: Automated Theorem Proving. Vieweg (1982). Second edition 1987

  11. Bibel, W., Otten, J.: From Schütte’s formal systems to modern automated deduction. In: Kahle, R., Rathjen, M. (eds.) The Legacy of Kurt Schütte, chap. 13, pp. 215–249. Springer (2020)

  12. Bonacina, M.P., Johansson, M.: On interpolation in decision procedures. In: TABLEAUX 2011, LNCS (LNAI), vol. 6793, pp. 1–16. Springer (2012)

  13. Bonacina, M.P., Johansson, M.: Interpolation systems for ground proofs in automated deduction: a survey. J. Autom. Reason. 54(4), 353–390 (2015)

    Article  MathSciNet  Google Scholar 

  14. Bonacina, M.P., Johansson, M.: On interpolation in automated theorem proving. J. Autom. Reason. 54(1), 69–97 (2015)

    Article  MathSciNet  Google Scholar 

  15. Borgida, A., de Bruijn, J., Franconi, E., Seylan, I., Straccia, U., Toman, D., Weddell, G.: On finding query rewritings under expressive constraints. In: SEBD 2010. Esculapio Editore (2010)

  16. Brand, D.: Proving theorems with the modification method. SIAM J. Comput. 4(4), 412–430 (1975)

    Article  MathSciNet  Google Scholar 

  17. Brillout, A., Kroening, D., Rümmer, P., Wahl, T.: An interpolating sequent calculus for quantifier-free Presburger arithmetic. J. Autom. Reason. 47(4), 341–367 (2011)

    Article  MathSciNet  Google Scholar 

  18. Bry, F., Manthey, R.: SATCHMO: A theorem prover implemented in Prolog. In: CADE-9, LNCS, vol. 310, pp. 415–434. Springer (1988)

  19. Bárány, V., Benedikt, M., ten Cate, B.: Rewriting guarded negation queries. In: MFCS 2013, LNCS, vol. 8087, pp. 98–110. Springer (2013)

  20. Chang, C.L., Lee, R.C.T.: Symbolic Logic and Automated Theorem Proving. Academic Press, Cambridge (1973)

    MATH  Google Scholar 

  21. Christ, J., Hoenicke, J.: Instantiation-based interpolation for quantified formulae. In: Decision Procedures in Software, Hardware and Bioware, vol. 10161. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2010)

  22. Cimatti, A., Griggio, A., Schaafsma, B.J., Sebastiani, R.: The MathSAT5 SMT solver. In: TACAS 2013, LNCS, vol. 7795, pp. 93–107. Springer (2013)

  23. Craig, W.: Linear reasoning. A new form of the Herbrand-Gentzen theorem. J. Symb. Log. 22(3), 250–268 (1957)

    Article  MathSciNet  Google Scholar 

  24. Craig, W.: Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory. J. Symb. Log. 22(3), 269–285 (1957)

    Article  MathSciNet  Google Scholar 

  25. Craig, W.: The road to two theorems of logic. Synthese 164(3), 333–339 (2008)

    Article  MathSciNet  Google Scholar 

  26. Dahn, I., Wernhard, C.: First order proof problems extracted from an article in the Mizar mathematical library. In: FTP’97, RISC-Linz Report Series No. 97–50, pp. 58–62. Joh. Kepler Univ., Linz, Austria (1997)

  27. Dershowitz, N., Jouannaud, J.: Notations for rewriting. Bull. EATCS 43, 162–174 (1991)

    MATH  Google Scholar 

  28. Eder, E.: An implementation of a theorem prover based on the connection method. In: AIMSA’84, pp. 121–128. North-Holland (1985)

  29. Eén, N., Biere, A.: Effective preprocessing in SAT through variable and clause elimination. In: SAT ’05, LNCS, vol. 3569, pp. 61–75. Springer (2005)

  30. Fagin, R., Kolaitis, P.G., Miller, R.J., Popa, L.: Data exchange: semantics and query answering. Theor. Comput. Sci. 336(1), 89–124 (2005)

    Article  MathSciNet  Google Scholar 

  31. Fitting, M.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, Berlin (1995)

    MATH  Google Scholar 

  32. Gabbay, D., Ohlbach, H.J.: Quantifier elimination in second-order predicate logic. In: KR’92, pp. 425–435. Morgan Kaufmann (1992)

  33. van Gelder, A., Topor, R.W.: Safety and translation of relational calculus queries. ACM Trans. Database Syst. 16(2), 235–278 (1991)

    Article  MathSciNet  Google Scholar 

  34. Grau, B.C., Horrocks, I., Krötzsch, M., Kupke, C., Magka, D., Motik, B., Wang, Z.: Acyclicity notions for existential rules and their application to query answering in ontologies. JAIR 47, 741–808 (2013)

    Article  MathSciNet  Google Scholar 

  35. Hoder, K., Holzer, A., Kovács, L., Voronkov, A.: Vinter: A Vampire-based tool for interpolation. In: APLAS 2012, LNCS, vol. 7705, pp. 148–156. Springer (2012)

  36. Huang, G.: Constructing Craig interpolation formulas. In: COCOON ’95, LNCS, vol. 959, pp. 181–190. Springer (1995)

  37. Hudek, A., Toman, D., Wedell, G.: On enumerating query plans using analytic tableau. In: TABLEAUX 2015, LNCS (LNAI), vol. 9323, pp. 339–354. Springer (2015)

  38. Hähnle, R.: Tableaux and related methods. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automatic Reasoning, chap. 3, vol. 1, pp. 101–178. Elsevier, Amsterdam (2001)

    Chapter  Google Scholar 

  39. Jacobs, S., Waldmann, U.: Comparing instance generation methods for automated reasoning. J. Autom. Reason. 38(1–3), 57–78 (2007)

    Article  MathSciNet  Google Scholar 

  40. Järvisalo, M., Biere, A., Heule, M.: Blocked clause elimination. In: TACAS 2010, LNCS, vol. 6015, pp. 129–144 (2010)

  41. Kaliszyk, C.: Efficient low-level connection tableaux. In: TABLEAUX 2015, LNCS (LNAI), vol. 9323, pp. 102–111. Springer (2015)

  42. Kaliszyk, C., Urban, J.: FEMaLeCoP: Fairly efficient machine learning connection prover. In: LPAR-20, LNCS, vol. 9450, pp. 88–96. Springer (2015)

  43. Kiesl, B., Suda, M.: A unifying principle for clause elimination in first-order logic. In: CADE 26, LNCS (LNAI), vol. 10395, pp. 274–290. Springer (2017)

  44. Kiesl, B., Suda, M., Seidl, M., Tompits, H., Biere, A.: Blocked clauses in first-order logic. In: LPAR-21, EPiC, vol. 46, pp. 31–48 (2017)

  45. Kovács, L., Voronkov, A.: First-order interpolation and interpolating proof systems. In: LPAR-21, EPiC, vol. 46, pp. 49–64. EasyChair (2017)

  46. Leone, N., Pfeifer, G., Faber, W., Eiter, T., Gottlob, G., Perri, S., Scarcello, F.: The DLV system for knowledge representation and reasoning. ACM Trans. Comput. Log. 7(3), 499–562 (2006)

    Article  MathSciNet  Google Scholar 

  47. Letz, R.: Clausal tableaux. In: Bibel, W., Schmitt, P.H. (eds.) Automated Deduction - A Basis for Applications, vol. I, pp. 43–72. Kluwer Academic Publishers, Amsterdam (1998)

    Google Scholar 

  48. Letz, R.: First-order tableau methods. In: M. D’Agostino, D. M. Gabbay, R. Hähnle, J. Posegga (eds.) Handb. of Tableau Methods, pp. 125–196. Kluwer Academic Publishers (1999)

  49. Letz, R.: Tableau and connection calculi. structure, complexity, implementation. Habilitationsschrift, TU München (1999). http://www2.tcs.ifi.lmu.de/~letz/habil.ps. Accessed 7 June 2020

  50. Letz, R., Mayr, K., Goller, C.: Controlled integration of the cut rule into connection tableaux calculi. J. Autom. Reason. 13(3), 297–337 (1994)

    Article  Google Scholar 

  51. Letz, R., Schumann, J., Bayerl, S., Bibel, W.: SETHEO: a high-performance theorem prover. J. Autom. Reason. 8(2), 183–212 (1992)

    Article  MathSciNet  Google Scholar 

  52. Letz, R., Stenz, G.: Model elimination and connection tableau procedures. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automatic Reasoning, vol. 1, pp. 2015–2114. Elsevier, Amsterdam (2001)

    Chapter  Google Scholar 

  53. Loveland, D.W.: Automated Theorem Proving: A Logical Basis. North-Holland, Amsterdam (1978)

    MATH  Google Scholar 

  54. Lyndon, R.: An interpolation theorem in the predicate calculus. Pac. J. Math. 9, 129–142 (1959)

    Article  MathSciNet  Google Scholar 

  55. Maier, D., Mendelzon, A.O., Sagiv, Y.: Testing implications of data dependencies. ACM Trans. Database Syst. 4(4), 455–469 (1979)

    Article  Google Scholar 

  56. Marx, M.: Queries determined by views: Pack your views. In: PODS ’07, pp. 23–30. ACM (2007)

  57. McCune, W.: Prover9 and Mace4 (2005–2010). http://www.cs.unm.edu/~mccune/prover9

  58. McMillan, K.L.: Interpolation and SAT-based model checking. In: CAV 2003, LNCS, vol. 2725, pp. 1–13. Springer (2003)

  59. McMillan, K.L.: Applications of Craig interpolants in model checking. In: TACAS 2005, LNCS, vol. 3440, pp. 1–12. Springer (2005)

  60. McMillan, K.L.: An interpolating theorem prover. Theor. Comput. Sci. 345(1), 101–121 (2005)

    Article  MathSciNet  Google Scholar 

  61. Moser, M., Ibens, O., Letz, R., Steinbach, J., Goller, C., Schumann, J., Mayr, K.: SETHEO and E-SETHEO - the CADE-13 systems. J. Autom. Reason. 18(2), 237–246 (1997)

    Article  Google Scholar 

  62. Motik, B., Shearer, R., Horrocks, I.: Hypertableau reasoning for description logics. JAIR 36, 165–228 (2009)

    Article  MathSciNet  Google Scholar 

  63. Motohashi, N.: Equality and Lyndon’s interpolation theorem. J. Symb. Log. 49(1), 123–128 (1984)

  64. Nash, A., Segoufin, L., Vianu, V.: Views and queries: Determinacy and rewriting. ACM Trans. Database Systems 35(3) (2010)

  65. Oliver, B.E., Otten, J.: Equality preprocessing in connection calculi. In: PAAR-2020, CEUR Workshop Proceedings (2020)

  66. Otten, J.: Restricting backtracking in connection calculi. AI Commun. 23(2–3), 159–182 (2010)

    Article  MathSciNet  Google Scholar 

  67. Pelzer, B., Wernhard, C.: System description: E-KRHyper. In: CADE-21, LNCS (LNAI), vol. 4603, pp. 503–513. Springer (2007)

  68. Plaisted, D.A., Greenbaum, S.: A structure-preserving clause form translation. J. Symb. Comput. 2, 293–304 (1986)

    Article  MathSciNet  Google Scholar 

  69. Reckhow, R.A.: On the lengths of proofs in the propositional calculus. Ph.D. thesis, University of Toronto (1975). https://www.cs.toronto.edu/~sacook/homepage/reckhow_thesis.pdf. Accessed 7 June 2020

  70. Schulz, S., Cruanes, S., Vukmirovic, P.: Faster, higher, stronger: E 2.3. In: CADE 27, LNCS, vol. 11716, pp. 495–507. Springer (2019)

  71. Scott, D.: A decision method for validity of sentences in two variables. J. Symb. Log. 27(4), 477 (1962)

    Google Scholar 

  72. Segoufin, L., Vianu, V.: Views and queries: determinacy and rewriting. In: PODS 2005, pp. 49–60. ACM (2005)

  73. Smullyan, R.M.: First-Order Logic. Springer (1968). Also republished with corrections by Dover publications (1995)

  74. Stickel, M.E.: A Prolog technology theorem prover: implementation by an extended Prolog compiler. J. Autom. Reason. 4(4), 353–380 (1988)

    Article  MathSciNet  Google Scholar 

  75. Tarski, A.: Einige methologische Untersuchungen zur Definierbarkeit der Begriffe. Erkenntnis 5, 80–100 (1935)

    Article  Google Scholar 

  76. Toman, D., Weddell, G.: Fundamentals of Physical Design and Query Compilation. Morgan & Claypool, New York (2011)

    Book  Google Scholar 

  77. Toman, D., Weddell, G.: An interpolation-based compiler and optimizer for relational queries (system design report). In: IWIL 2017 Workshop and LPAR-21 Short Presentations, Kalpa, vol. 1. EasyChair (2017)

  78. Tseitin, G.S.: On the complexity of derivation in propositional calculus. In: Slisenko, A.O. (ed.) Studies in Constructive Mathematics and Mathematical Logic, vol. Part II, pp. 115–125. Steklov Mathematical Institute, London (1970)

    Google Scholar 

  79. Wernhard, C.: System Description: KRHyper. Tech. Rep. Fachberichte Informatik 14–2003, Universität Koblenz-Landau, Koblenz, Germany (2003)

  80. Wernhard, C.: Semantic knowledge partitioning. In: JELIA 04, LNAI, vol. 3229, pp. 552–564. Springer (2004)

  81. Wernhard, C.: The PIE system for proving, interpolating and eliminating. In: PAAR-2016, CEUR Workshop Proceedings, vol. 1635, pp. 125–138 (2016)

  82. Wernhard, C.: Craig interpolation and access interpolation with clausal first-order tableaux. CoRR abs/1802.04982 (2018). (Tech. rep. Technische Universität Dresden, KRR 18-01)

  83. Wernhard, C.: Facets of the PIE environment for proving, interpolating and eliminating on the basis of first-order logic. In: DECLARE 2019, LNCS (LNAI), vol. 12057, pp. 160–177 (2020)

Download references

Acknowledgements

This research was in part supported by Deutsche Forschungsgemeinschaft (DFG) with grant WE 5641/1-1. The author thanks anonymous reviewers of previous versions for numerous very helpful suggestions and remarks.

Author information

Authors and Affiliations

  1. Berlin, Germany

    Christoph Wernhard

Authors
  1. Christoph Wernhard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christoph Wernhard.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wernhard, C. Craig Interpolation with Clausal First-Order Tableaux. J Autom Reasoning 65, 647–690 (2021). https://doi.org/10.1007/s10817-021-09590-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10817-021-09590-3

Keywords

Search

Navigation