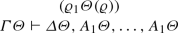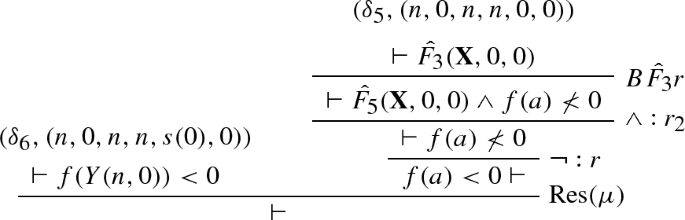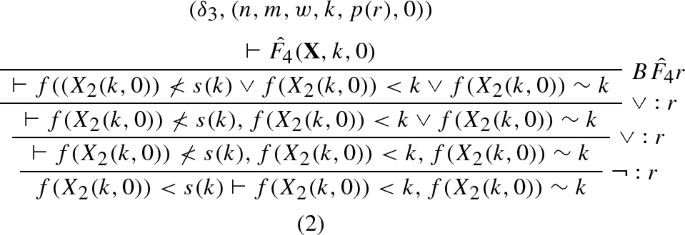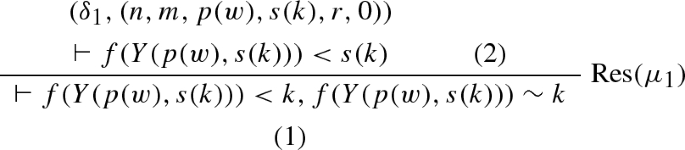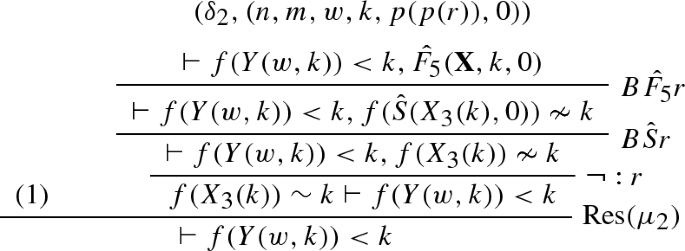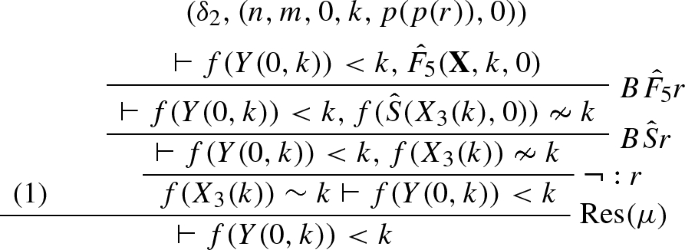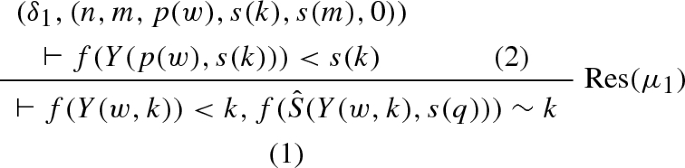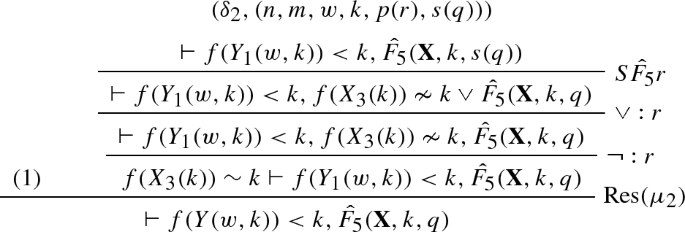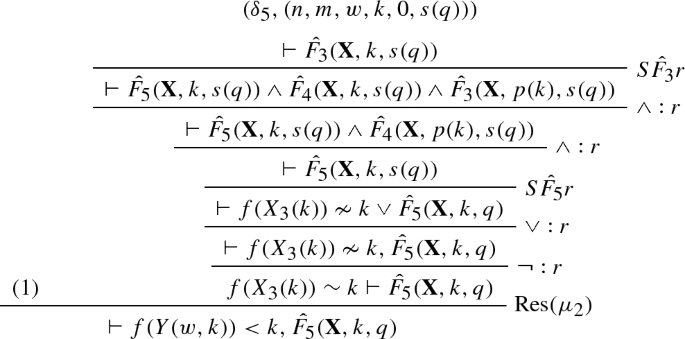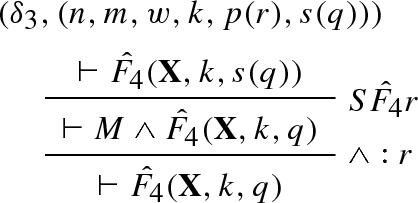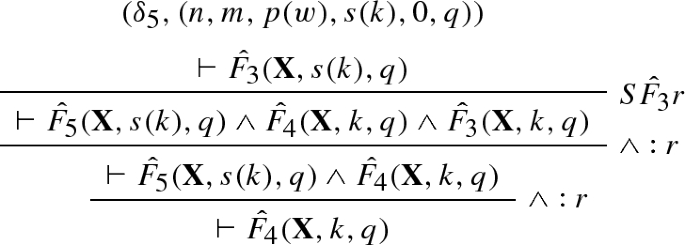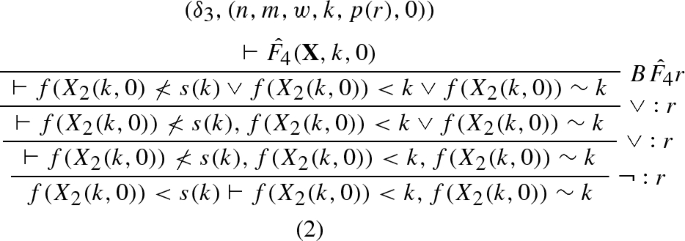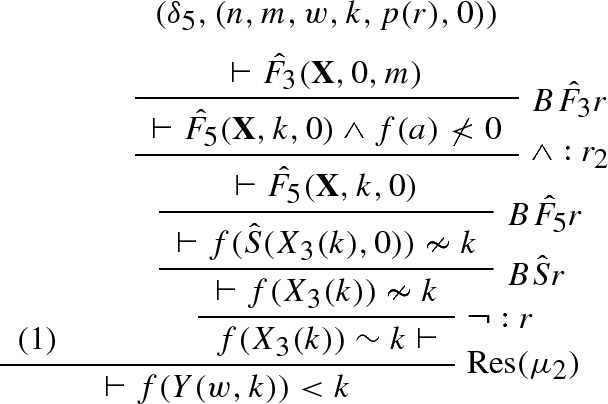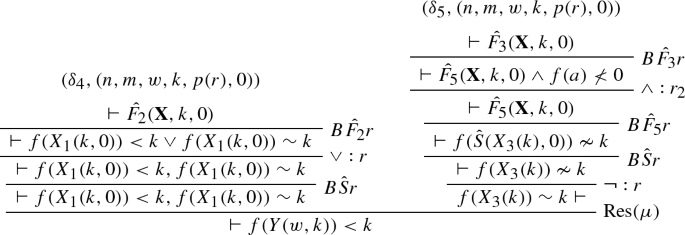Abstract
Proof schemata are infinite sequences of proofs which are defined inductively. In this paper we present a general framework for schemata of terms, formulas and unifiers and define a resolution calculus for schemata of quantifier-free formulas. The new calculus generalizes and improves former approaches to schematic deduction. As an application of the method we present a schematic refutation formalizing a proof of a weak form of the pigeon hole principle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recursive definitions of functions play a central role in computer science, particularly in functional programming. While recursive definitions of proofs are less common they are of increasing importance in automated proof analysis. Proof schemata, i.e. recursively defined infinite sequences of proofs, serve as an alternative formulation of induction. Prior to the formalization of the concept, an analysis of Fürstenberg’s proof of the infinitude of primes [5] suggested the need for a formalism quite close to the type of proof schemata we will discuss in this paper. The underlying method for this analysis was CERES [6] (cut-elimination by resolution) which, unlike reductive cut-elimination, can be applied to recursively defined proofs by extracting a schematic unsatisfiable formula and constructing a recursively defined refutation. Moreover, Herbrand’s theorem can be extended to an expressive fragment of proof schemata, that is those formalizing k-induction [11, 14]. Unfortunately, the construction of recursively defined refutations is a highly complex task. In previous work [14] a superposition calculus for certain types of formulas was used for the construction of refutation schemata, but only works for a weak fragment of arithmetic and is hard to use interactively.
The key to proof analysis using CERES in a first-order setting is not the particularities of the method itself, but the fact that it provides a bridge between automated deduction and proof theory. In the schematic setting, where the proofs are recursively defined, a bridge over the chasm has been provided [11, 14], but there has not been much development on the other side to reap the benefits of. The few existing results about automated deduction for recursively defined formulas barely provide the necessary expressive power to analyse significant mathematical argumentation. Applying the earlier constructions to a weak mathematical statement such as the eventually constant schema required much more work than the value of the provided insights [10]. The resolution calculus we introduce in this work generalizes resolution and the first-order language in such a way that it provides an excellent environment for carrying out investigations into decidable fragments of schematic propositional formulas beyond those that are known. Furthermore, concerning the general unsatisfiability problem for schematic formulas, our formalism provides a perfect setting for interactive proof construction.
Proof schema is not the first alternative formalization of induction with respect to Peano arithmetic [17]. However, all other existing examples [8, 9, 15] that provide calculi for induction together with a cut-elimination procedure do not allow the extraction of Herbrand sequentsFootnote 1 [12, 17] and thus Herbrand’s theorem cannot be realized. In contrast, in [14] finite representations of infinite sequences of Herbrand sequents are constructed, so-called Herbrand systems. Of course, such objects do not describe finite sets of ground instances, though instantiating the free parameters (i.e. variables that can be instantiated with numerals) of Herbrand systems does result in sequents derivable from a finite set of ground instances.
The formalism developed in this paper extends and improves the formal framework for refuting formula schemata in [11, 14] in several ways: 1. The new calculus can deal with arbitrary quantifier-free formula schemata (not only with clause schemata), 2. we extend the schematic formalism to multiple parameters (in [11] and in [14] only schemata defined via one parameter were admitted); 3. we strongly extend the recursive proof specifications by allowing mutual recursion (formalizable by so-called called point transition systems). Note that in [11] a complicated schematic clause definition was used, while the schematic refutations in [14] were based on negation normal forms and on a complicated translation to the n-clause calculus. Moreover, the new method presented in this paper provides a simple, powerful and elegant formalism for interactive use. The expressivity of the method is illustrated by an application to a (weak) version of the pigeon hole principle.
2 A Motivational Example
In [10], proof analysis of a mathematically simple statement, the Eventually Constant Schema, was performed using an early formalism developed for schematic proof analysis [11]. The Eventually Constant Schema states that any monotonically decreasing function with a finite range is eventually constant. The property of being eventually constant may be formally written as follows:
where f is an uninterpreted function symbol with the following property
for some \(n\in {\mathbb {N}}\). The method defined in [11] requires a strong quantifier-free end sequent, thus implying the proof must be skolemized. The skolemized formulation of the eventually constant property is \(\exists x( x\le g(x) \rightarrow f(x) = f(g(x)))\) where g is the introduced Skolem function. The proof presented in [10] used a sequence of \(\varSigma _2\)-cuts
Also, the Skolem function was left uninterpreted for the proof analysis. The resulting cut-structure, when extracted as an unsatisfiable clause set, has a fairly simple refutation. Thus, with the aid of automated theorem provers, a schema of refutations was constructed.
The use of an uninterpreted Skolem function greatly simplified the construction presented in [10]. In this paper we will interpret the function g as the successor function. Note that using the axioms presented in [10] the following statement
is not provable. Note that we drop the implication of Equation 1 and the antecedent of the implication given that \(x\le suc (x)\) is a trivial property of the successor function. However, using an alternative set of axioms and a weaker cut we can prove this statement. The additional axioms are as follows:
For the most part these axioms are harmless, however the axiom \(f( suc (x))< s(k) \vdash f( suc (x)) = k, f(x) < k\) implies that f has some monotonicity properties similar to the eventually constant schema.
Note that the mentioned axiom \(f(x)< s(k) \vdash f(x) = k, f(x) < k\) is equivalent to
in the standard model. Thus this axiom describes an increase of values, not a decrease! For example consider the following interpretation of f for \(n=2\):
Here we have \(f(1)<2\), but \(f(2)=2\) and \(f(z)=2\) for all \(z>1\).
Being that our proof enforces this property using the following \(\varDelta _2\)-cut formula we are guaranteed to reach a value in the domain above which f is constant. The cut formula is:
One additional point which the reader might notice is that we use what seems to be the less than relation and equality relation of the natural numbers, but do not concern ourselves with substitutivity of equality nor transitivity of <. While including these properties will change the formal proof we present below, the argument will still require a free numeric parameter denoting the size of the range of f and the number of positions we require to map to the same value.
We will refer to this version of the eventually constant schema as the successor eventually constant schema. While this results in a new formulation of the eventually constant schema under an interpretation of the Skolem function as the successor function, we have not taken complete advantage of this new interpretation taking into account that this re-formulation is actually of lower complexity than the eventually constant schema. For example in Fig. 1 we provide the output of Peltier’s superposition induction prover [3] when ran on the clausified form of the cut structure of the successor eventually constant schema. The existence of this derivation implies that the proof analysis method of [14] may be applied to the successor eventually constant schema. Unfortunately, the prover does not find the invariant discovered in [10], but this may have more to do with the choice of axioms rather than the statement being beyond the capabilities of the prover.
Output of Peltier et al.’s Prover9 extension [13]
We can strengthen the successor eventually constant schema beyond the capabilities of [13] easily by adding a second parameter as follows:
We refer to this problem as the m-successor eventually constant schema. Applying this transformation to the eventually constant schema of [10] is not so trivial being that the axioms used to construct the proof do not easy generalize. However, for the successor eventually constant schema the generalization is trivial and is provided below:
Similar to the previous case, the last axiom may be interpreted as
over the standard model, where \({ s uc}^r(x) = x+r\). Again, it describes an increase of values. Furthermore, the cut formula can be trivially extended as follows:
Given that the m-successor eventually constant schema contains two parameters it is beyond the capabilities of [13]. Interesting enough, the prover can find invariants for each value of m in terms of n, though, these invariants get impressively large quite quickly. The cut structure of the m-successor eventually constant schema may be extracted as an inductive definition of an unsatisfiable negation normal form formula. We provide this definition below:
where a is some arbitrary constant. We will show how our new formalism can provide a finite representation of the refutations of the inductive definition even though our refutation requires the use of mutual recursion as well as multiple parameters (six in total).
3 Schematic Language
Large parts of mathematics can be formalized in a natural way in second-order logic [16]. However, most methods for proof analysis and transformation are particularly suited for first-order logic and thus, second-order formalizations have to be projected to first-order ones. The most appropriate way to deal with this projection is the introduction of a many-sorted language. As in [11, 14] we choose to work in a two-sorted version of classical first-order logic with one sort for a standard first-order term language and one for numerals.
The first sort we consider is \(\omega \), in which every ground term normalizes to a numeral, i.e. a term inductively constructable over the signature \(\varSigma _{\omega } = \{0, s(\cdot )\}\) as follows \(N \Rightarrow s(N) \ | \ 0\), s.t. \(s(N) \not = 0\) and \(s(N) = s(N') \rightarrow N = N'\). Natural numbers (\({\mathbb {N}}\)) will be denoted by lower-case Greek letters (\(\alpha \), \(\beta \), \(\gamma \), etc); The numeral \(s^\alpha 0\), \(\alpha \in {\mathbb {N}}\), will be written as \({\bar{\alpha }}\). The set of numerals is denoted by \({ Num}\). When describing sequences of objects such as \(t_1,\cdots , t_{\alpha }\), if it is possible to avoid confusion, we will abbreviate the sequence by \(\overrightarrow{t}_{\alpha }\).
Furthermore, the \(\omega \) sort includes a countable set of variables \(\mathcal {N}\) called parameters. Parameters are denoted by \(k,l,n,m,k_1,k_2,\ldots ,l_1,l_2,\ldots ,n_1,n_2,\ldots ,m_1,m_2,\) \(\ldots \). The set of parameters occurring in an expression E is denoted by \(\mathcal {N}(E)\). The set of free \(\omega \)-terms, denoted by \(\mathcal {T}^{\omega }_0\) contains all terms inductively constructable over \(\varSigma _{\omega }\) and \(\mathcal {N}\) as follows:
-
If \(t\in \mathcal {N}\) or \(t\in Num \), then \(t\in \mathcal {T}^{\omega }_0\)
-
If \(t\in \mathcal {T}^{\omega }_0\), then \(s(t) \in \mathcal {T}^{\omega }_0\)
In addition to the signature \(\varSigma _{\omega }\), the \(\omega \) sort allows defined function symbols, the set of which will be denoted by \({\hat{\varSigma }}_{\omega }\). These symbols will be denoted using \({\hat{\cdot }}\) and have a fixed finite arity. The set of \(\omega \)-terms, denoted by \(T^{\omega }\) contains all terms inductively constructable over \(\varSigma _{\omega }\), \({\hat{\varSigma }}_{\omega }\), and \(\mathcal {N}\), i.e.
-
If \(t\in T^{\omega }_0 \), then \(t \in T^{\omega }\)
-
If \(t_1,\cdots t_{\alpha }\in T^{\omega }\) and \({\hat{f}}\in {\hat{\varSigma }}_{\omega }\), s.t. \({\hat{f}}\) has arity \(\alpha \ge 1\) , then \({\hat{f}}(\overrightarrow{t}_{\alpha })\in T^{\omega }\)
The second sort, the \(\iota \)-sort (individuals), also has two associated signatures, the set of free function symbols, \(\varSigma _{\iota }\), and the set of defined function symbols, \({\hat{\varSigma }}_{\iota }\). Similarly, defined symbols will be denoted by \({\hat{\cdot }}\) and have a fixed finite arity. Variables of the \(\iota \)-sort are what we refer to as global variables, that is variables which take numeric arguments, i.e. \(X(\overrightarrow{t}_{\alpha })\) where \(\overrightarrow{t}_{\alpha }\in T^{\omega }\) for \(\alpha \ge 0\). Note that \(\alpha \) is fixed and finite. The set of all global variables will be denoted by \(V^{G}\), and terms of the form \(X(\overrightarrow{t}_{\alpha })\) will be referred to as V-terms over X. The set of V-terms whose arguments are numerals (from \({ Num}\)) will be denoted by \(V^{\iota }\). Such terms are referred to as individual variables. We will often denote the set of individual variables contained in some object \({\mathbf {T}}\) by \(V^{\iota }({\mathbf {T}})\), e.g. a substitution, an \(\iota \) term, a set of \(\iota \) terms, etc. A similar construction will be used for other types of objects defined in this section.
Thus, the set of free \(\iota \)-terms, denoted by \(\mathcal {T}^{\iota }_0\) is inductively constructed from \(\varSigma _{\iota }\) and \(V^{G}\) as follows:
-
If \({\bar{\alpha }}_1,\cdots , {\bar{\alpha }}_{\beta }\in Num \) and \(X\in V^{G}\), then \( X(\overrightarrow{{\bar{\alpha }}_{\beta }})\in \mathcal {T}^{\iota }_0\)
-
If \(t_1,\cdots , t_{\alpha }\in \mathcal {T}^{\iota }_0\) and \(f\in \varSigma _{\iota }\) s.t. f has arity \(\alpha \ge 0\), then \(f(\overrightarrow{t}_{\alpha }) \in \mathcal {T}^{\iota }_0\)
The set of \(\iota \)-terms, denoted by \(\mathcal {T}^{\iota }\) is inductively constructed from \(\varSigma _{\iota }\), \({\hat{\varSigma }}_{\iota }\), and \(V^{G}\) as follows:
-
If \(t\in \mathcal {T}^{\iota }_0\), then \(t\in \mathcal {T}^{\iota }\)
-
If \(t_1,\cdots , t_{\alpha }\in \mathcal {T}^{\omega }\) and \(X\in V^{G}\), then \( X(\overrightarrow{t_{\alpha }})\in \mathcal {T}^{\iota }\)
-
If \(t_1,\cdots , t_{\alpha }\in \mathcal {T}^{\iota }\), \({\hat{f}}\in {\hat{\varSigma }}_{\iota }\), \(\overrightarrow{X_{\beta }}\in V^G\), and \(\overrightarrow{n_{\alpha +1}}\in \mathcal {N}\) s.t. \({\hat{f}}\) has arity \(\alpha +\beta +1\) for \(\alpha ,\beta \ge 0\), then \({\hat{f}}(\overrightarrow{X_{\beta }},\overrightarrow{n_{\alpha +1}})\in \mathcal {T}^{\iota }\)
Remark 1
In this work we will define schematic refutations and schematic unifiers. In previous work (see [14]) in principle only an implicit representation of unification schemata could be obtained, an explicit representation was impossible due to the restrictions of the formalism. If we however allow for the use of indexed variables, we obtain a stronger formalism in the sense that schematic variables, and thus unifiers, can be defined. The use of global variables will be vital for the definition of schematic substitutions and unifiers later in the paper.
The third and final sort we consider is that of formulas which will be denoted by o. Formulas are constructed using the signature \(\varSigma _{o} = \{\lnot , \wedge , \vee \}\), a countably infinite set of predicate symbols \(\mathcal {P}\) with fixed and finite arity, and a countably infinite set of formula variables \(V^F\). The set of formula terms, denoted by \(\mathcal {T}^{o}_V\) is constructed inductively as follows:
-
if \(t\in V^{F}\), then \(t\in \mathcal {T}^{o}_V\)
-
if \(t_1,\dots , t_{\alpha } \in T^{\iota }\) and \(P\in \mathcal {P}\) s.t. P has arity \(\alpha \ge 0\), then \(P(\overrightarrow{t_{\alpha }})\in \mathcal {T}^{o}_V\).
-
if \(t\in \mathcal {T}^{o}_V\), then \(\lnot t\in \mathcal {T}^{o}_V\)
-
if \(t_1,t_2 \in \mathcal {T}^{o}_V\) and \(\star \in \{\vee , \wedge \}\), then \(t_1\star t_2 \in \mathcal {T}^{o}_V\)
We refer to Boolean expressions as the subset of \({\mathcal {T}}^{o}_V\) constructed without symbols of \(V^F\). For \(t\in {\mathcal {T}}^{o}_V\), by \(V^{F}(t)\subset V^{F}\) we denote the set of formula variables occurring in t. The set of Boolean expressions will be denoted by \(\mathcal {T}^{o}_0\) and is constructed as follows:
-
if \(t_1,\dots , t_{\alpha } \in T^{\iota }\) and \(P\in \mathcal {P}\) s.t. P has arity \(\alpha \ge 0\), then \(P(\overrightarrow{t_{\alpha }})\in \mathcal {T}^{o}_0\).
-
if \(t\in \mathcal {T}^{o}_0\), then \(\lnot t\in \mathcal {T}^{o}_0\)
-
if \(t_1,t_2 \in \mathcal {T}^{o}_0\) and \(\star \in \{\vee , \wedge \}\), then \(t_1\star t_2 \in \mathcal {T}^{o}_0\)
Formula schemata are constructed using formula terms by allowing defined predicate symbols to occur. Similarly as in the previous cases, defined symbols will be denoted by \({\hat{\cdot }}\) and have a fixed finite arity. The set of defined predicate symbols is denoted by \(\hat{\mathcal {P}}\). The set of formula schemata is denoted by \(\mathcal {T}_{o}(\varSigma _{o},\mathcal {P},V^F,V^G,\mathcal {N},\hat{\mathcal {P}})\) and is constructed inductively as follows:
-
if \(t\in \mathcal {T}^{o}_V\), then \(t\in \mathcal {T}^{o}\)
-
If \(t_1,\cdots , t_{\alpha }\in \mathcal {T}^{o}\), \({\hat{P}}\in \hat{\mathcal {P}}\), \(\overrightarrow{X_{\beta }}\in V^G\), and \(\overrightarrow{n_{\alpha +1}}\in \mathcal {N}\) s.t. \({\hat{P}}\) has arity \(\alpha +\beta +1\) for \(\alpha ,\beta \ge 0\), then \({\hat{P}}(\overrightarrow{X_{\beta }},\overrightarrow{n_{\alpha +1}})\in \mathcal {T}^{o}\)
-
if \(t\in \mathcal {T}^{o}\), then \(\lnot t\in \mathcal {T}^{o}\)
-
if \(t_1,t_2 \in \mathcal {T}^{o}\) and \(\star \in \{\vee , \wedge \}\), then \(t_1\star t_2 \in \mathcal {T}^{o}\)
Furthermore, for \(x\in \{\omega ,\iota ,o\}\), \({\hat{\varSigma }}_{x}\) has an associated irreflexive, transitive, and Noetherian order \(<_{x}\).
For every defined symbol \({\hat{f}}\in {\hat{\varSigma }}_{\omega }\cup {\hat{\varSigma }}_{\iota }\cup {\hat{\varSigma }}_{o}\) there exists a set of defining equations \(D({\hat{f}})\) which expresses a primitive recursive definition of \({\hat{f}}\).
Definition 1
(Defining equations) Let \(x\in \{\omega ,\iota ,o\}\), \(\alpha ,\beta \ge 0\), and \(\bullet \) is a member of \(\mathcal {N}\),\(V^{\iota }\), or \(V^{F}\) depending on x. For every \({\hat{f}}\in \varSigma _x\), we define a set \(D({\hat{f}})\) consisting of two equations:
-
(1)
If \({\hat{f}}\) is minimal:
-
(a)
if \(x\in \{\omega ,\iota \}\), then \(t^{{\hat{f}}}_B,t^{{\hat{f}}}_S \in T^x_0\)
-
(b)
if \(x= o\), then \(t^{{\hat{f}}}_B \in T^o_0\), \(t^{{\hat{f}}}_S \in T^o_V\), and \(|V^{F}(t^{{\hat{f}}}_S)|\le 1\).
-
(a)
-
(2)
If \({\hat{f}}\) is non-minimal: \(t^{{\hat{f}}}_B,t^{{\hat{f}}}_S\in T^x\) where \(t^{{\hat{f}}}_B,t^{{\hat{f}}}_S\) may contain only defined function symbols smaller than \({\hat{f}}\) in \(<_{x}\). If \(x=o\), then \(|V^{F}(t^{{\hat{f}}}_S)|\le 1\) and \(|V^{F}(t^{{\hat{f}}}_B)|= 0\).
Additionally, \(\mathcal {N}(t^{{\hat{f}}}_B) \subseteq \{n_1,\ldots ,n_\beta \}\), \(\mathcal {N}(t^{{\hat{f}}}_S) \subseteq \{n_1,\ldots ,n_\beta \} \cup \{m,\bullet \}\) (if \(\bullet \in \mathcal {N}\)), and the only global variables occurring in \(t_B\) and \(t_S\) are \(\overrightarrow{X}_{\alpha }\cup \{\bullet \}\) (if \(\bullet \in V^{\iota }\)). We define \(D^x = \bigcup \{D({\hat{f}}) \mid {\hat{f}}\in \hat{\varSigma _x}\}\).
Remark 2
We frequently write \(t_B\) instead of \(t^{{\hat{f}}}_B\) and \(t_S\) instead of \(t^{{\hat{f}}}_S\) when the defined symbol is clear from the context.
Definition 2
(Closed symbol set) Let S be a finite set of symbols in \({\hat{\varSigma }}_\omega \cup {\hat{\varSigma }}_\iota \cup {\hat{\varSigma }}_o\). We call S closed if for any \({\hat{f}}\in S\) all defined symbols occurring in \(t^{{\hat{f}}}_B\) and in \(t^{{\hat{f}}}_S\) belong to S.
Definition 3
(Theory) Let S be a closed set of symbols. Then the tuple \((S,{\hat{f}},{{\mathcal {D}}})\) is a theory of \({\hat{f}}\) if
-
\({\hat{f}}\in S\) and \({\hat{f}}\) is maximal in S,
-
\({{\mathcal {D}}}= \bigcup \{D({\hat{f}}) \mid {\hat{f}}\in S\}\).
Example 1
For \({\widehat{p}}\in \varSigma _{\omega }\), \(D({\widehat{p}}) = \left\{ {\widehat{p}}({\bar{0}}) = {\bar{0}},\ {\widehat{p}}(s(m)) = m\right\} \), \(t_B = {\bar{0}}\), \(t_s = m\).
Let \({\hat{f}},{\hat{g}}\in \varSigma _{\omega }\) s.t. \({\hat{f}}\) is minimal and \({\hat{f}}<_{\omega } {\hat{g}}\). We define \(D({\hat{f}})\) as
for \(t_B = n\) and \(t_S = s(\bullet )\). Then, obviously, \({\hat{f}}\) defines \(+\). Now we define \(D({\hat{g}})\) as
where \(t'_B = {\bar{0}}\) and \(t'_S = {\hat{f}}(n,\bullet )\). Then \({\hat{g}}\) defines \(*\). In both cases \(\bullet \) is any fresh parameter in \(\mathcal {N}\). The corresponding theory is \(\left( \{ {\hat{p}},{\hat{f}},{\hat{g}}\}, \{{\hat{g}} \}, D({\hat{p}})\cup D({\hat{f}})\cup D({\hat{g}})\right) .\)
Example 2
As a second example consider \(g\in \varSigma _{\iota }\) and \({\hat{f}}\in {\hat{\varSigma }}_{\iota }\). We define \(D({\hat{f}})\) as
Here, \(t_B = X(0), t_S = g(X(m+1),\bullet )\).
It is easy to see that, given any parameter assignment, all terms in \(T^\omega \) evaluate to numerals. The defined symbols in our language introduce an equational theory and without restrictions on the use of these equalities the word problem is undecidable. Furthermore, the evaluation of equations can be nonterminating. However, in this work the equations can be oriented to terminating and confluent rewrite systems and thus termination of the evaluation procedure is easily verified.
Definition 4
(Rewrite systems) Let \(x\in \{\omega ,\iota ,o\}\), and \({\hat{f}}\in \varSigma _x\). Then \(R({\hat{f}})\) is the set of the following rewrite rules obtained from \(D({\hat{f}})\):
\(R^x = \bigcup \{R({\hat{f}}) \mid {\hat{f}}\in {\hat{{{\mathcal {F}}}}}_x\}\). When a term \(s \in T^x\) rewrites to t under \(R^x\) we write \(s \rightarrow _x t\). for a term \(s \in T^x\), such that \(\mathcal {N}(s) = \emptyset \), we denote exhaustive application of \(R^x\) to s by \(s\downarrow _{x}\), i.e. normalization of s.
Definition 4 implies that parameters ought to be replaced by numerals prior to normalization.
Definition 5
(Parameter assignment) A function \(\sigma :\mathcal {N}\rightarrow { Num}\) is called a parameter assignment. \(\sigma \) is extended to \(\mathcal {T}^{\omega }\) homomorphically:
-
\(\sigma ({\bar{\beta }}) = {\bar{\beta }}\) for numerals \({\bar{\beta }}\).
-
\(\sigma (s(t)) = s(\sigma (t))\)
-
\(\sigma ({\hat{f}}(\overrightarrow{t_\alpha })) = {\hat{f}}(\sigma (\overrightarrow{t_\alpha }))\downarrow _{\omega }\) for \({\hat{f}}\in \varSigma _{\omega }\) and \(\overrightarrow{t_\alpha }\in T^\omega \).
The set of all parameter assignments is denoted by \({{\mathcal {S}}}\).
Note that parameter assignments (Definition 5) can be extended to \(\iota \) and o terms in an obvious way. While numeric terms evaluate to numerals under parameter assignments, terms in \(T^\iota \) evaluate to terms in \(T^\iota _0\), i.e. to ordinary first-order terms, and terms in \(T^o\) evaluate to terms in \(T^o_0\), i.e. Boolean expressions. Like for the terms in \(T^\omega \) the evaluation is defined via a rewrite system. To evaluate a term \(t \in T^\iota \) under \(\sigma \in {{\mathcal {S}}}\) we have to combine \(\rightarrow _\omega \) and \(\rightarrow _\iota \).
Definition 6
(Evaluation of \(T^\iota \)) Let \(\sigma \in {{\mathcal {S}}}\) and \(t \in T^\iota \). We define \(\sigma (t)\downarrow _\iota \):
-
\(t = X(\overrightarrow{s_\alpha })\) for \(X\in V^G\) then \(\sigma (X(\overrightarrow{s_\alpha }))\downarrow _\iota = X(\overrightarrow{\sigma (s_\alpha })\downarrow _\omega )\).
-
\(t= f(\overrightarrow{s_{\alpha }})\) for \(f \in \varSigma _\iota \),then \(\sigma (f(\overrightarrow{s}_\alpha ))\downarrow _\iota = f(\sigma (\overrightarrow{s}_\alpha )\downarrow _\iota ).\)
-
\(t={\hat{f}}(\overrightarrow{X}_{\alpha },\overrightarrow{t}_{\beta +1})\) for \({\hat{f}}\in {\hat{\varSigma }}_\iota \), then \(\sigma ({\hat{f}}(\overrightarrow{X}_{\alpha },\overrightarrow{t}_{\beta +1}))\downarrow _\iota = {\hat{f}}(\overrightarrow{X}_{\alpha }, \sigma (\overrightarrow{t}_{\beta +1})\downarrow _\omega )\downarrow _\iota .\)
Remark 3
Concerning global variables and normalization, we should consider the following: Let \(t_1,\cdots t_{\alpha },s_1,\cdots s_{\alpha } \in \omega \), \(X,Y \in V^G\), then we say \(X(t_1,\cdots t_{\alpha }) = Y(s_1,\cdots s_{\alpha })\) iff \(X=Y\) and for any parameter assignment \(\sigma \) we have \(\sigma (t_i)\downarrow _\omega = \sigma (s_i)\downarrow _\omega \) for \(1\le i \le \alpha \).
Example 3
Let us consider the evaluation of the term \(g(X(n),{\hat{f}}(X,m+1))\) with respect to the parameter assignment \(\sigma (m)= 2\), \(\sigma (n)= 2\), using the defining equations provided in Example 2.
To evaluate a term \(t \in T^o\) under \(\sigma \in {{\mathcal {S}}}\) we have to combine \(\rightarrow _\omega \), \(\rightarrow _\iota \), and \(\rightarrow _o\).
Definition 7
(Evaluation of \(T^o\)) Let \(\sigma \in {{\mathcal {S}}}\); we define \(\sigma (t)\downarrow _o\) for \(t \in T^o\).
-
\(t\in V^F\), then \(\sigma (t)\downarrow _o = t\).
-
\(t= P(\overrightarrow{t_{\alpha }})\) for \(P\in \varSigma _o\), then \(\sigma (P(\overrightarrow{t_{\alpha }}))\downarrow _o = P(\overrightarrow{\sigma (t_{\alpha })}\downarrow _\iota ).\)
-
\(t={\hat{P}}(\overrightarrow{X}_{\alpha },\overrightarrow{t}_{\beta +1})\) for \({\hat{P}}\in {\hat{\varSigma }}_o\), then \({\hat{P}}(\overrightarrow{X}_{\alpha }, \sigma (\overrightarrow{t}_{\beta +1})\downarrow _\omega )\downarrow _o\)
-
\(t = \lnot t'\), then \(\sigma (\lnot t')\downarrow _o = \lnot \sigma (t')\downarrow _o\).
-
\(t = t_1 \circ t_2\), then \(\sigma (t)\downarrow _o = \sigma (t_1)\downarrow _o \circ \sigma (t_2)\downarrow _o\) for \(\circ \in \{\wedge ,\vee \}\).
Proposition 1
.
-
\(R^x\) is a canonical rewrite system for \(x\in \{\omega ,\iota , o\}\).
-
Let \(t \in T^x\) and \(\sigma \in {{\mathcal {S}}}\). Then the (unique) normal form of \(\sigma (t)\) under \(R^x\), \(\sigma (t)\downarrow _x\), is a member of \(\mathcal {T}^x_0\).
Proof
Concerning \(R^{\omega }\), termination and confluence are well known, see e.g. [4]. In particular, \({\bar{0}},s\) and \(R({\hat{\varSigma }}_\omega )\) define a language for computing the set of primitive recursive functions; in particular the recursions are well founded. A formal proof of termination requires double induction on \(<_{\omega }\) and the value of the recursion parameter. The proofs for \(R^{\iota }\) and \(R^{o}\) are slightly more complex. Given the similarity of the two rule sets we will only provide formal proof for \(R^{\iota }\). In particular, we show that given \(t \in T^\iota \) and \(\sigma \in {{\mathcal {S}}}\) then \(\sigma (t)\downarrow _\iota \in T^\iota _0\). We proceed according to Definition 6.
-
if \(t=X(\overrightarrow{s_\alpha })\) then \(\sigma (\overrightarrow{s_\alpha })\downarrow _\omega = \overrightarrow{\bar{\gamma _\alpha }}\) for \(\bar{\gamma _\alpha } \in Num \) and \(\sigma (X(\overrightarrow{s_\alpha }))\downarrow _\iota = X(\overrightarrow{\bar{\gamma _\alpha }}) \in V^{\iota }\).
-
if \(t = f(\overrightarrow{s_\alpha })\) for \(f \in \varSigma _{\iota }\), then \(\sigma (f(\overrightarrow{s_\alpha }))\downarrow _\iota = f(\overrightarrow{\sigma (s_\alpha })\downarrow _\iota )\). By induction we may assume that \(\overrightarrow{s_\alpha '} = \overrightarrow{\sigma (s_\alpha })\downarrow _\iota \in T^\iota _0\), thus \(f(s'_1,\ldots ,s'_\alpha ) \in T^\iota _0\).
-
if \({\hat{f}}(\overrightarrow{X}_{\alpha },\overrightarrow{t_\beta },t_{\beta +1})\) for \({\hat{f}}\in {\hat{\varSigma }}_{\iota }\) and \({\hat{f}}\) is minimal in \(<_{\iota }\), then we distinguish two cases
-
1.
\(\sigma (t_{\beta +1})\downarrow _\omega = {\bar{0}}\). Then, \(\sigma ({\hat{f}}(\overrightarrow{X}_{\alpha },\overrightarrow{t_\beta },t_{\beta +1}))\downarrow _\iota )) = {\hat{f}}(\overrightarrow{X}_{\alpha }, \overrightarrow{{\bar{\gamma }}_\beta },{\bar{0}})\) for \(\overrightarrow{\bar{\gamma _i}} \in Num \). According to Definition 4\({\hat{f}}(\overrightarrow{X}_{\alpha }, \overrightarrow{{\bar{\gamma }}_\beta },{\bar{0}})\) rewrites to \(t_B \in T^\iota _0\).
-
2.
\(\sigma (t_{\beta +1})\downarrow _\omega = \bar{p+1}\) for \(p>0\). Then \({\hat{f}}(\overrightarrow{X}_{\alpha }, \overrightarrow{{\bar{\gamma }}_\beta },\bar{p+1})\) rewrites to the term \(t_S\{\bullet \leftarrow {\hat{f}}(\overrightarrow{X}_{\alpha }, \overrightarrow{{\bar{\gamma }}_\beta },{\bar{p}})\}\) where \(t_S \in T^\iota _0\). By induction on p we infer that \({\hat{f}}(\overrightarrow{X}_{\alpha }, \overrightarrow{{\bar{\gamma }}_\beta },{\bar{p}})\downarrow _\iota \in T^\iota _0\) and so \({\hat{f}}(\overrightarrow{X}_{\alpha }, {\bar{\gamma }}_\beta ,\bar{p+1})\) rewrites to a term in \(T^\iota _0\).
-
1.
-
if \({\hat{f}}(\overrightarrow{X}_{\alpha },\overrightarrow{t_\beta },t_{\beta +1})\) for \({\hat{f}}\in {\hat{\varSigma }}_{\iota }\) and \({\hat{f}}\) is not minimal in \(<_{\iota }\), then we have to add induction on \(<_{\iota }\) with the base cases shown above.
\(\square \)
Example 4
We consider the theory \((\{{\hat{f}}\},{\hat{f}},{{\mathcal {D}}})\) where \({{\mathcal {D}}}= \{D({\hat{f}})\}\) for \(D({\hat{f}})\) defined below. Let \(X,Y\in V^G\), \(g \in \varSigma _{\iota }\), and n, m parameters. Assume \({\hat{f}}\) is defined as follows: Let \(D({\hat{f}})\) consist of the two equations
We evaluate \({\hat{f}}(X,Y,n,m)\) under \(\sigma \), where \(\sigma (n) = {\bar{1}}, \sigma (m) = {\bar{2}}\) and \(\sigma (k) = {\bar{0}}\) for \(k \not \in \{n,m\}\).
When we write \(x_1\) for \(X({\bar{1}},{\bar{1}})\) and \(x_2\) for \(X({\bar{1}},{\bar{0}})\) and y for Y we get the term in the common form \(g(x_1,g(x_2,y))\).
The last point we would like to make concerning terms \(\mathcal {T}^o\) is that we designed the language to finitely express infinite sequences of quantifier free first-order formula. In particular, we are interested in infinite sequences of unsatisfiable formula whose refutations are finitely describable using the resolution calculus introduced later in this paper. We end this section with examples of such formulas.
Definition 8
(Unsatisfiable schemata) Let \(F \in \mathcal {T}^o\). Then F is called unsatisfiable if for all \(\sigma \in {{\mathcal {S}}}\) the formula \(\sigma (F)\downarrow _o\) is unsatisfiable.
Example 5
Let \(a\in \varSigma _\iota \), \(P \in \varSigma _o\), \({\hat{f}}\) as in Example 2, \({\hat{P}},{\hat{Q}}\in {\hat{\varSigma }}_o\) such that \({\hat{P}}<_{o}{\hat{Q}}\). We consider the theory \((\{{\hat{P}},{\hat{Q}},{\hat{f}}\},{\hat{Q}},\{D({\hat{P}}),D({\hat{Q}}),D({\hat{f}})\})\). The defining equations for \({\hat{P}}\) and \({\hat{Q}}\) are:
It is easy to see that the schema \({\hat{Q}}(X,Y,n,m)\) is unsatisfiable. Let us consider \(\sigma ({\hat{Q}}(X,Y,n,m))\downarrow _o\) for \(\sigma \) with \(\sigma (m) = {\bar{2}}, \sigma (n) = {\bar{3}}\):
Note that for \(\sigma (n) = {\bar{\alpha }}\) the number of different variables in \(\sigma ({\hat{Q}}(X,Y,n,m))\downarrow _o\) is \(\alpha +2\); so the number of variables increases with the parameter assignments.
Example 6
Let us now consider the schematic formula representation of the inductive definition extracted from the m-successor eventually constant schema presented in Sect. 2. This requires us to define five defined predicate symbols \({{\hat{F}}_1},{{\hat{F}}_2},{{\hat{F}}_3},{{\hat{F}}_4}\), and \({{\hat{F}}_5}\) such that \({{\hat{F}}_5}<_{o}{{\hat{F}}_4}<_{o}{{\hat{F}}_3}<_{o}{{\hat{F}}_2} <_{o}{{\hat{F}}_1}\). Furthermore, the defining equations associated with these defined predicate symbols contain the symbols \(\sim ,< \in \varSigma _o\), \(a,f, suc \in \varSigma _{\iota }\), and \(n,m\in \mathcal {N}\). We also require a defined function symbol \({\hat{S}}\in {\hat{\varSigma }}_{\iota }\). Note that in this case the sort \(\iota \) is identical to \(\omega \). Using these symbols we can rewrite the inductive definition provided in Sect. 2 into the theory \((S,\hat{F_1},{{\mathcal {D}}})\) where \(S = \{{\hat{F}}_1,\ldots ,{\hat{F}}_5,{\hat{S}}\}\) and \({{\mathcal {D}}}\) consists of the equations below (\({\mathbf {X}} = (X_1,X_2,X_3)\)):
In dealing with term schemata we have to consider schematic substitutions, particularly when we are interested in unification. Below we develop some formal tools to describe such schemata. Note that for two term schemata to be unifiable, they have to be unifiable for all parameter assignments. Here the use of global variables plays a vital role. Although there are unifiable term schemata that are defined without global variables, allowing this kind of indexed variables in the construction of term schemata simplifies the formalism. As shown below in Example 7, there are term schemata (which are defined without using global variables) that are unifiable for some, but not all parameter assignments.
Example 7
Let us consider \({{\hat{f}}}\),\({{\hat{f}}_1}\), and \({{\hat{g}}}\) with the defining equations
Note that \({{\hat{f}}_1} > {{\hat{f}}}\). Consider the parameter assignment \(\sigma = \{ n\rightarrow 2\}\) and the evaluation of \({\hat{f}}_1(x,y,n)\):
We can define unification problems such as
Consider \(\sigma _0 = \{ n\rightarrow 0\}\) and \(\sigma _1 = \{ n\rightarrow 1\}\). Then, the unification problem evaluates to
both of which are unifiable. However, for \(\sigma _2 = \{ n\rightarrow 2\}\) the unification problem evaluates to
After two steps unification fails due to occurs check.
On the other hand,
is a unifiable unification problem. The evaluation for \(\sigma _2 = \{ n\rightarrow 2\}\) is
A unifier for this problem is \(\theta = \)
The substitution schema is
As term schemata that are defined without the use of global variables repeat a finite set of variables arbitrarily often, in many cases the unification problem of term schemata will result in occurrence check failure. We can tackle this problem by using global variables. Usually, we do not desire all variables occurrences to be the same nor do we desire them to all be different. These extreme cases can be described through quantification. Let P be a one-place predicate symbol, then \(P({\hat{f}}(x,n))\) can be interpreted as
The use of global variables allows for the syntactic description of properties of the quantifier prefix. Moreover, it reduces unwanted occurrence check failure. The domain of a unifier of term schemata, that are constructed using global variables, is by construction dependent on the numeric parameter. These kind of unifiers are called s-unifiers. Before introducing s-unification formally, we need some preliminaries.
The class \(T^\omega _0\) which represents the free algebra based on s and \({\bar{0}}\) is not very expressive while \(T^\omega \) is too strong (many properties are undecidable). For our proof analysis in Sect. 6 we need a slight extension of \(T^\omega _0\); besides the successor, we add the predecessor in order to define recursive calls. For this reason we extend our class \(T^\omega _0\) by adding the defined function symbol \({\hat{p}}\) as defined in Example 1.
Definition 9
(\(T^\omega _1\)) Let \({\hat{p}}\in \hat{\varSigma _\omega }\) and \(D({\hat{p}})\) as in Example 1. The class \(T^\omega _1\) is defined inductively as follows.
-
\({\bar{0}} \in T^\omega _1\),
-
\(\mathcal {N}\subseteq T^\omega _1\),
-
if \(t \in T^\omega _1\) then \(s(t) \in T^\omega _1\),
-
if \(t \in T^\omega _1\) then \({\hat{p}}(t) \in T^\omega _1\).
Definition 10
(Essentially distinct) Let \(\overrightarrow{s}_1 = (s_1,\ldots ,s_\alpha )\) for \(s_1,\ldots ,s_\alpha \in T^\omega _1\) and \(\overrightarrow{s}_2 = (s'_1,\ldots ,s'_\beta )\) for \(s'_1,\ldots ,s'_\beta \in T^\omega _1\). \(\overrightarrow{s}_1\) and \(\overrightarrow{s}_2\) are called essentially distinct if either \(\alpha \ne \beta \) or for all \(\sigma \in {{\mathcal {S}}}\) there exists an \(i \in \{1,\ldots ,\alpha \}\) such that \(\sigma (s_i)\downarrow _\omega \ne \sigma (s'_i)\downarrow _\omega \).
Proposition 2
Let \(\alpha \ge 0\), \(\overrightarrow{s}_1 = (s_1,\ldots ,s_\alpha )\) for \(s_1,\ldots ,s_\alpha \in T^\omega _1\) and \(\overrightarrow{s}_2 = (s'_1,\ldots ,s'_\alpha )\) for \(s'_1,\ldots ,s'_\alpha \in T^\omega _1\), and \(\varGamma = \{ s_1{\mathop {=}\limits ^{?}} s'_1, \cdots , s_\alpha {\mathop {=}\limits ^{?}} s'_\alpha \}\). Then \(\varGamma \) is unifiable over \(T^\omega _1\) (i.e. in the theory \((\{{\hat{p}}\},\{{\hat{p}}\},\{D({\hat{p}})\})\) over \(T^\omega _1\)) iff \(\overrightarrow{s}_1\) and \(\overrightarrow{s}_2\) are not essentially distinct.
Proposition 3
It is decidable whether \(\overrightarrow{s},\overrightarrow{t}\) are essentially distinct for term tuples \(\overrightarrow{s},\overrightarrow{t}\) in \(T^\omega _1\).
Proof
If the arity of \(\overrightarrow{s}\) and \(\overrightarrow{t}\) is different the problem is trivial. Therefore we consider terms of the form
By Proposition 2\(\overrightarrow{s},\overrightarrow{t}\) are not essentially distinct iff
is solvable over \(T^\omega _1\). We present an algorithm for deciding solvability of such a system \(\varGamma \).
Let t be a term in \(T^\omega _1\). Then t is either of the form \(f_1 \cdots f_\beta n\) for \(n \in \mathcal {N}\) or \(f_1 \cdots f_\beta {\bar{0}}\) where \(f_1,\ldots ,f_\beta \in \{s,{\hat{p}}\}\). To each such term and \(\sigma \in {{\mathcal {S}}}\) we assign an arithmetic expression \(\pi (\sigma ,t)\):
-
If \(t = f_1 \cdots f_\beta {\bar{0}}\) then \(\pi (\sigma ,t) = \alpha \) for \(f_1 \cdots f_\beta {\bar{0}}\downarrow _\omega = {\bar{\alpha }}\).
-
If \(t = f_1 \cdots f_\beta n\) we define
-
\(\nu _s(t) =\) number of occurrences of s in t,
-
\(\nu _{{\hat{p}}}(t) =\) number of occurrences of \({\hat{p}}\) in t.
$$\begin{aligned} \pi (\sigma ,t)= & {} n+\nu _s(t) - \nu _{{\hat{p}}}(t) \text{ for } \sigma (n) \ge \overline{\nu _{{\hat{p}}}(t)},\\= & {} \alpha _i \text{ for } \bar{\alpha _i} = f_1\cdots f_\beta {\bar{i}}\downarrow _\omega \text{ and } \sigma (n) = {\bar{i}}, i<\nu _{{\hat{p}}}(t). \end{aligned}$$
-
Now let \({{\mathcal {T}}}(n)\) be all terms of the form \(f_1 \cdots f_\beta n\) in \(\varGamma \). Select the t in \({{\mathcal {T}}}(n)\) where \(\nu _{{\hat{p}}}(t)\) is maximal and define \(r(n) = \nu _{{\hat{p}}(t)}\). If \(n_1,\ldots ,n_\gamma \) are all the variables in \(\varGamma \) we obtain numbers \(r(n_1),\ldots ,r(n_\gamma )\). For all terms t of the form \(f_1 \cdots f_\beta n\) we define now
Now consider the valid formula
and transform it into an equivalent DNF F. Then every conjunct C in F defines a condition on \(\sigma \) such that the \(\pi (\sigma ,s_i),\pi (\sigma ,t_i)\) are uniquely defined and every C defines a system
The solvability of \({{\mathcal {E}}}(C,\sigma )\) is easy to check as all equations are of the form \(m \circ i = n \star j\), \(m \circ i = j\) or \(i=j\) for \(\circ ,\star \in \{+,-\}\), m, n integer variables and \(i,j \in \mathrm{I\!N}\). But \(\varGamma \) is solvable iff all the \({{\mathcal {E}}}(C,\sigma )\) are solvable. Hence the decision algorithm consists in checking all equational systems \({{\mathcal {E}}}(C,\sigma )\) for solvability. \(\square \)
Example 8
Let \(\overrightarrow{s} = ({\hat{p}}s n,m,n),\ \overrightarrow{t} = ({\hat{p}}{\hat{p}}n,n,s k)\). For m, k we get \(\pi (\sigma ,m)=m, \pi (\sigma ,s k) = k+1\). We have two terms “ending” with n, namely \({\hat{p}}s n\) and \({\hat{p}}{\hat{p}}n\). Here we get
We obtain \(r(n)=2\) and obtain the formula \(n=0 \vee n=1 \vee n \ge 2\) which is already in DNF. The corresponding equation systems are
All equation systems are unsolvable and thus \(\overrightarrow{s},\overrightarrow{t}\) are essentially distinct. It is easy to see that the first equation system is solvable if we change the term \(\overrightarrow{t}\) to \(\overrightarrow{t'} = ({\hat{p}}{\hat{p}}n,n,k)\). So \(\overrightarrow{s},\overrightarrow{t'}\) are not essentially distinct.
Definition 11
(s-substitution) Let \(\varTheta \) be a finite set of pairs \((X(\overrightarrow{s}_{\alpha }),t)\) where \(X(\overrightarrow{s}_{\alpha }) \in T^\iota _V\), \(\overrightarrow{s}_\alpha \) a tuple of terms in \(T^\omega _1\) and \(t \in T^\iota \). Note that the global variables occurring in \(\varTheta \) need not be of the same type. \(\varTheta \) is called an s-substitution if for all \((X(\overrightarrow{s}_{\alpha }),t)\) , \((Y(\overrightarrow{s'}_{\alpha }),t') \in \varTheta \) either \(X \ne Y\) or the tuples \(\overrightarrow{s}_{\alpha }\) and \(\overrightarrow{s'}_{\alpha }\) are essentially distinct. For \(\sigma \in {{\mathcal {S}}}\) we define \(\varTheta [\sigma ] =\{X(\sigma (\overrightarrow{s}_{\alpha })\downarrow _\omega ) \leftarrow t\sigma \downarrow _\iota \mid (X(\overrightarrow{s}_{\alpha }),t) \in \varTheta \}.\)
We define \(\mathop { dom}(\varTheta ) = \{X(\overrightarrow{s}_{\alpha }) \mid (X(\overrightarrow{s}_{\alpha }),t) \in \varTheta \}\) and \(\mathop { rg}(\varTheta ) = \{t \mid (X(\overrightarrow{s}_{\alpha }),t) \in \varTheta \}\).
Proposition 4
For all \(\sigma \in {{\mathcal {S}}}\) and every s-substitution \(\varTheta \), \(\varTheta [\sigma ]\) is a (first-order) substitution.
Proof
It is enough to show that for all \((X(\overrightarrow{s}_{\alpha }),t),(Y(\overrightarrow{s'}_{\alpha '}),t') \in \varTheta \) \(X(\sigma (\overrightarrow{s}_{\alpha })\downarrow _\omega )\) \(\ne Y(\sigma (\overrightarrow{s'}_{\alpha '})\downarrow _\omega )\) and \(\sigma (t)\downarrow _\iota , \sigma (t')\downarrow _\iota \in T^\iota _0\) (follows from Proposition 1), for all \(\sigma \in {{\mathcal {S}}}\). If \(X \ne Y\) this is obvious; if \(X =Y\) then, by definition of \(\varTheta \), \(\overrightarrow{s}_{\alpha }\) and \(\overrightarrow{s'}_{\alpha }\) are essentially distinct and so for each \(\sigma \in {{\mathcal {S}}}\) we have \(X(\sigma (\overrightarrow{s}_{\alpha })\downarrow _\omega ) \ne X(\sigma (\overrightarrow{s'}_{\alpha '})\downarrow _\omega )\). Thus \(\varTheta [\sigma ]\) is indeed a substitution as for \(X(\overrightarrow{s}_{\alpha }) \in T^\iota _V\) \(X(\sigma (\overrightarrow{s}_{\alpha })) \in V^{\iota }\). \(\square \)
Example 9
The following expression is an s-substitution
for \({\hat{S}}\) as in Example 6.
The application of an s-substitution \(\varTheta \) to terms in \(T^\iota \) is defined inductively on the complexity of term definitions as usual.
Definition 12
Let \(\varTheta \) be an s-substitution and \(\sigma \) a parameter assignment. We define \(t\varTheta [\sigma ]\) for terms \(t \in T^\iota \):
-
if t is a constants of type \(\iota \), then \(t\varTheta [\sigma ] = t\),
-
if \(t = X(\overrightarrow{s}_{\alpha })\) and \((X(\overrightarrow{s'}_{\alpha }),t') \in \varTheta \) such that \(X(\sigma (\overrightarrow{s'}_{\alpha })) = X(\sigma (\overrightarrow{s}_{\alpha }))\), then \(X(\overrightarrow{s}_\alpha )\varTheta [\sigma ] = \sigma (t')\downarrow _\iota \), otherwise \(X(\overrightarrow{s}_{\alpha })\varTheta [\sigma ] = X(\sigma (\overrightarrow{s}_\alpha ))\);
-
if \(f \in {{\mathcal {F}}}_{\iota }\), \(f:\iota ^\alpha \rightarrow \iota \), \(s_1,\ldots ,s_\alpha \in T^\iota \) then \(f(s_1,\ldots ,s_\alpha )\varTheta [\sigma ] = f(s_1\varTheta [\sigma ],\ldots ,\) \(s_\alpha \varTheta [\sigma ])\),
-
if \({\hat{f}}\in {\hat{\varSigma }}_{\iota }\), \({\hat{f}}:\tau (\gamma (1),\ldots ,\gamma (\alpha _1)) \times \omega ^{\beta +1} \rightarrow \iota \), then
$$\begin{aligned} {\hat{f}}(\overrightarrow{X}_{\alpha _1}, t_1,\ldots ,t_{\beta +1})\varTheta [\sigma ] = {\hat{f}}(\overrightarrow{X}_{\alpha _1},\sigma (t_1)\downarrow _\omega ,\ldots ,\sigma (t_{\beta +1})\downarrow _\omega )\downarrow _\iota \varTheta [\sigma ]. \end{aligned}$$
Example 10
Let us consider the following defined function symbol:
and the parameter assignment \(\sigma = \left\{ n\leftarrow 0 , m\leftarrow s(0) \right\} \). Then the evaluation of the term \({\hat{g}}(X,n,m)\) by the s-substitution \(\varTheta \) from Example 9 proceeds as follows:
where
for \({\hat{S}}\) as in Example 6.
The composition of s-substitutions is not trivial as, in general, there is no uniform representation of composition under varying parameter assignments.
Example 11
Let \(\varTheta _1 = \{(X_1(n),f(X_1(n))\}\) and \(\varTheta _2 = \{(X_1(0),g(a))\}\). Then, for \(\sigma \in {{\mathcal {S}}}\) s.t. \(\sigma (n)=0\) we get
On the other hand, for \(\sigma ' \in {{\mathcal {S}}}\) with \(\sigma '(n)=1\) we obtain
Or take \(\varTheta '_1 = \{(X_1(n),X_2(n))\}\) and \(\varTheta '_2 = \{(X_2(m),X_1(m))\}\).
Let \(\sigma (n)=\sigma (m)=0\) and \(\sigma '(n)=0,\sigma '(m)=1\). Then
The examples above suggest the following restrictions on s-substitutions with respect to composition. The first definition ensures that domain and range are variable-disjoint.
Definition 13
Let \(\varTheta \) be an s-substitution. \(\varTheta \) is called normal if for all \(\sigma \in {{\mathcal {S}}}\) \(\mathop { dom}(\varTheta [\sigma ]) \cap V^{\iota }(\mathop { rg}(\varTheta [\sigma ])) = \emptyset \).
Example 12
The s-substitution in Example 9 is normal. The substitutions \(\varTheta '_1\) and \(\varTheta '_2\) in Example 11 are normal. \(\varTheta _1\) in Example 11 is not normal.
Proposition 5
It is decidable whether a given s-substitution is normal.
Proof
Let \(\varTheta \) be an s-substitution. We search for equal global variables in \(\mathop { dom}(\varTheta )\) and in \(\mathop { rg}(\varTheta )\); if there are none then \(\varTheta \) is trivially normal. So let \(X \in V^G(\mathop { dom}(\varTheta ))\) \(\cap V^G(\mathop { rg}(\varTheta ))\). For every \(X(\overrightarrow{s}_{\alpha }) \in \mathop { dom}(\varTheta )\) and for every \(X(\overrightarrow{t}_{\alpha })\) occurring in \(\mathop { rg}(\varTheta )\) we test unifiability of the arguments in the sense of Proposition 2. \(\varTheta \) is normal iff for no pair \(X(\overrightarrow{s}_{\alpha }\) and \(X(\overrightarrow{t}_{\alpha } )\) are the arguments unifiable in the sense of Proposition 2. \(\square \)
Example 11 shows also that normal s-substitutions cannot always be composed to an s-substitution; thus we need an additional condition.
Definition 14
Let \(\varTheta _1,\varTheta _2\) be normal s-substitutions. \((\varTheta _1,\varTheta _2)\) is called composable if for all \(\sigma \in {{\mathcal {S}}}\)
-
1.
\(\mathop { dom}(\varTheta _1[\sigma ]) \cap \mathop { dom}(\varTheta _2(\sigma )) = \emptyset \),
-
2.
\(\mathop { dom}(\varTheta _1[\sigma ]) \cap V^{\iota }(\mathop { rg}(\varTheta _2[\sigma ])) = \emptyset \).
Proposition 6
It is decidable whether \((\varTheta _1,\varTheta _2)\) is composable for two normal s-substitutions \(\varTheta _1, \varTheta _2\).
Proof
Like in Proposition 5 we use Proposition 2 to test unifiability of arguments for variables \(X(\overrightarrow{s}),X(\overrightarrow{t})\) occurring in the sets under consideration. \(\square \)
Definition 15
Let \(\varTheta _1,\varTheta _2\) be normal s-substitutions and \((\varTheta _1,\varTheta _2)\) composable. Assume that
Then the composition \(\varTheta _1 \star \varTheta _2\) is defined as
The following proposition shows that \(\varTheta _1 \star \varTheta _2\) really represents composition.
Proposition 7
Let \(\varTheta _1,\varTheta _2\) be normal s-substitutions and \((\varTheta _1,\varTheta _2)\) be composable then for all \(\sigma \in {{\mathcal {S}}}\) \((\varTheta _1 \star \varTheta _2)[\sigma ] = \varTheta _1[\sigma ] \circ \varTheta _2[\sigma ]\).
Proof
Let
Then \(\varTheta _1 \star \varTheta _2\) is defined as
We write \(x_i\) for \(X_i(\sigma (\overrightarrow{s_i})))\) and \(y_j\) for \(Y_j(\sigma (\overrightarrow{w_j}))\), \(\theta _1\) for \(\varTheta _1[\sigma ]\) and \(\theta _2\) for \(\varTheta _2[\sigma ]\). Moreover let \(t'_i = \sigma (t_i)\downarrow _\iota , r'_j = \sigma (r_j)\downarrow _\iota \). Then
As \((\varTheta _1,\varTheta _2)\) is composable we have
-
1.
\(\{x_1,\ldots ,x_\alpha \} \cap \{y_1,\ldots ,y_\beta \} = \emptyset \), and
-
2.
\(\{x_1,\ldots ,x_\alpha \} \cap V^{\iota }(\{r'_1,\ldots ,r'_\beta \}) = \emptyset \).
So \(\theta _1\theta _2 =\{ x_1 \leftarrow t'_1,\ldots ,x_\alpha \leftarrow t'_\alpha )\}\theta _2= \{x_1 \leftarrow t'_1\theta _2,\ldots ,x_\alpha \leftarrow t'_\alpha \theta _2\} \cup \theta _2\). The last substitution is just \((\varTheta _1 \star \varTheta _2)[\sigma ]\). \(\square \)
Proposition 8
Let \(\varTheta _1,\varTheta _2\) be normal s-substitutions and \((\varTheta _1,\varTheta _2)\) composable. Then \(\varTheta _1 \star \varTheta _2\) is normal.
Proof
Like in the proof of Proposition 7 let \(\varTheta _1[\sigma ] =\theta _1,\varTheta _2[\sigma ] = \theta _2\). We have to show that \(\mathop { dom}(\theta _1\theta _2) \cap V^{\iota }(\mathop { rg}(\theta _1\theta _2) = \emptyset \). We have
As \(\theta _1\) is normal we have \(V^{\iota }(t'_i) \cap \{x_1,\ldots ,x_\alpha \} =\emptyset \) for \(i = 1,\ldots ,\alpha \). By definition of composability \(\mathop { rg}(\theta _2) \cap \{x_1,\ldots ,x_\alpha \} = \emptyset \), and therefore
So \(\{x_1 \leftarrow t'_1\theta _2,\ldots ,x_\alpha \leftarrow t'_\alpha \theta _2\}\) is normal. As also \(\varTheta _2\) is normal we have \(\mathop { dom}(\theta _2) \cap V^{\iota }(\mathop { rg}(\theta _2) = \emptyset \). Hence we obtain \(\mathop { dom}(\theta _1\theta _2) \cap V^{\iota }(\mathop { rg}(\theta _1\theta _2)) = \emptyset .\) \(\square \)
Definition 16
(s-unifier) Let \(t_1,t_2 \in T^\iota \). An s-substitution \(\varTheta \) is called an s-unifier of \(t_1,t_2\) if for all \(\sigma \in {{\mathcal {S}}}\) \((t_1\sigma \downarrow _\iota )\varTheta [\sigma ] = (t_2\sigma \downarrow _\iota )\varTheta [\sigma ]\). We refer to \(t_1,t_2\) as s-unifiable if there exists an s-unifier of \(t_1,t_2\). s-unifiability can be extended to more than two terms and to formula schemata (to be defined below) in an obvious way.
Example 13
Consider the following theory \(\left( \{{\hat{f}},{\hat{g}}\},\{{\hat{f}}\}, D({\hat{f}})\cup D({\hat{g}})\right) \) where
and
Using these schemata we can define the unification problem
which has as a unification schema \({\hat{\varTheta }}: \left\{ X(n)\leftarrow {\hat{h}}(n)\right\} \) where \({\hat{h}}(n)\) is as follows:
\({\hat{\varTheta }}(n)\) is an s-unifier within the extended theory
Definition 17
An s-unifier \(\varTheta \) of \(t_1,t_2\) is called restricted to \(\{t_1,t_2\}\) if \(T^\iota _V(\varTheta ) \subseteq T^\iota _V(\{t_1,t_2\})\).
Remark 4
It is easy to see that for any s-unifier \(\varTheta \) of \(\{t_1,t_2\}\) there exists an s-unifier \(\varTheta '\) of \(\{t_1,t_2\}\) which is restricted to \(\{t_1,t_2\}\).
Most general unification is defined modulo the set of parameter substitutions \(\mathcal {S}\).
Definition 18
A restricted s-unifier \(\varTheta \) of \(\{t_1,t_2\}\) is a most general unifier if for all parameter substitutions \(\sigma \in \mathcal {S}\), \( \varTheta \left[ \sigma \right] \) is a most general unifier of \(\{\sigma (t_1)\downarrow _{\iota },\sigma (t_2)\downarrow _{\iota }\}\).
Remark 5
For example, the s-unifier from Example 13 is a most general unifier. Note that it is not clear if a most general unifier always exists. We do not have a decision procedure for the unification problem, not even for restricted classes.
4 The Resolution Calculus
The basis of our calculus for refuting formula schemata is a calculus \(\mathrm{RPL}_0\) for quantifier-free formulas, which combines dynamic normalization rules (a la Andrews, see [1]) with the resolution rule. In contrast to [1] we do not restrict the resolution rule to atomic formulas. We denote as \(\mathrm{PL}_0\) the set of quantifier-free formulas in predicate logic; for simplicity we omit \(\rightarrow \) and represent it by \(\lnot \) and \(\vee \) in the usual way. Sequents are objects of the form \(\varGamma \vdash \varDelta \) where \(\varGamma \) and \(\varDelta \) are multisets of formulas in \(\mathrm{PL}_0\).
Definition 19
(\(\mathrm{RPL}_0\)) The axioms of \(\mathrm{RPL}_0\) are sequents \(\vdash F\) for \(F \in \mathrm{PL}_0\). The rules are the elimination rules for the connectives



the introduction rules for the connectives



the resolution rule

\(\vartheta \) is an m.g.u. of \(\{A_1,\ldots ,A_k,B_1,\ldots ,B_l\}\), \(V(\{A_1,\ldots ,A_k\}) \cap V(\{B_1,\ldots ,B_l\}) = \emptyset \).
We will extend \(\mathrm{RPL}_0\) by rules handling schematic formula definitions. But we have to consider another aspect as well: in inductive proofs the use of lemmas is vital, i.e. an ordinary refutational calculus (which has just a weak capacity of lemma generation) may fail to derive the desired invariant. To this aim we added introduction rules for the connectives, which gives us the potential to derive more complex formulas. Note that our aim is to use the calculi in an interactive way and not fully automatic, which justifies this process of “anti-refinement”.
Proposition 9
\(\mathrm{RPL}_0\) is sound and refutationally complete, i.e.
-
(1)
all rules in \(\mathrm{RPL}_0\) are sound and
-
(2)
for any unsatisfiable formula \(\forall F\) and \(F \in \mathrm{PL}_0\) there exists a \(\mathrm{RPL}_0\)-derivation of \(\vdash \) from axioms of the form \(\vdash F\vartheta \) where \(\vartheta \) is a renaming of V(F).
Proof
(1) is trivial: if \({{\mathcal {M}}}\) is a model of the premise(s) of a rule then \({{\mathcal {M}}}\) is also a model of the conclusion.
For proving (2) we first derive the standard clause set \({{\mathcal {C}}}\) of F. Therefore, we apply the rules of \(\mathrm{RPL}_0\) to \(\vdash F\), decomposing F into its subformulas, until we cannot apply any rule other than the resolution rule res. The last subformula obtained in this way is atomic and hence a clause. The standard clause set \({{\mathcal {C}}}\) of F is comprised of the clauses obtained in this way. As \(\forall F\) is unsatisfiable, its standard clause set is refutable by resolution. Thus, we apply res to the clauses and obtain \(\vdash \). The whole derivation lies in \(\mathrm{RPL}_0\). \(\square \)
In extending \(\mathrm{RPL}_0\) to a schematic calculus we have to replace unification by s-unification. Formally we have to define how s-substitutions are extended to formula schemata and sequent schemata.
Definition 20
Let \(\varTheta \) be an s-substitution. We define \(F\varTheta \) for all \(F \in \mathcal {T}^{o}\) which do not contain formula variables.
-
Let \(P(t_1,\ldots ,t_\alpha ) \in T^o\) and \(P \in {{\mathcal {P}}}\). Then \(P(t_1,\ldots ,t_\alpha )\varTheta = P(t_1\varTheta ,\ldots ,\) \(t_\alpha \varTheta )\).
-
Let \({\hat{P}}\in {\hat{{{\mathcal {P}}}}}\) and \({\hat{P}}(X_1,\ldots ,X_\alpha ,t_1,\ldots ,t_{\beta +1}) \in T^o\), then
$$\begin{aligned} {\hat{P}}(X_1,\ldots ,X_\alpha ,t_1,\ldots ,t_{\beta +1})\varTheta = {\hat{P}}(X_1,\ldots ,X_\alpha ,t_1\varTheta ,\ldots ,t_{\beta +1}\varTheta ). \end{aligned}$$ -
\((\lnot F)\varTheta = \lnot F\varTheta \).
-
If \(F_1,F_2 \in \mathcal {T}^{o}\) then
$$\begin{aligned} (F_1 \wedge F_2)\varTheta = F_1\varTheta \wedge F_2\varTheta ,\quad (F_1 \vee F_2)\varTheta = F_1\varTheta \vee F_2\varTheta . \end{aligned}$$
Let \(S:A_1,\ldots , A_\alpha \vdash B_1,\ldots ,B_\beta \) be a sequent schema. Then
In the resolution rule we have to ensure that the sets of variables in \(\{A_1,\ldots ,A_k\}\) and \(\{B_1,\ldots ,B_l\}\) are pairwise disjoint. We need a corresponding concept of disjointness for the schematic case.
Definition 21
(Essentially disjoint) Let \({{\mathcal {A}}},{{\mathcal {B}}}\) be finite sets of schematic variables in \(T^\iota _V\). \({{\mathcal {A}}}\) and \({{\mathcal {B}}}\) are called essentially disjoint if for all \(\sigma \in {{\mathcal {S}}}\) \({{\mathcal {A}}}[\sigma ] \cap {{\mathcal {B}}}[\sigma ] = \emptyset \).
Definition 22
(\(\mathrm{RPL}_0^\varPsi \)) Let \(\varPsi :(S,{\hat{Q}},{{\mathcal {D}}})\) be a theory of the schematic predicate symbol \({\hat{Q}}\) then, for all schematic predicate symbols \({\hat{P}}\in S\) for
elimination of defined symbols


introduction of defined symbols


We also adapt the resolution rule to the schematic case:
Let \(T^\iota _V(\{A_1,\ldots ,A_\alpha \}), T^\iota _V(\{B_1,\ldots ,B_\beta \})\) be essentially disjoint sets of schematic variables and \(\varTheta \) be an s-unifier of \(\{A_1,\ldots ,A_\alpha ,B_1,\ldots ,B_\beta \}\). Then the resolution rule is defined as

The refutational completeness of \(\mathrm{RPL}_0^\varPsi \) is not an issue as already \(\mathrm{RPL}_0\) is refutationally complete for \(\mathrm{PL}_0\) formulas [3, 14]. Note that this is not the case any more if parameters occur in formulas. Indeed, due to the usual theoretical limitations, the logic is not semi-decidable for schematic formulas [2]. \(\mathrm{RPL}_0^\varPsi \) is sound if the defining equations are considered.
Proposition 10
Let the sequent S be derivable in \(\mathrm{RPL}_0^\varPsi \) for \(\varPsi = (S',{\hat{P}},{{\mathcal {D}}})\). Then \({{\mathcal {D}}}\models S\).
Proof
The introduction and elimination rules for defined predicate symbols are sound with respect to \({{\mathcal {D}}}\); also the resolution rule (involving s-unification ) is sound with respect to \({{\mathcal {D}}}\). \(\square \)
Definition 23
An \(\mathrm{RPL}_0^\varPsi \) derivation \(\varrho \) is called a cut-derivation if the s-unifiers of all resolution rules are empty.
Remark 6
A cut-derivation is an \(\mathrm{RPL}_0^\varPsi \) derivation with only propositional rules. Such a derivation can be obtained by combining all unifiers to a global unifier.
In computing global unifiers we have to apply s-substitutions to proofs. However, not every s-substitution applied to a \(\mathrm{RPL}_0^\varPsi \) derivation results in a \(\mathrm{RPL}_0^\varPsi \) derivation again. Just assume that an s-unifier in a resolution is of the form \((X_1(s),X_2(s'))\); if \(\varTheta = \{(X_1(s),a),(X_2(s'),b)\}\) for different constant symbols a, b then \(X_1(s)\varTheta \) and \(X_2(s')\varTheta \) are no longer unifiable and the resolution is blocked.
Definition 24
Let \(\rho \) be a derivation in \(\mathrm{RPL}_0^\varPsi \) which does not contain the resolution rule; then for any s-substitution \(\varTheta \) \(\rho \varTheta \) is the derivation in which every sequent occurrence S is replaced by \(S\varTheta \). We say that \(\varTheta \) is admissible for \(\rho \). Now let \(\rho =\)

where \(\varTheta '\) is an s-unifier of \(\{A_1,\ldots ,A_\alpha ,B_1,\ldots ,B_\beta \}\). Let us assume that \(\varTheta \) is admissible for \(\rho _1\) and \(\rho _2\). We define that \(\varTheta \) is admissible for \(\rho \) if the set
is s-unifiable. If \(\varTheta ^*\) is an s-unifier of U then we can define \(\rho \varTheta \) as

Definition 25
Let \(\varrho \) be an \(\mathrm{RPL}_0^\varPsi \) derivation and \(\varTheta \) be an s-substitution which is admissible for \(\varrho \). \(\varTheta \) is called a global unifier for \(\varrho \) if \(\varrho \varTheta \) is a cut-derivation.
In order to compute global unifiers we need \(\mathrm{RPL}_0^\varPsi \) derivations in some kind of “normal form”. Below we define two necessary restrictions on derivations.
Definition 26
An \(\mathrm{RPL}_0^\varPsi \) derivation \(\varrho \) is called normal if all s-unifiers of resolution rules in \(\varrho \) are normal and restricted.
Remark 7
Note that, in case of s-unifiability, we can always find normal and restricted s-unifiers; thus the definition above does not really restrict the derivations, it only requires some renamings.
Definition 27
An \(\mathrm{RPL}_0^\varPsi \) derivation \(\varrho \) is called regular if for all subderivations \(\varrho '\) of \(\varrho \) of the form

we have \(V^G(\varrho '_1) \cap V^G(\varrho '_2) = \emptyset \).
Note that the condition \(V^G(\varrho '_1) \cap V^G(\varrho '_2) = \emptyset \) in Definition 27 guarantees that, for all parameter assignments \(\sigma \), \(\varrho '_1[\sigma ]\) and \(\varrho '_2[\sigma ]\) are variable-disjoint.
We write \(\varrho ' \le _{ss}\varrho \) if there exists an s-substitution \(\varTheta \) s.t. \(\varrho '\varTheta = \varrho \).
Proposition 11
Let \(\varrho \) be a normal \(\mathrm{RPL}_0^\varPsi \) derivation. Then there exists a \(\mathrm{RPL}_0^\varPsi \) derivation \(\varrho '\) s.t. \(\varrho ' \le _{ss}\varrho \) and \(\varrho '\) is normal and regular.
Proof
By renaming of variables in subproofs and in s-unifiers. \(\square \)
Proposition 12
Let \(\varrho \) be a normal and regular \(\mathrm{RPL}_0^\varPsi \) derivation. Then there exists a global s-unifier \(\varTheta \) for \(\varrho \) which is normal and \(V^G(\varTheta ) \subseteq V^G(\varrho )\).
Proof
By induction on the number of inferences in \(\varrho \).
Induction base: \(\varrho \) is an axiom. \(\emptyset \) is a global s-unifier which trivially fulfils the properties.
For the induction step we distinguish two cases.
-
The last rule in \(\varrho \) is unary. Then \(\varrho \) is of the form

By induction hypothesis there exists a global substitution \(\varTheta '\) which is a global unifier for \(\varrho '\) s.t. \(\varTheta '\) is normal and \(V^G(\varTheta ') \subseteq V^G(\varrho ')\). We define \(\varTheta = \varTheta '\). Then, trivially, \(\varTheta \) is normal and a global unifier of \(\varrho \). Moreover, by definition of the unary rules in \(\mathrm{RPL}_0^\varPsi \), we have \(V^G(\varrho ') = V^G(\varrho )\) and so \(V^G(\varTheta ) \subseteq V^G(\varrho )\).
-
\(\varrho \) is of the form

As \(\varrho \) is a normal \(\mathrm{RPL}_0^\varPsi \) derivation the unifier \(\varTheta \) is normal. By regularity of \(\varrho \) we have \(V^G(\varrho _1) \cap V^G(\varrho _2) = \emptyset \).
By induction hypothesis there exist global normal unifiers \(\varTheta _1,\varTheta _2\) for \(\varrho _1\) and \(\varrho _2\) s.t. \(V^G(\varTheta _1) \subseteq V^G(\varrho _1)\) and \(V^G(\varTheta _2) \subseteq V^G(\varrho _2)\). By \(V^G(\varrho _1) \cap V^G(\varrho _2) = \emptyset \) we also have \(V^G(\varTheta _1) \cap V^G(\varTheta _2) = \emptyset \).
We show now that \((\varTheta _1,\varTheta )\) and \((\varTheta _2,\varTheta )\) are composable. As \(\varTheta _1\) is normal we have for all \(\sigma \in {{\mathcal {S}}}\)
$$\begin{aligned} V^{\iota }(\{A_1,\ldots ,A_\alpha \}[\sigma ]) \cap \mathop { dom}(\varTheta _1[\sigma ]) = \emptyset . \end{aligned}$$Similarly we obtain
$$\begin{aligned} V^{\iota }(\{B_1,\ldots ,B_\beta \}[\sigma ]) \cap \mathop { dom}(\varTheta _2[\sigma ]) = \emptyset . \end{aligned}$$As \(\varTheta \) is normal and restricted we have for all \(\sigma \in {{\mathcal {S}}}\)
$$\begin{aligned} V^{\iota }(\varTheta [\sigma ]) \subseteq V^{\iota }(\sigma \{A_1,\ldots ,A_\alpha ,B_1,\ldots ,B_\beta \}\downarrow _o). \end{aligned}$$Therefore \((\varTheta _1,\varTheta )\) and \((\varTheta _2,\varTheta )\) are both composable. As \(\varTheta _1,\varTheta _2,\varTheta \) are normal so are \(\varTheta _1 \star \varTheta \) and \(\varTheta _2 \star \varTheta \). As \(\varTheta _1,\varTheta _2\) are essentially disjoint we can define
$$\begin{aligned} \varTheta (\varrho ) = \varTheta _1 \star \varTheta \cup \varTheta _2 \star \varTheta . \end{aligned}$$\(\varTheta (\varrho )\) is a normal s-substitution and \(V^G(\varTheta (\varrho )) \subseteq V^G(\varrho )\).
\(\varTheta (\varrho )\) is also a global unifier of \(\varrho \). Indeed, \(\varrho _1\varTheta (\varrho )=\)
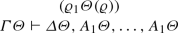
and \(\varrho _2\varTheta (\varrho )=\)

So we obtain the derivation

which is an instance of \(\varrho \) and a cut derivation (note that every instance of a cut derivation is a cut derivation as well).
-
\(\varrho \) is of the form

where \(\chi \) is a binary rule different from resolution.
As \(\varrho \) is a normal \(\mathrm{RPL}_0^\varPsi \) derivation all occurring s-unifiers in \(\varrho _1\) and \(\varrho _2\) are normal. By regularity of \(\varrho \) we have that \(V^G(\varrho _1) \cap V^G(\varrho _2) = \emptyset \).
By induction hypothesis there exist global normal unifiers \(\varTheta _1,\varTheta _2\) for \(\varrho _1\) and \(\varrho _2\) s.t. \(V^G(\varTheta _1) \subseteq V^G(\varrho _1)\) and \(V^G(\varTheta _2) \subseteq V^G(\varrho _2)\). By \(V^G(\varrho _1) \cap V^G(\varrho _2) = \emptyset \) we also have \(V^G(\varTheta _1) \cap V^G(\varTheta _2) = \emptyset \). Moreover, there is no overlap between the domain variables of the unifiers \(\varTheta _1\) and \(\varTheta _2\), i.e. \(\mathop { dom}(\varTheta _1[\sigma ]) \cap \mathop { dom}(\varTheta _2(\sigma )) = \emptyset \) for all \(\sigma \in {{\mathcal {S}}}\). Therefore, we can define \(\varTheta = \varTheta _1 \cup \varTheta _2\), which is obviously a global s-unifier of \(\varrho \). Furthermore, \(V^G(\varTheta ) = V^G(\varTheta _1) \cup V^G(\varTheta _2)\), therefore \(V^G(\varTheta ) \subseteq V^G(\varrho _1) \cup V^G(\varrho _2)\) and by definition of binary introduction rules in \(\mathrm{RPL}_0^\varPsi \), we have \(V^G(\varTheta ) \subseteq V^G(\varrho )\).\(\square \)
Example 14
We provide a simple \(\mathrm{RPL}_0^\varPsi \) refutation using the schematic formula constructed in Example 6. We will only cover the \(\mathrm{RPL}_0^\varPsi \) derivation of the base case and wait for the introduction of proof schemata to provide a full refutation. We abbreviate \(X_1,X_2,X_3\) by \({\mathbf {X}}\).



The labels \((\delta ^1_0,(0,0)),\ldots ,(\delta ^3_0,(0,0)\) can be ignored for the moment. They become important when the derivation above becomes part of a proof schema to be defined in Sect. 6.
\(\mathrm{RPL}_0^\varPsi \)-derivations can be evaluated under parameter assignments. Let \(\varphi \) be an \(\mathrm{RPL}_0^\varPsi \)-derivation and \(\sigma \) a parameter assignment, then \(\varphi \downarrow _\sigma \) denotes the \(\mathrm{RPL}_0\)-derivation defined by \(\varphi \) under \(\sigma \). Note that, if the parameters are all replaced by numerals then occurrences and introductions of defined symbols can be treated as instances of definition rules (see Section 7.3 [7]). Removal of defined symbols can be treated as definition rule elimination (a cosmetic change) and thus \(\varphi \downarrow _\sigma \) is indeed an \(\mathrm{RPL}_0\)-derivation.
5 Point Transition Systems
For our specification of schematic proofs we will use complex call structures beyond primitive recursion. To characterize such complex recursion types we develop an abstract framework.
Consider, e.g., the primitive recursive definitions of \(+\) and \(*\) (we write p for \(+\), t for \(*\) and s for successor):
In defining t we assume that p has been defined “before”, while p is defined via recursion and the successor s (which is a base symbol). In fact we can order the function symbols t and p by defining \(p<t\), where < is irreflexive and transitive. The relation < prevents that both \(p<t\) and \(t <p\) holds, as then we would get \(p<p\) contradicting irreflexivity. So primitive recursion, being based on orderings of function symbols, excludes the use of mutual recursion. However, mutual recursion is a very powerful specification principle which, even when equivalent primitive recursive specifications exist, may provide simpler and more elegant representations.
Example 15
We assume that \(+\) is already defined (e.g. as p above). We define three functions f, g, h, where f is defined via f and g and g via f and h making an ordering of the symbols f, g impossible.
f and g are not defined via primitive recursion and therefore it is not so simple to prove that f and g are indeed total and thus recursive. That the above type of mutual recursion is terminating is based on \((n+1,m+1)> (n+1,m), (n+1,m+1) > (n+1,m)\) and \((n+1,m) > (n,m)\) where > is the lexicographic tuple ordering. That the definition is also well defined (we obtain a value for all \((n,m) \in {\mathbb {N}}^2\)) follows from the following partitions of \({\mathbb {N}}^2\):
In this section we abstract from the computation of functions and even of values of any kind. Instead our aim is to focus on the underlying recursion itself. For Example 15 above we choose a symbol \(\delta _1\) for f, \(\delta _2\) for g, \(\delta _3\) for h and \(\delta _4,\ldots ,\delta _8\) as termination symbols. Then the recursion of the example can be represented by the following conditional reduction rules:
We call such a system a point transition system; the formal definitions are given below.
Definition 28
(Point) A point is an element of \({{\mathcal {P}}}^\alpha \) for \({{\mathcal {P}}}\subseteq T^\omega \) and some \(\alpha \ge 1\).
Definition 29
(Labeled point) Let \(\varDelta \) be an infinite set of symbols called labels. A labeled point is a pair \((\delta ,p)\) where p is a point and \(\delta \in \varDelta \).
Definition 30
(Condition) An atomic condition is either \(\top \), \(\bot \) or of the form \(s < t\), \(s>t\), \(s=t\), \(s \ne t\) for \(s,t \in T^\omega _0\). Let \(\mathrm{ATC}\) be the set of all atomic conditions. We define the set \(\mathrm{COND}\) of all conditions inductively:
-
\(\mathrm{ATC}\subseteq \mathrm{COND}\),
-
if \(C \in \mathrm{COND}\) then \(\lnot C \in \mathrm{COND}\),
-
if \(C_1,C_2 \in \mathrm{COND}\) then \(C_1 \wedge C_2 \in \mathrm{COND}\) and \(C_1 \vee C_2 \in \mathrm{COND}\).
Example 16
\(k=0\) and \(m < n\) are atomic conditions. \(k =0 \wedge m < n\) and \((k=0 \wedge m<n) \vee m=n\) are conditions.
Definition 31
(Semantics of conditions) For every \(C \in \mathrm{COND}\) and \(\sigma \in {{\mathcal {S}}}\) we define \(\sigma [C] \in \{\top ,\bot \}\):
-
\(\sigma [\top ] = \top ,\ \sigma [\bot ] = \bot \).
-
\(\sigma [s = t] = \top \) if \(s\downarrow _\sigma = t\downarrow _\sigma \), and \(\bot \) otherwise.
-
\(\sigma [s < t] = \top \) if \(s\downarrow _\sigma < t\downarrow _\sigma \), and \(\bot \) otherwise.
-
\(\sigma [s > t] = \top \) if \(s\downarrow _\sigma > t\downarrow _\sigma \), and \(\bot \) otherwise.
-
\(\sigma [s \ne t]= \top \) iff \(\sigma [s=t] = \bot \).
-
\(\sigma [C_1 \wedge C_2]=\top \) if \(\sigma [C_1] = \top \) and \(\sigma [C_2] = \top \), and \(\bot \) otherwise.
-
\(\sigma [C_1 \vee C_2]=\top \) if \(\sigma [C_1] = \top \) or \(\sigma [C_2] = \top \), and \(\bot \) otherwise.
A condition C is called valid if for all \(\sigma \in {{\mathcal {S}}}:\sigma [C] = \top \). C is called unsatisfiable if for all \(\sigma \in {{\mathcal {S}}}:\sigma [C] = \bot \).
Definition 32
(Point transition) A point transition is an expression of the form \((\delta ,p) \rightarrow {{\mathcal {P}}}:C\) where \((\delta ,p)\) is a labeled point and \({{\mathcal {P}}}\) is a nonempty finite set of labeled points and C is a condition. We define functions l, r, c on point transitions t as follows: if \(t = (\delta ,p) \rightarrow {{\mathcal {P}}}:C\) then \(l(t) = (\delta ,p),\ r(t) = {{\mathcal {P}}},\ c(t) = C\).
Definition 33
(Point transition cluster) A finite set of point transitions \({\mathbf {P}}\) is called a point transition cluster if for all \(\delta \in \varDelta \) and points p, q such that \((\delta ,p)\) and \((\delta ,q)\) occur in \({\mathbf {P}}\) (as l(t) or in r(t) for a \(t \in {\mathbf {P}}\)) there exists an \(\alpha \ge 1\) such that \(p,q \in {{\mathcal {P}}}^\alpha \). That means for all \(\delta \) occurring in \({\mathbf {P}}\) (for this set we write \(\varDelta ({\mathbf {P}})\)) the corresponding points are all of the same arity; this arity is denoted by \(A(\delta )\).
Example 17
Let
Then \({\mathbf {P}}_1\) is a point transition cluster. Here we have \(A(\delta )=2, A(\delta ')=3\). The following set \({\mathbf {P}}_2\) of point transitions for
is not a point transition cluster as \(A(\delta )\) cannot be defined consistently.
Point transition systems are restricted forms of point transition clusters where the labeled points and the conditions are subject to further restrictions.
Definition 34
(Partition) Let \({{\mathcal {C}}}= \{C_1,\ldots ,C_\alpha \}\) be a set of conditions. \({{\mathcal {C}}}\) is called a partition if \(C_1 \vee \cdots \vee C_\alpha \) is valid and for all \(i,j \in \{1,\ldots ,\alpha \}\) and \(i \ne j\) \(C_i \wedge C_j\) is unsatisfiable.
Definition 35
(Regular point transition) Let \({\mathbf {p}}:(\delta ,p) \rightarrow {{\mathcal {P}}}:C\) be a point transition in a point transition cluster and \(p \in {{\mathcal {P}}}^\alpha \). \({\mathbf {p}}\) is called regular if
-
\(p = (n_1,\ldots ,n_\alpha )\) for distinct parameters \(n_1,\ldots ,n_\alpha \),
-
for all \((\delta ',q) \in {{\mathcal {P}}}\) \(V(q) \subseteq \{n_1,\ldots ,n_\alpha \}\),
-
\(V(C) \subseteq \{n_1,\ldots ,n_\alpha \}\).
Definition 36
(Point transition system) Let \({\mathbf {P}}\) be a point transition cluster \(\delta _0 \in \varDelta ({\mathbf {P}})\). Then the tuple \({\mathbf {P}}^\star :(\delta _0,\varDelta ^*,\varDelta _e,{\mathbf {P}})\) is called a point transition system if the following conditions are fulfilled:
-
1.
\(\delta _0 \in \varDelta ^*\),
-
2.
\(\varDelta ^* = \varDelta ({\mathbf {P}})\)
-
3.
All point transitions in \({\mathbf {P}}\) are regular.
-
4.
Let \(t_1,t_2 \in {\mathbf {P}}\) with \(l(t_1) = (\delta ,p)\) and \(l(t_2) = (\delta ,q)\); then \(p=q\). That means every left-hand side of a point transition with \(\delta \) is related to a unique point p; we call p the source of \(\delta \).
-
5.
Let \({\mathbf {P}}(\delta )\) be the set \(\{(\delta ,p) \rightarrow {{\mathcal {P}}}_1:C_1, \ldots , (\delta ,p) \rightarrow {{\mathcal {P}}}_\alpha :C_\alpha \}\) consisting of all \(t \in {\mathbf {P}}\) with \(l(t) = (\delta ,p)\) (for the source p of \(\delta \)). Then, in case \({\mathbf {P}}(\delta ) \ne \emptyset \), \(\{C_1,\ldots ,C_\alpha \}\) is a partition.
-
6.
\({\mathbf {P}}(\delta _0) \ne \emptyset \).
-
7.
\({\mathbf {P}}(\delta ) = \emptyset \) for \(\delta \in \varDelta _e\).
The label \(\delta _0\) is called the start label of \({\mathbf {P}}^\star \), the \(\delta \) in \(\varDelta _e\) are called end labels.
Every point transition system defines a kind of computation for a given \(\sigma \in {{\mathcal {S}}}\).
Definition 37
(\(\sigma \)-trees) Let \({\mathbf {P}}^\star :(\delta _0,\varDelta ^*,\varDelta _e,{\mathbf {P}})\) be a point transition system, \(\sigma \in {{\mathcal {S}}}\) and \((\delta ,p)\) be a labeled point in \({{\mathcal {P}}}\). We define the \(\sigma \)-tree on a labeled point \((\delta ,p)\) inductively:
-
\(T({\mathbf {P}},(\delta ,p),\sigma ,0)\) is the tree consisting only of a root node labeled with
\((\delta ,\sigma (p)\downarrow )\).
-
Let us assume that \(T({\mathbf {P}},(\delta ,p),\sigma ,\alpha )\) is already defined. For every leaf \(\nu \) of \(T_\alpha \) labeled with \((\delta ',q)\) we check whether \({{\mathcal {P}}}(\delta ') = \emptyset \); if this is the case then \(\nu \) remains a leaf node.
If \({{\mathcal {P}}}(\delta ') \ne \emptyset \) then
$$\begin{aligned} {{\mathcal {P}}}(\delta ') = \{(\delta ',p') \rightarrow {{\mathcal {P}}}_1:C_1, \ldots , (\delta ',p') \rightarrow {{\mathcal {P}}}_\beta :C_\beta \} \end{aligned}$$Let us assume that \(q \in {{\mathcal {P}}}^\alpha \) and q is a tuple of numerals . Then, as \({{\mathcal {P}}}(\delta ')\) is a set of regular point transitions, \(p' = (n_1,\ldots ,n_\alpha )\) for distinct parameters \(n_1,\ldots ,n_\alpha \). As q is a tuple of numerals \((q_1,\ldots ,q_\alpha )\) \(q = \sigma '(p')\downarrow \) for a parameter assignment \(\sigma '\) where \(\sigma '(n_i) = q_i\) for \(i=1,\ldots , \alpha \). As all point transitions in \({{\mathcal {P}}}(\delta ')\) are regular we have \(V(C_i) \subseteq \{n_1,\ldots ,n_\alpha \}\) for \(i=1,\ldots ,\beta \). Now, \(\{C_1,\ldots ,C_\beta \}\) is a partition, thus there exists exactly one \(i \in \{1,\ldots ,\beta \}\) such that \(\sigma '[C_i] = \top \). Let \({{\mathcal {P}}}_i = \{(\delta ^i_1,q^i_1), \ldots , (\delta ^i_{r(i)},q^i_{r(i)})\}\). Then we create new nodes \(\mu _1,\ldots ,\mu _{r(i)}\) labeled with the labeled points
$$\begin{aligned}&(\delta ^i_1,\sigma '(q^i_1)\downarrow ), \ldots , (\delta ^i_{r(i)},\sigma '(q^i_{r(i)})\downarrow ) \text{ and } \text{ add } \text{ the } \text{ edges } \\&\quad (\nu ,\mu _1), \ldots , (\nu ,\mu _{r(i)}) \text{ to } T(\alpha ) \end{aligned}$$By the regularity of \({\mathbf {P}}^\star \) the points \(\sigma '(q^i_j)\downarrow \) are all tuples of numerals. We call the tree obtained from \(T({\mathbf {P}},(\delta ,p),\sigma ,\alpha )\) via the procedure above
\(T({\mathbf {P}},(\delta ,p),\sigma ,\alpha +1)\).
Let \(T({\mathbf {P}},(\delta ,p),\sigma ,\alpha ) = (V_\alpha ,E_\alpha )\) for all \(\alpha \in \mathrm{I\!N}\). Note that for all \(\alpha \) we have \(V_\alpha \subseteq V_{\alpha +1}\) and \(E_\alpha \subseteq E_{\alpha +1}\). So, when we define \(V_\infty = \bigcup _{\alpha \in \mathrm{I\!N}}V_\alpha \) and \(E_\infty = \bigcup _{\alpha \in \mathrm{I\!N}}E_\alpha \), then \((V_\infty ,E_\infty )\) is a tree; we call this tree the \(\sigma \)-tree on \((\delta ,p)\) and denote it by \(T({\mathbf {P}},(\delta ,p),\sigma )\). Note that the tree \(T({\mathbf {P}},(\delta ,p),\sigma )\) may be infinite. It is finite if there exists an \(\alpha \) such that \(T(\alpha ) = T(\alpha +1)\) The result of a computation of \({\mathbf {P}}^\star \) with respect to \(\sigma \) is defined by \(T_{{\mathbf {P}}^\star }[\sigma ] = T({\mathbf {P}},(\delta _0,p_0),\sigma )\).
We have seen that for every point transition system \({\mathbf {P}}^\star \) and \(\sigma \in {{\mathcal {S}}}\) \(T_{{\mathbf {P}}^\star }[\sigma ]\) is a tree with nodes labeled by labeled points describing the computation of \({\mathbf {P}}^\star \) on input \(\sigma \). However, \(T_{{\mathbf {P}}^\star }[\sigma ]\) may be infinite what means that the computation is nonterminating.
Example 18
Let \({\mathbf {P}}^\star = (\delta ,\{\delta ,\delta '\},\{\delta '\},{\mathbf {P}})\) for
\({\mathbf {P}}^\star \) is a point transformation system. The source of \(\delta \) is n and \(\{0<n, n=0\}\) is a partition. For \(\sigma \) with \(\sigma (n) = {\bar{0}}\) we obtain \(T_{{\mathbf {P}}^\star }[\sigma ] =\)

But for every \(\sigma \) with \(\sigma (n) = {\bar{\alpha }} > {\bar{0}}\) we obtain the infinite tree

Indeed, for every \(i \in \mathrm{I\!N}\), \(T(i+1) \ne T(i)\) for T(i) as defined in Definition 37. So the computation of \({\mathbf {P}}^\star \) on \(\sigma \) is nonterminating.
Definition 38
Let \({{\mathcal {P}}}^\star \) be a point transition system. \({{\mathcal {P}}}^\star \) is called terminating if \(T_{{{\mathcal {P}}}^\star }[\sigma ]\) is finite for all \(\sigma \in {{\mathcal {S}}}\).
To ensure termination of a point transition system we have to define a well-founded order on the set of labeled points. The ordering \(<_P\) defined below will be used in Sect. 6 for recursive definitions of proofs.
Definition 39
(\(<_P\)) We define an order on the set of all labeled points \((\delta ,p)\) where \(\delta \in \varDelta _0\) for a finite subset \(\varDelta _0\) of \(\varDelta \). We partition \(\varDelta _0\) in two disjoint subsets \(\varDelta _1,\varDelta _2\) where \(\varDelta _2\) will be reserved for mutual recursion and \(\varDelta _1\) stands for primitive recursive order types. We define an irreflexive, transitive relation \(<_{\varDelta _0}\) on \(\varDelta _0\) such that \(\delta <_{\varDelta _0}\delta '\) for all \(\delta \in \varDelta _1\) and \(\delta ' \in \varDelta _2\).
Let \(\alpha >0\) and \({{\mathcal {P}}}^\alpha _0\) be the subspace of the point space \({{\mathcal {P}}}^\alpha \) consisting of \(\alpha \)-tuples of numerals only. For \({{\mathcal {P}}}^\alpha _0\) we have a well-founded total order \(<_\alpha \). We extend \(<_\alpha \) to \({{\mathcal {P}}}^\alpha \) by defining
We are now extending the orderings to an order \(<_P\) of labeled points over \(\varDelta _0\). Let \((\delta ,p),(\delta ',q)\) two such points. We define \((\delta ,p) <_P(\delta ',q)\) if
-
(P1)
\(\delta ,\delta ' \in \varDelta _2\), \(A(\delta ) = A(\delta ')\) and \(p <_\alpha q\) for \(\alpha = A(\delta )\) or
-
(P2)
\(\delta ,\delta ' \in \varDelta _2\) and \(A(\delta ') < A(\delta )\) or
-
(P3)
\(\delta \in \varDelta _1\), \(\delta ' \in \varDelta _2\) or
-
(P4)
\(\delta ,\delta ' \in \varDelta _1\) and \(\delta <_{\varDelta _0}\delta '\) or
-
(P5)
\(\delta ,\delta ' \in \varDelta _1\), \(\delta = \delta '\) and \(p <_\alpha q\) for \(\alpha = A(\delta )\).
It is easy to see that the conditions (P1)–(P5) exclude each other. Note that (P3) implies \(\delta <_{\varDelta _0}\delta '\).
The relation \(<_P\) is stable under parameter assignments and is well founded.
Proposition 13
Let \((\delta ,p) <_P(\delta ',q)\) and \(\sigma \in {{\mathcal {S}}}\). Then \((\delta ,\sigma (p)\downarrow ) <_P(\delta ',\sigma (q)\downarrow )\).
Proof
For (P1), (P5) this follows directly from the definition of \(<_\alpha \) on \({{\mathcal {P}}}^\alpha \). (P2)–(P4) are invariant under parameter assignments. \(\square \)
Proposition 14
\(<_P\) is well-founded.
Proof
We show first that \(<_P\) is irreflexive and transitive. That \(<_P\) is irreflexive can be immediately read of from the conditions (P1)–(P5). It remains to show transitivity. To this aim we have to check all combinations of (P1)–(P5). Let us assume \((\delta ,p) <_P(\delta ',q)\) and \((\delta ',q) <_P(\delta '',r)\).
- (P1)–(P1)::
-
Here we have \(A(\delta )=A(\delta ')=A(\delta '')\) and \(p <_\alpha q\), \(q <_\alpha r\). By transitivity of \(<_\alpha \) we obtain \(p <_\alpha r\) and \((\delta ,p) <_P(\delta '',r)\) by (P1).
- (P1)–(P2)::
-
we have \(A(\delta ) = A(\delta ')\) and \(A(\delta '')<A(\delta ')\); so \(A(\delta '')<A(\delta )\) and \((\delta ,p) <_P(\delta '',r)\) by (P2).
(P1)–(P3), (P1)–(P4) and (P1)–(P5) are impossible as \(\varDelta _1 \cap \varDelta _2 = \emptyset \) and thus \(\delta ' \in \varDelta _1\) and \(\delta ' \in \varDelta _2\) is impossible.
- (P2)–(P1)::
-
\(A(\delta ')< A(\delta )\) and \(A(\delta '') = A(\delta ')\) gives \(A(\delta '')<A(\delta )\) and so \((\delta ,p) <_P(\delta '',r)\) by (P2).
- (P3)–(P1)::
-
Here we have \(\delta \in \varDelta _1\), \(\delta ',\delta '' \in \varDelta _2\). Therefore \((\delta ,p) <_P(\delta '',r)\) by (P3).
(P4)–(P1), (P5)–(P1) and (P2)–(P4), (P2)–(P5) are impossible.
- (P3)–(P2)::
-
\(\delta \in \varDelta _1\), \(\delta ',\delta '' \in \varDelta _2\) and so \((\delta ,p) <_P(\delta '',r)\) by (P3).
The combinations (P4)–(P2), (P5)–(P2), (P3)–(P3), (P3)–(P4) and (P3)–(P5) are all impossible.
- (P4)–(P3)::
-
we have \(\delta ,\delta ' \in \varDelta _1\) and \(\delta '' \in \varDelta _2\) and therefore \((\delta ,p) <_P(\delta '',r)\) by (P3).
- (P5)–(P3)::
-
the same as for (P4)–(P3).
- (P4)–(P4)::
-
\(<_{\varDelta _0}\) is transitive.
- (P4)–(P5)::
-
We have \(\delta <_{\varDelta _0}\delta '\) and \(\delta '' = \delta '\); so \((\delta ,p) <_P(\delta '',r)\) by (P4).
- (P5)–(P4)::
-
\(\delta = \delta '\) and \(\delta ' <_{\varDelta _0}\delta ''\); therefore \((\delta ,p) <_P(\delta '',r)\) by (P4).
- (P5)–(P5)::
-
Here \(\delta =\delta '=\delta ''\), \(p <_\alpha q\), \(q <_\alpha r\). By transitivity of \(<_\alpha \) we get \(p <_\alpha r\) and \((\delta ,p) <_P(\delta '',r)\) by (P5).
Now assume that \(<_P\) is not well-founded. Then there exists an infinite sequence \(\eta :(\delta _i,p_i)_{i \in \mathrm{I\!N}}\) such that \((\delta _{i+1},p_{i+1}) <_P(\delta _i,p_i)\) for all \(i \in \mathrm{I\!N}\). As \(\varDelta _0\) is finite there exists a \(\delta \in \varDelta _0\) appearing infinitely often in \(\eta \). That means there exists an infinite subsequence \(\eta ^*\) of \(\eta \) which is of the form
and \((\delta ,q_{i+1}) <_P^* (\delta ,q_i)\) for \(i \in \mathrm{I\!N}\) and the transitive closure \(<_P^*\) of \(<_P\). We have shown that \(<_P\) is transitive and therefore \(<_P= <_P^*\), hence \((\delta ,q_{i+1}) <_P(\delta ,q_i)\) for \(i \in \mathrm{I\!N}\).
It remains to distinguish two cases:
-
\(\delta \in \varDelta _1\): then, for all \(i \in \mathrm{I\!N}\), \((\delta ,q_{i+1}) <_P(\delta ,q_i)\) by (P5) and (for \(A(\delta ) = \alpha \)) \(q_{i+1} <_\alpha q_i\) for all \(i \in \mathrm{I\!N}\). But this is impossible because \(<_\alpha \) is well-founded.
-
\(\delta \in \varDelta _2\): analogous to \(\delta \in \varDelta _1\) with (P1) instead of (P5). Again we obtain a contradiction to the well-foundedness of \(<_\alpha \).
We have shown that \(\eta \) does not exist and \(<_P\) is well-founded. \(\square \)
Definition 40
(Canonic point transition system) Let \({\mathbf {P}}^\star :(\delta _0,\varDelta ^*,\varDelta _e,{\mathbf {P}})\) be a point transition system. \({\mathbf {P}}^\star \) is called canonic
Theorem 1
(Termination) Canonic point transition systems are terminating, i.e. if \({{\mathcal {P}}}^\star \) is a canonic point transition system and \(\sigma \in {{\mathcal {S}}}\) then \(T_{{{\mathcal {P}}}^\star }[\sigma ]\) is finite.
Proof
By contradiction. Assume that \({\mathbf {P}}^\star \) is a canonic point transition system and \(T_{{\mathbf {P}}^\star }[\sigma ]\) is infinite for some \(\sigma \in {{\mathcal {S}}}\). Then \(T_{{\mathbf {P}}^\star }[\sigma ]\) is an infinite tree with finite node degree. By König’s lemma \(T_{{\mathbf {P}}^\star }[\sigma ]\) has an infinite path \(\eta \) for
By definition of \(T_{{{\mathcal {P}}}^\star }[\sigma ]\), for each \((\delta _i,p_i),(\delta _{i+1},p_{i+1})\) in \(\eta \), there exists a point transition \((\delta _i,p) \rightarrow {{\mathcal {P}}}:C\) in \({{\mathcal {P}}}\) “matching” \((\delta _i,p_i)\). More precisely, there exists a parameter assignment \(\sigma '\) such that \(\sigma '(p)\downarrow = p_i\), \(\sigma '[C]=\top \) and \((\delta _{i+1},p_{i+1})\) is obtained via a \((\delta _{i+1},q) \in {{\mathcal {P}}}\) and \(p_{i+1} = \sigma '(q)\downarrow \). As \({{\mathcal {P}}}^*\) is canonic we have \((\delta _{i+1},q) <_P(\delta _i,p)\). By Proposition 13 we obtain \((\delta _{i+1},\sigma '(q)\downarrow ) <_P(\delta _i,\sigma '(p)\downarrow )\) what yields just \((\delta _{i+1},p_{i+1}) <_P(\delta _i,p_i)\) for all \(i \in \mathrm{I\!N}\). But by Proposition 14\(<_P\) is a well-ordering contradicting the existence of the infinite chain \(\eta \). Therefore there exists no infinite \(\sigma \)-chain in \({{\mathcal {P}}}^*\) and \(T_{{\mathbf {P}}^\star }[\sigma ]\) is finite. \(\square \)
Example 19
Let \({\mathbf {P}}^\star :(\delta _1,\varDelta ^*,\varDelta _e,{\mathbf {P}})\) be the point transition system corresponding to Example 15 for \(\varDelta ^* = \{\delta _1,\ldots ,\delta _8\}\) and \(\varDelta _e = \{\delta _4,\ldots ,\delta _8\}\). Here \({\mathbf {P}}\) consists of the following point transition rules:
It is easy to see that \({\mathbf {P}}^\star \) is canonic when we define \(\varDelta _1 = \{\delta _4,\ldots , \delta _8\}\) and \(\varDelta _2 =\{\delta _1,\delta _2,\delta _3\}\). Then, by definition of \(<_P\), we have \(\delta _i <_P\delta _j\) for \(i \in \{4,\ldots ,8\}, \ j \in \{1,2,3\}\). Therefore the transitions 2,3,4,6 and 8 are decreasing via (P3). Transition 1 is decreasing via (P1), transition 5 via (P1) and (P2); finally transition 7 is decreasing via (P1). Therefore \(T_{{\mathbf {P}}^\star }[\sigma ]\) is finite for all \(\sigma \in {{\mathcal {S}}}\) and, in particular, the function f in Example 15 is total and thus recursive. Also \(T({\mathbf {P}},(\delta _2,(n,m)),\sigma )\) is finite for all \(\sigma \in {{\mathcal {S}}}\), so the function g is recursive as well.
6 Schematic \(\mathrm{RPL}_0^\varPsi \) Derivations
Schematic \(\mathrm{RPL}_0^\varPsi \) derivations are extension of \(\mathrm{RPL}_0^\varPsi \) derivations where, besides the formulas to be refuted, new kinds of axioms (in the form of labeled sequents) are included. These labeled sequents serve the purpose to establish recursive call structures in the proof. For constructing schematic \(\mathrm{RPL}_0^\varPsi \) derivations we introduce a countably infinite set \(\varDelta \) of proof symbols which are used to label the individual proofs of a proof schema. A particular proof schema uses a finite set of proof symbols \(\varDelta ^*\subset \varDelta \). Like for point transition systems we assign an arity \(A(\delta )\) to every \(\delta \in \varDelta ^*\); \(A(\delta )\) is just the arity of the input parameters for the proof labeled by \(\delta \). Also, we need a concept of proof labels which serve the purpose to relate some leafs of the proof tree to recursive calls.
Definition 41
(Proof label) Let \(\delta \in \varDelta \) and \(\vartheta \) be a parameter substitution. Then the pair \((\delta ,\vartheta )\) is called a proof label.
We will need to locate specific occurrences of sequents in a proof \(\pi \); to this aim we define \(\varLambda _\pi \) as the set of all sequent occurrences in \(\pi \). By \(|\pi |_\lambda \) we denote the sequent occurring at position \(\lambda \) for \(\lambda \in \varLambda _\pi \). Furthermore, let \(\rho \) be a proof with the end-sequent \(|\pi |_\lambda \); then by \(\pi [\rho ]_\lambda \) we denote the proof which results from replacing in \(\pi \) the derivation at \(\lambda \) by \(\rho \).
Definition 42
(Labeled sequents and derivations) Let S be a sequent and \((\delta ,\vartheta )\) a proof label, them \((\delta ,\vartheta ):S\) is a labeled sequent. A labeled \(\mathrm{RPL}_0^\varPsi \) derivation is an \(\mathrm{RPL}_0^\varPsi \) derivation \(\pi \) where all leaves are labeled. We distinguish axiom labels and nonaxiom labels. By \(\mathrm{Axiom}(\pi )\) we denote the set of occurrences of leaves labeled by axiom labels, the set of the occurrences of leaves with nonaxiom labels is denoted by \(\mathrm{Naxiom}(\pi )\). The set of all occurrences of leaves in \(\pi \) is denoted by \(\mathrm{leaves}(\pi )\); so \(\mathrm{leaves}(\pi ) = \mathrm{Axiom}(\pi ) \cup \mathrm{Naxiom}(\pi )\) and \(\mathrm{Axiom}(\pi ) \cap \mathrm{Naxiom}(\pi ) = \emptyset \).
We will define proof schemata in the spirit of point transition systems. Before giving a formal definition the following example should serve the purpose to reveal the intuition behind the concept.
Example 20
We define a refutation schema for the theory
provided in Example 5. The defining equations for \({\hat{P}}\) and \({\hat{Q}}\) are:
For \({\hat{f}}\) we have \({\hat{f}}(X,0) = X(0),\ {\hat{f}}(X,m+1) = g(X(m+1),{\hat{f}}(X,m))\).
We create a proof symbol \(\delta _0\) which stands for the refutation of \({\hat{Q}}(X,Y,n,m)\). For this refutation we consider the partition \(n=0\) (base case) and \(n>0\) (step case). In order to refute \({\hat{Q}}(X,Y,n,m)\) for \(n >0\) we will need an auxiliary deduction which deduces \({\hat{Q}}(X,Y,0,m)\) from the axioms \({\hat{Q}}(X,Y,n,m)\). In defining this derivation, which we give the label \(\delta _1\), we will need additional parameters k, l which do not occur in the definition of \({\hat{Q}}\) but are needed to control the recursions. For every proof symbol we have a parameter tuple, it is (n, m) for \(\delta _0\) and (n, m, k, l) for \(\delta _1\). For \(\delta _0\) we define the proof schema via the reduction system \(\varPi (\delta _0,X,Y,n,m)\) and the specification of the end-sequent \(S(\delta _0,X,Y,n,m) =\ \vdash \). We define
which means that for \(n=0\) we select the proof \(\rho _0(\delta _0,X,Y,n,m)\) for \(n>0\) the proof \(\rho _1(\delta _0,X,n,m)\). By \(\rho _0(\delta _0,X,Y, n,m)\) we denote the following derivation:

where \(\sigma _1 = \{X(0) \leftarrow {\hat{f}}(Y(0),m), Y(1) \leftarrow {\hat{f}}(a,0)\}\).Obviously, \(\rho (\delta _0,X,Y,0,m)\) is a \(\mathrm{RPL}_0^\varPsi \) refutation of \({\hat{Q}}(X,Y,0,m)\). The label \((\delta '_1,\emptyset )\) means that \(\delta '_1\) is an axiom label for the case (0, m). By \(\rho _1(\delta _0,X,Y, n,m)\) we denote the following derivation:

In contrast to \(\rho _0(\delta _0,X,Y, n,m)\) \({\hat{Q}}(X,Y,0,m)\) is not an axiom in the proof but rather the end-sequent. The label \((\delta _1,(n,m,n,0))\) represents a call of the proof \(\rho (\delta _1,X,Y,m,n,k,l)\) where k is replaced by n and l by 0. For the proof symbol \(\delta _1\) we select the partition \(\{n=0,\ n>0 \wedge l<n,\ n>0 \wedge l \ge n\}\), define a reduction system \(\varPi (\delta _1,X,Y,m,n,k,l)\) and a sequent \(S(\delta _1,X,Y,n,m,k,l) = {\hat{Q}}(X,Y,l,m)\). We define \(\varPi (\delta _1,X,Y,n,m,k,l) =\)
where
\((\delta '_2,(n,m,k,l))\) and \((\delta '_3,(n,m,k,l))\) are axiom labels where the computation of the proof stops. The most involved proof is \(\rho _1(\delta _1,X,Y,m,n,k,l)\) which performs the real induction. It derives the end sequent \(\vdash {\hat{Q}}(X,Y,l,m)\) from the sequent \((\delta _1,(m,n,p(k),\) \(s(l))):{\hat{Q}}(X,Y,s(l),m)\). If \(l<n\) then (m, n, p(k), s(l)) represents a further call of \(\rho _1(\delta _1,X,Y,m,n,k,l)\). By this call the leaf \({\hat{Q}}(X,Y,s(l),m)\) is replaced by a derivation of \({\hat{Q}}(X,Y,s(l),m)\) with leaves \({\hat{Q}}(X,Y,ss(l),m)\) and so on. If the counter reaches \(l=n\) the computation stops and we have reached the axioms \({\hat{Q}}(X,Y,n,m)\). Note that, in the whole proof system, we start with \(l=0\) and \(k=n\) via the call from \(\delta _0\). That is, via the initiation given by the call from \(\delta _0\), we obtain a derivation of \(\vdash {\hat{Q}}(X,Y,0,m)\) from axioms \(\vdash {\hat{Q}}(X,Y,n,m)\). Putting \(\delta _0\) and \(\delta _1\) together where \(\delta _0\) is the main symbol we eventually obtain a refutation of \(\vdash {\hat{Q}}(X,Y,n,m)\).
By \(\rho _1(\delta _1,X,Y,m,n,k,l)\) we denote the following derivation:


where \(\sigma _2 = \{X(l) \leftarrow {\hat{f}}(Y(0),m), Y(1) \leftarrow {\hat{f}}(a,l)\}\).

Definition 43
(\(\mathrm{RPL}_0^\varPsi \) schema) Let \({{\mathcal {D}}}\) be the tuple \((\varPsi ,\delta _0,\varDelta ^*,\varDelta _a,\mathbf {X}, \varPi )\). \({{\mathcal {D}}}\) is called an \(\mathrm{RPL}_0^\varPsi \) schema if the following conditions are fulfilled:
-
\(\varPsi :(S,{\hat{P}},{{\mathcal {T}}})\) is a theory as in Definition 3.
-
\(\varDelta ^*\) be a finite subset of \(\varDelta \).
-
\(\delta _0 \in \varDelta ^*\), \(\delta _0\) is called the main symbol.
-
\(\varDelta _a \subseteq \varDelta ^*\), the axiom symbols.
-
\(\mathbf {X}\) is a tuple of global variables.
-
To every \(\delta \in \varDelta ^*\) we assign a parameter tuple \(\mathbf {n}_\delta \) of pairwise different parameters and a partition \({{\mathcal {C}}}_\delta = \{C^\delta _1,\ldots ,C^\delta _{k(\delta )}\}\) of \({{\mathcal {S}}}\) where the \(C^\delta _i\) contain only parameters in \(\mathbf {n}_\delta \).
-
\(\varPi \) is a set of pairs \( \left\{ (\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta ),S(\delta ,\mathbf {X},\mathbf {n}_\delta ))\ \vert \ \delta \in \varDelta ^* \right\} \) where \(S(\delta ,\mathbf {X},\mathbf {n}_\delta )\) is a sequent over the global variables \(\mathbf {X}\) and the parameters in \(\mathbf {n}_\delta \), and \(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta )\) is defined as follows:
$$\begin{aligned} \{(\delta ,\mathbf {X},\mathbf {n}_\delta ) \rightarrow \rho _1(\delta ,\mathbf {X},\mathbf {n}_\delta ):C^\delta _1,\ldots ,(\delta ,\mathbf {X},\mathbf {n}_\delta ) \rightarrow \rho _{k(\delta )}(\delta ,\mathbf {X},\mathbf {n}_\delta ):C^\delta _{k(\delta )}\} \end{aligned}$$Note the following, for each \(i \in \{1,\ldots ,k(\delta )\}\) \(\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta )\) is a labeled \(\mathrm{RPL}_0^\varPsi \) derivation of \(S(\delta ,\mathbf {X},\mathbf {n}_\delta )\) and for each leaf \(\lambda \in \mathrm{leaves}(\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta ))\) we have
-
\(|\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta )|_\lambda = (\delta ',\mathbf {n}_\delta ):\vdash \; {\hat{P}}(\mathbf {Z},\mathbf {r})\) for \(\lambda \in \mathrm{Axiom}(\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta ))\) where \({\hat{P}}(\mathbf {Z},\mathbf {r})\) is a variant of the main atom of \(\varPsi \), \(\delta ' \in \varDelta _a\), \(A(\delta ') = A(\delta )\) and \(\mathbf {Z}\) is a tuple of global variables which is a subtuple of \(\mathbf {X}\).
-
\(|\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta )|_\lambda = (\delta ',\mathbf {s}):S(\delta ',\mathbf {X},\mathbf {s})\) for \(\lambda \in \mathrm{Naxiom}(\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta ))\) where \(\delta ' \in \varDelta ^* {\setminus } \varDelta _a\), and \(\mathbf {s}\) is an \(A(\delta ')\) tuple of terms in \(T^\omega _1\) containing only parameters in \(\mathbf {n}_\delta \).
-
Furthermore,
-
\(\mathbf {n}_\delta = (\mathbf {r},\mathbf {m}_\delta )\), the first part being the parameter tuple \(\mathbf {r}\) for the main symbol of the theory \(\varPsi \). The arity of \(\mathbf {m}_\delta \) depends on \(\delta \).
-
\(\varPi (\delta _0,\mathbf {X},\mathbf {n}_{\delta _0}) \ne \emptyset \),
-
for all \(\delta \in \varDelta _a\) \(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta ) = \emptyset \),
\({{\mathcal {D}}}\) is called a refutation schema of \(\varPsi \) if \(S(\delta _0,\mathbf {X},\mathbf {n}_{\delta _0}) =\, \vdash \).
Remark 8
In defining \(\mathbf {n} = (\mathbf {r},\mathbf {m}_\delta )\) we distinguish the static parameters in \(\mathbf {r}\) (which are used in the recursive formula definition) and the dynamic parameters in \(\mathbf {m}_\delta \) which are used for carrying out the inductive steps. In Example 20\(\delta _0\) has no dynamic parameters, but \(\delta _1\) has the dynamic parameters k and l. In a recursive call only dynamic parameters are substituted. The tuple \(\mathbf {Z}\) of global variables is chosen in a way to guarantee essential disjointness of global variables in the resolution steps.
Given a parameter assignment \(\sigma \), every proof schema defines a sequence of proofs in the following way: either we arrive at an axiom and stop or we find a leaf in the proof of the form \((\delta ,\mathbf {p}):S(\delta ,\mathbf {X},\mathbf {p})\); in the latter case we identify the right condition \(C^\delta _i\) and the proof \(\rho _i(\delta ,\mathbf {X},\mathbf {p})\) and replace the leaf by the derivation \(\rho _i(\delta ,X,\mathbf {p})\). If this sequence converges we obtain an \(\mathrm{RPL}_0^\varPsi \) proof corresponding to \(\sigma \). The formal definition is given below.
Definition 44
(Semantics of proof schemata) Let \({{\mathcal {D}}}\) be a proof schema
Let \(\sigma \in {{\mathcal {S}}}\); we define define a sequence \({{\mathcal {D}}}(\sigma ,\alpha )_{\alpha \in \mathrm{I\!N}}\) and call it the proof sequence corresponding to \(\sigma \). Let
As \(\{ C^{\delta _0}_1, \ldots , C^{\delta _0}_{k(\delta _0)} \}\) is a partition there is exactly one \(i \in \{1,\ldots ,k(\delta _0)\}\) such that \(\sigma [C^{\delta _0}_i] = \top \). Let \(\sigma (\mathbf {n}_{\delta _0}) = \mathbf {k}\) where \(\mathbf {k} = (\mathbf {r}_0,\mathbf {s})\) for \(\sigma (\mathbf {r})\downarrow _\omega = \mathbf {r}_0\). Then we define
Note that \(\rho _i(\delta _0,\mathbf {X},\mathbf {k})\) is an \(\mathrm{RPL}_0^\varPsi \) derivation of \(S(\delta _0,X,\mathbf {k})\) and the leaves of \(\rho _i(\delta _0,\mathbf {X},\mathbf {k})\) are either axioms of the form \((\delta '_0,\mathbf {k}):{\hat{P}}(\mathbf {X},\mathbf {r}_0)\) for \(\delta '_0 \in \varDelta _a\), or they are of the form \((\delta ,\mathbf {l}):S(\delta ,\mathbf {X},\mathbf {l})\) where \(\delta \in \varDelta ^*{\setminus } \varDelta _a\) and \(\mathbf {l}\) is a ground term tuple obtained in replacing the original one by substituting parameters by numerals.
Assume that \({{\mathcal {D}}}(\sigma ,\alpha )\) is already defined. We distinguish two cases:
-
(a)
All leaves in \({{\mathcal {D}}}(\sigma ,\alpha )\) are of the form \((\delta ,\mathbf {p}):{\hat{P}}(\mathbf {Z},\mathbf {s})\) for \(\delta \in \varDelta _a\) where \({\hat{P}}\) is the main symbol of \(\varPsi \). Then we define \({{\mathcal {D}}}(\sigma ,\alpha +1) = {{\mathcal {D}}}(\sigma ,\alpha )\).
-
(b)
There are leaves of the form \((\delta ,\mathbf {k}):S(\delta ,\mathbf {X},\mathbf {k})\) for an \(A(\delta )\) ground term tuple \(\mathbf {k}\) and \(\delta \in \varDelta ^* {\setminus } \varDelta _a\). For each leaf of this form we consider
$$\begin{aligned} \varPi (\delta ,\mathbf {X},\mathbf {n}_{\delta })= & {} \{(\delta ,\mathbf {X},\mathbf {n}_{\delta }) \rightarrow \rho _1(\delta ,\mathbf {X},\mathbf {n}_{\delta }):C^{\delta }_1,\\&\ldots ,(\delta ,\mathbf {X},\mathbf {n}_{\delta }) \rightarrow \rho _{k(\delta )}(\delta ,\mathbf {X},\mathbf {n}_{\delta }):C^{\delta }_{k(\delta )}\}. \end{aligned}$$Let \(\sigma ' \in {{\mathcal {S}}}\) such that \(\sigma '(\mathbf {n}_\delta ) = \mathbf {k}\). As \(\{ C^{\delta }_1, \ldots , C^{\delta }_{k(\delta )} \}\) is a partition there is exactly one \(i \in \{1,\ldots ,k(\delta )\}\) such that \(\sigma '[C^{\delta }_i] = \top \). Now we have to select the production
$$\begin{aligned} (\delta ,\mathbf {X},\mathbf {n}_{\delta }) \rightarrow \rho _i(\delta ,\mathbf {X},\mathbf {n}_{\delta }) :C^{\delta }_i \end{aligned}$$from \(\varPi (\delta ,\mathbf {X},\mathbf {n}_{\delta })\). Finally we replace the leaf \((\delta ,\mathbf {k}):S(\delta ,\mathbf {X},\mathbf {k})\) by the \(\mathrm{RPL}_0^\varPsi \) derivation \(\rho _i(\delta ,\mathbf {X},\mathbf {k})\). We perform this transformation for all leaves with \(\delta \in \varDelta ^* {\setminus } \varDelta _a\) and obtain a new \(\mathrm{RPL}_0^\varPsi \) derivation which we call \({{\mathcal {D}}}(\sigma ,\alpha +1)\).
If the sequence converges, i.e. \({{\mathcal {D}}}(\sigma ,\alpha ) = {{\mathcal {D}}}(\sigma ,\alpha +1)\) for some \(\alpha \) we obtain an \(\mathrm{RPL}_0^\varPsi \) proof as a result. Of course it is desirable to obtain such a proof for all parameter assignments \(\sigma \).
Definition 45
Let \(\varphi = {{\mathcal {D}}}(\sigma ,\alpha )\) where \({{\mathcal {D}}}(\sigma ,\alpha ) = {{\mathcal {D}}}(\sigma ,\alpha +1)\). Then we say that \({{\mathcal {D}}}(\sigma ,\alpha )_{\alpha \in \mathrm{I\!N}}\) converges and converges to \(\varphi \). \({{\mathcal {D}}}\) is called convergent if, for all \(\sigma \in {{\mathcal {S}}}\), \({{\mathcal {D}}}(\sigma ,\alpha )_{\alpha \in \mathrm{I\!N}}\) converges.
If \({{\mathcal {D}}}(\sigma ,\alpha )_{\alpha \in \mathrm{I\!N}}\) converges then it converges to a proof \(\varphi \in \mathrm{RPL}_0^\varPsi \) which is parameter free. But \(\varphi \) can be further reduced to an \(\mathrm{RPL}_0\) derivation \(\varphi \downarrow \) via the method defined in Sect. 4. We can now extend the semantics to \(\mathrm{RPL}_0\)-proofs:
Definition 46
Let \({{\mathcal {D}}}\) be a proof schema which, for a \(\sigma \in {{\mathcal {S}}}\), converges to an \(\mathrm{RPL}_0^\varPsi \) derivation \(\varphi (\sigma )\). Then \(\varphi (\sigma )\downarrow \) is called the \(\mathrm{RPL}_0\) proof defined by \({{\mathcal {D}}}\) under \(\sigma \). If \({{\mathcal {D}}}\) converges for all \(\sigma \) then \(\{\varphi (\sigma )\downarrow \mid \sigma \in {{\mathcal {S}}}\}\) is called the \(\mathrm{RPL}_0\) proof set defined by \({{\mathcal {D}}}\).
Example 21
Let \({{\mathcal {D}}}\) be the proof schema from Example 20. We compute \({{\mathcal {D}}}(\sigma ,\alpha )\) for two different \(\sigma \in {{\mathcal {S}}}\). Let \(\sigma _0(n)={\bar{0}},\ \sigma _0(m) = {\bar{2}}\) and \(\sigma _0(k) = {\bar{1}}\) for all parameters \(k \not \in \{n,m\}\). We start with \({{\mathcal {D}}}(\sigma _0,0)\). As \(\sigma _0(n)={\bar{0}}\) we have to replace \((\delta _0,X,Y,(n,m))\) by the proof \(\rho _0(\delta _0,X,Y,({\bar{0}},{\bar{2}}))\). So we define \({{\mathcal {D}}}(\sigma _0,0)=\)

for \(\sigma '_1 = \{X(0) \leftarrow {\hat{f}}(Y(0),2), Y(1) \leftarrow {\hat{f}}(a,0)\}\). In \(\rho _0(\delta _0,X,Y,({\bar{0}},{\bar{2}}))\) all leaves are labeled by the axiom labels \(\delta '_1\) and there is no leaf to expand; thus \({{\mathcal {D}}}(\sigma _0,1) = {{\mathcal {D}}}(\sigma _0,0)\) and \({{\mathcal {D}}}(\sigma _0,\alpha )_{\alpha \in \mathrm{I\!N}}\) converges to \(\rho _0(\delta _0,X,Y,(0,2))\).
Now let \(\sigma _1(p) = \sigma _0(p)\) for \(p \ne n\) and \(\sigma _1(n)=1\). In this case the condition \(n>0\) holds and we have to choose the proof \(\rho _1(\delta _0,X,Y, 1,2)\). We obtain \({{\mathcal {D}}}(\sigma _1,0)=\)

Now both leaves in \(\rho _1(\delta _0,X,Y,1,2)\) represent a call to the proof labeled by \(\delta _1\). In \(\varPi (\delta _1,X,Y,n,m,k,l)\) we have to choose the proof \(\rho _1(\delta _1,X,Y,1,2,1,0)\) via \(\sigma '(n)=1,\ \sigma '(m)=2,\ \sigma '(k)=1,\ \sigma '(l)=0\) (the second condition applies). So we obtain \({{\mathcal {D}}}(\sigma _1,1)=\)

Now \(\rho _1(\delta _1,X,Y,(1,2,1,0))=\)


where \(\sigma _2 = \{X(0) \leftarrow {\hat{f}}(Y(0),2), Y(1) \leftarrow {\hat{f}}(a,0)\}\).

In \({{\mathcal {D}}}(\sigma ,1)\) we have the leaves \(\vdash (\delta _1,(1,2,0,1) ):{\hat{Q}}(X,Y,1,2)\). Again we have to call \(\delta _1\), this time via \(\sigma ''\) for \(\sigma ''(n)=1,\sigma ''(m)=2,\sigma ''(k)=0,\sigma ''(l)=1\). As now \(\sigma ''(l) = \sigma ''(n)\) we have to call \(\rho _2(\delta _1,X,Y,(1,2,0,1))\). But
where \(\delta '_3 \in \varDelta _a\). So we obtain \({{\mathcal {D}}}(\sigma _1,2)\) from \({{\mathcal {D}}}(\sigma _1,1)\) by replacing the leaves \(\vdash (\delta _1,(1,2,0,1) ):{\hat{Q}}(X,Y,1,2)\) by the axiom leaves \((\delta '_3,(1,2,0,1)):Q(X,Y,1,2)\). In \({{\mathcal {D}}}(\sigma _1,2)\) all leaves are axiom leaves and so \({{\mathcal {D}}}(\sigma _1,3) = {{\mathcal {D}}}(\sigma _1,2)\). Therefore also \({{\mathcal {D}}}(\sigma _1,\alpha )_{\alpha \in \mathrm{I\!N}}\) converges. It is easy to see that \({{\mathcal {D}}}\) itself is convergent. The means to prove this formally will be developed below.
The concept of proof schema \({{\mathcal {D}}}\) is defined in a way that the skeleton of \({{\mathcal {D}}}\) is, in fact, a point transition system: we just strip the schema of its logical part and obtain the remaining “call part” of the schema.
Definition 47
Let \({{\mathcal {D}}}:(\varPsi ,\delta _0,\varDelta ^*,\varDelta _a,\mathbf {X},\varPi )\) be a proof schema. Assume that for \(\delta \in \varDelta ^*\) we have
Let \(t:(\delta ,\mathbf {X},\mathbf {n}_\delta ) \rightarrow \rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta ):C^\delta _i\) be a production in \(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta )\). Let \(\varLambda (\delta ,i)\) the set of all leaves in the proof \(\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta )\) . For every \(\lambda \in \varLambda (\delta ,i)\) of the form \(\lambda :(\delta ',\mathbf {p}):F\) we define \({ pts}(\lambda ) = (\delta ',\mathbf {p})\).
Then we replace the production t in \(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta )\) by
and \(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta )\) by
Finally we define \({\mathbf {P}}(\delta ) = { pts}(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta ))\) for all \(\delta \in \varDelta ^*\) and set
Proposition 15
Let \({{\mathcal {D}}}:(\varPsi ,\delta _0,\varDelta ^*,\varDelta _a,\mathbf {X},\varPi )\) be a proof schema. Then \({ pts}({{\mathcal {D}}})\) is a point transition system.
Proof
Immediate by the Definitions 36, 43 and 47. \(\square \)
Example 22
Let \({{\mathcal {D}}}\) be the proof schema in Example 20. Then \({ pts}({{\mathcal {D}}})\) is the point transition system \((\delta _0,\varDelta ^*,\varDelta _a,{\mathbf {P}})\), where \(\varDelta ^* = \{\delta _0,\delta _1,\delta '_1,\delta '_2,\delta '_3\}\), \(\varDelta _a = \{ \delta '_1,\delta '_2,\delta '_3\}\) and \({\mathbf {P}}\) defined below:
Note that the righthandsides of the productions in \({ pts}({{\mathcal {D}}})\) are sets—not multisets. Therefore we count different leaves with the same labels just once. It is easy to see that \({ pts}({{\mathcal {D}}})\) is a canonic point transition system and thus terminating. We will prove below that this implies that \({{\mathcal {D}}}\) is convergent.
Lemma 1
Let \({{\mathcal {D}}}(\sigma ,\alpha )\) be as in Definition 44 and \(T({\mathbf {P}}^\star ,(\delta ,p),\sigma ,\alpha )\) as in Definition 37. Then, for any \(\alpha \in \mathrm{I\!N}\):
-
(a)
if \((\delta ,\mathbf {k}):S\) is a leaf node in \({{\mathcal {D}}}(\sigma ,\alpha )\) then \((\delta ,\mathbf {k})\) is a leaf node in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha +1)\);
-
(b)
if \((\delta ,\mathbf {k})\) is a leaf node in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha +1)\) then there exists a sequent S such that \((\delta ,\mathbf {k}):S\) is a leaf node in \({{\mathcal {D}}}(\sigma ,\alpha )\).
Proof
We prove (a) by induction on \(\alpha \). Let \(\alpha = 0\). Let us consider
and \(\sigma [C^{\delta _0}_i] = \top \). Then \({{\mathcal {D}}}(\sigma ,0)\) is defined as \(\rho _i(\delta _0,\mathbf {X},\sigma (\mathbf {n}_{\delta _0}))\). Now let \((\delta _j,\mathbf {p}_j):F_j\) be the leaves in in \(\rho _i(\delta _0,\mathbf {X},\mathbf {n}_{\delta _0})\) for \(j=1,\ldots ,\beta \); then \((\delta _j,\sigma (\mathbf {p}_j)):\sigma (F_j))\) are the leaves in \(\rho _i(\delta _0,\mathbf {X},\sigma (\mathbf {n}_{\delta _0}))\). By Definition 47\({ pts}(\varPi (\delta _0,\mathbf {X},\mathbf {n}_{\delta _0}))\) contains the production
Hence, by Definition 37\(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,1)\) has exactly the leaves \((\delta _j,\sigma (\mathbf {p}_j))\). This concludes the case \(\alpha = 0\).
Now assume that, for any leaf \((\delta ,\mathbf {k}):F\) in \({{\mathcal {D}}}(\sigma ,\alpha )\) there exists a leaf \((\delta ,\mathbf {k})\) in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha +1)\). If \(\delta \in \varDelta _a\) then, by definition, \((\delta ,\mathbf {k}):F\) is a leaf in \({{\mathcal {D}}}(\sigma ,\alpha +1)\) and \((\delta ,\mathbf {k})\) is a leaf in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha +2)\). Otherwise assume that \(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta ) \ne \emptyset \) and
Let \(\sigma ' \in {{\mathcal {S}}}\) such that \(\sigma '(\mathbf {n}_\delta ) = \mathbf {k}\) and \(\sigma '[C^{\delta }_i] = \top \). Now we have to select the production
from \(\varPi (\delta ,\mathbf {X},\mathbf {n}_{\delta })\). Again, assume that \((\delta _j,\mathbf {p}_j):F_j\) are the leaves in \(\rho _i(\delta ,\mathbf {X},\mathbf {n}_\delta )\) for \(j=1,\ldots ,\gamma \), and so \((\delta _j,\sigma '(\mathbf {p}_j)):\sigma '(F_j)\) are the leaves in in \(\rho _i(\delta ,\mathbf {X},\sigma '(\mathbf {n}_\delta ))\). By Definition 47\({ pts}(\varPi (\delta ,\mathbf {X},\mathbf {n}_\delta ))\) contains the production
By Definition 37 , \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha +2)\) contains (new) leaves of the form \((\delta _j,\sigma '(\mathbf {p}_j))\).
The proof of (b) is analogous to that of (a). \(\square \)
Theorem 2
Let \({{\mathcal {D}}}\) be a proof schema. \({{\mathcal {D}}}\) is convergent iff \({ pts}({{\mathcal {D}}})\) is terminating.
Proof
\({{\mathcal {D}}}\) is convergent \(\Rightarrow \):
For all \(\sigma \in {{\mathcal {S}}}\) there exists an \(\alpha \) such that \({{\mathcal {D}}}(\sigma ,\alpha ) = {{\mathcal {D}}}(\sigma ,\alpha +1)\). By definition of \({{\mathcal {D}}}\) this happens only if for all leaves \((\delta ,\mathbf {k}):S\) in \({{\mathcal {D}}}(\sigma ,\alpha )\) we have \(\delta \in \varDelta _a\). By Lemma 1 all leaves in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha +1)\) are of the form \((\delta ,\mathbf {k})\) for \(\delta \in \varDelta _a\). As \(\varDelta _a\) is the set of all end labels in \({ pts}({{\mathcal {D}}})\) we get
and, for all \(\sigma \), \({ pts}({{\mathcal {D}}})\) terminates on \(\sigma \); thus \({ pts}({{\mathcal {D}}})\) is terminating.
\({ pts}({{\mathcal {D}}})\) is terminating \(\Rightarrow \):
For all \(\sigma \in {{\mathcal {S}}}\) there exists an \(\alpha \) such that
For all \(\alpha > 0\) this implies that, for all leaves \((\delta ,\mathbf {k})\) in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha )\), \(\delta \in \varDelta _a\). Now let \((\delta ',\mathbf {p}):S\) be a leaf in \({{\mathcal {D}}}(\sigma ,\alpha -1)\); by Lemma 1\((\delta ',\mathbf {p})\) is a leaf in \(T({ pts}({{\mathcal {D}}}),(\delta _0,\mathbf {n}_{\delta _0}),\sigma ,\alpha )\) and, by assumption, \(\delta ' \in \varDelta _a\). Therefore, by definition of \({{\mathcal {D}}}(\sigma ,\alpha +1)\), we get \({{\mathcal {D}}}(\sigma ,\alpha +1) = {{\mathcal {D}}}(\sigma ,\alpha )\) and \({{\mathcal {D}}}\) converges on \(\sigma \). \(\square \)
We can now characterize the convergence of proof schemata via point transition systems:
Theorem 3
Let \({{\mathcal {D}}}\) be a proof schema. Then \({{\mathcal {D}}}\) is convergent if \({ pts}({{\mathcal {D}}})\) is canonic.
Proof
Immediate by the Theorems 1 and 2. \(\square \)
Now it is easily verified that the proof schema \({{\mathcal {D}}}\) from Example 20 is convergent. The point transition system \({ pts}({{\mathcal {D}}})\) shown in Example 22 is canonic: for the ordering \(<_P\) we use the lexicographic tuple ordering and we partition \(\varDelta ^*\) into \(\varDelta _1\), \(\varDelta _2\) by \(\varDelta _1 = \varDelta _a\), \(\varDelta _2 = \{\delta _0,\delta _1\}\).
Example 23
Below is the complete refutation schema for the schematic formula provided in Example 6. In addition to the construction provided in Example 6 we require an additional global variable Y with a two arguments. Let \(\mathcal {D} = (\varPsi ,\delta _0,\varDelta ^*,\) \(\varDelta _a,\mathbf {X}\cup \{Y\},\varPi )\) be an \(\mathrm{RPL}_0^\varPsi \) schema where \(\varPsi \) is the theory presented in Example 6, \(\varDelta ^* {=}\{\delta _0, \cdots , \delta _6,\delta _0^1,\delta _0^2,\delta _0^3,\delta _0^4,\delta _4',\delta _5'\}\), \(\varDelta _a = \{ \delta _0^1,\delta _0^2,\delta _0^3,\delta _0^4,\delta _4', \delta _5'\}\), and
where,
-
\(\varPi _0(\delta _0,\mathbf {X},Y,n,m) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _0,\mathbf {X},Y,n,m) \rightarrow \rho _1(\delta _0,\mathbf {X},Y,n,m):n>0 \wedge m>0\\ (\delta _0,\mathbf {X},Y,n,m) \rightarrow \rho _2(\delta _0,\mathbf {X},Y,n,m):n=0 \wedge m>0\\ (\delta _0,\mathbf {X},Y,n,m) \rightarrow \rho _3(\delta _0,\mathbf {X},Y,n,m):n>0 \wedge m=0\\ (\delta _0,\mathbf {X},Y,n,m) \rightarrow \rho _4(\delta _0,\mathbf {X},Y,n,m):n=0 \wedge m=0\\ \end{array}\right\} . \end{aligned}$$\(\rho _{4}(\delta _0,\mathbf {X},Y,n,m)\) is defined in Example 14.
The other proofs are as follows:
-
\(\bullet \) \(\rho _1(\delta _0,\mathbf {X},Y, n,m)\)

where \(\mu = \left\{ Y(n,0)\leftarrow a \right\} \).
-
\(\bullet \) \(\rho _2(\delta _0,\mathbf {X},Y, n,m)\)

where \(\mu = \left\{ Y(0,0)\leftarrow a \right\} \).
-
\(\bullet \) \(\rho _3(\delta _0,\mathbf {X},Y, n,m)\)
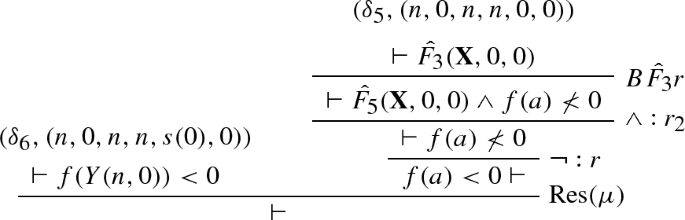
where \(\mu = \left\{ Y(n,0)\leftarrow a \right\} \).
-
-
\(\varPi _1(\delta _1,\mathbf {X},Y,n,m,w,k,r,q) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _1,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _1(\delta _1,\mathbf {X},Y,n,m,w,k,r,q):w>0\\ (\delta _1,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _2(\delta _1,\mathbf {X},Y,n,m,w,k,r,q):w=0 \\ \end{array}\right\} . \end{aligned}$$-
\(\bullet \) \(\rho _1(\delta _1,\mathbf {X},Y,n,m,w,k,r,q)\)
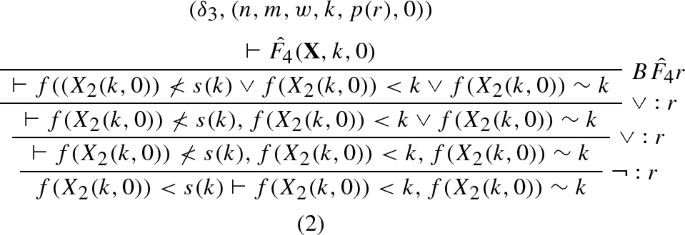
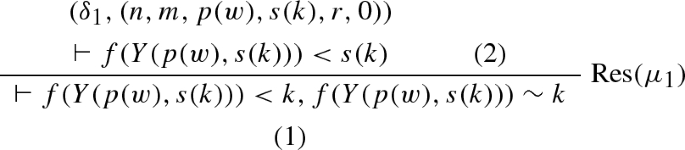
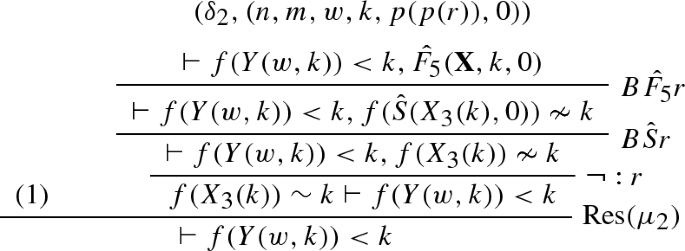
where \(\mu _1 = \left\{ \begin{array}{c} X_2(k,0)\leftarrow Y(p(w),s(k))\end{array}\right\} \) and
$$\begin{aligned} \mu _2 = \left\{ \begin{array}{c}Y(p(w),s(k))\leftarrow Y(w,k),\ X_3(k) \leftarrow Y(w,k)\end{array}\right\} \end{aligned}$$.
-
\(\bullet \) \(\rho _2(\delta _1,\mathbf {X},Y, n,m,w,k,r,q)\)

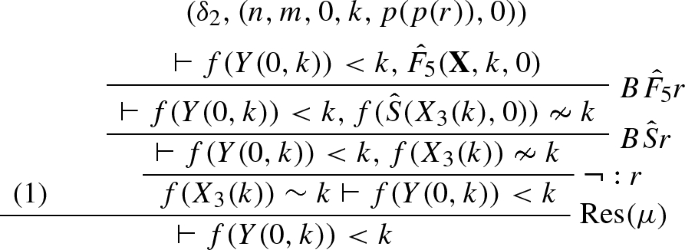
where \(\mu = \left\{ \begin{array}{c} X_1(k,0)\leftarrow Y(0,k)\ , \ X_3(k)\leftarrow Y(0,k) \end{array}\right\} \).
-
-
\(\varPi _2(\delta _2,\mathbf {X},Y,n,m,w,k,r,q) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _2,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _1(\delta _2,\mathbf {X},Y,n,m,w,k,r,q):r>0\\ (\delta _2,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _2(\delta _2,\mathbf {X},Y,n,m,w,k,r,q):r=0 \\ \end{array}\right\} . \end{aligned}$$-
\(\bullet \) \(\rho _1(\delta _2,\mathbf {X},Y, n,m,w,k,r,q)\)

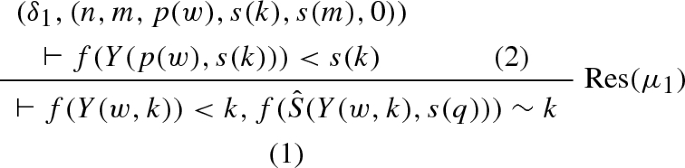
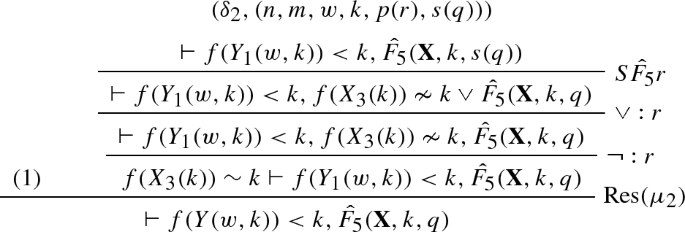
where
$$\begin{aligned} \mu _1 = \left\{ \begin{array}{c} X_2(k,s(q))\leftarrow Y(w,k),\ Y(p(w),s(k)) \leftarrow {\hat{S}}(Y(w,k),s(q)) \end{array}\right\} , \end{aligned}$$and
$$\begin{aligned} \mu _2 = \left\{ \begin{array}{c} Y_1(w,k)\leftarrow Y(w,k),\ X_3(k) \leftarrow {\hat{S}}(Y(w,k),s(q)) \end{array}\right\} . \end{aligned}$$ -
\(\bullet \) \(\rho _2(\delta _2,\mathbf {X},Y, n,m,w,k,r,q)\)


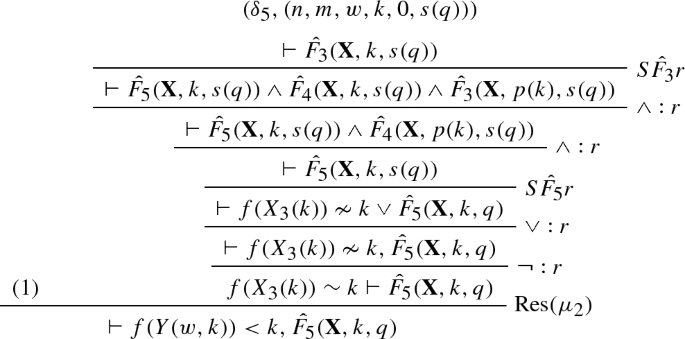
-
where
$$\begin{aligned} \mu _1 = \left\{ \begin{array}{c} X_2(k,s(q))\leftarrow Y(w,k),\ Y(p(w),s(k))\leftarrow {\hat{S}}(Y(w,k),s(q))\end{array}\right\} , \end{aligned}$$and
$$\begin{aligned} \mu _2 = \left\{ \begin{array}{c} X_3(k)\leftarrow {\hat{S}}(Y(w,k),s(q))\end{array}\right\} . \end{aligned}$$
-
-
\(\varPi _3(\delta _3,\mathbf {X},Y,n,m,w,k,r,q) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _3,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _1(\delta _3,\mathbf {X},Y,n,m,w,k,r,q):r>0\\ (\delta _3,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _2(\delta _3,\mathbf {X},Y,n,m,w,k,r,q):r=0 \\ \end{array}\right\} . \end{aligned}$$-
\(\bullet \) \(\rho _1(\delta _3,\mathbf {X},Y, n,m,w,k,r,q)\)
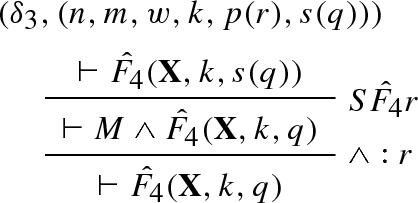
where M denotes
$$\begin{aligned}&(\lnot f({\hat{S}}(X_2(k,s(q)),s(q)))< s(k)\vee f(X_2(k,s(q))) < k \vee \\&\quad f({\hat{S}}(X_2(k,s(q)),s(q))) \sim k ). \end{aligned}$$ -
\(\bullet \) \(\rho _2(\delta _3,\mathbf {X},Y,n,m,w,k,r,q)\)
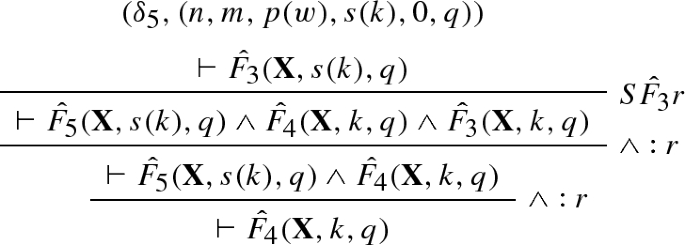
-
-
\(\varPi _4(\delta _4,\mathbf {X},Y,n,m,w,k,r,q) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _4,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _1(\delta _4,\mathbf {X},Y,n,m,w,k,r,q):r>0\\ (\delta _4,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _2(\delta _4,\mathbf {X},Y,n,m,w,k,r,q):r=0 \\ \end{array}\right\} . \end{aligned}$$-
\(\bullet \) \(\rho _1(\delta _4,\mathbf {X},Y, n,m,w,k,r,q)\)

-
\(\bullet \) \(\rho _2(\delta _4,\mathbf {X},Y,n,m,w,k,r,q)\)

-
-
\(\varPi _5(\delta _5,\mathbf {X},Y,n,m,w,k,r,q) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _5,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _1(\delta _5,\mathbf {X},Y,n,m,w,k,r,q):w>0\\ (\delta _5,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _2(\delta _5,\mathbf {X},Y,n,m,w,k,r,q):w=0 \\ \end{array}\right\} . \end{aligned}$$-
\(\bullet \) \(\rho _1(\delta _5,\mathbf {X},Y,n,m,w,k,r,q)\)

-
\(\bullet \) \(\rho _2(\delta _5,\mathbf {X},Y,n,m,w,k,r,q)\)

-
-
\(\varPi _6(\delta _6,\mathbf {X},Y,n,m,w,k,r,q) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _6,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _1(\delta _6,\mathbf {X},Y,n,m,w,k,r,q):w>0\\ (\delta _6,\mathbf {X},Y,n,m,w,k,r,q) \rightarrow \rho _2(\delta _6,\mathbf {X},Y,n,m,w,k,r,q):w=0 \\ \end{array}\right\} . \end{aligned}$$-
\(\bullet \) \(\rho _1(\delta _6,\mathbf {X},Y, n,m,w,k,r,q)\) denotes
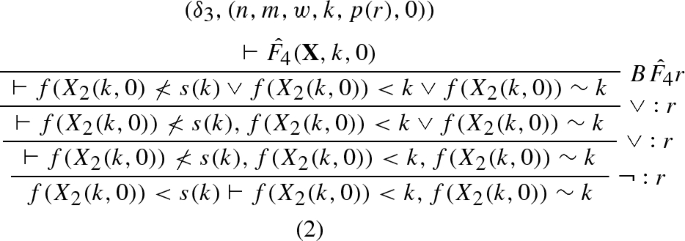

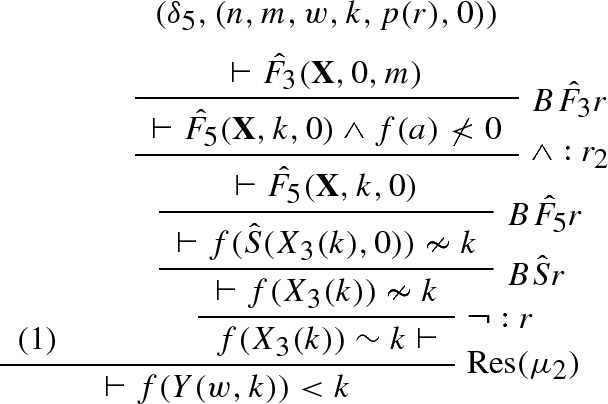
where
$$\begin{aligned} \mu _1 = \left\{ \begin{array}{c} X_2(k,0)\leftarrow Y(p(w),s(k))\end{array}\right\} , \end{aligned}$$and
$$\begin{aligned} \mu _2 = \left\{ \begin{array}{c} Y(p(w),s(k))\leftarrow Y(w,k)\ , \ X_3(k)\leftarrow Y(w,k)\end{array}\right\} . \end{aligned}$$ -
\(\bullet \) \(\rho _2(\delta _6,\mathbf {X},Y n,m,w,k,r,q)\)
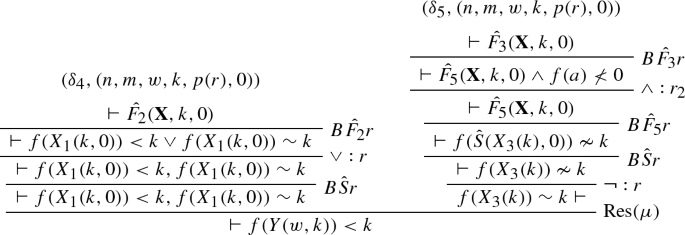
where \(\mu = \left\{ \begin{array}{c} X_1(k,0)\leftarrow Y(w,k)\ , \ X_3(k)\leftarrow Y(w,k) \end{array}\right\} \).
-
In Example 23 we constructed an \(\mathrm{RPL}_0^\varPsi \) refutation \(\mathcal {D}\). From this refutation we may extract a point transition system following the construction outlined in Definition 47.
Example 24
The point transition system for \(\mathcal {D}\), as defined in Example 23, is \({ pts}({{\mathcal {D}}}) = (\delta _0,\varDelta ^*,\varDelta _a,{\mathbf {P}}),\) for \({\mathbf {P}}=\bigcup P_{\delta _i}\) where the \(P_{\delta _i}\)’s are defined as follows:
-
\(P_{\delta _0} = { pts}(\varPi _0(\delta _0,\mathbf {X},Y,n,m)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _0,(n,m)) \rightarrow \left\{ \begin{array}{c} (\delta _1, (n,m,n,n,s(m),0))\\ (\delta _5, (n,m,n,n,0,m)) \end{array} \right\} :n>0 \wedge m>0\\ (\delta _0,(n,m)) \rightarrow \left\{ \begin{array}{c} (\delta _1,(0,m,0,0,s(m),0)) \\ (\delta _0^{4},(0,m))\end{array} \right\} :n=0 \wedge m>0\\ (\delta _0,(n,m)) \rightarrow \left\{ \begin{array}{c} (\delta _5,(n,0,n,n,0,0)),\\ (\delta _6,(n,0,n,n,s(0),0)) \end{array} \right\} :n>0 \wedge m=0\\ (\delta _0,(n,m)) \rightarrow \left\{ \begin{array}{c} (\delta _0^1,(0,0))\\ (\delta _0^2,(0,0))\\ (\delta _0^3,(0,0))\end{array} \right\} :n=0 \wedge m=0\\ \end{array}\right\} \end{aligned}$$ -
\(P_{\delta _1} = { pts}(\varPi _1(\delta _1,\mathbf {X},Y,n,m,w,k,r,q)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _1,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _1,( n,m,p(w),s(k),r,0)),\\ (\delta _2,(n,m,w,k,p(p(r)),0)),\\ (\delta _3,(n,m,w,k,p(r),0)) \end{array} \right\} :w>0\\ (\delta _1,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _4, (n,m,0,k,p(r),0)),\\ (\delta _2, (n,m,0,k,p(p(r)),0))\end{array} \right\} :w=0 \\ \end{array}\right\} \end{aligned}$$ -
\(P_{\delta _2} = { pts}(\varPi _2(\delta _2,\mathbf {X},Y,n,m,w,k,r,q)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _2,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _2, (n,m,w,k,p(r),s(q))),\\ (\delta _1, (n,m,p(w),s(k),s(m),0)),\\ (\delta _3, (n,m,w,k,p(r),s(q))) \end{array} \right\} :r>0\\ (\delta _2,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _1, n,m,p(w),s(k),s(m),0) ,\\ (\delta _3, n,m,w,k,0,s(q)), \\ (\delta _5, n,m,w,k,0,s(q))\end{array} \right\} :r=0 \\ \end{array}\right\} \end{aligned}$$ -
\(P_{\delta _3} = { pts}(\varPi _3(\delta _3,\mathbf {X},Y,n,m,w,k,r,q)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _3,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _3, n,m,w,k,p(r),s(q)) ,\\ \end{array} \right\} :r>0\\ (\delta _3,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _5, n,m,p(w),s(k),0,q) \end{array} \right\} :r=0 \\ \end{array}\right\} \end{aligned}$$ -
\(P_{\delta _4} = { pts}(\varPi _4(\delta _4,\mathbf {X},Y,n,m,w,k,r,q)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _4,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _4, n,m,w,k,p(r),s(q)) ,\\ \end{array} \right\} :r>0\\ (\delta _4,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _4', n,m,w,k,r,q) \end{array} \right\} :r=0 \\ \end{array}\right\} \end{aligned}$$ -
\(P_{\delta _5} = { pts}(\varPi _5(\delta _5,\mathbf {X},Y,n,m,w,k,r,q)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _5,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _5, n,m,p(w),s(k),r,q) ,\\ \end{array} \right\} :w>0\\ (\delta _5,(n,m,w,k,r,q)) \rightarrow \left\{ \begin{array}{c} (\delta _5', n,m,w,k,r,q) \end{array} \right\} :w=0 \\ \end{array}\right\} \end{aligned}$$ -
\(P_{\delta _6} = { pts}(\delta _6,\mathbf {X},Y,n,m,w,k,r,q)) = \)
$$\begin{aligned} \left\{ \begin{array}{c} (\delta _6, n,m,w,k,r,q) \rightarrow \left\{ \begin{array}{c} (\delta _1, n,m,p(w),s(k),r,0),\\ (\delta _5, n,m,w,k,p(r),0),\\ (\delta _3, n,m,w,k,p(r),0) \end{array} \right\} :w>0\\ (\delta _6, n,m,w,k,r,q) \rightarrow \left\{ \begin{array}{c} (\delta _4, n,m,0,k,p(r),0),\\ (\delta _5, n,m,0,k,p(r),0)\end{array} \right\} :w=0 \\ \end{array}\right\} \end{aligned}$$
By inspection one can see that \({ pts}({{\mathcal {D}}})\) is in fact a point transition system.
Theorem 4
Let \(\varPsi \) be the theory in Example 6. Then \({{\mathcal {D}}}\) in Example 23 is a convergent refutation schema of \(\varPsi \).
Proof
That \({{\mathcal {D}}}\) is a refutation schema of \(\varPsi \) is easy to see as \(S(\delta _0,X,Y,n,m) = \; \vdash \). It remains to show that \({{\mathcal {D}}}\) is convergent. By the Theorems 1 and 2 it is sufficient to prove that \({ pts}({{\mathcal {D}}})\) (see Example 24) is canonic. We have \(\varDelta ^* = \{\delta _0,\ldots ,\delta _6\} \cup \varDelta _a\) for \(\varDelta _a = \{\delta ^1_0,\ldots ,\delta ^1_4,\delta '_4,\delta '_5\}\). According to Definition 39 we have to partition \(\varDelta ^*\) into \(\varDelta _1,\varDelta _2\) for defining the order \(<_P\). We define \(\varDelta _2 = \{\delta _0,\ldots ,\delta _6\}\) and \(\varDelta _1 = \varDelta _a\). Then it is easy to check that \({ pts}({{\mathcal {D}}})\) is canonic. \(\square \)
7 Future Work and Applications
The initial intention of this research was to develop a schematic resolution calculus and thus allowing interactive proof analysis using CERES-like methods [5] in the presence of induction. More precisely, the resolution calculus introduced in this work will provide the basis for a schematic CERES method more expressive than the methods proposed in [11, 14]. As already indicated, the key to proof analysis using CERES lies in the fact that it provides a bridge between automated deduction and proof theory. In the schematic setting a bridge has been provided [11, 14], and the formalism presented here provides a setting to study automated theorem proving for schematic first-order logic.
Our recursive semantics (defined in Sect. 5) separates local resolution derivations from the global “shape” of the refutation, an essential characteristic of induction. While constructing a recursive resolution refutation for a recursive unsatisfiable formula schema is incomplete, it is not clear whether the problem remains incomplete when the point transition system is fixed. In other words, we may instead ask: “Is providing a recursive resolution refutation, with respect to a given point transition system, for recursive formulas complete?” The answer to this question is not so clear in that it depends on the resolution calculus itself as well as on the associated unification problem. Both concepts are developed in this paper.
Concerning the resolution calculus presented in Sect. 4, both the Andrew’s calculus-like sequent rules and the introduction of global variables provide the necessary extensions to resolution accommodating the recursive nature of our formulas. The unification problem discussed in Sect. 3 has not been addressed so far, and furthermore it may have interesting decidable fragments impacting schematic proof analysis as well as other fields.
Overall, the avenues we leave for future investigations provide ample opportunities for studying schematic theorem proving.
Notes
Herbrand sequents allow the representation of the propositional content of first-order proofs.
References
Andrews, P.B.: Resolution in type theory. J. Symb. Log. 36(3), 414–432 (1971)
Aravantinos, V., Caferra, R., Peltier, N.: Decidability and undecidability results for propositional schemata. J. Artif. Intell. Res. 40(1), 599–656 (2011)
Aravantinos, V., Mnacho, E., Nicolas, P.: A resolution calculus for first-order schemata. Fundam. Inform. 125, 101–133 (2013)
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Baaz, M., Hetzl, S., Leitsch, A., Richter, C., Spohr, H.: Ceres: an analysis of Fürstenberg’s proof of the infinity of primes. Theor. Comput. Sci. 403(2–3), 160–175 (2008)
Baaz, M., Leitsch, A.: Cut-elimination and redundancy-elimination by resolution. J. Symb. Comput. 29, 149–176 (2000)
Baaz, M., Leitsch, A.: Methods of Cut-elimination, vol. 34. Springer, Berlin (2011)
Brotherston, J.: Cyclic proofs for first-order logic with inductive definitions. In: TABLEAUX. Lecture Notes in Computer Science, vol. 3702, pp. 78–92. Springer, Berlin (2005)
Brotherston, J., Simpson, A.: Sequent calculi for induction and infinite descent. J. Logic Comput. 21(6), 1177–1216 (2010)
Cerna, D.M., Leitsch, A.: Schematic cut elimination and the ordered pigeonhole principle. In: Automated Reasoning—8th International Joint Conference, IJCAR 2016, Coimbra, Portugal, June 27–July 2, 2016, Proceedings, pp. 241–256 (2016). Peer Reviewed
Dunchev, C., Leitsch, A., Rukhaia, M., Weller, D.: Cut-elimination and proof schemata. In: TbiLLC. Lecture Notes in Computer Science, vol. 8984 , pp. 117–136. Springer (2013)
Hetzl, S., Leitsch, A., Weller, D., Paleo, B.W.: Herbrand sequent extraction. In: Intelligent Computer Mathematics, pp. 462–477. Springer (2008)
Kersani, A.: Preuves par induction dans le calcul de superposition. (Induction proof in superposition calculus). PhD thesis, Grenoble Alpes University, France (2014)
Leitsch, A., Peltier, N., Weller, D.: CERES for first-order schemata. J. Log. Comput. 27(7), 1897–1954 (2017)
Mcdowell, R.: Cut-elimination for a logic with definitions and induction. Theor. Comput. Sci. 232, 91–119 (1997)
Simpson, S.G.: Subsystems of Second Order Arithmetic. Perspectives in Mathematical Logic. Springer, Berlin (1999)
Takeuti, G.: Proof Theory. Studies in Logic and the Foundations of Mathematics, vol. 81. American Elsevier Pub., New York (1975)
Acknowledgements
This work was partially supported by the Linz Institute of Technology (LIT) \(\hbox {Math}_{{LP}}\) project (LIT- 2019-7-YOU-213) funded by the state of upper Austria.
Funding
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cerna, D.M., Leitsch, A. & Lolic, A. Schematic Refutations of Formula Schemata. J Autom Reasoning 65, 599–645 (2021). https://doi.org/10.1007/s10817-020-09583-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-020-09583-8