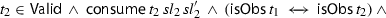CoCon: A Conference Management System with Formally Verified Document Confidentiality

Abstract

We present a case study in formally verified security for realistic systems: the information flow security verification of the functional kernel of a web application, the CoCon conference management system. We use the Isabelle theorem prover to specify and verify fine-grained confidentiality properties, as well as complementary safety and “traceback” properties. The challenges posed by this development in terms of expressiveness have led to bounded-deducibility security, a novel security model and verification method generally applicable to systems describable as input/output automata.

1 Introduction

Information flow security is concerned with preventing or facilitating (un)desired flow of information in computer systems, covering aspects such as confidentiality, integrity and availability of information. Dieter Gollmann wrote in 2005 [27]: “Currently, information flow and noninterference models are areas of research rather than the bases of a practical methodology for the design of secure systems.” The situation has undergone steady improvements in the past fourteen years. A number of practical systems, some of which are surveyed by Murray et al.  [58], have been formally certified for information flow security—covering hardware, operating systems, programming languages, web browsers and web applications.

This paper gives a detailed presentation of the verification work that went into one such system. CoCon is a full-fledged conference management system, handling multiple users and multiple conferences and offering a similar functionality (though fewer features and less customization) to that of popular systems such as EasyChair [76] and HotCRP [77].

CoCon’s high-level architecture (depicted in Fig. 1) follows the paradigm of security by design. It consists of a verified kernel and some trusted components. Namely:

• We formalize and verify the kernel of the system in the Isabelle proof assistant [60, 61].

• The formalization is automatically translated into a functional programming language.

• The translated program is wrapped in a web application.

Conference management systems are widely used in the scientific community. EasyChair alone claims more than two million users. Moreover, the information flow in these systems possesses enough complexity so that errors can sneak into their specifications or implementations. For example, Fig. 2 shows a confidentiality violation in a past version of HotCRP [77], probably stemming from the logic of the system: It gives the authors capabilities to read confidential comments by the program committee (PC).

Fig. 1

CoCon’s high-level architecture

Fig. 2

Confidentiality bug in HotCRP

The main focus of the verification work presented in this paper is guarding against confidentiality violations (although our methods would equally apply to integrity violations). We verify that CoCon’s kernel satisfies properties such as the following, where Dis addresses the problem in Fig. 2:

• Pap $_1$: A group of users learns nothing about a paper (i.e., about its title, author name list, abstract and content) unless one of them becomes an author of that paper or becomes a PC member at the paper’s conference and the conference has reached the bidding phase.

• Pap $_2$: A group of users learns nothing about a paper beyond the last submitted version unless one of them becomes an author of that paper.

• Rev: A group of users learns nothing about the content of a paper’s review beyond the last submitted version before the discussion phase and the later versions unless one of them is that review’s author.

• Dis: The authors learn nothing about the discussion of their paper.

In general, we will be concerned with properties restricting the information flow from the various sensitive documents maintained by the system (papers, reviews, comments, decisions) towards the users of the system. The restrictions refer to certain conditions (e.g., authorship, PC membership) as well as to upper bounds (e.g., at most the last submitted version) for information release. We consider groups of users rather than single users in order to ensure stronger properties, guaranteeing that information does not leak even if unauthorized users cooperate with each other, combining their partial knowledge.

Here is the structure of this paper. We start with a description of CoCon’s kernel, formalized in Isabelle as an executable input/output (I/O) automaton (Sect. 2).

Then we move on to describing the first main contribution of this paper: a general security model called bounded-deducibility (BD) security (Sect. 3). It is applicable to any I/O automaton and allows the precise formulation of triggers and (upper) bounds for the controlled release of information, also known as declassification. The framework is instantiated to provide a comprehensive coverage of CoCon’s confidentiality properties of interest, including the ones discussed in this introduction. To address information flow security concerns more thoroughly, we discover the additional need for a form of traceback properties (Sect. 3.6), which naturally complement BD Security by showing that the declassification triggers cannot be forged.

Our second main contribution is a verification infrastructure for BD Security, centered around an unwinding proof technique (Sect. 4), which we have applied to CoCon’s confidentiality properties. In the process of verifying confidentiality, we also needed to prove several safety properties (system invariants). The Isabelle scripts, covering both the abstract framework and the CoCon instances, are available from this paper’s website [36].

We used CoCon to manage the submission and reviewing process of two international conferences: TABLEAUX 2015 [19] and ITP 2016 [11]. In Sect. 5, we discuss CoCon’s implementation and holistic security concerns, and describe our experience with its deployment—including facing a critical bug in the (unverified) web application wrapper.

The current paper is an extended version of a conference paper presented at CAV 2014 [39]. In addition to the material in the conference paper, it includes:

• the detailed description of some of the verified confidentiality properties (in Sect. 3.4) and of the unwinding relations used in their verification (in Sect. 4.3)

• a presentation of CoCon’s traceback properties (in Sect. 3.6)

• the full definition of the abstract unwinding conditions (in Sect. 4.1) and their compositionality oriented theorems (in Sect. 4.2)

• a discussion of CoCon’s deployment to conferences (in Sect. 5)

Notation We write function application by juxtaposition, without placing the argument in parentheses, as in $f\,a$, unless required for disambiguation, e.g., $f\,(g\,a)$. Multiple-argument functions will be considered in curried form—e.g., we think of $f: A \rightarrow B \rightarrow C$ as a two-argument function, and $f\,a\,b$ denotes its application to a and b. We write “$\circ$” for function composition.

For the purpose of this paper, “set” and “type” will be synonymous. Particular types are the inductive datatypes (which are heavily used in proof assistants such as Isabelle/HOL): They consist of expressions freely generated by applying the indicated constructors.

Also, “list” and “sequence” will be synonymous. We write $[a_1,\ldots ,a_n]$ for the list consisting of the indicated elements; in particular, [] is the empty list and [a] is a singleton list. We write “$\cdot$” for list concatenation. Applied to a non-empty list $[a_1,\ldots ,a_n]$, the functions ${{\mathsf {head}}}$, ${{\mathsf {tail}}}$ and ${{\mathsf {last}}}$ return $a_1$, $[a_2,\ldots ,a_n]$ and $a_n$ respectively. Given the function f, $\mathsf {{map}}\,f\,[a_1,\ldots ,a_n]$ returns $[f\,a_1,\ldots ,f\,a_n]$. Given a predicate P, ${{\mathsf {filter}}}\,P\,[a_1,\ldots ,a_n]$ returns the sublist of all elements $a_i$ satisfying P. If A is a set, $\textsf {List}\,(A)$ denotes the set of lists with elements in A. As a general convention, if a, b denote elements in A, automatically $\textit{al},\textit{bl}$ will denote elements of $\textsf {List}\,(A)$. An exception will be the system traces—even though they are lists of transitions t, for them we will use the customized notation ${ tr }$.

2 System Specification

CoCon is inspired by EasyChair, which was created by Andrei Voronkov. It hosts multiple users and conferences, allowing the creation of new users and conferences at any time. It has a superuser, which we call voronkov as a tribute to EasyChair. The voronkov is the first user of the system, and his role is to approve new-conference requests.

2.1 CoCon’s Workflow

A conference goes through several phases.

No-Phase Any user can apply for a new conference, with the effect of registering it in the system as initially having “no phase.” After approval from the voronkov, the conference moves to the setup phase, with the applicant becoming a conference chair.

Setup A conference chair can add new chairs and new regular PC members. From here on, moving the conference to successor phases can be done by the chairs.

Submission Any user can list the conferences awaiting submissions (i.e., being in the submission phase). A user can submit a paper, upload new versions, or indicate other users as coauthors thereby granting them reading and editing rights.

Bidding Authors are no longer allowed to upload or register new papers, and PC members are allowed to view the submitted papers. PC members can place bids, indicating for each paper one of the following preferences: “want to review”, “would review”, “no preference”, “would not review”, and “conflict”. If the preference is “conflict”, the PC member cannot be assigned that paper, and will not see its discussion. “Conflict” is assigned automatically to papers authored by a PC member.

Reviewing Chairs can assign papers to PC members for reviewing either manually or by invoking an external program to establish fair assignment based on some parameters: preferences, number of papers per PC member, and number of reviewers per paper. The assigned reviewers can edit their reviews.

Discussion All PC members having no conflict with a paper can see its reviews and can add comments. The reviewers can still edit their reviews, but in a transparent manner—so that the overwritten versions are still visible to the non-conflict PC members. Also, chairs can edit the decision.

Notification The authors can read the reviews and the accept/reject decision, which no one can edit any longer.

Closing The conference becomes inactive. All users can still read the documents previously readable, but nothing is editable any longer.

2.2 CoCon’s I/O Automaton

The state stores the lists of registered conference IDs, user IDs and paper IDs; and, for each ID, the state stores actual conference, user or paper information. For user IDs, the state also stores (hashed) passwords. In the context of a conference, each user is assigned one or more of the roles described by the following Isabelle datatype:

$$\begin{aligned} \texttt {datatype}\,\, \, \textsf {Role}\,=\, {{\mathsf {Chair}}}\,\mid \, {{\mathsf {PC}}}\,\mid \, {{\mathsf {Aut}}}\,\textsf {PaperID}\,\mid \, {{\mathsf {Rev}}}\,\textsf {PaperID}\,\textsf {Nat}\end{aligned}$$

with the following meanings, assuming ${ pid }$ is a paper ID and n is a number:

• ${{\mathsf {Chair}}}$: The user is a chair of the conference

• ${{\mathsf {PC}}}$: The user is a member of the program committee

• ${{\mathsf {Aut}}}~{ pid }$: The user is an author of the paper with ID pid

• ${{\mathsf {Rev}}}~{ pid }~n$: The user is the n’th reviewer of the paper with ID ${ pid }$

In a state, each paper ID is assigned a paper having title, abstract, content, and, in due time, a list of reviews, a discussion text, and a decision. We keep different versions of the decision and of each review, as they may transparently change during the discussion phase. This means that a decision is a list of strings representing its different versions, ${{\mathsf {Dec}}}= \textsf {List}\,(\textsf {String})$. Similarly, a review is a list of review contents representing its different versions, $\textsf {Review}= \textsf {List}\,(\textsf {Review\_Content})$, where $\textsf {Review\_Content}$ consists of triples (expertise, text, score).

In addition, the state stores: for each conference, the list of (IDs of) papers submitted to that conference, the list of news updated by the chairs, and the current phase; for each user and paper, the preferences resulted from biddings; for each user and conference, a list of roles. We will mainly access the roles through discriminators. For example, ${{\mathsf {isPC}}}\,\sigma \,{ cid }\,{ uid }$ returns True just in case in state $\sigma$ the user ${ uid }$ is a PC member for conference ${ cid }$. Here is the formal structure of the state:

$$\begin{aligned} \begin{array}{l} \texttt {record}\,\,\textsf {State}\,=\, \\ \begin{array}{lll} {{\mathsf {confIDs}}}: \textsf {List}\,(\textsf {ConfID}) &{}&{}{{\mathsf {conf}}}: \textsf {ConfID}\rightarrow \textsf {Conf}\\ {{\mathsf {userIDs}}}: \textsf {List}\,(\textsf {UserID}) &{}&{}{{\mathsf {pass}}}: \textsf {UserID}\rightarrow \textsf {Pass}\\ {{\mathsf {user}}}: \textsf {UserID}\rightarrow \textsf {User}&{}&{}{{\mathsf {roles}}}: \textsf {ConfID}\rightarrow \textsf {UserID}\rightarrow \textsf {List}\,(\textsf {Role}) \\ {{\mathsf {paperIDs}}}: \textsf {ConfID}\rightarrow \textsf {List}\,(\textsf {PaperID}) &{}&{}{{\mathsf {paper}}}: \textsf {PaperID}\rightarrow \textsf {Paper}\\ {{\mathsf {pref}}}: \textsf {UserID}\rightarrow \textsf {PaperID}\rightarrow \textsf {Pref}&{}&{} {{\mathsf {voronkov}}}: \textsf {UserID}\\ {{\mathsf {news}}}: \textsf {ConfID}\rightarrow \textsf {List}\,(\textsf {String}) &{}&{} {{\mathsf {phase}}}: \textsf {ConfID}\rightarrow \textsf {Phase}\end{array} \end{array} \end{aligned}$$

The initial state of the system, ${{\mathsf {istate}}}\in \textsf {State}$, is the one with a single user, the voronkov, and no conferences.

Actions are parameterized by user IDs and passwords. There are 45 actions forming five categories: creation, update, nondestructive update, reading and listing.

The creation actions register new objects (users, conferences, chairs, PC members, papers, authors), assign reviewers (by registering new review objects), and declare conflicts. For example, ${{\mathsf {cPaper}}}\,{ cid }\,{ uid }\,{ pw }\,{ pid }\,{ title }\,{ abs }$ is an action by user ${ uid }$ with password ${ pw }$ attempting to register to conference ${ cid }$ a new paper ${ pid }$ with indicated title and abstract. Moreover, ${{\mathsf {cAuthor}}}\,{ cid }\,{ uid }\,{ pw }\,{ pid }\,{ uid }'$ expresses an attempt of user ${ uid }$ with password ${ pw }$ to create a new (co)author for the paper ${ pid }$ in the context of the conference ${ cid }$—namely, to set the user ${ uid }'$ as this new author.

The update actions modify the various documents of the system: user information and password, paper content, reviewing preference, review content, etc. For example, ${{\mathsf {uPaperC}}}\,{ cid }\,{ uid }\,{ pw }\,{ pid }\,{ pct }$ is an attempt by user ${ uid }$ with password ${ pw }$ to upload a new version of paper ${ pid }$ by modifying its content to ${ pct }$.

The nondestructive update actions are similar, but also record the history of a document’s versions. For example, if a reviewer decides to change their review during the discussion phase, then the previous version is still stored in the system and visible to the other PC members (although never to the authors). Other documents subject to nondestructive updates are the news, the discussion, and the accept–reject decision.

The reading actions access the content of the system’s documents: papers, reviews, comments, decisions, news. The listing actions produce lists of IDs satisfying various filters—e.g., all conferences awaiting paper submissions, all PC members of a conference, all the papers submitted by a given user, etc.

The different categories of actions are wrapped in a single datatype through specific constructors:

$$\begin{aligned} \begin{array}{l} \texttt {datatype}\,\, \textsf {Act}\,= {{\mathsf {Cact}}}\,\textsf {cAct}\mid {{\mathsf {Uact}}}\,\textsf {uAct}\mid {{\mathsf {UUact}}}\,\textsf {uuAct}\mid {{\mathsf {Ract}}}\,\textsf {rAct}\mid {{\mathsf {Lact}}}\,\textsf {lAct}\end{array} \end{aligned}$$

Note that the first three categories of actions are aimed at modifying the state, and the last two are aimed at observing the state through outputs. However, the modification actions also produce a simple output, since they may succeed or fail. Moreover, the observation actions can also be seen as changing the state to itself. Therefore we can assume that both types produce a pair consisting of a new state and an output.

Outputs include some generic output types, like ${{\mathsf {outOK}}}$ for a successful update action and ${{\mathsf {outErr}}}$ for a failed action. Moreover, outputs for various datatypes are defined, e.g., for Booleans, lists of strings, lists of pairs of strings, etc. Similarly to the case of actions, all these types of outputs are wrapped together in a single type $\textsf {Out}$.

Finally, we define the step function ${{\mathsf {step}}}: \textsf {State}\rightarrow \textsf {Act}\rightarrow \textsf {Out}\times \textsf {State}$ that operates by determining the type of the action and dispatching specialized handler functions. We illustrate the definition of ${{\mathsf {step}}}$ by zooming into one of its subcases:

Above, we only showed one subcase of the creation-action case in full. The semantics of each type of action (e.g., ${{\mathsf {cAuthor}}}$, which is itself a subtype of creation actions) has an associated test for enabledness (here, ${{\mathsf {e\_createAuthor}}}$) and an effect function (here, ${{\mathsf {createAuthor}}}$).

The enabledness test checks if it is allowed to perform the requested action: if the IDs of the involved users and conferences exist (expressed by a generic predicate ${{\mathsf {IDsOK}}}$), if the password matches the acting user’s ID, if the conference phase is appropriate, if the acting user holds the appropriate role, etc.

The effect is only applied if the action is enabled; otherwise an error output is issued. In this example, the effect is to add an author ${ uid }'$ to the existing paper ${ pid }$, as well as a conflict in the system database between the author and the paper:

To the outside world, i.e., to the web application wrapper, our specification only exports the initial state ${{\mathsf {istate}}}: \textsf {State}\rightarrow \textsf {bool}$ and the step function ${{\mathsf {step}}}: \textsf {State}\rightarrow \textsf {Act}\rightarrow \textsf {Out}\times \textsf {State}$, i.e., it exports an I/O automaton.

3 Security Model

As a starting point towards a framework where we can express CoCon’s desired security properties, we recall the classic notion of nondeducibility. Then we proceed with a generalization that replaces non with bounded deducibility.

3.1 Sutherland’s Nondeducibility Recalled

In its most abstract form, Sutherland’s early notion of nondeducibility [74] is parameterized by a set of worlds $\textsf {World}$ and two functions $F : \textsf {World}\rightarrow J$ and $H : \textsf {World}\rightarrow K$. For example, the worlds could be the valid traces of the system, F could select the actions of certain users (potential attackers), and H could select the actions of other users (intended as being secret). Nondeducibility of H from F says that the following holds for all $w_1 \in \textsf {World}$: For all $k_2$ in the image of H, there exists $w_2 \in \textsf {World}$ such that $F\,w_2 = F\,w_1$ and $H\,w_2 = k_2$. Intuitively, from what the attacker (modeled as F) knows about the actual world $w_1$, the secret actions (the value of H) could be anything (in the image of H)—hence cannot be “deduced.” The generality of this framework allows one to fine-tune both the location of the relevant events in the trace and their secrets.

But generality is no free lunch: Unlike in other less expressive settings (some of them recalled in Sect. 6), it is not clear how to provide an incremental proof method in the style of unwinding—a (bi)simulation-like [54, 72] method pioneered by Goguen and Meseguer in the context of proving noninterference [26], which has been applied widely and successfully in the world of information flow security [48].

3.2 Bounded-Deducibility Security

We introduce a notion of information flow security that:

• retains the precision and versatility of nondeducibility;

• factors in declassification as required by our motivating examples;

• is amenable to a general unwinding technique.

We will formulate security in general, not only for CoCon’s I/O automaton described in Sect. 2.2, but for any I/O automaton indicated by the following data, which will be considered fixed throughout this subsection: sets of states, $\textsf {State}$, actions, $\textsf {Act}$, and outputs, $\textsf {Out}$, an initial state ${{\mathsf {istate}}}\in \textsf {State}$, and a step function ${{\mathsf {step}}}: \textsf {State}\rightarrow \textsf {Act}\rightarrow \textsf {Out}\times \textsf {State}$.

We let $\textsf {Trans}$, the set of transitions, be $\textsf {State}\times \textsf {Act}\times \textsf {Out}\times \textsf {State}$. Thus, a transition is a tuple ${ t }= (\sigma ,a,{ o },\sigma ')$, where $\sigma$ indicates the source, a the action, ${ o }$ the output, and $\sigma '$ the target of ${ t }$. The transition ${ t }$ is called valid if it has been induced by the step function, namely ${{\mathsf {step}}}\,\sigma \,a = ({ o },\sigma ')$.

A trace ${ tr }\in \textsf {Trace}$ is any list of transitions: $\textsf {Trace}= \textsf {List}\, ({{\mathsf {Trans}}})$. For any $\sigma \in \textsf {State}$, the set of valid traces starting in $\sigma$, ${{\mathsf {Valid}}}_\sigma \subseteq \textsf {Trace}$, consists of the traces of the form $[{ t }_1,\ldots ,{ t }_n]$ for some n, where each ${ t }_i$ is a valid transition, the source of ${ t }_1$ is $\sigma$ and, for all $i \in \{2,\ldots ,n\}$, the source of ${ t }_i$ is the target of ${ t }_{i-1}$. We will be mostly interested in the valid traces starting in the initial state ${{\mathsf {istate}}}$—we simply call these valid traces and write ${{\mathsf {Valid}}}$ for ${{\mathsf {Valid}}}_{{\mathsf {istate}}}$.

For a system specified as an I/O automaton, we want to verify that there are no unintended flows of information to attackers who can observe and influence certain aspects of the system execution. To this end, we specify:

• 1. what the capabilities of the attacker are;

• 2. which information is (potentially) confidential;

• 3. which flows are allowed.

The first point is captured by a function ${{\mathsf {O}}}: \textsf {Trace}\rightarrow \textsf {List}\,(\textsf {Obs})$ taking a trace and returning the observable part of that trace—where $\textsf {Obs}$ is a chosen domain of observations. Similarly, the second point is captured by a function ${{\mathsf {S}}}: \textsf {Trace}\rightarrow \textsf {List}\,(\textsf {Sec})$ taking a trace and returning the sequence of secrets occurring in that trace—where $\textsf {Sec}$ is a chosen domain of secrets.

We think of the above as an instantiation of the abstract framework for nondeducibility recalled in Sect. 3.1, where $\textsf {World}= {{\mathsf {Valid}}}$, $F = {{\mathsf {O}}}$, and $H = {{\mathsf {S}}}$. Thus, nondeducibility states that the observer ${{\mathsf {O}}}$ may learn nothing about ${{\mathsf {S}}}$.

However, here we are concerned with a more fine-grained analysis, in terms of which flows are allowed (our third point). To this end, we ask what may the observer ${{\mathsf {O}}}$ learn about ${{\mathsf {S}}}$. Using the idea underlying nondeducibility (and, more broadly, the concept of knowledge), we can answer this question precisely: Given a trace ${ tr }_1 \in {{\mathsf {Valid}}}$, the observer sees ${{\mathsf {O}}}\,{ tr }_1$ and therefore can infer that ${{\mathsf {S}}}\,{ tr }_1$ belongs to the set of all sequences of secrets of the form ${{\mathsf {S}}}\,{ tr }_2$ for some ${ tr }_2 \in {{\mathsf {Valid}}}$ such that ${{\mathsf {O}}}\,{ tr }_2 = {{\mathsf {O}}}\,{ tr }_1$. In other words, the observer can infer that the sequence of secrets is in the set ${{\mathsf {S}}}\,({{\mathsf {O}}}^{-1}({{\mathsf {O}}}\,{ tr }_1)\,\cap \,{{\mathsf {Valid}}})$, and nothing beyond this (where ${{\mathsf {O}}}^{-1} : \textsf {Obs}\rightarrow \textsf {Set}\,(\textsf {Trace})$ is the usual nondeterministic inverse of ${{\mathsf {O}}}$, defined by ${{\mathsf {O}}}^{-1}\,{ tr }= \{{ ol }\mid {{\mathsf {O}}}\,{ ol }= { tr }\}$). We call this set the declassification associated to ${ tr }_1$, written ${{\mathsf {Dec}}}_{{ tr }_1}$.

We want to establish, under certain conditions, upper bounds for declassification, or, in terms of set-theoretic inclusion, lower bounds for ${{\mathsf {Dec}}}_{{ tr }_1}$. For this, we further consider two parameters:

• a relation ${{\mathsf {B}}}: \textsf {List}\,(\textsf {Sec}) \rightarrow \textsf {List}\,(\textsf {Sec}) \rightarrow \textsf {Bool}$, which we call declassification bound;

• a predicate ${{\mathsf {T}}}: {{\mathsf {Trans}}}\rightarrow \textsf {Bool}$, which we call declassification trigger.

Given some list of secrets ${ sl }_1$, ${{\mathsf {B}}}$ will delimit a set $\{{ sl }_2 \mid {{\mathsf {B}}}\,{ sl }_1\,{ sl }_2\}$ that represents a lower bound on the intended attacker uncertainty about ${ sl }_1$, i.e., an upper bound on the information about ${ sl }_1$ that the attacker should be allowed to learn, in the absence of the trigger ${{\mathsf {T}}}$ firing. This leads to the following definition: The system is said to be bounded-deducibility secure (BD Secure) if for all ${ tr }_1 \in {{\mathsf {Valid}}}$ such that ${{\mathsf {never}}}\,{{\mathsf {T}}}\,{ tr }_1$, it holds that $\{{ sl }_2 \mid {{\mathsf {B}}}\,({{\mathsf {S}}}\,{ tr }_1)\,{ sl }_2\} \subseteq {{\mathsf {Dec}}}_{{ tr }_1}$, where “${{\mathsf {never}}}\,{{\mathsf {T}}}\,{ tr }_1$” means “${{\mathsf {T}}}$ holds for no transition in ${ tr }_1$.”

Informally, BD Security can be summarized as follows:

• If trigger ${{\mathsf {T}}}$ never holds,¹then attacker ${{\mathsf {O}}}$ can learn nothing about secrets ${{\mathsf {S}}}$ beyond ${{\mathsf {B}}}$.

We can think of ${{\mathsf {B}}}$ positively, as an upper bound for declassification, or negatively, as a lower bound for uncertainty. On the other hand, ${{\mathsf {T}}}$ is a trigger removing the bound ${{\mathsf {B}}}$: As soon as ${{\mathsf {T}}}$ becomes true, the containment of declassification is no longer guaranteed. In the extreme case of ${{\mathsf {B}}}$ being everywhere true and ${{\mathsf {T}}}$ everywhere false, we have no declassification, i.e., total uncertainty—in other words, standard nondeducibility.

Expanding some of the above definitions, we can alternatively express BD Security as the following implication holding for all ${ tr }_1 \in {{\mathsf {Valid}}}$ and ${ sl }_1,{ sl }_2 \in \textsf {List}\,(\textsf {Sec})$:

$$\begin{aligned} \begin{array}{l} {{\mathsf {never}}}\,{{\mathsf {T}}}\,{ tr }_1 \,\wedge \, {{\mathsf {S}}}\,{ tr }_1 = { sl }_1 \,\wedge \, {{\mathsf {B}}}\,{ sl }_1\,{ sl }_2 \,\rightarrow \, (\exists { tr }_2 \in {{\mathsf {Valid}}}.\,{{\mathsf {O}}}\,{ tr }_2 = {{\mathsf {O}}}\,{ tr }_1 \,\wedge \, {{\mathsf {S}}}\,{ tr }_2 = { sl }_2) \end{array} \,\,\,\,\,\,(*) \end{aligned}$$

Fig. 3

BD Security illustrated. (The figure uses colors.) Here the red trace $[t_1,t_1',t_1'']$ has been formed, with each of $t_1,t_1',t_1''$ satisfying $\lnot {{\mathsf {T}}}$, producing secrets $[s_1,s_1',s_1'']$ and observations $[o_1,o_1'']$. Say the secrets $[s_1,s_1',s_1'']$ are related under ${{\mathsf {B}}}$ to other secrets $[s_2,s_2'']$, shown in green. BD Security requires the existence of a second trace that produces these alternative secrets $[s_2,s_2'']$ and the same observations, namely $[o_1,o_1'']$. In the figure this alternative trace is $[t_2,t_2',t_2'']$, shown in green

In the rest of the paper we will refer to this last formulation of the definition. In this context, we will call ${ tr }_1$ “the original trace” (since, in our scenario, ${ tr }_1$ actually occurred when running the system) and ${ tr }_2$ “the alternative trace” (since, for what the observer knows, ${ tr }_2$ could have alternatively occurred). We will also apply the qualifiers “original” and “alternative” to ${ tr }_1$’s and ${ tr }_2$’s produced sequences of observations and secrets. Note that BD Security is a $\forall \exists$-property—quantified universally over the original trace ${ tr }_1$ and the alternative secrets ${ sl }_2$, and then existentially over the alternative trace ${ tr }_2$. (The additional universal quantification over the original secrets ${ sl }_1$ is done only for clarity; it could have been avoided, since ${ sl }_1$ is determined by ${ tr }_1$.) This $\forall \exists$ structure will be essential for the (game-like) unwinding proof method we devise in Sect. 4.1.

Regarding the parameters ${{\mathsf {O}}}$ and ${{\mathsf {S}}}$, we assume that they are defined componentwise, in terms of functions on individual transitions:

• ${{\mathsf {isObs}}}: {{\mathsf {Trans}}}\rightarrow \textsf {Bool}$, filtering the transitions that produce observations;

• ${{\mathsf {getObs}}}: {{\mathsf {Trans}}}\rightarrow \textsf {Obs}$, producing an observation out of a transition;

• ${{\mathsf {isSec}}}: {{\mathsf {Trans}}}\rightarrow \textsf {Bool}$, filtering the transitions that produce secrets;

• ${{\mathsf {getSec}}}: {{\mathsf {Trans}}}\rightarrow \textsf {Sec}$, producing a secret out of a transition.

We define ${{\mathsf {O}}}= \mathsf {{map}}\,{{\mathsf {getObs}}}\,\circ \,\textsf {filter}\,{{\mathsf {isObs}}}$ and ${{\mathsf {S}}}= \mathsf {{map}}\,{{\mathsf {getSec}}}\,\circ \,\textsf {filter}\,{{\mathsf {isSec}}}$. Thus, ${{\mathsf {O}}}$ uses ${{\mathsf {filter}}}$ to select the transitions in a trace that are (partially) observable according to ${{\mathsf {isObs}}}$, and then applies ${{\mathsf {getObs}}}$ to each selected transition. Similarly, ${{\mathsf {S}}}$ produces sequences of secrets by filtering with ${{\mathsf {isSec}}}$ and applying ${{\mathsf {getSec}}}$.

Figure 3 contains a visual illustration of BD Security’s two-dimensional nature: The system traces (displayed on the top left corner) produce observations (on the bottom left), as well as secrets (on the top right). The figure also includes an abstract example of traces and their observation and secret projections. The original trace ${ tr }_1$ consists of three transitions, ${ tr }_1 = [t_1,t_1',t_1'']$, of which all produce secrets, $[ s _1, s _1', s _1'']$, and only the first and the third produce observations, $[ o _1, o _1'']$—all these are depicted in red. The alternative trace ${ tr }_2$ also consists of three transitions, ${ tr }_2 = [t_2,t_2',t_2'']$, of which the first and the third produce secrets, $[ s _2, s _2'']$, and the first two produce observations, $[ o _2, o _2']$—all these are depicted in green.² Thus, the figure’s functions ${{\mathsf {O}}}$ and ${{\mathsf {S}}}$ are given by filters and producers behaving as follows:

$$\begin{aligned} \begin{array}{c|c|c|c|c} &{} {{\mathsf {isObs}}}&{} {{\mathsf {getObs}}}&{} {{\mathsf {isSec}}}&{} {{\mathsf {getSec}}}\\ \hline t_1 &{} \mathsf {{True}}&{} o_1 &{} \mathsf {{True}}&{} s_1\\ t_1' &{} \mathsf {{False}}&{} &{} \mathsf {{True}}&{} s_1'\\ t_1'' &{} \mathsf {{True}}&{} o_1'' &{} \mathsf {{True}}&{} s_1''\\ t_2 &{} \mathsf {{True}}&{} o_2 &{} \mathsf {{True}}&{} s_2\\ t_2' &{} \mathsf {{True}}&{} o_2' &{} \mathsf {{False}}&{}\\ t_2'' &{} \mathsf {{False}}&{} &{} \mathsf {{True}}&{} s_2''\\ \end{array} \end{aligned}$$

The empty slots in the table correspond to values of ${{\mathsf {getObs}}}$ and ${{\mathsf {getSec}}}$ that are irrelevant, since the corresponding values of ${{\mathsf {isObs}}}$ and ${{\mathsf {isSec}}}$ are $\mathsf {{False}}$. Here is how to read BD Security’s $\forall \exists$ structure on the figure: Given the original trace, here $[t_1,t_1',t_1'']$ (which produces the shown observations and secrets and has all its transitions satisfying $\lnot \,{{\mathsf {T}}}$) and given some alternative secrets, here $[s_2,s_2'']$, located within the bound ${{\mathsf {B}}}$ of the original secrets, BD Security requires the existence of the alternative trace, here $[t_2,t_2',t_2'']$, producing the same observations and producing the alternative secrets.

In summary, BD Security is parameterized by the following data:

• an I/O automaton $(\textsf {State},\textsf {Act},\textsf {Out},{{\mathsf {istate}}},{{\mathsf {step}}})$

• a security model, consisting of:

  • an observation infrastructure $(\textsf {Obs},{{\mathsf {isObs}}},{{\mathsf {getObs}}})$

  • a secrecy infrastructure $(\textsf {Sec},{{\mathsf {isSec}}},{{\mathsf {getSec}}})$

  • a declassification bound ${{\mathsf {B}}}$

  • a declassification trigger ${{\mathsf {T}}}$

3.3 Discussion

BD Security is a natural extension of nondeducibility. If one considers the latter as reasonably expressing the absence of information leak, then one is likely to accept the former as a reasonable means to indicate bounds on the leak. Unlike most notions in the literature, BD Security allows to express the bounds as precisely as desired.

As an extension of nondeducibility, BD Security is subject to the same criticism. The problem with nondeducibility [50, 52, 68] is that in some cases it is too weak, since it takes as plausible each possible explanation for an observation: If the observation sequence is, say, ${ ol }$, then any trace ${ tr }_1$ such that ${{\mathsf {O}}}\,{ tr }_1 = { ol }$ is plausible. But what if the low-level observers can synchronize their actions and observations with the actions of other entities, such as a high-level user or a Trojan horse acting on the user’s behalf, or even a third-party entity that is neither high nor low? Even without synchronization, the low-level observers may learn, from outside the system, of certain behavior patterns of the high-level users. Then the set of plausible explanations can be reduced, leading to information leaks.

In our case, the low-level observers are a group of users assumed to never acquire a certain status (e.g., authorship of a paper). The other users of the system are either “high-level” (e.g., the authors of the paper) or “third-party” (e.g., the non-author users not in the group of observers). Concerning the high-level users, it does not make sense to assume that they would cooperate to leak information through the system, since they certainly have better means to do that outside the system, e.g., via email. As for the possible third-party cooperation towards leaks of information, this is bypassed by our consideration of arbitrary groups of observers: In the worst case, all the unauthorized users can be placed in this group. However, the possibility to learn and exploit behavior patterns from outside the system is not explicitly addressed by BD Security—it would be best handled by a probabilistic analysis.

3.4 Instantiation to Our Running Examples

Recall that BD Security applies to I/O automata—in particular, to CoCon’s I/O automaton described in Sect. 2.2. As we are about to show, BD Security captures our running examples, as well as other information flow properties for CoCon, by suitably instantiating the parameters comprising the security model: secrecy infrastructure, observation infrastructure, declassification bound, and declassification trigger.

Common Observation Infrastructure For all our instance properties, we will consider the same observation infrastructure. We fix ${{\mathsf {UIDs}}}$, the set of IDs of the observing users. We let $\textsf {Obs}= \textsf {Act}\times \textsf {Out}$. We take ${{\mathsf {isObs}}}$ to hold for a transition iff its acting user is in ${{\mathsf {UIDs}}}$, and ${{\mathsf {getObs}}}$ to return its action and output:

$$\begin{aligned} \begin{array}{rcl} {{\mathsf {isObs}}}\,(\sigma ,a,{ o },\sigma ') &{}\,\equiv \,&{} {{\mathsf {userOf}}}\,a \in {{\mathsf {UIDs}}}\\ {{\mathsf {getObs}}}\,(\sigma ,a,{ o },\sigma ') &{}\equiv &{} (a,o) \end{array} \end{aligned}$$

${{\mathsf {O}}}\,{ tr }_1$ thus purges ${ tr }_1$ keeping only actions performed (or merely attempted) by users in ${{\mathsf {UIDs}}}$.

The secrecy infrastructure depends on the considered type of document.

Secrecy Infrastructure for Pap $_1$ and Pap $_2$ We fix ${{\mathsf {PID}}}$, the ID of the paper of interest. We let $\textsf {Sec}= \textsf {List}\,(\textsf {Paper\_Content})$. We take ${{\mathsf {isSec}}}$ to hold iff the transition is a successful upload of paper ${{\mathsf {PID}}}$’s content (denoted below by ${ pct }$), and ${{\mathsf {getSec}}}$ to return the uploaded content. ${{\mathsf {S}}}\,{ tr }_1$ thus returns the list of all uploaded paper contents for ${{\mathsf {PID}}}$:

$$\begin{aligned} \begin{array}{rcl} {{\mathsf {isSec}}}\,(\sigma ,a,{ o },\sigma ') &{}\,\equiv \,&{} { o }= {{\mathsf {outOK}}}\,\wedge \\ {} &{} &{} (\exists \,{ cid }\,{ uid }\,{ pw }\,{ pct }.\, a = {{\mathsf {Uact}}}\,({{\mathsf {uPaperC}}}\,{ cid }\,{ uid }\,{ pw }\,{{\mathsf {PID}}}\,{ pct })) \\ {{\mathsf {getSec}}}\,(\sigma ,a,{ o },\sigma ') &{}\,\equiv \,&{} { pct }\end{array} \end{aligned}$$

Above, the value ${ pct }$ from the righthand side of the definition of ${{\mathsf {getSec}}}\,(\sigma ,a,{ o },\sigma ')$ is the one uniquely determined by the condition defining ${{\mathsf {isSec}}}\,(\sigma ,a,{ o },\sigma ')$. (When ${{\mathsf {isSec}}}\,(\sigma ,a,{ o },\sigma ')$ does not hold, the result returned by ${{\mathsf {getSec}}}\,(\sigma ,a,{ o },\sigma ')$ is irrelevant.)

The declassification triggers and bounds are specific to each example.

Declassification Trigger and Bound for Pap $_1$ We define ${{\mathsf {T}}}(\sigma ,a,{ o },\sigma ')$ as “in state $\sigma '$, the paper ${{\mathsf {PID}}}$ is registered at some conference ${ cid }$ and some user in ${{\mathsf {UIDs}}}$ is an author of ${{\mathsf {PID}}}$ or a PC member of ${ cid }$ and the conference has reached the bidding phase,” formally:

Intuitively, the intent with Pap $_1$ is that, provided ${{\mathsf {T}}}$ never holds, users in ${{\mathsf {UIDs}}}$ learn nothing about the various consecutive versions of ${{\mathsf {PID}}}$. But is it true that they can learn absolutely nothing? There is the possibility that a user could infer that no version was submitted: Say the paper’s conference has not yet reached the submission phase; then the trace of paper uploads must be empty. But indeed, nothing beyond this quite harmless information should leak: Any nonempty sequence of secrets ${ sl }_1$ might as well have been any other (possibly empty) sequence ${ sl }_2$. Hence we define ${{\mathsf {B}}}\,{ sl }_1\,{ sl }_2$ as ${ sl }_1 \not = []$. It is interesting to notice here that, while a user could infer emptiness, this is not true for nonemptiness: If the trigger is not fired, there is no way for a user to say that there has been at least one upload of a given paper. In particular, the aforementioned mechanism that could allow a user to infer the absence of any uploads (namely probing the conference phase) is not useful for inferring the presence of any uploads. This shows that declassification bounds can be naturally asymmetric.

Declassification Trigger and Bound for Pap $_2$ The trigger only involves authorship, ignoring PC membership at the paper’s conference—we take ${{\mathsf {T}}}(\sigma ,a,{ o },\sigma ')$ to be

$$\begin{aligned} \exists { uid }\in {{\mathsf {UIDs}}}.\,\exists \,{ cid }.\,{{\mathsf {PID}}}\in {{\mathsf {paperIDs}}}\,\sigma '\,{ cid }\,\wedge \,{{\mathsf {isAut}}}\,\sigma '\,{ uid }\,{{\mathsf {PID}}}\end{aligned}$$

In the case of Pap $_2$, we have a nontrivial declassification bound: Since a PC member should only be able to learn the last submitted version of the considered paper’s content, we take ${{\mathsf {B}}}\,{ sl }_1\,{ sl }_2$ to be

$$\begin{aligned} { sl }_1 \not = [] \,\wedge \, { sl }_2 \not = [] \,\wedge \, {{\mathsf {last}}}\,{ sl }_1 = {{\mathsf {last}}}\,{ sl }_2 \end{aligned}$$

where the function ${{\mathsf {last}}}$ returns the last element of a list.

Instantiation for Rev To uniquely identify a review, we fix not only a paper ID ${{\mathsf {PID}}}$, but also a number ${{\mathsf {N}}}$—with the understanding that the pair $({{\mathsf {PID}}},{{\mathsf {N}}})$ denotes the ${{\mathsf {N}}}$’th review of the paper ${{\mathsf {PID}}}$. The secrecy infrastructure refers not only to the review’s content but also to the conference phase: $\textsf {Sec}= \textsf {List}\,(\textsf {Phase}\times \textsf {Review\_Content})$. The functions ${{\mathsf {isSec}}}$ and ${{\mathsf {getSec}}}$ are defined similarly to those for Pap $_1$ and Pap $_2$, mutatis mutandis. Thus, ${{\mathsf {isSec}}}$ checks whether the transition is a successful update or nondestructive update³ of the given review, namely $({{\mathsf {PID}}},{{\mathsf {N}}})$, and ${{\mathsf {getSec}}}$ returns a pair consisting of the conference’s current phase and the updated review’s content; hence ${{\mathsf {S}}}$ returns a list of such pairs.

The trigger ${{\mathsf {T}}}$ is similar to that of Pap $_2$ but refers to authorship of the paper’s ${{\mathsf {N}}}$’th review rather than paper authorship:

$$\begin{aligned} \begin{array}{rcl} {{\mathsf {T}}}\,(\sigma ,a,{ o },\sigma ')&\,\equiv \,&\exists { uid }\in {{\mathsf {UIDs}}}.\,\exists \,{ cid }.\,{{\mathsf {PID}}}\in {{\mathsf {paperIDs}}}\,\sigma '\,{ cid }\,\wedge \, {{\mathsf {isRevNth}}}\,\sigma '\,{ uid }\,{{\mathsf {PID}}}\,{{\mathsf {N}}}\end{array} \end{aligned}$$

One may wonder why do we keep the conference phase as part of the secrecy infrastructure for Rev, in other words, why do we have ${{\mathsf {getSec}}}$ return the conference phase in addition to the review content. The answer is that we need this information in order to formulate an appropriate bound ${{\mathsf {B}}}$, which is able to distinguish between updates occurring before the discussion phase and those occurring starting from the discussion phase—because these updates have different confidentiality statuses. It is a priori knowledge (i.e., knowledge that can be attained solely by studying the system’s specification) that review updates can only occur during the review and discussion phases, in this order—i.e., that any produced sequence of secrets ${ sl }_1$ has the form ${ ul }\cdot { wl }$ such that the pairs in ${ ul }$ have ${{\mathsf {Reviewing}}}$ as first component and the pairs in ${ wl }$ have ${{\mathsf {Discussion}}}$ as first component. Moreover, any PC member having no conflict with ${{\mathsf {PID}}}$ can additionally learn ${{\mathsf {last}}}\,{ ul }$ (the last submitted version before discussion), and ${ wl }$ (the versions updated during discussion); but (unless/until ${{\mathsf {T}}}$ holds) nothing beyond these. So we take ${{\mathsf {B}}}\,{ sl }_1\,{ sl }_2$ to state that ${ sl }_1$ decomposes as ${ ul }\cdot { wl }$ as indicated above, ${ sl }_2$ decomposes similarly as ${ ul }_2 \cdot { wl }$, and ${{\mathsf {last}}}\,{ ul }= {{\mathsf {last}}}\,{ ul }_2$.

Instantiation for Dis The property Dis needs rephrasing in order to be captured as BD Security. It can be decomposed into:

• Dis $_1$: An author always has a conflict with their own papers.

• Dis $_2$: A group of users learns nothing⁴ about a paper’s discussion unless one of them becomes a PC member at the paper’s conference having no conflict with the paper.

Dis $_1$ is a safety property (holding for all reachable states of the system). Dis $_2$ is an instance of BD Security defined as expected (in light of our previous analysis). In particular, the secrecy infrastructure focuses on the actions that (nondestructively) update the discussion section with comments.

3.5 More Instances

Table 1 shows, in informal notation, the entire array of confidentiality properties we have formulated as BD Security (and have also proved them, as discussed in Sect. 4.3). The observation infrastructure is always the same, given by the actions and outputs of a fixed group of observer users, as in Sect. 3.4.

There are several information sources, each yielding a different secrecy infrastructure. In rows 1–8, the sources are actual documents: paper content, review, discussion, decision. The properties Pap $_1$, Pap $_2$, Rev and Dis $_2$ form the rows 2, 1, 3, and 6, respectively. In rows 9 and 10, the source is the data about the reviewers assigned to a paper.

The declassification triggers express paper or review authorship (being or becoming an author of the indicated document) or PC membership at the paper’s conference. Some triggers are also listed with “phase stamps” that strengthen the statements. For example, “PC membership$^{\textsf {B}}$” should be read as “PC membership and paper’s conference phase being at least bidding.”

Table 1 CoCon’s confidentiality properties

Some of the triggers require lack of conflicts with the paper, which is often important for the security statement to be sufficiently strong. This is the case of Dis $_2$ (row 6), since without the non-conflict assumption Dis $_2$ and Dis $_1$ would no longer imply the desired property Dis. By contrast, lack of conflicts cannot be added to PC membership in Pap $_1$ (row 2), since such a stronger version would not hold: Even if a PC member decides to indicate a conflict with a paper, this happens after they had the opportunity to see the paper’s content.

Note that the listed properties capture exhaustively the information flow from the indicated sources, in the sense that they identify all the relevant roles that can influence these flows. This can be seen by traversing the rows for each source upwards—in the increasing order of the bound’s permissiveness, which is also the decreasing order of the trigger’s permissiveness—and recording the differences with respect to the triggers.

For example, for the review source, we have the following cases:

• Row 5: If a user is not the review’s author, not a non-conflict PC member in the discussion phase, and not the reviewed paper’s author in the notification phase, then they could learn about the absence of any edit—but nothing more.

• Subtracting row 4 from row 5: In addition, the reviewed paper’s authors will learn in the notification phase of the last edited version of the review before notification—but nothing more.

• Subtracting row 3 from row 4: In addition, non-conflict PC members will learn in the discussion phase of all the intermediate versions starting from the last one before the discussion phase and all the later versions (produced during the discussion phase)—but nothing more.

The role that persists even in the least permissive trigger (in row 3) is that of the review’s author, which obviously has no restriction.

As another example, consider the reviewer assignment source, where we have the cases:

• Row 10: If a user is not a non-conflict PC member in the reviewing phase and not the paper’s author in the notification phase, then they will have access to the a priori knowledge that reviewers are non-conflict PC members—but nothing more.

• Subtracting row 9 from row 10: In addition, the paper’s authors will learn in the notification phase of the number of reviewers (of course, inferring it from the number of reviews they receive as authors)—but nothing more.

Here, the role that persists in the least permissive trigger (in row 9) is that of PC member in the reviewing phase.

3.6 Traceback Properties

Our confidentiality properties show upper bounds on information release that are valid unless/until some trigger ${{\mathsf {T}}}$ occurs, e.g., chairness, PC membership, authorship, or the conference reaching a given phase. While ${{\mathsf {T}}}$ is allowed to depend on all four components of a transition $(\sigma ,{ o },a,\sigma ')$, our CoCon instances only depend on $\sigma '$, employing predicates such as ${{\mathsf {isAut}}}\,\sigma '\,{ uid }\,{{\mathsf {PID}}}$ and ${{\mathsf {isPC}}}\,\sigma '\,{ uid }\,{ cid }$. Two questions arise.

First, why do we consider the target state $\sigma '$ and not the source state $\sigma$? This is because our choice gives the more intuitive result: ${{\mathsf {never}}}\,{{\mathsf {T}}}$ holding for a valid trace $[(\sigma _1,a_1,{ o }_1,\sigma _2),\,(\sigma _2,a_2,{ o }_2,\sigma _3), \ldots , (\sigma _{n-1},a_{n-1},{ o }_n,\sigma _n)]$ means that the corresponding state condition fails for $\sigma _2,\ldots ,\sigma _n$ (importantly, also including the last state $\sigma _n$); and all our trigger conditions fail trivially for the initial state $\sigma _1 = {{\mathsf {istate}}}$, therefore not covering this state is not a problem.

Second, why do we formulate ${{\mathsf {T}}}$ “intensionally” as a state-based condition, and not “extensionally” as an action-based condition? For example, instead of asking that a user ${ uid }\in {{\mathsf {UIDs}}}$ be an author in the transition’s target state (${{\mathsf {isAut}}}\,\sigma '\,{ uid }\,{{\mathsf {PID}}}$), why not ask that the action of such a user becoming an author has occurred in the trace? The answer to this is pragmatic: The two choices are equivalent, while state-based conditions are easier to formulate since they don’t need to refer to entire traces.

However, the state-based versus action-based question leads us to a more fundamental concern about the security guarantees.⁵ We have proved that one does not acquire a certain information unless one acquires a certain role. But how can we know that only “lawfully” appointed users acquire that role? To fully answer this question, we trace back, within valid traces, all possible chains of events that could have led to certain roles and other information flow enabling situations—leading to what we call traceback properties.

For example, we prove that, if a user is currently a chair then they either must have been the original chair (who registered the conference), or, inductively, must have been appointed by another chair—and this of course in a well-founded fashion, in that the chain of chair appointments can always be traced back to the original chair and the registration of the conference.

Formally, we achieve this by introducing an alternative “is chair” predicate ${{\mathsf {isChair}}}' : \textsf {Trace}\rightarrow \textsf {ConfID}\rightarrow \textsf {UserID}\rightarrow \textsf {Bool}$, which is defined inductively to account for the lawful chair-appointment transitions on the trace:

• Create Conference: $\displaystyle \frac{{ t }= (\_,{{\mathsf {Cact}}}\,({{\mathsf {cConf}}}\,{ cid }\,{ uid }\,\_\,\_ \,\_),{{\mathsf {outOK}}},\_) }{ {{\mathsf {isChair}}}'\,({ tr }\cdot [{ t }])\,{ cid }\,{ uid }}$

• Add Chair: $\displaystyle \frac{ {{\mathsf {isChair}}}'\,tr\,{ cid }\,{ uid }' { t }= (\_,({{\mathsf {Cact}}}\,({{\mathsf {cChair}}}\,{ cid }\,{ uid }'\,\_\,{ uid })), {{\mathsf {outOK}}},\_) }{ {{\mathsf {isChair}}}'\,({ tr }\cdot [{ t }])\,{ cid }\,{ uid }}$

• Irrelevant Transition: $\displaystyle \frac{ {{\mathsf {isChair}}}'\,tr\,{ cid }\,{ uid }}{ {{\mathsf {isChair}}}'\,({ tr }\cdot [{ t }])\,{ cid }\,{ uid }}$

The chair-role traceback property rests on the equivalence between the original (state-based) predicate and this alternative trace-based predicate:

Prop 1

For all valid traces ${ tr }_1$ ending in state $\sigma$ , we have that

We formulate (and prove) such traceback properties for all the trigger components used in our security properties:

• 1. If a user is an author of a paper then either the user has registered the paper in the first place or, inductively, has been appointed as coauthor by another author

• 2. If a user is a PC member then the user either must have been the original chair or must have been appointed by a chair.

• 3. If a user is a paper’s reviewer, then the user must have been appointed by a chair (from among the PC members who have not declared a conflict with the paper).

• 4. If a user has a conflict with a paper, then the user is either an author of the paper or the conflict has been declared by that user or by a paper’s author, in such a way that between the moment when the conflict has been last declared and the current moment there is no transition that successfully removes the conflict.

• 5. If a conference is in a given phase different from “no phase,” then this has happened as a consequence of either a conference approval action by the voronkov (if the phase is ${{\mathsf {Setup}}}$) or a phase change action by a chair (otherwise).

As expected, some of the above traceback schemes rely on the others. For example, the scheme for the PC member role relies on that of the chair role, and that of reviewer relies on those of chair and PC member.

In conclusion, the BD Security instances for CoCon state that information disclosure is bounded, provided certain triggers are not fired. To complement these, we formulated traceback properties, stating that users cannot improperly fire the triggers. There is an analogy between traceback and accountability properties [80]: Say a certain situation occurs (e.g., a role acquisition), which could represent an “abuse”; our traceback property identifies the actions that have led to that, which also contain information about the “responsible” parties.

4 Verification

To cope with general declassification bounds, BD Security talks about system traces in conjunction with sequences of secrets that must be produced by these traces. We extend the unwinding proof technique to cope with this situation and employ the result to the verification of our confidentiality properties.

4.1 Unwinding Proof Method

Let us recall, looking at Sect. 3.2’s definition $(*)$, what it takes to prove BD Security: We are given the original (valid) trace ${ tr }_1$ which produces the sequence of secrets ${ sl }_1$ and for which ${{\mathsf {never}}}\,{{\mathsf {T}}}$ holds. We are also given an alternative sequence of secrets ${ sl }_2$ such that ${{\mathsf {B}}}\,{ sl }_1\,{ sl }_2$ holds. From these, we need to provide an alternative (valid) trace ${ tr }_2$ whose produced sequence of secrets is exactly ${ sl }_2$ and whose produced sequence of observations is the same as that of ${ tr }_1$.

Following the tradition of unwinding for noninterference [26, 48, 67], we wish to construct ${ tr }_2$ from ${ tr }_1$ incrementally: As ${ tr }_1$ grows, ${ tr }_2$ should grow nearly synchronously. If we adopted the traditional setting, we would take an unwinding to be a relation on states, connecting the states reached by the under-construction traces ${ tr }_1$ and ${ tr }_2$, assumed to satisfy some conditions connecting possible ways to extend ${ tr }_1$ by single transitions with ways to extend ${ tr }_2$ by matching transitions; and also, ideally, allowing for some slack in terms of unmatched unobservable transitions on each side (in the style of weak bisimulation). Proving a relation to be an unwinding would essentially be a two player game, where we, the prover, have control over the ${ tr }_2$ extensions and the opponent has control over the ${ tr }_1$ extensions.

In order for ${ tr }_2$ to have the same observation sequence (produced via ${{\mathsf {O}}}$) as ${ tr }_1$, we naturally commit to the requirement that the observable transitions of ${ tr }_2$ (i.e., those for which ${{\mathsf {isObs}}}$ holds) be perfectly synchronized with those of ${ tr }_1$ and produce the same observations (via ${{\mathsf {getObs}}}$). However, when dealing with sequences of secrets (produced via ${{\mathsf {S}}}$), there is a complication: In contrast to the traditional setting, we must consider an additional parameter, namely the a priori given ${{\mathsf {B}}}$-related sequences of secrets ${ sl }_1$ and ${ sl }_2$, such that (1) we can count on the fact that ${ tr }_1$ produces ${ sl }_1$ and (2) we must make sure that ${ tr }_2$ also produces ${ sl }_2$.

From the above discussion, we see that, in a presumptive unwinding game for BD Security, we must record not only pairs $(\sigma _1,\sigma _2)$, but quadruples $(\sigma _1,{ sl }_1,\sigma _2,{ sl }_2)$, where $\sigma _1$ and $\sigma _2$ are, as before, the states reached by the under-construction traces ${ tr }_1$ and ${ tr }_2$, while ${ sl }_1$ and ${ sl }_2$ are the sequences of secrets that must still be produced by the two traces.

Figure 4 illustrates, on Fig. 3’s abstract example, how such an unwinding game would work. (The figure uses colors.) We play with Green, having control over the alternative trace, with moves shown on the right of the figure, against our opponent, who plays Red, having control over the original trace, with moves shown on the left. The game starts with a pair of sequences of secrets, related by the bound ${{\mathsf {B}}}$: an original one ${ sl }_1 = [s_1,s_1',s_1'']$ (to be produced by the original trace) and an alternative one ${ sl }_2 = [s_2,s_2'']$ (to be produced by the alternative trace). Both the original trace ${ tr }_1$ and the alternative trace ${ tr }_2$ are initially empty—they will grow as the players make moves. Note that, even if the figure shows the traces ${ tr }_1$ and ${ tr }_2$, all the information needed in order to extend them are the states that they have reached (i.e., the target states of their last transitions), say, $\sigma _1$ and $\sigma _2$. In other words, we only need to store configurations $(\sigma _1,{ sl }_1,\sigma _2,{ sl }_2)$, as noted before. At the beginning, both $\sigma _1$ and $\sigma _2$ are the initial state ${{\mathsf {istate}}}$. The game proceeds as follows: Each time we, the Green, can choose between two options: (1) asking the opponent to move and then performing a Reaction, which can be either Ignore or Match, and (2) taking Independent Action.

In case we choose the first option, the opponent must make a move, which consists of extending the original trace with one transition; if this transition produces a secret, it must be the first in the remaining original sequence of secrets—and that secret will be crossed out, i.e., removed from the sequence. (This condition ensures that the under-construction original trace ${ tr }_1$ stays on track with respect to the to-be-produced secrets ${ sl }_1$).

Fig. 4

Illustration of BD security unwinding

To this move, we must react by either Ignore, thus changing nothing (an option made available to us only if the opponent’s last transition was unobservable, in order to keep our commitment to full synchronization with respect to observations) or Match. If we choose Match, we must extend the alternative trace with a transition, which must be equally observable and, if observable, it must produce the same observation as the opponent’s last transition (again, in line with our observation-synchronization commitment). Concerning the secrets, we have a restriction similar to the opponent’s: If our transition produces a secret, it must be the first in the remaining alternative sequence of secrets (and it will be crossed out).

In Fig. 4, we see how the first three pairs of moves are triggered by us repeatedly asking for a move from the opponent, who does the following:

• adds the transition $t_1$ (crossing out the first original secret $s_1$ and producing an observation $o_1$); to this, we react by the matching transition $t_2$ (crossing out the first alternative secret $s_2$ and producing an identical observation $o_2 = o_1$);

• adds a further transition $t_1'$ (crossing out the next original secret $s_1'$ and producing no observation); this we ignore (and we are allowed to do that, since $t_1'$ is unobservable);

• adds a further transition $t_1''$ (crossing out the next original secret $s_1''$ and producing an observation $o_1''$); to this, we react by the matching transition $t_2'$ (producing no secret and producing an identical observation $o_2' = o_1''$).

In case we choose the second option (Independent Action), the opponent waits and it is us who must make a move: by adding an unobservable transition and again committing to only producing, if any, the first secret in the remaining list of alternative secrets. In Fig. 4, the last move is Independent Action, which crosses out the remaining alternative secret.

When should the game be won? Traditionally with unwinding and the other notions in the (bi)simulation family, we win if we are able to stay in the game indefinitely—which is essentially a safety-like condition. However, in our case, due to the sequence-of-secrets components, we need an additional liveness-like twist: Provided the opponent has crossed out all their secrets (in the original sequence of secrets ${ sl }_1$), we must also eventually cross out all our secrets (in the alternative sequence of secrets ${ sl }_2$). We achieve this by the following mechanism: As soon as the opponent has crossed out all their secrets (meaning ${ sl }_1 = []$), provided we have not yet crossed out all our secrets (meaning ${ sl }_2 \not = []$), we are forced to choose Independent Action; moreover, we ask that Independent Action must always produce secrets. This last requirement also avoids the possibility of “filibustering” the game with observationless and secretless Independent Action moves—which would be unsound with respect to our goal of proving BD security.

Note that Fig. 4 does not show an entire run of the game, but only a prefix of such a run—corresponding to Fig. 3’s particular instantiation of BD Security’s $\forall$- and $\exists$-quantified variables. In order to prove BD security by this unwinding scheme, we must of course (symbolically) produce a strategy for winning the game for each ${{\mathsf {B}}}$-related sequences of secrets and each choice of moves by the opponent. In the configuration shown at the end of Fig. 4, we, the Green, have achieved an important milestone—by having crossed out all the secrets of the given instance. However, in order to win we would still need to show how we can stay in the game indefinitely—by being able to properly react to any of the opponent’s further moves. For example, a scenario in which we can still lose Fig. 4’s game is if we next choose Reaction and the opponent comes up with a further transition $t_1'''$ that produces no secret and produces an observation $o_1'''$ that we are not able to match with any available transition.

Considering all the above, we define an unwinding relation to be a quaternary relation $\varDelta : \textsf {State}\rightarrow \textsf {List}\,(\textsf {Sec}) \rightarrow \textsf {State}\rightarrow \textsf {List}\,(\textsf {Sec}) \rightarrow \textsf {Bool}$ satisfying the condition ${{\mathsf {unwind}}}\,\varDelta$ shown below, where ${{\mathsf {reach}}}: \textsf {State}\rightarrow \textsf {Bool}$ is the state reachability predicate and ${{\mathsf {reach}_{\,\lnot \,{{\mathsf {T}}}}}}: \textsf {State}\rightarrow \textsf {Bool}$ is its strengthening to reachability by transitions that do not satisfy ${{\mathsf {T}}}$:

$$\begin{aligned} \begin{array}{ll} {{\mathsf {unwind}}}\,\varDelta \,\equiv \, &{} \forall \sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2.\,{{\mathsf {reach}_{\,\lnot \,{{\mathsf {T}}}}}}\,\sigma _1 \,\wedge \, {{\mathsf {reach}}}\,\sigma _2\,\wedge \, \varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\rightarrow \\ &{}(({ sl }_1 \not = [] \,\vee \, { sl }_2 = [])\,\wedge \, {{\mathsf {reaction}}}\,\varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2) \,\vee \, \\ &{}{{\mathsf {iaction}}}\,\varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\vee \, \\ &{}({ sl }_1 \not = [] \,\wedge \, {{\mathsf {exit}}}\,\sigma _1\,({{\mathsf {head}}}\,{ sl }_1)) \end{array} \end{aligned}$$

The predicates ${{\mathsf {reaction}}}$ and ${{\mathsf {iaction}}}$ formalize Reaction and Independent Action, the former involving a disjunction of predicates formalizing Ignore and Match. To define all these, we first introduce the auxiliary predicate ${{\mathsf {consume}}}\,{ t }\,{ sl }_1\,{ sl }_1'$, stating that the transition ${ t }$ either produces a secret that is consumed from ${ sl }_1$ yielding ${ sl }_1'$ or produces no secret and ${ sl }_1 = { sl }_1'$, formally:

$$\begin{aligned} \hbox {if} \,{{\mathsf {isSec}}}\,{ t }\, \hbox {then} \,({ sl }_1 \not = [] \,\wedge \,{{\mathsf {getSec}}}\,{ t }= {{\mathsf {head}}}\,{ sl }_1 \,\wedge \, { sl }_1' = {{\mathsf {tail}}}\,{ sl }_1)\, \hbox {else} \,({ sl }_1' = { sl }_1) \end{aligned}$$

Now the predicates are defined as follows:

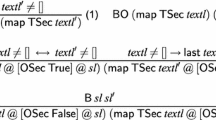
• ${{\mathsf {reaction}}}\,\varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2\, \equiv \,\,\forall a\,{ o }\,\sigma _1'.\,$ let ${ t }= (\sigma _1,a,{ o },\sigma _1')$ in       ${ t }\in {{\mathsf {Valid}}}\,\wedge \, \lnot \,{{\mathsf {T}}}\,{ t }\,\wedge \,{{\mathsf {consume}}}\,{ t }\,{ sl }_1\,{ sl }_1' \,\rightarrow$       ${{\mathsf {match}}}\,\varDelta \,\sigma _1\,\sigma _2\,{ sl }_2\,a\,{ o }\,\sigma _1'\,{ sl }_1' \,\vee \, {{\mathsf {ignore}}}\,\varDelta \,\sigma _1\,\sigma _2\,{ sl }_2\,a\,{ o }\,\sigma _1'\,{ sl }_1'$ where:

  • ${{\mathsf {ignore}}}\,\varDelta \,\sigma _1\,\sigma _2\,{ sl }_2\,a\,{ o }\,\sigma _1'\,{ sl }_1' \equiv \lnot \,{{\mathsf {isObs}}}\,(\sigma _1,a,{ o },\sigma _1') \,\wedge \, \varDelta \,\sigma _1'\,{ sl }_1'\,\sigma _2\,{ sl }_2$

  • ${{\mathsf {match}}}\,\varDelta \,\sigma _1\,\sigma _2\,{ sl }_2\,a\,{ o }\,\sigma _1'\,{ sl }_1' \equiv$       $\exists a_2\,{ o }_2\,\sigma _2'\,{ sl }_2'.$ let ${ t }_1 = (\sigma _1,a,{ o },\sigma _1')$ and ${ t }_2 = (\sigma _2,a_2,{ o }_2,\sigma _2')$ in 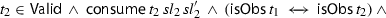             $({{\mathsf {isObs}}}\,{ t }_1 \rightarrow {{\mathsf {getObs}}}\,{ t }_1 = {{\mathsf {getObs}}}\,{ t }_2) \,\wedge \, \varDelta \,\sigma _1'\,{ sl }_1'\,\sigma _2'\,{ sl }_2'$

  • ${{\mathsf {iaction}}}\,\varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \equiv$       $\exists a_2\,{ o }_2\,\sigma _2'\,{ sl }_2'.$ let ${ t }_2 = (\sigma _2,a_2,{ o }_2,\sigma _2')$ in       ${ t }_2 \in {{\mathsf {Valid}}}\,\wedge \, {{\mathsf {consume}}}\,{ t }_2\,{ sl }_2\,{ sl }_2'\,\wedge \, {{\mathsf {isSec}}}\,{ t }_2\, \,\wedge \, \lnot \,{{\mathsf {isObs}}}\,{ t }_2\,\wedge \,\varDelta \,\sigma _1\,{ sl }_1\,\sigma _2'\,{ sl }_2'$

In the above definition of ${{\mathsf {unwind}}}$, there is a predicate ${{\mathsf {exit}}}$ which has not been defined or motivated yet. It performs an optimization that allows us to finish a game earlier by proving that the opponent cannot fulfill their contract. Namely, we note that BD Security holds trivially if the original trace ${ tr }_1$ cannot produce the sequence of secrets ${ sl }_1$, i.e., if ${{\mathsf {S}}}\,{ tr }_1 \not = { sl }_1$—this happens if and only if, at some point, an element s of ${ sl }_1$ can no longer be produced, i.e., for some decompositions ${ tr }_1 = { tr }_1' \cdot { tr }_1''$ and ${ sl }_1 = { sl }_1' \cdot [s] \cdot { sl }_1''$ of ${ tr }_1$ and ${ sl }_1$, it holds that ${{\mathsf {S}}}\,{ tr }_1' = { sl }_1'$ and $\forall { t }\in { tr }_1''.\,{{\mathsf {isSec}}}\,{ t }\rightarrow {{\mathsf {getSec}}}\,{ t }\not = s$. Can we detect such a situation from within $\varDelta$? The answer is an over-approximated yes, in that we can detect a sufficient (though not necessary) condition for this situation to occur: After $\varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2$ evolves by Reaction and Independent Action to $\varDelta \,\sigma _1'\,([s] \cdot { sl }_1'')\,\sigma _2'\,{ sl }_2'$ for some $\sigma _1'$, $\sigma _2'$ and ${ sl }_2'$ (presumably consuming ${ tr }_1'$ and producing the ${ sl }_1'$ prefix of ${ sl }_1$), then one can safely exit the game if one proves that no valid trace ${ tr }_1''$ starting from $\sigma _1'$ can ever produce s, in that it satisfies $\forall { t }\in { tr }_1''.\,{{\mathsf {isSec}}}\,{ t }\rightarrow {{\mathsf {getSec}}}\,{ t }\not = s$. The above justifies the following definition:

• ${{\mathsf {exit}}}\,\sigma _1\,s \,\equiv \, \forall \,{ tr }_1\,{ t }.\,{ tr }_1 \cdot [{ t }] \in {{\mathsf {Valid}}}_{\sigma _1} \,\wedge \,{{\mathsf {isSec}}}\,{ t }\rightarrow {{\mathsf {getSec}}}\,{ t }\not = s$

This predicate essentially expresses a safety property, and therefore can be verified in a trace-free manner by exhibiting an invariant $K : \textsf {State}\rightarrow \textsf {Bool}$ and proving that it holds for $\sigma _1$. Intuitively, the potential invariant K ensures that the secret s can never be produced:

Prop 2

Assume that, for all valid transitions ${ t }= (\sigma _1,a,{ o },\sigma _1')$, $K\,\sigma _1$ implies $K\,\sigma _1' \wedge \,({{{\mathsf {isSec}}}}\,{ t }\rightarrow {{{\mathsf {getSec}}}}\,{ t }\not = s)$. Then $\forall \sigma _1.\,K\,\sigma _1 \rightarrow \mathsf {exit}\,\sigma _1\,s$

We can now formulate our main result about unwinding:

Theorem 3

(Unwinding Theorem)Assume that the following hold:

• $\forall { sl }_1\,{ sl }_2.\,{{\mathsf {B}}}\,{ sl }_1\,{ sl }_2 \rightarrow \varDelta \,{{\mathsf {istate}}}\,{ sl }_1\,{{\mathsf {istate}}}\,{ sl }_2$

• ${{\mathsf {unwind}}}\,\varDelta$

Then the system is BD secure.

According to the theorem, our notion of unwinding is a sound proof method for BD Security: To check BD Security it suffices to define a relation $\varDelta$ and prove that it coincides with ${{\mathsf {B}}}$ on the initial state and that it is an unwinding.

To prove this theorem, we first prove that, given an unwinding relation $\varDelta$ and a configuration $(\sigma _1,{ sl }_1,\sigma _2,{ sl }_2)$ for which the relation holds and the states $\sigma _1$ and $\sigma _2$ are reachable via $\lnot \,{{\mathsf {T}}}$ transitions and respectively reachable, a generalization of BD Security holds—for traces starting in $\sigma _1$ and $\sigma _2$ instead of ${{\mathsf {istate}}}$:

Lemma 4

${{{\mathsf {unwind}}}}\,\varDelta \,\wedge \, \varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\wedge \, {{{{{\mathsf {reach}}}}_{\,\lnot \,{{\mathsf {T}}}}}}\,\sigma _1 \,\wedge \, {{{\mathsf {reach}}}}\,\sigma _2 \,\wedge \, { tr }_1 \in {{{\mathsf {Valid}}}}_{\sigma _1} \,\wedge \,$

${{{\mathsf {never}}}}\,{{{\mathsf {T}}}}\,{{ tr }}_{1} \,{\wedge }\, \mathsf {S}\,{{ tr }}_{1} = {{ sl }}_1 \,{\rightarrow }\, ({\exists } { tr }_2.\,{ tr }_2 \in {{{\mathsf {Valid}}}}_{\sigma _2} \,\wedge \, \mathsf {O}\,{ tr }_2 = \mathsf {O}\,{ tr }_1 \,\wedge \, \mathsf {S}\,{ tr }_2 = { sl }_2)$

Proof

By induction on ${{\mathsf {length}}}\,{ tr }_1 + {{\mathsf {length}}}\,{ sl }_2$: Our carefully chosen unwinding conditions ensure that, at each move in the unwinding game, either ${ tr }_1$ decreases or ${ sl }_2$ decreases. $\square$

The theorem follows immediately from the above lemma, taking $\sigma _1 = \sigma _2 = {{\mathsf {istate}}}$.

4.2 Compositional Reasoning

To keep each reasoning step manageable, we replace the monolithic unwinding relation $\varDelta$ with a network of relations, such that any relation may unwind to any number of relations in the network. To achieve this, we replace the single requirement ${{\mathsf {unwind}}}\,\varDelta$ with a set of requirements ${{\mathsf {unwind\_to}}}\,\varDelta \,{\varDelta { s }}$ with ${\varDelta { s }}$ being a set of relations. The predicate ${{\mathsf {unwind\_to}}}$ is defined similarly to ${{\mathsf {unwind}}}$, but employing disjunctions of the predicates in ${\varDelta { s }}$, written ${{\mathsf {disj}}}\,{\varDelta { s }}$:

$$\begin{aligned} \begin{array}{ll} {{\mathsf {unwind\_to}}}\,\varDelta \,{\varDelta { s }}\,\equiv \, &{} \forall \sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2.\,{{\mathsf {reach}_{\,\lnot \,{{\mathsf {T}}}}}}\,\sigma _1 \,\wedge \, {{\mathsf {reach}}}\,\sigma _2\,\wedge \, \varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\rightarrow \\ &{}(({ sl }_1 \not = [] \,\vee \, { sl }_2 = [])\,\wedge \, {{\mathsf {reaction}}}\,({{\mathsf {disj}}}\,{\varDelta { s }})\,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2) \,\vee \, \\ &{}{{\mathsf {iaction}}}\,({{\mathsf {disj}}}\,{\varDelta { s }})\,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\vee \, \\ &{}({ sl }_1 \not = [] \,\wedge \, {{\mathsf {exit}}}\,\sigma _1\,({{\mathsf {head}}}\,{ sl }_1)) \end{array} \end{aligned}$$

This enables a form of sound compositional reasoning: If we verify a condition as above for each component relation, we obtain an overall secure system.

Corollary 5

(Compositional Unwinding Theorem) Let ${\varDelta { s }}$ be a set of relations. For each $\varDelta \in {\varDelta { s }}$, let ${{\mathsf {next}}}_\varDelta \subseteq {\varDelta { s }}$ be a (possibly empty) “continuation” of $\varDelta$, and let $\varDelta _{\textsf {init}} \in {\varDelta { s }}$ be a chosen “initial” relation. Assume the following hold:

• $\forall { sl }_1\,{ sl }_2.\,\mathsf {B}\,{ sl }_1\,{ sl }_2 \rightarrow \varDelta _{\textsf {init}}\,{{\mathsf {istate}}}\,{ sl }_1\,{{\mathsf {istate}}}\,{ sl }_2$

• $\forall \varDelta \in {\varDelta { s }}.\,{\mathsf {unwind}\_{\mathsf {to}}}\,\varDelta \, \mathsf {next}_\varDelta$

Then the system is BD secure.

Proof

One can show that ${{\mathsf {unwind}}}\,({{\mathsf {disj}}}\,{\varDelta { s }})$ holds and use the original unwinding theorem. $\square$

Fig. 5

A network of unwinding components

The network of components can in principle form any directed graph, the only requirement being that each node has an outgoing edge—Fig. 5 shows an example. However, the unwinding proofs for our CoCon instances will follow the temporal evolution of the conference as witnessed by the phase change and other events. Hence the following essentially linear network will suffice (Fig. 6): Each $\varDelta _i$ unwinds either to itself, or to $\varDelta _{i+1}$ (if $i\not = n$), or to an exit component ${\varDelta _{{\mathsf {e}}}}$ that invariably chooses the “exit” unwinding condition. To capture this type of situation, we employ the predicate ${{\mathsf {unwind\_cont}}}$ that restricts the unwinding of $\varDelta _i$ to proper continuations (i.e., no exits) and the predicate ${{\mathsf {unwind\_exit}}}$ that restricts the unwinding of ${\varDelta _{{\mathsf {e}}}}$ to exits (as depicted in Fig. 6):

$$\begin{aligned} \begin{array}{rll} {{\mathsf {unwind\_cont}}}\,\varDelta \,{\varDelta { s }}&{} \,\equiv \, &{} \forall \sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2.\,{{\mathsf {reach}_{\,\lnot \,{{\mathsf {T}}}}}}\,\sigma _1 \,\wedge \, {{\mathsf {reach}}}\,\sigma _2\,\wedge \, \varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\rightarrow \\ &{}&{}(({ sl }_1 \not = [] \,\vee \, { sl }_2 = [])\,\wedge \, {{\mathsf {reaction}}}\,\,({{\mathsf {disj}}}\,{\varDelta { s }})\,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2) \,\vee \, \\ &{}&{}{{\mathsf {iaction}}}\,({{\mathsf {disj}}}\,{\varDelta { s }})\,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \\ {{\mathsf {unwind\_exit}}}\,\varDelta \, &{} \,\equiv \, &{} \forall \sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2.\,{{\mathsf {reach}_{\,\lnot \,{{\mathsf {T}}}}}}\,\sigma _1 \,\wedge \, {{\mathsf {reach}}}\,\sigma _2\,\wedge \, \varDelta \,\sigma _1\,{ sl }_1\,\sigma _2\,{ sl }_2 \,\rightarrow \\ &{}&{}{ sl }_1 \not = [] \,\wedge \, {{\mathsf {exit}}}\,\sigma _1\,({{\mathsf {head}}}\,{ sl }_1) \end{array} \end{aligned}$$

Corollary 6

(Sequential Unwinding Theorem) Consider the indexed set of relations $\{\varDelta _1,\ldots ,\varDelta _n\}$ such that the following hold:

• $\forall { sl }_1\,{ sl }_2.\,\mathsf {B}\,{ sl }_1\,{ sl }_2 \rightarrow \varDelta _1\,{{\mathsf {istate}}}\,{ sl }_1\,{{\mathsf {istate}}}\,{ sl }_2$

• $\forall i \in \{1,\ldots ,n-1\}.\,{{\mathsf {unwind}\_{\mathsf {cont}}}}\,\varDelta _i\,\{\varDelta _i,\varDelta _{i+1},{\varDelta _{{\mathsf {e}}}}\}$

• ${{\mathsf {unwind}\_{\mathsf {cont}}}}\,\varDelta _n\,\{\varDelta _n,{\varDelta _{{\mathsf {e}}}}\}$

• ${{\mathsf {unwind}\_{\mathsf {exit}}}}\,{\varDelta _{{\mathsf {e}}}}$

Then the system is BD secure.

Proof

From the compositional unwinding theorem, given that ${{\mathsf {unwind\_cont}}}$ and ${{\mathsf {unwind\_exit}}}$ are both subsumed by ${{\mathsf {unwind\_to}}}$. $\square$

We found the sequential unwinding theorem to represent a sweet spot between generality and ease of instantiation for our concrete unwinding proofs, which we discuss next. In fact, we even went a little further and partially instantiated this theorem with various fixed small numbers of non-terminal relations, namely 3, 4 and 5.

Fig. 6

A linear network with exit

4.3 Verification of the Concrete Instances

We have employed the sequential unwinding theorem to verify all the CoCon instances of BD Security listed in Table 1. We will explain our unwinding proofs quasi-informally, in terms of the strategy for incrementally building an alternative trace ${ tr }_1$ from an original trace ${ tr }_2$ (even though, strictly speaking, what the unwinding relation remembers are not the traces themselves, but only the states they have currently reached).

The choice of the relations $\varDelta _i$ required by the sequential unwinding theorem was guided by milestones in the journey of ${ tr }_1$ and ${ tr }_2$: changing a conference’s phase, registering a paper, registering a relevant agent such as a chair, a PC member or a reviewer, declaring or removing a conflict, etc. For example, here are the unwinding relations we used in the proof of Pap $_2$:

And here are the ones we used in the proof of Rev:

Above, ${{\mathsf {B}}}\,{ sl }_1\,{ sl }_2$ denotes the respective declassification bounds for these instances, and the changes from $\varDelta _i$ to $\varDelta _{i+1}$ have been emphasized.

Each BD Security instance has one or more critical phases, the only phases when the sequences of secrets ${ sl }_1$ and ${ sl }_2$ can be produced. For Pap $_2$, secret production means paper uploading, which is only possible in the submission phase—meaning that submission is the single critical phase. For Rev, secret production means review update; there is an update action available in the reviewing phase, and a nondestructive update action available in the discussion phase—so both these phases are critical. Until the critical phases, (the construction of) ${ tr }_2$ proceeds perfectly synchronously to ${ tr }_1$, taking the same actions—consequently, the states $\sigma _1$ and $\sigma _2$ stay equal in $\varDelta _1$ for Pap $_2$ and in $\varDelta _1$ and $\varDelta _2$ for Rev.

In the critical phases, the traces ${ tr }_1$ and ${ tr }_2$ will partly diverge, due to the need of producing possibly different (but ${{\mathsf {B}}}$-related) sequences of secrets. As a result, the equality between $\sigma _1$ and $\sigma _2$ is replaced with the weaker relation of equality everywhere except on certain components of the state. This is the case with the relation $\varDelta _2$ for Pap $_2$, where $=_{{\mathsf {PID}}}$ denotes equality everywhere except on the content of ${{\mathsf {PID}}}$. Similarly, in $\varDelta _3$ for Rev, $=_{{{\mathsf {PID}}},{{\mathsf {N}}}}$ denotes equality everywhere except on the content of ${{\mathsf {PID}}}$’s ${{\mathsf {N}}}$’th review.

At the end of the critical phases, ${ tr }_2$ will usually need to resynchronize with ${ tr }_1$ and hereafter proceed with identical actions. Consequently, $\sigma _1$ and $\sigma _2$ will become connected by a stronger “equality everywhere except” relation or even plain equality again—which is the case with $\varDelta _3$ for Pap $_2$ and with $\varDelta _4$ for Rev.

Besides the phase changes, other relevant events in the unwinding proofs of Pap $_2$ and Rev are the registration of the considered paper or review. For Pap $_2$, here is the informal reading of $\varDelta _1$–$\varDelta _3$ in light of such events:

• $\varDelta _1$: The paper ${{\mathsf {PID}}}$ is not registered yet, so the two states $\sigma _1$ and $\sigma _2$ are equal.

• $\varDelta _2$: The paper is registered and the phase is ${{\mathsf {Submission}}}$; now the two states can diverge on the content of ${{\mathsf {PID}}}$.

• $\varDelta _3$: The paper is registered, and both the original trace and the alternative trace have exhausted their to-be-produced secrets.

And here is the informal reading of the relations in the case of Rev:

• $\varDelta _1$: Either the paper ${{\mathsf {PID}}}$ is not registered yet or the phase is not yet ${{\mathsf {Reviewing}}}$, so the two states are equal.

• $\varDelta _2$: The paper is registered and the phase is ${{\mathsf {Reviewing}}}$ but the paper’s ${{\mathsf {N}}}$’th review is not registered yet, so the two states are still equal.

• $\varDelta _3$: Both the paper and its ${{\mathsf {N}}}$’th review are registered and the phase is ${{\mathsf {Reviewing}}}$; now the two states can diverge on the content of the review.

• $\varDelta _4$: The phase is either ${{\mathsf {Reviewing}}}$ or higher (e.g., ${{\mathsf {Discussion}}}$), both traces have exhausted their ${{\mathsf {Reviewing}}}$-tagged secrets, meaning that the remaining to-be-produced secrets must be ${{\mathsf {Discussion}}}$-tagged⁶ and are required to be equal; now the states must be equal too.

The smooth transition between consecutive components $\varDelta _i$ and $\varDelta _{i+1}$ that impose different state equalities is ensured by a suitable Independent-Action/Reaction strategy—which does not show up in the relations themselves, but only in our proofs that the relations constitute a linear network of unwindings. For Pap $_2$, the crucial part in the proof is the strategy for transitioning from $\varDelta _2$ to $\varDelta _3$, with emptying the sequences of secrets ${ sl }_1$ and ${ sl }_2$ at the same time: By Independent Action, ${ tr }_2$ will produce all secrets in ${ sl }_2$ save for the last one, which will be produced by Reaction in sync with ${ tr }_1$ when ${ tr }_1$ reaches the last secret in ${ sl }_1$; this is possible since ${{\mathsf {B}}}$ guarantees ${{\mathsf {last}}}\,{ sl }_1 = {{\mathsf {last}}}\,{ sl }_2$. And Rev has a similar strategy for the crucial move from $\varDelta _3$ to $\varDelta _4$, this time with emptying not the entire sequences of secrets, but only their ${{\mathsf {Reviewing}}}$-tagged components.

The exit component ${\varDelta _{{\mathsf {e}}}}$ collects unsound situations $(\sigma _1,{ sl }_1)$ (that cannot be produced from any system trace ${ tr }_1$), in order to exclude them via Exit. For Pap $_2$, such a situation is the paper’s conference phase (in state $\sigma _1$) exceeding ${{\mathsf {Submission}}}$ while there are still secrets in ${ sl }_1$ to be produced. The transition from $\varDelta _2$ to ${\varDelta _{{\mathsf {e}}}}$ occurs if a “premature” change-phase action is taken (from ${{\mathsf {Submission}}}$ to ${{\mathsf {Bidding}}}$), while ${ sl }_1$ is still nonempty. For Rev, ${\varDelta _{{\mathsf {e}}}}$ witnesses two unsound situations: when the phase exceeds ${{\mathsf {Reviewing}}}$ and either there is no ${{\mathsf {N}}}$’th review or ${ sl }_1$ still contains ${{\mathsf {Reviewing}}}$-tagged secrets.

In summary, employing the sequential unwinding theorem in our unwinding proofs had the benefit of allowing (and encouraging) a separation of concerns: the $\varDelta _i$’s and the transitions between them constitute the main sequential flow of the phase-directed proof, while ${\varDelta _{{\mathsf {e}}}}$ collects all unsound situations, taking them out of our way.

About 20 safety properties are needed in the unwinding proofs, among which:

• A paper is never registered at two conferences.

• An author always has conflicts with that author’s papers (Dis $_1$).

• A paper always has at least one author.

• A user never reviews a paper with which that user has a conflict.

• A user never gets to write more than one review for a given paper.

For example, the first property in the above list was needed in the proof of Pap $_2$, to make sure that no secret can be produced (i.e., ${{\mathsf {isSec}}}\,({{\mathsf {head}}}\,{ sl }_1)$ does not hold) from within $\varDelta _1$ or $\varDelta _2$, since no paper upload is possible without prior registration. Another safety property, which is important in itself, is that CoCon’s kernel is never accessed with a wrong user ID or password, more precisely:

• An action that is not a user-creation action and contains either a non-existing user ID or an incorrect (user ID, password) pair always yields an error output and does not change the state.

The verification took us three person months, which also counts the development of reusable proof infrastructure and automation. Eventually, we could prove the auxiliary safety properties quasi-automatically. By contrast, the unwinding proofs required interaction for indicating the Independent-Action/Reaction strategy.

5 Implementation and Deployment

CoCon has been developed as part of a research program aimed at illustrating the feasibility of practical systems based on formally verified, semantically justified information flow security. Therefore, we and our colleagues have invested some effort into a fairly practical implementation, which allowed us to deploy CoCon for real conferences.

5.1 Implemention Layers

CoCon’s implementation consists of three layers, depicted in Fig. 7: the kernel generated automatically from the Isabelle specification, the REST API layer, and the graphical user interface (GUI) layer. The last two were implemented manually. This is a refinement of Fig. 1 from the introduction, showing the separation of the web application wrapper in two layers.

Fig. 7

CoCon’s architecture in more detail

The kernel consists of the I/O automaton described in Sect. 2.2—extracted from the Isabelle specification to a Scala program using Isabelle’s code generator [31, 32]. Its verification has been the main topic of this paper.

The API, written with Scalatra (one of the standard web frameworks for Scala) [78], forwards requests back and forth between the kernel and the outside world. It converts the payload of http(s) requests into actions that are passed to the kernel; the output retrieved from the kernel is then converted into JSON output, which is delivered as the API response.

This layer also has a stateful part, which stores salts for passwords and an association between authentication tokens and pairs consisting of a user ID and a (hashed) password. When a user logs in with their ID and password, a (temporary) authentication token is issued, which is associated with the given pair (user ID, password). Upon the arrival of an http request containing the authentication token, the pair (user ID, password) is retrieved and is used to access the desired data through the kernel.

Special treatment is given to data that cannot be reasonably stored in memory, namely the pdf’s of the papers. These are stored on the disk, while the kernel state stores the paths to their locations. They are all placed in a single directory, and the names of the files are the (guaranteed to be nonoverlapping) paper IDs. When a user requests the read of a paper pdf, the API layer invokes the corresponding reading action from the kernel to retrieve the path to that file—then the pdf is provided as payload of the API response.

The GUI is a stateless layer written in AngularJS. It offers a menu system through which the users can perform high-level requests. This layer transforms each high-level request into one or more requests to the API layer, retrieves the data from the API, and finally processes and displays the results back to the user. Figure 8 shows a screenshot of CoCon’s GUI during a conference run.

5.2 Verified and Trusted Components

Our verification work targets confidentiality, safety and traceback properties of CoCon’s Isabelle kernel. In order for these guarantees to apply to the overall system (the entire web application), there are some components that we need to trust (or, in the future, verify).

Fig. 8

CoCon’s GUI: page of an author in the reviewing Phase

First, we need to trust Isabelle’s code generator. Its general-purpose design is quite flexible, supporting program and data refinement. In the presence of these rich features, the code generator is only known to preserve partial correctness, hence safety properties [31, 32]. However, here we use the code generator in a very restrictive manner, to “refine” an already deterministic specification which is an implementation in its own right, and is simply translated from the functional language of Isabelle to that of Scala. In addition, all the used Isabelle functions are proved to terminate, and nontrivial data refinement is disabled. These allow us to (informally) conclude that the synthesized kernel implementation is trace-isomorphic to the specification, hence the former has the same confidentiality and traceback properties as the latter, in particular, it leaks as little information as the latter according to our notion of leakage (which disregards timing channels).

Second, we need to trust that no leakage is introduced through the API layer (with all its employed library functions). As we have seen, this layer is a mostly stateless wrapper, forwarding information back and forth between the kernel and the outside world—which is an essentially safe behavior. An exception to statelessness is the user identity management component, which performs password hashing and issues and stores salts and authentication tokens. This trusted component is of course critical to the overall confidentiality guarantees, and is outside the scope of our verification. In fact, our security model assumes that the users act on behalf of themselves, hence our proved properties do not cover identity theft, i.e., the notion of an attacker (user of the system or not) impersonating another user—more about this in Sect. 5.3.

Finally, our verification targets only the server-side implementation logic. Lower-level attacks, as well as browser-level forging are out of its reach, but are orthogonal issues that could in principle be mitigated separately.

5.3 Deployment to Conferences and Critical Bug

CoCon has been deployed to two conferences, TABLEAUX 2015 and ITP 2016, hosting approximately 70 users and 110 users, respectively—consisting of PC members and authors.

As a program extracted from Isabelle to Scala, CoCon’s kernel stores its data in memory (except for the pdf files, which, as noted before, are subject to a special treatment). Therefore, when deploying CoCon to the conferences, the developers had to find a way to prevent loss of data due to server crashing or other accidents. It was decided to do that without any intrusion into the generated code—by using the backup facility of the Redis NoSQL database management system [75], configured to take snapshots of CoCon’s memory every second. This turned out to be a practical solution: It allowed the crash-safe use of an in-memory application, which delivered quicker responses compared to the alternative of retrieving data from a standard database. Of course, it also introduced an additional trusted component.

Unfortunately, the implementation of the API layer was plagued by a banal data race bug, caused by thread-unsafe code in the handler for authenticated requests. This made it possible that, under conditions of high traffic, the authentication tokens of two different users A and B be mixed up, meaning that A would be treated with the credentials of B.

The bug was difficult to catch because the data race occurred very seldom—apparently under the higher traffic conditions of ITP 2016, but not under the ones of TABLEAUX 2015 or our previous testing sessions. In addition, the data race was highly volatile: occurring per single http requests, then disappearing. It was discovered during the running of ITP 2016 by the PC member Andrew Tolmach, and took CoCon’s verifiers and developers an investigation of 3.5 days before a fix was deployed. This large amount of time was partly caused by the verifiers’ and developers’ doubt about the very existence of the bug, due to a misplaced confidence in the scope of verification: We were aware that CoCon had trusted components, but the notion of a user not accessing data that they are not supposed to access was exactly what our bullet-proof kernel protected against!

It did not help that the bug was also very hard to reproduce. Initially, we believed it was an (annoying but information-flow harmless) pseudo-bug, caused by the display of outdated information due to browser caching. After some effort, Tolmach was able to reproduce the bug and bring us evidence for the leak—by accessing, with the ITP 2016 chairs’ permission, some (quite harmless) information that should have been protected from that user. It was only then that we looked more closely for a problem with the identity management outside the kernel. As Tolmach put it: “In my opinion, the whole episode is an unusually clear illustration of the perils of overselling (even to oneself) the benefits of verification. The most interesting thing is not that CoCon had a bug, but rather that the developers were (temporarily) in denial about it.” (See also Fig. 9.)

In all probability, the damaging effect of the bug has been very limited. This is because CoCon’s users (authors and PC members) have used the system not through direct calls to the API, but through the graphical interface—which had the property that accessing sensitive information was at least two clicks away from the main menu, meaning that a leak required the unlikely occurrence of the data race two times in a row. In addition, the users were friendly, having no interest, desire, or attention span for malicious activity. Of course, a completely different situation would have been somewhere in the wild, with motivated attackers. For example, once Tolmach purposely set out to “attack” the system for reproducing the bug, it took him some effort but he did succeed fairly quickly.

Managing authentication tokens is a standard and well-understood activity. The bug was caused by our web developer’s lack of experience with the Scalatra web framework. In addition, the bug was in the scope of what static data-race analyzers would be able to detect. So far, while having invested a significant effort in the verification of CoCon’s kernel, we have lacked the resources and the inspiration to explore such complementary verification/bug-finding techniques for the outer components.

Fig. 9

CoCon’s login page before and after ITP 2016

6 Related Work

There is a vast amount of literature on information flow security models, with many variants of formalisms and verification/enforcement techniques.

6.1 Conceptual Frameworks for Information Flow Security

An important distinction is between models that completely forbid information flow (between designated sources and sinks) and models that only restrict the flow, allowing some declassification, i.e., controlled information release. Historically, the former were introduced first, and the latter were subsequently introduced as generalizations.

Absence of Information Flow The information flow security literature starts in the late 1970s and early 1980s [16, 25, 63], motivated by the desire to express the absence of information leaks of systems more abstractly and more precisely than by means of access control [8, 43].

Applied to our case of interest, the debate concerning information flow control versus access control can be summarized as follows: Wouldn’t properties such as “only users with a certain role can access certain data” suffice, where the data is identified as a particular state component, such as a stored document? In other words, isn’t the simpler access data a good substitute for learn information? More than twenty years ago, the security community has decisively established that the answer is “no”—McLean [52] gives a good early summary of the debate and its conclusion, which was reinforced by the subsequent abundant literature (including the works cited below). Indeed, while access control properties are partially reassuring, no collection of such properties can offer the level of assurance achieved by factoring in genuine information flow in the statements.

For example, proving that an author learns nothing about their paper’s reviews before the notification phase represents much more than proving that an author cannot access those reviews before the notification phase. Unlike the latter, the former is a global property of the system that excludes in one swoop a whole variety of potential leaks. Here is one leaking scenario: The PC members are shown all the papers, but the scores of the papers with which they have a conflict are omitted; moreover, the PC members clearly have conflicts with their own (authored) papers. But what if the current average score of the papers’ reviews is used to determine the order in which the papers are listed? Then a PC member may learn the current average score for their authored paper with high accuracy—in spite of being forbidden direct access to the scores. An ad hoc access control property can be designed to cope with this particular scenario, but there is an endless supply of such scenarios, which an information flow property would exclude without having to consider explicitly.

Influential early contributions to information flow security were Goguen and Meseguer’s noninterference [25] and its associated proof by unwinding [26]. Many other notions were introduced subsequently, either in specialized programming-language-based [69] or processalgebra-based [23, 68] settings or in purely semantic, event-system-based settings [50, 51, 62]. These notions are aimed at extending noninterference to nondeterministic systems, closing Trojan-horse channels, or achieving compositionality. The unwinding technique has been generalized for some of these variants—McLean [52] and Mantel [48] give overviews.

Even ignoring our aimed declassification aspect, most of these notions could not adequately capture our properties of interest for CoCon. One problem is that they are not flexible enough w.r.t. the observations. They state nondetectability of the presence or absence of certain events anywhere in a system trace. An exception is of course Sutherland’s nondeducibility (discussed in Sect. 3.1), which already holds the seeds for BD Security’s flexibility. Indeed, nondeducibility can express a more fine-grained positioning of such undetectable events, and also it can focus not only on entire events, but more precisely on designated secrets extracted from the events—e.g., the content of the uploaded paper, ignoring other data in the event such as the ID of the author who uploaded it.

Another line of work based on nondeducibility is Halpern and O’Neill’s [33]. They recast nondeducibility as a property called secrecy maintenance, in a multi-agent framework of runs-and-systems. Their formulation enables general-purpose epistemic logic [66] primitives for deducing the absence of leaks.

Restriction of Information Flow A large body of work on declassification was pursued in a (mostly) language-based setting. Sabelfeld and Sands [71] give an overview of the state of the art up to 2009. They identify some generic dimensions of declassification that are relevant for our CoCon case study:

• What information is released? Here, document content, e.g., of papers, reviews, etc.

• Where in the system is information released? In our case, the relevant “where” is a “from where” (referring to the source, not to the exit point): from selected places in the system trace, e.g., the last submitted version before the deadline.

• When can information be released? After a certain trigger occurs, e.g., authorship.

• Who releases the information? The users who are entitled, e.g., the authors of a document.

Rushby’s intransitive noninterference [47, 67] is an extension of noninterference targeting the “where” dimension of declassification. It allows the downgrading of information, say, from High to Low, via a controlled Declassifier level. It could be possible to encode aspects of our properties of interest as intransitive noninterference, e.g., we could encode the act of a user becoming an author as a declassifying action for the target paper.

Some information flow security concepts based on knowledge, similar in spirit to our BD Security, have been quite influential in the language-based setting. Zdancewic and Myers’s robust declassification [82] limits what a class of attackers can learn if allowed to (actively) modify the system in addition to what they can by (passively) observing the system—thus addressing the “who” dimension in a blend of confidentiality and integrity.

Sabelfeld and Myers’s delimited release [70] addresses the “what” dimension. It describes the containment of declassification to specified escape hatches as an end-to-end property, involving the initial and final states of program executions. It can be viewed as a particular form of BD Security, where secrets are only produced at the beginning and observations are only produced at the end of traces.

Perhaps most similar to BD Security are the concepts introduced in a series of papers by Askarov and collaborators [2,3,4,5]. Although their work is placed in a language-based setting, the core of their security properties refers to traces of events—hence could be routinely adapted to arbitrary I/O automata. They introduce gradual release [4] as an extensional means to capture the “where” dimension—defining knowledge along (low components of) traces similarly to how we define the declassification associated to a trace, ${{\mathsf {Dec}}}_{{ tr }}$, introduced in Sect. 3.2 to motivate BD Security. Gradual release requires that knowledge changes (increases) only at specifically indicated events. Unlike in the intransitive noninterference’s take on the “where” dimension, the security guarantees offered by gradual release also cover traces on which actual declassification occurs. An extension of gradual release [5] with ideas from delimited release achieves fine-grained control over “where” and “what” declassification similar to that of BD Security—a main difference being their focus on variation of knowledge at different points, contrasting BD Security’s focus on the overall knowledge acquired. Later refinements of gradual release account for integrity in addition to confidentiality [3] (also incorporating ideas from robust declassification) and for the presence of weaker, forgetful attackers [2]. As far as we see, forgetful attackers could also be modeled by an upgrade of BD Security: extending our simple filter-map observation infrastructure to a stateful one.

Finally, flexible declassification (especially along the “when” dimension) has been addressed by custom temporal logics. Dimitrova et al. introduce SecLTL [20], a linear temporal logic enriched with an information-hiding operator. Their motivating examples include the following properties, referring to a minimalistic, finite-state conference management system [20, §1]:

• Last accept/reject before Close remains secret until Release.

• All accept/reject’s except the last before Close remain secret forever.

These roughly correspond to the following BD Security properties:

• One learns nothing about the last accept/reject decision (where “last” means “last uploaded before a Close action occurs”), unless/until a Release action occurs.

• One learns nothing about all but the last accept/reject decision.

Thus, on a high level, SecLTL seems able to capture, if not arbitrary BD Security properties, at least (slight reformulations of) the instance triggers and bounds we employed for CoCon. But upon a closer look we find that the superficially similar formulations yield mathematically quite different properties. Indeed, whereas the BD Security instances are $\forall \exists$ properties (quantifying universally over the original trace ${ tr }_1$ and the bound-related secrets, and existentially over the alternative trace ${ tr }_2$), the SecLTL counterparts are $\forall \forall$ properties—as can be seen from unpacking the semantics of SecLTL’s information-hiding operator. A second important difference is that SecLTL keeps the traces ${ tr }_1$ and ${ tr }_2$ synchronized, in that any differences in their events (be they observable or not) can occur only after secrets are being produced—in the spirit of MAKS’s “backwards strict” properties [48, §3.4.4]. More general temporal logics for hyperproperties, such as HyperCTL$^*$ [15, 22, 64], allow for arbitrary alternations of quantifiers (including $\forall \exists$), but preserve the aforementioned built-in synchronization. Depicting the exact relationship between temporal-logic-based and knowledge-based definitions of information flow security would be interesting future work.

6.2 Information Flow Security for Conference Management Systems

Arapinis et al. [1] introduce ConfiChair, a conference management system that improves on the state of the art by guaranteeing that the cloud, consisting of the system provider, cannot learn the content of the papers and reviews, and cannot link users with their written reviews. This is achieved by a cryptographic protocol based on key translations and mixes. They encode the desired properties as strong secrecy (a property similar to Goguen-Meseguer noninterference) and verify them using the ProVerif [10] tool specialized in security protocols. Our work differs from theirs in three major aspects. First, they propose a cryptography-based enhancement, while we focus on a traditional conference system. Second, they manage to encode and verify the desired properties automatically, while we use interactive theorem proving. While their automatic verification is an impressive achievement, we cannot hope for the same with our targeted properties which, while having a similar nature, are more nuanced and complex. For example, the properties Pap $_2$ and Rev, with such precise indication of declassification bounds, go far beyond strong secrecy and require interactive verification. Finally, we synthesize functional code isomorphic to the specification, whereas they provide a separate implementation, not linked to the specification which abstracts away from many functionality aspects.

Qapla  [53] is a middleware tool for enforcing access control policies for database systems. It has been deployed to the HotCRP conference management system. An interesting future work would be to use BD Security to analyze the information flow content of the enforced policies. We expect that such an analysis would yield a certain overlap between the CoCon properties we have verified and the HotCRP properties that can be inferred from the Qapla policies.

6.3 Holistic Verification of Systems

Proof assistants are today’s choice for precise and holistic formal verification of hardware and software systems. Already legendary verification works are the AMD microprocessor floating-point operations [55], the CompCert C compiler [44] and the seL4 operating system kernel [40]. More recent developments include a range of microprocessors [34], Java and ML compilers [42, 46], and model checkers [21, 79].

Major holistic verification case studies in the area of information flow security are less well represented, perhaps due to the more complex nature of the involved properties compared to traditional safety and liveness [49]. They include a hardware architecture with information flow primitives [18], a separation kernel [17], and noninterference for seL4 [56, 57]. A substantial contribution to web client security is the Quark verified browser [37]. Our own line of work is concerned with proof assistant verification of web-based system confidentiality grounded in BD Security: It started in 2014 with CoCon and continued with the CoSMed social media platform  [7] and its extension to a distributed model, CoSMeDis  [6]. For most of the CoSMed/CoSMeDis properties of interest, the bounds ${{\mathsf {B}}}$ had to be significantly more complex, to account for the repeated opening and closing of access windows, i.e., the repeated firing and canceling of various triggers. This made the actual triggers ${{\mathsf {T}}}$ unnecessary, meaning they had to be instantiated to “vacuously false” [7, §3]. (In general, the triggers cannot be encoded in the bounds—but could be if we changed BD security to a more symmetric notion, requiring that all transitions in the alternative trace also falsify the trigger [7, §3.3].)

Outside the realm of proof-assistant based work, Ironclad [35] provides end-to-end security guarantees down to the binary code level and across the network. The information flow properties discussed in [35] focus on controlling where in the program information is declassified, e.g., in trusted declassification functions. A verified Ironclad app is deployed on a server, and a Trusted Platform Module certifies to remote users of the app that the code running on the server indeed corresponds to the verified code.

6.4 Automatic Analysis of Information Flow

There are quite a few programming languages and tools aimed at supporting information flow secure programming—such as Jif [38] and its distributed extension Fabric [45] and I/O-reactive extension JRIF [41], LIO [24] and its distribuetd extension Hails [24], Paragon [12], Spark [73], Jeeves [81] and Ur-Web [13]—as well as information flow tracking tools for the client side of web applications [9, 14, 29]. The properties specifiable in these tools are significantly weaker (and more tractable) compared to those we considered in this paper.

We believe the future of information flow security verification will see an increased cooperation between fully automatic tools and proof assistants; the former being employed for wide-covering lightweight properties and the latter being employed more sparingly, for heavier properties of clearly isolated relatively small cores of systems. Compositionality results for information flow security [6, 28, 30, 48, 59] will play a key role in achieving such a cooperation on a well-understood semantic basis.