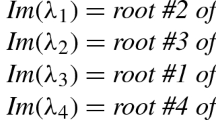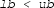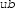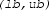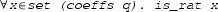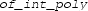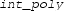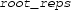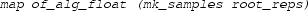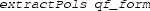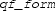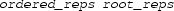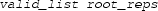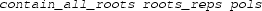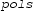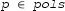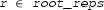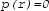Abstract
We present a proof procedure for univariate real polynomial problems in Isabelle/HOL. The core mathematics of our procedure is based on univariate cylindrical algebraic decomposition. We follow the approach of untrusted certificates, separating solving from verifying: efficient external tools perform expensive real algebraic computations, producing evidence that is formally checked within Isabelle’s logic. This allows us to exploit highly-tuned computer algebra systems like Mathematica to guide our procedure without impacting the correctness of its results. We present experiments demonstrating the efficacy of this approach, in many cases yielding orders of magnitude improvements over previous methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nonlinear polynomial systems are ubiquitous in science and engineering. As real-world applications of formal verification continue to grow and diversify, there is an increasing need for proof assistants (e.g., ACL2, Coq, Isabelle [27], HOL Light and PVS) to provide automation for reasoning about nonlinear systems over the reals [17, 24, 25].
Cylindrical algebraic decomposition (CAD) [8] is one of the most powerful known techniques for analysing non-linear polynomial systems. CAD-based methods have been implemented in various systems such as Z3 [9], QEPCAD [3], Mathematica and Maple. However, implementing CAD-based decision procedures within proof assistants has been hindered by the difficulty in formalising the mathematics justifying CAD computations.
In this paper, we present a formally verified procedureFootnote 1 based on CAD for univariate polynomial problems with rational coefficients. Goals such as
can be discharged by our tactic automatically. It should be noted that certifying a general multivariate CAD procedure is much harder, and the univariate version we describe in the paper is only a first step in that direction.
A key feature of our procedure is its certificate-based design in which an external untrusted (but ideally highly efficient) program is used to find certificates, and those certificates are then checked by verified internal procedures. Overall, the soundness of our procedure depends solely on the soundness of Isabelle’s logic (and code generationFootnote 2) rather than trusted external oracles. This is much like Isabelle’s sledgehammer tactic, which sceptically incorporates various external tools.
Our main contributions are:
-
An efficient formalised theory of Tarski queries,
-
An efficient approach to univariate sign determination at real algebraic points,
-
A practical formally verified procedure for real algebraic problems based on univariate CAD.
The paper continues at follows: A motivating example (Sect. 2) and a description of the overall design (Sect. 3) sketch the general idea of our procedure. The construction and manipulation of real algebraic numbers is developed in (Sect. 4), including a sign determination procedure for evaluating polynomials at real algebraic points (Sect. 5). The main proof is described in (Sect. 6), which is followed by a discussion of interaction with external solvers (Sect. 7). Next, experiments and related work (Sect. 8) are described along with further discussion of our tactic (Sect. 9). We then conclude with a look towards the future (Sect. 10).
2 A Motivating Example
Unlike the general case of \(\mathbb {R}^n\), the restriction of CAD to univariate problems (i.e., to \(\mathbb {R}^1\)) is relatively straight-forward. Suppose we wish to prove
where
To do so, we can decompose\(\mathbb {R}\) into disjoint connected components induced by the roots of P and Q. This is illustrated in Fig. 1:

and it can be observed that both P and Q have invariant signs over each of these components. For example, as can be seen from Fig. 1, \(P(x)<0\) and \(Q(x)>0\) hold for all \(x \in (-\sqrt{2},\sqrt{2})\). To decide the conjecture, we can pick sample points from each of these components and evaluate \(\lambda x.\, P(x) > 0 \vee Q(x) \ge 0\) at these points. That is,
since
Analogously, to decide an existential formula
we have
In performing these arguments, there were a few “obvious” subtleties:
-
The decomposition of \(\mathbb {R}\) into the seven regions given covered the entire real line. That is,
$$\begin{aligned} (-\infty ,-3) \cup \{-3\} \cup (-3,-\sqrt{2}) \cup \{-\sqrt{2}\} \cup (-\sqrt{2},\sqrt{2})\cup \{\sqrt{2}\} \cup (\sqrt{2},\infty ) = \mathbb {R}. \end{aligned}$$ -
The “sign-invariance” of P and Q over each region was exploited to allow only a single sample point to be selected from each region. This property holds as by the Intermediate Value Theorem, P and Q can only change sign by passing through a root.
-
The signs of univariate polynomials were evaluated at irrational real algebraic points like \(\sqrt{2}\) to determine the truth values of atomic formulas.
In creating our automatic proof procedure, all of this routine reasoning must, of course, be formalised. Moreover, the isolation of polynomial roots (and thus sign-invariant regions) and the sign determination for polynomials at real algebraic points are computationally expensive operations. Computer algebra systems like Mathematica have decades of tuning in their implementations of these core algebraic algorithms. To have a practical proof procedure, we wish to take advantage of these highly tuned external tools as much as possible. Let us next describe how this can be done.
3 A Sketch of Our Certificate-Based Design
There is a rich history of certificate-based, sceptical integrations between proof assistants and external solvers. Examples include John Harrison’s sums-of-squares method [17] and the Sledgehammer [31] command in Isabelle.
Certificate-based approaches are motivated by many observations, including:
-
External solvers are often highly tuned and run much faster than verified ones.
-
Verification of certificates from external solvers is usually much easier than finding them. Such verification ensures the soundness of the overall tactic.
-
Switching between different external solvers does not require changes in formal proofs.

Algorithm 1 sketches our idea for univariate universal formulas. In particular, in line 3, we use external programs to return real roots of polynomials (i.e., \(\mathfrak {P}\)) from the quantifier-free part of the formula (i.e., F(x)). Those roots (i.e., \( roots \)) correspond to a decomposition such that each polynomial from \(\mathfrak {P}\) has a constant sign over each component of this decomposition. Since the roots are returned by untrusted programs, in line 5, we not only check \(\forall x \in samples .\, F(x)\) as in Eq. (1) but also certify that these roots are indeed all real roots of \(\mathfrak {P}\).
The step in line 3 in Algorithm 1 is more commonly referred as (real) root isolation, which is a classic and well-studied topic in symbolic computing. Although we can in principle formalise our own root isolation procedure (e.g., using the Sturm–Tarski theorem), it is utterly unlikely that our implementation will be competitive with state-of-the-art ones, especially for polynomials of high degree, large bit-width, or whose roots are very close together. Therefore, we delegate this computationally expensive step to external tools.

With existential formulas, the situation is even simpler as illustrated in Algorithm 2, since we do not need to deal with the decomposition internally. Rather, all we need is a real algebraic witness that satisfies \(\lambda x.\, F(x)\) to certify \(\exists x.\, F(x)\). What is more interesting is that the satisfaction problem for \(\lambda x.\, F(x)\) can be not only solved by a CAD procedure, which is complete but not very fast due to its symbolic nature, but also be complemented by highly efficient incomplete numerical methods. Thus it is natural to externalize the step in line 2 in Algorithm 2.
4 Encoding Real Algebraic Numbers
External programs in either Algorithms 1 and 2 can return real algebraic numbers (e.g. \(\sqrt{2}\)). In this section, we see how to formalise such numbers in Isabelle/HOL.
The real algebraic numbers (\(\mathbb {R}_{\mathrm {alg}}\)) are real roots of non-zero polynomials with integer (equivalently, rational) coefficients. They form a countable, computable subfield of the real numbers. To encode them, we use a polynomial with integer coefficients and a root selection method to “pin down” the root in question. Common root selection methods include isolating intervals, root indices or Thom encodings. We use the root interval approach, that is, a real algebraic number \(r \in \mathbb {R}_{\mathrm {alg}}\) will be given by
-
A polynomial \(p \in \mathbb {Z}[x]\) s.t. \(p(r) = 0\), and
-
Two rationals \(a,b \in \mathbb {Q}\) s.t. r is the only root of p contained in [a, b].
To reason over the reals, we define a function

to embed those real algebraic numbers into the reals:

where

is a polynomial with integer coefficients and the two

arguments represent an interval. Note, a

in Isabelle/HOL is a dyadic rational number of the form
Compared to our previous work [21], where a pair of rational numbers is used to represent an interval, the dyadic rational approach is more efficient due to the elimination of ubiquitous greatest common divisor (gcd) operations within rational arithmetic.
In Isabelle/HOL, a real number is represented as a Cauchy sequence of type

, where a Cauchy sequence is defined as

We then convert an encoding of a real algebraic number into a sequence of type

. The idea is to bisect the isolating interval through each recursive call, and proceed with the half where the sign of the polynomial changes at its end points:

where

evaluates the polynomial

at the point

. Note,

encodes a real algebraic number here (rather than

), as we can embed

and

into

.
It can be then shown that the sequence constructed by

is indeed a Cauchy sequence and the real number represented by this sequence resides within the interval \([ lb , ub ]\), provided \( lb < ub \):


Note, the function

of type

constructs a real number from its underlying representation (i.e. a Cauchy sequence).
Finally, we can finish the definition of

:


where

ensures
-
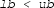
,
-
The polynomial

is of different signs (and non-zero) at

and
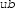
,
-
The polynomial

has exactly one real root within the interval
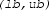
.
With the help of

, we can now encode the real algebraic number \(\sqrt{2}\) as

where

corresponds to the polynomial \(-2 x^0+ 0 x^1 + 1 x^2 = x^2-2\), and 1 and 2 are the lower bound and upper bound respectively, such that \(\sqrt{2}\) is the only root of \(x^2-2\) within the interval (1, 2).
Furthermore, we can formally derive that

is indeed a root of

within the interval

:

where

embeds the integer polynomial

into a real one.
5 Deciding the Sign of a Univariate Polynomial at Real Algebraic Points
In the previous section, we described how to encode a real algebraic number as an integer polynomial and two dyadic rational numbers. Now, suppose we have
where \((x^2-2,1,2)\) is abbreviated from

for the sake of readability. How can we computationally prove that
Considering that \(\mathbb {R}_{\mathrm {alg}}\) is a computable subfield of \(\mathbb {R}\) and has decidable arithmetic and comparison operations, it is natural to evaluate such formulas through algebraic arithmetic:
where \(\times _{\mathrm {alg}}\) and \(-_{\mathrm {alg}}\) are exact algebraic arithmetic operations that usually involve calculation of bivariate resultants. Although such computations are currently possible in Isabelle/HOL [21, 36], they are far from efficient.
In this section, we describe a verified procedure to decide the sign of univariate polynomials with rational coefficients at real algebraic points which uses only rational (or dyadic rational) arithmetic rather than costly algebraic arithmetic.
5.1 The Sturm–Tarski Theorem
We abbreviate \(\mathbb {R} \cup \{-\infty ,\infty \}\) as \(\overline{\mathbb {R}}\), the extended real numbers.
Definition 1
(Tarski Query) The Tarski query \(\mathrm {TaQ}(Q,P,a,b)\) is
where \(a,b \in \overline{\mathbb {R}}\), \(P, Q \in \mathbb {R}[X]\), \(P\ne 0\) and \(\mathrm {sgn}: \mathbb {R} \rightarrow \{-1,0,1\}\) is the sign function.
The Sturm–Tarski theorem [23, Chapter 8] (or Tarski’s theorem [2, Chapter 2]) is essentially an effective way to compute Tarski queries through some remainder sequences:
Theorem 1
(Sturm–Tarski) The Sturm–Tarski theorem states
where \(P \ne 0\), \(P,Q\in \mathbb {R}[X]\), \(P'\) is the first derivative of P, \(a,b \in \overline{\mathbb {R}}\), \(a<b\) and are not roots of P, \(\mathrm {SRemS}(P,P'Q)\) is the signed remainder sequence of P and \(P'Q\), and
is the difference in the number of sign variations (after removing zeroes) in the polynomial sequence \([p_0 , p_1 , \dots , p_n ]\) evaluated at a and b.
Note that the more famous Sturm’s theorem, which counts the number of distinct real roots (of a univariate polynomial) within an interval, is a special case of the Sturm–Tarski theorem when \(Q=1\).
5.2 A Formal Proof of the Sturm–Tarski Theorem
Our proof of the Sturm–Tarski theorem in Isabelle is based on Basu et al. [2, Chapter 2] and Cohen’s formalisation in Coq [6].
The core idea of our formal proof is built around the Cauchy index. First defined by Cauchy in 1837, the Cauchy index of a real rational function encodes deep properties of its roots and poles, and can be used as the basis of an algebraic method for computing Tarski queries.Footnote 3
Definition 2
Given \(P,Q \in \mathbb {R}[x]\) and \(x \in \mathbb {R}\), \(\mathrm {jump}(P,Q,x)\) is defined as
For example, let \(Q=x-4\) and \(P=(x-3)(x-1)^2(x+1)\). The graph of Q / P is shown in Fig. 2. We have
The Cauchy index

is the sum of the jumps of q / p over the interval (a, b):

By case analysis, we can prove a connection between the Tarski query and the Cauchy index:

where

is a formal definition of the Tarski query

and

is the first derivative of

.
Moreover, the Cauchy index can be related to Euclidean division (

) on polynomials by a recurrence:

where
A similar recurrence relation holds for the number of sign variations of the signed remainder sequences (

):

where

is defined as

and the signed remainder sequence (

) is defined as

and

returns the number of sign changes when evaluating a list of polynomials (

) at

.
Finally, by combining

,

and

, we derive the Sturm–Tarski theorem:

Note, this is just the bounded case of the Sturm–Tarski theorem. Proofs for the unbounded and half-bounded cases are similar.
5.3 Sign Determination Through the Sturm–Tarski Theorem
Given a polynomial q with rational coefficients and our encoding of a real algebraic number \(\alpha \)
where p is an integer polynomial, and \( lb \) and \( ub \) are dyadic rationals, we can effectively decide the sign of \(q(\alpha )\) using the Sturm–Tarski theorem, provided

holds. The rationale behind is that

ensures \(\alpha \) is the only root of p within the interval \(( lb , ub )\), hence
Importantly, it can be observed that evaluating \(\mathrm {Var}(\mathrm {SRemS}(p,p'q); lb , ub )\) requires only rational arithmetic rather than costly algebraic arithmetic.
To be even more efficient, we refine the procedure further to make use of dyadic rational arithmetic. The main advantage of dyadic rational arithmetic over rational arithmetic are reduced normalization steps and possible bit-level operations. For example, consider two rational numbers \(\frac{a_1}{b_1}\) and \(\frac{a_1}{b_2}\) where \(a_1,b_1,a_2,b_2 \in \mathbb {Z}\), their sum is
To counter the growth in the size of representations, we usually need to normalize the result by factoring out the gcd. Such gcd operations can be the source of major computational expense. Thankfully, they are unnecessary in the context of dyadic rationals. The sum of two dyadic rationals \((a_1,e_1)\) and \((a_2,e_2)\) where \(a_1,e_1,a_2,b_2 \in \mathbb {Z}\) is
Moreover, multiplications by powers of two, such as \(a_1 2^{e_1-e_2}\), can be optimised by shift operations.
However, the problem with dyadic rational numbers is that they do not have the division operation (e.g. \(1 \times 2^0\) divided by \(3 \times 2^0\) is no longer a dyadic rational), hence they do not form a field, while Euclidean division only works for polynomials over a field. This problem can be solved if we switch from Euclidean division (

and

):
to pseudo-division (

and

) [10]:
since pseudo-division can be carried out by polynomials over an integral domain (rather than a field).
Based on pseudo-division, the signed pseudo-remainder sequence (\(\mathrm {SPRemS}\)) can be defined:

where

is the scalar product on polynomials and

is the leading coefficient of

. Accordingly, the function to count the difference in sign variations can be refined:

and linked to the previous one based on signed remainder sequences (\(\mathrm {SRemS}\)):

where

embeds a

into

and

coverts a

(i.e. polynomial with dyadic rational coefficients) to a

by embedding each of the coefficients into

.
Finally, we define a function

that returns the sign of a univariate polynomial at some point:

Note, for now, if either

or any coefficient of

is an irrational real number (e.g. an irrational real algebraic number), evaluating

will raise an exception, as Isabelle/HOL, by default, only supports rational arithmetic. Although we can eliminate some such exceptions by loading any of the recent algebraic arithmetic libraries [21, 36], we consider exact algebraic arithmetic too slow for our purpose as stated at the beginning of Sect. 5. Alternatively, by proving some code equations, we can restore the executability of

when

is constructed by

and coefficients of

are rational reals:

where
-
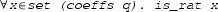
checks if each coefficient of

is rational,
-
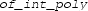
converts an integer polynomial into a dyadic rational one,
-
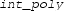
clears denominators in the coefficients by multiplying each coefficient by the least common multiple (of the denominators),
-

throws an exception, if either \((p, lb , ub )\) is an invalid representation of a real algebraic number or the polynomial

has any non-rational coefficient.
And note that evaluating

requires only dyadic arithmetic, which is much more efficient than exact algebraic arithmetic.
Moreover, the executability of

is restored similarly as well:

where

checks if the polynomial p has exactly one real root within the interval \(( lb , ub )\) by exploiting Sturm’s theorem (a special case of our formalised Sturm–Tarski theorem).
After restoring executability of

on real algebraic numbers, we can now check the sign of \(P(x)=\frac{1}{2}x^2-1\) at \(\sqrt{2}\) by typing the following command:

which returns 0 (i.e. \(P(\sqrt{2})=0\)).
5.4 Remark
A formal proof of the Sturm–Tarski theorem is not new among proof assistants: it has been formalised in PVS [25] and Coq [6]. However, as far as we know, we are the first to exploit this theorem to build a verified sign determination procedure of real algebraic numbers, which uses only rational or dyadic rational arithmetic.
Real algebraic numbers are essential in symbolic computing, and well studied. In general, exact real algebrac arithmetic is rarely used in modern computer algebra systems due to its extreme inefficiency. For example, consider the problem of isolating the real roots of a polynomial with real algebraic coefficients. Modern approaches usually use sophisticated techniques to soundly approximate those coefficients to a certain precision rather than carrying out exact algebraic arithmetic [5, 33, 35], relying on exact symbolic procedures as a fall-back in degenerate cases.
Following these efficient modern approaches, our sign determination procedure can be improved in at least the following ways:
-
Sophisticated interval arithmetic can be used to decide the sign before resorting to a remainder sequence, as has been done in Z3 [10]. This approach should help when the sign is non-zero.
-
Pseudo-division, which we are currently using for building remainder sequences, is not good for controlling coefficients growth. More sophisticated approaches, such as subresultant sequences and modular methods, can be used to optimise the calculation of remainder sequences.
6 The Formal Development of the Decision Procedure
In this section, we describe the main proof underlying our tactic.
6.1 Parsing Formulas
The first step of our tactic is to parse the target formula into a structured form. This process is usually referred as reification [4] in Isabelle/HOL. More specifically, given an Isabelle/HOL term e of type \(\tau \), we define a (more structured) datatype \(\delta \) and an interpretation function \( interp \) of type \(\delta \Rightarrow \tau \ list \Rightarrow \tau \), such that for some e‘ of type \(\delta \)
where \( xs \) is a list of free variables in e. Subsequently, instead of directly dealing with e, we now convert it into a more pleasant form \( interp \ e`\ xs \) where e‘ is in fact a formal language that captures the structure of e.
The datatypes we defined to capture the structure of target univariate formulas are as follows:




and the interpretation functions:




Given the definition of a (structured) datatype

and the corresponding interpretation function

, target formulas can now be parsed. For example, we can convert a univariate formula

into an equivalent form

In particular, note

in which inequalities have been parsed into a polynomial sign determination problem.
On the contrary, a bivariate non-closed formula such as

will be converted into

where the

constructor indicates that such formula is not supported by our current tactic.
6.2 Existential Case
To discharge a univariate existential formula is easy: we can computationally check if a certificate (i.e., a real algebraic number) returned by an external solver satisfies the quantifier-free part of the formula:

where

of type


is a certificate that is supposed to be instantiated by an external solver. The function

converts

from

to

. In other words, to prove an existential formula:

we can computationally check the truth value of the quantifier-free part of the formula at

:

which is possible due to the sign determination procedure described in Sect. 5.
6.3 Universal Case
For the universal case, the core lemma is as follows:

where

states that

is a bijective function between the decomposition

and the sample points

. Essentially, what the lemma

shows is that given a predicate

, an unbounded universal formula

is equivalent to a bounded one

, if the truth value of

is constant over each component of the decomposition:

.
On top of the lemma

, we similarly convert an unbounded univariate real formula into a bounded one:

where
-
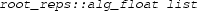
is a certificate that should be instantiated by an external solver. More specifically,
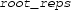
should be the representation of a list of real roots (in ascending order) of polynomials from the quantifier-free part of the target formula,
-
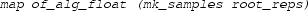
constructs sample points from the representation of a list of roots,
-
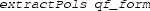
extracts polynomials from the quantifier-free part
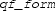
,
-
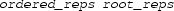
and
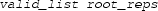
together ensure that the representation of roots are valid and those roots are in ascending order,
-
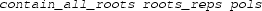
checks if
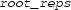
is a representation of all real roots of the polynomials
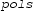
. Specifically, by Sturm’s theorem, the number of total distinct real roots of each
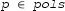
can be computed, which can be then compared with the number of
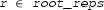
that
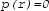
.
Most importantly, all assumptions of the lemma

and its right-hand side

can be computationally checked, through which we can prove an unbounded univariate universal formula:

.
7 Linking to an External Solver
Certificates for both existential and universal cases can be produced by any program performing univariate CAD. For now, we implement the program on top of Mathematica. More specifically, the universal certificates are constructed by the Mathematica command SemialgebraicComponentInstances, which gives sample points in each connected component of a semialgebraic set. The existential certificates are constructed by the command FindInstance, which incorporates powerful numerical methods to accelerate the search for real algebraic sample points.
Also, it may be worth mentioning that after a certificate has been found, our tactic will record it (as a string) so that repeating the proof no longer requires the external solver. This is much like the sums-of-squares tactic [17].
In general, the certificate-based design grants us much flexibility: We can easily switch to a more efficient external solver without modifying existing formal proofs. In fact, we were first using an implementation of univariate CAD built within MetiTarski, which turned out to be not very efficient, and we simply switched to the current one based on Mathematica. In the future, we plan to experiment with other open-source CAD implementations such as Z3 and QEPCAD to provide more options with external solvers.
8 Experiments and Related Work
The most relevant work is the recent tarski strategy by Narkawicz et al. [25] in PVS. Both their work and ours rely on a formal proof of the Sturm–Tarski theorem (which they call Tarski’s theorem) and handle roughly the same class of problemsFootnote 4 (i.e., first-order univariate formulas over reals). There are two main differences between their work and ours:
-
Their procedure resembles Tarski’s original quantifier elimination [2, Chapter 2] and Cyril Cohen’s quantifier elimination procedure in Coq [6, Chapter 12] by making use of both the Sturm–Tarski theorem and matrices. In contrast, our tactic is based on CAD and real algebraic numbers (instead of matrices).
-
Their procedure is entirely built within PVS, while ours sceptically makes use of efficient external programs to generate certificates.
To compare both tactics empirically, we have conducted experiments on several typical examples from their paperFootnote 5 and the MetiTarski projectFootnote 6 [29]. The experiments are run on a desktop with an Intel Core 2 Quad Q9400 (quad core, 2.66 GHz) CPU and 8 gigabytes RAM. Results of the experiments are illustrated in Fig. 3, where our

tactic includes both certificate searching and checking process, while the

does the checking part only (when repeating a proof with certificates already recorded as a string).
In general, the experiments indicate that our tactic outperforms the tarski strategy in PVS. Particularly, the advantage of our tactic becomes greater as the problems become more complex, which can be attributed to the fact that our tactic has much better worst-case computational complexity (polynomial vs. exponential in the number of polynomials).
In the case of general multivariate problems, the CAD procedure is doubly exponential while Tarski’s quantifier elimination procedure is non-elementary in the number of variables [2, Chapter 11]). When limited to univariate problems, the CAD procedure degenerates to root isolation and sign determination on a set of univariate polynomials, which is of polynomial complexity in the number of polynomials and their degree bound [2, Chapter 10]). In comparison, Tarski’s quantifier elimination procedure, even when limited to univariate problems, is still exponential in the number of polynomials [7].
In addition, it is worth noting that as the problems become more complex (e.g., ex6 and ex7 in Fig. 3), certificate checking becomes the bottleneck factor of our tactic (especially for universal problems). This indicates that, despite the fact that certificate searching is much harder than certificate checking, the Mathematica implementation is still much more efficient than our verified certificate-checking procedure. This leaves much room for future optimisations.
Our work has also been greatly inspired by Cyril Cohen’s PhD thesis [6], within which a quantifier elimination procedure has been built upon the Sturm–Tarski theorem and real algebraic numbers formalised within the Coq theorem prover. However, our goals and approaches are very different.
Cohen’s work is part of a large project that has formalised the Feit–Thompson theorem (odd order theorem) in Coq [15], and focuses more on theoretical developments than we do. For example, they proved the Sturm–Tarski theorem to construct an RCF quantifier elimination procedure in the spirit of Tarski’s original method, which has important theoretical properties but is not practical as a proof procedure. Moreover, he has formalised arithmetic on real algebraic numbers and shown that they form a real closed field via resultants. We have not formalised resultants at all. Our sign determination algorithm uses the Sturm–Tarski theorem, which is significantly more efficient in practice than using resultants. On the other hand, as it was unnecessary for our proof procedure, we have not proved in Isabelle that the real algebraic numbers form a real closed field. In general, compared to his work, ours stresses the practical side over the theoretical. Fundamentally, we want to build procedures to solve non-trivial problems in practice.
Decision procedures based on Sturm’s theorem have been implemented in Isabelle and PVS before [14, 26]. Their core idea is to count the number of real roots within a certain (bounded or unbounded) interval. Generally, they can only handle formulas involving a single polynomial, so they are not complete for first-order formulas (unlike our tactic and the tarski strategy in PVS).
Assia Mahboubi [22] has implemented the executable part of a general CAD procedure in Coq, but as far as we know, the correctness proof for her implementation is still ongoing. This is also one of the reasons for us to choose the certificate-based approach rather than directly verifying an implementation.
There are other methods to handle nonlinear polynomial problems in theorem provers, such as sums of squares [17], which is good for multivariate universal problems but is not applicable when the existential quantifier arises, and interval arithmetic [18, 34], which is very efficient for some cases but is not complete. These methods and ours should be used in a complementary way.
9 Discussion and Applications
One of our driving motivations is the integration of MetiTarski with Isabelle. MetiTarski [1] is a first-order theorem prover for real number inequalities involving transcendental functions such as \(\sin \), \(\tan \) and \(\exp \). It can automatically prove formulas like
The main idea behind MetiTarski is to approximate transcendental functions by polynomial or rational function bounds, and then solve the formula by a combination of a resolution theorem proving and an external Real Closed Field (RCF) decision procedure (QEPCAD, Mathematica or Z3). MetiTarski is a version of Joe Hurd’s Metis prover [19], modified to include arithmetic simplification and integration with RCF decision procedures, along with many other refinements.
Applications of MetiTarski include verification problems arising in air traffic control [13] and analogue circuit designs [11]. As some of the applications are safety critical, it is natural to consider to integrate MetiTarski with an existing interactive theorem prover, whose internal logic can be used to ensure the correctness of MetiTarski’s proofs. Besides, the automation provided by MetiTarski is generally useful to interactive theorem provers.
MetiTarski has been integrated with the PVS theorem prover [28] as a trusted oracle [12]. The authors state that the automation introduced by MetiTarski for closing sequents containing real-valued functions considerably outperforms existing tactics in PVS. However, this tactic should not be used in a certification environment, where external oracles are not allowed.
Our eventual goal is to integrate MetiTarski into the Isabelle/HOL theorem prover. Isabelle can verify purely logical inferences (in fact, it contains an internal copy of the Metis theorem prover), and the third author has just formalised most of the bounds of transcendental functions used by MetiTarski [30]. The primary remaining hurdle is the RCF decision procedure, and the work presented here is the first step towards it.
Finally, let us say a bit about how our work might be generalised to multivariate problems. In doing so, we plan to continue our certificate-based approach, as we are unlikely to implement a verified internal CAD procedure comparable in efficiency to a state-of-the-art implementation. It is still not obvious to us where the clear separation between search and verification should be in the multivariate case, but we have already made some progress:
-
The bivariate sign determination procedure based on recursive application of the Sturm–Tarski theorem described in our previous work [21] can be easily generalised to a multivariate one (i.e., a procedure to decide the sign of a multivariate polynomial at real algebraic points), which can be then used to efficiently certify purely existential multivariate formulas over reals.
-
Our recent formalisation of Cauchy’s residue theorem [20] can be used to certify a key theorem used in general CAD: that the complex roots of a polynomial continuously depend on its coefficients.
10 Conclusion
We have described our work of building a procedure for first-order univariate polynomial problems in Isabelle/HOL. Compared to existing tactics among proof assistants, noticeable features of our tactic are
-
It is based on univariate cylindrical algebraic decomposition (CAD).
-
It sceptically integrates efficient external solvers in a certificate-based way, so that its soundness solely depends on Isabelle’s logic (and code generation machinery) rather than the external solvers.
This is made possible by certificate-based approaches to real root isolation and sign-determination for evaluating polynomials at real algebraic points. As much of the novelty in our work is motivated by practical efficiency considerations, we have performed experiments comparing our procedure with another real algebraic proof procedure, the tarski method in PVS. By making use of efficient external solvers, our procedure is shown to empirically outperform this other method by substantial margins. We believe this adds further impetus to the certificate-based methods for a wide variety of formal proof procedures.
Certificate-based methods can be compared on the basis of how much mathematics and computation are required both to find and check their certificates. For example, to convert a Positivstellensatz certificate into a HOL-Light proof of a universal theorem, Harrison’s sums-of-squares tactic only requires simple sign-based reasoning and rational arithmetic, while in our case, we need more mathematics (e.g., real algebraic numbers and the Sturm–Tarski theorem) and more computation (especially for the universal case). A good certificate design needs to balance the difficulty of the formalisation effort and verified computation required to check the certificates with the efficiency improvements offered by offloading the construction of the certificates to high-performance external tools.
Notes
Code is available from https://bitbucket.org/liwenda1990/src_jar_2017.
As our tactic is computationally intense, our procedure makes use of the proof by reflection technique [16].
Besides the application described in this section, the Cauchy index also plays a critical role in the Routh–Hurwitz theorem. Interested readers may consult [32, Chapter 10, 11] for historical notes.
In fact, their tactic does not handle arbitrary boolean expressions like ours, but we believe this should not be too hard to overcome.
References
Akbarpour, B., Paulson, L.: MetiTarski: an automatic theorem prover for real-valued special functions. J. Autom. Reason. 44(3), 175–205 (2010)
Basu, S., Pollack, R., Roy, M.F.: Algorithms in Real Algebraic Geometry (Algorithms and Computation in Mathematics). Springer, New York (2006)
Brown, C.W.: QEPCAD B: a program for computing with semi-algebraic sets using CADs. ACM SIGSAM Bull. 37(4), 97–108 (2003)
Chaieb, A., et al.: Automated methods for formal proofs in simple arithmetics and algebra. Dissertation, Technische Universität, München (2008)
Cheng, J.S., Gao, X.S., Yap, C.K.: Complete numerical isolation of real zeros in zero-dimensional triangular systems. In: Proceedings of the 2007 International Symposium on Symbolic and Algebraic Computation, pp. 92–99. ACM (2007)
Cohen, C.: Formalized algebraic numbers: construction and first-order theory. Ph.D. thesis, École polytechnique (2012)
Cohen, C., Mahboubi, A., et al.: Formal proofs in real algebraic geometry: from ordered fields to quantifier elimination. Log. Methods Comput. Sci. 8(1: 02), 1–40 (2012)
Collins, G.E.: Quantifier elimination for real closed fields by cylindrical algebraic decomposition: a synopsis. ACM SIGSAM Bull. 10(1), 10–12 (1976)
De Moura, L., Bjørner, N.: Z3: An efficient SMT solver. In: Tools and Algorithms for the Construction and Analysis of Systems, pp. 337–340. Springer, Berlin (2008)
De Moura, L., Passmore, G.O.: Computation in real closed infinitesimal and transcendental extensions of the rationals. In: International Conference on Automated Deduction, pp. 178–192. Springer, Berlin (2013)
Denman, W., Akbarpour, B., Tahar, S., Zaki, M.H., Paulson, L.C.: Formal verification of analog designs using MetiTarski. In: Formal Methods in Computer-Aided Design, 2009. FMCAD 2009, pp. 93–100. IEEE (2009)
Denman, W., Muñoz, C.: Automated real proving in PVS via MetiTarski. In: FM 2014: Formal Methods, pp. 194–199. Springer (2014)
Denman, W., Zaki, M.H., Tahar, S., Rodrigues, L.: Towards flight control verification using automated theorem proving. In: NASA Formal Methods, pp. 89–100. Springer (2011)
Eberl, M.: A decision procedure for univariate real polynomials in Isabelle/HOL. In: Proceedings of the 2015 Conference on Certified Programs and Proofs, CPP ’15, pp. 75–83. ACM, New York (2015). doi:10.1145/2676724.2693166
Gonthier, G., Asperti, A., Avigad, J., Bertot, Y., Cohen, C., Garillot, F., Le Roux, S., Mahboubi, A., O’Connor, R., Ould Biha, S., Pasca, I., Rideau, L., Solovyev, A., Tassi, E., Théry, L.: A machine-checked proof of the odd order theorem. In: Blazy S., Paulin-Mohring C., Pichardie D. (eds.) Interactive Theorem Proving: 4th International Conference, ITP 2013, Rennes, France, July 22–26. Lecture Notes in Computer Science, vol. 7998, pp. 163–179. Springer, Berlin (2013)
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: International Symposium on Functional and Logic Programming, pp. 103–117. Springer (2010)
Harrison, J.: Verifying nonlinear real formulas via sums of squares. In: K. Schneider, J. Brandt (eds.) Proceedings of the 20th International Conference on Theorem Proving in Higher Order Logics, TPHOLs 2007, Lecture Notes in Computer Science, vol. 4732, pp. 102–118. Springer, Kaiserslautern (2007)
Hölzl, J.: Proving inequalities over reals with computation in Isabelle/HOL. In: International Workshop on Programming Languages for Mechanized Mathematics Systems, pp. 38–45 (2009)
Hurd, J.: Metis first order prover. http://gilith.com/software/metis (2007)
Li, W., Paulson, L.C.: A formal proof of Cauchy’s residue theorem. In: ITP 2016: Seventh International Conference on Interactive Theorem Proving (2016, to appear)
Li, W., Paulson, L.C.: A modular, efficient formalisation of real algebraic numbers. In: Proceedings of the 5th ACM SIGPLAN Conference on Certified Programs and Proofs, pp. 66–75. ACM (2016)
Mahboubi, A.: Implementing the cylindrical algebraic decomposition within the Coq system. Math. Struct. Comput. Sci. 17(1), 99–127 (2007)
Mishra, B.: Algorithmic Algebra. Springer, New York (1993)
Muñoz, C., Narkawicz, A.: Formalization of Bernstein polynomials and applications to global optimization. J. Autom. Reason. 51(2), 151–196 (2013). doi:10.1007/s10817-012-9256-3
Narkawicz, A., Munoz, C., Dutle, A.: Formally-verified decision procedures for univariate polynomial computation based on Sturm’s and Tarski’s theorems. J. Autom. Reason. 54(4), 285–326 (2015)
Narkawicz, A.J., Muñoz, C.A.: A formally-verified decision procedure for univariate polynomial computation based on Sturm’s theorem. Technical Memorandum NASA/TM-2014-218548, NASA, Langley Research Center, Hampton VA 23681-2199, USA (2014)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Springer, Berlin (2002)
Owre, S., Rushby, J.M., Shankar, N.: PVS: a prototype verification system. In: International Conference on Automated Deduction, pp. 748–752. Springer (1992)
Passmore, G.O., Paulson, L.C., De Moura, L.: Real algebraic strategies for MetiTarski proofs. In: International Conference on Intelligent Computer Mathematics, pp. 358–370. Springer (2012)
Paulson, L.C.: Real-valued special functions: upper and lower bounds. Archive of Formal Proofs (2014)
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: IWIL-2010, vol. 1 (2010)
Rahman, Q., Schmeisser, G.: Analytic Theory of Polynomials. London Mathematical Society Monographs. Clarendon Press, Oxford (2002). https://books.google.co.uk/books?id=FzFEEVO3PXYC
Sagraloff, M.: A general approach to isolating roots of a bitstream polynomial. Math. Comput. Sci. 4(4), 481–506 (2010)
Solovyev, A., Hales, T.C.: Formal verification of nonlinear inequalities with Taylor interval approximations. In: NASA Formal Methods, pp. 383–397. Springer, Berlin (2013)
Strzeboński, A.W.: Cylindrical algebraic decomposition using validated numerics. J. Symb. Comput. 41(9), 1021–1038 (2006)
Thiemann, R., Yamada, A.: Algebraic numbers in Isabelle/HOL. Archive of Formal Proofs (2015). http://isa-afp.org/entries/Algebraic_Numbers.shtml. Formal proof development
Acknowledgements
We thank Florian Haftmann for helping with code generation for our procedure. We are also grateful to the anonymous referees for their constructive suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
The first author was funded by the China Scholarship Council, via the CSC Cambridge Scholarship programme. The development of MetiTarski was supported by the Engineering and Physical Sciences Research Council [Grant Numbers EP/I011005/1, EP/I010335/1].
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, W., Passmore, G.O. & Paulson, L.C. Deciding Univariate Polynomial Problems Using Untrusted Certificates in Isabelle/HOL. J Autom Reasoning 62, 69–91 (2019). https://doi.org/10.1007/s10817-017-9424-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-017-9424-6