“Hence our truth is the intersection of independent lies” – Levins (1966, p. 423)

Introduction

From roads to footpaths to trails, the material traces of movement are thought to have preserved the decision-making processes of people in the past when traversing the landscape (Snead et al., 2009). When direct records of the decision-making processes used by past people are not available, it is by explaining past routes that we can aim to uncover why people in the past moved where they did. For proposed explanations to have explanatory power, it is however necessary that the model outcome sufficiently represents the outcome of the hypothesis of interest and not the artefacts of the specific mathematical formalisation used to represent the hypothesis.

A common method for explaining known past routes is the use of least-cost path (LCP) analysis (e.g. Fonte et al., 2017; Güimil-Fariña & Parcero-Oubiña, 2015; Herzog, 2013, 2022; Lewis, 2021). LCP analysis is predicated on the assumption that humans—whether modern or past—use all available information to economise their behaviour when traversing the landscape (Surface-Evans & White, 2012; Zipf, 1949). In this approach, a slope-based cost function that expresses the cost of traversing a specific slope gradient when walking, with cost often measured in time-taken or energy expended, is used to calculate an LCP between a specified origin and destination (Herzog, 2013). When the path of the calculated LCP and the to-be-explained known past route is deemed to be sufficiently similar,Footnote 1 it is suggested that the resulting LCP, and the hypothesis that its underlying cost function aims to represent, reflects the decision-making processes used by past people when creating the known past route. For example, if an LCP calculated using a time-based cost function representing the hypothesis ‘humans minimised time taken when traversing the landscape’ shares similarity with a known past route, it can be inferred that the placement of the known past route was chosen to minimise time.

Whilst the comparison of multiple LCPs derived using different slope-based cost functions estimating the cost of movement when walking has been used to assess which single cost function, and by extension hypothesis, best explains the known past route (e.g. Güimil-Fariña & Parcero-Oubiña, 2015; Herzog, 2013, 2020, 2022; see also Field et al., 2019 for a reconstructive example; but see Campbell et al., 2019 who argues against the notion of a single maximal cost function), this approach misrepresents what cost functions are, their relationship to the hypotheses that they aim to represent, and their role in explanation. For example, Güimil-Fariña and Parcero-Oubiña (2015) compared four cost functions, despite three of these aiming to represent the same hypothesis ‘humans minimise energy expenditure when traversing the landscape’. The ‘best’ cost function was subsequently used in Fonte et al. (2017)

Using the ideas of multiple model idealisation (hereafter MMI) and robustness analysis associated with Levins (1966) and further developed by Wimsatt (1981, 1987) and Weisberg (2006, 2007, 2013), this paper argues that for LCP results to have explanatory power focus should shift from comparing single cost functions—each constructed with their own assumptions and simplifications—and their ability to explain a known past route, to the comparison of hypotheses as represented by multiple cost functions. Within MMI, each individual model is deemed to be false but might still be useful when combined (Wimsatt, 1981, 1987). First, the combining of models defines “the extremes of a continuum of cases in which the real case is presumed to lie”, and second “to look for results that are true in all of the models and therefore presumably independent of the various specific assumptions that vary from model to model” (Wimsatt, 1987, pp. 30–32). This latter point is subsumed under robustness analysis (Levins, 1966; Wimsatt, 1981). When using LCP analysis to explain known past routes, it is thus not the cost function itself that is of interest—this is merely a simplifying device used to represent the relationship between cost and slope gradient and operationalised to calculate the LCP—but rather the hypothesis that multiple cost functions aim to represent. By producing model outcomes that sufficiently represent the outcome of the hypothesis and not the artefacts of a single cost function (sensu Levins, 1966), i.e. the hypothesis is shown to be robust, model outcomes can more credibly be used for explaining known past routes and more importantly the decision-making processes of past people. Or, as explained by Wimsatt (1981, p. 128) when discussing robustness analysis, “the distinguishing of the real from the illusory; the reliable from the unreliable; the objective from the subjective; the object of focus from artefacts of perspective; and, in general, that which is regarded as ontologically and epistemologically trustworthy and valuable from that which is unreliable, ungeneralisable, worthless, and fleeting”.

The theoretical and methodological basis of using cost functions when aiming to explain known past routes is examined in light of MMI and robustness analysis. This is followed by two case studies. First, a tactical simulation (sensu Orton, 1973), where LCP results from multiple time- and energy-based cost functions estimating the cost of movement when walking only are shown to be robust but underdetermined. As a result, whilst model outcomes are similar when comparing within hypotheses and thus are suggested to provide a credible realisation of the expected outcome given the hypothesis, different hypotheses can also produce similar model outcomes. Second, model outcomes from both hypotheses ‘humans minimise time taken / energy expended when traversing the landscape’, as represented using multiple time- and energy-based cost functions, are assessed for their ability to explain a known Roman road in south-west Sardinia. All data and code for the analyses are available at: https://doi.org/10.5281/zenodo.8278659.

Idealised Cost Functions and Multiple Models

All scientific models contain idealisations: the intentional misrepresentation of a target system. Using idealisations, phenomena in the world produced as a result of complex causal patterns become mathematically and computationally tractable, amongst other advantages (McMullin, 1985; Potochnik, 2017, pp. 41–50; Weisberg, 2007). Cost functions, themselves models, also contain idealisations; that is, they intentionally misrepresent—through different assumptions, approximations, and simplifications—the relationship between an associated cost and slope gradient. Differences in idealisation across cost functions can first be attributed to cost functions being created from data derived from participants of varying sexes, ages, and fitness levels, e.g. Campbell et al. (2019). Additional choices that influence the process of idealisation include what functional form is used to model the relationship, e.g. the bilateral exponential function used by Tobler’s Hiking function (Tobler, 1993) or the sixth degree polynomial by Herzog (2014c); what parameters are included within the model, e.g. whether to include an offset parameter to represent the anisotropic property of slope (e.g. Campbell et al., 2019; Tobler, 1993); to the specific parameter values used. Each cost function therefore represents a specific idealisation of the relationship between cost and slope gradient, each making varying trade-offs in their accuracy, precision, generality, and simplicity of representation (sensu Levins, 1966; Weisberg, 2007). As a result, no single cost function can simultaneously maximise all these properties (Levins, 1966). For LCP model outcomes to credibly explain the decision-making processes of past people when traversing the landscape, it is therefore necessary that model outcomes sufficiently represent the outcome of hypotheses, e.g. time or energy, rather than reflecting the specific simplifying assumptions within a single cost function: for each cost function contains idealisation and alone is an imperfect representation of the true relationship between the associated cost and slope gradient. Only when model outcomes sufficiently represent the outcome of the hypothesis of interest, i.e. the hypothesis is robust, can LCP model outcomes credibly be used for explaining why people in the past moved where they did.

Case Study 1: a Tactical Simulation

When using cost functions in LCP analysis to explain known past routes, it is necessary that cost functions are robust: that the model outcome depends not on the simplifying assumptions of a single cost function but the essentials, i.e. the hypothesis shared by multiple cost functions. If multiple cost functions representing the same hypothesis, e.g. the relationship between time taken and slope gradient, each similar but distinct in their idealisation, are able to produce similar results, then the shared hypothesis can be deemed robust (sensu Levins, 1966; Weisberg, 2006; Wimsatt, 2007, pp. 94–132). The need for multiple cost functions to produce similar—but not identical—model outcomes reflects that each cost function is its own idealisation. As a result, model outcomes are expected to slightly differ. Similarity here is defined subjectively; general patterns are more important than the specific similarity. Model outcomes should however aim to reflect the shared hypothesis, i.e. be robust, whilst also not being underdetermined, i.e. that model outcomes representing different hypotheses are distinguishable (sensu Perreault, 2019). Conversely, if robustness is not present, model outcomes can be deemed to not sufficiently represent the hypothesis of interest and thus do not provide a credible realisation of the expected outcome given the hypothesis. Or worse, if model outcomes using cost functions with different hypotheses are indistinguishable in their realisations, then the two hypotheses are underdetermined and thus do not provide adequate support for choosing which hypothesis best explains the decision-making processes used by past people when traversing the landscape.

Materials and Methods

To test the robustness and underdetermination of multiple cost functions sharing the same and different hypotheses, five simulated digital elevation models (DEMs) of 1 km by 1 km, with a spatial resolution of 1 m, were used. The elevation of the DEMs was scaled to reflect two different scenarios: 0 to 5 m and 0 to 10 m. The former ensures that the maximum slope gradient is below 30° and in-line with the proposed critical gradient, i.e. the maximum slope gradient an optimal route would take (Kay, 2012), and the latter including slope gradients above the proposed critical gradient but below 50°. Five synthetic DEMS with fractal dimensions of 2.20, 2.30, 2.40, 2.50, and 2.60 were generated using the spectral synthesis method (Saupe, 1988) as implemented in GRASS (GRASS Development Team, 2022) for the two scenarios. The fractal dimension of a surface quantities its complexity at different scales — a surface with a fractal dimension closer to 2 is smoother and lacks variation, whereas closer to 3 the surface is rougher and more irregular (Tate & Wood, 2001). Increasing the fractal dimension thereby results in simulated landscapes that have more complex surfaces and thus show greater topographic variability (Fig. 1).

Fig. 1
figure 1

Simulated digital elevation models representing five different landscape complexities as measured by fractal dimension for two different scenarios: elevation scaled to between 0 and 5 m (A) and elevation scaled to between 0 and 10 m (B)

Full size image

As a result of increasing landscape complexity, the range of slope gradients also increases (Fig. 2). With complexity of real landscapes ranging from a fractal dimension of 2.20 to 2.60 (Hofierka et al., 2009), the testing of five different landscape complexities across this range is deemed to sufficiently capture the variability present in real landscapes. With this, results presented here will be applicable across multiple landscape complexities and LCP analysis studies. This, however, does not assume that the only factor influencing past movement is the topography (see Murrieta-Flores, 2010). For example, the tactical simulation does not include the influence of rivers or different land types on the cost of movement when walking. Rather, the topography-only simulations provide a ‘laboratory’ where all other factors are not present and thus cannot influence the modelled results (sensu Bevan, 2013).

Fig. 2
figure 2

Range of degrees slope gradients present in the five simulated digital elevation models with increasing landscape complexities as measured by the fractal dimension for two different scenarios: elevation scaled to between 0 and 5 m (A) and elevation scaled to between 0 and 10 m (B). Slope gradients are calculated from each central cell to all other adjacent cells in the digital elevation models rather than just identifying the maximum slope gradient

Full size image

The robustness and underdetermination of the hypotheses as represented by multiple time- and energy-based cost functions were assessed using the following approach:

  1. 1.

    Two random points were selected within the extent of the five simulated DEMs for the two different scenarios. These points represent the origin and destination used when calculating the least-cost paths.

  2. 2.

    Fourteen least-cost paths, using fourteen different cost functions (Fig. 3), were calculated from the origin and destination. Least-cost paths were calculated using the leastcostpath R package (Lewis, 2023). Least-cost paths are calculated using the Dijkstra algorithm and a 4-adjacency neighbourhood.

    1. a.

      Time-based Tobler’s Hiking functions (Tobler, 1993), the modified Tobler’s Hiking function (Márquez-Pérez et al., 2017), the Irmischer-Clarke male and female on-path and off-path cost functions (Irmischer & Clarke, 2018), and the cost functions proposed by Rees (2004), Davey et al. (1994), Garmy et al. (2005), Kondo and Seino (2010), Naismith (1892), and Campbell et al. (2019) (50th percentile).

    2. b.

      The energy-based cost functions proposed by Herzog (2014c) and Llobera and Sluckin (2007).

  3. 3.

    Each calculated LCP for the two different scenarios was assigned a ‘hypothesis type’, that is time or energy, e.g. Tobler’s Hiking function was assigned the ‘time’ type whereas Herzog ‘energy’.

  4. 4.

    Pairwise maximum Euclidean distances calculated between each LCP to all other LCPs for the two different scenarios. For example, the Euclidean distance from the spatial coordinates of the time-based Tobler’s hiking function LCP was calculated to another LCP and the maximum Euclidean distance was retrieved. This was repeated for the other twelve LCPs. Henceforth, the maximum Euclidean distance is also termed ‘deviation’.

  5. 5.

    In total, 91 Euclidean distance values were calculated. The calculation of 91 distances reflects that there are fourteen LCPs, thirteen other LCPs, and that the distance between two LCPs is symmetrical (91 = 14 * 13/2).

Fig. 3
figure 3

Fourteen cost functions estimating cost in terms of time taken (s/m) (Campbell et al., 2019; Davey et al., 1994; Garmy et al., 2005; Irmischer & Clarke, 2018; Kondo & Seino, 2010; Márquez-Pérez et al., 2017; Naismith, 1892; Rees, 2004; Tobler, 1993) and energy expended (KJ/m) (Herzog, 2014c; Llobera & Sluckin, 2007) by degrees slope. Uphill/downhill slopes are denoted by positive/negative slope values respectively. Campbell et al. (2019) is based on the 50th percentile. Cost functions for the two different scenarios presented: elevation scaled to between 0 and 5 m (scenario 1) and elevation scaled to between 0 and 10 m (scenario 2). Note that the Irmischer and Clarke (2018) male and female off-path cost functions are multiplications of male and female on-path respectively and therefore produce identical least-cost paths

Full size image

Note that the energy-based cost function by Pandolf et al. (1977) was not included within the study. This is due to the cost function requiring additional parameters such as body mass, load mass, and terrain quality that are often not available within many archaeological contexts.

The approach outlined above was repeated 1000 times, generating two sets of 455,000 least-cost paths (91 LCPs * 5 landscapes * 1000 simulations for each scenario) and their accompanying Euclidean distance were calculated for both scenarios. To ease computational load, a different random sample was produced for each landscape complexity and scenario tested.

From the tactical simulation, there are four possible expectations with decreasing explanatory power (Fig. 4):

  1. 1)

    Assuming that the hypotheses as represented by multiple time- and energy-based cost functions are robust and not underdetermined, the model outcomes are expected to be similar within hypotheses and distinguishable across hypotheses (Fig. 4A). That is, the deviation as measured by Euclidean distance within model outcomes from multiple cost functions representing the same hypothesis, i.e. time or energy, is expected to be small, with differences in model outcomes attributed to the process of model idealisation. Deviation across model outcomes when comparing time- and energy-based cost functions is expected to be large, given that they represent different hypotheses;

  2. 2)

    If the deviation within and across model outcomes when comparing time- and energy-based cost functions is large, the hypotheses, whilst not underdetermined, are not robust (Fig. 4B). That is, whilst the large deviation across hypotheses means that the model outcomes are distinguishable, the large deviation within model outcomes from multiple cost functions representing the same hypothesis suggests that the model outcomes are reflecting not the essentials shared across the multiple cost functions, but rather the simplifying assumptions made during the process of model idealisation;

  3. 3)

    If the deviation within and across model outcomes is small, the hypotheses are deemed robust but underdetermined (Fig. 4C). That is, whilst model outcomes from multiple cost functions representing the same hypothesis are similar, the model outcomes when comparing time- and energy-based cost functions are also similar and therefore not distinguishable;

  4. 4)

    Lastly, if the deviation within model outcomes is large with deviation across model outcomes small, the hypotheses are both not robust and underdetermined (Fig. 4D). That is, model outcomes from multiple cost functions representing the same hypothesis are not similar, whilst model outcomes when comparing the two hypotheses are similar and therefore not distinguishable.

Fig. 4
figure 4

Four possible expectations from the tactical simulation: hypotheses are robust and not underdetermined (A), hypotheses are not robust and not underdetermined (B), hypotheses are robust but underdetermined (C), and hypotheses are not robust and underdetermined (D). Here robustness refers to the property of model outcomes being similar, whereas underdetermination is the ability to differentiate between hypotheses as represented by model outcomes. Expectations are in the order of decreasing explanatory power

Full size image

Results and Discussion

Figure 5 shows that for both scenarios, i.e. when elevation is scaled to between 0 to 5 m (Fig. 5A) and 0 to 10 m (Fig. 5B), the deviation within and across model outcomes is small. As a result, whilst the two hypotheses are robust, they are also underdetermined (Fig. 4C outcome). That is, although the model outcomes of the hypotheses ‘humans minimise time taken / energy expended when traversing the landscape’ as represented by multiple time- and energy-based cost functions are suggested to produce credible realisations of the expected outcome given the hypotheses, the two hypotheses also produce similar model outcomes when comparing across hypotheses. With this, it is difficult to discern between model outcomes from the two hypotheses; the expected deviation within the two hypotheses coincides with the expected deviation across hypotheses. This pattern is consistent across all landscape complexities and scenarios tested. This underdetermination impacts the support for choosing which hypothesis best explains the known past route when using LCP analysis, and by extension the explanatory power of these hypotheses for understanding past decision-making.

Fig. 5
figure 5

Square root Euclidean distance between least-cost paths within and across hypothesis types for the two different scenarios presented: elevation scaled to between 0 and 5 m (A) and elevation scaled to between 0 and 10 m (B). Within refers to model outcomes produced from the same hypothesis type, whereas across from different hypothesis types

Full size image

The range within energy-based cost functions also increases as landscape complexity increases for both scenarios (Fig. 6).

Fig. 6
figure 6

Square root Euclidean distance between least-cost paths within and across hypothesis types by fractal dimension for the two different scenarios presented: elevation scaled to between 0 and 5 m (A) and elevation scaled to between 0 and 10 m (B). Within refers to model outcomes produced from the same hypothesis type, whereas across from different hypothesis types

Full size image

This is however more pronounced for lower fractal dimensions in scenario two (Fig. 6B), where elevation is scaled to between 0 and 10 m. The increasing range as landscape complexity increases within the energy-based cost functions can be attributed to the process of model idealisation. As landscape complexity increases, the slope gradients within the landscapes also increase (Fig. 2). With this, the functional form used when creating the cost function becomes more influential on the model outcome. That is, at shallower slope gradients—more commonly occurring in scenario one given its less complex landscape—the relationship between slope gradient and cost is more similar across cost functions, i.e. shallower slope gradients require less energy to traverse. As slope gradient increases, differences in cost functions become more pronounced, resulting in a greater impact on the model outcome. This can be seen for the two energy-based cost functions tested, where the lack of data points available at steeper downhill gradients results in two differing cost functions (Fig. 3, bottom row). As a result, the model outcomes produced within more complex landscapes—and therefore containing steeper slope gradients—might not be reflecting the hypothesis shared across the two energy-based cost functions but the process of model idealisation. The smaller range within energy-based model outcomes compared to within time- and across hypotheses for the two scenarios for all landscape complexities tested can however be attributed to the fewer energy-based cost functions tested. That is, 2 energy-based cost functions compared to the 12 time-based cost functions. Whilst this suggests that the process of model idealisation for energy-based cost functions has less influence on the model outcome compared to time- and across hypotheses, this is not unexpected: both the energy-based cost functions tested are derived from the same data collected by Minetti et al. (2002), with the only difference in the cost functions resulting from the function used to fit the data.

Increasing the Euclidean distance between the origin and destination used when calculating the LCP also increases the deviation within and across hypotheses (Fig. 7). That is, model outcomes are both less similar within and across hypotheses as Euclidean distance increases. The difference in deviation between the two scenarios for the energy-based cost functions (Fig. 7, row 2) again highlights that the model outcomes from these cost functions are likely reflecting the process of model idealisation and not the shared hypothesis. The joint increase in both deviation within and across hypotheses as Euclidean distance increases nonetheless indicates that the two hypotheses remain underdetermined irrespective of distance between the origin and destination used when calculating the LCP. Given that increasing the Euclidean distance also increases the number of cells between the origin and destination, these results are also proposed to be applicable when calculating LCPs using DEMs with increasingly higher resolution from the same origin and destination. That is, as the resolution of the DEM increases, the number of cells between an origin and destination also increases.

Fig. 7
figure 7

Euclidean distance between least-cost paths within and across hypothesis types for the two different scenarios presented: elevation scaled to between 0 and 5 m (A) and elevation scaled to between 0 and 10 m (B) as a function of increasing Euclidean distance between the origin and destination location used to calculate the least-cost path. Within refers to model outcomes produced from the same hypothesis type, whereas across from different hypothesis types

Full size image

In summary, the tactical simulation shows that the model outcomes from both hypotheses ‘humans minimise time taken / energy expenditure when traversing the landscape’ as represented by multiple time- and energy-based cost functions are robust but underdetermined across landscapes with increasing complexity, different maximum slope gradients, and increasing distances between origin and destination locations when calculating the least-cost path. Therefore, whilst the model outcomes can be suggested to produce credible realisations of the expected outcome given the specific hypothesis, the two hypotheses can also produce similar model outcomes. As a result, it is difficult to discern which hypothesis produced the model outcome, with this impacting the support for choosing which hypothesis best explains the known past route. By extension, this also limits the explanatory power of these two hypotheses for understanding past decision-making. Despite the issue of underdetermination, the robustness of the two hypotheses does however suggest that the concurrent use of multiple time- and energy-based cost functions sufficiently represents the hypotheses ‘humans minimise time taken / energy expenditure when traversing the landscape’, respectively. Thus, when multiple cost functions representing the same hypothesis are used concurrently, the impact of the process of model idealisation on the model outcome is reduced. The underdetermination of the two hypotheses does however show that it is more likely that the model outcomes representing the two hypotheses will not be distinguishable in their realisation, i.e. it will remain difficult to identify which of the two hypotheses resulted in the model outcome, and therefore which decision-making process resulted in the known past route.

Case Study 2: Explaining the ‘a Karalibus Sulcos’ Roman Road in Sardinia

With individual hypotheses represented by multiple time- and energy-based cost functions shown to be robust but underdetermined, multiple time- and energy-based cost functions were used concurrently for explaining the ‘a Karalibus Sulcos’ Roman road in the south-west of Sardinia. With least-cost path analysis results previously shown to be impacted by random error within the DEM (Lewis, 2021), probabilistic least-cost paths were used within this case study. Through the use of multiple time- and energy-based cost functions and the incorporation of random error in the DEM, spurious results in calculated least-cost paths as a result of model idealisation when creating the cost functions and measurement error in the DEM will be reduced.

Background

Following Nuragic transhumance routes and Punic-era roads, the ‘a Karalibus Sulcos’ Roman road connected the city of Sulci in the south-west of Sardinia to the port at Carales in the south (Atzori, 2006; Mastino, 2005, pp. 382–385; Meloni, 1990, pp. 350–353). Providing an internal and more direct route than the road along the coast via Teluga and Nura (Fig. 8), the road was used to transport lead silver and wheat stored at Sulci to the port at Carales before being distributed to Italy (Atzori, 2006, pp. 11–13). Given its economic role, it is hypothesised that the ‘a Karalibus Sulcos’ Roman road followed a path that minimised cost from Sulci to Carales. Following similar studies (e.g. Fonte et al., 2017; Lewis, 2021), the model outcomes from both hypotheses ‘humans minimise time taken / energy expended when traversing the landscape’ will be assessed for their ability to explain the placement of the Roman road. Whilst it is possible that wheat and silver were transported using wheeled vehicles, the wheeled vehicle cost function developed by Llobera and Sluckin (2007) was not used within this study. Although the hypothesis could be formulated as ‘humans minimise steeper slope gradients when traveling by wheeled vehicles’, the critical gradient parameter within the cost function is not given a pre-defined value defined by the cost function but instead to be estimated from the past route being explained. Therefore, any modelled outcome that aims to represent the hypothesis should include an additional clause: ‘humans minimise steeper slope gradients than x critical gradient when traveling by wheeled vehicles’. As a result of this, each hypothesis become independent of one another and is not shared across cost functions with different critical gradient values. More importantly, the cost function itself, even with a pre-defined critical gradient value, is only a single model. Thus, any modelled outcome from this cost function would represent the artefacts of the specific mathematical formalisation used to represent the hypothesis and not the hypothesis itself.

Fig. 8
figure 8

Overview of Roman Sardinia, the Roman road system, and the ‘a Karalibus Sulcos’ Roman road. Road stations and overview of the Roman road system following Mastino (2005)

Full size image

Materials and Methods

The ‘a Karalibus Sulcos’ Roman road was based on that recorded by Atzori (2006, pp. 61–111). With a digitised version of the road by Atzori (2006) not available, the road was digitised by myself. The topography of Sardinia was represented using the TINITALY 10 m resolution DEM (RMSE, 4.3 m) (Tarquini et al., 2007). Whilst there are rivers within the study area that might have influenced the Roman road (Mastino, 2005, pp. 336, 340; Meloni, 1990, pp. 230–231; Talbert, 2000, pp. 736–746), it is difficult to know which of these rivers were passable and which would have required additional infrastructure such as fords or bridges to cross. Rather than assigning a constant cost value to all rivers as previously done, e.g. Güimil-Fariña and Parcero-Oubiña (2015), rivers were not incorporated within the analysis. Least-cost paths are calculated using the Dijkstra algorithm and a 16-adjacency neighbourhood. Fourteen time- and energy-based cost functions were used to represent the hypotheses ‘humans minimise time taken / energy expenditure when traversing the landscape’ (Fig. 3). Least-cost paths were calculated from the intersection of the ‘a Karalibus Sulcos’ Roman road and the Roman road along the western coast to the modern-day town of Decimomannu using the R package leastcostpath (Lewis, 2023).

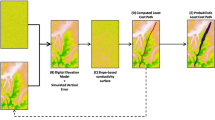
LCPs from multiple time- and energy-based cost functions were combined to create two probabilistic least-cost paths: one representing the model outcome from the hypothesis ‘humans minimise time taken when traversing the landscape’, the other from the hypothesis ‘humans minimise energy expenditure when traversing the landscape’. The uncertainty in the LCPs as a result of random error in the DEM was propagated through the analysis, with each LCP calculated fifty times with different realisations of random error (see Lewis, 2021 for methodology). In contrast to Lewis (2021), autocorrelation in random error was not accounted for, with completely random unfiltered error fields used instead (Wechsler & Kroll, 2006). The use of unfiltered error fields has two advantages: (1) reduction in computational burden as spatial autocorrelation does not need to be calculated, and (2) no assumptions are made about the spatial relationships of the random error. As a result of the second advantage, the effect of the random error fields can be deemed as the worst-case scenario (Wechsler & Kroll, 2006).

Results and Discussion

With the hypotheses ‘humans minimise time taken when traversing the landscape’ and ‘humans minimise energy expenditure when traversing the landscape’ as represented by multiple time- and energy-based cost functions shown to be robust, multiple time- and energy-based cost functions were used concurrently. Given that the two hypotheses have been shown to be underdetermined, it is to be expected that the model outcomes representing the two hypotheses will be similar in their realisations (Fig. 9). The lack of similarity between the ‘a Karalibus Sulcos’ Roman road and the expected outcome given the two hypotheses nonetheless shows that neither the minimisation of time or energy is able to explain the placement of the Roman road, and by extension the decision-making process of the Romans when constructing the road. Thus, the process of road construction for the ‘a Karalibus Sulcos’ Roman road cannot be credibly attributed to the desire to minimise time or energy when traversing on foot from the western coast to the modern-day town of Decimomannu, or, in short, these hypotheses are rejected as explaining the Roman road. Whilst other studies have identified a prioritisation for minimising energy expenditure, time taken, and cost when using animal-drawn wheeled vehicles as explaining the placement of Roman roads (e.g. Fonte et al., 2017; Güimil-Fariña & Parcero-Oubiña, 2015; Lewis, 2021; Parcero-Oubiña et al., 2019), it remains unclear whether these findings reflect the particular cost function idealisation used, the topography in which the Roman road was constructed in, or whether the result could be achieved given a different hypothesis as represented via multiple cost functions. With the use of probabilistic least-cost paths representing the outcome of a hypothesis and not a particular cost function, these issues are minimised.

Fig. 9
figure 9

Probabilistic time- and energy-based least-cost paths, (A) and (B) respectively. Probabilistic least-cost paths calculated from the concurrent use of multiple cost functions representing the same hypothesis and the incorporation of random error in the digital elevation model

Full size image

It should be noted, however, that a number of least-cost paths representing the hypothesis ‘humans minimise energy expenditure when traversing the landscape’ do follow a route similar to the ‘a Karalibus Sulcos’ Roman road (Fig. 9B). Whilst unlikely, given the low probability of the least-cost paths crossing those cells after incorporating random error, it is nonetheless possible that the route of the ‘a Karalibus Sulcos’ Roman road was chosen to minimise energy expenditure. It is also possible that the model outcomes following the Roman road are the result of modern-day roads captured within the high-resolution DEM. As discussed by Herzog and Yépez (2015), DEMs—unless corrected for—can contain modern-day activities that post-date the ancient landscape. Of the two energy-based cost functions tested, that is Herzog (2014c) and Llobera and Sluckin (2007), it is only however Herzog (2014c) that can produce the model outcomes that follow the Roman road (Fig. 10A). Given this, it is suggested that these model outcomes are more likely to be the product of model idealisation, and thus are not representative of the hypothesis but the artefacts of the specific cost function.

Fig. 10
figure 10

Probabilistic energy-based least-cost paths using the Herzog and Llobera-Sluckin cost function, (A) and (B) respectively. Probabilistic least-cost paths calculated from the incorporation of random error in the digital elevation model

Full size image

More generally, the lack of similarity between the probabilistic least-cost paths and the Roman road suggests that the use of pre-existing routes and settlements therein played a greater role in its placement than minimising time or energy when traversing on foot from the western coast to the modern-day town of Decimomannu. Whilst dating of settlements along the ‘a Karalibus Sulcos’ Roman road is difficult (Atzori, 2006, pp. 31–60), settlement continuity in south-west Sardinia from the pre-Roman to Roman period has been argued (Arca, 2018; Pietra, 2015; Tronchetti, 1995). Given that the pre-existing routes from Sulci to Carales are thought to have been the result of Nuragic transhumance routes, that is the seasonal movement of shepherds and their flocks between different regions, it is therefore possible that the Nuragic and later Punic routes—on which the Roman road also followed—took a route most preferable for the movement of animals. An alternative explanation is that one or more of the pre-Roman settlements influenced the road northwards before heading east towards Decimomannu, i.e. a historical dependency. Irrespective of the exact process, the use of pre-existing routes and settlements when constructing the Roman road meant that the movement of resources and local traffic across south-western Roman Sardinia could be controlled. The re-use and formalisation of pre-existing routes is not however unique to the ‘a Karalibus Sulcos’ Roman road, with this process occurring throughout Roman Sardinia (Barreca, 1974, pp. 65–68; Tetti, 1985), and the Roman Empire more generally.

Conclusion

Using the ideas of multiple model idealisation and robustness analysis, and examined in the tactical simulation, this paper has shown that both the hypotheses ‘humans minimise time taken when traversing the landscape’ and ‘humans minimise energy expenditure when traversing the landscape’ as represented by multiple time- and energy-based cost functions are robust but underdetermined across landscapes with increasing complexity, different maximum slope gradients, and increasing distances between origin and destination locations when calculating the least-cost path. Given this, similar model outcomes can be produced irrespective of whether the minimisation of time or energy hypothesis is employed. As a result, it is difficult to discern which hypothesis produced the model outcome, thereby impacting the support for choosing which hypothesis best explains the known past route, and by extension limits the explanatory power of these hypotheses for understanding the decision-making process used by people in the past.

Despite this epistemic limitation, this study has shown, through case study two, that multiple time- and energy-based cost functions can be used concurrently via probabilistic least-cost paths. With this, the probabilistic least-cost path aims to reflect the expected outcome given the hypothesis and not the artefacts of a single model. This both reduces the impact of model idealisation on the model outcome, whilst also accounting for random error in the digital elevation model. Furthermore, differences in model outcomes from cost functions sharing the same hypothesis can be examined, with the reason for these differences better understood.

Although limited by the issue of underdetermination, by accounting for the process of model idealisation and measurement error when using least-cost path analysis, the explanatory power of the two hypotheses is strengthened, with the risk of spurious results and interpretations reduced. With this, we can more towards a better understanding of the decision-making processes used by past people when traversing the landscape.