Beyond symmetry in generalized Petersen graphs

Abstract

A graph is a core or unretractive if all its endomorphisms are automorphisms. Well-known examples of cores include the Petersen graph and the graph of the dodecahedron—both generalized Petersen graphs. We characterize the generalized Petersen graphs that are cores. A simple characterization of endomorphism-transitive generalized Petersen graphs follows. This extends the characterization of vertex-transitive generalized Petersen graphs due to Frucht, Graver, and Watkins and solves a problem of Fan and Xie. Moreover, we study generalized Petersen graphs that are (underlying graphs of) Cayley graphs of monoids. We show that this is the case for the Petersen graph, answering a recent mathoverflow question, for the Desargues graphs, and for the Dodecahedron—answering a question of Knauer and Knauer. Moreover, we characterize the infinite family of generalized Petersen graphs that are Cayley graphs of a monoid with generating connection set of size two. This extends Nedela and Škoviera’s characterization of generalized Petersen graphs that are group Cayley graphs and complements results of Hao, Gao, and Luo.

1 Introduction

Let k, n be integers such that $0<k<\frac{n}{2}$. The generalized Petersen graph G(n, k) is the cubic graph on vertex set $V = V_I \cup V_O$, where $V_I = \{v_0, \ldots , v_{n-1}\}$ is the set of inner vertices and $V_O = \{u_0,\ldots , u_{n-1}\}$ the set of outer vertices. The edge set is partitioned into three parts (all subscripts are considered modulo n): the edges $E_O(n,k) = \{u_i u_{i+1} \, \vert \, 0 \le i \le n-1\}$ form the outer rim, inducing a cycle of length n; the edges $E_I(n,k) = \{v_i v_{i+k} \, \vert \, 0 \le i \le n-1\}$ form the inner rims, inducing $\gcd (n,k)$ cycles of length $\frac{n}{\gcd (n,k)}$; and the edges $E_S(n,k) = \{u_i v_i \, \vert \, 0 \le i \le n-1\}$ are called spokes and form a perfect matching of G(n, k). Generalized Petersen graphs were introduced by Coxeter [3] and named by Watkins [53]. Many known cubic graphs belong to this class, e.g., the Petersen graph G(5, 2) itself, the Dürer graph G(6, 2), the Möbius–Kantor graph G(8, 3) (Fig. 1), the Dodecahedron G(10, 2), the Desargues graph G(10, 3), the Nauru graph G(12, 5), and the n-prism G(n, 1). Coxeter even wrote a paper on G(24, 5), see [4]. Despite its simple definition, many important algebraic properties of G(n, k) depend on the particular k, n, e.g., isomorphisms [48], automorphism groups, edge-and vertex-transitivity [7], being Cayley graph of a group [34, 39].

Fig. 1

The Möbius–Kantor graph G(8, 3)

In the present paper, we study what are sometimes called “generalized symmetries” of generalized Petersen graphs, see e.g. [5]. This is, we study endomorphisms and retracts of G(n, k), as well as Cayley graphs of semigroups and monoids that are generalized Petersen graphs. Graph homomorphisms and in particular the structure of the endomorphism monoid of a graph are classical topics of research, with several books dedicated or closely related to them, see e.g. [9, 16, 32]. This type of questions concern the first part of the present paper. In particular, we characterize cores among generalized Petersen graphs (Theorem 2.1). The problem of describing cores among different families of graphs containing the Petersen graph has been several times addressed in the literature. For example, it is known that nontrivial Kneser graphs [9, Theorem 7.9.1] and graphs obtained from invertible hermitian matrices over the field with four elements [41] are cores. Also, cores in the family of complementary prisms are studied in [42]. As a corollary of Theorem 2.1 we obtain the characterization of endomorphism-transitive generalized Petersen graphs (Corollary 2.2). This settles a problem of Fan and Xie [5, 6]. This can be seen as an extension of the classical characterization of vertex-transitive generalized Petersen graphs of Frucht, Graver, and Watkins [7].

The second part of the paper is dedicated to Cayley graphs of monoids and semigroups. These form a more complicated class than their group counterpart and are related to regular languages in automata theory [44] and have applications in Data-Mining [18]. An important theoretical feature of Cayley graphs concerns the representation theory of monoids as endomorphism monoids of graphs, see [13,14,15]—an area with recent [40, Problem 19.2] and old questions [2]. In the study of Cayley graphs of semigroups two main directions can be identified. On the one hand properties of Cayley graphs of special classes of semigroups have been investigated, see [1, 10,11,12, 17, 20, 22,23,24,25,26, 28, 35, 37, 38, 51, 52]. On the other hand, Cayley graphs falling into a certain class of graphs have been studied, such as bidirected digraphs [19], vertex-transitive digraphs [8, 21], and bounded outdegree digraphs [31, 54]. Semigroups that admit a generating set such that the Cayley graph has given genus have been studied [29, 30, 46, 47, 55]. In the topological setting edge orientations, multiplicities, and loops can be ignored. This leads to simple undirected underlying graphs of Cayley graphs—a notion that in contrast to the group setting causes a significant loss of algebraic information. Only recently graphs that are not the underlying graph of Cayley graphs of monoids have been found [31]. The main question of the second part of the paper is:

Which generalized Petersen graphs are underlying graphs of Cayley graphs of monoids/semigroups?

First, as a corollary of our study of cores, we show that there are infinitely many generalized Petersen graphs which cannot be the underlying graph of a loopless Cayley graph of a semigroup (Corollary 3.4). This answers a question of [8, Question 6.6] and strengthens a result of [27] for monoids (Corollary 3.5). Moving on to general Cayley graphs (with possible loops), we answer the recent question on mathoverflow whether the Petersen graph is a Cayley graph of a group-like structure [45]. We present two different ways to represent the Petersen graph as a Cayley graph of a monoid (Proposition 3.6). Furthermore, we show that the Kronecker double cover of the Petersen graph—the Desargues graph is the underlying graph of a monoid Cayley graph (Proposition 3.8)

The planar connected Cayley graphs of groups are exactly the graphs of the Platonic and Archimedean solids except for the Dodecahedron and the Icosidodecahedron [36]. This led to the question whether the latter two are underlying graphs of Cayley graphs of semigroups or monoids, see [30, Problem 4]. We answer this question partially by providing a monoid representation of the Dodecahedron (Proposition 3.9). Finally, we characterize those generalized Petersen graphs that are Cayley graphs of a monoid with respect to a generating connection set of size two (Theorem 3.13). This extends Nedela and Škoviera’s [39] characterization of generalized Petersen graphs that are group Cayley graphs as well as results by Hao, Gao, and Luo [10, 11] about generalized Petersen graph as components of Cayley graphs of symmetric inverse and Brandt semigroups.

2 Cores and endomorphism-transitivity

A graph G is a core (or unretractive) if all its endomorphisms are automorphisms. A graph is vertex-transitive (respect. endomorphism-transitive) if for any two vertices u, v there exists an automorphism (respect. an endomorphism) of G sending u to v.

In this section we present a characterization of the unretractive generalized Petersen graphs. As a corollary we characterize all endomorphism-transitive generalized Petersen graphs—settling a problem of Fan and Xie [5, 6].

Unless the graph is just an edge or a vertex, bipartite graphs are not cores. Moreover, bipartite graphs without isolated vertices are endomorphism-transitive. For this reason in this section we will only consider non-bipartite graphs. It is easy to check that the generalized Petersen graph G(n, k) is bipartite if and only if n is even and k is odd.

Theorem 2.1

Let G(n, k) be a non-bipartite generalized Petersen graph. Then, the following conditions are equivalent:

• (a) G(n, k) is a core,

• (b) at least one shortest odd length cycle of G(n, k) uses a spoke,

• (c) If we denote by $d\!:= \gcd (n,k)$ and by $a \in {\mathbb {Z}}^+$ the only integer $0< a < \frac{n}{d}$ such that $ak \equiv d \ (\textrm{mod}\ n)$, then one of the following properties holds:

  • (c.1) $\frac{n}{d}$ is even, or

  • (c.2) $a + d$ is even and $a \ge d + 2$, or

  • (c.3) $a + d$ is odd and $a + d + 2 \le \frac{n}{d}$.

As a consequence we derive the following characterization of endomorphism-transitive generalized Petersen graphs.

Corollary 2.2

The endomorphism-transitive generalized Petersen graphs are exactly the vertex-transitive and the bipartite generalized Petersen graphs.

Before proving the main results of this section, we begin by summarizing the main results that we need about cores (see, e.g., [9, Section 6.2] for a proof of these statements) and about the automorphism group of generalized Petersen graphs. A subgraph X of G is a core of G if X is a core itself and there is a homomorphism from G to X. A retraction is a homomorphism f from G to a subgraph X such that f restricted to V(X) is the identity map. When there is a retraction from G to X we say that X is a retract of G. Clearly retracts have to be induced subgraphs and retracts of connected graphs have to be connected too. We call the odd girth of a non-bipartite G the length of a shortest odd cycle. Since homomorphic images of odd cycles are odd cycles, if G is non-bipartite with odd girth g and X is a retract of G, then there is a cycle of length g in X.

Proposition 2.3

Every graph G has an (up to isomorphism) unique core X. Moreover, X is a retract of G. As a consequence, if X is a core of G and there exists $\varphi \in \textrm{Aut}(G)$ such that $\varphi (x) = y$ for some $x,y \in V(X)$, then there exists $\phi \in \textrm{Aut}(X)$ such that $\phi (x) = y$.

The automorphism group of G(n, k) depends on the values of n, k and was completely described by Frucht, Graver and Watkins in [7]. Let V be the vertex set of G(n, k), and consider $\alpha ,\beta ,\gamma : V \longrightarrow V$ defined as

$$\begin{aligned} \alpha (u_i) = u_{i+1},&\alpha (v_i) = v_{i+1},&\quad \text {(rotation),} \end{aligned}$$

(1)

$$\begin{aligned} \beta (u_i) = u_{-i},&\beta (v_i) = v_{-i},&\quad \text {(reflection),} \end{aligned}$$

(2)

$$\begin{aligned} \gamma (u_i) = v_{ki},&\gamma (v_i) = u_{ki},&\quad \text {(inside-out).} \end{aligned}$$

(3)

Then $\alpha , \beta$ are always automorphisms of G(n, k) and, in particular, $\textrm{Aut}(G(n,k))$ has a dihedral subgroup $D_n$ or order 2n. As a consequence, we have that G(n, k) can be either vertex-transitive, or every $\varphi \in \textrm{Aut}(G(n,k))$ satisfies that $\varphi (V_I) = V_I$ (and $\varphi (V_O) = V_O)$. Moreover, $\gamma$ is an automorphism if and only if $k^2 \equiv \pm 1 \ (\textrm{mod}\ n)$. Except for seven exceptional cases (which are described in detail in [7]), the group $\textrm{Aut}(G(n,k))$ can be described with $\alpha , \beta$ and $\gamma$.

Theorem 2.4

[7] If (n, k) is not one of (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5) or (24, 5), then the following hold:

• if $k^2 \equiv 1 \ (\textrm{mod}\ n)$; then

  $$\begin{aligned} \textrm{Aut}(G(n,k)) = \langle \alpha , \beta , \gamma \, \vert \, \alpha ^n = \beta ^2 = \gamma ^2 = \textrm{id},\, \beta \alpha \beta = \alpha ^{-1},\, \gamma \beta = \beta \gamma ,\, \gamma \alpha \gamma = \alpha ^k \rangle , \end{aligned}$$

• if $k^2 \equiv -1 \ (\textrm{mod}\ n)$; then $\textrm{Aut}(G(n,k)) = \langle \alpha , \gamma \, \vert \, \alpha ^n = \gamma ^4 = \textrm{id},\, \gamma \alpha \gamma ^{-1} = \alpha ^k \rangle ,$

• if $k^2 \not \equiv \pm 1 \ (\textrm{mod}\ n)$; then $\textrm{Aut}(G(n,k)) = \langle \alpha , \beta \, \vert \, \alpha ^n = \beta ^2 = \textrm{id},\, \beta \alpha \beta = \alpha ^{-1}\rangle .$

As a consequence of this, in [7], they also get the following.

Corollary 2.5

The following are equivalent:

• (a) G(n, k) is vertex-transitive,

• (b) $k^2 \equiv \pm 1 \ (\textrm{mod}\ n)$ or $(n,k) = (10,2)$ (Dodecahedron),

• (c) the dihedral group $D_n$ is a proper subgroup of $\textrm{Aut}(G(n,k))$.

We will also use the following auxiliary result to prove that (b) implies (a) in Theorem 2.1.

Lemma 2.6

Let G be the graph consisting of two vertex disjoint cycles of the same length $C_1 = (x_0,\ldots ,x_{\ell -1})$, $C_2 = (y_0,\ldots ,y_{\ell -1})$ and $\ell$ disjoint paths of the same length $P_0,\ldots , P_{\ell -1}$, where $P_i$ joins $x_i$ with $y_i$ for all $i \in \{0,\ldots ,\ell -1\}$. Then, G is not a core.

Proof

Denote by k the length of $P_0,\ldots , P_{\ell -1}$ and write $P_i = (x_i = z_{i,0}, z_{i,1},\ldots ,z_{i,k} = y_i)$ for all $i \in \{0,\ldots ,\ell -1\}$. Now, we define $\varphi \in \textrm{End}(G)$ as $\varphi (z_{i,j}) = x_{i+j\ \textrm{mod} \ \ell }\$ for all $i \in \{0,\ldots ,\ell -1\}$. We have that $\varphi$ is not an automorphism and, thus, G is not a core. $\square$

Now, we can prove that (b) implies (a) in Theorem 2.1

Proposition 2.7

Let G(n, k) be a non-bipartite generalized Petersen graph of odd girth g. If there exists a cycle C of length g passing through both inner and outer vertices, then G(n, k) is a core.

Proof

We first observe that if G(n, 1) is non-bipartite, then its odd girth is n and there are no cycles of length n passing through inner and outer vertices. Take now G(n, k) a non-bipartite generalized Petersen graph having a cycle C of length g passing through both inner and outer vertices. By our previous observation we have that $k \ge 2$.

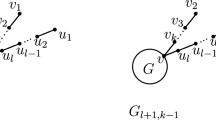
Let $C_g = (w_0,\ldots ,w_{g-1},w_0)$ be a cycle of length g and let us prove that there are no homomorphisms from G(n, k) to $C_g$. Assume on the contrary that there is such a homomorphism $\varphi$. Consider the 8-cycle $C_8 = (u_0,u_1,v_1, v_{k+1}, u_{k+1}, u_{k}, v_k, v_0, u_0)$ in G(n, k). One observes that for every two consecutive edges in $C_8$, one of them is a spoke (see Fig. 2). Thus, every three consecutive vertices in $C_8$ belong to a cycle of length g (this is because G(n, k) has an odd cycle of length g with inner, outer and spoke edges). Assume without loss of generality that $\varphi (u_0) = w_0$ and $\varphi (u_1) = w_1$. Since $v_1$ is adjacent to $u_1$, then $\varphi (v_1) \in \{w_0,w_2\}$. Moreover, we have that $u_0,u_1,v_1$ belong to a cycle C of length g, hence $\varphi$ restricted to the vertices of C has to be injective and, thus $\varphi (v_1) = w_2$. Repeating an analogous argument we get that $\varphi (v_{k+1}) = w_{3},\, \varphi (u_{k+1}) = w_{4},\ldots ,\, \varphi (u_0) = w_{8},$ where the subindices in the vertices of $C_g$ are taken modulo g. Thus, we get that $w_0 = \varphi (u_0) = w_{8}$ and g divides 8, a contradiction.

Fig. 2

The Dodecahedron graph G(10, 2) has odd girth equal to 5 and there exists a 5-cycle (in blue) passing through both inner and outer vertices. As a consequence, every three consecutive vertices of the 8-cycle $C_8$ (in red) belong to a 5-cycle (Color figure online)

Let X be a core of G(n, k). We know that X contains a cycle of length g but we have proved that X itself is not a cycle of length g. Since X has to be connected, then X has both inner and outer vertices of G(n, k). By Proposition 2.3, we also have that all inner (respect. outer) vertices have the same degree in X, which we denote $d_I$ (respect. $d_O$). We have that $d_I \ge 2$ and $d_O \ge 2$. Moreover, since X is connected and is not a cycle, then $d_I$ and $d_O$ cannot be both two. If $d_O = 3$, since X is an induced subgraph, we have that $X = G(n,k)$ and G(n, k) is a core. It only remains to prove that $d_I = 3$ and $d_O = 2$ cannot happen. We proceed by contradiction and consider $u_i$ an outer vertex that belongs to X such that its two neighbors in X are $v_i$ and $u_{i+1}$. Since $d_I = 3$, $u_i$ has a neighbor of degree 3 in X, so Proposition 2.3 implies that the same holds for all the outer vertices from X. Since $d_O = 2, d_I = 3$ and since X is a connected and induced subgraph of G(n, k), it thus follows that the vertex set of X consists of all the vertices $u_j$ and $v_j$, where j is of the form $i + sk$ or $i + sk + 1$, where $0 \le s < n/ \textrm{gcd}(n, k)$. It is now clear that X satisfies the assumptions of Lemma 2.6 with all of the connecting paths of length 3 and, hence, X is not a core, a contradiction. $\square$

Now we can proceed with the proof of the main result.

Proof of Theorem 2.1

$(b) \Longrightarrow (a)$ is Proposition 2.7. Let us prove $(c) \Longrightarrow (b)$. We observe that the subgraph induced by $V_I$ consists of d disjoint cycles of length $\frac{n}{d}$ and the subgraph induced by $V_0$ is just a cycle of n vertices. If (c.1) holds, then $\frac{n}{d}$ (and n) are even, so any odd cycle has inner and outer vertices. So, assume that $\frac{n}{d}$ is odd and let us prove that there exists a cycle of length at most n/d passing through inner and outer vertices. If (c.2) holds, the odd cycle

$$\begin{aligned} (v_d = v_{ak}, v_{(a+1)k}, \ldots , v_{\frac{n}{d} k} = v_0, u_0, u_{1},\ldots , u_d, v_d) \end{aligned}$$

has length $\frac{n}{d} - a + d + 2 \le \frac{n}{d}$, so we are done. If (c.3) holds, the odd cycle

$$\begin{aligned} (v_0, v_k, \ldots , v_{ak} = v_d, u_d, u_{d-1},\ldots , u_0, v_0) \end{aligned}$$

has length $a + d + 2 \le \frac{n}{d}$, so we are done.

Let us now prove the contrapositive statement of $(a) \Longrightarrow (c)$. So, we assume that $\frac{n}{d}$ is odd, and

• (i) if $a+d$ is even, then $a \le d$ and

• (ii) if $a+d$ is odd, then $a+d \ge \frac{n}{d}$,

and we aim at proving that G(n, k) is not a core in either case. If we consider $k'= n-k$, we have that $G(n, k) = G(n,k')$ (where $G(n,k')$ is a non-standard notation for a generalized Petersen graph because $k' > \frac{n}{2}$). One has that the only integer $0< a' < \frac{n}{d}$ such that $a'k' \equiv d \ (\textrm{mod}\ n)$ is $a' = \frac{n}{d} - a$. Thus, $a+d$ is odd if and only if $a' + d$ is even, and $a + d \ge \frac{n}{d}$ is equivalent to $a' \le d$. As a consequence, setting $\ell := k$ and $b := a$ in case (i), or $\ell := k'$ and $b:= a'$ in case (ii) we have that $b \ell \equiv d \ (\textrm{mod}\ n)$, $b+d$ is even and $b \le d$. To get the result it suffices to prove that $G(n,\ell )$ is not a core. For this purpose, we are going to describe a retraction f from $G(n,\ell )$ to one of the inner cycles, namely

$$\begin{aligned} C = (v_0, v_\ell , v_{2\ell }, \ldots , v_{(g-1)\ell }, v_{g\ell } = v_0), \end{aligned}$$

where $g:= \frac{n}{d}$. We observe that $v_d \in V(C)$ because $b \ell \equiv d \ (\textrm{mod}\ n)$.

We define f for the vertices in the outer rim as follows: for $i \in {\mathbb {Z}}$ we denote by q and r the quotient and remainder of the Euclidean division of i by d, i.e., $i = q d + r$ with $0 \le r < d$, and set

$$\begin{aligned} f(u_i) = \left\{ \begin{array}{lll} v_{qd + (r+1)\ell } &{}\quad \textrm{if} &{} r = 0,\ldots , b-1, \\ v_{(q+1)d+\ell } &{} \quad \textrm{if } &{} b \le r< d,\, r \equiv b\ (\textrm{mod}\ 2),\\ v_{(q+1)d} &{}\quad \textrm{if } &{} b< r < d,\, r \not \equiv b\ (\textrm{mod}\ 2). \end{array} \right. \end{aligned}$$

(4)

Concerning the inner rim: we set $f(v_j) = v_{t - \ell }$ whenever $f(u_j) = v_t$, for all $j \in {\mathbb {N}}$; as usual, all the subindices are taken modulo n (see Figs. 3, 4 and 5).

Fig. 3

Figure illustrating the retraction from G(15, 3) to the bold 5-cycle $C = (v_0,v_3,v_6,v_9,v_{12},v_0)$ described in (4). In this example $g = 5$, $d = 3$, $k = \ell = 3$ and $a = b = 1$

Fig. 4

Figure illustrating the retraction from G(15, 6) to the bold 5-cycle $C = (v_0,v_6,v_{12},v_3,v_{9},v_0)$ described in (4). In this example $g = 5$, $d = 3$, $k = \ell = 6$ and $a = b = 3$

The map f is well-defined. This holds since $f(u_{i+n}) = f(u_i)$ and $f(v_{i+n}) = f(v_i)$ for all $i \in {\mathbb {Z}}$.

The map f is a homomorphism. That is, if $xy \in E(G(n,\ell ))$, then $f(x) f(y) \in E(G(n,\ell ))$. To see that we separate three cases. Firstly, consider $xy \in E_S(n,\ell )$ a spoke, then we clearly have that $f(x)f(y) \in E(G(n,\ell ))$. Secondly, consider $u_i u_{i+1} \in E_O(n,\ell )$ an outer edge with $0 \le i \le n-1$. We denote by q (respect. $q'$) and r (respect. $r'$) the quotient and the remainder of the division of i (respect. $i+1$) by d.

• Case $r < d-1$: we have that $q = q'$, $r' = r+1$. Thus, $f(u_i) f(u_{i+1}) \in E(G(n,\ell ))$.

• Case $r = d-1$: we have that $q' = q+1$, $r' = 0$ and, since $r \not \equiv b \ (\textrm{mod}\ 2)$, it follows that $f(u_i) = v_{(q+1)d}$ and $f(u_{i+1}) = v_{q'd + \ell } = v_{(q+1)d+\ell }$. Thus, $f(u_i) f(u_{i+1}) \in E(G(n,\ell ))$.

Thirdly, consider $v_i v_{i+\ell } \in E_I(n,\ell )$ an inner edge. We observe that $f(v_i) f(v_{i+\ell }) \in E(G(n,\ell ))$ if and only if $f(u_i) f(u_{i+\ell }) \in E(G(n,\ell ))$. Moreover, denoting by q (respect. $q'$) and r (respect. $r'$) the quotient and the remainder of the division of i (respect. $i+\ell$) by d, we have that $q' = q + \frac{\ell }{d}$ and $r' = r$. It follows that if $f(u_i) = v_t$ then $f(u_{i+\ell }) = v_{t + \frac{\ell }{d}d} = v_{t+\ell }$. Thus $f(u_i) f(u_{i+\ell }) \in E(G(n,\ell ))$.

Finally, let us see that f is a retraction from $G(n,\ell )$ to C. It is clear that the image of every vertex lies in V(C), so it just remains to prove that $f(v) = v$ for all $v \in V(C)$. Take $v \in V(C)$, then $v = v_{\lambda \ell }$ for some $\lambda \in \{0,\ldots ,g - 1\}$. Following (4) we have that $f(u_{\lambda \ell }) = v_{\lambda \ell + \ell }$ and, thus, $f(u_{\lambda \ell }) = u_{\lambda \ell }$; and we are done. $\square$

Fig. 5

Figure illustrating the retraction from $G(10,4) = G(10,6)$ to the bold 5-cycle $C = (v_0,v_6,v_{2},v_8,v_{4},v_0)$ described in (4). In this example $g = 5$, $d = 2$, $k = 4, \ell = 10 - 4 = 6,\ a = 3$ and $b = 2$

As an easy consequence we have the following result:

Corollary 2.8

Let G(n, k) be a generalized Petersen graph. If $\gcd (n,k) = 1$, then G(n, k) is a core if and only if G(n, k) is not bipartite and $k \ne 1$, i.e., G(n, k) is not the n-prism.

Proof

By Lemma 2.6 we have that n-prisms are not cores, and bipartite (non-trivial) graphs are not cores either.

Let G(n, k) be a non-bipartite generalized Petersen graph with $k \ne 1$ and $\gcd (n,k) = 1$. Then, both the inner and the outer rims are cycles of length n.

If n is even, then all odd cycles pass through inner and outer vertices. Thus, G(n, k) is a core by Theorem 2.1.(b). Assume now that n is odd. We separate two cases. If k is even, we consider the odd cycle $C_1 = (u_0, u_1,\ldots , u_k, v_k, v_0, u_0)$ of length $k + 3 \le 2k + 1 \le n$. If k is odd (and $k \ne 1$), we consider the odd cycle $C_2 = (u_0, u_{n-1},\ldots ,u_k, v_k, v_0, u_0)$ of length $n - k + 3 \le n$. In both cases we have found an odd cycle of length at most n passing through inner and outer vertices. Hence, the result follows from Theorem 2.1.(b). $\square$

In Theorem 2.1 we actually proved that if G(n, k) is not bipartite and not a core, then its core (i.e. its minimal retract) is isomorphic to a g-cycle, where g is the odd grith of G(n, k). Moreover, the outer cycle is a core of G(n, k) only if G(n, k) is a n-prism with n odd. This is the main idea in the following proof of Corollary 2.2.

Proof of Corollary 2.2

Vertex-transitive and connected bipartite graphs are endomorphism-transitive, and core graphs are vertex-transitive if and only if they are endomorphism-transitive. So, to finish the proof it suffices to consider G(n, k) non-bipartite, not a core and endomorphism-transitive, and prove that it is vertex-transitive. Since G(n, k) is not a core, by Theorem 2.1.(b) we have that there is no odd cycle of length g passing through inner and outer vertices. As a consequence, the odd girth of G(n, k) is $g := \frac{n}{\gcd (n,k)}$ and the inner cycle $C = (v_0, v_k, \ldots , v_{kg} = v_0)$ is an odd cycle of length g. Consider now h an endomorphism such that $h(v_0) = u_0$. Since h is an endomorphism, $C' = (h(v_0) = u_0, h(v_k), \ldots , h(v_{kg}) = h(v_0) = u_0)$ has to be an odd cycle of length g and thus, $C'$ has to be the outer cycle and $\gcd (n,k) = 1$. Moreover, by Theorem 2.1.(c) we have that the value of a in the statement of the result is $a = 1$. Consequently, G(n, k) is the n-prism, which is vertex-transitive. $\square$

3 Cayley graphs

In this section we study the question which generalized Petersen graphs come from Cayley graphs of semigroups and monoids. All semigroups, monoids, groups and graphs considered are supposed to be finite. Before describing our results, we introduce some definitions. The (right) Cayley graph $\textrm{Cay}(S,C)$ of the semigroup S with respect to the connection set $C\subseteq S$ is the directed looped multigraph with vertex set S and one arc (s, sc) for each $s\in S$ and $c\in C$. The underlying graph of a directed looped multigraph is obtained by suppressing loops, forgetting orientations, and merging parallel edges into one. We say that G is a group graph, monoid graph, or semigroup graph, if G is the underlying graph of the Cayley graph of a group, monoid, and semigroup, respectively. If we want to specify a representation we say G is a semigroup graph $\textrm{Cay}(S,C)$, and similarly for the case of monoids and groups.

In [39] generalized Petersen graph that are group graph are characterized (see also [34]).

Theorem 3.1

[34, 39] G(n, k) is a group graph if and only if $k^2 \equiv 1 \ (\textrm{mod}\ n)$.

In the first part of this section we show that most generalized Petersen graphs that are cores, cannot be semigroup graphs unless $\textrm{Cay}(S,C)$ has loops. Together with Theorem 2.1 this gives an infinite such family and in particular by choosing any vertex-transitive (multi)orientation yields vertex-transitive digraphs, that are not directed Cayley graphs of a semigroup. This answers a question of [8, Question 6.6] and strengthens a result of [27] for monoids.

In the second part of this section, we show that several generalized Petersen graphs are monoid graphs. In particular, answering a question on mathoverflow asking whether the Petersen graph is the Cayley graph of a group-like structure [45], we present two different ways to represent the Petersen graph as a monoid graph (Proposition 3.6). Furthermore, we show that Desargues graph is the underlying graph of a monoid Cayley graph (Proposition 3.8). To prove this we use that the Desargues graph is the Kronecker double cover of the Petersen graph, where the Kronecker double cover of a graph G is the tensor product $G \times K_2$, i.e., it is formed by replacing each vertex of G by a pair of vertices and each edge by a pair of crossed edges. The graphs of all Platonic solids are known to be group graphs with the sole exception of the Dodecahedron, and it was asked whether it is a semigroup graph. In Proposition 3.9 we provide a positive answer, indeed, we prove that the Dodecahedron G(10, 2) is a monoid graph $\textrm{Cay}(M,C)$, where the connection set C has 3 elements and minimally generates M. Finally, we show an infinite family generalized Petersen graphs, that are monoid graphs (Theorem 3.11). Indeed, the used monoids are orthogroups, i.e. close to groups. Apart from the above mentioned group graph characterization, the only results into this direction so far have been by Hao, Gao, and Luo [10, 11] who show that every generalized Petersen graph appears as a certain subgraph of the Cayley graph of a symmetric inverse semigroup as well as a Brandt semigroup. However, these results have been improved recently by showing that every (directed) graph is a connected component of a monoid Cayley graph [31].

In the last part of this section we characterize generalized Petersen graphs that are monoid graphs with respect to a generating set of size 2 (Theorem 3.13), and provide several properties and a conjecture about generalized Petersen graphs that are monoid graphs with respect to a connection set of size 2.

3.1 Cores and loopless semigroup graphs

Lemma 3.2

Let $D=\textrm{Cay}(S,C)$ be a Cayley graph, then left multiplication by S yields a homomorphism from S to a subsemigroup of $\textrm{End}(D)$.

Proof

Let $\varphi : S \longrightarrow \textrm{End}(D)$ defined as $\varphi (s): S \longrightarrow S$, where $\varphi (s)(s') = s \cdot s'$. Let $s \in S$, it is easy to see that $\varphi (s)$ is an endomorphism of D. Indeed, if (u, v) is an arc of D, then $v = u \cdot c$ for some $c \in C$. As a consequence $s \cdot v = s \cdot (u \cdot c) = (s \cdot u) \cdot c$ and, then, there is an arc from $s \cdot u$ to $s \cdot v$. Moreover, we have that $\varphi (s \cdot s') = \varphi (s) \circ \varphi (s')$ because S is associative. $\square$

Lemma 3.3

If a core G without four-cycles is a semigroup graph $\textrm{Cay}(S,C)$, then $\textrm{Cay}(S,C)$ has loops or S is a group.

Proof

Suppose $D=\textrm{Cay}(S,C)$ has no loops and S is not a group. If $|C|\le 1$, then G either is a disjoint union of edges or pseudo-trees and not a core, or it is an odd cycle or an edge, in this case S is the cyclic group of order |V(D)| – contradiction. Thus, $|C|\ge 2$. By Lemma 3.2 left multiplication by S yields a homomorphism from S to a subsemigroup of $\textrm{End}(D)$. But Since D has no loops, the latter equals $\textrm{Aut}(D)$ since G is a core. If every two elements have different left-multiplication, then S is isomorphic to a subgroup of $\textrm{Aut}(D)$ (since $\textrm{Aut}(D)$ is finite, every subsemigroup of $\textrm{Aut}(D)$ is a group) – contradiction. Thus, two elements of $s,t\in S$ must have the same left-multiplication. Since left-multiplication is an automorphism of D, for any distinct $c,d\in C$, we have that $tc\ne td$. Thus, $s,sc=tc,t,td=sd$ is a four-cycle – contradiction. $\square$

Corollary 3.4

If G(n, k) is a core and $n \ne 4k$, then if G(n, k) is a semigroup graph Cay(S, C), then the latter has loops or S is a group.

Proof

It suffices to show that such graphs have no four-cycles. The rest follows from Lemma 3.3. So, assume that G(n, k) has a four-cycle. If it involves inner and outer vertices then it is an n-prism and, thus, not a core. If it only involves inner or outer vertices, then we have that $4 = \frac{ n}{\gcd (n,k)}$ and, since $0< k < \frac{n}{2}$, then $n = 4k$. $\square$

Corollary 3.4 provides us with an infinite family of negative instances of [8, Question 6.6]:

Corollary 3.5

There are infinitely many vertex-transitive digraphs, that are not the Cayley digraph of a semigroup.

Proof

Take any graph such that: it is vertex-transitive, it is a core, has no 4-cycles, and is not a group graph. Now, consider a biorientation of it, i.e., replace each edge by two oppositely oriented arcs. This digraph is vertex-transitive and, by Lemma 3.3, it is not the directed Cayley graph of a semigroup. Let us see that there is an infinite number of graphs satisfying these conditions within the family of generalized Petersen graphs.

For $(n,k) = (10,2)$ we have that G(10, 2) is vertex-transitive (Corollary 2.5), it is a core (Theorem 2.1), has no 4-cycles and is not a group graph (Theorem 3.1).

If n is odd and $k^2 \equiv -1\ (\textrm{mod}\ n)$, we have that G(n, k) is vertex-transitive (Corollary 2.5), it is not bipartite (because n is odd) and $\gcd (n,k) = 1$ , then it is a core (Corollary 2.8), if has no 4-cycles (because $n \ne 4k$) and is not a group graph (Theorem 3.1). This is an infinite family. $\square$

Clearly, the digraphs above have arcs in both directions and one could wonder whether this is essential for such a construction. A vertex-transitive digraph has at each vertex the same outdegree which also equals the indegree. Thus, if we want to have an example without multiple arcs, its underlying undirected graph has to be regular of even degree and thus cannot be found among generalized Petersen graphs. We believe, however that such graphs should be easy to find as well.

3.2 Positive results

In this section we study generalized Petersen graphs that are underlying graphs of Cayley graphs of semigroups or monoids.

Let us start with four semigroup representations of the Petersen graph G(5, 2). The semigroups $S,M,S',M'$ are given in Table 1. They yield the Petersen graph as their Cayley graph as depicted in Fig. 6, where also the connection sets are specified. Both S, M are unions of ${\mathbb {Z}}_6$ and the null semigroup $N_{[6,9]}$, i.e., $ab=9$ for all $a,b\in \{6,\ldots , 9\}$. Moreover, M is a monoid with neutral element 0. Similarly, $S',M'$ are unions of the dihedral group $D_3$ of order 6 and the null semigroup $N_{[6,9]}$ and $M'$ is a monoid with neutral element 5.

Table 1 Different ways to realize the Petersen graph

Together with Table 1 and Fig. 6 we conclude the above discussion:

Proposition 3.6

The Petersen graph G(5, 2) is a monoid graph.

The following is straight-forward and will be useful to show that the Desargues graph is a monoid graph:

Lemma 3.7

Let $R=S{{\dot{\cup }}} T$ be a semigroup such that $ST\subseteq T$ and $TS\subseteq T$ and $R'$ another semigroup. The set $R\times R'$ is a semigroup via $(s,i)(r,j)=(sr,i)$ and $(t,i)(r,j)=(tr,ij)$, for all $r\in R, s\in S, t\in T, i,j\in R'$ and the natural multiplication within R and $R'$, respectively. If both T and $R'$ are monoids, then so is the resulting semigroup.

Proof

We check associativity, where clearly the case where all three elements come from $S\times R'$ or $T\times R'$ , respectively, can be ignored because on these sets we have semigroup structure by hypothesis. The other six cases are straight-forward computations:

$$\begin{aligned}{} & {} ((s,i)(t,j))(t',k)=(st,i)(t',k)=(stt',i)=(s,i)(tt',jk)=(s,i)((t,j)(t',k)),\\{} & {} ((t,i)(s,j))(t',k)=(ts,ij)(t',k)=(tst',ij)=(t,i)(st',j)=(t,i)((s,j)(t',k)),\\{} & {} ((t,i)(t',j))(s,k)=(tt',ij)(s,k)=(tt's,ijk)=(t,i)(t's,jk)=(t,i)((t',j)(s,k)),\\{} & {} ((t,i)(s,j))(s',k)=(ts,ij)(s',k)=(tss',ij)=(t,i)(ss',j)=(t,i)((s,j)(s',k)),\\{} & {} ((s,i)(t,j))(s',k)=(st,i)(s',k)=(sts',i)=(s,i)(ts',jk)=(s,i)((t,j)(s',k)),\\{} & {} ((s,i)(s',j))(t,k)=(ss',i)(t,k)=(ss't,i)=(s,i)(s't,j)=(s,i)((s',j)(t,k)). \end{aligned}$$

Finally, if $e\in T$ and $e'\in R'$ are neutral elements, we clearly have $(e,e')(r,j)=(er,e'j)$, since $e\in T$. furthermore $(r,j)(e,e')=(r,j)$ independently of whether $r\in S$ or $r\in T$. $\square$

Proposition 3.8

The Desargues graph G(10, 3) is a monoid graph.

Proof

The Cayley graph is depicted in the left of Fig. 7. Let us see that this really is the Cayley graph of a monoid. In fact consider the monoid representation $\textrm{Cay}(M,\{1,6\})$ of the Petersen graph, where $M={\mathbb {Z}}_6\cup N_{[6,9]}$. Note in particular, that we have ${\mathbb {Z}}_6\cdot N_{[6,9]}\subseteq N_{[6,9]}$ and $N_{[6,9]}\cdot {\mathbb {Z}}_6\subseteq N_{[6,9]}$. Hence by Lemma 3.7 the set $M\times {\mathbb {Z}}_2$ carries a monoid structure ${\widetilde{M}}$. The graph in the left of Fig. 7 is $\textrm{Cay}({\widetilde{M}},\{(1,1),(6,0)\})$. Note however that $\{(1,1),(6,0)\}$ does not generate ${\widetilde{M}}$. $\square$

Fig. 6

From upper left to bottom right: $\textrm{Cay}(S,\{1,6\})$, $\textrm{Cay}(M,\{1,6\})$, $\textrm{Cay}(S',\{0,4,8\})$, $\textrm{Cay}(M',\{0,4,8\})$

Fig. 7

Left: a Cayley graph realizing the Desargues graph G(10, 3). Right: a Cayley graph realizing the Dodecahedron graph G(10, 2)

Now, let us consider the monoid M depicted in Table 2. This monoid is the disjoint union of the dihedral group $D_6$ on $\{0,\ldots 11\}$, and the two null semigroups $N_{[12,15]}$ and $N_{[16,19]}$. The Cayley graph $\textrm{Cay}(M,\{1,11,18\})$ depicted on the right of Fig. 7 realizes the Dodecahedron graph G(10, 2). We get:

Proposition 3.9

The Dodecahedron graph G(10, 2) is a monoid graph.

After having examined three particular generalized Petersen graphs, we proceed to construct an infinite family of generalized Petersen graphs that are monoid graphs. In the following we show that if $k^2 = \pm k \mod n$, then G(n, k) is a loopless monoid graph. For instance the Dürer graph G(6, 2) falls into this family and another example is displayed in Fig. 8. Before stating the result, we need one more lemma, that might be of independent interest. Recall that the the left-zero-band $L_I$ is defined on $\{\ell _i\mid i\in I\}$ via $\ell _i\ell _j=\ell _i$ for all $i,j\in I$.

Lemma 3.10

Let S, T, R be semigroups and $\varphi :S\rightarrow T$ and $\psi :S\rightarrow R$ two semigroup homomorphisms. Then $S\cup (T\times L_{R})$ carries a semigroup structure via $s(t,\ell _{r})=(\varphi (s)t,\ell _{\psi (s)r})$ and $(t,\ell _{r})s=(t\varphi (s),\ell _{r})$ and the natural multiplication in S and $T\times L_{T}$, respectively.

Table 2 A monoid representing the Dodecahedron

Proof

We check associativity, where clearly the case where all three elements come from S or $T\times L_{R}$, respectively, can be ignored because on these sets we have semigroup structure by hypothesis. The other six cases are straight-forward computations:

$$\begin{aligned}{} & {} (s(t,\ell _{r}))(t',\ell _{r'})=(\varphi (s)t,\ell _{\psi (s)r})(t',\ell _{r'})=(\varphi (s)tt',\ell _{\psi (s)r}) =s(tt',\ell _{r})=s((t,\ell _{r})(t',\ell _{r'})),\\{} & {} ((t,\ell _{r})s)(t',\ell _{r'})=(t\varphi (s),\ell _{r})(t',\ell _{r'}) =(t\varphi (s)t',\ell _{r})=(t,\ell _{r})(\varphi (s)t',\ell _{\psi (s)r'})=(t,\ell _{r})(s(t',\ell _{r'})),\\{} & {} ((t,\ell _{r})(t',\ell _{r'}))s=(tt',\ell _{r})s=(tt'\varphi (s),\ell _{r}) =(t,\ell _{r})(t'\varphi (s),\ell _{r'})=(t,\ell _{r})((t',\ell _{r'})s),\\{} & {} ((t,\ell _{r})s)s'=(t\varphi (s),\ell _{r})s'=(t\varphi (s)\varphi (s'),\ell _{r}) =(t\varphi (ss'),\ell _{r})=(t,\ell _{r})(ss'),\\{} & {} (s(t,\ell _{r}))s'=(\varphi (s)t,\ell _{\psi (s)r})s'=(\varphi (s)t\varphi (s'),\ell _{\psi (s)r})=s(t\varphi (s'),\ell _{r}) =s((t,\ell _{r})s'),\\{} & {} (ss')(t,\ell _{r})=(\varphi (ss')t,\ell _{\psi (ss')r})=(\varphi (s)\varphi (s')t,\ell _{\psi (s)\psi (s')r}) =s(\varphi (s')t,\ell _{\psi (s')r})=s(s'(t,\ell _{r})). \end{aligned}$$

$\square$

Recall, that a semigroup S is an orthogroup if S is the union of groups and its idempotent elements form a subsemigroup, see e.g. [43]. Note that none of the semigroups we have seen in this section so far is an orthogroup.

Theorem 3.11

If $k^2 \equiv \pm k \ (\textrm{mod}\ n)$, then G(n, k) is a monoid graph $\textrm{Cay}(M,C)$ where the latter is loopless and M is an orthogroup.

Proof

First observe that $k^2 \equiv \pm k \ (\textrm{mod}\ n)$ is equivalent to $k \equiv \pm 1 \ \left( \textrm{mod}\ \frac{n}{\gcd (n,k)}\right)$. Consider $S=A\cup A'$ with $A={\mathbb {Z}}_{n}$ and $A'={\mathbb {Z}}_{\frac{n}{\gcd (n,k)}}\times L_{\gcd (n,k)}$. Here $L_{\gcd (n,k)}:=L_{{\mathbb {Z}}_{\gcd (n,k)}}$. Since A is a group and $A'$ a left-group, i.e., the product of a group and a left-zero-band, we have that S is the union of groups. This already yields one of the properties required for an orthogroup.

Now, for $x\in {\mathbb {Z}}_{n}$ and $(i,\ell _j)\in {\mathbb {Z}}_{\frac{n}{\gcd (n,k)}}\times L_{\gcd (n,k)}$ define

$$\begin{aligned} x(i,\ell _j)=\left( x+i \mod \frac{n}{\gcd (n,k)},\ell _{x+j \mod \gcd (n,k)}\right) \end{aligned}$$

and

$$\begin{aligned} (i,\ell _j)x=\left( x+i \mod \frac{n}{\gcd (n,k)},\ell _j\right) . \end{aligned}$$

Fig. 8

Three Cayley graphs of the monoid from Theorem 3.11 with underlying graph G(10, 4), also see Remark 3.12

Note that defining $\varphi :{\mathbb {Z}}_{n}\rightarrow {\mathbb {Z}}_{\frac{n}{\gcd (n,k)}}$ as $x\mapsto x \mod \frac{n}{\gcd (n,k)}$ and $\psi :{\mathbb {Z}}_{n}\rightarrow {\mathbb {Z}}_{{\gcd (n,k)}}$ as $x\mapsto x \mod \gcd (n,k)$ we get two semigroup homomorphisms. By Lemma 3.10 our operation is a semigroup. Further note that $0\in {\mathbb {Z}}_n$ is a neutral element of this operation, so we do have a monoid. Finally, the set of idempotent elements I(S) of S consists of $0\in {\mathbb {Z}}_n$ and furthermore the set $\{0\}\times L_{\gcd (n,k)} \subseteq A'$. Clearly, $I(S)\cong L^+_{\gcd (n,k)}$, i.e., $L_{\gcd (n,k)}$ with an adjoint neutral element. In particular $I(S)<S$ is a subsemigroup, which concludes the proof that S is an orthogroup monoid.

Let now $C=\{1,(1,\ell _0)\}\subset S$. Clearly, $\textrm{Cay}(S, C)$ is loopless. Let us see that G(n, k) is the underlying graph of $\textrm{Cay}(S, C)$. We identify A with the outer vertices and $A'$ with the inner vertices. Clearly 1 generates the outer-rim on A and for each of the vertices $x \in A$ there is exactly one edge towards the inner vertices generated by $(1,\ell _0)$ and connecting x with $(x+1,\ell _x)$. Moreover both 1 and $(1,\ell _0)$ have the same right action on $A'$ and partition the inner vertices into the $\gcd (n,k)$ cycles of length $\frac{n}{\gcd (n,k)}$. We also observe that for all $i \in \{0,\ldots , \gcd (n,k)-1\}$, the inner neighbors of the vertices $\{x \, \vert \, x \equiv i \ (\textrm{mod}\ \gcd (n,k))\} \subseteq A$ are the vertices of one of the inner cycles, more precisely

$$\begin{aligned} \{x(1,\ell _0) \, \vert \, x \equiv i \ (\textrm{mod}\ \gcd (n,k))\} = {\mathbb {Z}}_{\frac{n}{\gcd (n,k)}} \times \{\ell _i\} \subseteq A'. \end{aligned}$$

Finally, we have that $x (1,\ell _0)$ (the inner neighbour of $x \in A$) and $(x+k) (1,\ell _0)$ (the inner neighbor of $x+k \in A$) are also neighbors, indeed,

• if $k \equiv 1\ (\textrm{mod}\ \frac{n}{\gcd (n,k)})$, then

  $$\begin{aligned} (x + k)(1,\ell _0) = (x+k+1, \ell _{x+k}) = (x+2,\ell _x) = x (1,\ell _0) (1, \ell _0), \end{aligned}$$

• if $k \equiv -1\ (\textrm{mod}\ \frac{n}{\gcd (n,k)})$, then

  $$\begin{aligned} (x + k)(1,\ell _0)(1,\ell _0) = (x+k+2,\ell _{x-k}) = (x+1,\ell _x) = x (1,\ell _0). \end{aligned}$$

This completes the proof. See the left of Fig. 8 for an example. $\square$

Remark 3.12

In the above construction we get interior double arcs which are parallel when $k^2 \equiv k \ (\textrm{mod} \ n)$, and anti-parallel when $k^2 \equiv -k \ (\textrm{mod} \ n)$. If we chose $C=\{1,(-1,\ell _0)\}$ in that construction the situation gets reversed, that is, we get the same underlying graph but the interior double arcs are anti-parallel for $k^2 \equiv k \ (\textrm{mod} \ n)$ and parallel when $k^2 \equiv -k \ (\textrm{mod} \ n)$. Moreover, if we choose $C=\{1,(0,\ell _0)\}$ we obtain a digraph with loops on the inner vertices but without multiple arcs whose underlying graph is G(n, k). See Fig. 8.

3.3 Generalized Petersen graphs that are 2-generated monoid graphs

The degree of the vertex e of a monoid graph $\textrm{Cay}(M,C)$ is at least |C| and the number of edges of the graph is at most |C| times its number of vertices. Hence, if a cubic graph is a monoid graph, then $2\le |C|\le 3$. The goal of this section is to study the case $|C|=2$. We prove Theorem 3.13, which characterizes all the generalized Petersen graphs that are monoid graphs with underlying Cayley graph $\textrm{Cay}(M,C)$ with $M = \langle C \rangle$ and $|C| = 2$. These graphs are exactly the ones obtained in the Theorem 3.11, the group Cayley graphs, and the Petersen graph.

Theorem 3.13

The generalized Petersen graph G(n, k) is a monoid graph $\textrm{Cay}(M,C)$ with $M = \langle C \rangle$ and $|C| = 2$ if and only if one of the following holds:

• (a) $(n,k)=(5,2)$ (Petersen graph),

• (b) $k^2 \equiv 1 \ (\textrm{mod}\ n),$ or

• (c) $k^2 \equiv \pm k\ (\textrm{mod}\ n)$.

Lemma 3.14

Let $G = \textrm{Cay}(M,C)$ be a cubic graph with $|C| = 2$, then there exists an invertible element $g \in C$ of order $o(g) > 2$. Moreover, $(e,g,g^2,\ldots ,g^{o(g)-1},e)$ is a cycle in G.

Proof

We observe that $C \subseteq N_G(e)$. Moreover, since G is a cubic graph and $|C| = 2$, then there exist $x \notin C$ and $g \in C$ such that $x g = e$. Let us see that g is invertible. We take $i \in {\mathbb {N}}$ the minimum value such that there exists a $j > i$ such that $g^i = g^j$ (such an i exists because M is finite), and let us see that $i = 0$. Indeed, if $i > 0$, then $g^{i-1} = (x g) g^{i-1} = x g^i = x g^j = (x g)g^{j-1} = g^{j-1}$, a contradiction. As a consequence g is invertible. Finally, we have that $g^2 \ne e$ because, otherwise $x = x g^2 = (xg) g = g \in C$, a contradiction. Clearly $(e,g,g^2,\ldots ,g^{o(g)-1},e)$ is a cycle in G. $\square$

In this section we will again make use of the rotation $\alpha$, reflection $\beta$, and the inside-out map $\gamma$ from the automorphism group of the generalized Petersen graph. In [39] (see also [34]), it is proven that G(n, k) is a group graph if and only if $k^2 \equiv 1 \ (\textrm{mod}\ n)$. In [34], the author observes that whenever G(n, k) is a group graph, it is $\textrm{Cay}(H,C)$ with $H = \langle \alpha , \gamma \, \vert \, \alpha ^n = \gamma ^2 = \textrm{id},\, \gamma \alpha \gamma = \alpha ^k \rangle$ and $C = \{\alpha ,\gamma \}$. Hence, one gets the following.

Corollary 3.15

If $k^2 \equiv 1 \ (\textrm{mod}\ n)$, then G(n, k) is the group graph of $\textrm{Cay}(H,C)$ with $H = \langle C \rangle$ a group and $|C| = 2.$

For a Cayley graph $\textrm{Cay}(M,C)$, a color endomorphism is a graph endomorphism $\varphi : M~\longrightarrow ~M$ such that $\varphi (m) c = \varphi (m c)$ for all $m \in M$, $c \in C$. Another ingredient we will use in the proof of Theorem 3.13 is the following variant of Lemma 3.10.

Theorem 3.16

[32, Theorem 7.3.7] Let M be a monoid with generating set $C \subseteq M$. Then, M is isomorphic to the monoid of color endomorphisms of $\textrm{Cay}(M,C)$. Moreover, the isomorphism is given by $m \mapsto \lambda _m$, being $\lambda _m$ the left-multiplication by m, i.e., $\lambda _m: M \longrightarrow M$ with $\lambda _m(m') = mm'$.

The statement of the following lemma is similar to the one of Theorem 3.13 but removing the hypothesis that the connection set C generates M. It will be used in all the main results of this section.

Lemma 3.17

If G(n, k) is a monoid graph $\textrm{Cay}(M,C)$ with $|C| = 2$, then one of the following holds:

• (a) $(n,k)=(5,2)$ (Petersen graph),

• (b) $(n,k)=(10,3)$ (Desargues graph) and there is an invertible $g \in C$ of order 6,

• (c) $k^2 \equiv 1 \ (\textrm{mod}\ n),$

• (d) $k^2 \equiv \pm k\ (\textrm{mod}\ n),$ or

• (e) $\gcd (n,k) \ne 1$ and there exists $g \in C$ such that $\lambda _g = \alpha ^k$ or $\lambda _g = \alpha ^{-k}$, where $\lambda _g$ and $\alpha$ are left-multiplication and rotation, respectively.

Proof

Let G(n, k) be a monoid graph that is the underlying graph of $\textrm{Cay}(M,C)$, where M is a monoid and $|C| = 2$, and assume that G(n, k) is not a group Cayley graph and $(n,k) \not = (5,2)$. By Lemma 3.14, there is an invertible element $g \in C$ such that $g^2 \ne 1$. In particular,

• (1) there exists an induced cycle $C' = (x_0,\ldots ,x_{\ell -1},x_{\ell } = x_0)$ of length $\ell := o(g)$, the order of g, and

• (2) there exists $\tau \in \textrm{Aut}(G(n,k))$ of order $\ell$ such that $\tau (x_i) = x_{i+1}$ for $i = 0,\ldots ,\ell -1$.

Indeed, $C' = (e,g,g^2,\ldots ,g^{o(g)-1},e)$ satisfies (1), and $\lambda _g$ satisfies (2).

Claim: Either (b) holds or there exists $\varphi \in \textrm{Aut}(G(n,k))$ such that $\varphi (C')$ is either the exterior or an interior cycle.

Proof of the claim. We separate four cases:

Case $(n,k) = (10,2)$. A computer assisted exhaustive search using SageMath [49] through all the automorphisms of G(10, 2) (its automorphism group is isomorphic to $A_5 \times {\mathbb {Z}}_2$) shows that the only values $\ell$ such that (1) and (2) hold are $\ell = 5$ and $\ell = 10$. Moreover, for $\ell = 5$, there is an automorphism $\varphi$ such that $\varphi (C')$ is an inner cycle, and for $\ell = 10$, there is an automorphism $\varphi$ such that $\varphi (C')$ is the outer cycle.

Case $(n,k) = (10,3)$. Again using SageMath [49] we analyze the automorphisms of G(10, 3) (its automorphism group is isomorphic to $S_5 \times {\mathbb {Z}}_2$) to find that the only values $\ell$ such that (1) and (2) hold are $\ell = 6$ and $\ell = 10$. If $\ell = 6$, then (b) holds. Moreover, if $\ell = 10$, then there is an automorphism $\varphi$ such that $\varphi (C')$ is the outer cycle.

Case $k^2 \not \equiv \pm 1 \ (\textrm{mod}\ n)$ and $(n,k) \ne (10,2)$. By Corollary 2.5 we have that $\textrm{Aut}(G(n,k)) = \langle \alpha , \beta \rangle \cong D_{n}$, and the only elements of order $> 2$ are of the form $\alpha ^i$, then $\lambda _g = \alpha ^i$. Since $C'$ is a cycle containing the edge $\{e,g\} = \{e, \alpha ^i(e)\}$, then either $i \in \{1,n-1\}$ and $C_g$ is the exterior cycle, or $i \in \{k,n-k\}$ and $C_g$ is an interior cycle.

Case $k^2 \equiv -1 \ (\textrm{mod}\ n)$ and $(n,k) \ne (10,3)$. Since $\gcd (n,k) = 1$ and $k \ne 1$, then there are no 3-cycles or 4-cycles in G(n, k). Hence $C'$ is a cycle of length $o(g) > 4$. By Theorem 2.4, every $\sigma \in \textrm{Aut}(G(n,k))$, can be written as $\sigma = \alpha ^i \gamma ^j$ for some $i \in \{0,\ldots ,n-1\}$ and $j \in \{0,1,2,3\}$. Moreover, if $j \ne 0$, then $k^{3j} + k^{2j} + k^j + 1 \equiv (-1)^j k^{j} + k^j + (-1)^j + 1 \equiv 0 \ (\textrm{mod}\ n)$ and $\sigma ^4 = \textrm{id}$. Hence, the only elements of order greater than 4 in $\textrm{Aut}(G(n,k))$ are of the form $\alpha ^i$ for some $1 \le i < n$. Hence we get that $\lambda _g = \alpha ^i$. Proceeding as in the previous case we get that $C_g$ is either the exterior or the interior cycle.

Thus, the claim follows.

As a consequence, one can assume without loss of generality that $C'$ itself is either the exterior cycle (and $\lambda _g = \alpha$ or $\lambda _g = \alpha ^{-1}$), or an interior cycle (and $\lambda _g = \alpha ^k$ or $\lambda _g = \alpha ^{-k}$).

If $C'$ has length $< n$, then (e) holds because $C'$ is necessarily an interior cycle and $\gcd (n,k) > 1$. Hence, it remains to consider when $C'$ is a a cycle of length n. We may also assume without loss of generality that it is the external cycle (if $\gcd (n,k) = 1$, taking $k'$ the inverse of k modulo n we have that $G(n,k) \cong G(n,k')$ and the isomorphism interchanges inner and outer vertices) and $\lambda _g = \alpha$ or $\lambda _g= \alpha ^{- 1}$.

We denote $C = \{g,h\}$. We observe that h is not invertible; otherwise $M = \langle g,h \rangle$ is a group. In particular, $h \notin \{g,g^{-1}\}$ and, then, h is the inner neighbor of e. Moreover, we have that $g^i h \notin V_O$ for all i, so $g^i h$ is the inner neighbor of $g^i$. As a consequence the vertex set of the inner cycle containing h is $V' = \{g^{\lambda k} h \, \vert \, 0 \le \lambda < \frac{n}{\gcd (n,k)}\}$. We split the proof in two cases.

Case 1: $h g = h$. As a consequence, for all $x \in V'$ we have $x g = x$. Consider the graph $D = \textrm{Cay}(V', \{h\})$, we know that D has to be a directed cycle (all the vertices in D have out-degree 1 and the underlying undirected graph is a cycle) and, hence, $V' = \{h^i \, \vert \, i \in {\mathbb {N}}\}$ is a set with at least 3 elements. Depending on the orientation of D, either $h^2 = g^k h$ or $h^2 = g^{-k}h$. In the first case, using that $h g^k = h$ we get $h^3 = h (g^k h) = (h g^k) h = h^2$, a contradiction. In the second one we have that $h^2 = g^{-k} h$ and using again that $h g^k = h$ we get $h^3 = (h g^k) h^2 = h (g^k h^2) = h^2$, a contradiction.

Case 2: $hg \ne h$. Since $hg \ne e$, then hg is an inner neighbor of h, we have that $hg = g^{\pm k} h$. We also take $\mu \in \{-1,0,1\}$ so that $h^2 = h g^\mu$. We claim that $h y = y h$ for all $y \in V'$. Indeed, if $y = h g^i = g^{\pm k i} h \in V',$ then $h y = h (hg^i) = h^2\,g^i = h g^{i+ \mu } = y g^{\mu }$ and $y h = g^{\pm ki } h^2 = g^{\pm ki} (h g^\mu ) = (g^{\pm ki} h) g^{\mu } = y g^{\mu }$. Taking $y = hg \in V'$, we have that

• $y h = (hg) h = g^{\pm k} h^2 = g^{\pm k} h g^{\mu } = g^{\pm k} g^{\pm k \mu }h,$ and

• $h y = h (hg) = h (g^{\pm k} h) = g^{(\pm k)^2} h^2 = g^{k^2} g^{\pm k \mu } h$.

Using that $y h = hy$ we finally get that $g^{\pm k} = g^{k^2}$. Hence $k^2 \equiv \pm k \ (\textrm{mod}\ n)$. $\square$

Now we can proceed with the proof of the main result.

Proof of Theorem 3.13

$(\Longleftarrow )$ Follows from Proposition 3.6 (for G(5, 2)), from Corollary 3.15 (for $k^2 \equiv 1 \ (\textrm{mod}\ n)$), and from Theorem 3.11 (for $k^2 \equiv \pm k \ (\textrm{mod}\ n)$).

$(\Longrightarrow )$ It only remains to prove that (b) and (e) in Lemma 3.17 cannot hold. Assume (b) holds and that $\tau \in \textrm{Aut}(G(10,3))$ satisfies conditions (1) and (2) in the proof of Lemma 3.17 with respect to a 6-cycle. An exhaustive search with SageMath [49] shows that, up to automorphism, there can be only one such cycle. Figure 9 displays the Desargues graph where the 6-fold rotation preserves the outer cycle X, generated by the invertible element $g\in C$. The blue arcs leaving this cycle correspond to the other generator $h\in C$. Since $\langle C \rangle =M$ each vertex of the graph has to be reachable by a directed path from $e\in X$. By the rotation symmetry this implies that both inner (white) vertices must be sinks. Since g is invertible, no element can have indegree larger than one with respect to g, both inner vertices are blue sinks and have a blue loop. In particular, $h^2=h^3$. Since the neighbors of X already have blue outdegree, in order to reach the inner cycle Y, the other arc leaving the neighbors of X has to be black. Since g is invertible, these edges must be black digons. Thus the arcs on Y the inner cycle must all be blue, in particular Y is directed and consists of six elements $\{hg,hgh,hgh^2,hgh^3,hgh^4,hgh^5\}$. This contradicts $h^2=h^3$.

Fig. 9

A hypothetical representation of the Desargues graph with two generators one being invertible of order 6

Assume (e) holds, then $\lambda _g = \alpha ^{\mu k}$ for some $\mu \in \{-1,1\}$. Consider $C'$ the inner cycle of length $\frac{n}{\gcd (n,k)} < n$ such that $e,g \in C'$. The outer neighbor of e is h. We separate three cases and we are going to prove that none of them is possible.

Case 1: $hg = h$. Since $M = \langle g,h \rangle$, then $x g = x$ for all $x \notin C'$. As a consequence, the number of edges of G(n, k) is at most $2n + \frac{n}{\gcd (n,k)} < 3n = |E(G(n,k))|.$

Case 2: $hg \ne h$ and $hg^2 = h$. Since $M = \langle g,h \rangle$, then $x g^2 = x$ for all $x \notin C'$. As a consequence, the number of edges of G(n, k) is at most $2n + \frac{n}{\gcd (n,k)} + \frac{1}{2} \left( n - \frac{n}{\gcd (n,k)}\right) = \frac{5}{2} n + \frac{n}{2 \gcd (n,k)} < 3n = |E(G(n,k))|$.

Case 3: $hg \ne h$ and $hg^2 \ne h$. We consider the closed walk $w = (h, hg, hg^2,\ldots ,hg^{o(g)} = h)$ of length $o(g) < n$ in the Cayley graph $\textrm{Cay}(V, \{g\})$ . Since the outer rim has length n, then the walk w has to pass through (at least) two spokes connecting the outer rim with the same inner rim. However, since $\lambda _g = \alpha ^{\pm k}$ is a color endomorphism (see Theorem 3.16), this implies that these spokes are bioriented, but this contradicts that fact that the out-degree of every vertex in $\textrm{Cay}(V, \{g\})$ is 1. $\square$

Theorem 3.13 is no longer true if we drop the assumption that $M = \langle C \rangle$ (i.e., when C is not a set of generators of M). Indeed, in Proposition 3.8 we proved that the Desargues graph G(10, 3) is a monoid graph $\textrm{Cay}(M,C)$ with $|C| = 2$. We are not aware of any further generalized Petersen graphs with the same behavior. Indeed, we believe that this is the only exception, and that the generalized Petersen graphs that are monoid Cayley graphs with connection set of size 2 are the ones described in Theorem 3.13 and the Desargues graph.

Conjecture 3.18

The generalized Petersen graph G(n, k) is a monoid graph $\textrm{Cay}(M,C)$ with $|C| = 2$ if and only if one of the following holds:

• (a) $(n,k)=(5,2)$ (Petersen graph),

• (b) $(n,k)=(10,3)$ (Desargues graph),

• (c) $k^2 \equiv 1 \ (\textrm{mod}\ n)$,

• (d) $k^2 \equiv \pm k\ (\textrm{mod}\ n)$.

We are able to prove this conjecture under the additional assumptions that $\gcd (n,k) = 1$ (Proposition 3.19), or that $\frac{n}{\gcd (n,k)}$ is odd (Proposition 3.20).

Proposition 3.19

Let $1 \le k < \frac{n}{2}$ such that $\gcd (n,k) = 1$. The generalized Petersen graph G(n, k) is a monoid graph $\textrm{Cay}(M,C)$ with $|C| = 2$ if and only if one of the following holds:

• (a) $(n,k)=(5,2)$ (Petersen graph),

• (b) $(n,k)=(10,3)$ (Desargues graph),

• (c) $k^2 \equiv 1 \ (\textrm{mod}\ n).$

Proof

$(\Longleftarrow )$ Follows from Proposition 3.6 (for G(5, 2)), from Proposition 3.8 (for G(10, 3)), and from Corollary 3.15 (for $k^2 \equiv 1 \ (\textrm{mod}\ n)$).

$(\Longrightarrow )$ Follows directly from Lemma 3.17 and observing that neither (d) nor (e) can hold because $\gcd (n,k) = 1$. Indeed, if $k^2 \equiv \pm k \ (\textrm{mod}\ n)$ and $\gcd (n,k) = 1$, then n divides $k \mp 1$, but this cannot happen because $k < \frac{n}{2}$. $\square$

Proposition 3.20

Let $1 \le k < \frac{n}{2}$ such that $\frac{n}{\gcd (n,k)}$ is odd. The generalized Petersen graph G(n, k) is a monoid graph $\textrm{Cay}(M,C)$ with $|C| = 2$ if and only if one of the following holds:

• (a) $(n,k)=(5,2)$ (Petersen graph),

• (b) $k^2 \equiv 1 \ (\textrm{mod}\ n)$,

• (c) $k^2 \equiv \pm k\ (\textrm{mod}\ n)$.

Proof

$(\Longleftarrow )$ Follows from Proposition 3.6 (for G(5, 2)), from Corollary 3.15 (for $k^2 \equiv 1 \ (\textrm{mod}\ n)$), and from Theorem 3.11 (for $k^2 \equiv \pm k \ (\textrm{mod}\ n)$).

$(\Longrightarrow )$ By Lemma 3.17 we just have to justify why (e) cannot hold. So assume that the cycle $C'$ in the proof of Lemma 3.17 is an inner cycle, that $o(g) = \frac{n}{\gcd (n,k)}$ is odd and $o(g) < n$. Take $y \in V_O$ and let us prove that $y g = y$. Indeed, consider the odd closed walk $w = (y, yg, yg^2,\ldots ,yg^{o(g)} = y)$ of length $o(g) < n$ in the Cayley graph $\textrm{Cay}(V, \{g\})$. Since the outer cycle has length n and $o(g) < n$ and is odd, then either $yg = y$ or the walk w has to pass through (at least) two spokes connecting the outer cycle with the same inner cycle. Let us confirm that the latter is not possible. Since $\lambda _g$ is a color endomorphism (see Theorem 3.16), then these spokes are bioriented, but this contradicts the fact that the out-degree of every vertex in $\textrm{Cay}(V, \{g\})$ is 1 and the walk is odd. Thus $yg = y$. As a consequence, the outer rim is $(h,h^2,\ldots ,h^{n+1} = h)$. However, in this case $h^{k+1} = g^{\pm 1} h$, which implies that $h^2 = (h g^{\pm 1}) h = h (g^{\pm 1} h) = h^{k+2}$, a contradiction. $\square$

As a consequence of Proposition 3.20, one gets that the Dodecahedron G(10, 2) is not a monoid graph $\textrm{Cay}(M,C)$ with $|C|=2$. However, as we have seen in Proposition 3.9 it is a monoid graph with $|C|=3$.

4 Conclusions

In the present paper we went beyond the classical symmetry properties for generalized Petersen graphs. We characterized cores and endomorphism-transitive members of this class, see also Fig. 10. This part of the research could be extended towards a deeper understanding of retracts of generalized Petersen graphs that are not cores. In particular, we believe that

Conjecture 4.1

The image of any endomorphism of a non-bipartite generalized Petersen graph is a retract.

Note that this statement is not true for bipartite generalized Petersen graphs as shown by the Möbius–Kantor graph G(8, 3) in Fig. 1. The white vertices are the image of an endomorphism but are not a retract because they do not induce an isometric subgraph.

Fig. 10

Cores, group Cayley graphs, and known (non-group) monoid Cayley graphs in the generalized Petersen plane

Furthermore, we described large families of generalized Petersen graphs that are monoid graphs, see Fig. 10. In particular, we characterized those generalized Petersen graphs that are monoid graphs with respect to a generating system of size 2. We conjecture that the Desargues graph is the only other generalized Petersen graph that is a monoid graph with respect to a connection set of size 2 (Conjecture 3.18). However, we also exposed the Dodecahedron being the only generalized Petersen graph we know of that is a monoid graph but only with respect to a connection set of size 3. This proves that all graphs of Platonic solids are monoid graphs. In order to establish the same for Archimedean solids, one needs to find a monoid representation for the graph of the Icosidodecahedron. It remains open whether all generalized Petersen graphs are monoid or semigroup graphse. In view of the results of this work, the first open case is G(7, 2) for which we know by Proposition 3.20 that, in case of being a monoid graph, it would need a connection set C of size 3. In a recent Bachelor Thesis [50] it was shown that moreover none of the elements of C may be invertible. Recall that while there are non-monoid graphs [31], it is open whether all graphs are semigroup graphs. We dare to conjecture:

Conjecture 4.2

All generalized Petersen graphs are semigroup graphs.

Given a loop-free semigroup representation of G, one easily gets one for the Kronecker double cover $G\times K_2$. However, comparing with [33] one finds that all Kronecker covers of graphs from the family in Theorem 3.11 that are generalized Petersen graphs fall into the same family. More generally, a covering map from a graph ${\hat{G}}$ to a graph G is a surjective graph homomorphism $\varphi :{\hat{G}}\rightarrow G$ such that for every vertex $v\in {\hat{G}}$, $\varphi$ induces a one-to-one correspondence between edges incident to v and edges incident to $\varphi (v)$. If there is a covering map from ${\hat{G}}$ to G, we say that ${\hat{G}}$ is a covering of G. For instance both the Dodecahedron and the Desargues graph are coverings of the Petersen graph. It is an interesting question to determine what further properties are needed in order to lift a loop-free semigroup representation a graph to its covering. On the other hand, generalizing results of [33], we wonder

Question 4.3

Which generalized Petersen graphs are (non-trivial) coverings of generalized Petersen graphs?