The core of a complementary prism

Abstract

The complementary prism $\Gamma {\bar{\Gamma }}$ is constructed from the disjoint union of a graph $\Gamma$ and its complement ${\bar{\Gamma }}$ if an edge is added between each pair of identical vertices in $\Gamma$ and ${\bar{\Gamma }}$. It generalizes the Petersen graph, which is obtained if $\Gamma$ is the pentagon. The core of the complementary prism is investigated for arbitrary simple graph $\Gamma$. In particular, it is shown that if $\Gamma$ is strongly regular and self-complementary, then $\Gamma {\bar{\Gamma }}$ is a core, i.e. all its endomorphisms are automorphisms.

1 Introduction

The existence of a homomorphism $\varphi : \Gamma _1\rightarrow \Gamma _2$ between two graphs provides information on the relation between the two values of various graph invariants for $\Gamma _1$ and $\Gamma _2$. For example, the clique number and the chromatic number of $\Gamma _1$ cannot exceed the corresponding value for $\Gamma _2$. Since many of these invariants are difficult to compute, the study of graph homomorphisms has gained in importance in the last couple of decades, and some systematic treatment appeared in the literature [20, 23, 26]. On the other hand it is also not surprising that exploring graph homomorphisms between two given graphs is often a hard task. Related to this research is a notion of a core, which is a graph with the property that each its endomorphism is an automorphism. Each graph $\Gamma$ has a subgraph $\Gamma '$, which is a core and such that there exists some homomorphism $\varphi : \Gamma \rightarrow \Gamma '$. It is referred as the core of $\Gamma$ and it is unique up to isomorphism. The investigation of cores is mostly focused on graphs that possess either some degree of ‘symmetry’ or some nice combinatorial properties. Often their definitions rely on some algebraic or geometric structure. It turns out that many such graphs are either cores or their cores are complete graphs. In fact, Cameron and Kazanidis [5] proved that this property is shared by all graphs with the automorphism group that acts transitively on (unordered) pairs of nonadjacent vertices. The same kind of a result was obtained by Godsil and Royle [21] for connected regular graphs with the automorphism group acting transitively on (unordered) pairs of vertices at distance two. Recently Roberson proved that each primitive strongly regular graph is either a core or its core is complete [45]. There are other examples of graphs with the same property, which show that the union of the graph families in [5, 21, 45] is not complete (cf. [38,39,40,41]). In these cases it is often very difficult to decide, which of the two possibilities regarding the core is true. In fact, for certain classes of graphs this question translates to some of longstanding open problems in finite geometry [5, 41]. For some other results related to cores see [18, 19, 31, 43, 44].

A famous core is the Petersen graph (cf. [20]). Its importance (cf. [27]) resulted in several generalizations of this graph. Perhaps the most known is the cubic version that was introduced in [12, 46] and whose endomorphisms were studied very recently in [16]. Yet there exist other generalizations with combinatorial/algebraic flavour. Among them the most studied family consists of Kneser graphs K(n, r), which are cores whenever $2r<n$ [20, Theorem 7.9.1]. If we consider the graph with the vertex set consisting of all invertible $n\times n$ Hermitian matrices over the field with four elements, where a pair of matrices $\{A, B\}$ form an edge if and only if ${\text {rank}}(A-B)=1$, we obtain another family of cores [40]. It generalizes the Petersen graph, which is obtained if $n=2$. In this paper we study the core of a complementary prism $\Gamma {\bar{\Gamma }}$ of a graph $\Gamma$. Graph $\Gamma {\bar{\Gamma }}$ was introduced in [24] and investigated in [1, 3, 6,7,8,9,10,11, 13,14,15, 22, 24, 25, 35, 37, 42, 47]. It is another generalization of the Petersen graph, which is obtained if $\Gamma$ is the pentagon. Since the later graph is strongly regular and self-complementary, the main aim in this paper is to study complementary prisms of strongly regular self-complementary graphs (Theorem 3.7). However, in Theorem 3.1 we provide substantial information on the core of $\Gamma {\bar{\Gamma }}$ for general finite simple graph $\Gamma$. Some special attention is given to the two cases, where either $\Gamma {\bar{\Gamma }}$ or its core is regular (Corollaries 3.4 and 3.6). All these results are contained in Sect. 3. In Sect. 2 we recall the necessary definitions and tools that are applied in the proofs.

2 Preliminaries

This section is split into three subsections.

2.1 Basic notation and tools

All graphs in this paper are finite and simple unless otherwise stated. Given a graph $\Gamma$, its vertex set and the edge set are denoted by $V(\Gamma )$ and $E(\Gamma )$, respectively. Given distinct vertices $u,v\in V(\Gamma )$, we write $u\sim _{\Gamma } v$ (or simply $u\sim v$) if $\{u,v\}\in E(\Gamma )$, and $u\not \sim _{\Gamma } v$ otherwise. We use $K_n$ and $P_n$ to denote the complete graph and the path on n vertices, respectively. A subset $C\subseteq V(\Gamma )$ is a clique if all its elements are pairwise adjacent. A subset $I\subseteq V(\Gamma )$ is independent if it is a clique in the complement ${\bar{\Gamma }}$ of graph $\Gamma$. The clique number $\omega (\Gamma )$ and the independence number $\alpha (\Gamma )$ are the orders of the largest clique and the largest independent set in $\Gamma$, respectively. Hence, $\omega ({\bar{\Gamma }})=\alpha (\Gamma )$. The chromatic number of a graph is denoted by $\chi (\Gamma )$. Clearly, $\chi (\Gamma )\ge \omega (\Gamma )$.

Example 2.1

Recall that the Kneser graph K(n, r), for $2r<n$, has the vertex set formed by all r-subsets in $\{1,2,\ldots ,n\}$, where two r-subsets form and edge if and only if they are disjoint. It is obvious that $\omega (K(n,r))=\left\lfloor \frac{n}{r}\right\rfloor$. On the other hand the Erdős-Ko-Rado theorem states that $\omega (\overline{K(n,r)})=\alpha (K(n,r))=\left( {\begin{array}{c}n-1\\ r-1\end{array}}\right)$ (cf. [20, Theorem 7.8.1]). The famous Lovász proof of the Kneser conjecture [29] implies that $\chi (K(n,r))=n-2r+2$ (see also [20, Theorem 7.11.4]). The chromatic number of the complement is computed in [2, Corollary 4, p. 93] and equals

$$\begin{aligned} \chi (\overline{K(n,r)})=\bigg \lceil \frac{\left( {\begin{array}{c}n\\ r\end{array}}\right) }{\left\lfloor \frac{n}{r}\right\rfloor }\bigg \rceil . \end{aligned}$$

$\square$

Given graphs $\Gamma _1, \Gamma _2$, a map $\varphi : V(\Gamma _1)\rightarrow V(\Gamma _2)$ is a graph homomorphism if it obeys the implication

$$\begin{aligned} \{u,v\}\in E(\Gamma _1)\Longrightarrow \{\varphi (u),\varphi (v)\}\in E(\Gamma _2) \end{aligned}$$

(1)

for all $u,v\in V(\Gamma _1)$. In particular, $\varphi (u)\ne \varphi (v)$ for the two endpoints of each edge in $\Gamma _1$. If in addition $\varphi$ is bijective, and the implication in (1) is replaced by the equivalence $\Longleftrightarrow$, then $\varphi$ is a graph isomorphism and graphs $\Gamma _1, \Gamma _2$ are isomorphic, which is denoted by $\Gamma _1\cong \Gamma _2$. If $\Gamma _1=\Gamma _2$, then a graph homomorphism/graph isomorphism is a graph endomorphism/automorphism, respectively. A graph $\Gamma$ is self-complementary if there exists some antimorphism (a.k.a. complementing permutation), which is a graph isomorphism $\varphi : \Gamma \rightarrow {\bar{\Gamma }}$. A graph $\Gamma$ is k-regular if each vertex $v\in V(\Gamma )$ has k neighbours. A k-regular graph on n vertices is strongly regular with parameters $(n,k,\lambda ,\mu )$ if each pair of adjacent vertices has $\lambda$ common neighbours, while each pair of distinct nonadjacent vertices has $\mu$ common neighbours.

Given a graph $\Gamma$ with the vertex set $\{v_1,\ldots ,v_n\}$ let A be its adjacency matrix, i.e. a $n\times n$ real matrix with (i, j)-th entry equal to 1 if $v_i\sim v_j$ and 0 otherwise. In this paper its eigenvalues are referred as the eigenvalues of $\Gamma$, and we number them in the decreasing order $\lambda _1\ge \cdots \ge \lambda _n$. If $\Gamma$ is k-regular, then $k=\lambda _1$ and the complement ${\bar{\Gamma }}$ has eigenvalues $n-k-1\ge -1-\lambda _n\ge \cdots \ge -1-\lambda _2$ (cf. [4]). Consequently, the largest eigenvalue of a regular self-complementary graph with n vertices equals $\frac{n-1}{2}$, while other eigenvalues occur in pairs $\{\lambda , -1-\lambda \}$ that are symmetric with respect to the value $-\frac{1}{2}$. More can be said in the case of strong regularity. In fact, the parameters $(n,k,\lambda ,\mu )$ of a strongly regular self-complementary graph are of the form $(n,\frac{n-1}{2},\frac{n-5}{4},\frac{n-1}{4})$ (see [36, Lemma 5.1.2] or [33, Theorem 2]). The spectrum of the adjacency matrix of a strongly regular graph is determined by its parameters (cf. [4, Theorem 9.1.3]). Consequently, we have the following lemma.

Lemma 2.2

Let $\Gamma$ be a strongly regular self-complementary graph on $n>1$ vertices. Then $\Gamma$ has eigenvalues $\frac{n-1}{2}, \frac{\sqrt{n}-1}{2}, \frac{-\sqrt{n}-1}{2}$ with multiplicities $1, \frac{n-1}{2}, \frac{n-1}{2}$, respectively.

2.2 Properties of graph homomorphisms and cores

In the paper we rely on some graph parameters that are homomorphism monotone, which means that the existence of a homomorphism between two graphs implies that the graph parameter of the first graph is not larger than the corresponding value on the second graph. Lemma 2.3 says that the clique number and the chromatic number are both homomorphism monotone. The claim (i) is obvious. The claim (ii) is also well known and can be found in [23].

Lemma 2.3

Let $\Gamma _1$ and $\Gamma _2$ be graphs such that there exists a homomorphism from $\Gamma _1$ to $\Gamma _2$. Then

• (i) $\omega (\Gamma _1)\le \omega (\Gamma _2)$,

• (ii) $\chi (\Gamma _1)\le \chi (\Gamma _2)$.

The Lovász theta function $\vartheta (\Gamma )$ of a graph $\Gamma$ with vertex set $\{v_1,\ldots , v_n\}$ was introduced in [30], and it can be defined as

$$\begin{aligned} \vartheta (\Gamma )=\inf _{M\in \mathcal{M}_{\Gamma }}\lambda _{1}(M), \end{aligned}$$

where the set $\mathcal{M}_{\Gamma }$ consists of all $n\times n$ real symmetric matrices $M=[m_{ij}]$ such that $m_{ij}=1$ whenever $i=j$ or $\{v_{i},v_{j}\}\notin E(\Gamma )$, and $\lambda _{1}(M)$ is the largest eigenvalue of M (see [4, 30]). The value $\vartheta ({{{\bar{\Gamma }}}})$ can be defined also in a different way. If $n=|V(\Gamma )|$ and $\nu <0$ is a real number, then consider the infinite graph $S(n,\nu )$ with the unit sphere $S^{n+1}:=\{\textbf{x}\in {\mathbb {R}}^n: \langle \textbf{x}, \textbf{x}\rangle _n=1\}$ as the vertex set and the edge set given by $\{\{\textbf{x}, \textbf{y}\}: \textbf{x},\textbf{y}\in S^{n+1}, \langle \textbf{x}, \textbf{y}\rangle _n=\nu \}$. Here, $\langle \textbf{x}, \textbf{y}\rangle _n=\sum _{i=1}^n x_i y_i$ is the dot product of vectors $\textbf{x}=(x_1,\ldots ,x_n)$ and $\textbf{y}=(y_1,\ldots ,y_n)$. In [28, Theorem 8.2] it was shown that the Lovász theta function of the complement $\vartheta ({{{\bar{\Gamma }}}})$ is the same as the infimum among all values $1-\frac{1}{\nu }$, where $\nu$ ranges over all negative values such that there exists a homomorphism $\varphi _{n,\nu }: \Gamma \rightarrow S(n,\nu )$. Consequently it was observed in [32] that $\vartheta ({{\overline{\Gamma }}_1})\le \vartheta ({{\overline{\Gamma }}_2})$ whenever there exists a homomorphism $\varphi : \Gamma _1\rightarrow \Gamma _2$ (see Lemma 2.4). In fact, if $n_1:=|V(\Gamma _1)|$, $n_2:=|V(\Gamma _2)|$, and $\varphi _{n_2,\nu }$ is a homomorphism between $\Gamma _2$ and $S(n_2,\nu )$, then the image of the map $\varphi _{n_2,\nu }\circ \varphi$ spans a vector subspace $U\subseteq {\mathbb {R}}^{n_2}$ of dimension $\dim U\le n_1$. If we choose any (linear) map $g: (U,\langle \cdot ,\cdot \rangle _{n_2})\rightarrow ({\mathbb {R}}^{\dim U}, \langle \cdot ,\cdot \rangle _{\dim U})$ that preserves the dot product, and the map $f: {\mathbb {R}}^{\dim U} \rightarrow {\mathbb {R}}^{n_1}$ that extends vectors by $n_1-\dim U$ zero entries, we deduce that the map $\varphi _{n_1,\nu }:=f\circ g\circ \varphi _{n_2,\nu }\circ \varphi$ is a homomorphism between $\Gamma _1$ and $S(n_1,\nu )$. Hence, $\vartheta ({{\overline{\Gamma }}_1})\le \vartheta ({{\overline{\Gamma }}_2})$.

Lemma 2.4

Let $\Gamma _1$ and $\Gamma _2$ be graphs such that there exists a homomorphism from $\Gamma _1$ to $\Gamma _2$. Then $\vartheta ({{\overline{\Gamma }}_1})\le \vartheta ({{\overline{\Gamma }}_2})$.

In the proof of Theorem 3.7 we rely also on the properties of $\vartheta$ that are given by Lemmas 2.5 and 2.6, and which were proved already by Lovász [30, Corollary 2, Theorem 9].

Lemma 2.5

Let $\Gamma$ be a graph on n vertices. Then $\vartheta (\Gamma )\vartheta ({\bar{\Gamma }})\ge n$.

Lemma 2.6

Let $\Gamma$ be a k-regular graph on n vertices. Then

$$\begin{aligned} \vartheta (\Gamma )\le \frac{n}{1-\frac{k}{\lambda _{n}}}, \end{aligned}$$

where $\lambda _{n}$ is the smallest eigenvalue of the adjacency matrix of $\Gamma$.

Remark 2.7

If we apply Lemmas 2.5 and 2.6 to a regular self-complementary graph, we deduce that its second eigenvalue $\lambda _2=-1-\lambda _n$ satisfies $\lambda _2\ge \frac{\sqrt{n}-1}{2}$. By Lemma 2.2, strongly regular self-complementary graphs satisfy the equality.

A graph $\Gamma$ is a core if all its endomorphisms are automorphisms. Simple examples include complete graphs and odd cycles. In fact, Lemma 2.3(ii) implies that all vertex-critical graphs are cores, i.e. graphs, where a removal of any vertex decreases the chromatic number. A subgraph $\Gamma '$ in a graph $\Gamma$ is a core of $\Gamma$, if $\Gamma '$ is a core and there exists some graph homomorphism from $\Gamma$ to $\Gamma '$. A core of a graph is an induced subgraph and is unique up to isomorphism [20, Lemma 6.2.2]. By ${\text {core}}(\Gamma )$ we denote any of the cores of $\Gamma$. There always exists a retraction $\psi : \Gamma \rightarrow {\text {core}}(\Gamma )$, i.e. a graph homomorphism that fixes each vertex in ${\text {core}}(\Gamma )$. Namely, if $\varphi : \Gamma \rightarrow {\text {core}}(\Gamma )$ is any graph homomorphism, then its restriction to the vertices of ${\text {core}}(\Gamma )$ is an automorphism of ${\text {core}}(\Gamma )$ and therefore $(\varphi \vert _{V({\text {core}}(\Gamma ))})^{-1}\circ \varphi$ is a retraction. The core of a graph $\Gamma$ is a complete graph if and only if $\chi (\Gamma )=\omega (\Gamma )$.

The following result is well known, and it can be found in [20, Lemma 6.2.3].

Lemma 2.8

Let $\Gamma _1$ and $\Gamma _2$ be graphs. Then there exist homomorphisms from $\Gamma _1$ to $\Gamma _2$ and from $\Gamma _2$ to $\Gamma _1$ if and only if ${\text {core}}(\Gamma _1)\cong {\text {core}}(\Gamma _2)$.

Remark 2.9

In particular, if $\psi$ is a retraction from $\Gamma$ onto its image, then $\Gamma$ and the graph induced by the image of $\psi$ have isomorphic cores.

Lemma 2.10 is also well known, but we did not find it in the literature.

Lemma 2.10

If graph $\Gamma$ is connected, then ${\text {core}}(\Gamma )$ is connected too.

Proof

Let u and v be arbitrary vertices in ${\text {core}}(\Gamma )$. Since ${\text {core}}(\Gamma )$ is a subgraph in the connected graph $\Gamma$, we can find a walk

$$\begin{aligned} u=u_0\sim _{\Gamma } u_1\sim _{\Gamma }\cdots \sim _{\Gamma }u_{d-1}\sim _{\Gamma } u_d=v \end{aligned}$$

in $\Gamma$ that joins u and v. If $\psi$ is any retraction of $\Gamma$ onto ${\text {core}}(\Gamma )$, then

$$\begin{aligned} u=u_0\sim _{\Gamma } \psi (u_1)\sim _{\Gamma }\cdots \sim _{\Gamma }\psi (u_{d-1})\sim _{\Gamma } u_d=v \end{aligned}$$

is a walk in ${\text {core}}(\Gamma )$ that joins u and v. $\square$

Remark 2.11

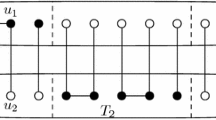
We end this subsection by emphasizing that the core of a regular graph is not necessarily regular. Consider for example the regular graph $\Gamma$ in Fig. 1. The map $\psi$ defined on the vertex set $\{1,\ldots ,9\}$ by $\psi (8)=4$, $\psi (9)=5$, and $\psi (i)=i$ for $i\le 7$, is a retraction onto the bold part of the graph. Since the bold part is a vertex-critical graph, it is a core of $\Gamma$. Clearly, it is not regular.

Fig. 1

A regular graph with a nonregular core

2.3 Complementary prisms

Let $\Gamma$ be a graph with the vertex set $V(\Gamma )=\{v_1,\ldots ,v_n\}$. The complementary prism of $\Gamma$ is the graph $\Gamma {\bar{\Gamma }}$, which is obtained by the disjoint union of $\Gamma$ and its complement ${\bar{\Gamma }}$, if we connect each vertex in $\Gamma$ to its copy in ${\bar{\Gamma }}$. More precisely, $V(\Gamma {\bar{\Gamma }}) = W_1\cup W_2$, where

$$\begin{aligned} W_1=W_1(\Gamma {\bar{\Gamma }})=\{(v_1,1),\ldots ,(v_n,1)\}\ {\text {and}}\ W_2=W_2(\Gamma {\bar{\Gamma }})=\{(v_1,2),\ldots ,(v_n,2)\}, \end{aligned}$$

and the edge set $E(\Gamma {\bar{\Gamma }})$ is given by the union

$$\begin{aligned}&\Big \{\{(u,1),(v,1)\}: \{u,v\}\in E(\Gamma )\Big \}\\&\quad \cup \Big \{\{(u,2),(v,2)\}: \{u,v\}\in E({\bar{\Gamma }})\Big \}\\&\quad \cup \Big \{\{(u,1),(u,2)\}: u\in V(\Gamma )\Big \}. \end{aligned}$$

In particular, $|V(\Gamma {\bar{\Gamma }})|=2n$ and $|E(\Gamma {\bar{\Gamma }})|=\left( {\begin{array}{c}n\\ 2\end{array}}\right) +n=\left( {\begin{array}{c}n+1\\ 2\end{array}}\right)$. Clearly, the complementary prism $\Gamma {\bar{\Gamma }}$ is regular if and only if $\Gamma$ is $\big (\frac{n-1}{2}\big )$-regular (see also [7, Theorem 3.6]).

Recall that the diameter of a connected graph is the length of the shortest path between the most distanced vertices. Lemma 2.12 is proved in [24, Theorem 2].

Lemma 2.12

Let $\Gamma$ be any graph. Then $\Gamma {\bar{\Gamma }}$ is a connected graph of diameter at most three. Moreover,

$$\begin{aligned} {\text {diam}}(\Gamma {\bar{\Gamma }})=1&\Longleftrightarrow \Gamma \cong K_1,\\ {\text {diam}}(\Gamma {\bar{\Gamma }})=2&\Longleftrightarrow {\text {diam}}(\Gamma )=2={\text {diam}}({\bar{\Gamma }}). \end{aligned}$$

Lemma 2.13 is proved in [7, Corollary 3.4].

Lemma 2.13

Let $\Gamma$ be a connected k-regular graph on n vertices, where $k=\lambda _1\ge \lambda _2\ge \dots \ge \lambda _n$ are the eigenvalues of the adjacency matrix of $\Gamma$. Then the set of all eigenvalues of the adjacency matrix of $\Gamma {\bar{\Gamma }}$ equals

$$\begin{aligned}&\left\{ \frac{n-1\pm \sqrt{(n-1-2k)^2+4}}{2}\right\} \end{aligned}$$

(2)

$$\begin{aligned}&\cup \left\{ \frac{-1\pm \sqrt{(2\lambda _i+1)^2+4}}{2} : 2\le i\le n\right\} . \end{aligned}$$

(3)

Corollary 2.14 is essential in the proof of Theorem 3.7.

Corollary 2.14

If $\Gamma$ is as in Lemma 2.13, then the largest and the smallest eigenvalues of $\Gamma {\bar{\Gamma }}$ equal

$$\begin{aligned} \frac{n-1+\sqrt{(n-1-2k)^2+4}}{2} \end{aligned}$$

(4)

and

$$\begin{aligned} \min \left\{ \frac{-1-\sqrt{(2\lambda _2+1)^2+4}}{2},\frac{-1-\sqrt{(2\lambda _n+1)^2+4}}{2}\right\} , \end{aligned}$$

(5)

respectively.

Proof

Obviously, (5) is the smallest among all values in (2)–(3). To see that (4) is the largest value, it suffices to prove that

$$\begin{aligned} n+\sqrt{(n-1-2k)^2+4}\ge \sqrt{(2\lambda _i+1)^2+4} \end{aligned}$$

for all $i\ge 2$. The left-hand side equals $n+\sqrt{m+n^2-2n-4nk}$, where $m=(2k+1)^2+4$, while the right-hand side is bounded above by $\sqrt{m}$. Therefore it suffices to prove that $n+\sqrt{m+n^2-2n-4nk}\ge \sqrt{m}$, which is obvious if $n^2-2n-4nk\ge 0$. On the other hand, if $n^2-2n-4nk<0$, then it suffices to prove the inequality

$$\begin{aligned}&n^2 \ge \big (\sqrt{m}-\sqrt{m+n^2-2n-4nk}\big )^2\\&\quad =2m+n^2-2n-4nk-2\sqrt{m(m+n^2-2n-4nk)}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \sqrt{m(m+n^2-2n-4nk)}\ge m-n-2nk. \end{aligned}$$

If the right-hand side is negative, then the inequality is obviously true. Otherwise we can square the inequality and rearrange it to deduce $n^2(m-4k^2-4k-1)\ge 0$, which is true since $m=4k^2+4k+5$. $\square$

3 The core of a complementary prism

We are now ready to state and prove the main results of this paper. We begin by studying the core of a complementary prism $\Gamma {\bar{\Gamma }}$ for general graph $\Gamma$. Beside the three expected situations (i), (ii), (iii) in Theorem 3.1, two additional and very restricted possibilities for ${\text {core}}(\Gamma {\bar{\Gamma }})$ can occur. Recall that $W_1$ and $W_2$ denote the parts of the vertex set $V(\Gamma {\bar{\Gamma }})$, which correspond to graphs $\Gamma$ and ${\bar{\Gamma }}$, respectively.

Theorem 3.1

Let $\Gamma$ be any graph that is not isomorphic to $K_2$ or $\overline{K_2}$. If ${\text {core}}(\Gamma {\bar{\Gamma }})$ is any core of $\Gamma {\bar{\Gamma }}$, then one of the following five possibilities is true.

• (i) Graph $\Gamma {\bar{\Gamma }}$ is a core.

• (ii) All vertices of ${\text {core}}(\Gamma {\bar{\Gamma }})$ are contained in $W_1$, in which case

  $$\begin{aligned} {\text {core}}(\Gamma {\bar{\Gamma }})\cong {\text {core}}(\Gamma ). \end{aligned}$$

• (iii) All vertices of ${\text {core}}(\Gamma {\bar{\Gamma }})$ are contained in $W_2$, in which case

  $$\begin{aligned} {\text {core}}(\Gamma {\bar{\Gamma }})\cong {\text {core}}({\bar{\Gamma }}). \end{aligned}$$

• (iv) The vertex set $V(\Gamma )=V({\bar{\Gamma }})$ can be written as a union $V_1\cup V_2\cup V_3$, where the pairwise disjoint sets $V_1,V_2,V_3$ are such that (at least) the sets $V_1,V_2$ are nonempty and the following statements are satisfied.

  • (a) The vertex set of ${\text {core}}(\Gamma {\bar{\Gamma }})$ equals

    $$\begin{aligned} \{(v,2): v\in V_1\cup V_2\}\cup \{(v,1): v\in V_2\}. \end{aligned}$$

    (6)

  • (b) In $\Gamma$, there is no edge with one endpoint in $V_1$ and the other endpoint in $V_2$.

  • (c) In $\Gamma$, each vertex in $V_3$ is adjacent to at most one vertex in $V_2$.

  • (d) In $\Gamma$, there exists a vertex in $V_2$ that has no neighbours in $V_3$.

  • (e) If $\Psi$ is any retraction from $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$, then

    $$\begin{aligned}&\Psi (\{(v,2) : v\in V_3\})\subseteq \{(v,2) : v\in V_1\}, \end{aligned}$$

    (7)
    $$\begin{aligned}&\Psi (\{(v,1) : v\in V_3\})\subseteq \{(v,2) : v\in V_1\cup V_2\}, \end{aligned}$$

    (8)
    $$\begin{aligned}&\Psi (\{(v,1) : v\in V_1\})\subseteq \{(v,2) : v\in V_1\cup V_2\}. \end{aligned}$$

    (9)

• (v) The vertex set $V(\Gamma )=V({\bar{\Gamma }})$ can be written as a union $V_1\cup V_2\cup V_3$, where the pairwise disjoint sets $V_1,V_2,V_3$ are such that (at least) the sets $V_1,V_2$ are nonempty and the following statements are satisfied.

  • (a) The vertex set of ${\text {core}}(\Gamma {\bar{\Gamma }})$ equals

    $$\begin{aligned} \{(v,1): v\in V_1\cup V_2\}\cup \{(v,2): v\in V_2\}. \end{aligned}$$

  • (b) In ${\bar{\Gamma }}$, there is no edge with one endpoint in $V_1$ and the other endpoint in $V_2$.

  • (c) In ${\bar{\Gamma }}$, each vertex in $V_3$ is adjacent to at most one vertex in $V_2$.

  • (d) In ${\bar{\Gamma }}$, there exists a vertex in $V_2$ that has no neighbours in $V_3$.

  • (e) If $\Psi$ is any retraction from $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$, then

    $$\begin{aligned}&\Psi (\{(v,1) : v\in V_3\})\subseteq \{(v,1) : v\in V_1\},\\&\Psi (\{(v,2) : v\in V_3\})\subseteq \{(v,1) : v\in V_1\cup V_2\},\\&\Psi (\{(v,2) : v\in V_1\})\subseteq \{(v,1) : v\in V_1\cup V_2\}. \end{aligned}$$

Proof

The vertex set of ${\text {core}}(\Gamma {\bar{\Gamma }})$ can be written as

$$\begin{aligned} \{(u,1): u\in U_1\}\cup \{(u,2): u\in U_2\}, \end{aligned}$$

where $U_1$, $U_2$ are two subsets of $V(\Gamma )$ and at least one of them is nonempty. If $U_2=\emptyset$, then the vertices of ${\text {core}}(\Gamma {\bar{\Gamma }})$ are contained in $W_1$ and any retraction of $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$ is a homomorphism from $\Gamma {\bar{\Gamma }}$ to $\Gamma$. Since $\Gamma$ is isomorphic to an induced subgraph in $\Gamma {\bar{\Gamma }}$ we have also the obvious homomorphism in the other direction. From Lemma 2.8 we infer that ${\text {core}}(\Gamma {\bar{\Gamma }})\cong {\text {core}}(\Gamma )$, i.e. (ii) is true. If $U_1=\emptyset$, then we deduce that (iii) is true in the same way. In what follows we assume that $U_1\ne \emptyset \ne U_2$. Moreover, Lemmas 2.12 and 2.10 imply that ${\text {core}}(\Gamma {\bar{\Gamma }})$ is connected. Hence, $U_1\cap U_2\ne \emptyset$. We now separate three cases.

Case 1 Let $U_1=U_2$. If both sets equal $V(\Gamma )$, then (i) is true. We next show that the inequality in $U_1=U_2\ne V(\Gamma )$ leads to a contradiction.

Firstly, if $|U_1|=1$, then $|V(\Gamma )\backslash U_1|=1$ is ruled out by the assumption, since $\Gamma$ is not isomorphic to $K_2$ or $\overline{K_2}$. Suppose that $|U_1|=1$ and $|V(\Gamma )\backslash U_1|\ge 2$. Pick arbitrary distinct vertices $v,v'\in V(\Gamma )\backslash U_1$ and denote the unique vertex in $U_1$ by u. Then either $v\sim _{\Gamma } v'$ or $v\sim _{{\bar{\Gamma }}} v'$. In the former case, u cannot be $\Gamma$-adjacent to both v and $v'$. In fact, the opposite would imply that $\Gamma$ contains a triangle, while ${\text {core}}(\Gamma {\bar{\Gamma }})\cong K_2$, a contradiction by Lemma 2.3(ii). Hence, $\Gamma {\bar{\Gamma }}$ contains one of the following three 5-cycles

$$\begin{aligned}&(u,1), (v,1), (v',1), (v',2), (u,2), (u,1),\\&(u,1), (v',1), (v,1), (v,2), (u,2), (u,1),\\&(u,2), (v,2), (v,1), (v',1), (v',2), (u,2), \end{aligned}$$

which implies a contradiction by Lemma 2.3(ii) in the same way as above. If $v\sim _{{\bar{\Gamma }}} v'$ we get a contradiction in a symmetrical way.

Next, observe that $|U_1|=2$ is not possible, since it would imply that ${\text {core}}(\Gamma {\bar{\Gamma }})$ is isomorphic to a path on four vertices, which is not a core.

Finally, assume that $|U_1|\ge 3$. Pick arbitrary $v\in V(\Gamma )\backslash U_1$ and any retraction $\Psi$ from $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$. Suppose that $\Psi (v,1)=(u,1)$ for some $u\in U_1=U_2$. Then $(v,1)\not \sim (u,1)$, i.e. $(v,2)\sim (u,2)$ and consequently, $(u,2)\sim \Psi (v,2)\sim \Psi (v,1)=(u,1)$, which is not possible, since (u, 1) and (u, 2) do not have common neighbours. Hence,

$$\begin{aligned} \Psi (v,1)=(u,2) \end{aligned}$$

(10)

for some $u\in U_1=U_2$. In symmetrical way we deduce that $\Psi (v,2)=({\dot{u}},1)$ for some ${\dot{u}}\in U_1=U_2$. Since $\Psi (v,1)\sim \Psi (v,2)$ it follows that ${\dot{u}}=u$, i.e.

$$\begin{aligned} \Psi (v,2)=(u,1). \end{aligned}$$

(11)

Since $|U_1|\ge 3$, we can find distinct $\ddot{u},\dddot{u}\in U_1$ such that either $(\ddot{u},1)\sim (v,1)\sim (\dddot{u},1)$ or $(\ddot{u},2)\sim (v,2)\sim (\dddot{u},2)$. Consequently, either

$$\begin{aligned} (\ddot{u},1)\sim \Psi (v,1)\sim (\dddot{u},1)\quad {\text {or}}\quad (\ddot{u},2)\sim \Psi (v,2)\sim (\dddot{u},2), \end{aligned}$$

which contradicts either (10) or (11).

Case 2 Let $U_2\backslash U_1\ne \emptyset$. We prove that in this case (iv) is true. Denote $V_1:=U_2\backslash U_1$ and $V_2:=U_1\cap U_2$. Then $V_1\ne \emptyset \ne V_2$ and $V_1\cap V_2=\emptyset$. Pick any retraction $\Psi$ from $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$.

Suppose that (b) is not true, i.e. there are vertices $v_1\in V_1$ and $v_2\in V_2$ such that $v_1\sim _{\Gamma } v_2$. Since $(v_2,1)$ and $(v_1,2)$ are vertices in ${\text {core}}(\Gamma {\bar{\Gamma }})$ and $(v_1,2)\sim (v_1,1)\sim (v_2,1)$ it follows that

$$\begin{aligned} (v_1,2)\sim \Psi (v_1,1)\sim (v_2,1). \end{aligned}$$

This is a contradiction, since $\Psi (v_1,1)\ne (v_1,1)$. In fact, $\Psi (v_1,1)$ is a vertex in ${\text {core}}(\Gamma {\bar{\Gamma }})$, while $(v_1,1)$ is not. Hence, the claim in (b) is correct.

Next we prove (9). If $v_1\in V_1$, then $(v_1,1)$ is not a vertex in ${\text {core}}(\Gamma {\bar{\Gamma }})$. Consequently $(v_1,1)\ne \Psi (v_1,1)\sim \Psi (v_1,2)=(v_1,2)$, which implies that

$$\begin{aligned} \Psi (v_1,1)\in \{(u,2): u\in U_2\}, \end{aligned}$$

(12)

i.e. (9).

To prove the claim (a), assume the contrary, i.e. $U_1\backslash U_2\ne \emptyset$. Then we show as in the previous two paragraphs that there are no edges in ${\bar{\Gamma }}$ with one endpoint in $V_1':=U_1\backslash U_2$ and the other endpoint in $V_2$, and for arbitrary $v_1'\in V_1'$ we have

$$\begin{aligned} \Psi (v_1',2)\in \{(u,1): u\in U_1\}. \end{aligned}$$

(13)

Let $v_1\in V_1$ be arbitrary. Recall that vertices $(v_1,1)$ and $(v_1',2)$ are not contained in ${\text {core}}(\Gamma {\bar{\Gamma }})$, that is, $(v_1,1)\notin \{(u,1): u\in U_1\}$ and $(v_1',2)\notin \{(u,2): u\in U_2\}$. Since either

$$\begin{aligned} \Psi (v_1,1)\sim \Psi (v_1',1)=(v_1',1)\quad {\text {or}}\quad \Psi (v_1',2)\sim \Psi (v_1,2)=(v_1,2), \end{aligned}$$

we get in contradiction with (12) or (13), respectively. Hence, $U_1\backslash U_2=\emptyset$ and the claim (a) is true.

Let $V_3:=V(\Gamma )\backslash U_2$. Then $V(\Gamma )$ is the union of pairwise disjoint sets $V_1,V_2,V_3$.

To prove (c) assume the contrary, that is, there exist $v_3\in V_3$ and distinct $v_2,v_2'\in V_2$ such that $v_2 \sim _{\Gamma } v_3\sim _{\Gamma } v_2'$. Then $(v_2,1)\sim (v_3,1)\sim (v_2',1)$ and consequently $W_1 \ni (v_2,1)=\Psi (v_2,1) \sim \Psi (v_3,1)\sim \Psi (v_2',1)=(v_2',1)\in W_1$. Therefore $\Psi (v_3,1)\in W_1$. By (a) it follows that

$$\begin{aligned} \Psi (v_3,1)=(v_2'',1) \end{aligned}$$

for some $v_2''\in V_2\backslash \{v_2,v_2'\}$. Consequently, $(v_2'',1)\not \sim (v_3,1)$, i.e. $(v_2'',2)\sim (v_3,2)\sim (v_3,1)$ and therefore $(v_2'',2)\sim \Psi (v_3,2)\sim (v_2'',1)$, which is not possible, as $(v_2'',1)$ and $(v_2'',1)$ do not have common neighbours. Hence, (c) is true.

Suppose that inclusion (7) is not true. Then by (a) there exist $v_3\in V_3$ and $v_2\in V_2$ such that $\Psi (v_3,2)=(v_2,i)$ for some $i\in \{1,2\}$. Assume firstly that $i=2$. Then, $(v_3,2)\not \sim (v_2,2)$, i.e. $(v_3,1)\sim (v_2,1)$. Consequently

$$\begin{aligned} (v_2,1)=\Psi (v_2,1)\sim \Psi (v_3,1)\sim \Psi (v_3,2)=(v_2,2), \end{aligned}$$

which is not possible. Assume now that $i=1$, that is,

$$\begin{aligned} \Psi (v_3,2)=(v_2,1). \end{aligned}$$

(14)

It follows from (c) that $(v_3,2)$ is adjacent to all vertices of the form (v, 2) where $v\in V_2$, with one possible exception. Since $\Psi (v,2)=(v,2)$ and $\Psi (v_3,2)\in W_1$, it follows that $|V_2|\in \{1,2\}$. Moreover, if $|V_2|=2$, then

$$\begin{aligned} (v_3,2)\ {\text {is adjacent to precisely one vertex of the form}}\ (v,2),\ v\in V_2. \end{aligned}$$

(15)

Suppose that $|V_2|=2$, i.e. $V_2=\{v_2,v\}$ for some $v\ne v_2$. Then (14)–(15) imply

$$\begin{aligned} (v_3,2)\sim (v_2,2)\ {\text {and}}\ (v_3,1)\sim (v,1), \end{aligned}$$

since the opposite would yield $(v_2,1)=\Psi (v_3,2)\sim \Psi (v,2)=(v,2)$, which is not true. Consequently,

$$\begin{aligned} (v_2,1)=\Psi (v_3,2)\sim \Psi (v_3,1)\sim \Psi (v,1)=(v,1). \end{aligned}$$

This is a contradiction, since $(v_2,1)$ and (v, 1) do not have common neighbours in ${\text {core}}(\Gamma {\bar{\Gamma }})$ as they are its unique vertices that are contained in $W_1$. On the other hand if $|V_2|=1$, i.e. $V_2=\{v_2\}$, then the graph with vertex set (6) is not a core. In fact, in such a case a map ${\dot{\Psi }}$, which satisfies ${\dot{\Psi }}(v_2,1)=(v_1,2)$ for arbitrary $v_1\in V_1$ and fixes all other vertices of ${\text {core}}(\Gamma {\bar{\Gamma }})$ is a nonbijective endomorphism of ${\text {core}}(\Gamma {\bar{\Gamma }})$. Hence inclusion (7) is correct.

If (8) is not true, then there are $v_3\in V_3$, $v_2\in V_2$ such that $\Psi (v_3,1)=(v_2,1)$. Since $\Psi (v_3,2)\sim \Psi (v_3,1)$, we get in contradiction with (7), and (8) is correct.

It remains to prove the statement (d). Suppose that each vertex $v_2\in V_2$ has at least one $\Gamma$-neighbour in the set $V_3$. Fix one of them and denote it by $f(v_2)$. Choose an arbitrary retraction $\Psi$ from $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$. Define a map $\ddot{\Psi }$ on the vertex set of ${\text {core}}(\Gamma {\bar{\Gamma }})$, which is described in (6), by

$$\begin{aligned} \ddot{\Psi }(v,i):=\left\{ \begin{array}{ll}(v,i) &{} {\text {if}}\ v\in V_1\cup V_2\ {\text {and}}\ i=2,\\ \Psi (f(v),2) &{} {\text {if}}\ v\in V_2\ {\text {and}}\ i=1.\end{array}\right. \end{aligned}$$

We claim that $\ddot{\Psi }$ is a nonbijective endomorphism of ${\text {core}}(\Gamma {\bar{\Gamma }})$. This gives the desired contradiction that proves (d). Pick any $v_2\in V_2$. Then (7) implies that $\Psi (f(v_2),2)=(v_1,2)$ for some $v_1\in V_1$. Consequently

$$\begin{aligned} \ddot{\Psi }(v_2,1)=\Psi (f(v_2),2)=(v_1,2)=\ddot{\Psi }(v_1,2), \end{aligned}$$

which shows that the map $\ddot{\Psi }$ is not bijective. Moreover, since

$$\begin{aligned} (v_2,1)=\Psi (v_2,1)\sim \Psi (f(v_2),1), \end{aligned}$$

it follows from (8) that each $v_2\in V_2$ satisfies

$$\begin{aligned} \Psi (f(v_2),1)=(v_2,2). \end{aligned}$$

(16)

To prove that $\ddot{\Psi }$ is an endomorphism, suppose that $(v,i)\sim (u,j)$ are two adjacent vertices in ${\text {core}}(\Gamma {\bar{\Gamma }})$. If $i=2=j$, then $\ddot{\Psi }(v,i)=(v,i)\sim (u,j)=\ddot{\Psi }(u,j)$. If $\{i,j\}=\{1,2\}$, say $i=1$ and $j=2$, then $v=u\in V_2$ and (16) implies that

$$\begin{aligned} \ddot{\Psi }(u,j)=\ddot{\Psi }(v,2)=(v,2)=\Psi (f(v),1)\sim \Psi (f(v),2)=\ddot{\Psi }(v,1)=\ddot{\Psi }(v,i). \end{aligned}$$

If $i=1=j$, then $v,u\in V_2$, and (16) implies that

$$\begin{aligned} \Psi (f(v),1)=(v,2)\not \sim (u,2)=\Psi (f(u),1). \end{aligned}$$

Hence, $(f(v),1)\not \sim (f(u),1)$, i.e. $(f(v),2)\sim (f(u),2)$. Consequently,

$$\begin{aligned} \ddot{\Psi }(v,i)=\ddot{\Psi }(v,1)=\Psi (f(v),2)\sim \Psi (f(u),2)=\ddot{\Psi }(u,1)=\ddot{\Psi }(u,j), \end{aligned}$$

which shows that $\ddot{\Psi }$ is an endomorphism of ${\text {core}}(\Gamma {\bar{\Gamma }})$.

Case 3 Let $U_1\backslash U_2\ne \emptyset$. Then we proceed symmetrically as in Case 2 to deduce that (v) is true. $\square$

Remark 3.2

The set $V_3$ in Theorem 3.1 is allowed to be empty. In this case either $\Gamma$ or ${\bar{\Gamma }}$ is disconnected.

Example 3.3

The possibilities (iv),(v) in Theorem 3.1 can occur even if the graph $\Gamma$ is regular. For example, if $\Gamma$ is a (disjoint) union of a triangle and a pentagon, then the core of $\Gamma {\bar{\Gamma }}$ is the graph, which is induced by all vertices in $W_2$ together with the triangle part of $W_1$. The verification of this fact is left to the reader. On the other hand it seems mysteriously complicated to provide an example of a regular graph $\Gamma$, where both $\Gamma$ and ${\bar{\Gamma }}$ are connected and the possibility (iv) or (v) occurs for ${\text {core}}(\Gamma {\bar{\Gamma }})$. Below we provide an example of such graph $\Gamma$ on 505 vertices that is 194-regular, but firstly some preparation is needed.

Observe from Example 2.1 that the Kneser graph K(10, 4) satisfies

$$\begin{aligned} \omega (K(10,4))=2,\ \chi (K(10,4))=4,\ \omega (\overline{K(10,4)})=84,\ \chi (\overline{K(10,4)})=105. \end{aligned}$$

Moreover, if $V=\{S\subseteq \{1,2,\ldots ,10\}: |S|=4 \}$ is the vertex set of K(10, 4), then a proper 4-vertex-colouring $c: V\rightarrow \{1,2,3,4\}$ can be obtained by defining $c(S)=\min _{s\in S} s$ whenever $\min _{s\in S}\le 3$ and $c(S)=4$ otherwise. Hence, if we add the edge $e=\{\{1,2,3,4\},\{2,3,4,5\}\}$ to graph K(10, 4), then the newly obtained graph $K(10,4) + e$ satisfies

$$\begin{aligned} \chi (K(10,4) + e)=4\ {\text {and}}\ \omega (K(10,4) + e)\ge 2, \end{aligned}$$

(17)

whereas the graph $\overline{K(10,4)} - e$ that is obtained by deleting the edge e satisfies

$$\begin{aligned} \chi (\overline{K(10,4)} - e)\ge 104 \ {\text {and}}\ \omega (\overline{K(10,4)} - e)\le 84. \end{aligned}$$

(18)

Now, consider the complement of the complete graph on 99 vertices, $\overline{K_{99}}$, the graph $\overline{K(10,4)} - e$, and the Cayley graph ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$, where ${\mathbb {F}}_{49}$ and ${\mathbb {F}}_{4}=\{0,1,\imath ,1+\imath \}$ are finite fields with 49 and 4 elements, respectively, and $S=\{(x,y): 0\ne x\in {\mathbb {F}}_{49}, y\in \{0,1\}\}$. Recall that ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$ has the additive group ${\mathbb {F}}_{49}\times {\mathbb {F}}_4$ as the vertex set and two vertices (x, y), $(x',y')$ form an edge if and only if $(x,y) - (x',y')\in S$. Moreover, the graph ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$ has two connected components, namely

$$\begin{aligned} \mathcal{C}_1=\{(x,y): x\in {\mathbb {F}}_{49}, y\in \{0,1\}\}\ {\text {and}}\ \mathcal{C}_2=\{(x,y): x\in {\mathbb {F}}_{49}, y\in \{\imath ,1+\imath \}\}. \end{aligned}$$

Fix any $(x_1,y_1)\in \mathcal{C}_1$ and $(x_2,y_2)\in \mathcal{C}_2$ and number the vertices $\{w_1,\ldots ,w_{196}\}$ of ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$ in such way that $w_{195}=(x_1,y_1)$ and $w_{196}=(x_2,y_2)$. Further, number the vertices $\{v_1,\ldots ,v_{99}\}$ of $\overline{K_{99}}$ in some order and let $u_1,u_2$ be the two endpoints of the deleted edge e in $\overline{K(10,4)} - e$. We form the graph $\Gamma$ from the disjoint union of graphs $\overline{K_{99}}$, $\overline{K(10,4)} - e$, ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$ by adding the following edges:

• $\{w_{195},u_1\}$, $\{w_{196},{u_2}\}$,

• $\{w_{195},v_i\}$, $\{w_{196},v_i\}$ where $i\in \{1,\ldots ,97\}$,

• $\{w_j,v_{98}\}$, $\{w_j,v_{99}\}$ where $j\in \{1,\ldots ,194\}$,

• $\{v_i,w_{s}\}$ where $i\in \{1,\ldots ,97\}$ and $s\in \{1,\ldots ,194\}\backslash \{i,i+97\}$.

Observe that the graph $\Gamma$ is 194-regular. The connectedness of $\overline{K(10,4)} - e$ implies the connectedness of $\Gamma$. The connectedness of ${\bar{\Gamma }}$ is obvious. We next prove that the vertices of a core of $\Gamma {\bar{\Gamma }}$ are contained in the set $X_1\cup X_2$, where

$$\begin{aligned} X_1&=\left\{ (u,1) : u\in V\big (\overline{K(10,4)} - e\big )\right\} ,\\ X_2&=\left\{ (u,2) : u\in V\big (\overline{K(10,4)} - e\big )\right\} \cup \{(v_1,2),\ldots ,(v_{99},2)\}, \end{aligned}$$

and none of the possibilities (i), (ii), (iii) of Theorem 3.1 can occur. Observe that the sets

$$\begin{aligned} C=\{(x,0): x\in {\mathbb {F}}_{49}\}\quad {\text {and}}\quad I=\{(0,y): y\in {\mathbb {F}}_{4}\} \end{aligned}$$

are a clique and an independent set in ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$, respectively. Since each Cayley graph is vertex-transitive it follows from [17, Corollaries 2.1.2, 2.1.3] that the product of its clique and independence numbers does not exceed the number of its vertices. Consequently, the orders of the clique C and the independent set I are the largest possible and the maps $p_1: (x,y)\mapsto (x,0)$ and $p_2: (x,y)\mapsto (0,y)$ are endomorphisms of ${\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)$ and $\overline{{\text {Cay}}({\mathbb {F}}_{49}\times {\mathbb {F}}_4, S)}$ onto their maximum cliques, respectively (compare with [41, Proposition 1]). Let $f_1: C\rightarrow \{v_1,\ldots ,v_{49}\}$ and $f_2: I\rightarrow \{v_{50},v_{51},v_{52},v_{53}\}$ be any bijections and consider the map $\Psi$ on $\Gamma {\bar{\Gamma }}$, which fixes the vertices in $X_1\cup X_2$ and satisfies

$$\begin{aligned} \Psi (w_j,1)&=\left\{ \begin{array}{ll}\big (f_1(p_1(w_j)),2\big )&{} {\text {if}}\ j\in \{1,\ldots ,194\},\\ (u_1,2)&{} {\text {if}}\ j=195,\\ (u_2,2)&{} {\text {if}}\ j=196,\\ \end{array}\right. \\ \Psi (w_j,2)&=\left\{ \begin{array}{ll}\big (f_2(p_2(w_j)),2\big )&{} {\text {if}}\ j\notin \{50,\ldots ,53,147,\ldots ,150\},\\ (v_{54},2)&{} {\text {if}}\ j=50,\\ (v_{55},2)&{} {\text {if}}\ j=51,\\ (v_{56},2)&{} {\text {if}}\ j=52,\\ (v_{57},2)&{} {\text {if}}\ j=53,\\ (v_{58},2)&{} {\text {if}}\ j=147,\\ (v_{59},2)&{} {\text {if}}\ j=148,\\ (v_{60},2)&{} {\text {if}}\ j=149,\\ (v_{61},2)&{} {\text {if}}\ j=150, \end{array}\right. ,\\ \Psi (v_i,1)&=\left\{ \begin{array}{ll}(v_{62},2)&{}\qquad \quad \ \; {\text {if}}\ i\ne 62,\\ (v_{63},2)&{}\qquad \quad \ \; {\text {if}}\ i=62. \end{array}\right. \end{aligned}$$

It is straightforward to check that $\Psi$ is a retraction. Since it is not bijective, the claim (i) in Theorem 3.1 is not true. Moreover, Remark 2.9 implies that

$$\begin{aligned} {\text {core}}(\Gamma {\bar{\Gamma }})\cong {\text {core}}(\langle X_1\cup X_2\rangle ), \end{aligned}$$

where $\langle X_1\cup X_2\rangle$ is the subgraph, which is induced by the set $X_1\cup X_2$. If the claim (ii) in Theorem 3.1 is true, then

$$\begin{aligned} {\text {core}}(\Gamma )\cong {\text {core}}(\langle X_1\cup X_2\rangle ) \end{aligned}$$

and consequently Lemmas 2.8, 2.3(i), and (17)–(18) imply that

$$\begin{aligned} 101&\le \omega (K_{99})+\omega (K(10,4) + e)=\omega (\langle X_2\rangle )\\&\le \omega (\langle X_1\cup X_2\rangle )=\omega (\Gamma )=\omega (\overline{K(10,4)} - e)\le 84, \end{aligned}$$

a contradiction. Next observe that $\Psi$ maps $W_2$ into $\langle X_2\rangle$. Hence, Lemma 2.3(ii) implies that

$$\begin{aligned} \chi ({\bar{\Gamma }})\le \chi (\langle X_2\rangle ). \end{aligned}$$

(19)

If the claim (iii) in Theorem 3.1 is true, then

$$\begin{aligned} {\text {core}}({\bar{\Gamma }})\cong {\text {core}}(\langle X_1\cup X_2\rangle ) \end{aligned}$$

and consequently Lemmas 2.8, 2.3(ii), (17)–(18), and (19) imply that

$$\begin{aligned} 104&\le \chi (\overline{K(10,4)} - e)= \chi (\langle X_1\rangle ) \le \chi (\langle X_1\cup X_2\rangle )\\&=\chi ({\bar{\Gamma }})\le \chi (\langle X_2\rangle )=\chi (K_{99})+\chi (K(10,4) + e)=103, \end{aligned}$$

a contradiction.$\Box$

Next we consider the case of a regular complementary prism $\Gamma {\bar{\Gamma }}$.

Corollary 3.4

Let $\Gamma$ be any graph on n vertices that is $\big (\frac{n-1}{2}\big )$-regular. Then only the statements (i), (ii), (iii) in Theorem 3.1 are possible.

Proof

Suppose the claim (iv) from Theorem 3.1 is true. Then $V\big ({\text {core}}(\Gamma {\bar{\Gamma }})\big )$ equals (6). Let $n_i=|V_i|$ for $i=1,2,3$. Then $n_1,n_2\ge 1$. By statement (b), each vertex in $V_1$ is adjacent to each vertex in $V_2$, viewed in the graph ${\bar{\Gamma }}$, which is $\big (\frac{n-1}{2}\big )$-regular. Hence, $n_2\le \frac{n-1}{2}$. Consequently, each vertex $v\in V_2$ has some neighbour $f(v)\in V_3$, viewed in graph $\Gamma$. In fact, the opposite would imply that v has at least $n_1+n_3=n-n_2\ge n-\frac{n-1}{2}=\frac{n+1}{2}$ neighbours in ${\bar{\Gamma }}$, which is not possible. By statement (c), the map $f: V_2\rightarrow V_3$ is injective. Hence,

$$\begin{aligned} n_3\ge n_2. \end{aligned}$$

(20)

Moreover, each vertex $v\in V_2$ has zero and at most $n_2-1$ $\Gamma$-neighbours in $V_1$ and $V_2$, respectively. Consequently, it has at least $\frac{n-1}{2}-(n_2-1)$ $\Gamma$-neighbours in $V_3$. By (c) it follows that $n_3\ge \big (\frac{n-1}{2}-(n_2-1)\big )n_2$. Since $n=n_1+n_2+n_3$, we deduce that

$$\begin{aligned} (n_2-n_1-1)n_2\ge (n_2-2)n_3. \end{aligned}$$

(21)

Further observe that

$$\begin{aligned} n_2\ge 2, \end{aligned}$$

since the equality $n_2=1$ would imply that the graph with vertex set (6) is not a core. We claim also that

$$\begin{aligned} n_1\ge 2. \end{aligned}$$

(22)

If $n_1=1$, then we infer from inclusion (7) that in graph ${\bar{\Gamma }}$ there are no edges inside the set $V_3$ and there are no edges connecting the vertex in $V_1$ with some vertex in $V_3$. Consequently, we deduce by the statement (b) in Theorem 3.1 (iv) that a vertex $f(v)\in V_3$ as above, has in graph $\Gamma$ (at least)

$$\begin{aligned} (n_3-1)+1+1\ge \left( \frac{n-1}{2}-1\right) +1+1=\frac{n+1}{2} \end{aligned}$$

neighbours. This is a contradiction that proves bound (22). Consequently, the equality $n_2=2$ is not possible by (21)–(22), while the inequality $n_2>2$ transforms (21) into

$$\begin{aligned} \frac{n_2-n_1-1}{n_2-2} n_2\ge n_3, \end{aligned}$$

which contradicts (20).

In the same way we see that the claim (v) in Theorem 3.1 is not true. $\square$

Example 3.5

In Corollary 3.4 the possibility (ii) or (iii) may occur even if a $(\frac{n-1}{2})$-regular graph is self-complementary. Consider the graph $\Gamma$ on the vertex set $\{1,2,\ldots ,13\}$ with the adjacency matrix as in Fig. 2. The map $\sigma : \Gamma \rightarrow {\bar{\Gamma }}$, which maps vertices $1,2,\ldots ,13$ into

$$\begin{aligned} 1,8,9,10,11,12,13,5,4,3,2,7,6, \end{aligned}$$

respectively, is an antimorphism. Any core of the graph $\Gamma {\bar{\Gamma }}$ is isomorphic to the complete graph on five vertices. For example, vertices

$$\begin{aligned} (1,1), (2,1), (3,1), (4,1), (5,1) \end{aligned}$$

form such a core C, yielding the possibility (ii). In fact, if we denote

$$\begin{aligned} U_1&=\{(1,1), (8,1), (9,1), (10,1), (4,2), (5,2), (11,2)\},\\ U_2&=\{(2,1), (6,1), (7,1), (1,2), (3,2)\},\\ U_3&=\{(3,1), (11,1), (2,2), (8,2)\},\\ U_4&=\{(4,1), (12,1), (7,2), (9,2), (13,2)\},\\ U_5&=\{(5,1), (13,1), (6,2), (10,2), (12,2)\}, \end{aligned}$$

then the map $\Psi$ on $V(\Gamma {\bar{\Gamma }})$, which maps vertices from the set $U_i$ into (i, 1), for all $i\in \{1,2,3,4,5\}$, is a retraction onto C. If we replace edges $\{3,9\}$, $\{4,10\}$ in graph $\Gamma$ by edges $\{3,10\}$, $\{4,9\}$, we obtain a graph $\Gamma '$, which has the same properties as $\Gamma$. Namely, $\sigma$ is an antimorphism of $\Gamma '$ and $\Psi$ is a retraction onto the clique C. Both graphs $\Gamma$, $\Gamma '$ were found with the help of the database [34].$\Box$

Fig. 2

The adjacency matrix of the graph $\Gamma$ in Example 3.5 and the graph $\Gamma {\bar{\Gamma }}$

In Corollary 3.6 we obtain the same conclusion as in Corollary 3.4 if we move the regularity assumption from $\Gamma {\bar{\Gamma }}$ to ${\text {core}}(\Gamma {\bar{\Gamma }})$ and if we exclude some small examples.

Corollary 3.6

Let $\Gamma$ be any graph on n vertices, which is not isomorphic to $K_2$, $\overline{K_2}$, $P_3$, or $\overline{P_3}$. If ${\text {core}}(\Gamma {\bar{\Gamma }})$ is regular, then only the statements (i), (ii), (iii) in Theorem 3.1 are possible.

Recall from Remark 2.11 that the core of a regular graph is not necessarily regular. Hence, Corollary 3.4 does not follow from Corollary 3.6.

Proof of Corollary 3.6

Suppose the claim (iv) from Theorem 3.1 is true. Let $\overline{\Gamma _1},\Gamma _2,\overline{\Gamma _2}$ be the subgraphs in $\Gamma {\bar{\Gamma }}$, which are induced by the vertex sets

$$\begin{aligned} \{(v,2): v\in V_1\},\quad \{(v,1): v\in V_2\},\quad \{(v,2): v\in V_2\}, \end{aligned}$$

(23)

respectively. Since ${\text {core}}(\Gamma {\bar{\Gamma }})$ is regular, it follows from (6) and the statement (b) in Theorem 3.1 (iv) that all three graphs $\overline{\Gamma _1},\Gamma _2,\overline{\Gamma _2}$ are regular. If ${\bar{k}}_1, n_1$ and ${\bar{k}}_2, n_2$ are the degree and the order of $\overline{\Gamma _1}$ and $\overline{\Gamma _2}$, respectively, then it follows from (6) that the degree of a vertex in $\Gamma {\bar{\Gamma }}$ equals

$$\begin{aligned} {\bar{k}}_1+n_2=(n_2-{\bar{k}}_2-1)+1={\bar{k}}_2+n_1+1, \end{aligned}$$

depending on part (23) of the vertex set that it belongs. From the first equality we deduce that ${\bar{k}}_1+{\bar{k}}_2=0$ and hence ${\bar{k}}_1=0={\bar{k}}_2$. The second equality yields $n_2=n_1+1$. Consequently, $\overline{\Gamma _1}\cong \overline{K_{n_1}}$, $\Gamma _2\cong K_{n_1+1}$, $\overline{\Gamma _2}\cong \overline{K_{n_1+1}}$. If $\Psi$ is a retraction from $\Gamma {\bar{\Gamma }}$ onto ${\text {core}}(\Gamma {\bar{\Gamma }})$, then a vertex in the set $\{(v,1): v\in V_1\}$ cannot be mapped into $\{(v,2): v\in V_1\}$ by $\Psi$, since $\overline{\Gamma _1}\cong \overline{K_{n_1}}$. Consequently, it follows from (9) that $n_1=1$, ${\text {core}}(\Gamma {\bar{\Gamma }})$ is isomorphic to a pentagon, and

$$\begin{aligned} \Psi (v_1,1)=(v_2,2) \end{aligned}$$

for some $v_2\in V_2$, where $V_1=\{v_1\}$. Since $\Gamma \ncong \overline{P_3}$, it follows that $V_3\ne \emptyset$. Let $w\in V_3$. From (7) we deduce that $\Psi (w,2)=(v_1,2)$. In particular, $(v_1,2)\not \sim (w,2)$, i.e. $(v_1,1)\sim (w,1)\sim (w,2)$. Consequently, $(v_2,2), \Psi (w,1), (v_1,2)$ form a triangle in the pentagon ${\text {core}}(\Gamma {\bar{\Gamma }})$, a contradiction.

In the same way we see that the claim (v) in Theorem 3.1 can be true only if $\Gamma$ is isomorphic to the path on three vertices. $\square$

A well-known core is the Petersen graph (cf. [20, 40]), which is the complementary prism $C_5\overline{C_5}$ constructed from the pentagon graph. Since $C_5$ is self-complementary and strongly regular, it is natural to ask if these two properties of a graph $\Gamma$ are sufficient for $\Gamma {\bar{\Gamma }}$ to be a core. Theorem 3.7 provides an affirmative answer.

Theorem 3.7

If $\Gamma$ is a strongly regular self-complementary graph, then $\Gamma {\bar{\Gamma }}$ is a core.

Proof

The claim is obvious if $n:=|V(\Gamma )|=1$. Let $n>1$. By Corollary 3.4 only the statements (i), (ii), (iii) in Theorem 3.1 could be possible. Since $\Gamma$ is self-complementary it suffices to prove that (iii) leads to a contradiction. Hence, assume that ${\text {core}}(\Gamma {\bar{\Gamma }})\cong {\text {core}}({\bar{\Gamma }})$. By Lemma 2.8 there exists a homomorphism between $\Gamma {\bar{\Gamma }}$ and ${\bar{\Gamma }}$. Hence, Lemma 2.4 implies that $\vartheta \big (\overline{\Gamma {\bar{\Gamma }}}\big )\le \vartheta (\Gamma )$ and Lemma 2.5 yields

$$\begin{aligned} \frac{2n}{\vartheta (\Gamma {\bar{\Gamma }})}\le \vartheta (\Gamma ). \end{aligned}$$

(24)

Recall that graphs $\Gamma$ and $\Gamma {\bar{\Gamma }}$ are regular of degree $\frac{n-1}{2}$ and $\frac{n+1}{2}$, respectively. Moreover, by Lemma 2.2 and Corollary 2.14, their smallest eigenvalues equal $\frac{-\sqrt{n}-1}{2}$ and $\frac{-\sqrt{n+4}-1}{2}$, respectively. Hence, Lemma 2.6 gives the inequalities $\vartheta (\Gamma )\le \sqrt{n}$ and

$$\begin{aligned} \vartheta (\Gamma {\bar{\Gamma }})\le \frac{2n}{1+\frac{n+1}{\sqrt{n+4}+1}}. \end{aligned}$$

If we combine them with (24), then we deduce that

$$\begin{aligned} n+1\le (\sqrt{n}-1)(\sqrt{n+4}+1). \end{aligned}$$

However, the inequality between the geometric and the arithmetic means yields

$$\begin{aligned} (\sqrt{n}-1)(\sqrt{n+4}+1)&=\sqrt{n(n+4)}+\sqrt{n}-\sqrt{n+4}-1\\&<\sqrt{n(n+4)}-1\\&\le \frac{n+(n+4)}{2}-1=n+1, \end{aligned}$$

a contradiction. $\square$

¹