1 Introductory remarks

The Erdős-Ko-Rado theorem [9], one of the central results in extremal combinatorics, which gives a bound on the size of a family of intersecting k-subsets of a set and classifies the families satisfying the bound, has been extended in various ways. This paper is concerned with an extension of this theorem to the ambient of transitive permutation groups and vertex-transitive graphs.

For a finite set V let \({\textrm{Sym}}(V)\) denote the corresponding symmetric group, and if \(|V|=n\), the notation \(S_n\) will be adopted. Given a permutation group \(G \le {\textrm{Sym}}(V)\), two elements \(g,h\in G\) are said to be intersecting if there exists \(v \in V\) such that \(g(v)=h(v)\). We will use the notation \(g\cap h\) in this case. Further, a subset \(\mathcal {F}\) of G is called intersecting if every two elements of \(\mathcal {F}\) are intersecting. The intersection density \(\rho (\mathcal{F})\) of the intersecting set \(\mathcal{F}\) is defined to be the quotient

$$\begin{aligned} \rho (\mathcal{F})=\frac{|\mathcal{F}|}{\max \{|G_v|:v\in V\}}, \end{aligned}$$

where \(G_v\) is the point stabilizer of \(v\in V\), and the intersection density \(\rho (G)\) (see [15, 17, 18, 21]) of a group G, is the maximum value of \(\rho (\mathcal{F})\) where \(\mathcal{F}\) runs over all intersecting sets in G.

Clearly, every coset \(gG_v\), \(v\in V\) and \(g\in G\), is an intersecting set, referred to as a canonical intersecting set. Consequently, \(\rho (G)\ge 1\). We say that G has the Erdős-Ko-Rado property (in short EKR-property), if the size of a maximum intersecting set is equal to the order of the largest point stabilizer, and is said to have the strict Erdős-Ko-Rado property (in short strict-EKR-property) if every maximum intersecting set of G is a coset of a point stabilizer. It is clear that strict-EKR-property implies EKR-property, but the converse does not hold. In particular, if G is transitive then \(\rho (G)= 1\) if and only if the maximum cardinality of an intersecting set is |G|/|V|. Note that if \(\mathcal {F}\) is an intersecting set of G and \(f\in \mathcal {F}\) then \(f^{-1}\mathcal {F}\) is an intersecting set of G (see [14, Proposition 2.3]). Therefore without loss of generality one can consider intersecting sets containing the identity. We will refer to such sets as basic intersecting sets.

Although there are numerous constructions of transitive permutation groups with intersection density greater than 1, such groups remain a hot topic of research. This brings us to the class of transitive permutation groups without regular subgroups. Namely, it is known that regular groups have intersection density equal to 1 [14, Proposition 2.6.], and that the intersection density of a transitive permutation group cannot exceed that of any of its transitive subgroups [20, Lemma 6.5]. Now, moving to vertex-transitive graphs, this means that the above question is for the most part a question about non-Cayley graphs. Namely, there do exist Cayley graphs containing transitive subgroups of automorphisms containing no regular subgroups whose intersection densities are greater than 1 (see Example 2.6). Let us remark that the generalization of the question regarding intersecting sets to the class of all vertex-transitive graphs is indeed a natural one. Namely, the original Erdős-Ko-Rado theorem may be rephrased in a graph-theoretic language as the classification of independent sets of maximal cardinality of the Kneser graphs, see [11]. Of course, the Kneser graphs are vertex-transitive, and therefore a generalization can go in two directions: first, from a special class of vertex-transitive graphs to the whole class of vertex-transitive graphs, and second, from intersecting density of the full automorphism groups to intersection density arrays of the graphs in question.

The intersection density array \(\rho (\Gamma )=[\rho _0,\rho _1,...,\rho _{k-1}]\) of a vertex-transitive graph \(\Gamma \) is defined as a “collection” of increasing intersection densities of transitive subgroups of \({\textrm{Aut}}\,(\Gamma )\), that is, for any transitive subgroup G of \({\textrm{Aut}}\,(\Gamma )\), we have \(\rho (G) = \rho _i\) for some \(i \in \mathbb {Z}_k\), with \(\rho _i<\rho _{i+1}\). Furthermore a vertex-transitive graph \(\Gamma \) is said to be intersection density stable if \(\rho (G) = \rho (H)\) for any two transitive subgroups G and H of \({\textrm{Aut}}\,(\Gamma )\). In short, if the above array consists of a single item. In particular, in line with the concept of EKR-property of transitive pemutation groups we say that a vertex-transitive graph with intersection density array [1] has the EKR-property. Of particular interest are graphs with non-trivial intersection densities, that is, graphs without the EKR-property. When restricting ourselves to symmetric graphs, that is, arc-transitive graphs, we say that the weak intersection density array \(\bar{\rho }(\Gamma )\) of a symmetric graph X is a subarray of \(\rho (\Gamma )\) consisting only of intersection densities realized by arc-transitive subgroups of \({\textrm{Aut}}\,(\Gamma )\). Furthermore, we say that \(\Gamma \) is weakly intersection density stable provided \(\rho (G) = \rho (H)\) for any two arc-transitive subgroups G and H of \({\textrm{Aut}}\,(\Gamma )\), and that \(\Gamma \) has the weak EKR-property if its weak intersection density array is equal to [1].

This paper initiates a program aimed at obtaining an understanding, as thorough as possible, of intersection densities of cubic symmetric graphs. (The connectedness of these graphs is tacitly assumed throughout the rest of the paper.) These graphs arise naturally from transitive permutation groups with self-paired suborbits of length 3. This paper is therefore a natural follow-up of [13] where intersection densities of transitive permutation groups with point stabilizers of prime order were studied. In particular, it was proved there that solvable groups with point stabilizers of prime order have the EKR property (see [13, Proposition 4.1]), implying that in our investigation of intersection density stable graphs we may restrict ourselves to non-solvable groups. It is well known that there are 17 types of cubic symmetric graphs. These types are defined with respect to (non)existence of different s-arc-regular subgroups for \(s\in \{1,2,3,4,5\}\) (see Sect. 2). As a starting point of a project aimed at obtaining a deeper understanding of intersection density arrays of cubic symmetric graphs, we choose to consider the subclass of cubic symmetric graphs which admit a 1-arc-regular subgroup of automorphisms. Out of the above-mentioned 17 types of cubic symmetric graphs five contain graphs admitting a 1-arc-regular subgroup of automorphisms: \(\{1\}\), \(\{1,2^1\}\), \(\{1,2^1,2^2,3\}\), \(\{1,4^1\}\) and \(\{1,4^1,4^2,5\}\). Graphs belonging to the latter two are obtained, respectively, as covers of the Heawood graph \(\textrm{F}14\) and the Biggs-Conway graph of order 2.352, and are therefore Cayley graphs. The corresponding Cayley groups are necessary contained in all arc-transitive subgroups with the exception of a \(4^2\)-arc-regular subgroup, for which the intersection density needs to be computed directly, see Proposition 3.3. In this sense, as far as the intersection density is concerned, the interesting families of graphs are those of types \(\{1\}\), \(\{1,2^1\}\) and \(\{1,2^1,2^2,3\}\). (Throughout the paper the notation \(\textrm{F} n\textrm{A}\), \(\textrm{F} n\textrm{B}\), etc. will refer to the corresponding graphs in the Foster census of all cubic symmetric graphs on up to 512 vertices  [3]. For cubic symmetric graphs on more vertices and in the appendix the notation from [4] is used).

The paper is organized as follows. In Sect. 2 we introduce the standard terminology and gather certain results on cubic symmetric graphs needed later on in the paper, and give examples of intersection density arrays for some of these graphs. In Sect. 3 certain properties of intersecting sets in graphs admitting 1-arc-regular actions are singled out. In Sect. 4 a sufficient condition for a cubic symmetric graph of type \(\{1,2^1\}\) to be non-trivial weakly intersection density stable is given (see Corollary 4.4). An infinite family of such graphs is also constructed (see Theorem 4.8).

Finally, in the Appendixthe list of all cubic symmetric graphs up to order 2.048 is given together with the following information for each of the graphs: order of the graph, its girth, is it bipartite or not, its type, is it density stable or not, its density array, all transitive subgroups of its automorphism group together with their densities, information if they contain a regular subgroup or not, information on s-arc-regularity in case they act arc-transitively on the graph, and the lengths of consistent cycles. (In the table \(\top \) always indicates a true statement and \(\bot \) a false statement.) The list was created using Magma [2] and the well-known list of these graphs due to Conder [4]. Computations were based on the fact that the intersecting density of a subgroup can be reduced to finding a maximal sized clique in the corresponding derangement graph. (The derangement graph \(\Gamma _G={\textrm{Cay}}(G,\mathcal{D})\) is a Cayley graph of a group G with the edge set consisting of all pairs \((g,h)\in G\times G\) such that \(gh^{-1}\in \mathcal{D}\), where \(\mathcal{D}\) is the set of all fixed-point-free elements (i.e., derangements) of G, see for example [20, 21].) In Table 1 we summarize all values of intersection density arrays that occur for cubic symmetric graphs of order up to 2.048.

Table 1 Values of intersection density arrays that occur for cubic symmetric graphs of order up to 2.048. The smallest examples of graphs of types \(\{4^2\}\), \(\{1,4^1,4^2,5\}\), \(\{4^1,5\}\) and \(\{5\}\) are of order more than 2.048, and so these types do not occur in the table
Full size table

2 Intersection density arrays of some cubic symmetric graphs

When attempting to gain a thorough understanding of symmetric graphs, it is often helpful to know the structure of vertex-stabilizers and how they act, both locally and globally. In particular, for symmetric cubic graphs the structure of vertex-stabilizers is well known. Tutte proved in two seminal papers [23, 24] that every finite symmetric cubic graph is s-arc-regular for some \(s \le 5\). Some further insight into the structure of symmetric cubic graphs was given by Djoković and Miller, who proved in [8] that each vertex-stabilizer in an s-arc-regular subgroup of automorphisms of a symmetric cubic graph is isomorphic to \(\mathbb {Z}_3\), \(S_3\), \(S_3 \times \mathbb {Z}_2\), \(S_4\) or \(S_4 \times \mathbb {Z}_2\), when \(s=1,2,3,4\) or 5, respectively. Also, for \(s\in \{1,3,5\}\) there is just one possibility for edge-stabilizers, while for \(s\in \{2,4\}\) there are two possibilities for edge-stabilizers (see [5, 8]). The resulting seven classes of arc-transitive finite group actions on cubic graphs are summarized in Table 2, where \(D_n\) denotes the dihedral group of degree n and order 2n (see also [10]). In particular, for \(s=2\) the edge-stabilizer (of order 4) is isomorphic to either \(V_4 \cong \mathbb {Z}_2\times \mathbb {Z}_2\) or \(\mathbb {Z}_4\), while for \(s=4\) the edge-stabilizer (of order 16) is isomorphic to either \(D_{8}\) or the quasi-dihedral group \(QD_{8}\).

Table 2 Vertex and edge-stabilizers of an s-arc-regular group G of automorphisms of a cubic graph
Full size table

More recently, Conder and Nedela [6] proved that there are exactly 17 combinations of the above seven classes realizable by the arc-transitive subgroups of the full automorphism group of a finite cubic symmetric graph X; see Table 3. For example, a cubic symmetric graph is said to be of type \(\{1,2^1,2^2,3\}\) if its automorphism group is 3-arc-regular, admitting two 2-arc-regular subgroups, with respective edge-stabilizers isomorphic to \(\mathbb {Z}_2\times \mathbb {Z}_2\) and \(\mathbb {Z}_4\), and admitting also a 1-arc-regular subgroup.

Table 3 The 17 possible types for symmetric cubic graphs
Full size table

We now give the intersection density arrays of some well-known cubic symmetric graphs. The computation was done by Magma [2]. We start with the complete bipartite graph \(K_{3,3}\), the Petersen graph and the Coxeter graph.

Example 2.1

The complete bipartite graph \(K_{3,3}\) is a cubic symmetric graph of type \(\{1,2^1,2^2,3\}\). The full automorphism group \(S_3^2\rtimes \mathbb {Z}_2\) as well as all of its subgroups acting transitively on vertices have intersection density 1, and so \(K_{3,3}\) is an example of a trivial intersection density stable graph.

Example 2.2

The Petersen graph is a cubic symmetric graph of type \(\{2^1,3\}\) with three subgroups of the automorphism group acting transitively on the set of vertices. The full automorphism group \(S_5\) has intersection density 1, while the index 2 subgroup isomorphic to \(A_5\) has intersection density 2. There is a third subgroup of order 20 isomorphic to \(\mathbb {Z}_5\rtimes \mathbb {Z}_4\) with intersection density 1. (For the reference of these results see [14].) The Petersen graph, with intersection density array [1, 2], is therefore not intersection density stable.

Example 2.3

The Coxeter graph is a cubic symmetric graph of type \(\{2^2,3\}\) with two subgroups of the automorphism group acting transitively on the vertex set. The full automorphism group \(\textrm{PGL}(2,7)\) has intersection density 1, while the index 2 subgroup isomorphic to \(\textrm{PSL}(2,7)\) has intersection density 2, and so the Coxeter graph has intersection density array equal to [1, 2] and is not intersection density stable.

In the next two examples, we give intersection density arrays of two non-Cayley cubic symmetric graphs of type \(\{1,2^1\}\). The first one has the intersection density array [1, 4/3], while the second one is intersection density stable and does not have the EKR-property.

Example 2.4

The cubic symmetric graph \(\textrm{F}220\textrm{B}\) has order 220 and is of type \(\{1,2^1\}\). The intersection density of the full automorphism group is equal to 1, whereas a 1-arc-regular subgroup has intersection density equal to 4/3. Hence this graph is not intersection density stable.

Example 2.5

The cubic symmetric graph \(\textrm{F}240\textrm{C}\) has order 240 and is of type \(\{1,2^1\}\). The intersection density of its full automorphism group as well as of the index 2 subgroups is equal to 3. As there are no other transitive subgroups of automorphisms we conclude that this graph is intersection density stable and of course it does not have the EKR property.

The fact that permutation groups which act regularly have intersection density 1, suggests that Cayley graphs are natural candidates for graph with EKR-property. Interestingly, however, there are Cayley graphs which are not intersection density stable, meaning that they have a transitive subgroup of automorphisms with intersection density not equal to 1. Of course this subgroup does not contain a regular subgroup. A classical example is the Kneser graph K(8, 3) of valency 10. In the example below, however, we give a cubic symmetric Cayley graph without the EKR property.

Example 2.6

The cubic symmetric graph \(\textrm{F}220\textrm{C}\) has order 220 and is of type \(\{2^1,2^2,3\}\). It is a Cayley graph with intersection density array [1, 2]. More precisely, both of the two 2-arc-regular subgroups have intersection density 2 while the full automorphism group and, of course, the regular subgroup, have intersection density 1.

3 Intersecting sets in graphs admitting 1-arc-regular actions

The following is a straightforward generalization of [13, Proposition 5.2]. The proof is omitted (see also [12]).

Proposition 1.7

Let G be a 1-arc-regular group acting on a cubic symmetric graph \(\Gamma \), and let \(\mathcal {F}\) be a basic intersecting set of G containing two elements x and y from different vertex stabilizers of G. Then \(T=\langle xy,xy^{-1}x\rangle \) is a normal abelian subgroup of \(\langle x,y\rangle \) such that \(\langle x,y\rangle / T \cong \mathbb {Z}_3\). In particular, if \((xy)^3=1\) then \(\langle x,y\rangle \) is either isomorphic to \(\mathbb {Z}_3^2\) or to the unique non-abelian group of order 27 with exponent 3.

For example, in the dodecahedron \(\textrm{F}20\textrm{A}\) the 1-arc-regular subgroup (isomorphic to \(A_5\)) has density 4/3, any maximal basic intersecting set consists of elements \(\{1,x,y,z\}\) where x, y, z are non-commuting elements from different vertex stabilizers such that \(\langle x,y\rangle \cong \langle y,z\rangle \cong \langle z,x\rangle \cong A_4\). On the other hand, in the cubic symmetric graph \(\textrm{C}720.5\), which is of type \(\{1,2^1\}\), a maximum intersecting set for a 1-arc-regular group has 9 elements while a maximum intersecting set for the full automorphism group has 10 elements. In particular, there exists a basic intersecting set \(\mathcal {F}\) for the 1-arc-regular group with 9 elements and the two non-commuting elements \(x,y\in \mathcal {F}\) generate the non-abelian group of order 27 with exponent 3 as predicted by Proposition 3.1.

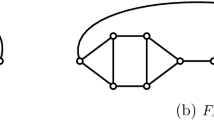
In the proof of the next proposition, the concept of rigid cells is needed. These are explored in detail in [7, 16]. Given a graph \(\Gamma \) and an automorphism \(\alpha \) of \(\Gamma \) let \(\text {Fix}(\alpha )\) denote the set of all vertices of \(\Gamma \) fixed by \(\alpha \). With the assumption that \(\text {Fix}(\alpha )\ne \emptyset \) we call the subgraph \(\Gamma [\text {Fix}(\alpha )]\) induced on \(\text {Fix}(\alpha )\) the rigid subgraph of \(\alpha \) or, in short, the \(\alpha \)-rigid subgraph. Every connected component of \(\Gamma [\text {Fix}(\alpha )]\) is referred to as an \(\alpha \)-rigid cell. It was proved in [16] that possible rigid cells in cubic symmetric graphs depending on the s-arc-regularity are as shown in Fig. 1.

Fig. 1
figure 1

I-tree, H-tree, Y-tree, and A-tree

Full size image

Proposition 1.8

Let \(\Gamma \) be a cubic symmetric graph whose automorphism group is either 4-arc-regular or 5-arc-regular. Then a transitive subgroup of \({\textrm{Aut}}\,(\Gamma )\) is either regular or acts transitively on arcs.

Proof

Suppose that there exists a transitive group G in \({\textrm{Aut}}\,(\Gamma )\) which is neither arc-transitive nor regular. Then G has two edge orbits on \(\Gamma \) consisting of a collection of cycles \(\mathcal {C}\) of the same length and a 1-matching. But in order for all arcs arising from a cycle \(C\in \mathcal {C}\) to be in the same orbit of G there must exist an involution \(\tau \) in G fixing C set-wise and as such it has at most two fixed (non-adjacent) vertices on this cycle. Since \(\Gamma \) is 4-arc-regular or 5-arc-regular, it follows by [16, Propositions 3.4. and 3.5.] that every involution must have either an H-tree or an A-tree as a rigid cell. In case of the involution \(\tau \), however, a corresponding rigid cell would consist only of a vertex \(v\in V(C)\) and its third neighbor outside C. \(\square \)

Proposition 1.9

Let \(\Gamma \) be a cubic symmetric graph either of type \(\{1,4^1\}\) or of type \(\{1,4^1,4^2,5\}\). Then \(\rho (\Gamma )=[1]\).

Proof

Suppose first that \(\Gamma \) is of type \(\{1,4^1\}\). Then, by [6], \(\Gamma \) is a regular cover of the Heawood graph \(\Gamma _0=\textrm{F}14\). In view of [14, Lemma 3.1] it suffices to show that \(\rho (\Gamma _0)=[1]\). First, by Proposition 3.2, every transitive subgroup of \({\textrm{Aut}}\,(\Gamma _0)\) is either regular or arc-transitive. In fact, \(\Gamma _0\) is a Cayley graph of the dihedral group \(D_{14}\) which is contained in every arc-transitive subgroup of \({\textrm{Aut}}\,(\Gamma _0)\), and the result follows.Similarly, if \(\Gamma \) is of type \(\{1,4^1,4^2,5\}\) then, by [6], it is a regular cover of the Biggs-Conway graph \(\Gamma _0\) of order 2352 [1], which is a Cayley graph and, as was checked by Magma [2], with \(\rho (\Gamma _0)=[1]\), and so [14, Lemma 3.1] implies that \(\rho (\Gamma )=[1]\) as well. \(\square \)

4 Intersection density stable graphs of type \(\{1,2^1\}\)

The next two results will be used in the proof of Theorem 4.3 which gives a sufficient condition for a cubic symmetric graph of type \(\{1,2^1\}\) to be weakly intersection density stable.

Lemma 1.10

Let \(\Gamma \) be a cubic symmetric graph admitting a 1-arc-regular subgroup G and a 2-arc-regular subgroup \(G^*\) such that

$$\begin{aligned} x\cap 1 \text { and } y\cap 1 \text { implies } xy\cap 1 \text { whenever } xy=yx \ (x,y\in G). \end{aligned}$$
(1)

If \(\mathcal {F}\) is a basic intersecting set of G such that \(\mathcal {F}\cup \{p,q\}\), \(p,q\in G^*\setminus G\), is an intersecting set of \(G^*\), then \(pq\in C_G(\mathcal {F})\) and \(\mathcal {F}\cup \{pq\}\) is an intersecting set of G.

Proof

Observe that in view of the assumptions the elements \(p,q\in G^*{\setminus } G\) belong to a basic intersecting set of \(G^*\) and since stabilizers in \(G^*\) are isomorphic to \(S_4\) it follows that p and q are involutions. We need to show that \(x\cap pq\) for each \(x\in \mathcal {F}\). Since \(p\cap q\) there exists a vertex \(v\in V(\Gamma )\) such that \(p(v)=q(v)\), implying \(v=pq(v)\), and so

$$\begin{aligned} pq\cap 1. \end{aligned}$$
(2)

In particular, since \(p,q\in G^*\), it follows that \(pq\in G\) generates a vertex stabilizer isomorphic to \(\mathbb {Z}_3\), and so \((pq)^3=1\). If \(x\ne 1\) then to show that \(x\cap pq\) observe that \(x\cap p\) and \(x\cap q\) imply that \(px\cap 1\) and \(qx\cap 1\), respectively. Hence \(px,qx\in G^*\setminus G\) belong to stabilizers and so \((px)^2=1=(qx)^2\). In other words \(px=x^{-1}p\) and \(qx=x^{-1}q\), and so \(pq,qp\in C_G(x)\). Consequently, \((xqp)^3=x^3(qp)^3=1\). Since \(x\cap 1\) it follows by (2) that the condition (1) is satisfied for \(y=pq\). We conclude that \(xqp\cap 1\), and so \(xq\cap p\), and finally \(x\cap pq\). Therefore \(\mathcal {F}\cup \{pq\}\) is an intersecting set of G. \(\square \)

As a direct consequence of Lemma 4.1 we have the following result.

Corollary 1.11

Let \(\Gamma \), \(G^*\) and G be as in the statement of Lemma 4.1. If \(\mathcal {F}\) is a maximal basic intersecting set of G and \(\mathcal {F}\cup \{p,q\}\), \(p,q\in G^*{\setminus } G\), is an intersecting set of \(G^*\) then \(pq\in \mathcal {F}\).

Theorem 1.12

Let \(\Gamma \), \(G^*\) and G be as in the statement of Lemma 4.1. If \(\rho (G)=\rho (G^*)\ne 1\) then \(\rho (G)=3^k\), \(k\in \mathbb {Z}\), and there exists a basic intersecting set \(\mathcal {F}\) of \(G^*\) which is a group such that \(\mathcal {F}\cap G\cong \mathbb {Z}_3^k\) and \(\mathcal {F}\cong \mathbb {Z}_3^k\rtimes \mathbb {Z}_2\).

Proof

Let \(\rho =\rho (G)=\rho (G^*)\). Among all basic intersecting sets let \(\mathcal {F}\) be such that \(P=\mathcal {F}\setminus G\) is of maximal cardinality. Let \( H= \mathcal {F}\cap G\). Then

$$\begin{aligned} H= \{x_i:i\in \mathbb {Z}_m\} \text { and } P=\{p_i :i\in \mathbb {Z}_n\} \end{aligned}$$

where \(x_0=1\) and \(x_i^3=1\) for every \(i\in \mathbb {Z}_m\), and \(p_i^2=1\) for every \(i\in \mathbb {Z}_n\). Also, \(|\mathcal {F}|=6\rho \), and furthermore \(|H|=3\rho =|P|\), for otherwise either \(\mathcal {F}\cap G\) or \(p(\mathcal {F}{\setminus } G)\) for some \(p\in P\) would be an intersecting set of G of size greater than \(3\rho \). Therefore \(m=3\rho =n\). Clearly \(n\ge 4\) as \(\rho (G^*)\ne 1\).

By Corollary 4.2 we have that \(pq\in H\) for any two elements \(p,q\in P\), and since \(|pP|=n\) for each \(p\in P\), it follows that \(p P=H\) for each \(p\in P\). Since, by Lemma 4.1, \(pP\subseteq C_G(H)\) it follows that every two elements in H commute. We now show that H is in fact an elementary abelian 3-group. Let \(x,y\in H\) be arbitrary. Then there exists p, q, r such that \(x=pq\) and \(y=pr\). Then \(x^{-1}y=qr\in H\), and so H is a subgroup of G, in fact an elementary abelian 3-group. This completes the proof of Theorem 4.3. \(\square \)

The corollary below gives a necessary and sufficient condition for a cubic symmetric graph of type \(\{1,2^1\}\) satisfying the condition (1) to be weakly intersection density stable.

Corollary 1.13

Let \(\Gamma \) be a cubic symmetric graph of type \(\{1,2^1\}\) admitting a 1-arc-regular subgroup G with the full automorphism group \(G^*\) such that \(x\cap 1\) and \(y\cap 1\) implies \(xy\cap 1\) whenever \(xy=yx\) (\(x,y\in G\)). Then \(\Gamma \) is weakly intersection density stable if and only if \(\rho (G)=3^k\), \(k\in \mathbb {Z}\), and there exists a basic intersecting set \(\mathcal {F}\) of \(G^*\) which is a group such that \(\mathcal {F}\cap G\cong \mathbb {Z}_3^k\) and \(\mathcal {F}\cong \mathbb {Z}_3^k\rtimes \mathbb {Z}_2\).

As a consequence of Corollary 4.4 we also have the following result.

Corollary 1.14

Let \(\Gamma \) be a cubic symmetric graph of type \(\{1,2^1\}\) admitting a 1-arc-regular subgroup G with the full automorphism group \(G^*\) with no semiregular automorphisms of order 3. Then \(\Gamma \) is weakly intersection density stable if and only if \(\rho (G)=3^k\), \(k\in \mathbb {Z}\), and there exists a basic intersecting set \(\mathcal {F}\) of \(G^*\) which is a group such that \(\mathcal {F}\cap G\cong \mathbb {Z}_3^k\) and \(\mathcal {F}\cong \mathbb {Z}_3^k\rtimes \mathbb {Z}_2\).

We now give a construction of an infinite family of non-trivial intersection density stable cubic symmetric graphs of type \(\{1,2^1\}\). These graphs arise from the action of the group \(\textrm{PSL}(2,3^n)\), \(n\ge 3\), on cosets of \(\mathbb {Z}_3\) and satisfy the conditions from Theorem 4.3. The group \(\textrm{PSL}(2,9)\) is not considered here because none of its orbitals in the action on cosets of a subgroup of order 3 is self-paired and connected. This is a direct consequence of the fact that, by [19], \(\textrm{PSL}(2,9)\) cannot be generated by an involution and an element of order 3, while for \(n\ge 3\) the group \(\textrm{PSL}(2,3^n)\) is generated by an involution and an element of order 3. Thus the result below proved in [13], implies the existence of cubic symmetric graphs admitting a 1-arc-regular action of \(\textrm{PSL}(2,3^n)\) whose intersection density is a power of 3.

Proposition 1.15

[13, Theorem 7.2] Let G be a transitive permutation group arising from \(\textrm{PSL}(2,3^n)\), \(n\ge 3\), acting on cosets of a subgroup of order 3. Then

$$\begin{aligned} \rho (G)= & {} {\left\{ \begin{array}{ll} 3^{n-1} &{} \text {if}\,\,n\,\,\text {is odd}, \\ 3^{n/2-1} &{} \text {if}\,\,n\,\,\text {is even}. \end{array}\right. } \end{aligned}$$
(3)

For brevity reasons, let X(n) denote a cubic symmetric graph arising from the action of \(\textrm{PSL}(2,3^n)\), \(n\ge 3\), given in Proposition 4.6. In Theorem 4.8 below we show that these graphs are non-trivial intersection density stable graphs of type \(\{1,2^1\}\).

Lemma 1.16

Let \(q=3^n\), \(n\ge 3\), \(G^*=\textrm{PGL}(2,q)\) and \(G=\textrm{PSL}(2,q)\). Then there exist \(h,a\in G\) and \(p\in G^*\setminus G\) such that \(G^*=\langle h,a,p :h^3=a^2=p^2=1, h^p=h^{-1}, ap=pa,\ldots \rangle \) and \(G=\langle h,a :h^3=a^2=1,\ldots \rangle \).

Proof

By [6] there exists an element h of order 3 and an involution a such that \(G=\langle h,a\rangle \). We can choose h to be \( \left[ \begin{array}{cc} 1 &{} 1 \\ 0 &{} 1\\ \end{array} \right] \) in view of the fact that for n odd all subgroups of order 3 are conjugate while for n even the two conjugate class of elements order 3 in G merge in \(G^*\). As for the involution \(a= \left[ \begin{array}{cc} x &{} y \\ z &{} -x\\ \end{array} \right] \) to be an element of G we just need that \(x^2+yz=\pm 1\). Next, we need to find an involution \(p\in G^*{\setminus } G\) such that \(ap=pa\) and \(h^p=h^{-1}\). It follows that p has to be of the form \( \left[ \begin{array}{cc} u &{} v \\ 0 &{} -u\\ \end{array} \right] \) where \(2xu=-zv\), and consequently \(p=uI\cdot \left[ \begin{array}{cc} 1 &{} -\frac{2x}{z} \\ 0 &{} 1\\ \end{array} \right] \) where \(u^2\ne \pm 1\) (in order for p to be in \(G^* {\setminus } G\)). \(\square \)

Theorem 1.17

Let q, \(G^*\) and G be as in the statement of Lemma 4.7 and let X(n) be the orbital graph of the action of \(G^*\) on the cosets of \(H^*=\langle h,p\rangle \) with respect to the suborbit arising from the arc \((H^*,H^*a)\). Then X(n) is an intersection density stable cubic symmetric graph of type \(\{1,2^1\}\) with \(\rho (X(n))\) equal to \([3^{n-1}]\) if n is odd and to \([3^{n/2-1}]\) if n is even.

Proof

The fact that X(n) is a cubic symmetric graph follows from the choice of h, a and p. Also the action of \(G^*\) is clearly 2-arc-regular and the action of G is 1-arc-regular. Namely, every coset \(H^*x\) is of the form \(H^*ah^{\pm 1}ah^{\pm 1}\ldots ah^{\pm 1}\) or \(H^*ah^{\pm 1}ah^{\pm 1}\ldots a\), and so clearly a multiplication by \(x^{-1}\in G\) takes \(H^*x\) to \(H^*\).

In order to see that the graph is indeed of type \(\{1,2^1\}\) we only need to show that X(n) is not 3-arc-regular. In other words, we need to show that X(n) is not of type \(\{1,2^1,2^2,3\}\). By Conder [6], we have that all cubic symmetric graphs of type \(\{1,2^1,2^2,3\}\) are bipartite, while X(n) is not bipartite in view of the fact that G has no subgroup of index 2.

Moreover, X(n) arises also as an orbital graph of the action of G on cosets of \(H=\langle h\rangle \), and so we conclude, by Proposition 4.6, that the intersection density of G is equal to \([3^{n-1}]\) if n is odd and to \([3^{n/2-1}]\) if n is even.

It follows by the proof of Proposition 4.6 that the maximum intersecting set \(\mathcal {F}\) giving rise to the corresponding intersection density of the action of G on H is an elementary abelian 3-group consisting of upper triangle matrices. One can then check that for any element \(k\in \mathcal {F}\) we have \(pkp=k^{-1}\), and consequently, we can conclude that \(\mathcal {F}\cup p\mathcal {F}\) is an intersecting set of \(G^*\) in its action on the costs of \(H^*\). Hence \(\rho (G^*)\ge \rho (G)\), and so \(\rho (G^*)= \rho (G)\).

To complete the proof of this theorem we just need to show that X(n) does not admit a transitive subgroup of automorphisms with two or three edge orbits on X(n), that is, a transitive subgroup of automorphisms with vertex stabilizer isomorphic to \(\mathbb {Z}_2\) or with trivial vertex stabilizer. In both cases this would imply the existence of a subgroup of index 3 in G which is clearly not the case (see, for example, [22, Theorems 6.25 and 6.26]). \(\square \)

Remark 4.9

As for future research of intersection density arrays of cubic symmetric graphs, our first goal should be obtaining a complete description of all possibilities that can occur with respect to intersection density arrays of cubic symmetric graphs of type \(\{1,2^1\}\). In this respect, understanding the relationship between the intersection densities \(\rho (G)\) and \(\rho (G^*)\) of the 1-arc-regular and 2-arc-regular groups G and \(G^*\), respectively, will be needed. We conjecture that it all comes down to essentially three different possibilities. The first possibility covers the situation where \(\rho (G^*)=\max \{1,\rho (G)/2\}\). In other words, a maximal intersecting set of \(G^*\) is either a vertex stabilizer \(G^*_v\) or it coincides with a maximal intersecting set of G. Second, drawing from Theorem 4.3 and Corollary 4.4 which give a necessary condition for the groups G and \(G^*\) to have the same intersection density, we hope to be able to complete the intersection density stable end of the spectrum of possible intersection density arrays. Finally, we believe that in all remaining cases a maximal intersecting set of \(G^*\) consists of a union of a maximal intersecting set of G and a single element from \(G^*\setminus G\), and consequently, \(\rho (G^*)=\rho (G)/2+1/6.\)