Addition–deletion results for the minimal degree of logarithmic derivations of hyperplane arrangements and maximal Tjurina line arrangements

Abstract

We study the change of the minimal degree of a logarithmic derivation of a hyperplane arrangement under the addition or the deletion of a hyperplane and give a number of applications. First, we prove the existence of Tjurina maximal line arrangements in a lot of new situations. Then, starting with Ziegler’s example of a pair of arrangements of $d=9$ lines with $n_3=6$ triple points in addition to some double points, having the same combinatorics, but distinct minimal degree of a logarithmic derivation, we construct new examples of such pairs, for any number $d\ge 9$ of lines, and any number $n_3\ge 6$ of triple points. Moreover, we show that such examples are not possible for line arrangements having only double and triple points, with $n_3 \le 5$.

1 Introduction

Let ${\mathbb {K}}$ be a field of characteristic zero, consider the polynomial ring $S={\mathbb {K}}[x_1,\ldots ,x_{\ell }]$ with the usual grading, i.e., $S=\oplus _{d \in {\mathbb {Z}}_{\ge 0}} S_d$, and for an S-graded module M, let $M=\oplus _{d \in {\mathbb {Z}}} M_d$ be its decomposition according to the grading. Let X be a reduced projective hypersurface in ${\mathbb {P}}^{\ell -1}$, defined by a homogeneous polynomial $f\in S_d$ of degree d. We assume that X is essential, that is, X is not the cone over a projective hypersurface in some ${\mathbb {P}}^n$ with $n <\ell -1$. When $X={{\mathcal {A}}}$ is a hyperplane arrangement, the main situation considered below, this definition agrees with the usual one. The details will be recalled in the next section. Let

$$\begin{aligned} {{\,\mathrm{Der}\,}}S:=\oplus _{i=1}^\ell S \partial _{x_i} \end{aligned}$$

be the module of derivations of S, a ${\mathbb {Z}}$-graded free S-module of rank $\ell$. Here, $0 \ne \theta \in {{\,\mathrm{Der}\,}}S$ is homogeneous of degree e if $\theta (g)$ is zero or homogeneous of degree e for all $g \in S_1$. For example, the Euler derivation $\theta _E:=\sum _{i=1}^\ell x_i \partial _{x_i}$ is homogeneous of degree 1. The logarithmic derivation module D(X) of the hypersurface X is defined by

$$\begin{aligned} D(X):=\{\theta \in {{\,\mathrm{Der}\,}}S \mid \theta (f) \subset (f)\}, \end{aligned}$$

where (f) denotes the principal ideal generated by f in S. It is known that D(X) is an S-graded reflexive module, but not free in general. It is clear that $\theta _E \in D(X)$. We say that X has exponents $\exp (X)=(d_1,\ldots ,d_k)$ if there are homogeneous derivations $\theta _1=\theta _E,\ldots ,\theta _k$ with $\deg \theta _j=d_j$ which form a minimal set of generators for the graded S-module D(X). Since X is essential, it follows that $d_j>0$ for all j. When these integers $d_j$ are written in increasing order, we use the notation

$$\begin{aligned} (d_1,\ldots ,d_k)_{\le }. \end{aligned}$$

Consider the graded S-submodule $D_0(X)=\{ \theta \in D(X) \mid \theta (f) =0\}$ in D(X) and note the decomposition $D(X)=D_0(X) \oplus S \theta _E.$ Because of this decomposition, it is usual to choose the minimal generators $\theta _j$ above such that $\theta _j \in D_0(X)$ for $j>1$. If $\theta =\sum _{i=1}^{\ell }a_i\partial _{x_i}$ with $a_i \in S_r$ for some integer r, the condition $\theta (f) =0$ translates into the following homogeneous Jacobian relation or Jacobian syzygy

$$\begin{aligned} \sum _{i=1}^{\ell }a_if_{x_i}=0, \end{aligned}$$

(1.1)

involving the partial derivatives $f_{x_i}=\partial _{x_i}f$ of the polynomial f. In this way, the generators $\theta _j$ for $j>1$ are sometimes identified with Jacobian relations. This explains the following.

Definition 1.1

The minimal degree of a Jacobian relation of X, denoted by r(X) or mdr(X), is defined by

$$\begin{aligned} r(X)=\min _{r \in {\mathbb {Z}}} \{r \mid D_0(X)_r \ne (0)\}. \end{aligned}$$

In other words, r(X) is exactly the ${\alpha }$-invariant ${\alpha }(D_0(X))$, or the initial degree $indeg(D_0(X))$, of the graded S-module $D_0(X)$, see [20, 21]. If $(d_1,\ldots ,d_k)_{\le }$ are the exponents of X, then $d_1=1$ and $d_2=r(X)$. We say that the hypersurface X is free if $k=\ell$, i.e., the graded S-module D(X) is free. When this happens, one has

$$\begin{aligned} d_1+\ldots +d_{\ell }=d. \end{aligned}$$

In particular, for a free plane curve X (the case when $\ell =3$), the exponents are determined by r(X), namely

$$\begin{aligned} \exp (X)=(1,r(X),d-1-r(X)), \end{aligned}$$

(1.2)

and $r(X) \le (d-1)/2$. Recall that a plane curve X is nearly free when its exponents are given by $\exp (X)=(1,r(X),d-r(X),d-r(X))$ with the unique relation at degree $d-r(X)+1$, see [14, 16].

The main motivation of this paper, and the reason to study the invariant r(X), is the following conjecture due to H. Terao.

Conjecture 1.2

Let ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ be two hyperplane arrangements, having isomorphic intersection lattices $L({{\mathcal {A}}}) \cong L({{\mathcal {B}}})$. If ${{\mathcal {A}}}$ is free, then ${{\mathcal {B}}}$ is also free.

For more on Terao’s conjecture, as well as for basic information on hyperplane arrangements, we refer to [8, 23]. This conjecture is open, even in the case of line arrangements in ${\mathbb {P}}^2$, in spite of a lot of work and partial results in the recent years, see [2, 3, 13, 28]. Note that the freeness of a line arrangement ${{\mathcal {A}}}$ is not determined by the weak combinatorics of ${{\mathcal {A}}}$, namely the numbers $n_j$ of points in ${{\mathcal {A}}}$ of multiplicity $j\ge 2$, see [22]. In the case of line arrangements, using (1.2) and a result by A. du Plessis and C.T.C. Wall quoted below in Theorem 4.2, Terao’s conjecture can be restated as follows.

Conjecture 1.3

Let ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ be two line arrangements, having isomorphic intersection lattices $L({{\mathcal {A}}}) \cong L({{\mathcal {B}}})$. If ${{\mathcal {A}}}$ is free, then $r({{\mathcal {A}}})=r({{\mathcal {B}}})$.

It is known that the intersection lattice $L({{\mathcal {A}}})$ does not determine the integer $r({{\mathcal {A}}})$ in general: indeed, G. Ziegler produced two arrangements ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ of $d=9$ lines, having only double and triple points, such that $L({{\mathcal {A}}}) \cong L({{\mathcal {B}}})$, and $5=r({{\mathcal {A}}}) \ne r({{\mathcal {B}}})=6$, see Remark 3.9 for more details. However, the following stronger form of Terao’s conjecture might be true.

Conjecture 1.4

Let ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ be two arrangements of d lines, having isomorphic intersection lattices $L({{\mathcal {A}}}) \cong L({{\mathcal {B}}})$. If $r({{\mathcal {A}}})<d/2$, then $r({{\mathcal {A}}})=r({{\mathcal {B}}})$.

Note that in [22], the authors produce two arrangements ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ of d lines, having the same weak combinatorics, and such that $r({{\mathcal {A}}}) <d/2$ and $r({{\mathcal {A}}}) \ne r({{\mathcal {B}}})$. Conjecture 1.4 can be stated in a more geometric way as follows, when ${\mathbb {K}}={\mathbb {C}}$. Let $E({{\mathcal {A}}})$ be the rank 2 vector bundle on ${\mathbb {P}}^2$ naturally associated with the reflexive graded S-module $D_0({{\mathcal {A}}})$. For a generic line L in ${\mathbb {P}}^2$, the restriction $E({{\mathcal {A}}})|L$ splits as a direct sum ${{\mathcal {O}}}_L(-e_1)\oplus {{\mathcal {O}}}_L(-e_2)$. The pair $(e_1,e_2)$ is called the generic splitting type of the bundle $E({{\mathcal {A}}})$, and it is known that the two pairs $(e_1,e_2)$ and $(d,r({{\mathcal {A}}}))$ determine each other when $r({{\mathcal {A}}})<d/2$, with $d=|{{\mathcal {A}}}|$, see [5, Propositions 3.1 and 3.2] and [11, Theorem 1.2]. When $r({{\mathcal {A}}})\ge d/2$, it follows from [5, 11] that the generic splitting type $(e_1,e_2)$ is determined by d and the global Tjurina number $\tau ({{\mathcal {A}}})$, which is determined in turn by the weak combinatorics of ${{\mathcal {A}}}$ via the well-known formula

$$\begin{aligned} \tau (A)=\sum _{j\ge 2} n_j(j-1)^2. \end{aligned}$$

(1.3)

Hence, Conjecture 1.4 is equivalent, when ${\mathbb {K}}={\mathbb {C}}$, to the following conjecture, which has already appeared in [7, Question 7.12] and in [5].

Conjecture 1.5

Let ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ be two line arrangements, having isomorphic intersection lattices $L({{\mathcal {A}}}) \cong L({{\mathcal {B}}})$. Then, the rank 2 vector bundles $E({{\mathcal {A}}})$ and $E({{\mathcal {B}}})$ have the same generic splitting type.

Note that in spite of Ziegler’s example mentioned above, Conjecture 1.5 holds for line arrangements having only double and triple points, see Remark 4.21.

In this paper, we start a detailed investigation of the dependence of the minimal degree $r({{\mathcal {A}}})$ of a Jacobian relation of a hyperplane arrangement ${{\mathcal {A}}}$ on the combinatorics of ${{\mathcal {A}}}$. As a first step, we study the change of the invariant $r({{\mathcal {A}}})$ of a hyperplane arrangement ${{\mathcal {A}}}$ under the addition or the deletion of a hyperplane H and give a number of applications.

In Sect. 2, after some preliminary material on arrangements, we establish the main general addition–deletion result for the invariant $r({{\mathcal {A}}})$ of a hyperplane arrangement ${{\mathcal {A}}}$, see Theorem 2.14. The special case of free hyperplane arrangements is discussed in Theorem 2.18. Other authors have considered addition–deletion to study the logarithmic derivation module $D({{\mathcal {A}}})$, see, for instance, [24, 26], but without paying attention to the invariant $r({{\mathcal {A}}})$.

In Sect. 3, we concentrate our attention to a line arrangement ${{\mathcal {A}}}$ in ${\mathbb {P}}^2$. The corresponding addition–deletion results for $r({{\mathcal {A}}})$ are stated in Theorems 3.3 and 3.4, while the case of free line arrangements is discussed in Theorem 3.6. We then recall the relation between the invariant $r({{\mathcal {A}}})$ and the maximal multiplicity $m({{\mathcal {A}}})$ of an intersection point of the line arrangement ${{\mathcal {A}}}$ following [9]. Corollary 3.8 says that $r({{\mathcal {A}}})$ is determined by the weak combinatorics of ${{\mathcal {A}}}$ when $2m({{\mathcal {A}}}) \ge |{{\mathcal {A}}}|$.

In Sect. 4, we give some applications of the above results. The result by A. du Plessis and C.T.C. Wall quoted below in Theorem 4.2 gives an upper bound $\tau (d,r)_{max}$ for the global Tjurina number $\tau (C)$ of a reduced plane curve C, in terms of its degree d and the invariant $r=r(C)$. A curve C, for which the equality $\tau (C)=\tau (d,r)_{max}$ holds, is called a maximal Tjurina curve of type (d, r). For any pair (d, r), with $1 \le r <d/2$, a maximal Tjurina curve of type (d, r) is nothing else but a free curve C of degree d with $r(C)=r$, and the existence of such curves, even in the class of line arrangements, follows from [14]. For the pairs of the form $(d=2r,r)$, a maximal Tjurina curve of type (d, r) is nothing else but a nearly free curve C of degree $d=2r$ with $r(C)=r$, and the existence of such curves, even in the class of line arrangements, follows again from [14]. The existence of maximal Tjurina curves of type (d, r) when $d/2<r\le d-2$, is much more subtle. The following conjecture was stated in [17].

Conjecture 1.6

For any integer $d \ge 5$ and for any integer r such that $d/2 < r\le d-2$, there are maximal Tjurina line arrangements of type (d, r).

As noted in [17], the generic line arrangement of d lines is Tjurina maximal of type $(d,d-2)$ for any $d \ge 2$, see also Remark 4.12 below. Line arrangements which are potentially maximal Tjurina of the following types:

• (1) $(d,r)=(2r-1,r)$ for $r \ge 3$,

• (2) $(d,r)=(d,d-4)$ for $d \ge 8$, and

• (3) $(d,r)=(d,d-3)$ for $d \ge 7$

have been put forth in [17], following numerical experiments with SINGULAR. The fact that these arrangements are indeed maximal Tjurina is proved here, see Corollary 4.5 for type (1), Theorem 4.10 for type (2), and Theorem 4.11 for type (3). As a result, Conjecture 1.6 holds in all these extremal cases for r in the interval $d/2<r< d-2$. The existence of maximal Tjurina curves of type (d, r) when $d/2<r< d-2$, in a lot of new cases, is proved in Theorem 4.4, Proposition 4.6 and Remark 4.8.

We continue Sect. 4 by investigating the effect on $r({{\mathcal {A}}})$ of adding a generic line, either passing through a point of maximal multiplicity of ${{\mathcal {A}}}$, or just transversal to ${{\mathcal {A}}}$, see Propositions 4.14 and 4.15 . Using these results and our main addition–deletion result, Theorem 3.3, we determine the invariant $r({{\mathcal {A}}})$ in the case of line arrangements having only double and triple points, when the number of triple points $n_3$ is $\le 5$, see Theorem 4.18. The conclusion is that in these cases the invariant $r({{\mathcal {A}}})$ is determined by the combinatorics of ${{\mathcal {A}}}$, in a precise, but rather complicated way. Ziegler’s example, which was the only known example of this type until now, shows that this result is sharp, i.e., it does not extend for the situation $n_3 \ge 6$, see Corollary 4.20. In fact, using Ziegler’s example and adding well-chosen lines, we can construct similar examples of pairs of arrangements of d lines, having only double and triple points, for any $d \ge 9$ and any possible weak combinatorial data $(n_2,n_3)$, when $n_3 \ge 6$, see the Proof of Corollary 4.20.

We also note that results in this paper are used in [12] to prove the irreducibility of the unexpected curves of minimal possible degree in many situations, see [7] for the relevant definitions.

We would like to thank the referee for the careful reading of our manuscript.

2 Hyperplane arrangements

2.1 Preliminaries

First, we recall some definitions and notations. Let $V={\mathbb {K}}^\ell$, $x_1,\ldots ,x_\ell$ a basis for $V^*$ and let $S:=\text{ Sym}^*(V^*)={\mathbb {K}}[x_1,\ldots ,x_\ell ]$. We say that ${{\mathcal {A}}}$ is a hyperplane arrangement in V if ${{\mathcal {A}}}$ is a finite set of linear hyperplanes in V. We say that ${{\mathcal {A}}}$ is essential if $\cap _{H \in {{\mathcal {A}}}} H =\{0\}$. We assume that all arrangements are essential unless otherwise specified. For $H \in {{\mathcal {A}}}$, let ${{\mathcal {A}}}^H:=\{H \cap L \mid L \in {{\mathcal {A}}}\setminus \{H\}\}$ be the restriction of ${{\mathcal {A}}}$ to H. Let $L({{\mathcal {A}}}):=\{ \cap _{H \in {{\mathcal {B}}}} H \mid {{\mathcal {B}}}\subset {{\mathcal {A}}}\}$ be the intersection lattice of ${{\mathcal {A}}}$. Then, we can define the Möbius function $\mu :L({{\mathcal {A}}}) \rightarrow {\mathbb {Z}}$ by $\mu (V)=1$, and by

$$\begin{aligned} \mu (X):=-\sum _{X \subsetneq Y \subset V,\ Y \in L({{\mathcal {A}}})} \mu (Y). \end{aligned}$$

Then, we can define the characteristic polynomial $\chi ({{\mathcal {A}}};t)$ by

$$\begin{aligned} \chi ({{\mathcal {A}}};t):=\sum _{X \in L({{\mathcal {A}}})} \mu (X)t^{\dim X}=\sum _{i=0}^\ell b_i({{\mathcal {A}}})t^i. \end{aligned}$$

If ${{\mathcal {A}}}\ne \emptyset$, then $\chi ({{\mathcal {A}}};t)$ is divisible by $(t-1)$. Let

$$\begin{aligned} \chi _0({{\mathcal {A}}};t):=\chi ({{\mathcal {A}}};t)/(t-1)=\sum _{i=0}^{\ell -1} b_i^0({{\mathcal {A}}}) t^i. \end{aligned}$$

It is easy to show that

$$\begin{aligned} b_1({{\mathcal {A}}})=|{{\mathcal {A}}}|, b_1^0({{\mathcal {A}}})=|{{\mathcal {A}}}|-1,\ b_2^0({{\mathcal {A}}})=b_2({{\mathcal {A}}})-|{{\mathcal {A}}}|+1. \end{aligned}$$

For $H \in {{\mathcal {A}}}$ fix a linear form $\alpha _H \in V^*$ such that $\ker \alpha _H=H$. Then, the logarithmic derivation module $D({{\mathcal {A}}})$ can be defined in this situation as follows:

$$\begin{aligned} D({{\mathcal {A}}}):=\{\theta \in {{\,\mathrm{Der}\,}}S \mid \theta (\alpha _H) \in S\alpha _H\ (\forall H \in {{\mathcal {A}}})\}. \end{aligned}$$

For $Q({{\mathcal {A}}}):= \prod _{H \in {{\mathcal {A}}}} \alpha _H$, one has as in the Introduction

$$\begin{aligned} D_0({{\mathcal {A}}}):=\{ \theta \in {{\,\mathrm{Der}\,}}S \mid \theta (Q({{\mathcal {A}}}))=0\}. \end{aligned}$$

The first easy, but important lemma is the following.

Lemma 2.2

(Lemma 1.33, [28]) For $H \in {{\mathcal {A}}}$, let $D_H({{\mathcal {A}}}):=\{ \theta \in D({{\mathcal {A}}}) \mid \theta (\alpha _H)=0\}$. Then,

$$\begin{aligned} D({{\mathcal {A}}})=D_0({{\mathcal {A}}}) \oplus S \theta _E= D_H({{\mathcal {A}}}) \oplus S \theta _E. \end{aligned}$$

In particular, if ${{\mathcal {A}}}\ne \emptyset$,

$$\begin{aligned} D_0({{\mathcal {A}}}) \simeq D({{\mathcal {A}}})/S \theta _E \simeq D_H({{\mathcal {A}}}) \end{aligned}$$

for any $H \in {{\mathcal {A}}}$.

Lemma 2.2 is a well-known classical result in arrangement theory. It implies in particular the equality

$$\begin{aligned} r({{\mathcal {A}}})=\min _{d \in {\mathbb {Z}}} \{d \mid D_H({{\mathcal {A}}})_d \ne (0)\}, \end{aligned}$$

(2.1)

for any $H \in {{\mathcal {A}}}$. In the study of $r({{\mathcal {A}}})$, Lemma 2.2 shows a big difference of hyperplane arrangements compared with, say, the case of general plane curves. The reason is that, for $L\in {{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$, Lemma 2.2 and the definition of logarithmic vector fields show that

$$\begin{aligned} D_0({{\mathcal {A}}}) \simeq D_L({{\mathcal {A}}}) \subset D_L({{\mathcal {A}}}') \simeq D_0({{\mathcal {A}}}'). \end{aligned}$$

Thus, we can directly compare $r({{\mathcal {A}}})$ and $r({{\mathcal {A}}}')$. To compare them more precisely, the following result due to Terao always plays the key role.

Theorem 2.3

(Terao’s polynomial B-theory, [25]) Let $H \in {{\mathcal {A}}}$, ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$, and let us define the homogeneous degree $|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|$-polynomial B by

$$\begin{aligned} B:=\prod _{X \in {{\mathcal {A}}}^H} \alpha _{\nu (X)}, \end{aligned}$$

where $\nu :{{\mathcal {A}}}^H \rightarrow {{\mathcal {A}}}$ is a section satisfying that $\nu (X) \cap H=X$. Then,

• (1) for an arbitrary $\theta \in D({{\mathcal {A}}}')$, it holds that

  $$\begin{aligned} \theta (\alpha _H) \in (\alpha _H,B), \end{aligned}$$

  where $(\alpha _H,B)$ denotes the ideal of S generated by $\alpha _H$ and B. Thus, $\theta \in D({{\mathcal {A}}}')$ is in $D({{\mathcal {A}}})$ if $\deg \theta <|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|$.

• (2) Assume that there is $\varphi \in D({{\mathcal {A}}}')$ such that $\deg \varphi =|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|$ and that $\varphi \not \in D({{\mathcal {A}}})$. Then for $\theta \in D({{\mathcal {A}}}')$, there is $f \in S$ such that $\theta -f \varphi \in D({{\mathcal {A}}})$. Thus,

  $$\begin{aligned} D({{\mathcal {A}}}')=D({{\mathcal {A}}})+S\cdot \varphi . \end{aligned}$$

To compare algebraic structures of $D({{\mathcal {A}}})$ and $D({{\mathcal {A}}}')$, the most useful tool is Terao’s addition–deletion. Since $r({{\mathcal {A}}})$ sees only the lowest degree generator of $D_0({{\mathcal {A}}})$, the following variant of the addition–deletion theorem is useful.

Theorem 2.4

(Multiple deletion theorem, [6]) Let ${{\mathcal {A}}}$ be a free hyperplane arrangement with $\exp ({{\mathcal {A}}})=(1,d_2,\ldots ,d_\ell )_\le$. If there is $H \in {{\mathcal {A}}}$ such that $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|=d_2$, then ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$ is free with $\exp ({{\mathcal {A}}}')=(1,d_2-1,d_3,\ldots ,d_\ell )_\le$.

To compare $r({{\mathcal {A}}})$, the following two restriction maps play important roles. Let us introduce them. First, the Euler restriction $\rho :D({{\mathcal {A}}}) \rightarrow D({{\mathcal {A}}}^H)$ is defined by

$$\begin{aligned} \rho (\theta )({\overline{f}}):=\overline{\theta (f)} \end{aligned}$$

for $\theta \in D({{\mathcal {A}}}),\ f \in S/\alpha _H S$. Here ${\overline{f}}$ denotes the image of $f \in S$ by the canonical surjection $S \rightarrow S/\alpha _H S$. It is well known that there is an exact sequence

$$\begin{aligned} 0 \rightarrow D({{\mathcal {A}}}\setminus \{H\}) {\mathop {\rightarrow }\limits ^{\cdot \alpha _H }} D({{\mathcal {A}}}) {\mathop {\rightarrow }\limits ^{\rho }} D({{\mathcal {A}}}^H). \end{aligned}$$

Also, we have the other restriction. To introduce it, let us recall multiarrangements. For an arrangement ${{\mathcal {A}}}$, let $m:{{\mathcal {A}}}\rightarrow {\mathbb {Z}}_{>0}$ be a multiplicity, and the pair $({{\mathcal {A}}},m)$ is called a multiarrangement. For $H \in {{\mathcal {A}}}$, let $\delta _H$ be a multiplicity on ${{\mathcal {A}}}$ defined by $\delta _H(L)=1$ if $L=H$, and 0 otherwise. We can define its logarithmic derivation module $D({{\mathcal {A}}},m)$ by

$$\begin{aligned} D({{\mathcal {A}}},m):=\{\theta \in {{\,\mathrm{Der}\,}}S \mid \theta (\alpha _H) \in S \alpha _H^{m(H)}\ (\forall H \in {{\mathcal {A}}})\}. \end{aligned}$$

We can define the freeness and exponents of $D({{\mathcal {A}}},m)$ in the same manner as for ${{\mathcal {A}}}$. We can construct multiarrangements canonically from an arrangement ${{\mathcal {A}}}$ and $H \in {{\mathcal {A}}}$ as follows. Define the Ziegler multiplicity $m^H$ on ${{\mathcal {A}}}^H$ by

$$\begin{aligned} m^H(X):=|\{ L \in {{\mathcal {A}}}\setminus \{H\} \mid L \cap H=X\} \end{aligned}$$

for $X \in {{\mathcal {A}}}^H$. Then, the pair $({{\mathcal {A}}}^H,m^H)$ is called the Ziegler restriction of ${{\mathcal {A}}}$ onto H, and the map $\pi =\pi _H:D_H({{\mathcal {A}}}) \rightarrow D({{\mathcal {A}}}^H,m^H)$ obtained by taking modulo $\alpha _H$ is called the Ziegler restriction map. The most important results related to multiarrangements are the following two.

Theorem 2.5

( [29]) Let ${{\mathcal {A}}}$ be free with exponents $(1,d_2,\ldots ,d_\ell )$, and $H \in {{\mathcal {A}}}$. Then, $({{\mathcal {A}}}^H,m^H)$ is free with exponents $(d_2,\ldots ,d_\ell )$ for any $H \in {{\mathcal {A}}}$.

Theorem 2.6

( [27]) Let $\ell =3$, $H \in {{\mathcal {A}}}$ and $\exp ({{\mathcal {A}}}^H,m^H)=(d_2,d_3)$. Let $\pi :D_H({{\mathcal {A}}}) \rightarrow D({{\mathcal {A}}}^H,m^H)$ be the Ziegler restriction map. Then,

$$\begin{aligned} \dim _{\mathbb {K}}{{\,\mathrm{coker}\,}}\pi =b_2^0({{\mathcal {A}}})-d_2d_3, \end{aligned}$$

and the equality holds if and only if ${{\mathcal {A}}}$ is free with exponents $(1,d_2,d_3)$.

If we can determine the whole algebraic structure of $D({{\mathcal {A}}})$, then of course we can see $r({{\mathcal {A}}})$, which is in general very difficult unless ${{\mathcal {A}}}$ is free. By [4], we can do it for the arrangement that can be obtained by deleting one hyperplane from free one.

Theorem 2.7

(Theorem 1.4, [4]) Let ${{\mathcal {A}}}$ be free with $\exp ({{\mathcal {A}}})=(1,d_2,\ldots ,d_\ell )$. Let $H \in {{\mathcal {A}}}$ with $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|=:d+1$. If ${{\mathcal {A}}}':= {{\mathcal {A}}}\setminus \{H\}$ is not free, then $D({{\mathcal {A}}}')$ has a minimal set of generators

$$\begin{aligned} \theta _E,\theta _2,\ldots ,\theta _\ell ,\varphi \end{aligned}$$

such that $\theta _E,\theta _2,\ldots ,\theta _\ell$ form a basis for $D({{\mathcal {A}}})$ with $\deg \theta _i=d_i$, $\varphi \not \in D({{\mathcal {A}}})$ is of degree d, and there is the unique relation

$$\begin{aligned} \sum _{i=1}^\ell f_i \theta _i+\alpha _H\varphi =0 \end{aligned}$$

for $\theta _1:=\theta _E,\ f_i \in S$.

Theorem 2.8

(Theorem 5.5, [4]) Let $\ell =3$, $H \in {{\mathcal {A}}}$ and ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$. Assume that ${{\mathcal {A}}}$ is not free. Then, ${{\mathcal {A}}}'$ is free with $\exp ({{\mathcal {A}}}')=(1,d_2,d_3)$ if and only if $D({{\mathcal {A}}})$ is generated by derivations $\theta _E,\theta _2,\theta _3,\varphi$ of degrees $\deg \theta _i=d_i+1,\ \deg \varphi =|{{\mathcal {A}}}^H|-1$ and there is the unique relation

$$\begin{aligned} f_1 \theta _E+f_2\theta _2+f_3 \theta _3+\alpha _H \varphi =0. \end{aligned}$$

Since such arrangements are useful, we give them a name as follows.

Definition 2.9

(Definition 1.1, [4]) We say that ${{\mathcal {A}}}$ is plus-one generated (POG) with ${{\,\mathrm{POexp}\,}}({{\mathcal {A}}})=(d_1,\ldots ,d_\ell )$ and level d if $D({{\mathcal {A}}})$ has a minimal set of generators

$$\begin{aligned} \theta _E,\theta _2,\ldots ,\theta _\ell ,\varphi \end{aligned}$$

such that $\deg \theta _i=d_i$, $\deg \varphi =d$, and there is the unique relation

$$\begin{aligned} \sum _{i=1}^\ell f_i \theta _i+\alpha \varphi =0 \end{aligned}$$

for some $\alpha \in V^*$.

We say that ${{\mathcal {A}}}$ is strongly plus-one generated (SPOG) with ${{\,\mathrm{POexp}\,}}({{\mathcal {A}}})=(d_1,\ldots ,d_\ell )$ and level d if $D({{\mathcal {A}}})$ has a minimal set of generators

$$\begin{aligned} \theta _E,\theta _2,\ldots ,\theta _\ell ,\varphi \end{aligned}$$

such that $\deg \theta _i=d_i$, $\deg \varphi =d$, and there is the unique relation

$$\begin{aligned} \sum _{i=1}^\ell f_i \theta _i+\alpha \varphi =0 \end{aligned}$$

for some $\alpha \in V^* \setminus \{0\}$. Such a $\varphi$ is called the level element, and such a set of minimal generators is said to be a SPOG generator.

Remark 2.10

Note that when $\ell =3$ all POG arrangements are SPOG by Proposition 5.1, [4].

2.2 Addition–deletion theorems on $r({{\mathcal {A}}})$ for hyperplane arrangements

First let us show the most fundamental results on $r({{\mathcal {A}}})$.

Proposition 2.12

Let $\ell \ge 2$, $H \in {{\mathcal {A}}},\ {{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$. Then,

• (1) $r({{\mathcal {A}}}') \le r({{\mathcal {A}}}) \le r({{\mathcal {A}}}')+1$.

• (2) If $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|>r({{\mathcal {A}}})$, then $r({{\mathcal {A}}})=r({{\mathcal {A}}}')$.

• (3) If $|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|>r({{\mathcal {A}}}')$, then $r({{\mathcal {A}}})=r({{\mathcal {A}}}')$.

Proof

Let $L \in {{\mathcal {A}}}'$. Since $\text{ ch }({\mathbb {K}})=0$, it holds that

$$\begin{aligned} D_0({{\mathcal {A}}}') \simeq D_L({{\mathcal {A}}}'),\ D_0({{\mathcal {A}}}) \simeq D_L({{\mathcal {A}}}). \end{aligned}$$

So we may consider only derivations in $D_L({{\mathcal {A}}})$ and $D_L({{\mathcal {A}}}')$. First assume that $r({{\mathcal {A}}}') \le r({{\mathcal {A}}})-2$. Let $\theta \in D_L({{\mathcal {A}}}')$ be of degree $r({{\mathcal {A}}}')$. Then, $\alpha _H \theta \in D_L({{\mathcal {A}}})$ is zero by the definition of $r({{\mathcal {A}}})$. Thus, $r({{\mathcal {A}}}')+1 \ge r({{\mathcal {A}}})$. Since $D_L({{\mathcal {A}}}') \supset D_L({{\mathcal {A}}})$, $r({{\mathcal {A}}}) \ge r({{\mathcal {A}}}')$, completing the Proof of (1).

Next let us prove (2). Assume that $r({{\mathcal {A}}}')+1=r({{\mathcal {A}}})=:r$. Let $0 \ne \theta \in D_L({{\mathcal {A}}}')_{r-1}$. By Theorem 2.3, it holds that $D_L({{\mathcal {A}}}')_{<|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|} =D_L({{\mathcal {A}}})_{<|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|}$. In particular, $D_L({{\mathcal {A}}}')_{r-1}=D_L({{\mathcal {A}}})_{r-1}$. So $\theta \in D_L({{\mathcal {A}}})_{r-1}=(0)$. This is absurd. The same argument shows (3). A quick proof can also be obtained using [23, Lemma 4.39 and Proposition 4.41], which in turn are based on Theorem 2.3. $\square$

For an arrangement ${{\mathcal {A}}}$, to study $r({{\mathcal {A}}})$, the Euler derivation does not appear, but it is very important in the following sense.

Lemma 2.13

Let ${{\mathcal {A}}}\ne \emptyset$ and $0 \ne \theta \in D({{\mathcal {A}}})_d$. Then, $r({{\mathcal {A}}}) \le d$ if $\theta \not \in S \theta _E$.

Proof

Let $\theta ':=\theta -\frac{\theta (\alpha _H)}{\alpha _H} \theta _E \in D_H({{\mathcal {A}}})_d$ for some $H \in {{\mathcal {A}}}$. By the assumption, $\theta ' \ne 0$, which completes the proof. $\square$

Now let us introduce the addition–deletion theorems for $r({{\mathcal {A}}})$ in an arbitrary dimension.

Theorem 2.14

(Addition–deletion theorem for $r({{\mathcal {A}}})$) Let $\ell \ge 2$, $H \in {{\mathcal {A}}}$ and ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$. Let $r=r({{\mathcal {A}}})$, $r'=r({{\mathcal {A}}}')$ and $r''=r({{\mathcal {A}}}''):=r({{\mathcal {A}}}^H)$. Then, $r=r'+1$ if $r'<r''$.

Proof

Assume that $r'<r''$ and $r=r'$. Then, there is $0\ne \theta \in D_H({{\mathcal {A}}}')_{r=r'}$ such that $\theta \in D_H({{\mathcal {A}}})_r$ by Lemma 2.2. Let $\rho :D({{\mathcal {A}}}) \rightarrow D({{\mathcal {A}}}^H)$ be the Euler restriction. Since $r''>r$ and $\deg \rho (\theta )=r<r''$, $\rho (\theta )$ is of the form $\rho (f \theta _E)$ by Lemma 2.13. Since $\theta \not \in S \theta _E$, we may replace $\theta$ by $\theta - f\theta _E \not \in S \theta _E$ and we may assume that $\rho (\theta )=0$. Thus, $\theta =\alpha _H \theta '$ with $S \theta _E \not \ni \theta ' \in D({{\mathcal {A}}}')_{r-1=r'-1}$. By Lemma 2.13, $\theta ' \ne 0$ implies that $r({{\mathcal {A}}}') \le r'-1$, a contradiction. $\square$

The addition–deletion theorem is related with the restriction theorem in general. For the effect of restriction on $r({{\mathcal {A}}})$, however, we cannot say much.

Proposition 2.15

Let $\ell \ge 2$, $H \in {{\mathcal {A}}}$ and ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$. Let $r=r({{\mathcal {A}}})$, $r'=r({{\mathcal {A}}}')$ and $r''=r({{\mathcal {A}}}'')=r({{\mathcal {A}}}^H)$. Then, $r'' \le r$ if $r=r'$.

Proof

By the same proof as in Theorem 2.14, there is a common $0 \ne \theta \in D({{\mathcal {A}}}')_{r=r'} \cap D({{\mathcal {A}}})_{r}$, and we may assume that $0 \ne \rho (\theta )\in D({{\mathcal {A}}}^H)_r \setminus (S/\alpha _HS)\rho (\theta _E)$. Therefore, one has $r''\le r$.$\square$

Remark 2.16

One can obtain a quick Proof of Theorem 2.14 and Proposition 2.15 using the exact sequence in [23, Proposition 4.45].

2.3 The case of free hyperplane arrangements

We can explicitly describe the behavior of $r({{\mathcal {A}}})$ when ${{\mathcal {A}}}$ is free.

Theorem 2.18

Let ${{\mathcal {A}}}$ be free with $\exp ({{\mathcal {A}}})=(1,d_2,\ldots ,d_\ell )_\le$. Let $H \in {{\mathcal {A}}}$ and ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$. Then, $r({{\mathcal {A}}}')=d_2-1$ if and only if $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|=d_2$. Otherwise $r({{\mathcal {A}}}')=d_2$.

Proof

Recall that $r({{\mathcal {A}}})=d_2$. If $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|=d_2$, then ${{\mathcal {A}}}'$ is free with exponents $(1,d_2-1,d_3,\ldots ,d_\ell )$ by Theorem 2.4. Assume that $r':=r({{\mathcal {A}}}')=d_2-1$. Then, $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|$ has to be $d_2$ if ${{\mathcal {A}}}'$ is free. Assume that ${{\mathcal {A}}}'$ is not free. Then by Theorem 2.7, ${{\mathcal {A}}}'$ is strictly plus-one generated with exponents $(1,d_2,\ldots ,d_\ell )_\le$ and level $|{{\mathcal {A}}}|-|{{\mathcal {A}}}^H|-1=:d$. Let us show that $d \ge d_2-1$. Assume that $d < d_2-1$. Note that

$$\begin{aligned} \frac{\overline{Q({{\mathcal {A}}})}}{\prod _{X \in {{\mathcal {A}}}^H} \alpha _{\nu {X} }}\pi (\theta _E)=:\theta _E^H \in D({{\mathcal {A}}}^H,m^H) \end{aligned}$$

and $d_2>d+1 =\deg \theta _E^H$, where $\pi :D_H({{\mathcal {A}}}) \rightarrow D({{\mathcal {A}}}^H,m^H)$ is the Ziegler restriction map and $\nu$ is the section in Theorem 2.3. Since $D({{\mathcal {A}}}^H,m^H)$ is free with exponents $(d_2,\ldots ,d_\ell )$ by Theorem 2.5, this is a contradiction. $\square$

3 Line arrangements

3.1 Addition–deletion theorems on $r({{\mathcal {A}}})$ for line arrangements

First, let us recall Terao’s addition–deletion theorem for line arrangements.

Theorem 3.2

(Terao’s addition–deletion theorem, [25]) Let $\ell =3$, $H \in {{\mathcal {A}}}$ and ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$. Then,

• (1) ${{\mathcal {A}}}$ is free with $\exp ({{\mathcal {A}}})=(1,a,b+1)$ if ${{\mathcal {A}}}'$ is free with $\exp ({{\mathcal {A}}}')=(1,a,b)$ and $|{{\mathcal {A}}}^H|=a+1$.

• (2) ${{\mathcal {A}}}'$ is free with $\exp ({{\mathcal {A}}}')=(1,a,b-1)$ if ${{\mathcal {A}}}$ is free with $\exp ({{\mathcal {A}}})=(1,a,b)$ and $|{{\mathcal {A}}}^H|=a+1$.

When $\ell =3$, Theorem 2.14 is more combinatorial.

Theorem 3.3

(Addition theorem for $r({{\mathcal {A}}})$) Let $\ell =3$ and ${{\mathcal {A}}}:={{\mathcal {A}}}' \cup \{H\}$ with $H \not \in {{\mathcal {A}}}'$. Assume that $r({{\mathcal {A}}}')=r'$. If $|{{\mathcal {A}}}^H| \ge r'+2$, then $r({{\mathcal {A}}})=r'+1$.

Proof

Since $\exp ({{\mathcal {A}}}^H)=(1,|{{\mathcal {A}}}^H|-1)$, $|{{\mathcal {A}}}^H| \ge r'+2$ shows that $r''>r'$. Now apply Theorem 2.14. $\square$

Theorem 3.4

(Deletion theorem for $r({{\mathcal {A}}})$) Let $\ell =3$ and ${{\mathcal {A}}}:={{\mathcal {A}}}' \cup \{H\}$ with $H \not \in {{\mathcal {A}}}'$. Assume that $r({{\mathcal {A}}})=r$. If $|{{\mathcal {A}}}^H| \ge r+2$, then $r({{\mathcal {A}}}')=r-1$.

Proof

Apply the same proof as in Theorem 3.3. $\square$

3.2 The case of free line arrangements

By the same reason as above, we can describe $r({{\mathcal {A}}})$ when $\ell =3$ and the arrangement ${{\mathcal {A}}}$ is free.

Theorem 3.6

Let $\ell =3$, $H \in {{\mathcal {A}}}$ and ${{\mathcal {A}}}':={{\mathcal {A}}}\setminus \{H\}$.

• (1) Assume that ${{\mathcal {A}}}$ is free with $\exp ({{\mathcal {A}}})=(1,d_2,d_3)_\le$. Then, $r({{\mathcal {A}}}')=d_2-1$ if and only if $|{{\mathcal {A}}}^H|=1+d_3$. Otherwise $r({{\mathcal {A}}}')=d_2$.

• (2) Assume that ${{\mathcal {A}}}'$ is free with $\exp ({{\mathcal {A}}}')=(1,d_2,d_3)_\le$. Then, $r({{\mathcal {A}}})=d_2+1$ if and only if $|{{\mathcal {A}}}^H|\ne 1+d_2$. Otherwise $r({{\mathcal {A}}})=d_2$.

Proof

(1) follows from Theorem 2.18. Let us show (2). By [1], ${{\mathcal {A}}}$ is free with exponents $(1,d_2+1,d_3)$ if and only if $|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|=d_3$, and

$$\begin{aligned} |{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|=d_3,\ \text{ or }\ |{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H|\le d_2. \end{aligned}$$

If ${{\mathcal {A}}}$ is not free, then ${{\mathcal {A}}}$ is strictly plus-one generated with exponents $(1,d_2+1,d_3+1)$ and level $d=|{{\mathcal {A}}}^H|-1$ by Theorem 2.7. Since $\ell =3$, ${{\mathcal {A}}}$ is SPOG. Thus, $d \ge d_3+1$. Thus, $mdr(A)=d_2+1$. Since this occurs if and only if $|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H| \ne d_2,d_3$, it suffices to show that $r:=mdr({{\mathcal {A}}})=d_2$ if $|{{\mathcal {A}}}'|-|{{\mathcal {A}}}^H| = d_3$, which is trivial since $\exp ({{\mathcal {A}}})=(1,d_2,d_3+1)$ by Theorem 3.2. $\square$

3.3 Points of high multiplicity and the invariant $r({{\mathcal {A}}})$

In this subsection ${{\mathcal {A}}}':f'=0$ is a line arrangement, and $p=(1:0:0)$ is an intersection point on ${{\mathcal {A}}}'$ of maximal multiplicity, say $m'={{\,\mathrm{mult}\,}}({{\mathcal {A}}}',p)$. To this situation, one can associate a primitive Jacobian syzygy as explained in [9, Section 2.2]. We recall this construction here. Let $g=0$ be the equation of the subarrangement of ${{\mathcal {A}}}'$ formed by the $m'$ lines in ${{\mathcal {A}}}'$ passing through p. Then, we can write $f'=gh$ for some polynomial $h \in S$. Since g is a product of linear factors of the form $sy+tz$, it follows that $f'_x=gh_x$ and hence $g=G.C.D.(f',f'_x)$. The syzygy constructed as explained there is primitive and has degree $r'_p=d'-m'$. As shown in [9, Theorem 1.2], the following cases are possible for $r'=r({{\mathcal {A}}}')$.

Case A: $r'=r'_p=d'-m'$, in other words the constructed syzygy has minimal degree.

Case B: $r'<r'_p=d'-m'$, in other words the constructed syzygy has not minimal degree. Then, two situations are possible, namely

Subcase B1: $r'=m'-1$, and then, $2m'<d'+1$ and ${{\mathcal {A}}}'$ is free with exponents $d_1=1, d_2=m'-1<d_3=d'-m'$, or

Subcase B2: $m' \le r' \le d'-m'-1$, and then $2m' <d'$.

This discussion implies the following.

Corollary 3.8

If the line arrangement ${{\mathcal {A}}}'$ satisfies $2m' \ge d'$, then $r'=r({{\mathcal {A}}}')$ is determined by the weak combinatorics of ${{\mathcal {A}}}'$.

Proof

If $2m' \ge d'+1$, it follows that only Case A is possible, and hence, $r'=d'-m'$. When $2m'=d'$, then both Case A and Subcase B1 are possible; hence, we have either $r'=m'-1$ or $r'=d'-m'=m'$. If ${{\mathcal {A}}}'$ is in the situation of Subcase B1, then we know that

$$\begin{aligned} \tau ({{\mathcal {A}}}')=(d'-1)^2-r'(d-r'-1)=(d'-1)^2-(m'-1)(d'-m'). \end{aligned}$$

On the other hand, if ${{\mathcal {A}}}'$ is in the situation of Case A, then we know that

$$\begin{aligned} \tau ({{\mathcal {A}}}') \le (d'-1)^2-r'(d-r'-1)-1=(d'-1)^2-(d'-m')(m'-1)-1, \end{aligned}$$

see [10, 18]. Since the total Tjurina number is determined by the weak combinatorics, recall (1.3), this completes the proof. $\square$

Remark 3.9

In Ziegler’s celebrated example, see [30], we have two line arrangements ${{\mathcal {A}}}'_1$ and ${{\mathcal {A}}}'_2$ of degree $d'=9$ and such that $m'=3$ in both cases. For one of them, say for ${{\mathcal {A}}}'_1$, the six triple points are on a conic, and one has $r'_1=5 =d'-m'-1$; hence, we are in Subcase B2 above. For the other one, say for ${{\mathcal {A}}}'_2$, the six triple points are not on a conic, and one has $r'_2=6=d'-m'$, so we are in Case A. This shows that the combinatorics of ${{\mathcal {A}}}'$ cannot decide in which case A, B1 or B2 we are in the above discussion. This example is discussed in [8, Remark 8.5]. One can find there some equations for the arrangements ${{\mathcal {A}}}'_1$ and ${{\mathcal {A}}}'_2$, namely

$$\begin{aligned}&{{\mathcal {A}}}'_1: xy(x-y-z)(x-y+z)(2x+y-2z)\\&\quad \times (x+3y-3z)(3x+2y+3z)(x+5y+5z)(7x-4y-z)=0 \end{aligned}$$

and

$$\begin{aligned}&{{\mathcal {A}}}'_2: xy(4x-5y-5z)(x-y+z)(16x+13y-20z)\\&\quad \times (x+3y-3z)(3x+2y+3z)(x+5y+5z)(7x-4y-z)=0. \end{aligned}$$

In fact, the equation for ${{\mathcal {A}}}'_2$ given in [8, Remark 8.5] is not correct, and we take the opportunity here to correct this equation.

4 Applications

4.1 Line arrangements which are Tjurina maximal

Recall that the global Tjurina number $\tau (C)$ of the plane curve $C:f=0$ can be defined as either the degree of the Jacobian ideal $J_f=(f_x,f_y,f_z)$, or as the sum of the Tjurina numbers of all the singularities of the curve C. It was shown by A. du Plessis and C.T.C. Wall that one has the following result, see [18, Theorem 3.2], and also [19, Theorem 20] for a new approach.

Theorem 4.2

Let $C:f=0$ be a reduced plane curve of degree d and let $r=mdr(C)$. Then, the following hold.

• (1) If $r <d/2$, then $\tau (C) \le \tau (d,r)_{max}= (d-1)(d-r-1)+r^2$ and the equality holds if and only if the curve C is free.

• (2) If $d/2 \le r \le d-1$, then $\tau (C) \le \tau (d,r)_{max}$, where, in this case, we set

  $$\begin{aligned} \tau (d,r)_{max}=(d-1)(d-r-1)+r^2-{ 2r-d+2 \atopwithdelims ()2}. \end{aligned}$$

The curve $C:f=0$ in this Theorem is called maximal Tjurina of type (d ,  r) if one has the equality

$$\begin{aligned} \tau (C) = \tau (d,r)_{max}. \end{aligned}$$

The characterization and the existence of maximal Tjurina curves of type (d, r), with $d/2 \le r \le d-1$ is discussed in [17]. In this note we prove the existence of maximal Tjurina curves of type (d, r) in many cases. We start with the following.

Proposition 4.3

If ${{\mathcal {A}}}':f'=0$ is a Tjurina maximal line arrangement of type $(d',r')$ with $r' \ge (d'-1)/2$ and H is a new line in ${\mathbb {P}}^2$ such that

$$\begin{aligned} |{{\mathcal {A}}}' \cap H|=r'+2, \end{aligned}$$

then ${{\mathcal {A}}}={{\mathcal {A}}}' \cup H$ is a Tjurina maximal line arrangement of type (d, r) with $d=d'+1$ and $r=r'+1$.

Proof

First note that Theorem 3.3 implies that $r=r({{\mathcal {A}}})=r({{\mathcal {A}}}')+1=r'+1$. Hence to show that ${{\mathcal {A}}}$ is a Tjurina maximal line arrangement of type (d, r), it is enough to show that it has the global Tjurina number $\tau ({{\mathcal {A}}})=\tau (d,r)_{max}$, given by the formula in Theorem 4.2 (2). Indeed, it is clear that $r' \ge (d'-1)/2$ implies $r \ge (d-1)/2$. A direct computation shows that this yields the following

$$\begin{aligned} \tau ({{\mathcal {A}}})-\tau ({{\mathcal {A}}}')=2d'-r'-2. \end{aligned}$$

(4.1)

To measure the difference $\tau ({{\mathcal {A}}})-\tau ({{\mathcal {A}}}')$, assume that ${{\mathcal {A}}}' \cap H$ consists of s points, say $p_1,\ldots ,p_s$, with multiplicities $m_1, \ldots ,m_s$ regarded as points on ${{\mathcal {A}}}'$. When we add the new line H, the point $p_j$ will have multiplicity $m_j+1$, so the increase in Tjurina number at $p_j$ is

$$\begin{aligned} m_j^2-(m_j-1)^2=2m_j-1. \end{aligned}$$

It follows that

$$\begin{aligned} \tau ({{\mathcal {A}}})-\tau ({{\mathcal {A}}}')=\sum _{j=1,s}(2m_j-1)=2d'-s. \end{aligned}$$

(4.2)

This ends the proof of the claim. $\square$

Theorem 4.4

Given a pair of positive integers (d, r) such that $d\ge 4$ and

$$\begin{aligned} \frac{d}{2} \le r \le \frac{2}{3}(d-1), \end{aligned}$$

then there is a real line arrangement ${{\mathcal {A}}}$ in ${\mathbb {P}}^2$ which is Tjurina maximal of type (d, r).

Proof

We set $r=d-k$ for some $k \ge 2$, and the equalities involving d and r in Theorem 4.4 are equivalent to

$$\begin{aligned} 2k \le d \le 3k-2. \end{aligned}$$

Hence, we have to show the existence of a real line arrangement ${{\mathcal {A}}}$ in ${\mathbb {P}}^2$ which is Tjurina maximal of type $(d,d-k)$, where d and k satisfy the above inequalities. We start with the line arrangement

$$\begin{aligned} {{\mathcal {A}}}_0: f_0(x,y,z)=x(x-z) \ldots (x-(k-2)z)y(y-z) \ldots (y-(k-2)z)z=0, \end{aligned}$$

which is free, even supersolvable, and also Tjurina maximal of type $(2k-1,k-1)$. If we add the line

$$\begin{aligned} H_1: y=x+z, \end{aligned}$$

then we can apply Proposition 4.3 with ${{\mathcal {A}}}'={{\mathcal {A}}}_0$ and $H=H_1$, since

$$\begin{aligned} |H_1 \cap {{\mathcal {A}}}_0|=k+1, \end{aligned}$$

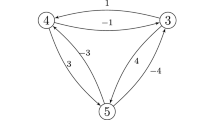
see Fig. 1 to understand why this equality holds, or read the explanation in the general case given below when we add $H_{j+1}$ to ${{\mathcal {A}}}_j$. We get that

$$\begin{aligned} {{\mathcal {A}}}_1={{\mathcal {A}}}_0\cup H_1: f_1(x,y,z)=f_0(x,y,z)(x-y+z)=0 \end{aligned}$$

is a Tjurina maximal line arrangement of type (2k, k). Then, we add the line

$$\begin{aligned} H_2: y=x+2z, \end{aligned}$$

and apply Proposition 4.3 with ${{\mathcal {A}}}'={{\mathcal {A}}}_1$ and $H=H_2$. We get that

$$\begin{aligned} {{\mathcal {A}}}_2={{\mathcal {A}}}_1\cup H_2: f_2(x,y,z)=f_0(x,y,z)(x-y+z)(x-y+2z)=0 \end{aligned}$$

is a Tjurina maximal line arrangement of type $(2k+1,k+1)$. Assume now that ${{\mathcal {A}}}_j$ has been constructed, for $2 \le j < k-2$, and it is a Tjurina maximal line arrangement of type $(2k+j-1,k+j-1)$. Then, we construct ${{\mathcal {A}}}_{j+1}$ by adding the new line

$$\begin{aligned} H_{j+1}: y=x+(j+1)z \end{aligned}$$

and apply Proposition 4.3 with ${{\mathcal {A}}}'={{\mathcal {A}}}_j$ and $H=H_{j+1}$. Indeed, the new line $H=H_{j+1}$ intersects the line arrangement ${{\mathcal {A}}}'={{\mathcal {A}}}_j$ in $k-j-2$ double points of ${{\mathcal {A}}}'$, $2j+2$ simple points of ${{\mathcal {A}}}'$ and one point of multiplicity $j+1$ of ${{\mathcal {A}}}'$, namely (1 : 1 : 0). Bezout theorem yields

$$\begin{aligned} 2(k-j-2)+(2j+2)+j+1=2k+j-1= \deg ({{\mathcal {A}}}_j), \end{aligned}$$

and this shows that we have listed all the intersection points. It follows that

$$\begin{aligned} |{{\mathcal {A}}}_j\cup H_{j+1}|=(k-j-2)+(2j+2)+1=k+j+1=r({{\mathcal {A}}}_j)+2, \end{aligned}$$

and hence indeed one can apply Proposition 4.3. We get that

$$\begin{aligned} {{\mathcal {A}}}_{j+1}= & {} {{\mathcal {A}}}_j\cup H_{j+1}: f_{j+1}(x,y,z)\\= & {} f_0(x,y,z)(x-y+z)\ldots (x-y+(j+1)z)=0 \end{aligned}$$

is a Tjurina maximal line arrangement of type $(2k+j,k+j)$. This construction ends when we construct ${{\mathcal {A}}}_{k-1}$, because after this value the hypothesis of Proposition 4.3 is no longer verified. $\square$

Corollary 4.5

For any odd degree $d=2r-1\ge 7$, there is a maximal Tjurina real line arrangement of type $(2r-1,r)$.

Proof

Just consider the arrangement ${{\mathcal {A}}}_2$ in the above proof. $\square$

Note that the last arrangement ${{\mathcal {A}}}_{k-1}$ constructed in the Proof of Theorem 4.4 consists of the line at infinity $z=0$ and three families of parallel lines, each containing $k-1$ lines. Hence, this arrangement has three points of maximal multiplicity equal to k on the line at infinity. When $d-r=k=2k'+1$ is odd, we can continue the above construction and get a stronger result.

Proposition 4.6

Given a pair of positive integer (d, r) such that $d\ge 4$, $k=d-r$ is odd and

$$\begin{aligned} \frac{d}{2} \le r \le \frac{3}{4}(d-1), \end{aligned}$$

then there is a real line arrangement ${{\mathcal {A}}}$ in ${\mathbb {P}}^2$ which is Tjurina maximal of type (d, r).

Proof

When $d-r=k=2k'+1$ is odd, we can continue the above construction in two steps, as follows. Recall that ${{\mathcal {A}}}_{k-1}$ is a Tjurina maximal line arrangement of type $(3k-2,2k-2)$. To get ${{\mathcal {A}}}_{k}$ from ${{\mathcal {A}}}_{k-1}$ we add the line

$$\begin{aligned} H_k: x+y=3k'z. \end{aligned}$$

Note that $H_k$ does the following.

• a) It intersects vertical lines $x - az = 0$ in $(a : 3k'- a : 1)$;

• b) It intersects horizontal lines $y- bz = 0$ in $(3k'-b : b : 1)$;

• c) It intersects oblique lines $y = x + cz$ in $(3k'- c : 3k' + c : 2)$.

One can see when two such points are the same, and when they are not, and use inclusion–exclusion principle to count them only once. In this way we get that line $H_k$ intersects the line arrangement ${{\mathcal {A}}}_0$ in $3k'+2$ points, namely one point on the line at infinity, $k'+1$ points situated only on vertical lines $x-az=0$ for $0 \le a \le k'$, $k'+1$ points situated only on horizontal lines $y-az=0$ for $0 \le a \le k'$, and $k'-1$ points situated at the intersection of a vertical line $x-az=0$ with a horizontal line $y-(3k'-a)z=0$ for $k'+1 \le a \le 2k'-1$. The intersection of $H_k$ with the line $y-x-bz=0$ for $1 \le b \le k-1=2k'$ is the point

$$\begin{aligned} (3k'-b:3k'+b:2). \end{aligned}$$

This point gives a new intersection point of $H_k$ with the line arrangement ${{\mathcal {A}}}_{k-1}$ exactly when $k'-b$ is an odd integer. Since b can take $k'$ even values and $k'$ odd values, this happens exactly $k'$ times. It follows that

$$\begin{aligned} | H_k \cap {{\mathcal {A}}}_{k-1} |=3k'+2+k'=4k'+2=2k=(2k-2)+2. \end{aligned}$$

Hence, we can use Proposition 4.3 and we get that ${{\mathcal {A}}}_k$ is a Tjurina maximal line arrangement of type $(3k-1,2k-1)$. Then, in the first step, we add the lines

$$\begin{aligned} H_j: x+y=(3k'+j-k)z, \end{aligned}$$

for $j=2k'+2,..., 3k'$, to get new line arrangements ${{\mathcal {A}}}_j={{\mathcal {A}}}_{k-1} \cup H_k \cup \ldots \cup H_j$, which are Tjurina maximal of type $(2k+j-1, k+j-1)$ for each $j=2k'+2,..., 3k'$. Indeed, in each case one can count the intersection points in $H_j \cap {{\mathcal {A}}}_{j-1}$ as above, and conclude that Proposition 4.3 may be applied. If we increase the coefficient of z beyond this value $6k'-k=2k-3$, the number of intersection points in ${{\mathcal {A}}}' \cap H$ is no longer a strictly increasing sequence $q, q+1,q+2,...$ as until now, but has repetitions of the form $q,q, q+1,q+1,q+2,q+2,...$, and hence, we have a choice in selecting the new line to add between two possibilities. This is the second step in this construction. The largest type we can get in this way is $(4k-3,3k-3)$, and we denote such an arrangement by ${{\mathcal {A}}}_{2k-2}$, since it is obtained from ${{\mathcal {A}}}_0$ by adding $2k-2$ lines. $\square$

Note that the last arrangement ${{\mathcal {A}}}_{2k-2}$ constructed in the Proof of Proposition 4.6 consists of the line at infinity $z=0$ and four families of parallel lines, each containing $k-1$ lines. Hence, this arrangement has four points of maximal multiplicity equal to k on the line at infinity.

Example 4.7

As an illustration, consider the case $k=7$, and hence, $k'=3$. The first sequence of line arrangements constructed in the Proof of Theorem 4.4 has the following equations

$$\begin{aligned} {{\mathcal {A}}}_0: f_0(x,y,z)=x(x-z) \ldots (x-5z)y(y-z) \ldots (y-5z)z=0, \end{aligned}$$

and

$$\begin{aligned} {{\mathcal {A}}}_j: f_j(x,y,z)=f_0(x,y,z)(x-y+z)(x-y+2z) \ldots (x-y+jz)=0, \end{aligned}$$

for $j=1,2,...,6$. In other words $H_j: x-y+jz=0$, see Figure 1. The arrangements constructed in the first step in Proposition 4.6 consist of the following two arrangements

$$\begin{aligned} {{\mathcal {A}}}_7={{\mathcal {A}}}_6 \cup \{H_7\}: f_7(x,y,z)=f_6(x,y,z)(x+y-9z) \end{aligned}$$

and

$$\begin{aligned} {{\mathcal {A}}}_8={{\mathcal {A}}}_7 \cup \{H_8\}: f_8(x,y,z)=f_7(x,y,z)(x+y-10z). \end{aligned}$$

The second sequence of arrangements constructed in Proposition 4.6, when a choice is possible, consists of the following four arrangements obtained by taking the minimal absolute value for the coefficient of z:

$$\begin{aligned} {{\mathcal {A}}}_9= & {} {{\mathcal {A}}}_8 \cup \{H_9\}: f_{9}(x,y,z)=f_8(x,y,z)(x+y-11z),\\ {{\mathcal {A}}}_{10}= & {} {{\mathcal {A}}}_9 \cup \{H_{10}\}: f_{10}(x,y,z)=f_9(x,y,z)(x+y-13z),\\ {{\mathcal {A}}}_{11}= & {} {{\mathcal {A}}}_{10} \cup \{H_{11}\}: f_{11}(x,y,z)=f_{10}(x,y,z)(x+y-15z), \end{aligned}$$

and

$$\begin{aligned} {{\mathcal {A}}}_{12}={{\mathcal {A}}}_{11} \cup \{H_{12}\}: f_{12}(x,y,z)=f_{11}(x,y,z)(x+y-17z). \end{aligned}$$

Note that ${{\mathcal {A}}}_0$ has $2k-1=13$ lines, and ${{\mathcal {A}}}_{12}$ has $13+12=25=4k-3$ lines, as expected. Here ${{\mathcal {A}}}_j$ is a Tjurina maximal line arrangement of type $(13+j,6+j)$ for $j=0,1,...,12$.

Fig. 1

The arrangements from Example 4.7. The line at infinity $z=0$ is not drawn

Remark 4.8

When $k=2k'$ is even, then there are two cases. When $k'$ is odd, we have found no simple way to add a new line to ${{\mathcal {A}}}_{k-1}$ in order to get a larger Tjurina maximal line arrangement. This is due to the fact that the number of intersection points in ${{\mathcal {A}}}' \cap H$ in this case, for H a line of the form to $x+y-az=0$, has repetitions and gaps of the form $2q+1,2q+1,2q+3,2q+3,...$, i.e., we get only odd numbers, and hence, it is impossible to apply Proposition 4.3. When $k'$ is even, we can construct ${{\mathcal {A}}}_k$ as follows: we add the line

$$\begin{aligned} H_k: x+y=(3k'-2)z. \end{aligned}$$

Using Proposition 4.3 we get that ${{\mathcal {A}}}_k$ is a Tjurina maximal line arrangement of type $(3k-1,2k-1)$. However, this construction stops here, since in this case the number of intersection points in ${{\mathcal {A}}}' \cap H$ has repetitions and gaps of the form $2q,2q,2q+2,2q+2,...$.

Example 4.9

As an illustration, consider the case $k=8$, and hence, $k'=4$. The first sequence of line arrangements constructed in the Proof of Theorem 4.4 has the following equations

$$\begin{aligned} {{\mathcal {A}}}_0: f_0(x,y,z)=x(x-z) \ldots (x-6z)y(y-z) \ldots (y-6z)z=0, \end{aligned}$$

and

$$\begin{aligned} {{\mathcal {A}}}_j: f_j(x,y,z)=f_0(x,y,z)(x-y+z)(x-y+2z) \ldots (x-y+jz)=0, \end{aligned}$$

for $j=1,2,...,7$. The largest line arrangement constructed in Remark 4.8 is the following:

$$\begin{aligned} {{\mathcal {A}}}_8: f_8(x,y,z)=f_7(x,y,z)(x+y-10z). \end{aligned}$$

Here ${{\mathcal {A}}}_j$ is a Tjurina maximal line arrangement of type $(15+j,7+j)$ for $j=0,1,...,8$.

Consider now the question of the existence of maximal Tjurina line arrangements ${{\mathcal {A}}}$ of d lines with large invariant $r=r({{\mathcal {A}}})$ with respect to d. The first case we consider is $r=d-4$, see Remark 4.12 below. To give a positive answer to this question, consider the following arrangements ${{\mathcal {A}}}_{3p+2}$ for $p\ge 2$, defined by

$$\begin{aligned}&xy\left( \frac{x}{2^{p+1}}+\frac{y}{3^{p+1}}-z\right) \prod _{j=1}^{p} \left( \frac{x}{2^j}+\frac{y}{3^j}-z\right) \left( \frac{x}{2^j}+\frac{y}{3^{j+1}}-z\right) \\&\qquad \times \prod _{j=1}^{p-1} (\frac{x}{2^j}+\frac{y}{3^{j+2}}-z)=0,\\&{{\mathcal {A}}}_{3p+3}={{\mathcal {A}}}_{3p+2} \cup \{H_1\} \end{aligned}$$

with $H_1:27x-8y=0$, and

$$\begin{aligned} {{\mathcal {A}}}_{3p+4}={{\mathcal {A}}}_{3p+3} \cup \{H_2\} \end{aligned}$$

with $H_2:x-y=0$. Using these three families of line arrangements, we can define ${{\mathcal {A}}}_d$ for all $d\ge 8$. The following result proves a conjecture made in [17], where it was shown that ${{\mathcal {A}}}_d$ is a maximal Tjurina line arrangement of type $(d,d-4)$ if and only if $r({{\mathcal {A}}}_d)=d-4$.

Note that the line

$$\begin{aligned} \frac{x}{2^c} + \frac{y}{3^d}- z = 0 \end{aligned}$$

intersects the line

• i) $x = 0$ in $(0 : 3^d : 1)$;

• ii) $y = 0$ in (2c : 0 : 1);

• iii) $\frac{x}{2^a} +\frac{y}{3^b}-z = 0$ in

$$\begin{aligned} ((3^b - 3^d)2^{a+c} : (2^c- 2^a)3^{b+d} : 3^b2^c- 3^d2^a). \end{aligned}$$

Note that, if $a = c$ (and necessarily, $b\ne d$), we get the point $(2^c : 0 : 1)$; and if $b = d$ (and necessarily, $a\ne c$) we get the point $(0 : 3^d : 1)$.

Theorem 4.10

Let ${{\mathcal {A}}}_d$ be the arrangement defined above. Then, $r({{\mathcal {A}}}_{d})=d-4$ for all $d \ge 8$.

Proof

We know that the statement is true when d is small by [17]. We use first a recursive argument on $p\ge 2$ to show that $r({{\mathcal {A}}}_{3p+2}) = 3p -2$. The inductive step will be to go from ${{\mathcal {A}}}_{3p+2}$ to ${{\mathcal {A}}}_{3p(p+1)+2} = {{\mathcal {A}}}_{3p+5}$, and to do this we apply Theorem 3.3 three times. To fill in the gaps not covered by this induction, one can similarly apply Theorem 3.3 for each of the steps ${{\mathcal {A}}}_{3p+2} \rightarrow {{\mathcal {A}}}_{3p+3}$ and ${{\mathcal {A}}}_{3p+3} \rightarrow {{\mathcal {A}}}_{3p+4}$

Here are the details for the first step. We add three lines, namely we set ${{\mathcal {B}}}={{\mathcal {A}}}_{3p+2}$, ${{\mathcal {B}}}'={{\mathcal {B}}}\cup H'$ where

$$\begin{aligned} H': \frac{x}{2^{p}}+\frac{y}{3^{p+2}}-z=0, \end{aligned}$$

${{\mathcal {B}}}''={{\mathcal {B}}}' \cup H''$ where

$$\begin{aligned} H'': \frac{x}{2^{p+1}}+\frac{y}{3^{p+2}}-z=0 \end{aligned}$$

and ${{\mathcal {B}}}'''={{\mathcal {B}}}'' \cup H'''= {{\mathcal {A}}}_{3p+5}$ where

$$\begin{aligned} H''': \frac{x}{2^{p+2}}+\frac{y}{3^{p+2}}-z=0. \end{aligned}$$

Then, we apply Theorem 3.3 three times. First we have to pass from ${{\mathcal {B}}}$ to ${{\mathcal {B}}}'$, and to do this we have to check that $|{{\mathcal {B}}}\cap H'| \ge r({{\mathcal {B}}})+2=3p$. The line $H'$ intersects ${{\mathcal {B}}}$ transversely, except at one double point, located at $(2^p:0:1)$. It follows that $|{{\mathcal {B}}}\cap H'|=\deg {{\mathcal {B}}}-1=(3p+2)-1=3p+1$, and hence, we can apply Theorem 3.3 and get that $r({{\mathcal {B}}}')=r({{\mathcal {B}}})+1=3p-1$. Then, we check that $|{{\mathcal {B}}}' \cap H''| \ge r({{\mathcal {B}}}')+2=3p+1$. The line $H''$ intersects ${{\mathcal {B}}}'$ transversely, except at two double points, located at $(2^{p+1}:0:1)$ and $(0:3^{p+2}:1)$. It follows that $|{{\mathcal {B}}}' \cap H''|=\deg {{\mathcal {B}}}' -2=(3p+3)-2=3p+1$, and hence, we can apply Theorem 3.3 and get that $r({{\mathcal {B}}}'')=r({{\mathcal {B}}}')+1=3p$. Finally, we have to check that $|{{\mathcal {B}}}'' \cap H'''| \ge r({{\mathcal {B}}}'')+2=3p+2$. The line $H'''$ intersects ${{\mathcal {B}}}''$ transversely, except at one triple point, located at $(0:3^{p+2}:1)$. It follows that $|{{\mathcal {B}}}'' \cap H'''|=\deg {{\mathcal {B}}}'' -2=(3p+4)-2=3p+2$, and hence, we can apply Theorem 3.3 and get that $r({{\mathcal {B}}}''')=r({{\mathcal {B}}}'')+1=3p+1=deg({{\mathcal {B}}}''')-4$. This ends the proof for the passage from ${{\mathcal {A}}}_{3p+2}$ to ${{\mathcal {A}}}_{3p+5}$. The case $p=2$ is represented in Figure 2. The other two passages can be justified in a completely similar manner. $\square$

Fig. 2

The arrangements from the Proof of Theorem 4.10, case $p=2$. The line at infinity is not in these arrangements

Finally, consider the question of the existence of maximal Tjurina line arrangement of d lines with $r=d-3$. Define the families of line arrangements ${{\mathcal {B}}}_{2p}$ by

$$\begin{aligned} xy\prod _{j=1}^{p-1} \left( \frac{x}{2^j}+\frac{y}{3^j}-z\right) \left( \frac{x}{2^j}+\frac{y}{3^{j+1}}-z\right) =0, \end{aligned}$$

and ${{\mathcal {B}}}_{2p+1}$ by

$$\begin{aligned} xy \left( \frac{x}{2^p}+\frac{y}{3^p}-z\right) \prod _{j=1}^{p-1} \left( \frac{x}{2^j}+\frac{y}{3^j}-z\right) \left( \frac{x}{2^j}+\frac{y}{3^{j+1}}-z\right) =0, \end{aligned}$$

Using these two families, we can define ${{\mathcal {B}}}_d$ for all $d\ge 7$. In [17, Subsection 4.12] it was shown that ${{\mathcal {B}}}_d$ is a maximal Tjurina line arrangement of type $(d,d-3)$ if and only if $r({{\mathcal {B}}}_d)=d-3$, and it was conjectured that one has $r({{\mathcal {B}}}_d)=d-3$. By the same proof as in Theorem 4.10, we can prove this conjecture.

Theorem 4.11

Let ${{\mathcal {B}}}_d$ be the arrangement defined above. Then, $r({{\mathcal {B}}}_{d})=d-3$ for all $d \ge 7$.

Proof

For small values of d the claim was established in [17] by a direct computation. Assume now the claim holds for ${{\mathcal {B}}}_{2p+1}$, for some value of p. Then, to get ${{\mathcal {B}}}_{2p+2}$ from ${{\mathcal {B}}}_{2p+1}$ we have to add the line

$$\begin{aligned} H': \frac{x}{2^p}+\frac{y}{3^{p+1}}-z =0. \end{aligned}$$

This line $H'$ intersects ${{\mathcal {B}}}_{2p+1}$ transversely, except at one double point, located at $(2^p:0:1)$. It follows that

$$\begin{aligned}|{{\mathcal {B}}}_{2p+1} \cap H'|=\deg {{\mathcal {B}}}_{2p+1}-1=2p= r({{\mathcal {B}}}_{2p+1})+2, \end{aligned}$$

and hence we can apply Theorem 3.3 and get that

$$\begin{aligned} r({{\mathcal {B}}}_{2p+2})=r({{\mathcal {B}}}_{2p+1})+1=2p-1=\deg ({{\mathcal {B}}}_{2p+2})-3. \end{aligned}$$

Next, to pass from ${{\mathcal {B}}}_{2p+2}$ to ${{\mathcal {B}}}_{2p+3}$ we have to add the line

$$\begin{aligned} H'': \frac{x}{2^{p+1}}+\frac{y}{3^{p+1}}-z =0. \end{aligned}$$

This line $H''$ intersects ${{\mathcal {B}}}_{2p+2}$ transversely, except at one double point, located at $(0: 3^{p+1}:1)$. It follows that

$$\begin{aligned} |{{\mathcal {B}}}_{2p+2} \cap H''|=\deg {{\mathcal {B}}}_{2p+2}-1=2p+1= r({{\mathcal {B}}}_{2p+2})+2. \end{aligned}$$

Hence, we can apply Theorem 3.3 and get that

$$\begin{aligned} r({{\mathcal {B}}}_{2p+3})=r({{\mathcal {B}}}_{2p+2})+1=2p=\deg ({{\mathcal {B}}}_{2p+3})-3. \end{aligned}$$

$\square$

Remark 4.12

For any line arrangement with $d \ge 2$, one has $r \le d-2$, by our discussion before Corollary 3.8. Any generic line arrangement is maximal Tjurina of type $(d,d-2)$ when $d \ge 2$, see [17, Remark 2.2]; hence, the cases $r=d-4$ and $r=d-3$ considered in Theorems 4.10 and 4.11 are the largest possible values of r where the existence of a maximal Tjurina line arrangement of type (d, r) is not obvious.

4.2 Adding a generic line to a line arrangement

First we take a generic secant passing through the point p of maximal multiplicity $m'$ for the line arrangement ${{\mathcal {A}}}'$.

Proposition 4.14

Let ${{\mathcal {A}}}':f'=0$ be a line arrangement, let L be a generic line passing through the maximal multiplicity intersection point $p \in {{\mathcal {A}}}'$, and let ${{\mathcal {A}}}={{\mathcal {A}}}' \cup L:f=0$. Then, one has the following.

• (1) The (weak) combinatorics of the line arrangement ${{\mathcal {A}}}'$ determines the (weak) combinatorics of the line arrangement ${{\mathcal {A}}}$. In particular, one has

  $$\begin{aligned} \tau ({{\mathcal {A}}})=\tau ({{\mathcal {A}}}')+d'+m'-1. \end{aligned}$$

• (2) $r= r'+1$ if $r' <d'-m'$.

• (3) $r=r'$ if $r'=d'-m'$.

Proof

The first claim is obvious. To prove the second claim, we use Theorem 3.3. The number of intersection points of ${{\mathcal {A}}}$ on L is $|{{\mathcal {A}}}^L|=1+d'-m'$ and hence the condition in Theorem 3.3, namely

$$\begin{aligned} |{{\mathcal {A}}}^L| \ge r'+2 \end{aligned}$$

is equivalent to

$$\begin{aligned} 1+d'-m'\ge r'+2 \end{aligned}$$

or

$$\begin{aligned} r' \le d'-m'-1. \end{aligned}$$

This condition is satisfied by our assumption $r'<d'-m'$. To prove the claim (3), note that by Proposition 2.12 we have $d'-m'=r' \le r$. On the other hand, [9, Theorem 1.2] implies $r \le d-m=(d'+1)-(m'+1)=d'-m'$, where $m={{\,\mathrm{mult}\,}}({{\mathcal {A}}},p)$. $\square$

Next we add a generic line, meeting ${{\mathcal {A}}}'$ only at simple points.

Proposition 4.15

Let ${{\mathcal {A}}}':f'=0$ be a line arrangement with $d' \ge 2$ and L be a generic line. Consider the new line arrangement ${{\mathcal {A}}}={{\mathcal {A}}}' \cup L:f=0$. Then, one has the following.

• (1) The (weak) combinatorics of the line arrangement ${{\mathcal {A}}}'$ determines the (weak) combinatorics of the line arrangement ${{\mathcal {A}}}$. In particular, one has

  $$\begin{aligned} \tau ({{\mathcal {A}}})=\tau ({{\mathcal {A}}}')+d'. \end{aligned}$$

• (2) $r= r'+1$.

In particular, if ${{\mathcal {A}}}$ is a generic arrangement of $d \ge 2$ lines, then $r({{\mathcal {A}}})=d-2$.

Proof

The intersection points in ${{\mathcal {A}}}$ which are not the same as the corresponding ones in ${{\mathcal {A}}}'$ are the $d'$ double points along the line L. These points add $d'$ to the global Tjurina number of ${{\mathcal {A}}}$. The number of intersection points of ${{\mathcal {A}}}$ on L is $|{{\mathcal {A}}}^L|=d'$ and hence the condition in Theorem 3.3, namely

$$\begin{aligned} |{{\mathcal {A}}}^L| \ge r'+2 \end{aligned}$$

is equivalent to

$$\begin{aligned} d' \ge r'+2 \end{aligned}$$

This condition is satisfied, since $r' \le d'-m' \le d'-2$. The last claim is obvious for $d=2$, since the equation for ${{\mathcal {A}}}$ can be chosen to be $xy=0$. The case $d>2$ follows by induction on d, using the point (2) above. $\square$

Example 4.16

Consider again Ziegler’s arrangements ${{\mathcal {A}}}'_1$ and ${{\mathcal {A}}}'_2$ from Remark 3.9. If we apply Proposition 4.14 (2) to the arrangement ${{\mathcal {A}}}'_1$, we get a new arrangement with $r_1=r'_1+1=5+1=6$. If we apply Proposition 4.14 (3) to the arrangement ${{\mathcal {A}}}'_2$, we get a new arrangement with $r_2=r'_2=6$. Hence by adding a generic line through a triple point, the difference between $r_1'$ and $r_2'$ disappears. On the other hand, if we add a generic line L to both arrangements ${{\mathcal {A}}}'_1$ and ${{\mathcal {A}}}'_2$, we get again two line arrangements ${{\mathcal {A}}}_1$ and ${{\mathcal {A}}}_2$ with $d=10$, $r_1=5+1=6 <r_2=6+1=7$ and having the same combinatorics. By continuing to add generic lines we can construct such pairs for any $d \ge 9$.

4.3 On line arrangements with double and triple points

Note that Ziegler’s arrangements ${{\mathcal {A}}}'_1$ and ${{\mathcal {A}}}'_2$ have both only double and triple points; more precisely, $n_2= 18$ and $n_3=6$. The following result says that $n_3=6$ is the minimal value for which such pairs with the same combinatorics but distinct values for r can be constructed.

Theorem 4.18

Let ${{\mathcal {A}}}$ be a line arrangement with $d=|{{\mathcal {A}}}| \ge 2$, having $n_2$ double points, $n_3$ triple points and no points of higher multiplicity.

• (1) If $n_3=0$, then $r({{\mathcal {A}}})=d-2$.

• (2) If $1 \le n_3 \le 3$, then $r({{\mathcal {A}}})=d-3$.

• (3) If $n_3=4$, then $r({{\mathcal {A}}})=d-3$, unless any line of the arrangement ${{\mathcal {A}}}$, passing through a triple point of ${{\mathcal {A}}}$, contains an extra triple point of ${{\mathcal {A}}}$. In this latter situation, ${{\mathcal {A}}}$ is obtained, up to a change of coordinates, from the arrangement

  $$\begin{aligned} {{\mathcal {A}}}(2,2,3): (x^2-y^2)(x^2-z^2)(y^2-z^2)=0 \end{aligned}$$

  by adding $d-6$ generic lines, and then, $r({{\mathcal {A}}})=d-4$.

• (4) If $n_3=5$, then there are two possibilities.

• (A) There is at least one triple point p in ${{\mathcal {A}}}$ and a line L in ${{\mathcal {A}}}$, passing through p and containing only p as a triple point. If the line arrangement ${{\mathcal {A}}}'={{\mathcal {A}}}\setminus L$ is obtained, up to a change of coordinates, from the arrangement ${{\mathcal {A}}}(2,2,3)$ by adding $d-7$ generic lines, then $r({{\mathcal {A}}})=d-4$. Otherwise $r({{\mathcal {A}}})=d-3$.

• (B) For any of the five triple points, the three lines meeting at this point contain each at least an extra triple point, and then, $r({{\mathcal {A}}})=d-4$. The intersection lattice of ${{\mathcal {A}}}$ in this case is the same as the intersection lattice of the arrangement obtained by adding $d-7$ generic lines to the following arrangement

  $$\begin{aligned} {{\mathcal {B}}}: y(y+x)(y-x)(y+x-2z)(y-x-2z)(3y+x-2z)(3y-x-2z)=0. \end{aligned}$$

Proof

The claim (1) is well known, see, for instance, 4.15.

Consider now the claim (2). Let p be a triple point, and note that, since $n_3 \le 3$, there is a line L in ${{\mathcal {A}}}$, passing through p, containing only p as a triple point. Indeed, otherwise, we get at least three new triple points in ${{\mathcal {A}}}$, at least one on each of the three lines through p, which is a contradiction. Since $r({{\mathcal {A}}})\le d-m=d-3$, it is enough to show that $r=r({{\mathcal {A}}}) \le d-4$ leads to a contradiction.

Apply Theorem 3.4 to the arrangement ${{\mathcal {A}}}'={{\mathcal {A}}}\setminus L$ and the line L. The number of intersection points of ${{\mathcal {A}}}$ on L is $|{{\mathcal {A}}}^L|=d-2$ and hence the condition in Theorem 3.4, namely

$$\begin{aligned} |{{\mathcal {A}}}^L| \ge r'+2, \end{aligned}$$

where $r'=r({{\mathcal {A}}}')$, is satisfied by our assumption. It follows that $r'=r-1 \le d-5=d'-4$. We start with the case $n_3=1$. Then, ${{\mathcal {A}}}'$ is nodal, so $r'=d'-2$ a contradiction. Hence, in this case $r=d-3$. The cases $n_3=2$ and $n_3=3$ can be treated in exactly the same way, using the previous cases.

To treat the claim (3), note that there are two possibilities. The first one is that there is a triple point p and a line L in ${{\mathcal {A}}}$, passing through p and containing only p as a triple point. Then, we can repeat the argument in the case (2) and get $r=d-3$. The second case is when, for any of the four triple points, the three lines meeting at this point contain each an extra triple point. Let p one of these triple points, denote by $L_1$, $L_2$ and $L_3$ the 3 lines passing through p, and let $q_j \in L_j$ be the unique triple point on $L_j$ distinct from p, for $j=1,2,3$. Since any line through a triple point contains at least another one, it follows that all the lines $L_{ij}$ determined by $q_i$ and $q_j$ for $i \ne j$ are in ${{\mathcal {A}}}$. Indeed, $p,q_1,q_2$ and $q_3$ are the only triple points in ${{\mathcal {A}}}$. This situation occurs for the arrangement ${{\mathcal {A}}}(2,2,3)$, and it is known that this arrangement has $r=2=d-4$. If we are in this situation, the six lines determined by the four triple points form an arrangement which is, up to a linear change of coordinates, the arrangement ${{\mathcal {A}}}(2,2,3)$. The additional lines must create only double points, so they are generic lines. Using Proposition 4.15, we see that for any arrangement ${{\mathcal {A}}}$ constructed in this way we get $r=d-4$.

In the final claim (4), if we are in case (A), we can delete the line L, and the resulting arrangement ${{\mathcal {A}}}'$ has $n_3=4$. Hence, the two cases discussed in (3) are possible. More precisely, we know that $r \le d-m=d-3$. Assume $r \le d-4$ and apply Theorem 3.4. We get as above $r' =r-1\le d-5=d'-4$. Using the claim (3), we infer that in this case ${{\mathcal {A}}}'$ is obtained from the arrangement ${{\mathcal {A}}}(2,2,3)$ by adding $d-7$ generic lines.

If we are in case (B), it is enough to check that for the arrangement ${{\mathcal {B}}}$ of seven lines we have $r({{\mathcal {B}}})=3$, which follows by a direct computation using SINGULAR, and then, we use Proposition 4.15.

The possible configurations of the five triple points in ${{\mathcal {A}}}$ are discussed next, and this discussion shows that only the situations (A) and (B) are possible.

Case 1: Assume first that each line in ${{\mathcal {A}}}$ contains at most two triple points. If each triple point p is connected to three other triple points by lines in ${{\mathcal {A}}}$, it means that there is a unique triple point $p'$ not connected to p. The five triple points are in this way divided in a number of pairs $\{p,p'\}$, a contradiction. Hence, in this case we are in the situation (A).

Case 2: Assume next that there is a unique line $L'$ in ${{\mathcal {A}}}$ containing three or more triple points. If $L'$ contains at least four triple points, the claim is clear, any triple point p on $L'$ is a good choice, to see that we are again in situation (A). Assume now that $L'$ contain three points $p_1,p_2$ and $p_3$, and the remaining triple points are $q_1$ and $q_2$ are not on $L'$. Each of the points $p_j$ has to be connected with both points $q_1$ and $q_2$, in order to avoid being again in the situation (A). In this way, by considering these seven lines, we get a line arrangement with the same combinatorics as ${{\mathcal {B}}}$. Therefore, if this happens, we are in the situation (B).

Case 3: Assume finally that there are two lines $L'$ and $L''$ in ${{\mathcal {A}}}$ containing each three triple points. Then, the intersection point $p=L' \cap L''$ has to be a triple point, and the third line through p, call it L, contains no triple points except p. Therefore, we are in the situation (A). $\square$

Example 4.19

(i) The arrangement

$$\begin{aligned} {{\mathcal {A}}}: f=xyz(x+z)(x+y-z)(2x-y)(x+y+3z)=0 \end{aligned}$$

has $d=7$, $n_3=4$ and $r=d-3=4$. Hence, it illustrates the case (3), when $r=d-3$ in Theorem 4.18. The line $L:x+y-z=0$ contains a unique triple point, namely the point $p=(1:-1:0)$.

(ii) The arrangement

$$\begin{aligned} {{\mathcal {A}}}: f=xyz(x+z)(x+y-z)(2x-y)(x+y+3z)(y+z)=0 \end{aligned}$$

has $d=8$, $n_3=5$ and $r=d-3=5$. Hence, it illustrates the case (4), subcase (A), when $r=d-3$ in Theorem 4.18. The line $L:x+y-z=0$ contains a unique triple point, namely $p=(1:-1:0)$, and also the line $L':y+z=0$ contains a unique triple point, namely $p'=(1:0:0)$.

Corollary 4.20

Let ${{\mathcal {A}}}:f=0$ be a line arrangement with $d=|{{\mathcal {A}}}| \ge 2$, having $n_2$ double points, $n_3$ triple points and no points of higher multiplicity. The invariant $r({{\mathcal {A}}})$ is determined by the combinatorics of ${{\mathcal {A}}}$ if and only if $n_3 \le 5$.

Proof

The claim that $r({{\mathcal {A}}})$ is determined by the combinatorics of ${{\mathcal {A}}}$ if $n_3 \le 5$ follows from Theorem 4.18. The claim that $r({{\mathcal {A}}})$ is not determined by the combinatorics of ${{\mathcal {A}}}$ if $n_3 =6$ follows from Ziegler’s example of arrangements ${{\mathcal {A}}}'_j$ for $j=1,2$ discussed in Remark 3.9 and in Example 4.16, where we show that any $d \ge 9$ can be realized. To increase the number of triple points, it is enough to pick a double point p in ${{\mathcal {A}}}'_j$ for $j=1,2$ and add a generic line L passing through p. We can apply Theorem  3.3 and show that the arrangements ${{\mathcal {A}}}_j={{\mathcal {A}}}'_j \cup L$ have $r_1=r_1'+1=6$ and $r_2=r_2'+1=7$, and they both have $n_3=7$ and the same combinatorics. Note that $|{{\mathcal {A}}}_1^L|=8>r_1'+2=7$, and $|{{\mathcal {A}}}_2^L|=8=r_2'+2$; hence, we need the full strength of Theorem  3.3.

Proceeding in this way, it is clear that for any $n_3 \ge 6$, one can construct a pair of line arrangements having only double points and $n_3$ triple points, with the same combinatorics, but distinct invariants r. $\square$

Remark 4.21

Using [5, Proposition 3.2, (3) and (4)] and [15, Theorem 3.2 (1)], it follows that Conjecture 1.5 holds for the line arrangements having only double and triple points. More precisely, [15, Theorem 3.2 (1)] shows that an arrangement ${{\mathcal {A}}}$ of d lines, having only double and triple points, satisfies

$$\begin{aligned} r({{\mathcal {A}}}) \ge \frac{d-2}{2}. \end{aligned}$$

Then, [5, Proposition 3.2, (3) and (4)] shows that in this case, the generic splitting type $(e_1,e_2)$ is determined by d.