Quotients of the Hermitian curve from subgroups of $\mathrm{PGU}(3,q)$ without fixed points or triangles

Abstract

In this paper, we deal with the problem of classifying the genera of quotient curves ${\mathcal {H}}_q/G$, where ${\mathcal {H}}_q$ is the ${\mathbb {F}}_{q^2}$-maximal Hermitian curve and G is an automorphism group of ${\mathcal {H}}_q$. The groups G considered in the literature fix either a point or a triangle in the plane $\mathrm{PG}(2,q^6)$. In this paper, we give a complete list of genera of quotients ${\mathcal {H}}_q/G$, when $G \le \mathrm{Aut}({\mathcal {H}}_q) \cong \mathrm{PGU}(3,q)$ does not leave invariant any point or triangle in the plane. Also, the classification of subgroups G of $\mathrm{PGU}(3,q)$ satisfying this property is given up to isomorphism.

1 Introduction

Let ${\mathbb {F}}_q$ be a finite field of order q and $\mathcal X$ be a projective, irreducible, non-singular algebraic curve of genus g defined over ${\mathbb {F}}_{q}$. The problems of determining the maximum number of points over ${\mathbb {F}}_{q}$ that $\mathcal X$ can have and finding examples of algebraic curves $\mathcal X$ with many rational points have been important, not only from the theoretic perspective, but also for applications in Coding Theory; see, for instance, [11, 32, 33]. The Hasse–Weil theorem provides an upper bound for the number of rational points $|\mathcal X({\mathbb {F}}_q)|$ that a curve $\mathcal X$ defined over ${\mathbb {F}}_q$ can have, namely $|\mathcal X({\mathbb {F}}_q)| \le q+1+2g \sqrt{q}$. If $|\mathcal X({\mathbb {F}}_q)| =q+1+2g \sqrt{q}$, then the curve $\mathcal X$ is said to be ${\mathbb {F}}_q$-maximal. Clearly, $\mathcal X$ can be ${\mathbb {F}}_q$-maximal only if either g is zero or q is a square. A natural question in this context is: Over a finite field ${\mathbb {F}}_{q^2}$ of square cardinality, which nonnegative integers g can be realized as the genera of maximal curves over ${\mathbb {F}}_{q^2}$?

A leading example of a maximal curve is the Hermitian curve $\mathcal H_q$ over ${\mathbb {F}}_{q^2}$, where q is a power of a prime p. It is defined as the non-singular plane curve admitting one of the following birational equivalent plane models: $X^{q+1}+Y^{q+1}+Z^{q+1}=0$ and $X^qZ+XZ^q=Y^{q+1}$.

For fixed q, the curve $\mathcal H_q$ has the largest genus $g(\mathcal H_q)=q(q-1)/2$ that an ${\mathbb {F}}_{q^2}$-maximal curve can have; see [12] and references therein. The full automorphism group $\mathrm{Aut}(\mathcal H_q)$ is isomorphic to $\mathrm{PGU}(3,q)$, the group of projectivities of $\mathrm{PG}(2,q^2)$ commuting with the unitary polarity associated with $\mathcal H_q$. The automorphism group $\mathrm{Aut}(\mathcal H_q)$ is extremely large with respect to the value $g(\mathcal H_q)$. Indeed, it is known that the Hermitian curve is the unique curve of genus $g \ge 2$ up to isomorphisms admitting an automorphism group of order at least $16g^4$.

By a result commonly referred to as the Kleiman–Serre covering result, see [24] and [25, Proposition 6], a curve defined over ${\mathbb {F}}_{q^2}$ which is ${\mathbb {F}}_{q^2}$-covered by an ${\mathbb {F}}_{q^2}$-maximal curve is ${\mathbb {F}}_{q^2}$-maximal as well. In particular, ${\mathbb {F}}_{q^2}$-maximal curves can be obtained as Galois ${\mathbb {F}}_{q^2}$-subcovers of an ${\mathbb {F}}_{q^2}$-maximal curve $\mathcal X$, that is, as quotient curves $\mathcal X/G$ where G is a finite ${\mathbb {F}}_{q^2}$-automorphism group of $\mathcal X$. Since $\mathrm{Aut}(\mathcal H_q)$ is large and has plenty of non-conjugated subgroups, it seems to be natural to construct maximal curves as Galois ${\mathbb {F}}_{q^2}$-subcovers $\mathcal H_q/G$ of the Hermitian curve $\mathcal H_q$ with $G \le \mathrm{PGU}(3,q)$. Indeed, most of the known maximal curves are constructed in this way; see, for instance, [7, 12, 13, 28, 29] and references therein. The most significant cases treated in the literature are the following:

• G fixes an ${\mathbb {F}}_{q^2}$-rational point of $\mathcal H_q$; see [1, 3, 12].

• G normalizes a Singer subgroup of $\mathcal H_q$ acting on three ${\mathbb {F}}_{q^6}$-rational points of $\mathcal H_q$; see [6, 12].

• G has prime order; see [7].

• G fixes an ${\mathbb {F}}_{q^2}$-rational point off $\mathcal H_q$; see [8, 29, 30].

• G fixes a self-polar triangle in $\mathrm{PG}(2,q^2)$; see [8].

From these results, in order to obtain the complete list of genera of quotients $\mathcal H_q/G$ of the Hermitian curve $\mathcal H_q$, only the following cases for $G\le \mathrm{Aut}(\mathcal H_q)$ still have to be described and characterized completely:

• (1) G fixes a self-polar triangle in $\mathrm{PG}(2,q^2)$;

• (2) G fixes a point $P \in \mathcal H_q({\mathbb {F}}_{q^2})$, with $p=2$ and $|G|=p^\ell d$ where $p^\ell \le q$ and $d \mid (q-1)$;

• (3) G fixes an ${\mathbb {F}}_{q^2}$-rational point $P\notin \mathcal H_q$, with $q\not \equiv 1\pmod 4$;

• (4) G does not fix any point or triangle in $\mathrm{{PG}}(2,q^6)$.

The structure of maximal subgroups of $\mathrm{PGU}(3,q)$ fixing a point or a triangle in $\mathrm{{PG}}(2,q^6)$ is known, see [19, 27]; yet, the structure of subgroups $\mathrm{PGU}(3,q)$ fixing no points nor triangles is not explicitly described when $3 \mid (q+1)$, that is, when $\mathrm{PGU}(3,q)\ne \mathrm{PSU}(3,q)$. Also, the groups $G\le \mathrm{PGU}(3,q)$ considered in the literature always have a fixed point or a fixed triangle in $\mathrm{{PG}}(2,q^6)$ (with the single exception of [28, Proposition 5.1]).

In this paper, we give the complete list of genera of quotients $\mathcal H_q/G$ when G does not fix any point or triangle in $\mathrm{{PG}}(2,q^6)$. To this aim, we also provide the list of such subgroups of $\mathrm{PGU}(3,q)$ up to isomorphisms, and we give explicitly the list of maximal subgroups of $\mathrm{PGU}(3,q)$, which was already provided in [19, 27] for $3\not \mid (q+1)$.

The organization of the paper is the following. Section 2 provides preliminary results on the structure of $\mathrm{PGU}(3,q)$ and $\mathrm{PSU}(3,q)$ and on the Riemann–Hurwitz formula applied to quotients of the Hermitian curve. Section 3 contains a description of the maximal subgroups of $\mathrm{PGU}(3,q)$ in relation to the maximal subgroups of $\mathrm{PSU}(3,q)$. Also, Sect. 3 lists the subgroups of $\mathrm{PGU}(3,q)$ acting on the plane without fixed points or triangles. Section 4 applies the results of Sects. 2 and 3 to compute the genus of $\mathcal H_q/G$, whenever G does not fix any point or triangle; examples of new genera of maximal curves are collected in Table 2.

2 Preliminary results

Throughout the paper, q will denote a power $p^n$ of a prime p. Maximal subgroups of $\mathrm{PSU}(3,q)$ were explicitly described in [19, 27], see also [20, Theorem A.10].

The structure of maximal subgroups M of the automorphism group $\mathrm{Aut}(\mathcal H_q)\cong \mathrm{PGU}(3,q)$ of the Hermitian curve $\mathcal H_q$ which fix a point or a triangle in $\mathrm{{PG}}(2,{\bar{{\mathbb {F}}}}_{q^2})$ is known, and the genera of quotients $\mathcal H_q/G$ with $G\le M$ have been deeply investigated; see, for instance, [3, 6,7,8, 12, 26, 28, 29]. Such maximal subgroups are the following, up to conjugation.

• (I) The stabilizer $M_1$ of a point $P\in \mathcal H_q({\mathbb {F}}_{q^2})$. The group $M_1$ has order $q^3(q^2-1)$ and is a semidirect product of its unique Sylow p-subgroup of order $q^3$ and a cyclic group C of order $q^2-1$. The group C fixes also another point $Q\ne P$ with $Q\in \mathcal H_q({\mathbb {F}}_{q^2})$.

• (II) The stabilizer $M_2$ of a pole-polar pair $(P,\ell )$ with respect to the unitary polarity associated with $\mathcal H_q$, with $P\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$ and $P\notin \ell$. The group $M_2$ has order $q(q+1)^2(q-1)$ and is a semidirect product isomorphic to $\mathrm{{SL}}(2,q)\rtimes C_{q+1}$, where $C_{q+1}$ is cyclic of order $q+1$.

• (III) The stabilizer $M_3$ of a self-polar triangle $T=\{P_1,P_2,P_3\}$ with respect to the unitary polarity associated with $\mathcal H_q$, with $P_i\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$. The group $M_3$ has order $6(q+1)^2$ and is a semidirect product of an abelian group $C_{q+1}\times C_{q+1}$ fixing T pointwise and a symmetric group $S_3$ acting faithfully on T.

• (IV) The stabilizer $M_4$ of a triangle $T=\{P_1,P_2,P_3\}\subset \mathcal H_q({\mathbb {F}}_{q^6}){\setminus }\mathcal H_q({\mathbb {F}}_{q^2})$ which is invariant under the Frobenius automorphism $(X,Y,Z)\mapsto (X^{q^2},Y^{q^2},Z^{q^2})$. The group $M_4$ has order $3(q^2-q+1)$ and is a semidirect product $C_{q^2-q+1}\rtimes C_3$, where $C_{q^2-q+1}$ is a Singer group acting semiregularly on $\mathrm{{PG}}(2,q^2)$ and fixing T pointwise, and $C_3$ has a unique orbit on T.

For any $i\in \{1,2,3,4\}$, the intersection $\mathrm{PSU}(3,q)\cap M_i$ of $\mathrm{PSU}(3,q)$ with the maximal subgroup $M_i$ listed above is a maximal subgroup of $\mathrm{PSU}(3,q)$ with index $\gcd (3,q+1)$ in $M_i$; see [19, 27].

Theorem 2.1

([19, 27]) If p is odd, then the maximal subgroups of $\mathrm{PSU}(3,q)$ not fixing a point nor a triangle are the following:

• (i) the Hessian groups of order 216 when $9\mid (q+1)$, and of order 72 when $3\mid (q+1)$ and $9\not \mid (q+1)$;

• (ii) $\mathrm{PGL}(2,q)$ preserving a conic;

• (iii) $\mathrm{PSL(2,7)}$ when $p=7$ or $-7$ is not a square in ${\mathbb {F}}_q$;

• (iv) the alternating group $\mathrm{A}_6$ when either $p=3$ and n is even, or 5 is a square in ${\mathbb {F}}_q$, but ${\mathbb {F}}_q$ contains no primitive cube roots of unity;

• (v) a group of order 720 containing the alternating group $\mathrm{A}_6$ as a normal subgroup when $p=5$ and n is odd;

• (vi) the alternating group $\mathrm{A}_7$ when $p=5$ and n is odd;

• (vii) $\mathrm{PSU}(3,p^m)$ where n / m is an odd prime different from 3;

• (viii) subgroups containing $\mathrm{PSU}(3,p^m)$ as a normal subgroup of index 3, when $m\mid n$, $n/m=3$, and $3\mid (q+1)$.

If $p=2$, then the maximal subgroups of $\mathrm{PSU}(3,q)$ not fixing a point nor a triangle are the following:

(vii$^\prime$):

$\mathrm{PSU}(3,2^m)$ where $m\mid n$ and n / m is an odd prime different from 3; when $m=1$, this is the Hessian group of order 72;

(viii$^\prime$):

subgroups containing $\mathrm{PSU}(3,2^m)$ as a normal subgroup of index 3, where $n/m=3$ and $3\mid (q+1)$. For $m=1$, this is the Hessian group of order 216;

(ix$^\prime$):

a group of order 36, which exists as a maximal subgroup when $n=1$.

The following lemma recalls how an element of $\mathrm{PGU}(3,q)$ of a given order acts on $\mathrm{{PG}}(2,\overline{{\mathbb {F}}}_{q^2})$, and in particular on $\mathcal H_q({\mathbb {F}}_{q^2})$; for the usual terminology about collineations of projective planes, see [21].

Lemma 2.2

([29, Lemma 2.2]) For a non-trivial element $\sigma \in \mathrm{PGU}(3,q)$, one of the following cases holds.

• (A) $\mathrm{ord}(\sigma )\mid (q+1)$, and $\sigma$ is a homology whose center P is a point off $\mathcal H_q$ and whose axis $\ell$ is a chord of $\mathcal H_q({\mathbb {F}}_{q^2})$ such that $(P,\ell )$ is a pole-polar pair with respect to the unitary polarity associated with $\mathcal H_q({\mathbb {F}}_{q^2})$.

• (B) $\mathrm{ord}(\sigma )$ is coprime to p and $\sigma$ fixes the vertices $P_1,P_2,P_3$ of a non-degenerate triangle T.

  • (B1) The points $P_1,P_2,P_3$ are ${\mathbb {F}}_{q^2}$-rational, $P_1,P_2,P_3\notin \mathcal H_q$ and the triangle T is self-polar with respect to the unitary polarity associated with $\mathcal H_q({\mathbb {F}}_{q^2})$. Also, $o(\sigma )\mid (q+1)$.

  • (B2) The points $P_1,P_2,P_3$ are ${\mathbb {F}}_{q^2}$-rational, $P_1\notin \mathcal H_q$, $P_2,P_3\in \mathcal H_q$. Also, $o(\sigma )\mid (q^2-1)$ and $\mathrm{ord}(\sigma )\not \mid (q+1)$.

  • (B3) The points $P_1,P_2,P_3$ have coordinates in ${\mathbb {F}}_{q^6}{\setminus }{\mathbb {F}}_{q^2}$, $P_1,P_2,P_3\in \mathcal H_q$. Also, $\mathrm{ord}(\sigma )\mid (q^2-q+1)$.

• (C) $\mathrm{ord}(\sigma )=p$, and $\sigma$ is an elation whose center P is a point of $\mathcal H_q$ and whose axis $\ell$ is a tangent of $\mathcal H_q({\mathbb {F}}_{q^2})$; here, $(P,\ell )$ is a pole-polar pair with respect to the unitary polarity associated with $\mathcal H_q({\mathbb {F}}_{q^2})$.

• (D) $\mathrm{ord}(\sigma )=p$ with $p\ne 2$, or $\mathrm{ord}(\sigma )=4$ and $p=2$. In this case, $\sigma$ fixes an ${\mathbb {F}}_{q^2}$-rational point P, with $P \in \mathcal H_q$, and a line $\ell$ which is a tangent of $\mathcal H_q({\mathbb {F}}_{q^2})$; here, $(P,\ell )$ is a pole-polar pair with respect to the unitary polarity associated with $\mathcal H_q({\mathbb {F}}_{q^2})$.

• (E) $p\mid \mathrm{ord}(\sigma )$, $p^2\not \mid \mathrm{ord}(\sigma )$, and $\mathrm{ord}(\sigma )\ne p$. In this case, $\sigma$ fixes two ${\mathbb {F}}_{q^2}$-rational points P, Q, with $P\in \mathcal H_q$, $Q\notin \mathcal H_q$.

Throughout the paper, a non-trivial element of $\mathrm{PGU}(3,q)$ is said to be of type (A), (B), (B1), (B2), (B3), (C), (D), or (E), as given in Lemma 2.2; G always stands for a subgroup of $\mathrm{PGU}(3,q)$.

Every subgroup G of $\mathrm{PGU}(3,q)$ produces a quotient curve $\mathcal H_q/G$, and the cover $\mathcal H_q\rightarrow \mathcal H_q/G$ is a Galois cover defined over ${\mathbb {F}}_{q^2}$ where the degree of the different divisor $\Delta$ is given by the Riemann–Hurwitz formula [31, Theorem 3.4.13],

$$\begin{aligned} \Delta =(2g(\mathcal H_q)-2)-|G|(2g(\mathcal H_q/G)-2). \end{aligned}$$

On the other hand, $\Delta =\sum _{\sigma \in G{\setminus }\{id\}}i(\sigma )$, where $i(\sigma )\ge 0$ is given by the Hilbert’s different formula [31, Thm. 3.8.7], namely

$$\begin{aligned} \textstyle {i(\sigma )=\sum _{P\in \mathcal H_q({\bar{{\mathbb {F}}}}_{q^2})}v_P(\sigma (t)-t),} \end{aligned}$$

(1)

where t is a local parameter at P.

By analyzing the geometric properties of the elements $\sigma \in \mathrm{PGU}(3,q)$, it turns out that there are only few possibilities for $i(\sigma )$, as stated in the following theorem.

Theorem 2.3

([29, Theorem 2.7]) For a non-trivial element $\sigma \in \mathrm{PGU}(3,q)$, one of the following cases occurs.

• (1) If $\mathrm{ord}(\sigma )=2$ and $2\mid (q+1)$, then $\sigma$ is of type (A) and $i(\sigma )=q+1$.

• (2) If $\mathrm{ord}(\sigma )=3$, $3 \mid (q+1)$, and $\sigma$ is of type (B3), then $i(\sigma )=3$.

• (3) If $\mathrm{ord}(\sigma )\ne 2$, $\mathrm{ord}(\sigma )\mid (q+1)$, and $\sigma$ is of type (A), then $i(\sigma )=q+1$.

• (4) If $\mathrm{ord}(\sigma )\ne 2$, $\mathrm{ord}(\sigma )\mid (q+1)$, and $\sigma$ is of type (B1), then $i(\sigma )=0$.

• (5) If $\mathrm{ord}(\sigma )\mid (q^2-1)$ and $\mathrm{ord}(\sigma )\not \mid (q+1)$, then $\sigma$ is of type (B2), and $i(\sigma )=2$.

• (6) If $\mathrm{ord}(\sigma )\ne 3$, and $\mathrm{ord}(\sigma )\mid (q^2-q+1)$, then $\sigma$ is of type (B3) and $i(\sigma )=3$.

• (7) If $p=2$ and $\mathrm{ord}(\sigma )=4$, then $\sigma$ is of type (D) and $i(\sigma )=2$.

• (8) If $\mathrm{ord}(\sigma )=p$, $p \ne 2$, and $\sigma$ is of type (D), then $i(\sigma )=2$.

• (9) If $\mathrm{ord}(\sigma )=p$ and $\sigma$ is of type (C), then $i(\sigma )=q+2$.

• (10) If $\mathrm{ord}(\sigma )\ne p$, $p\mid \mathrm{ord}(\sigma )$, and $\mathrm{ord}(\sigma )\ne 4$, then $\sigma$ is of type (E) and $i(\sigma )=1$.

3 On maximal subgroups of $\mathrm{PGU}(3,q)$

Since we were not able to find references for the complete list of maximal subgroups of $\mathrm{PGU}(3,q)$, we determine it in this section when $3 \mid (q+1)$, that is, when $\mathrm{PGU}(3,q)\ne \mathrm{PSU}(3,q)$. The result is the following.

Theorem 3.1

Let $q=p^n$ be a prime power such that $3 \mid (q+1)$. Then, the following is the list of maximal subgroups of $\mathrm{PGU}(3,q)$.

• (1) The stabilizer $M_1$ of a point $P\in \mathcal H_q({\mathbb {F}}_{q^2})$. The group $M_1$ has order $q^3(q^2-1)$ and is a semidirect product of its unique Sylow p-subgroup of order $q^3$ and a cyclic group C of order $q^2-1$. The group C fixes also another point $Q\ne P$ with $Q\in \mathcal H_q({\mathbb {F}}_{q^2})$.

• (2) The stabilizer $M_2$ of a pole-polar pair $(P,\ell )$ with respect to the unitary polarity associated with $\mathcal H_q$, with $P\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$ and $P\notin \ell$. The group $M_2$ has order $q(q+1)^2(q-1)$ and is a semidirect product isomorphic to $\mathrm{{SL}}(2,q)\rtimes C_{q+1}$, where $C_{q+1}$ is cyclic of order $q+1$.

• (3) The stabilizer $M_3$ of a self-polar triangle $T=\{P_1,P_2,P_3\}$ with respect to the unitary polarity associated with $\mathcal H_q$, with $P_i\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$. The group $M_3$ has order $6(q+1)^2$ and is a semidirect product of an abelian group $C_{q+1}\times C_{q+1}$ fixing T pointwise and a symmetric group $S_3$ acting faithfully on T.

• (4) The stabilizer $M_4$ of a triangle $T=\{P_1,P_2,P_3\}\subset \mathcal H_q({\mathbb {F}}_{q^6}){\setminus }\mathcal H_q({\mathbb {F}}_{q^2})$ which is invariant under the Frobenius automorphism $(X,Y,Z)\mapsto (X^{q^2},Y^{q^2},Z^{q^2})$. The group $M_4$ has order $3(q^2-q+1)$ and is a semidirect product $C_{q^2-q+1}\rtimes C_3$, where $C_{q^2-q+1}$ is a Singer group acting semiregularly on $\mathrm{{PG}}(2,q^2)$ and fixing T pointwise, and $C_3$ has a unique orbit on T.

• (5) The normal subgroup $\mathrm{PSU}(3,q)$ of index 3 in $\mathrm{PGU}(3,q)$.

• (6) The Hessian group $H_{216} \cong \mathrm{PGU}(3,2)$, if p is odd and $9 \not \mid (q+1)$.

• (7) $\mathrm{PGU}(3,p^m)$ where $m \mid n$ and n / m is an odd prime different from 3.

In order to prove Theorem 3.1, we proceed with a case-by-case analysis on maximal subgroups M of $\mathrm{PGU}(3,q)$ containing a maximal subgroup H of $\mathrm{PSU}(3,q)$ not fixing a point nor a triangle, as listed in Theorem 2.1.

Remark 3.2

Let $3\mid (q+1)$, H be a maximal subgroup of $\mathrm{PSU}(3,q)$, and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, the maximality of H in $\mathrm{PSU}(3,q)$ implies either $M\cap \mathrm{PSU}(3,q)=H$ or $M\cap \mathrm{PSU}(3,q)=\mathrm{PSU}(3,q)$. If $M\cap \mathrm{PSU}(3,q)=H$, then

$$\begin{aligned} 3\cdot |\mathrm{PSU}(3,q)|=|\mathrm{PGU}(3,q)|=|\mathrm{PSU}(3,q)M|=|\mathrm{PSU}(3,q)|\cdot |M|\,/\,|H|, \end{aligned}$$

and hence, $[M:H]=3$. Also, H is normal in M since $\mathrm{PSU}(3,q)$ is normal in $\mathrm{PGU}(3,q)$.

3.1 Hessian groups

Proposition 3.3

Let $q=p^n$ be a power of an odd prime p such that $9\mid (q+1)$. Let $H\cong \mathrm{PGU}(3,2)$ be a maximal subgroup of $\mathrm{PSU}(3,q)$ isomorphic to the Hessian group of order 216, and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M\cong \mathrm{PSU}(3,q)$.

Proof

Assume by contradiction $M\not \cong \mathrm{PSU}(3,q)$. Then, $M\cap \mathrm{PSU}(3,q)=H$ and $|M|=648$ by Remark 3.2. By direct checking with MAGMA [4], there are exactly three groups of order 648 containing a subgroup of order 216 isomorphic to $\mathrm{PGU}(3,2)$, namely SmallGroup(648, i) with $i \in \{702,756,757\}$.

• $M\cong SmallGroup(648,702)$. In this case, M has a normal subgroup of order 3, say $\langle \alpha \rangle$; hence, M acts on the points fixed by $\alpha$. By Lemma 2.2, $\alpha$ is either of type (A), or (B1), or (B3); hence, either M fixes a pole-polar pair $(P,\ell )$ with $P\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$, or M stabilizes a self-polar triangle $\{P_1,P_2,P_3\}\subseteq \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$, or M stabilizes a Frobenius-invariant triangle $\{P_1,P_2,P_3\}\subseteq \mathcal H_q({\mathbb {F}}_{q^6}){\setminus }\mathcal H_q({\mathbb {F}}_{q^2})$. Then, M is properly contained in one of the maximal subgroups $M_1,M_2,M_3,M_4$ described in Theorem 3.1, a contradiction to the maximality of M.

• $M\cong SmallGroup(648,756)$. In this case, M has a normal subgroup of order 2, say $\langle \alpha \rangle$; hence, M acts on the points fixed by $\alpha$. By Lemma 2.2, $\alpha$ is of type (A) and fixes a point $P \in PG(2,q^2) {\setminus } \mathcal H_q$. Thus, M fixes P and is properly contained in the maximal subgroup $M_2$ of $\mathrm{PGU}(3,q)$, a contradiction.

• $M\cong SmallGroup(648,757)$. In this case, M has a normal subgroup of order 2, and a contradiction follows as in the previous case.

Then, $M\cap \mathrm{PSU}(3,q)=\mathrm{PSU}(3,q)$ and the claim is proved. $\square$

Proposition 3.4

Let $q=p^n$ be a power of an odd prime p such that $3 \mid (q+1)$ and $9 \not \mid (q+1)$. Let $H\cong \mathrm{PSU}(3,2)$ be a maximal subgroup of $\mathrm{PSU}(3,q)$ isomorphic to the Hessian group of order 72, and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M \cong \mathrm{PGU}(3,2)$ is isomorphic to the Hessian group of order 216.

Proof

Arguing as in the proof of Theorem 9 in [27], one can explicitly construct a subgroup M of $\mathrm{PGL}(3,q^2)$ containing H as a normal subgroup of index 3 and isomorphic to the Hessian group $\mathrm{PGU}(3,2)$ of order 216. By direct computation, the generators of M leave invariant the Hermitian curve $\mathcal H_q$ in its Fermat equation $X^{q+1}+Y^{q+1}+Z^{q+1}=0$; hence, M is a subgroup of $\mathrm{PGU}(3,q)$. Also, M is not contained in $\mathrm{PSU}(3,q)$. Now, we show that M is maximal in $\mathrm{PGU}(3,q)$.

Suppose by contradiction there exists a proper subgroup $M^\prime$ of $\mathrm{PGU}(3,q)$ containing M properly. By [27, Theorem 9], M is the unique tame subgroup of $\mathrm{PGU}(3,q)$ such that M does not leave invariant a point, or a line, or a triangle and M contains homologies of order 3. Since $M\subseteq M^\prime$, also $M^\prime$ does not leave invariant a point, or a line, or a triangle and $M^\prime$ contains homologies of order 3. Then, $M^\prime$ contains p-elements, which are clearly elements of $\mathrm{PSU}(3,q)$ because $p\not \mid [\mathrm{PGU}(3,q):\mathrm{PSU}(3,q)]$. From [27, Theorem 18], $M^\prime$ contains elements of type (C) because $M^\prime$ cannot contain only p-elements of type (D). From [27, Theorem 28], $M^\prime$ contains the entire $\mathrm{PSU}(3,q)$; since $M^\prime$ is not contained in $\mathrm{PSU}(3,q)$, this implies $M^\prime =\mathrm{PGU}(3,q)$, a contradiction. $\square$

3.2 $\mathrm{PGL}(2,q)$ preserving a conic

Proposition 3.5

Let $q=p^n$ be a power of an odd prime p with $3 \mid (q+1)$. Let H be a maximal subgroup of $\mathrm{PSU}(3,q)$ such that $H \cong \mathrm{PGL}(2,q)$ and H fixes a conic $\mathcal C$. Let M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M \cong \mathrm{PSU}(3,q)$.

Proof

Assume by contradiction $M\not \cong \mathrm{PSU}(3,q)$. By Remark 3.2, $H=M\cap \mathrm{PSU}(3,q)\triangleleft M$ and $[M:H]=3$. From [14, Remark 6.14], M is a semidirect product $M=\mathrm{PGL}(2,q) \rtimes C_3$ where $C_3=\langle \alpha \rangle$ is a cyclic group of order 3 and $3 \mid n$. Let $I=\mathcal H_q\cap \mathcal C$ be the set of the $q+1$ points of intersection between $\mathcal H_q$ and $\mathcal C$. The set I is the unique orbit of size $q+1$ of H on $\mathcal H_q$; see [5, Lemma 3.1]. Since M normalizes H, M acts on the set of orbits of H on $\mathcal H_q$ having the same size; hence, M acts on I. By Lemma 2.2, $\alpha$ is either of type (A), or of type (B1), or of type (B3).

• (1) Assume that $\alpha$ is a homology, with center P and axis $\ell$. Recall that $\mathcal C$ is irreducible, and let r be a secant line to $\mathcal C$ passing through P. Then, the size of $(r\cap \mathcal H_q){\setminus }\ell$ is 1 or 2, according to $r\cap \ell \in \mathcal C$ or $r\cap \ell \notin \mathcal C$, respectively. Since r and $\ell$ are fixed by $\alpha$, we have that $\alpha$ acts on the 1 or 2 points of $(r\cap \mathcal H_q){\setminus }\ell$. This is a contradiction to the action on the plane of $\alpha$, which has long orbits of size 3 out of $\ell$ and P.

• (2) Assume that $\alpha$ is of type (B1). Since $o(\alpha )=3$, this implies that $\alpha \in \mathrm{PSU}(3,q)$. In fact, we can use the Fermat model $X^{q+1}+Y^{q+1}+Z^{q+1}=0$ of $\mathcal H_q$ and assume up to conjugation that $\alpha$ fixes the fundamental triangle, so that $\alpha$ is represented by a diagonal matrix $\mathrm{diag}(\lambda ,\mu ,1)$ with $\lambda ^{3}=\mu ^{3}=1$. As $\alpha$ is of type (B1), we have $\lambda \ne 1$, $\mu \ne 1$, $\mu \ne \lambda$. Then, $\mu =\lambda ^{-1}$ and $\mathrm{det}(\alpha )=1$, so that $\alpha \in \mathrm{PSU}(3,q)$. This contradicts $M\not \subseteq \mathrm{PSU}(3,q)$.

• (3) Assume that $\alpha$ is of type (B3). By the Orbit-Stabilizer theorem, the stabilizer $M_P$ in M of a point $P\in I$ has order $3q(q-1)$. From $P\in \mathcal H_q$ and [20, Lemma 11.44], we have that $M_P$ is a semidirect product $M_P={M}_P^1 \rtimes {M}_P^2$, where ${M}_P^1$ is the Sylow p-subgroup of $M_P$ and ${M}_P^2$ is cyclic of order $3(q-1)$. Analogously, the stabilizer $H_P$ of P in H satisfies $H_P={H}_P^1 \rtimes {H}_P^2$ with $|{H}_P^2|=q-1$; up to conjugation, ${M}_P^2$ contains ${H}_P^2$. Since $3 \not \mid (q-1)$, there exists an element $\beta \in {M}_P^2 {\setminus } H$ of order 3. As $\beta$ fixes an ${\mathbb {F}}_{q^2}$-rational point P of $\mathcal H_q$, $\beta$ is a homology by Lemma 2.2. Then, $M=H\rtimes \langle \beta \rangle$ and a contradiction is obtained as in Case (1). $\square$

3.3 $\mathrm{PSL}(2,7)$ when $p=7$ or $\sqrt{-7}\notin {\mathbb {F}}_q$

Proposition 3.6

Let $q=p^n$ be a power of an odd prime p such that $3 \mid (q+1)$ and either $p=7$ or $\sqrt{-7}\notin {\mathbb {F}}_q$. Let H be a maximal subgroup of $\mathrm{PSU}(3,q)$ with $H \cong \mathrm{PSL}(2,7)$, and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M \cong \mathrm{PSU}(3,q)$.

Proof

Assume by contradiction $M\not \cong \mathrm{PSU}(3,q)$. By Remark 3.2, $H\triangleleft M$ and $[M:H]=3$. From [14, Remark 6.14] and [34, Proposition 1.2 (i)], we obtain that $M=H \times C_3$. Hence, H acts on the points fixed by $C_3\triangleleft M$. By Lemma 2.2, this means that H is contained in one of the maximal subgroups $M_2,M_3,M_4$ described in Theorem 3.1, a contradiction to Theorem 2.1. $\square$

3.4 The group SmallGroup(720, 765) when $p=5$ and n is odd

From [27], $\mathrm{PSU}(3,q)$ has a maximal subgroup H of order 720 which contains a normal subgroup of order 360 isomorphic to the alternating group $\mathrm{A}_6$, when $p=5$ and q is odd power of p. The following lemma gives H explicitly in the GAP notation.

Lemma 3.7

Let q be an odd power of 5 and H be a subgroup of $\mathrm{PSU}(3,q)$ of order 720 containing $\mathrm{A}_6$. Then, H is isomorphic to the subgroup of $\mathrm{P \Gamma L}(2,9)$ named SmallGroup(720,765).

Proof

By direct checking, there are exactly four groups of order 720 containing a subgroup isomorphic to $\mathrm{A}_6$, namely the direct product $\mathrm{A}_6 \times C_2$, the symmetric group $\mathrm{S}_6$, a semidirect product $SmallGroup(720,764)\cong \mathrm{A}_6\rtimes C_2$, and SmallGroup(720, 765).

• Suppose that $M\cong \mathrm{A}_6\times C_2$, say $C_2=\langle \alpha \rangle$. Then, by Lemma 2.2, $\alpha$ is of type (A). Since $C_2$ is normal in H, H fixes the center of $\alpha$ and is contained in the maximal subgroup $M_2$ of $\mathrm{PGU}(3,q)$ described in Theorem 3.1. By the maximality of H in $\mathrm{PSU}(3,q)$, we have $H=M_2\cap \mathrm{PSU}(3,q)$, which is a contradiction to $720=|H|\ne |M_2\cap \mathrm{PSU}(3,q)|=q(q+1)^2(q-1)/3$.

• Suppose that $H\cong \mathrm{S}_6$. Then, H contains an elementary abelian subgroup of order 8. This is a contradiction to the fact that for odd q, there are at most three involutions which commute pairwise; see also [23, Lemma 2.2 (viii)].

• Suppose that H is the semidirect product $\mathrm{SmallGroup}(720,764)\cong \mathrm{A}_6\rtimes C_2$. Then, H contains a cyclic subgroup $C_{10}$ of order 10; by Lemma 2.2, $C_{10}$ is generated by an element of type (E), and the elements of order 5 in $C_{10}$ are of type (C). Also, H contains a dihedral subgroup $D_5$ of order 10. If an involution normalizes an elation, then they commute, as they are both contained in a maximal subgroup of type $M_2$ and the involution is in the center of $M_2$; see [28] for the structure of $M_2$. Hence, the elements of order 5 in $D_5$ are of type (D). But H has a unique conjugacy class of elements of order 5, so that we cannot have elements of type (C) and elements of type (D).

Then, $H\cong \mathrm{SmallGroup}(720,765)$ and the claim is proved. $\square$

Proposition 3.8

Let q be an odd power of 5, H be a maximal subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{SmallGroup(720,765)}$, and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M=\mathrm{PSU}(3,q)$.

Proof

Assume by contradiction $M\not \cong \mathrm{PSU}(3,q)$. By Remark 3.2, $H=M\cap \mathrm{PSU}(3,q)\triangleleft M$ and $|M|=3|H|=2160$. Also, $\mathrm{A}_6\triangleleft M$ since $\mathrm{A}_6$ is characteristic in H. Hence, $M/\mathrm{Ker}(\varphi )$ is isomorphic to an automorphism group of $\mathrm{A}_6$, where $\mathrm{Ker}(\varphi )$ is the kernel of the action by conjugation of M on $\mathrm{A}_6$. As $\mathrm{A}_6\cong \mathrm{PSL}(2,9)$, $M/\mathrm{Ker}(\varphi )$ is isomorphic to a subgroup of $\mathrm{P\Gamma L}(2,9)$. Since the largest subgroup of ${P\Gamma L}(2,9)$ has order 720 and the order of $M/\mathrm{Ker}(\varphi )$ is at least $|H|=720$, we have $|\mathrm{Ker}(\varphi )|=3$. Thus, $M{\setminus } \mathrm{A}_6$ contains an element $\alpha$ of order 3 commuting with $\mathrm{A}_6$ elementwise. As $3\mid (q+1)$, $\alpha$ is either of type (A), or of type (B1), or of type (B3), by Lemma 2.2. Hence, H is contained in one of the maximal subgroups $M_2,M_3,M_4$ described in Theorem 3.1, a contradiction to Theorem 2.1. $\square$

3.5 The alternating group $\mathrm{A}_6$ when either $p=3$ and n is even, or 5 is a square in ${\mathbb {F}}_q$, but ${\mathbb {F}}_q$ contains no primitive cube roots of unity

Proposition 3.9

Let $q=p^n$, where either $p=3$ and n is even, or 5 is a square in ${\mathbb {F}}_q$, but ${\mathbb {F}}_q$ contains no primitive cube roots of unity. Let H be a maximal subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{A}_6$ and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M=\mathrm{A}_6$ if $p=3$ and $M=\mathrm{PSU}(3,q)$ otherwise.

Proof

The claim is trivial for $p=3$ by Theorem 2.1, as $\mathrm{PGU}(3,q)=\mathrm{PSU}(3,q)$. If $p\ne 3$ and ${\mathbb {F}}_q$ contains no primitive cube roots of unity, then $3\mid (q+1)$. Assume by contradiction $M\not \cong \mathrm{PSU}(3,q)$. By Remark 3.2, $H=M\cap \mathrm{PSU}(3,q)\triangleleft M$ and $[M:H]=3$. Arguing as in the proof of Proposition 3.8, it can be shown that $M/\mathrm{Ker}(\varphi )$ is isomorphic to a subgroup of $\mathrm{P\Gamma L}(2,9)$, where $\varphi$ is the action by conjugation of M on H; H commutes elementwise with an element of order 3 in $M{\setminus } H$; H is contained either in $M_2$ or in $M_3$ or in $M_4$ as described in Theorem 3.1, a contradiction to Theorem 2.1. $\square$

3.6 The alternating group $\mathrm{A}_7$ when $p=5$ and n is odd

Proposition 3.10

Let q be an odd power of $p=5$, H be a maximal subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{A}_7$, and M be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing H. Then, $M=\mathrm{PSU}(3,q)$.

Proof

Assume by contradiction $M\not \cong \mathrm{PSU}(3,q)$. By Remark 3.2, $H=M\cap \mathrm{PSU}(3,q)\triangleleft M$ and $[M:H]=3$. Thus, $M/\mathrm{Ker}(\varphi )$ is isomorphic to an automorphism group of H, where $\varphi$ is the action by conjugation of M on H. Since $|\mathrm{Aut}(\mathrm{A}_7)|=2|\mathrm{A}_7|$ and $H\le M$, we conclude that $Ker(\varphi )$ is cyclic of order 3. Hence, H commutes with an element $\alpha$ of order 3, and H acts on the points fixed by $\alpha$. This is a contradiction to Theorem 2.1, according to which H cannot fix a point nor a triangle. $\square$

3.7 $\mathrm{PSU}(3,p^m)$ where $m\mid n$ and n / m is odd

In this section, $q=p^n$ can be even or odd. Let H be a subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{PSU}(3,{\bar{q}})$, where ${\bar{q}}=p^m$, m divides n, and n / m is odd. We start with some lemmas on maximal subgroups of $\mathrm{PSU}(3,q)$ containing H which we were not able to find clearly stated in [19, 27] nor elsewhere.

Lemma 3.11

Let $q=p^n$ be a prime power and H be a subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{PSU}(3,p^m)$, where $m\mid n$ and m / n is odd. Then, $\mathrm{PSU}(3,q)$ contains a unique conjugacy class of subgroups isomorphic to H. Also, H is not maximal in $\mathrm{PSU}(3,q)$ unless n / m is prime.

Proof

Consider the Hermitian curve $\mathcal H_q$ in its Norm–Trace equation $x^{q+1}=y^q+y$, let $P_{\infty }\in \mathcal H_q$ be the unique point at infinity of $\mathcal H_q$, and $\mathcal A(P_{\infty })$ be the stabilizer of $P_{\infty }$ in $\mathrm{PGU}(3,q)$; we follow here the notation in [12]. From [12], $\mathcal A(P_{\infty })$ has order $q^3(q^2-1)$ and is a semidirect product ${\mathcal {A}}(P_\infty )={\mathcal {A}}_1(P_\infty ) \rtimes {\mathcal {C}}(P_\infty )$ where ${\mathcal {A}}_1(P_\infty )$ is the unique Sylow p-subgroup of ${\mathcal {A}}(P_\infty )$ and ${\mathcal {C}}(P_\infty )$ is cyclic of order $q^2-1$. If $\sigma \in {\mathcal {A}}_1(P_\infty )$, then $\sigma (x)=x+b$ and $\sigma (y)=y+b^qx+c$, for some $b,c \in {\mathbb {F}}_{q^2}$ satisfying $c^q+c=b^{q+1}$; if $\sigma \in {\mathcal {C}}(P_\infty )$, then $\sigma (x)=ax$ and $\sigma (y)=a^{q+1}y$ with $a \in {\mathbb {F}}_{q^2}$. Also, $\mathrm{PGU}(3,q)=\langle {\mathcal {A}}(P_\infty ),w \rangle$, where w is the involution defined as $w(x)=\frac{x}{y}$, $w(y)=\frac{1}{y}$. The subgroup $\mathrm{PSU}(3,q)$ is generated by $\mathrm{PSU}(3,q)=\langle \mathrm{PSU}(3,q)\cap \mathcal A(P_\infty ),w\rangle$, where $\mathrm{PSU}(3,q)\cap \mathcal A(P_\infty )={\mathcal {A}}_1(P_\infty ) \rtimes (\mathrm{PSU}(3,q)\cap {\mathcal {C}}(P_\infty ))$ and $|\mathrm{PSU}(3,q)\cap {\mathcal {C}}(P_\infty )|=(q^2-1)/\gcd (3,q+1)$. Let

$$\begin{aligned} K_1= & {} \{\sigma \in {\mathcal {A}}_1(P_\infty ) \mid \sigma \mathrm{\ is \ defined \ over} \ {\mathbb {F}}_{p^{2m}}\},\\ K_2= & {} \{\sigma \in {\mathcal {C}}(P_\infty ) \cap \mathrm{PSU}(3,q) \mid \sigma \mathrm{\ is \ defined \ over} \ {\mathbb {F}}_{p^{2m}}\}, \end{aligned}$$

and $\mathcal A_m(P_\infty )=\langle K_1,K_2\rangle$. Clearly, $|K_2|=p^{2m}-1$. To show that $|K_1|=p^{3m}$, let $b,c\in {\mathbb {F}}_{p^{2m}}$. By direct checking, the condition $c^q+c=b^{q+1}$ holds if and only if $c^{p^{m(r-2)}}+c=b^{p^{m(r-2)}+1}$, where $r=n/m$. If $r=3$, the condition reads $c^{p^m}+c=b^{p^{m(r-2)}+1}$ and has $p^{3m}$ solutions $(b,c)\in {\mathbb {F}}_{p^{2m}}$ by the properties of the norm and trace functions. If $r\ge 5$, then by writing $m(r-2)=2m+m(r-4)$, we have that $c^{q}+c=b^{q+1}$ is equivalent to $c^{p^{m(r-4)}}+c=b^{p^{m(r-4)}+1}$; by induction, we obtain $|K_1|=p^{3m}$. Since $K_2$ normalizes $K_1$, we have ${\mathcal {A}}_m(P_\infty )=K_1 \rtimes K_2$ and $|{\mathcal {A}}_m(P_\infty )|=p^{3m}(p^{2m}-1)$. Clearly, the involution w is defined over ${\mathbb {F}}_{p^{2m}}$. Hence, the group $\langle \mathcal A_m(P_\infty ),w\rangle$ is defined over ${\mathbb {F}}_{p^{2m}}$ and is isomorphic to $\mathrm{PSU}(3,p^m)$, since it preserves the Hermitian curve $x^{p^m+1}=y^{p^m}+y$.

If $H\le \mathrm{PSU}(3,q)$ is isomorphic to $\mathrm{PSU}(3,p^m)$, write $H=\langle S\rtimes C,{\tilde{w}}\rangle$, where $|S|=p^{3m}$, C is cyclic of order $p^{2m}-1$, and ${\tilde{w}}$ is an involution. The group $S\rtimes C$ fixes a point $P\in \mathcal H_q({\mathbb {F}}_{q^2})$ as $\mathcal H_q$ has p-rank zero (see [20, Theorem 11.133]), and ${\tilde{w}}$ maps P to another point $Q \in \mathcal H_q({\mathbb {F}}_{q^2})$. Since $\mathrm{PSU}(3,q)$ is doubly transitive on $\mathcal H_q({\mathbb {F}}_{q^2})$ and transitive on $\mathrm{PG}(2,q^2) {\setminus } \mathcal H_q$, we have up to conjugation in $\mathrm{PSU}(3,q)$ that $P=P_\infty$, Q is the other fixed point of w, and ${\tilde{w}}=w$, so that $H=\langle \mathcal A_m(P_\infty ),w\rangle$. Hence, subgroups isomorphic to $\mathrm{PSU}(3,p^m)$ are conjugated in $\mathrm{PSU}(3,q)$ to the subgroup $\langle \mathcal A_m(P_\infty ),w\rangle$ described above. This implies that $\mathrm{PSU}(3,{\bar{q}})$ is not maximal in $\mathrm{PSU}(3,q)$ unless n / m is prime; in fact, if $n/m=d_1 d_2$ with $d_1,d_2>1$, then there exists a proper subgroup $\mathrm{PSU}(3,p^{md_1})$ of $\mathrm{PSU}(3,q)$ which contains $\mathrm{PSU}(3,{\bar{q}})$ properly. $\square$

Lemma 3.12

Let $q=p^n$ be a prime power and H be a subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{PSU}(3,p^m)$, where $m \mid n$ and n / m is an odd prime.

• If $n/m \ne 3$ or $3 \not \mid (q+1)$, then H is maximal in $\mathrm{PSU}(3,q)$.

• If $n/m=3$ and $3 \mid (q+1)$, then a maximal subgroup M of $\mathrm{PSU}(3,q)$ containing H is isomorphic to $\mathrm{PGU}(3,p^m)$.

Proof

As shown in the proof of Lemma 3.11, we can assume up to conjugation that H consists of the ${\mathbb {F}}_{p^{2m}}$-rational elements of $\mathrm{PSU}(3,q)$. Let M be a maximal subgroup of $\mathrm{PSU}(3,q)$ containing H. Since M does not leave invariant any point or triangle, we have by Theorem 2.1 that either $M\cong \mathrm{PSU}(3,p^k)$, where $k\mid n$ and n / k is odd; or M contains $\mathrm{PSU}(3,p^k)$ as a normal subgroup of index 3, where $k\mid n$, $3\mid n/m$, and $3\mid (q+1)$. Hence, if the odd prime n / m is different from 3 or $3\not \mid (q+1)$, then the second case cannot occur, and $M\cong H$ follows. Then, we can suppose that $n/m=3$ and $3\mid (q+1)$; this implies also $3\mid (p^k+1)$, so that $\mathrm{PSU}(3,p^m)\ne \mathrm{PGU}(3,p^m)$.

Let M be the subgroup of $\mathrm{PGU}(3,q)$ made by the elements of $\mathrm{PGU}(3,q)$ which are defined over ${\mathbb {F}}_{p^{2m}}$; note that $H\le M$. By arguing as in the proof of Lemma 3.11, we obtain that M is isomorphic to $\mathrm{PGU}(3,p^m)$, and hence, $\mathrm{PSU}(3,p^m)$ has index 3 in M. For any $\sigma \in M$, $\sigma$ has a representative in $\mathrm{GL}(3,p^{2m})$, whose determinant is in ${\mathbb {F}}_{p^{2m}}$ and hence is a cube in ${\mathbb {F}}_{q^2}$, because ${\mathbb {F}}_{q^2}$ is a cubic extension of ${\mathbb {F}}_{p^{2m}}$. Thus, M is a subgroup of H and satisfies the statement of this lemma.

Let ${\tilde{M}}$ be a maximal subgroup of $\mathrm{PSU}(3,q)$ containing H as a normal subgroup of index 3; the claim follows if we prove that the case ${\tilde{M}}\not \cong \mathrm{PGU}(3,p^m)$ cannot occur. If ${\tilde{M}}\not \cong \mathrm{PGU}(3,p^m)$, then from [14, Remark 6.14], it follows that ${\tilde{M}}$ is a semidirect product $H\rtimes C_3$. Let $C_3=\langle \alpha \rangle$; clearly, $\alpha \notin M\cong \mathrm{PGU}(3,p^m)$, and otherwise, ${\tilde{M}}$ and M coincide. By Lemma 2.2, $\alpha$ is either of type (A), or of type (B1), or of type (B3).

• Suppose that $\alpha$ is of type (A) or (B1). As in Case (2), in the proof of Proposition 3.5, we can use the Fermat model of $\mathcal H_q$ and assume up to conjugation that $\alpha$ is a diagonal matrix of type $\mathrm{diag}(\lambda ,\mu ,1)$, where $\lambda ^3=\mu ^3=1$; here, $\lambda =\mu$ or $\lambda \ne \mu$ according to $\alpha$ being of type (A) or (B1), respectively. In any case, $\alpha$ is defined over ${\mathbb {F}}_{p^{2m}}$ as $3\mid (p^m+1)$, and hence, $\alpha \in M\cong \mathrm{PGU}(3,p^m)$, a contradiction.

• Suppose that $\alpha$ is of type (B3), and let T be the ${\mathbb {F}}_{q^6}$-rational triangle fixed pointwise by $\alpha$. Then, $\alpha$ is an element of the pointwise stabilizer of T in $\mathrm{PSU}(3,q)$, which has order $(q^2-q+1)/3$. This is a contradiction to $o(\alpha )=3\not \mid (q^2-q+1)/3$.

$\square$

Proposition 3.13

Let $q=p^n$ be a prime power and H be a subgroup of $\mathrm{PSU}(3,q)$ isomorphic to $\mathrm{PSU}(3,p^m)$, where $m \mid n$ and n / m is an odd prime. Let M be a maximal subgroup of $\mathrm{PSU}(3,q)$ containing H, so that

• if $n/m\ne 3$ or $3\not \mid (q+1)$, then $M\cong \mathrm{PSU}(3,p^m)$;

• if $n/m=3$ and $3\mid (q+1)$, then $M\cong \mathrm{PGU}(3,p^m)$.

Let ${\tilde{M}}$ be a maximal subgroup of $\mathrm{PGU}(3,q)$ containing M.

• If $n/m \ne 3$ or $3 \not \mid (q+1)$, then ${\tilde{M}} \cong \mathrm{PGU}(3,p^m)$.

• If $n/m=3$ and $3 \mid (q+1)$, then ${\tilde{M}} \cong \mathrm{PSU}(3,q)$.

Proof

Assume without restriction that $\mathcal H_q$ has Norm–Trace equation $x^{q+1}=y^q+y$ and, up to conjugation, the elements of H are defined over ${\mathbb {F}}_{p^{2m}}$. The claim on M follows from Lemma 3.12. If $3 \not \mid (q+1)$, then $\mathrm{PSU}(3,q)=\mathrm{PGU}(3,q)$, and hence, ${\tilde{M}}=M \cong \mathrm{PGU}(3,p^m)$ by Lemma 3.12.

Now suppose that $n/m \ne 3$ and $3 \mid (q+1)$. Then, either ${\tilde{M}} \cap \mathrm{PSU}(3,q)=M$, or $\tilde{M}=\mathrm{PSU}(3,q)$. We prove the claim by providing a maximal subgroup ${{\hat{M}}}$ of $\mathrm{PGU}(3,q)$ isomorphic to $\mathrm{PGU}(3,p^m)$ and showing that the case ${\tilde{M}}\not \cong {{\hat{M}}}$ cannot occur. Arguing as in the proof of Lemma 3.11, let ${{\hat{M}}}$ be the subgroup of $\mathrm{PGU}(3,q)$ made by the elements which are defined over ${\mathbb {F}}_{p^{2m}}$. Then, ${{\hat{M}}}\cong \mathrm{PGU}(3,q)$. Since ${{\hat{M}}}$ and $\mathrm{PSU}(3,q)$ are maximal in $\mathrm{PGU}(3,q)$, we have ${{\hat{M}}}\cap \mathrm{PSU}(3,q)=M\cong \mathrm{PSU}(3,p^m)$ and $[{{\hat{M}}} : M]=3$. Let N be a maximal subgroup of $\mathrm{PGU}(3,q)$ such that ${{\hat{M}}}\le N$. Then, $N\cap \mathrm{PSU}(3,q)\ne \mathrm{PSU}(3,q)$ by the maximality of $\mathrm{PSU}(3,q)$ in $\mathrm{PGU}(3,q)$; hence, $N\cap \mathrm{PSU}(3,q)=M$ by the maximality of M in $\mathrm{PSU}(3,q)$, and $[N:M]=3$. Thus, $|N|=|M|$ and $N=M$, proving that ${{\hat{M}}}$ is maximal in $\mathrm{PGU}(3,q)$. Assume by contradiction that ${\tilde{M}}\not \cong {{\hat{M}}}$. Then, by [14, Remark 6.14], ${\tilde{M}}$ is a semidirect product $H\rtimes C_3$, where $C_3=\langle \alpha \rangle$ and $\alpha \notin {\hat{M}}$. By Lemma 2.2, $\alpha$ is either of type (A), or of type (B1), or of type (B3). If $\alpha$ is of type (A) or (B1), a contradiction follows as in the proof of Lemma 3.12. If $\alpha$ is of type (B3) and T is the ${\mathbb {F}}_{q^6}$-rational triangle fixed by $\alpha$, then $\alpha$ is the unique element of order 3 in the pointwise stabilizer C of T in $\mathrm{PGU}(3,q)$, which has order $q^2-q+1$. Since $n/m\ne 3$, it is easily seen that $(p^{2m}-p^m+1)\mid (q^2-q+1)$. Thus, the intersection $C\cap {\hat{M}}\cong \mathrm{PGU}(3,p^m)$ has order $p^{2m}-p^m+1$, which is divisible by 3; hence, $\alpha \in {{\hat{M}}}$, a contradiction.

Finally, suppose that $n/m=3$ and $3\mid (q+1)$. Assume by contradiction that ${\tilde{M}}\ne \mathrm{PSU}(3,q)$, so that ${\tilde{M}} \cap \mathrm{PSU}(3,q)=M$ and $|{\tilde{M}}|=3|M|=9|\mathrm{PSU}(3,p^m)|$. Since M is normal in ${\tilde{M}}$, we have from [14, Remark 6.14] that ${\tilde{M}}$ is a semidirect product $\mathrm{PGU}(3,p^m) \rtimes C_3$ and $3 \mid m$. Let $C_3=\langle \alpha \rangle$, so that by Lemma 2.2, $\alpha$ is either of type (A), or of type (B1), or of type (B3). Arguing as above, $\alpha \notin \mathrm{PSU}(3,q)$ implies that $\alpha$ is of type (B3). Since the elements of type (A) cannot stabilize the ${\mathbb {F}}_{q^6}$-rational triangle fixed pointwise by $\alpha$, we have that $\alpha$ does not commute elementwise with $\mathrm{PGU}(3,p^m)$. Hence, ${\tilde{M}}$ is a subgroup of the automorphism group $\mathrm{P\Gamma U}(3,p^m)=\mathrm{PGU}(3,p^m)\rtimes C_m$ of $\mathrm{PGU}(3,p^m)$; here, $C_m$ has order m and is generated by the Frobenius automorphism $\varphi :(X,Y,Z)\mapsto (X^p,Y^p,Z^p)$. Up to multiplying by an element of $\mathrm{PGU}(3,p^m)$, we can assume that $\alpha \in C_m$. Thus, $\alpha$ commutes with those elements of $\mathrm{PGU}(3,p^m)$ which are defined over ${\mathbb {F}}_{p}$; in particular, $\alpha$ commutes with the elements $\sigma :(x,y)\mapsto (ax,a^{q+1}y)$, $a\in {\mathbb {F}}_p$, which are of type (B2). This implies that $\alpha$ fixes a point $P\in \mathrm{PG}(2,q^2){\setminus }\mathcal H_q$, a contradiction to $\alpha$ being of type (B3). $\square$

3.8 The group $\mathrm{SmallGroup}(36,9)$ when $q=2$

From [19], $\mathrm{PSU}(3,2)$ has a maximal subgroup H of order 36. By direct checking, $H\cong \mathrm{SmallGroup}(36,9)$ in the GAP notation.

Proposition 3.14

Let $q=2^n$. Then, $\mathrm{PSU}(3,q)$ contains a subgroup isomorphic to $\mathrm{SmallGroup}(36,9)$ if and only if n is odd.

Proof

If n is odd, the claim follows from Theorem 2.1 as $\mathrm{PSU}(3,q)$ contains $\mathrm{PSU}(3,2)$. Conversely, suppose by contradiction that $\mathrm{SmallGroup}(36,9)\le \mathrm{PSU}(3,q)$ with n even. Then, $\mathrm{PSU}(3,q)$ contains an elementary abelian 3-subgroup E of order 9, whose non-trivial elements are of type (B2) from Lemma 2.2. Let $\sigma ,\tau \in E{\setminus }\{id\}$ with $\tau \notin \langle \sigma \rangle$; then, $\tau$ acts on the fixed points $\{P_1,P_2,P_3\}$ of $\sigma$, where $P_1\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$ and $P_2,P_3\in \mathcal H_q({\mathbb {F}}_{q^2})$. By $E\le \mathrm{Aut}(\mathcal H_q)$ and the Orbit-Stabilizer theorem, E fixes $\{P_1,P_2,P_3\}$ pointwise. Hence, E is cyclic by [20, Lemma 11.44 (c)], a contradiction. $\square$

Remark 3.15

Let q be an odd power of 2. Then, the only subgroups of $\mathrm{PGU}(3,q)$ properly containing $\mathrm{SmallGroup}(36,9)$ are $\mathrm{PSU}(3,2^k)$ and $\mathrm{PGU}(3,2^k)$, where $k\mid n$.

In fact, by direct checking, any degree 3, extension M of $\mathrm{SmallGroup}(36,9)$ contains a normal subgroup of order 3; if $M\le \mathrm{PGU}(3,q)$, then M would fix a point or a triangle and the same does $\mathrm{SmallGroup}(36,9)$, a contradiction. Then, the claim follows from Theorem 2.1.

Remark 3.16

When q is even, the only subgroups G of $\mathrm{PSU}(3,q)$ which do not fix any point or triangle are $G\cong \mathrm{PSU}(3,2^k)$ when $k\mid n$, n is odd, and 3 divides n / k; $G\cong \mathrm{PGU}(3,2^k)$ when $k\mid n$ ; and $G\cong \mathrm{SmallGroup}(36,9)$ when n is even.

In fact, from Theorem 2.1, either $q=2$ and $G\le \mathrm{SmallGroup}(36,9)$; or $G\le \mathrm{PSU}(3,2^k)$; or $G\le \mathrm{PGU}(3,2^k)$. If $G< \mathrm{SmallGroup}(36,9)$, then G contains a cyclic normal subgroup, and hence, G fixes a point or a triangle. If $G<\mathrm{PSU}(3,2^k)$ or $G<\mathrm{PGU}(3,2^k)$, apply inductively the same argument.

3.9 The subgroups of $\mathrm{PGU}(3,q)$ without fixed points or triangles

We conclude Sect. 3 with the list of subgroups of $\mathrm{PGU}(3,q)$ which do not fix a point or a triangle in $\mathrm{{PG}}(2,q^6)$. This result can be deduced from Theorem 2.1 and the analysis ruled out in this section.

Theorem 3.17

Let $q=p^n$ be a prime power. The subgroups of $\mathrm{PGU}(3,q)$ which do not fix a point or a triangle are the following.

• (1) $\mathrm{PSU}(3,p^m)$, when $m\mid n$ and n / m is odd.

• (2) $\mathrm{PGU}(3,p^m)$, when $m\mid n$ and n / m is odd.

  For $p>2$, also the following subgroups.

• (3) The Hessian groups of order 216, 72, and 36; they are isomorphic to $\mathrm{PGU}(3,2)$, $\mathrm{PSU}(3,2)$, and $\mathrm{SmallGroup}(36,9)$, respectively.

• (4) $\mathrm{PGL}(2,q)$ fixing a conic.

• (5) $\mathrm{PSL}(2,7)$, when $p=7$ or $-7$ is not a square in ${\mathbb {F}}_{q}$.

• (6) The alternating group $A_6$, when $p=3$ and n is even, or 5, is a square in ${\mathbb {F}}_q$, and ${\mathbb {F}}_q$ contains no primitive cube roots of unity.

• (7) A group of order 720 containing the alternating group $A_6$ when $p=5$ and n is odd, isomorphic to $\mathrm{SmallGroup}(720,765)$ in the GAP notation.

• (8) The alternating group $A_7$, when $p=5$ and n is odd.

  When q is an odd power of 2, also a group of order 36 isomorphic to $\mathrm{SmallGroup}(36,9)$ in the GAP notation.

4 Genera of $\mathcal H_q/G$ when $G\le \mathrm{PGU}(3,q)$ has no fixed points or triangles in $\mathrm{{PG}}(2,{\bar{{\mathbb {F}}}}_{q^2})$

In this section, we compute the genera of all quotients $\mathcal H_q/G$ such that $G\le \mathrm{PGU}(3,q)$ has no fixed points (hence also no fixed lines) nor fixed triangles in the plane $\mathrm{{PG}}(2,{\bar{{\mathbb {F}}}}_{q^2})$. This is equivalent to require that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$ (see Lemma 2.2). We proceed with a case-by-case analysis on maximal subgroups M of $\mathrm{PSU}(3,q)$ and $\mathrm{PGU}(3,q)$ containing G, as described in Theorem 2.1 and Sect. 3. In order to avoid the subgroups $G\le \mathrm{PGU}(3,q)$ which fix a point or a triangle, the following remark will be useful.

Remark 4.1

If $G\le \mathrm{PGU}(3,q)$ has a cyclic normal subgroup C, then G fixes either a point or a triangle in $\mathrm{{PG}}(2,q^6)$. In fact, G acts on the points fixed by a generator $\alpha$ of C; hence, according to Lemma 2.2, G fixes either a point, if the type of $\alpha$ is (A) or (B2) or (C) or (D) or (E); or a triangle, otherwise.

4.1 G is a subgroup of the Hessian group $H_{216}\cong \mathrm{PGU}(3,2)$

Proposition 4.2

Let $q=p^n$ be a power of an odd prime p with $3\mid (q+1)$, and H be a subgroup of $\mathrm{PGU}(3,q)$ isomorphic to the Hessian group $H_{216}\cong \mathrm{PGU}(3,2)$. If G is a subgroup of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$, then the genus of $\mathcal H_q/G$ is one of the following:

$$\begin{aligned}&\frac{q^2-34q+397-48\gamma -54\delta }{432},\qquad \frac{q^2-10q+133-54\delta }{144},\nonumber \\&\quad \frac{q^2-10q+61-18\delta }{72}, \end{aligned}$$

(2)

$$\begin{aligned}&\text {where}\qquad \gamma ={\left\{ \begin{array}{ll} 0, &{} \text {if}\quad 9\mid (q+1), \\ 3, &{} \text {if}\quad 9\not \mid (q+1), \end{array}\right. }\qquad \delta ={\left\{ \begin{array}{ll} 0, &{} \text {if}\quad 4\mid (q+1), \\ 2, &{} \text {if}\quad 4\mid (q-1), \end{array}\right. } \end{aligned}$$

(3)

and $G\cong \mathrm{PGU}(3,2)$, $G\cong \mathrm{PSU}(3,2)$, and $G\cong \mathrm{SmallGroup}(36,9)$, respectively. Conversely, if ${\bar{g}}$ is one of the integers in Eq. (2), then there exists a subgroup G of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$ and $g(\mathcal H_q/G)={\bar{g}}$.

Proof

By direct checking, $H\cong \mathrm{PGU}(3,2)$ has just three conjugacy classes of subgroups which do not admit cyclic normal subgroups; namely, they are H itself, $K\cong \mathrm{PSU}(3,2)$ (which is normal in H), and three groups $L_1,L_2,L_3\cong \mathrm{SmallGroup}(36,9)$ of order 36 (which are normal in K). By Remark 4.1, we only have to consider the cases $G\in \{H,K,L_1\}$. To prove the claim, we will show that the first, second, and third value in Eq. (23) are the genus of $\mathcal H_q/G$ with $G=H$, $G=K$, and $G=L_1$, respectively.

Case $G=H\cong \mathrm{PGU}(3,2)$. The group G contains

• a conjugacy class $S_1$ consisting of nine elements of order 2;

• a conjugacy class $S_2$ consisting of eight elements of order 3;

• a conjugacy class $G_3$ consisting of 12 subgroups of order 3; $G_3$ splits into two conjugacy classes $S_3$, $S_3^{\prime }$, each one consisting of 12 elements of order 3;

• a conjugacy class $G_4$ consisting of 24 subgroups of order 3; $G_4$ splits into two conjugacy classes $S_4$, $S_4^{\prime }$, each one consisting of 24 elements of order 3;

• a conjugacy class $S_5$ consisting of 54 elements of order 4;

• a conjugacy class $G_6$ consisting of 36 cyclic subgroups of order 6; $G_6$ splits into two conjugacy classes $S_6$, $S_6^{\prime }$, each one consisting of 36 elements of order 6.

We use Lemma 2.2 to determine the type of non-trivial elements $\sigma \in G$. If $\sigma \in S_1$, then $\sigma$ is of type (A).

Let $\sigma \in S_5$. If $4\mid (q-1)$, then $\sigma$ is of type (B2). If $4\mid (q+1)$, then $\sigma$ is of type (B1). In fact, if $\sigma$ is not of type (B1), then $\sigma$ is of type (A) and $S_5$ contains only another element $\tau$ different from $\sigma$ such that $\tau ^2=\sigma ^2$, namely $\tau =\sigma ^{-1}$, because the homologies with given center form a cyclic group; but the number $|S_1|=9$ of involutions in G is strictly smaller than $|S_5|$, a contradiction.

Let $\sigma \in S_6$. Recall that $6\mid (q+1)$. Since a cyclic group of order 6 contains exactly 2 elements of order 6 and $|S_6|/2 >|C_1|$, the same argument used for $S_5$ shows that $\sigma$ is of type (B1).

Let $\sigma \in S_2$. By direct checking, $\sigma$ is contained in a subgroup $S_3=\langle \sigma \rangle \rtimes C_2$ of H. Hence, an involution acts on the fixed points of $\sigma$, so that $\sigma$ is not of type (B3), because an element of type (A) cannot fix a point which is not ${\mathbb {F}}_{q^2}$-rational. The elements of $S_2$, together with the identity, form an elementary abelian group $C_3\times C_3$. Being conjugated, the elements of $S_2$ are all of the same type. If $C_3\times C_3$ is generated by elements of type (A), then $C_3\times C_3$ contains 2 elements of type (B1); in fact, using the Fermat model of $\mathcal H_q$, we have up to conjugation in $\mathrm{PGU}(3,q)$ that $C_3\times C_3=\{\mathrm{diag}(\lambda ,\mu ,1)\mid \lambda ^3=\mu ^3=1\}$, and $\mathrm{diag}(\rho ,\rho ^{-1},1)$, $\mathrm{diag}(\rho ^{-1},\rho ,1)$ are of type (B1), where $\rho$ is a primitive cube root of unity. Therefore, the elements of $S_2$ are of type (B1).

Let $\sigma \in S_3$ or $\sigma \in S_3^{\prime }$; since elements of $S_3$ and elements of $S_3^{\prime }$ are inverse each other, they are of the same type. As $\langle \sigma \rangle$ is normalized by an involution, the same argument used for $S_2$ shows that $\sigma$ is not of type (B3). We show that $\sigma$ is of type (A); to this aim, assume by contradiction that the elements of $S_3$ and $S_3^{\prime }$ are of type (B1). By direct checking, $\sigma$ is contained in an elementary abelian 3 group $E=C_3\times C_3$; E contains a subgroup ${\bar{C}}_3$ of order 3 whose non-trivial elements are in $S_2$, while every element in $E{\setminus }{\bar{C}}_3$ is in $S_3$ or $S_3^{\prime }$. Let $\sigma ^{\prime }\in E{\setminus }\langle \sigma \rangle$, and denote by $T=\{P_1,P_2,P_3\}$ and $T^{\prime }=\{P_1^{\prime },P_2^{\prime },P_3^{\prime }\}$ the triangles fixed pointwise by $\sigma$ and $\sigma ^{\prime }$, respectively. Then, $T\ne T^{\prime }$, since there are just 3 elements of order 3 and type (B1) which fix T pointwise. Also, T and $T^{\prime }$ have no vertex in common. In fact, $\sigma$ acts on $T^{\prime }$, because $\sigma$ and $\sigma ^{\prime }$ commute; if $T\ne T^{\prime }$ and $P_1=P_1^{\prime }$ (as represented in the following picture), then $\sigma$ acts on $\{P_2^{\prime },P_3^{\prime }\}$ with long orbits, a contradiction to $o(\sigma )=3$.

Therefore, the vertices of the triangles $T_1,T_2,T_3,T_4$ fixed pointwise by some non-trivial element of E are 12 distinct points altogether. By direct checking, the normalizer of E in G contains a subgroup $N\cong E\rtimes C_2$ of order 18. Let $C_2=\langle \tau \rangle$. Since $\tau$ normalizes E, $\tau$ acts on $T_1,T_2,T_3,T_4$. By direct checking, N contains elements of order 6. Hence, $\tau$ commutes with some non-trivial $\alpha \in E$, and thus, $\tau$ fixes pointwise a triangle $T_i$, say $T_1=\{P,Q,R\}$; we can assume that the center of the homology $\tau$ is P. Then, the involution $\tau$ acts on the remaining 9 vertices and thus fixes another point S, vertex of a triangle $\{S,U,V\}$. Since $\tau$ fixes S and S cannot be the center of $\tau$, S is a point of the axis QR of $\tau$, as represented in the following picture.

Since $\alpha$ acts on the line QR and $\alpha$ acts also on the triangle $\{S,U,V\}$, $\alpha$ should fix the point S, a contradiction. We have then shown that the elements in $S_3$ and $S_3^{\prime }$ are of type (A).

Let $\sigma \in S_4$ or $\sigma \in S_4^{\prime }$; the elements of $S_4$ and $S_4^{\prime }$ are of the same type as they are inverse each other. Let $\gamma \in \{0,3,q+1\}$ be such that $i(\sigma )=\gamma$. Then, by the Riemann–Hurwitz formula and Theorem 2.3,

$$\begin{aligned} q^2-q-2=216\left( 2g(\mathcal H_q/G)-2\right) +9(q+1)+24(q+1)+48 \gamma + 54 \delta , \end{aligned}$$

where $\delta =0$ if $4\mid (q+1)$, and $\delta =2$ if $4\mid (q-1)$. As $g(\mathcal H_q/G)$ is an integer, we have $(q+1)(q-26)\equiv 48\gamma \pmod {27}$. This implies $\gamma =3$ if $9\not \mid (q+1)$, and $\gamma \in \{0,q+1\}$ if $9\mid (q+1)$. We now suppose that $9\mid (q+1)$ and show that $\gamma =0$. By direct checking, H contains eight elementary abelian 3-subgroups $E_1,\ldots ,E_8$ of order 9; for any $i=1,\ldots ,8$, $L_i$ contains 2 elements of $S_2$ and 6 elements of $S_4\cup S_4^{\prime }$; for any $\tau \in S_2$, there exist exactly 2 indexes $i,j\in \{1,\ldots ,8\}$ such that $\langle \tau \rangle \subset E_i$ and $\langle \tau \rangle \subset E_j$. Assume by contradiction that $\gamma =q+1$. Hence, the elements of $E_i{\setminus }\langle \tau \rangle$ and $E_j{\setminus }\langle \tau \rangle$ are of type (A). Then, $E_i$ and $E_j$ are generated by elements of type (A), so that they fix pointwise two triangles $T_i$ and $T_j$. Thus, $\tau$ is an element of type (B1) fixing both $T_i$ and $T_j$ pointwise; this implies $T_i=T_j$. This yields the contradiction $E_i=E_j$, because the pointwise stabilizer of $T_i$ has the form $C_{q+1}\times C_{q+1}$ which has a unique elementary abelian 3-subgroup of order 9.

To sum up, the elements of $S_1$, $S_3$, and $S_3^{\prime }$ are of type (A); the elements of $S_2$, $S_6$, and $S_6^{\prime }$ are of type (B1); the elements of $S_4$ and $S_4^{\prime }$ are of type (B3) or (B1) according to $9\not \mid (q+1)$ or $9\mid (q+1)$, respectively; the elements of $S_5$ are of type (B1) or (B2) according to $4\mid (q+1)$ and $4\mid (q-1)$, respectively. By the Riemann–Hurwitz formula and Theorem 2.3,

$$\begin{aligned} g(\mathcal H_q/G)=\frac{q^2-34q+397-54\delta }{432},\qquad \text {where}\quad \delta ={\left\{ \begin{array}{ll} 0, &{} \text {if}\quad 4\mid (q+1), \\ 2, &{} \text {if}\quad 4\mid (q-1). \end{array}\right. } \end{aligned}$$

Case $G=K\cong \mathrm{PSU}(3,2)$. The group G contains nine elements of order 2, 54 elements of order 4, and eight elements of order 3 contained in $S_2$. By the Riemann–Hurwitz formula,

$$\begin{aligned} q^2-q-2=72\left( 2g(\mathcal H_q/G)-2\right) +9(q+1)+54\delta +8\cdot 0, \end{aligned}$$

and hence

$$\begin{aligned} g(\mathcal H_q/G)=\frac{q^2-10q+133-54\delta }{144}. \end{aligned}$$

Case $G=L_1\cong \mathrm{SmallGroup}(36,9)$. The group G contains nine elements of order 2, 18 elements of order 4, and eight elements of order 3 contained in $S_2$. By the Riemann–Hurwitz formula,

$$\begin{aligned} g(\mathcal H_q/G)=\frac{q^2-10q+61-18\delta }{72}. \end{aligned}$$

Finally, we note that $L_1$ does not fix any point or triangle, and hence, the same holds for K and H which contain $L_1$. In fact, the group $L_1$ cannot fix any point $P\in \mathcal H_q$, since $L_1$ contains elements of type (B1). The group $L_1$ cannot fix any point $P\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$, since $L_1$ contains an elementary abelian 3-subgroup $C_3\times C_3$ whose non-trivial elements are of type (B1); so that if $\sigma _1,\sigma _2\in (C_3\times C_3){\setminus }\{id\}$ and $\sigma _2\notin \langle \sigma _1\rangle$, then $\sigma _2$ acts without fixed points on the three points fixed by $\sigma _1$. The group $L_1$ cannot fix any triangle $T\subset \mathcal H_q({\mathbb {F}}_{q^6})$, since the stabilizer of T in $\mathrm{PGU}(3,q)$ has odd order $3(q^2-q+1)$ unlike $L_1$. The group $L_1$ cannot fix any triangle $T\subset \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$, since the elements of order 4 should fix a vertex of T and interchange the other two vertexes of T; so that their squares, that is the nine involutions of $L_1$, should fix T pointwise, a contradiction to the fact that there are exactly three involutions in $\mathrm{PGU}(3,q)$ fixing T pointwise. $\square$

4.2 G is a subgroup of $\mathrm{PGL}(2,q)$ preserving a conic

Recall that $\mathrm{PGU}(3,q)$ contains a subgroup $H\cong \mathrm{PGL}(2,q)$ preserving a conic $\mathcal C$, namely a Baer conic, i.e., the restriction of an irreducible conic to a Baer subplane of $\mathrm{{PG}}(2,q^2)$; see [5] for a description of $\mathcal C$ and H.

Proposition 4.3

Let $q=p^n$ be a power of an odd prime p, and $H\cong \mathrm{PGL}(2,q)$ be a subgroup of $\mathrm{PGU}(3,q)$ preserving an irreducible conic $\mathcal C$. If G is a subgroup of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$, then the genus of $\mathcal H_q/G$ is one of the following:

$$\begin{aligned} \frac{q^2-16q+103-24\gamma -20\delta }{120}, \end{aligned}$$

(4)

when $p=5$ or $5\mid (q^2-1)$, with $G\cong \mathrm{A}_5$ and

$$\begin{aligned} \delta ={\left\{ \begin{array}{ll} 2, \ if \ either \ p=3 \ or \ 3 \mid (q-1), \\ 0, \ if \ 3 \mid (q+1),\end{array}\right. } \quad and \quad \gamma ={\left\{ \begin{array}{ll} 0, \ if \ 5 \mid (q+1), \\ 2, \ if \ p=5 \ or \ 5 \mid (q-1); \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \frac{q^2-q-2-\Delta }{{\bar{q}} ({\bar{q}} +1)({\bar{q}} -1)}+1, \end{aligned}$$

(5)

where $q=\bar{q}^h$, ${\bar{q}}\ne 3$, $G\cong \mathrm{PSL}(2,{\bar{q}})$, and

• $\Delta =+\,2({\bar{q}} -1)( {\bar{q}}+1) +2 \frac{{\bar{q}}({\bar{q}}+1)}{2} \bigg ( \frac{{\bar{q}}-1}{2}-2\bigg )+\frac{{\bar{q}} ( {\bar{q}}+1)}{2}(q+1)+ \delta \frac{{\bar{q}}({\bar{q}}-1)}{2} \bigg ( \frac{{\bar{q}}+1}{2}-1\bigg ),$ if ${\bar{q}} \equiv 1 \pmod 4$,

• $\Delta =+\, 2({\bar{q}} -1)( {\bar{q}}+1) + 2\frac{{\bar{q}}({\bar{q}}+1)}{2} \bigg ( \frac{{\bar{q}}-1}{2}-1\bigg )+\frac{{\bar{q}} ( {\bar{q}}-1)}{2}(q+1)+\delta \frac{{\bar{q}}({\bar{q}}-1)}{2} \bigg ( \frac{{\bar{q}}+1}{2}-2\bigg )$, if ${\bar{q}} \equiv 3 \pmod 4$,

  $$\begin{aligned} \mathrm{with} \ \delta ={\left\{ \begin{array}{ll} 2, \ if \ h \ is \ even, \\ 0, \ otherwise ;\end{array}\right. } \end{aligned}$$

$$\begin{aligned} \frac{q^2-q-2-\Delta }{2{\bar{q}} ({\bar{q}} +1)({\bar{q}} -1)}+1, \end{aligned}$$

(6)

where $q=\bar{q}^h$, ${\bar{q}}\ne 3$, $G\cong \mathrm{PGL}(2,{\bar{q}})$, and

$$\begin{aligned} \Delta= & {} 2({\bar{q}}-1)({\bar{q}}+1)+\frac{{\bar{q}} ( {\bar{q}}+1)}{2}(q+1)+\frac{{\bar{q}} ( {\bar{q}}-1)}{2}(q+1)\\&\quad +\,2\frac{{\bar{q}} ( {\bar{q}}+1)}{2}({\bar{q}}-1-2)+\delta \frac{{\bar{q}} ( {\bar{q}}-1)}{2}({\bar{q}}+1-2) \end{aligned}$$

and

$$\begin{aligned} \delta ={\left\{ \begin{array}{ll} 2, \ if \ h \ is \ even, \\ 0, \ otherwise .\end{array}\right. } \end{aligned}$$

Conversely, if ${\bar{g}}$ is one of the integers in Eqs. (4)–(6), then there exists a subgroup G of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$ and $g(\mathcal H_q/G)={\bar{g}}$.

Proof

If G has no fixed points or triangles, then the following holds: G has no cyclic normal subgroups, by Remark 4.1; G has no elementary abelian normal 2-subgroups of order 4; G has no normal p-subgroups. Then, by [22, Hauptsatz 8.27], $G=K_1\cong \mathrm{A}_5$ with $p=5$ or $5\mid (q^2-1)$, or $G=K_2\cong \mathrm{PSL}(2,{\bar{q}})$, or $G=K_3\cong \mathrm{PGL}(2,{\bar{q}})$, with $q=\bar{q}^h$.

Elements $\alpha$ of order p in H are of type (D). In fact, suppose by contradiction that $\alpha$ is an elation. Then, $\alpha$ fixes a point $P \in \mathcal H_q \cap \mathcal C$, where $\mathcal C$ is the fixed conic, and its tangent line pointwise; also, it acts with long orbits on the remaining q points belonging to each other line containing P. Since every of these lines intersects the conic $\mathcal C$ in either 1 or 2 points, and this intersection is preserved by $\sigma$, each line must be tangent to $\mathcal C$ at P, a contradiction.

Elements $\alpha$ of order dividing $q+1$ and different from 2 are of type (B1). In fact, H contains a dihedral group $D=\langle \alpha \rangle \rtimes C_2$ and hence, $\langle \alpha \rangle$ is normalized by an involution. If $\alpha$ is a homology, then $\alpha$ and the involution commute, a contradiction. Also, no elements of type (B3) are normalized by an involution.

Suppose that $G=K_1$. By the Riemann–Hurwitz formula and Theorem 2.3, the genus of $\mathcal H_q/G$ is given by Eq. (4). Suppose that $G=K_2$ or $G=K_3$. The order statistics of G follow from the analysis of $\mathrm{PSL}(2,{\bar{q}})$ and $\mathrm{PGL}(2,{\bar{q}})$ in [22, Chapter II.8]. Together with the Riemann–Hurwitz formula and Theorem 2.3, Eqs. (5) and (6) provide the genus of $\mathcal H_q/K_2$ and $\mathcal H_q/K_3$, respectively.

Finally, we show that $K_1$, $K_2$, and $K_3$ do not fix any point or triangle. The group $K_1$ contains 15 involutions which form five elementary abelian 2-groups $E_1,\ldots ,E_5$ of order 4, that intersect pairwise trivially. Hence, the triangles fixed pointwise by $E_i$ and $E_j$ are disjoint for $i\ne j$. This implies that $K_1$ cannot fix any point $P\in \mathcal H_q$ nor any self-polar triangle $T\subset \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$; also, $K_1$ cannot fix any triangle $T\subset \mathcal H_q({\mathbb {F}}_{q^6})$ as $K_1$ has even order. The groups $K_2$ and $K_3$ contain p-elements. The groups $K_2$ and $K_3$ cannot fix a point $P\in \mathcal H_q({\mathbb {F}}_{q^2})$, since $K_2$ and $K_3$ contain elementary abelian 2-subgroups of order 4. The groups $K_2$ and $K_3$ cannot fix a point $P\in \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q({\mathbb {F}}_{q^2})$ as they contain p-elements of type (D). The groups $K_2$ and $K_3$ cannot fix a triangle $T\subset \mathcal H_q({\mathbb {F}}_{q^6})$ as they have even order. The groups $K_2$ and $K_3$ cannot fix a triangle $T\subset \mathrm{{PG}}(2,q^2){\setminus }\mathcal H_q$. Otherwise, they contain an abelian subgroup of index dividing 6, namely the pointwise stabilizer of T; since an abelian subgroup has order at most $q+1$, this yields ${\bar{q}}=3$. $\square$

4.3 G is a subgroup of $\mathrm{PSL}(2,7)$ with $p=7$ or $\sqrt{-7}\notin {\mathbb {F}}_q$

Proposition 4.4

Let $q=p^n$ be a power of an odd prime p, where either $p=7$ or $\sqrt{-7}\notin {\mathbb {F}}_q$, and $H \le \mathrm{PGU}(3,q)$ be isomorphic to $\mathrm{PSL}(2,7)$. Then, the genus of the quotient curve $\mathcal H_q/H$ is

$$\begin{aligned} \frac{q^2-22q+313-56\alpha -48\beta -42\gamma }{336}, \end{aligned}$$

where

$$\begin{aligned} \alpha= & {} {\left\{ \begin{array}{ll} 0, \ if \ 3 \mid (q+1), \\ 2, \ otherwise; \end{array}\right. }\\ \beta= & {} {\left\{ \begin{array}{ll} 0, \ if \ 7 \mid (q+1), \\ 3, \ if \ 7 \mid (q^2-q+1), \\ 2, \ otherwise; \end{array}\right. }\\ \ and \ \gamma= & {} {\left\{ \begin{array}{ll} 0, \ if \ 4 \mid (q+1), \\ 2, \ otherwise. \end{array}\right. } \end{aligned}$$

Also, every proper subgroup of H fixes a point or a triangle.

Proof

The group H contains 21 elements of order 2, 56 elements of order 3, 48 elements of order 7, and 42 elements of order 4.

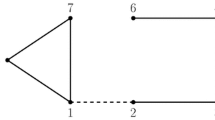
Case $p=7$. We prove that elements of order 7 are of type (D); note that all elements $\sigma \in H$ of order 7 are of the same type, as they form a unique conjugacy class in H. Assume by contradiction that $\sigma$ is of type (C). Since $\sigma$ does not commute with any involution, $\sigma$ acts with long orbits on the 21 centers $P_1,\ldots ,P_{21}$. Hence, $P_1,\ldots ,P_{21}$ are on three lines $\ell _1,\ell _2,\ell _3$ containing the center P of $\sigma$, as represented in the following picture.

Consider an elementary abelian 2-subgroup E of order 4 in H, which fixes pointwise a self-polar triangle $T=\{P_1,P_2,P_3\}$ with $P_i \in \ell _1 \cup \ell _2 \cup \ell _3$. Thus, one of the following cases occurs, up to relabeling:

• (1) $P_1,P_2\in \ell _3$ and $P_3 \in \ell _2$, or

• (2) $P_i \in \ell _i$ for $i=1,2,3$.

Suppose that Case (2) occurs. Then, there exists k such that $\sigma ^k(P_1)=P_2$. This implies that $\sigma ^k(T)=T$ and hence, $\sigma ^k$ normalizes E, a contradiction to $7\not \mid |N_{\mathrm{PGU} (3,q)}(E)|$. Hence, Case (1) occurs. Since H contains 14 elementary abelian 2-subgroups of order 4 and just 21 involutions, there exists a self-polar triangle $T^\prime =\{P^\prime _1,P^\prime _2,P^\prime _3\}\ne T$ fixed by an elementary abelian 2-subgroup $E^{\prime }\ne E$ such that $|E\cap E^{\prime }|=2$. Hence, two vertices of T and $T^\prime$ coincide, say $P_1=P_1^\prime$ and $P_2=P_2^\prime$, while $P_3 \ne P_3^\prime$ as $E\ne E^{\prime }$. This is a contradiction, because $P_3$ is uniquely determined by its polar line $P_2 P_3$. This shows that the elements of order 7 in H are not elations and hence are of type (D). The claim follows by the Riemann–Hurwitz formula and Theorem 2.3.

Case $p \ne 7$ and $\sqrt{-7}\notin {\mathbb {F}}_q$. The condition $\sqrt{-7}\notin {\mathbb {F}}_{q}$ implies that $p \equiv 2,5,6 \pmod 7$ and n is odd. Note that H contains dihedral groups of order 6 and 8, proving that if $3 \mid (q+1)$ (resp. $4 \mid (q+1)$), then an element of order 3 (resp. of order 4) is of type (B1). The claim follows by the Riemann–Hurwitz formula and Theorem 2.3.

If K is a proper subgroup of H, then either K contains a cyclic normal subgroup of order 3 or 7, and hence, K fixes a point or a triangle by Remark 4.1; or K contains a elementary abelian normal 2-subgroup of order 4, and hence, K fixes a self-polar triangle. $\square$

Remark 4.5

All the congruences of p modulo 4 and 3 listed in Proposition 4.4 can occur. Table 1 provides a list of examples.

Table 1 Possible values for q in Proposition 4.4

4.4 G is a subgroup of $\mathrm{SmallGroup}(720,765)$, when q is an odd power of 5

Proposition 4.6

Let q be an odd power of 5 and H be a subgroup of $\mathrm{PGU}(3,q)$, $H \cong \mathrm{SmallGroup(720,765)}$. If G is a subgroup of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$, then the genus of $\mathcal H_q/G$ is one of the following:

$$\begin{aligned}&\frac{q^2-10q+25}{72},\quad \frac{q^2-16q+55}{120}, \quad \frac{q^2-10q+25}{144},\nonumber \\&\quad \frac{q^2-46q+205}{720}, \quad \frac{q^2-46q+205}{1440}. \end{aligned}$$

(7)

where $G\cong \mathrm{SmallGroup}(36,9)$, $G\cong \mathrm{A}_5$, $G\cong \mathrm{PSU}(3,2)$, and $G\cong \mathrm{A}_6$, $G=H$, respectively. Conversely, if ${\bar{g}}$ is one of the integers in Eq. (7), then there exists a subgroup G of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$ and $g(\mathcal H_q/G)={\bar{g}}$.

Proof

By direct checking, either $G\cong \mathrm{SmallGroup}(36,9)$, $G\cong \mathrm{A}_5$, $G\cong \mathrm{PSU}(3,2)$, $G\cong \mathrm{A}_6$, $G=H$; or G contains a normal subgroup which is cyclic or elementary abelian of order 4, and hence, G fixes a point or a triangle. If $G\cong \mathrm{SmallGroup}(36,9)$ or $G\cong \mathrm{PSU}(3,2)$, or $G\cong \mathrm{A}_5$, then G has no fixed points or triangles and the genus of $\mathcal H_q/G$ is computed in Propositions 4.2 or 4.3, respectively.

Elements $\sigma$ of order 3 are of type (B1); in fact, H contains dihedral subgroups of order 6 containing $\sigma$, implying that $\sigma$ cannot be neither of type (B3) nor of type (A). Elements of order 5 are of type (D), because they are contained in dihedral groups of order 10. The genus of $\mathcal H_q/G$ for $G\cong \mathrm{A}_6$ and $G=H$ can be computed by the Riemann–Hurwitz formula and Theorem 2.3.

Finally, we note that if $G=H$ or $G\cong \mathrm{A}_6$, then G does not fix any point or triangle, because G contains a subgroup isomorphic to $\mathrm{A}_5$ which fixes no points or triangles. $\square$

4.5 G is a subgroup of $\mathrm{A}_6$, when q is an even power of $p=3$, or 5 is a square in ${\mathbb {F}}_q$, but ${\mathbb {F}}_q$ contains no primitive cube roots of unity

Proposition 4.7

Let $q=p^n$ be a power of an odd prime p, where either $p=3$ and n is even, or $\sqrt{5}\in {\mathbb {F}}_q$ and ${\mathbb {F}}_q$ contains no primitive cube roots of unity. Let H be a maximal subgroup of $\mathrm{PSU}(3,q)$ isomorphic to the alternating group $\mathrm{A}_6$. If G is a subgroup of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$, then the genus of $\mathcal H_q/G$ is one of the following:

$$\begin{aligned}&\frac{q^2-46q+673-80\alpha -90\beta -144\gamma }{720},\quad \frac{q^2-16q+103-20\alpha -24\gamma }{120}, \end{aligned}$$

(8)

$$\begin{aligned}&\frac{q^2-10q+61-18\beta }{72}, \end{aligned}$$

(9)

where

$$\begin{aligned} \alpha= & {} {\left\{ \begin{array}{ll} 2, \ if \ p=3, \\ 0, \ otherwise; \end{array}\right. } \\ \beta= & {} {\left\{ \begin{array}{ll} 2, \ if \ p=3 \ or \ q \equiv 1 \pmod 4, \\ 0, \ otherwise; \end{array}\right. } \\ \gamma= & {} {\left\{ \begin{array}{ll} 0, \ if \ 5 \mid (q+1), \\ 2, \ otherwise,\end{array}\right. } \end{aligned}$$

and $G\cong \mathrm{A}_6$, $G\cong \mathrm{A}_5$, and $G\cong \mathrm{SmallGroup}(36,9)$, respectively. Conversely, if ${\bar{g}}$ is one of the integers in Eq. (8), or $p\ne 3$ and ${\bar{g}}$ is the integer in Eq. (9), then there exists a subgroup G of H such that G has no fixed points or triangles and $g(\mathcal H_q/G)={\bar{g}}$.

Proof

If G has a normal subgroup which is either cyclic or of order 4, then G fixes a point or a triangle. Hence, we can assume that $G\cong \mathrm{A}_6$, or $G\cong \mathrm{A}_5$, or $G\cong \mathrm{SmallGroup}(36,9)$. Also, if $p=3$ and $G\cong \mathrm{SmallGroup}(36,9)$, then G fixes a point $P\in \mathcal H_q({\mathbb {F}}_{q^2})$ because G has a normal Sylow 3-subgroup.

Elements of order 3 are either of type (D) or of type (B1), according to $p=3$ or $p\ne 3$, because they are contained in dihedral subgroups of order 6. If $p=5$ or $5\mid (q+1)$, then elements of order 5 are of type (D) or (B1), respectively, because they are contained in dihedral subgroups of order 10. If $4\mid (q+1)$, then elements of order 4 are of type (B1), because they are contained in dihedral subgroups of order 8. Then, Eq. (8) follows from the Riemann–Hurwitz formula together with Theorem 2.3.

If $p\ne 3$ and $G\cong \mathrm{SmallGroup}(36,9)$, then by Proposition 4.2, G fixes no points nor triangles; if $p\ne 3$ and $G\cong \mathrm{A}_5$ or $G\cong \mathrm{A}_6$, then G fixes no points or triangles because G contains $\mathrm{SmallGroup}(36,9)$. If $p=3$ and $G\cong \mathrm{A}_5$, then G cannot fix any point or triangle, since G contains both elements of order 3 and elementary abelian 2-subgroups of order 4. If $p=3$ and $G\cong \mathrm{A}_6$, then G fixes no points nor triangles as G contains $\mathrm{A}_5$. $\square$

4.6 G is a subgroup of $\mathrm{A}_7$, when q is an odd power of $p=5$

Proposition 4.8

Let q be an odd power of 5, and let H be a subgroup of $\mathrm{PGU}(3,q)$ isomorphic to the alternating group $\mathrm{A}_7$. If G is a subgroup of H such that G has no fixed points or triangles in $\mathrm{{PG}}(2,q^6)$, then the genus of $\mathcal H_q/G$ is one of the following:

$$\begin{aligned}&\frac{q^2-106q+2665-720\beta }{5040},\quad \frac{q^2-46q+205}{720},\quad \frac{q^2-22q+229-48\beta }{336},\qquad \end{aligned}$$

(10)

$$\begin{aligned}&\frac{q^2-26q+105}{240},\quad \frac{q^2-16q+55}{120},\quad \frac{q^2-10q+25}{72}, \end{aligned}$$

(11)

where

$$\begin{aligned} \beta ={\left\{ \begin{array}{ll} 0, &{} \text {if}\quad 7\mid (q+1), \\ 3, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

and $G\cong \mathrm{A}_7$, $G\cong \mathrm{A}_6$, $G\cong \mathrm{PSL}(2,7)$, $G\cong \mathrm{A}_5\rtimes C_2$, $G\cong \mathrm{A}_5$, and $G\cong \mathrm{SmallGroup}(36,9)$, respectively. Conversely, if ${\bar{g}}$ is one of the integers in Eqs. (10) and (11), then there exists a subgroup G of H such that G has no fixed points or triangles and $g(\mathcal H_q/G)={\bar{g}}$.

Proof

By direct checking, either $G\cong \mathrm{A}_7$, $G\cong \mathrm{A}_6$, $G\cong \mathrm{PSL}(2,7)$, $G\cong \mathrm{A}_5\rtimes C_2$, $G\cong \mathrm{A}_5$, $G\cong \mathrm{SmallGroup}(36,9)$, or G a normal subgroup which is cyclic or of order 4 and hence, G fixes a point or a triangle. If $G\cong \mathrm{A}_6$ or $G\cong \mathrm{PSL}(2,7)$ or $G\cong \mathrm{A}_5$ or $G\cong \mathrm{SmallGroup}(36,9)$, then G has no fixed points or triangles and the genus of $\mathcal H_q/G$ is computed by Propositions 4.4, 4.7, and 4.2.

Elements of order 3 (resp. 5) are of type (B1) because they are contained in dihedral subgroups of order 6 (resp. 10). Elements of order 6 are of type (B1) because their squares are of type (B1). If $7\mid (q+1)$, then elements of order 7 are of type (B1), since they are contained in semidirect products of order 21 but not in cyclic subgroups of order 21. Now, Eqs. (10) and (11) follow from the Riemann–Hurwitz formula and Theorem 2.3.

If $G\cong \mathrm{A}_5 \rtimes C_2$ or $G=H$, then G has no fixed points or triangles because G contains $\mathrm{A}_5$. $\square$

4.7 G is a subgroup of $\mathrm{PGU}(3,p^m)$ with $m\mid n$ and n / m odd

Let G be a subgroup of $\mathrm{PGU}(3,p^m)$ with $m\mid n$ and n / m odd such that G does not fix any point or triangle in $\mathrm{{PG}}(2,q^6)$. By Theorem 3.1 and Proposition 3.14, either $G\cong \mathrm{SmallGroup}(36,9)$ when q is an odd power of 2; or $G\cong \mathrm{PSU}(3,p^k)$ or $G\cong \mathrm{PGU}(3,p^k)$ where $k\mid m$ and m / k is odd.

Proposition 4.9

Let $q=p^n$ be a power of a prime p, and G be a subgroup of $\mathrm{PGU}(3,q)$ such that either

• (i) q is an odd power of 2 and $G=G_1\cong \mathrm{SmallGroup}(36,9)$; or

• (ii) $G=G_2\cong \mathrm{PGU}(3,p^k)$ with $k\mid n$ and n / k odd; or

• (iii) $G=G_3\cong \mathrm{PSU}(3,p^k)$ with $3\mid (q+1)$, $k\mid n$ and n / k odd.

Then

$$\begin{aligned} g(\mathcal H_q/G_1)= & {} \frac{q^2-10q+16}{72}; \end{aligned}$$

(12)

$$\begin{aligned} g(\mathcal H_q/G_2)= & {} 1+\frac{q^2-q-2-\Delta }{2{{\bar{q}}}^3({{\bar{q}}}^3+1)({{\bar{q}}}^2-1)}, \end{aligned}$$

(13)

where

$$\begin{aligned} \Delta= & {} ({\bar{q}} -1)({\bar{q}}^3+1)\cdot (q+2) + ({\bar{q}}^3-{\bar{q}})({\bar{q}}^3+1)\cdot 2 + {\bar{q}}({{\bar{q}}}^4-{{\bar{q}}}^3+{{\bar{q}}}^2)\cdot (q+1)\\&+ \,({{\bar{q}}}^2-{{\bar{q}}}-2)\frac{({{\bar{q}}}^3+1){{\bar{q}}}^3}{2}\cdot 2 + ({{\bar{q}}}-1){{\bar{q}}}({{\bar{q}}}^3+1){{\bar{q}}}^2\cdot 1\\&\quad +\, ({{\bar{q}}}^2-{{\bar{q}}})\frac{{{\bar{q}}}^6+{{\bar{q}}}^5-{{\bar{q}}}^4-{{\bar{q}}}^3}{3}\cdot \gamma , \end{aligned}$$

with

$$\begin{aligned} \gamma = {\left\{ \begin{array}{ll} 3, &{} \text {if} \quad ({{\bar{q}}}^2-{{\bar{q}}}+1)\mid (q^2-q+1)\;\text { and }\;{{\bar{q}}}\ne 2, \\ 0, &{} \text {if} \quad ({{\bar{q}}}^2-{{\bar{q}}}+1)\mid (q+1)\;\text { and }\;{{\bar{q}}}\ne 2,\\ 3, &{} \text {if} \quad {{\bar{q}}}=2\;\text {and}\;3\mid (q+1)\;\text {and}\;3\not \mid n,\\ 0, &{} \text {if} \quad {{\bar{q}}}=2\;\text {and}\;3\mid (q+1)\;\text {and}\;3\mid n;\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} g(\mathcal H_q/G_3)=\frac{3(q^2-q-2-\Delta )}{2{{\bar{q}}}^{3}({{\bar{q}}}^{2}-1) ({{\bar{q}}}^{3}+1)}+1, \end{aligned}$$

(14)

where

$$\begin{aligned} \Delta= & {} ({\bar{q}} -1)({\bar{q}}^3+1)\cdot (q+2) + ({\bar{q}}^3-{\bar{q}})({\bar{q}}^3+1)\cdot 2 \\&+\, (({\bar{q}}+1)/3-1)({{\bar{q}}}^4-{{\bar{q}}}^3+{{\bar{q}}}^2)\cdot (q+1)\\&+ \,(({\bar{q}}^2-1)/3-({\bar{q}}+1)/3)\frac{({\bar{q}}^3+1){\bar{q}}^3}{2} \cdot 2 \\&+ \,({{\bar{q}}}-1)(({{\bar{q}}}+1)/3-1)({{\bar{q}}}^3+1){{\bar{q}}}^2 \cdot 1\\&+\,(({\bar{q}}^2-{\bar{q}}+1)/3-1)\frac{{\bar{q}}^6 +{\bar{q}}^5-{\bar{q}}^4-{\bar{q}}^3}{3}\cdot \delta , \end{aligned}$$

with

$$\begin{aligned} \delta ={\left\{ \begin{array}{ll}3, \ if \ ({{\bar{q}}}^2-{{\bar{q}}}+1)/3 \mid (q^2-q+1),\\ 0, \ if \ ({{\bar{q}}}^2-{{\bar{q}}}+1)/3 \mid (q+1). \end{array}\right. } \end{aligned}$$

Proof

Suppose that $G=G_1$. Elements of order 3 are of type (B1), since they are contained in dihedral subgroups of order 6. Then, Eq. (12) follows from the Riemann–Hurwitz formula and Theorem 2.3.

Suppose that $G=G_2$. Then, the genus of $\mathcal H_q/G_2$ has been computed in [28, Proposition 5.1], and Eq. (13) follows.

Suppose that $G=G_3$. As pointed out in Lemma 3.11, we can assume up to conjugation in $\mathrm{PGU}(3,q)$ that G is the subgroup of elements $\sigma \in \mathrm{PSU}(3,q)$ such that $\sigma$ is defined over ${\mathbb {F}}_{{\bar{q}}^2}$. First, we classify the elements of $\mathrm{PSU}(3,{\bar{q}})$ seen as the automorphism group of a Hermitian curve $\mathcal H_{{\bar{q}}}$, using the order statistics of $\mathrm{PSU}(3,{\bar{q}})$.

• (1) There are exactly $({\bar{q}} -1)({{\bar{q}}}^3+1)$ elements of type (C). In fact, for each $P\in \mathcal H_{{\bar{q}}}({\mathbb {F}}_{{{\bar{q}}}^2})$, there exist exactly ${\bar{q}}-1$ elations in $\mathrm{PSU}(3,{\bar{q}})$ with center P.

• (2) There are exactly $({\bar{q}}^3-{\bar{q}})({\bar{q}}^3+1)$ elements of type (D). In fact, they are the p-elements of $\mathrm{PSU}(3,{\bar{q}})$ which are not of type (C).

• (3) There are exactly $(({\bar{q}}+1)/3-1)({\bar{q}}^4-{\bar{q}}^3+{\bar{q}}^2)$ elements of type (A). In fact, for each $P\in \mathrm{{PG}}(2,{\bar{q}}^2){\setminus }\mathcal H_{{\bar{q}}}$, there exist exactly $({\bar{q}}+1)/3-1$ homologies in $\mathrm{PSU}(3,{\bar{q}})$ with center P.

• (4) There are exactly $(({\bar{q}}^2-1)/3-({\bar{q}}+1)/3)\frac{({\bar{q}}^3+1){\bar{q}}^3}{2}$ elements of type (B2). In fact, for each pair $\{P,Q\}\subset \mathcal H_{{\bar{q}}}({\mathbb {F}}_{{\bar{q}}^2})$, there exist exactly $({\bar{q}}^2-1)/3-1$ non-trivial elements of $\mathrm{PSU}(3,{\bar{q}})$ fixing P and Q, and $({\bar{q}}+1)/3-1$ of them are homologies with axis PQ.

• (5) There are exactly $(({\bar{q}}^2-{\bar{q}}+1)/3-1)\frac{{\bar{q}}^6+{\bar{q}}^5-{\bar{q}}^4-{\bar{q}}^3}{3}$ elements of type (B3). In fact, any point $P\in \mathcal H_{{\bar{q}}^2}({\mathbb {F}}_{{\bar{q}}^6}){\setminus }\mathcal H_{{\bar{q}}}({\mathbb {F}}_{{\bar{q}}^2})$ determines a unique triangle $\{P,\Phi _{{\bar{q}}^2}(P),\Phi _{{\bar{q}}^2}^2(P)\}\subset \mathcal H_{{\bar{q}}}({\mathbb {F}}_{{\bar{q}}^6})$ fixed by a Singer subgroup of order $({\bar{q}}^2-{\bar{q}}+1)/3$; see [29].

• (6) There are exactly $({{\bar{q}}}-1)(({{\bar{q}}}+1)/3-1)({{\bar{q}}}^3+1){{\bar{q}}}^2$ elements of type (E). In fact, consider a pair $\{P,Q\}$ with $P\in \mathcal H_{{\bar{q}}}({\mathbb {F}}_{{\bar{q}}^2})$ and $Q\in \mathrm{{PG}}(2,{\bar{q}}^2)\cap \ell _P$, where $\ell _P$ is the tangent line to $\mathcal H_{{\bar{q}}}$ at P. Any element of type (E) fixing P and Q is uniquely obtained as the product of an elation of center P and a homology of center Q; thus, there exist exactly $({{\bar{q}}}-1)(({{\bar{q}}}+1)/3-1)$ such elements.

• (7) The remaining $(q^8-3q^7+8q^6-11q^5+9q^4-4q^3)/18=q^3(q-1)(q^2-q+1)(q^2-q+4)/18$ non-trivial elements are of type (B1).

Now, we describe the elements in each class (1)–(7) according to their geometry with respect to $\mathcal H_q$.

• (i) The elements in class (1) are of type (C). In fact, let $\bar{S}$ be one of the ${{\bar{q}}}^3+1$ Sylow p-subgroups of $\mathrm{PSU}(3,{{\bar{q}}})$ and S be the Sylow p-subgroup of $\mathrm{PSU}(3,q)$ containing $\bar{S}$. Note that S is a trivial intersection set, since $\mathcal H_q$ has zero p-rank; see [20, Theorem 11.133]. Consider the explicit representation of S given in [12, Section 3], where $\mathcal H_q$ has Norm–Trace equation and S fixes the point at infinity. By direct computation, there are ${{\bar{q}}}$ elements of $\bar{S}$ in the center of S. Thus, $\bar{S}$ has exactly ${{\bar{q}}}-1$ elements of type (C); see [12, Eq. (2.12)].

• (ii) The elements in class (2) are of type (D). In fact, with $\bar{S}$ as in Case (i), the claim follows from Case

  (i) counting the remaining non-trivial elements of $\bar{S}$.

• (iii) Let $\sigma \in \mathrm{PGU}(3,{{\bar{q}}})$ be in class (3). Then, $\sigma$ is contained in the pointwise stabilizer D of a self-polar triangle with respect to $\mathcal H_{{\bar{q}}}$ and D is an abelian group of order $({\bar{q}}+1)^2/3$; see [27]. Let $C_{q+1}\times C_{q+1}\le \mathrm{PGU}(3,q)$ be the pointwise stabilizer of a self-polar triangle ${\mathcal {T}}$ with respect to $\mathcal H_q$, such that $D\le (C_{q+1}\times C_{q+1})\cap \mathrm{PSU}(3,q)$ which is an abelian group of order $(q+1)^2/3$.

  Up to conjugation, $\mathcal H_q$ has Fermat equation and ${\mathcal {T}}$ is the fundamental triangle, so that

  $$\begin{aligned} D=\{(X,Y,Z)\mapsto (\lambda X,\mu Y,Z)\mid \lambda ^{{{\bar{q}}}+1},\mu ^{{{\bar{q}}}+1}=1\} \cap \mathrm{PSU}(3,q). \end{aligned}$$

  By direct computation, D contains $3(({{\bar{q}}}+1)/3-1)$ elements of type (A) and $({{\bar{q}}}^2-{{\bar{q}}}+4)/3$ elements of type (B1).

  Since $\mathrm{PSU}(3,{{\bar{q}}})$ is transitive on $\mathrm{{PG}}(2,{{\bar{q}}}^2){\setminus }\mathcal H_{q}$, there are exactly $\frac{| \mathrm{PSU} (3,{{\bar{q}}}) |}{6|D|}$ self-polar triangles ${\mathcal {T}}^\prime$ with respect to $\mathcal H_q$, whose pointwise stabilizer $D^\prime$ is conjugated to D under $\mathrm{PSU}(3,{{\bar{q}}})$.

  Note that D and $D^\prime$ intersect non-trivially if and only if ${\mathcal {T}}$ and ${\mathcal {T}}^\prime$ have a vertex P in common; in this case, $(D\cap D^\prime ){\setminus }\{id\}$ is made by $({{\bar{q}}}+1)/3-1$ homologies with center P. The number of points in $\mathrm{{PG}}(2,{{\bar{q}}}^2){\setminus }\mathcal H_{q}$ lying on the polar of P is ${{\bar{q}}}^2-{{\bar{q}}}$; hence, the number of $D^\prime$ which intersect D non-trivially is $(({{\bar{q}}}+1)/3-1)({{\bar{q}}}-1)/2$.

  Therefore, by direct computation, the number of elements of type (A) in $\mathrm{PSU}(3,{{\bar{q}}})$ is exactly the number $(({{\bar{q}}}+1)/3-1)({{\bar{q}}}^4-{{\bar{q}}}^3+{{\bar{q}}}^2)$ of elements in class (3), and the remaining $(q^8-3q^7+8q^6-11q^5+9q^4-4q^3)/18$ elements of the subgroups of $\mathrm{PSU}(3,{{\bar{q}}})$ conjugated to D are of type (B1) and in class (7).

• (iv) Let $\sigma \in \mathrm{PSU}(3,{{\bar{q}}})$ be in class (4). Since the order $o(\sigma )$ of $\sigma$ divides ${{\bar{q}}}^2-1$ but not ${{\bar{q}}}+1$, we have that $o(\sigma )$ divides $q^2-1$ but not $q+1$, as q is an odd power of ${{\bar{q}}}$. Therefore, $\sigma$ is of type (B2).

• (v) Let $\sigma \in \mathrm{PSU}(3,{{\bar{q}}})$ be in class (6). Since the order of $\sigma$ is $p\cdot d$ where $d>1$ and $p\not \mid d$, $\sigma$ is of type (E).

• (vi) Let $\sigma \in \mathrm{PSU}(3,{{\bar{q}}})$ be in class (5). By direct checking, the order $o(\sigma )$ of $\sigma$ divides either $q^2-q+1$ or $q+1$. Note that $({{\bar{q}}}^2-{{\bar{q}}}+1)/3$ is not divisible by 3. If $({{\bar{q}}}^2-{{\bar{q}}}+1) \mid (q^2-q+1)$, then every $\sigma$ in class (5) is of type (B3), by [29].

  If $({{\bar{q}}}^2-{{\bar{q}}}+1) \mid (q+1)$, then $\sigma$ is either of type (A) or (B1). We note that $\sigma$ is contained in the maximal subgroup (iv) of $\mathrm{PSU}(3,{{\bar{q}}})$ in [27], which is a semidirect product $C_{({{\bar{q}}}^2-{{\bar{q}}}+1)/3} \rtimes C_3$, where $\sigma \in C_{({{\bar{q}}}^2-{{\bar{q}}}+1)/3}$ and $C_3$ does not commute with any subgroup of $C_{({{\bar{q}}}^2-{{\bar{q}}}+1)/3}$. Therefore, $\sigma$ cannot be of type (A), because otherwise every element which normalizes $\sigma$ should commute with $\sigma$. Then, $\sigma$ is of type (B1).

Now, Eq. (14) follows from the Riemann–Hurwitz formula and Theorem 2.3. $\square$

4.8 New genera of ${\mathbb {F}}_{q^2}$-maximal curves

The results of Sect. 4 provide new genera of maximal curves over finite fields, with respect to the genera obtained in [1,2,3, 7,8,9,10, 12, 15,16,18, 26, 28, 30]. Table 2 collects some examples.

Table 2 New genera for maximal curves