Combinatorial invariance of Kazhdan–Lusztig–Vogan polynomials for fixed point free involutions

Abstract

When $\mathrm {Sp}(2n,\mathbb {C})$ acts on the flag variety of $\mathrm {SL}(2n,\mathbb {C})$, the orbits are in bijection with fixed point free involutions in the symmetric group $S_{2n}$. In this case, the associated Kazhdan–Lusztig–Vogan polynomials $P_{v,u}$ can be indexed by pairs of fixed point free involutions $v\ge u$, where $\ge$ denotes the Bruhat order on $S_{2n}$. We prove that these polynomials are combinatorial invariants in the sense that if $f:[u,w_0]\rightarrow [u',w_0]$ is a poset isomorphism of upper intervals in the Bruhat order on fixed point free involutions, then $P_{v,u} = P_{f(v),u'}$ for all $v\ge u$.

1 Introduction

Let (W, S) be a Coxeter system with W ordered by the Bruhat order. Every interval [u, v] in this poset comes with an associated Kazhdan–Lusztig (KL) polynomial $\mathcal {P}_{u,v}$, introduced in [13]. When W is a Weyl group, the polynomials carry detailed information about the singularities of the Schubert varieties indexed by W [14]. Evaluated at 1, they provide composition factor multiplicities of Verma modules; this is one of the original Kazhdan–Lusztig conjectures from [13] which was independently proven by Beilinson and Bernstein [1] and by Brylinski and Kashiwara [5].

The KL polynomial $\mathcal {P}_{u,v}$ can be computed merely in terms of the structure of the lower interval [e, v], where $e\in W$ is the identity element, which is the minimum in the Bruhat order. The procedure relies on detailed knowledge about the elements of [e, v]. It has, however, been conjectured independently by Dyer [8] and Lusztig that the KL polynomial is an invariant of the poset isomorphism class of [u, v]. This is known as the combinatorial invariance conjecture. Most substantial progress towards this conjecture has had to do with lower intervals and is captured in the following statement:

Theorem 1.1

Let $v,v'\in W$ and suppose $f:[e,v]\rightarrow [e,v']$ is a poset isomorphism. Then, $\mathcal {P}_{u,v} = \mathcal {P}_{f(u),v'}$ for all $u\le v$.

For W of general type, this result is due to Brenti et al. [4] and independently to Delanoy [6]. The methods build on earlier work by Brenti [3] and du Cloux [7], where the result was established in certain types.

The more general family of Kazhdan–Lusztig–Vogan (KLV) polynomials was introduced in [15, 18]. Let G be a complex connected reductive algebraic group with non-compact real form $G_\mathbb {R}$. Let $\theta :G\rightarrow G$ be the complexification of a Cartan involution of $G_\mathbb {R}$. The fixed point subgroup $K=G^\theta$ acts on the flag variety G / B with finitely many orbits [16], B being a $\theta$-stable Borel subgroup. Each of the indices u and v of a KLV polynomial $P_{u,v}$ consists of a K-orbit closure together with a choice of local system on it. These polynomials describe the singularities of K-orbit closures and, evaluated at 1, provide character coefficients for $G_\mathbb {R}$-representations [15, 18].

In this paper, we confine ourselves to the setting $G=\mathrm {SL}(2n,\mathbb {C})$, $G_\mathbb {R}= \mathrm {SU}^*(2n)$, $K=\mathrm {Sp}(2n,\mathbb {C})$. The following combinatorially appealing situation then arises: we may think of the indices u and v simply as fixed point free involutions in the symmetric group $S_{2n}$ of permutations of $\{1,\ldots ,2n\}$. Moreover, $P_{u,v}$ is nonzero if and only if $u\ge v$ in the Bruhat order on $S_{2n}$. Denote by $\mathrm {Br}(F_{2n})$ its subposet induced by the fixed point free involutions. The maximum of $\mathrm {Br}(F_{2n})$ is the reverse permutation $w_0$, the longest element in $S_{2n}$. Our main result is the following combinatorial invariance assertion for KLV polynomials:

Theorem 1.2

If $f: [u,w_0] \rightarrow [u',w_0]$ is a poset isomorphism of upper intervals in $\mathrm {Br}(F_{2n})$, then $P_{v,u}= P_{f(v),u'}$ for all fixed point free involutions $v\ge u$.

The fixed point free involutions $u\in S_{2n}$ which satisfy $u(i)>n$ for all $i\le n$ form a subposet of $\mathrm {Br}(F_{2n})$ which is isomorphic to the dual of the Bruhat order on $S_n$. When restricted to such u, Theorem 1.2 specializes to the type A version of Theorem 1.1, which is the main result of Brenti’s aforementioned work [3].

In order to briefly outline the proof idea, let us first describe Brenti’s approach from [3]. First, Brenti observed that combinatorial invariance of KL polynomials is equivalent to that of the associated KL R-polynomials. At the heart of the recurrence relation for the R-polynomials is the map $x\mapsto xs$ for $x\in W$, $s\in S$. Brenti’s key idea was to replace such maps by special matchings, which are defined solely in terms of poset properties. By studying the possible special matchings of lower Bruhat intervals, Brenti was able to deduce the key fact, namely that the resulting poset theoretic recurrence actually is well-defined and computes the R-polynomials.

Our overall approach is very similar to that of Brenti. Instead of KL R-polynomials, we study what we call Q-polynomials, which are a slight variation of Vogan’s KLV R-polynomials. In our setting, Vogan’s recurrence for the latter boils down to a recurrence for Q-polynomials which relies on the conjugation map $x\mapsto sxs$ of fixed point free involutions x. In order to obtain a poset theoretic recurrence, we replace such conjugation maps by special partial matchings which are similar to special matchings, except that they may have fixed elements. Again, the crux is to show that this indeed yields a recurrence which computes Q-polynomials. Rather than fixed point free involutions, we mostly work with the set of twisted identities $\iota \subset S_{2n}$; multiplication by $w_0$ provides a bijection between the two which reverses the Bruhat order. This viewpoint gives us convenient access to combinatorial tools already developed for twisted identities.

The remainder of the paper is structured as follows. In the next section, we agree on notation and recall important definitions and tools. Section 3 contains some observations about twisted identities. Special partial matchings are introduced in Sect. 4, where technical assertions about the structure of such partial matchings are collected. In the final section we use them in order to prove our main result.

2 Preliminaries

Let n be a positive integer and denote by $W = S_{2n}$ the symmetric group of permutations of the set $[2n] = \{1,\ldots ,2n\}$. Then, W is a Coxeter group with set of Coxeter generators $S=\{s_1,\ldots ,s_{2n-1}\}$, where the $s_i = (i\,\,\,i+1)$ are the adjacent transpositions. If $w= s_{i_1}\cdots s_{i_k}$, the word $s_{i_1}\cdots s_{i_k}$ is an expression for w which is reduced if k is minimal; then $k = \ell (w)$ is the number of inversions of w, i.e. the number of pairs $1\le i < j \le 2n$ such that $w(i)>w(j)$.

A generator $s\in S$ is called a (right) descent of $w\in W$ if $\ell (ws)<\ell (w)$. The set of descents of w is denoted by $D_{\mathrm {R}}(w)$. Clearly, $s_i\in D_{\mathrm {R}}(w)$ if and only if $w(i)>w(i+1)$.

2.1 Twisted involutions and twisted identities

Define an involutive automorphism $\theta : W\rightarrow W$ by $\theta (s_i)=s_{2n-i}$. This is the only nontrivial (if $n>1$) automorphism of W which preserves S.

Let $\mathcal {I}= \mathcal {I}(\theta ) = \{w\in W\ \mid \theta (w)=w^{-1}\}$ be the set of twisted involutions and $\iota = \iota (\theta )=\{\theta (w^{-1})w\ \mid w\in W \}\subset \mathcal {I}$ the subset of twisted identities. In other words, $\iota$ is the orbit of the identity element e when W acts (from the right, say) on itself by twisted conjugation. Let $*$ denote this action; i.e. $x*w = \theta (w^{-1})xw$ for $x,w\in W$.

Next we recall some properties of $\mathcal {I}$ and $\iota$. All unjustified claims can be gleaned from [17] or [10]. Our notation follows the latter reference. Define a set of symbols $\underline{S}=\{\underline{s}_i \mid i \in [2n-1]\}$. There is an action of the free monoid $\underline{S}^*$ on the set W defined by

$$\begin{aligned} w\underline{s}= {\left\{ \begin{array}{ll} w s &{}\quad \text { if } w *s =w, \\ w *s &{}\quad \text { otherwise.} \end{array}\right. } \end{aligned}$$

It is convenient to use the notational conventions $w\underline{s}_{i_1}\cdots \underline{s}_{i_k}=(\cdots ((w\underline{s}_{i_1})\underline{s}_{i_2})\cdots )\underline{s}_{i_k}$ and $\underline{s}_{i_1}\cdots \underline{s}_{i_k} = e\underline{s}_{i_1}\cdots \underline{s}_{i_k}$, where e is the identity permutation. For instance when $n=2$, $\underline{s}_1=s_3s_1$, $\underline{s}_2=s_2$, and $\underline{s}_1\underline{s}_2=s_2s_3s_1s_2$, etc.

The orbit of e under this action is $\mathcal {I}$. Thus, if $w\in \mathcal {I}$, we have $w = \underline{s}_{i_1}\cdots \underline{s}_{i_k}$ for some $i_j$. We refer to the word $\underline{s}_{i_1}\cdots \underline{s}_{i_k}$ as an $\underline{S}$-expression for w and say it is reduced if k is minimally chosen among all such expressions; in that case $\rho (w) = k$ is called the rank of w. Here are some key properties of $\ell$ and $\rho$:

Lemma 2.1

Suppose $w\in \mathcal {I}$, $s\in S$. Then,

• $\ell (w*s) = \ell (w) \Leftrightarrow w*s = w$,

• $\rho (w\underline{s})=\rho (w)\pm 1$,

• $\rho (w\underline{s}) = \rho (w)-1 \Leftrightarrow s\in D_{\mathrm {R}}(w)$,

• $\ell (w) \le 2\rho (w)$,

• $\ell (w) = 2\rho (w) \Leftrightarrow w\in \iota$.

A useful consequence is that $w\underline{s}\in \iota$ holds whenever $w\in \iota$, $s\in D_{\mathrm {R}}(w)$. Thus, if $w*s = w$ for $w\in \iota$, $s\in S$, then $s\not \in D_{\mathrm {R}}(w)$.

Just as with ordinary expressions, the Coxeter relations can be applied to reduced $\underline{S}$-expressions: $\cdots \underline{s}_i\underline{s}_{i+1}\underline{s}_i\cdots = \cdots \underline{s}_{i+1}\underline{s}_i\underline{s}_{i+1}\cdots$ and $\cdots \underline{s}_i \underline{s}_j\cdots = \cdots \underline{s}_j\underline{s}_i\cdots$ if $|i-j|> 2$. Unlike for ordinary expressions this is not in general the case for arbitrary $\underline{S}$-expressions. For example, with $n=2$,

$$\begin{aligned} \underline{s}_2\underline{s}_3\underline{s}_2\underline{s}_1\underline{s}_2 = \underline{s}_2\underline{s}_1\underline{s}_3 = s_1s_3s_2s_1s_3 = 4231 \end{aligned}$$

which is different from

$$\begin{aligned} \underline{s}_2\underline{s}_3\underline{s}_1\underline{s}_2\underline{s}_1 = \underline{s}_1\underline{s}_2\underline{s}_3 = s_2s_3s_1s_2s_3 = 3421. \end{aligned}$$

2.2 The Bruhat order

When applied to elements of W, $\le$ denotes the Bruhat order. We shall make use of several well-known characterisations which all can be found in [2]:

Theorem 2.2

(Subword property of W) Let $x,y\in W$, and suppose $s_{i_1}\cdots s_{i_k}$ is a reduced expression for y. Then, $x\le y$ holds if and only if $x = s_{i_{j_1}}\cdots s_{i_{j_l}}$ for some $1\le j_1<\cdots <j_l\le k$.

For $x\in W$, let $x_{i,k}$ denote the i-th element when $x(1), x(2), \ldots , x(k)$ are rearranged increasingly.

Theorem 2.3

(Tableau criterion) Given $x,y\in W$, the following conditions are equivalent:

• (i) $x \le y$.

• (ii) $x_{i,k} \le y_{i,k}$ for all $s_k \in D_{\mathrm {R}}(x)$ and $1 \le i \le k$.

• (iii) $x_{i,k} \le y_{i,k}$ for all $s_k \in S {\setminus } D_{\mathrm {R}}(y)$ and $1 \le i \le k$.

Theorem 2.4

Given $x,y\in W$, $x\le y$ holds if and only if $x[i,j] \le y[i,j]$ for all $i,j\in [2n]$, where $w[i,j] = |\{k\in \{i,\ldots ,2n\}\mid w(k)\le j\}|$.

The Bruhat order on W is a graded poset with minimum element the identity permutation e, maximum element the reverse permutation $w_0$ defined by $w_0(i)= 2n+1-i$, and rank function $\ell$. For any subset $X\subseteq W$, $\mathrm {Br}(X)$ indicates the subposet of the Bruhat order induced by X. Obviously, the previous three results may be applied in the context of any $\mathrm {Br}(X)$ just by replacing W with X. We next discuss some additional tools which are applicable when $X=\mathcal {I}$. Because W is a Weyl group, most are consequences of Richardson and Springer’s [17, Section 8], although the terminology there differs somewhat from that employed here. In our language, everything can be found in [10].

The following counterpart of Theorem 2.2 can be deduced from [17, Corollary 8.10]:

Theorem 2.5

(Subword property of $\mathcal {I}$) Let $x,y\in \mathcal {I}$, and suppose $\underline{s}_{i_1}\cdots \underline{s}_{i_k}$ is a reduced $\underline{S}$-expression for y. Then, $x\le y$ holds if and only if $x = \underline{s}_{i_{j_1}}\cdots \underline{s}_{i_{j_l}}$ for some $1\le j_1<\cdots <j_l\le k$.

Comparing Theorem 2.2 with Theorem 2.5 it should not be too surprising that $\mathrm {Br}(\mathcal {I})$ is graded with rank function $\rho$. This is in fact also true for $\mathrm {Br}(\iota )$, where $\rho = \ell /2$. Both have e as minimum element. The maximum in $\mathrm {Br}(\mathcal {I})$ is $w_0$, whereas the maximum in $\mathrm {Br}(\iota )$ is $w_0s_1s_3\cdots s_{2n-1}$.

Let $I_{2n}$ be the set of (ordinary) involutions in W. There exists a poset isomorphism between $\mathrm {Br}(I_{2n})$ and the dual of $\mathrm {Br}(\mathcal {I})$ as we will show below. Incitti [12] showed that $\mathrm {Br}(I_{2n})$ is Eulerian. In particular it and its dual $\mathrm {Br}(\mathcal {I})$ are thin, meaning that all rank two intervals consist of exactly four elements. Rank two intervals in the subthin poset $\mathrm {Br}(\iota )$ have either four or three elements.

The lifting property is a classical result on $\mathrm {Br}(W)$; see [9, Theorem 1.1]. We shall not make explicit use of it, but instead use the following completely analogous result for $\mathrm {Br}(\mathcal {I})$ which follows from [17, Proposition 8.13]:

Lemma 2.6

(Lifting property of $\mathcal {I}$) Let $u,w\in \mathcal {I}$ with $u\le w$ and suppose $s\in D_{\mathrm {R}}(w)$. Then,

• (i) $u\underline{s}\le w$.

• (ii) $s\in D_{\mathrm {R}}(u)\Rightarrow u\underline{s}\le w \underline{s}$.

• (iii) $s\notin D_{\mathrm {R}}(u)\Rightarrow u\le w \underline{s}$.

Consider the following subset of $\iota$:

$$\begin{aligned} \mathcal {S}_n= \{w\in \iota \mid \underline{s}_n \not \le w\}. \end{aligned}$$

Every element in $\mathcal {S}_n$ has a reduced $\underline{S}$-expression which consists entirely of letters in $\{\underline{s}_1,\ldots ,\underline{s}_{n-1}\}$. Given such an expression, one obtains a reduced expression for an element in $S_n$ by removing the lines under the letters: $\underline{s}_{i_1}\cdots \underline{s}_{i_k}\mapsto s_{i_1}\cdots s_{i_k}$. This map is a bijection $\varphi : \mathcal {S}_n\rightarrow S_n$. It preserves the Bruhat order, yielding $\mathrm {Br}(\mathcal {S}_n)\cong \mathrm {Br}(S_n)$. When restricted to $\mathcal {S}_n$, the main results of the present paper coincide with Brenti’s results on the symmetric group [3].

2.3 Permutation diagrams, symmetries and cover relations

The inversion map $x\mapsto x^{-1}$ is a poset automorphism of $\mathrm {Br}(W)$ and, since it preserves $\iota$, of $\mathrm {Br}(\iota )$. Left and right multiplication by the reverse permutation $w_0$ yield poset antiautomorphisms of $\mathrm {Br}(W)$. Composing them, we recover the automorphism $\theta$; i.e. $\theta (w) = w_0ww_0$. Therefore, $x\mapsto w_0x$ and $x\mapsto xw_0$ provide poset isomorphisms $\mathrm {Br}(\mathcal {I})\cong \mathrm {Br}(I_{2n})^*$, where $P^*$ denotes the dual poset of P. Under both isomorphisms, $\iota$ is sent to the conjugacy class of $w_0$, namely the set $F_{2n}\subset W$ of fixed point free involutions, so that $\mathrm {Br}(\iota )\cong \mathrm {Br}(F_{2n})^*$.

We shall sometimes represent $w\in W$ by means of its diagram, i.e. the graph of w. It has a dot in the plane with coordinates (i, j) whenever $w(i) = j$. Theorem 2.4 can then be interpreted as follows: $x\le y$ iff for every $(i,j)\in [2n]^2$, there are at least as many dots weakly southeast of (i, j) in the diagram of y as there are in the diagram of x.¹

Left multiplication by $w_0$ amounts to an upside down flip of the diagram, whereas taking inverses is reflection in the diagonal line through (1, 1) and (2n, 2n). It follows that $\mathcal {I}$ consists of the permutations whose diagrams are invariant under reflection in the line through (1, 2n) and (2n, 1), and that $\iota$ is the subset of elements without any dots on this line.

Two dots in a permutation diagram form a rise if the rightmost dot is also the uppermost; otherwise the dots form a fall.

We shall reserve the notation $u\triangleleft w$ to mean that u is covered by w in $\mathrm {Br}(\mathcal {I})$ (hence in $\mathrm {Br}(\iota )$ if $u,w\in \iota$). In [12], Incitti characterised the cover relation of $\mathrm {Br}(I_{2n})$ in terms of the diagrams of the involved involutions. By taking duals and/or restricting, we obtain for free the cover relations in $\mathrm {Br}(\mathcal {I})$, $\mathrm {Br}(\iota )$ and $\mathrm {Br}(F_{2n})$. We reproduce Incitti’s description in Fig. 1, adapted to the setting of $\mathrm {Br}(\mathcal {I})$. Observe that only two of the six kinds of covers, namely those without dots on the diagonal, occur in $\mathrm {Br}(\iota )$. In particular, every cover in $\mathrm {Br}(\iota )$ (respectively, $\mathrm {Br}(F_{2n})$) is given by twisted (respectively, ordinary) conjugation by a transposition. That is, if $u\triangleleft w$ and $u,w\in \iota$, then $u = w*t$ (respectively, $w_0u = tw_0wt$) for some transposition t.

Fig. 1

All types of covers that occur in $\mathrm {Br}(\mathcal {I})$. If w covers u, the diagram of u is indicated by white dots and w is represented by black dots. Dots shared by both diagrams are omitted. Shaded regions are empty. The pictures are reproduced from [12]

By inspecting Fig. 1, the next lemma follows immediately.

Lemma 2.7

Given $w\in \mathcal {I}{\setminus } \iota$, there exists at most one $u\in \iota$ such that $u\triangleleft w$.

Most of the action of the present paper takes place in $\mathrm {Br}(\iota )$. However, other subposets of $\mathrm {Br}(W)$ turn up frequently in our arguments. In order to mitigate possible confusion we shall employ the following poset interval notation for $u,w\in W$:

$$\begin{aligned}{}[u,w]= & {} \{x\in W\mid u\le x \le w\},\\ [u,w]_\mathcal {I}= & {} [u,w]\cap \mathcal {I},\\ [u,w]_\iota= & {} [u,w]\cap \iota .\\ \end{aligned}$$

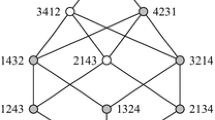
Some examples can be found in Fig. 2.

Fig. 2

Pictures of $\mathrm {Br}(\iota ) = [e,\underline{s}_1\underline{s}_2\underline{s}_1\underline{s}_3\underline{s}_4\underline{s}_2]_\iota$ (left) and $[e,\underline{s}_2\underline{s}_1\underline{s}_3\underline{s}_2]_\mathcal {I}$ (right) when $n=3$. Twisted identities correspond to black dots, whereas white dots signal elements of $\mathcal {I}{\setminus } \iota$. The labels are index sequences of reduced $\underline{S}$-expressions. For example, “232” represents the twisted involution $\underline{s}_2\underline{s}_3\underline{s}_2 = s_3s_4s_2s_3s_2$

2.4 Kazhdan–Lusztig–Vogan polynomials

Introduced in [15, 18], the Kazhdan–Lusztig–Vogan (KLV) polynomials are at the heart of the representation theory of real reductive groups much in the same way that Kazhdan–Lusztig polynomials describe representations for complex groups.

In general, a KLV polynomial $P_{\gamma , \delta }(q)$ is indexed by two local systems $\gamma$ and $\delta$ on orbits of a symmetric subgroup K on a flag manifold G / B. In the present paper we shall restrict to the setting $G = \mathrm {SL}(2n,\mathbb {C})$, $K=\mathrm {Sp}(2n,\mathbb {C})$. In this case, every local system is trivial and the orbits are indexed by $\iota$ (or, as was done in the introduction, by $F_{2n}$; hence the title of the present paper). Moreover, $\mathrm {Br}(\iota )$ coincides with the inclusion order among orbit closures; the details of this correspondence are described by Richardson and Springer [17, Example 10.4]. Thus, we may in this setting consider KLV polynomials to be indexed by pairs of twisted identities. When doing so, we shall use the superscript $\iota$ to avoid confusion with the polynomials indexed by $F_{2n}$ in the introduction. In other words, $P^\iota _{u,w} = P_{w_0u,w_0w}$ whenever $u,w\in \iota$. For fixed $w\in \iota$, we then have the following identity in the free $\mathbb {Z}[q,q^{-1}]$-module with basis $\iota$:

$$\begin{aligned} q^{-\rho (w)}\sum _{v\in [e,w]_\iota }P^\iota _{v,w}(q)v = \sum _{v\in [e,w]_\iota }\sum _{u\in [e,v]_\iota }(-1)^{\rho (u)-\rho (v)}q^{-\rho (v)}P^\iota _{v,w}(q^{-1})R_{u,v}(q)u; \end{aligned}$$

(1)

cf. Vogan’s [18, Corollary 6.12]. Here, $R_{u,v}$ denotes a KLV counterpart of the classical Kazhdan–Lusztig (KL) R-polynomials.

Introducing the convenient variation $Q_{u,w}(q) = (-q)^{\rho (w)-\rho (u)}R_{u,w}(q^{-1})$ and comparing the coefficients of a fixed element $u\in \iota$ on each side of (1) one obtains the, from the theory of KL polynomials, familiar-looking

$$\begin{aligned} q^{\rho (w)}P^\iota _{u,w}(q^{-1}) = q^{\rho (u)}\sum _{v\in [u,w]_\iota }P^\iota _{v,w}(q)Q_{u,v}(q). \end{aligned}$$

(2)

Together with the restrictions $P^\iota _{x,x} = 1$ and $\deg P^\iota _{u,w} \le (\rho (w)-\rho (u)-1)/2$, this recurrence uniquely determines the KLV polynomials. In order to use it, one must first know the Q-polynomials (which are polynomials). They are completely determined by the following recurrence and initial values; see [11, Proposition 5.3].

Proposition 2.8

Let $u,w\in \iota$. If $s\in D_{\mathrm {R}}(w)$, then

$$\begin{aligned} Q_{u,w}(q) = {\left\{ \begin{array}{ll} Q_{u*s,w*s}(q) &{} \text { if } u*s \triangleleft u, \\ qQ_{u*s,w*s}(q)+(q-1)Q_{u,w*s}(q) &{} \text { if } u*s \triangleright u, \\ qQ_{u,w*s}(q) &{} \text { if } u*s = u. \end{array}\right. } \end{aligned}$$

Moreover $Q_{u,u}(q)=1$, and $Q_{u,w}(q) = 0$ if $u\not \le w$.

When restricted to $u,w\in \mathcal {S}_n\subset \iota$, $R_{u,w}$ coincides with $Q_{u,w}$; this is then the ordinary KL R-polynomial of $S_n$ indexed by $\varphi (u)$ and $\varphi (w)$, where $\varphi$ is the bijection $\varphi : \mathcal {S}_n\rightarrow S_n$ introduced above, and the $P^\iota _{u,w}$ of course restrict to the ordinary KL polynomials, i.e. $\mathcal {P}_{\varphi (u),\varphi (w)} = P^\iota _{u,w}$.

3 Structural properties of $\iota$

In this section we obtain some information about the structure of $\iota$ which shall be of use in the sequel.

Lemma 3.1

Suppose $u,u',w,w'\in \iota$ are such that $|[u,w]_\iota | = |[u',w']_\iota | = 3$. Then, $|[u,w]_\iota \cap [u',w']_\iota |\ne 2$.

Proof

Since $\mathrm {Br}(\mathcal {I})$ is thin, the corresponding intervals $[u,w]_\mathcal {I}$ and $[u',w']_\mathcal {I}$ have four elements each. Hence, the interval $(w_0w,w_0u)$ in $\mathrm {Br}(I_{2n})$ consists of exactly two elements x and y where x is fixed point free and y has exactly two fixed points. Now consult Incitti’s [12] characterisation of the covering relation in Fig. 1. The only possibility is that $w_0w < y$ is a cover as in the lower middle picture, $y<w_0u$ is as in the upper left, $w_0w < x$ lower right and, finally, $x<w_0u$ is of the lower left form. All except four dots in two common two-cycles are left unchanged by all these cover operations. In particular, this implies that the disjoint cycle decompositions of $w_0w$, x and $w_0u$ have $n-2$ two-cycles in common. Inspecting any two of these three elements is sufficient to determine all those common two-cycles. Since exactly three fixed point free involutions have $n-2$ fixed two-cycles in common, we conclude that $|[u,w]_\iota \cap [u',w']_\iota |\ge 2$ implies $[u,w]_\iota =[u',w']_\iota$. $\square$

The preceding lemma immediately yields a simple description of the twisted identities that cover exactly one element:

Lemma 3.2

Let $w\in \iota$ and suppose $|\{x\in \iota \ |\ x\triangleleft w\}|=1$. Then, either $w=\underline{s}_{n-1}\underline{s}_n$ or $\rho (w) = 1$.

Proof

It is easy to verify the assertion for all w that satisfy $\rho (w)\le 2$ or $\underline{s}_{n-1}\underline{s}_n \triangleleft w$. Suppose w is some other element and that $x\triangleleft w$. Applying induction on the rank, we may assume x covers at least two elements. By Lemma 3.1, so does w. $\square$

We shall only need the following simple lemma for $w\in \iota$. Proving it for $w\in \mathcal {I}$ costs, however, no extra effort.

Lemma 3.3

Define $\tau =\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1}$, where $2\le i \le n-2$, and let $w\in \mathcal {I}$. Then, $\tau \nleq w$ if and only if $w([i-1])\subseteq [i+1]$.

Proof

Let $w\in W$ and notice that $\tau =s_{2n-(i-1)}s_{2n-i}s_{2n-(i+1)}s_{i+1}s_is_{i-1}.$ Thus, $D_{\mathrm {R}}(\tau )=\{s_{i-1},s_{2n-i-1}\}$. Following the notation used in Theorem 2.3, $(\tau _{1,i-1},\ldots ,\tau _{i-1,i-1})=(1,\ldots ,i-2,i+2)$ and $(\tau _{1,2n-i-1},\ldots ,\tau _{2n-i-1,2n-i-1})=(1,\ldots ,2n-i-2,2n-i+2)$. Now, $\tau \le w$ if and only if $\tau _{k,i-1}\le w_{k,i-1}$ for all $1\le k\le i-1$ and $\tau _{k,2n-i-1}\le w_{k,2n-i-1}$ for all $1\le k\le 2n-i-1$. Therefore, $\tau \le w$ if and only if $\max (w(1),\ldots , w(i-1))\ge i+2$ and $\max (w(1),\ldots , w(2n-i-1))\ge 2n-i+2$. Hence $\tau \nleq w$ if and only if $w([i-1])\subseteq [i+1]$ or $w([2n-i-1])\subseteq [2n-i+1]$. If $w\in \mathcal {I}$, diagram symmetry yields that both inclusions are equivalent, and the result follows. $\square$

Lemma 3.4

Let $a = \underline{s}_{i}\underline{s}_{i-1}\underline{s}_i$ and $b = \underline{s}_i\underline{s}_{i+1}\underline{s}_i$ for some $2\le i \le n-2$. If $c\in \iota$ covers both a and b, then $c= \underline{s}_i\underline{s}_{i-1}\underline{s}_{i+1}\underline{s}_i$.

Proof

If $\underline{s}_n\le c$, the subword property shows that c is obtained by inserting the letter $\underline{s}_n$ somewhere inside some reduced $\underline{S}$-expression for a. Since $s_n$ commutes with every generator $s_i\le a$, we may in fact assume that $\underline{s}_n$ is inserted as the first letter. This, however, contradicts $c \in \iota$. We conclude that $c\in \mathcal {S}_n$. Therefore, the assertion of the lemma is equivalent to $c' = s_is_{i-1}s_{i+1}s_i$ being the only element which covers $a' = s_is_{i-1}s_i$ and $b' = s_is_{i+1}s_i$ in the (ordinary) Bruhat order on $S_n$. To see that this holds, note that the reduced expressions that were just used for $a'$ and $b'$ are the only ones that contain only single occurrences of $s_{i-1}$ and $s_{i+1}$, respectively. Hence an element which covers both must have a reduced expression which simultaneously can be obtained by inserting $s_{i-1}$ into $s_is_{i+1}s_i$ and by inserting $s_{i+1}$ into $s_is_{i-1}s_i$. $\square$

The final result of this section shows that a twisted identity is nearly always determined by the elements that it covers.

Proposition 3.5

Suppose $v,w\in \iota$ cover the same set of elements in $\mathrm {Br}(\iota )$. Then either $v=w$ or $\rho (v)=\rho (w)\le 2$.

Proof

Assume that $v\ne w$ and that $u\triangleleft v \Leftrightarrow u\triangleleft w$ for $u\in \iota$. Choose descents $s\in D_{\mathrm {R}}(v)$ and $s'\in D_{\mathrm {R}}(w)$, if possible so that $v\underline{s}\ne w\underline{s}'$.

Suppose first that, indeed, $v\underline{s}\ne w\underline{s}'$ and let $\tau = v\underline{s}'$. By the lifting property, $w\triangleleft \tau$. Lemma 2.7 then implies $\tau \in \iota$. We claim that $\tau$ covers no element except v and w. Indeed, if $v\ne x \triangleleft \tau$, lifting yields $x\underline{s}' \triangleleft v$ and thus $x\underline{s}' \triangleleft w$. Since $w\underline{s}'$ is the only element which does not have $s'$ as a descent among those covered by w, $x\underline{s}' = w\underline{s}'$ so that $x=w$ as needed. Now, lifting shows $v\underline{s}\underline{s}' \triangleleft v\underline{s}$. Thus, $\tau$ has a reduced $\underline{S}$-expression which ends with $\underline{s}'\underline{s}\underline{s}'$. In particular, $\{s,s'\} = \{s_i,s_{i+1}\}$ for some i, and $\tau \underline{s}\underline{s}'\underline{s}= \tau \underline{s}'\underline{s}\underline{s}'$. This means that the $\{\underline{s},\underline{s}'\}^*$-orbit of $\tau$ contains exactly six elements, ordered as $\tau \underline{s}\underline{s}'\underline{s}\triangleleft v\underline{s},w\underline{s}' \triangleleft v,w \triangleleft \tau$. Assuming without loss of generality that $s = s_i$, it follows that the disjoint cycle decompositions of the corresponding fixed point free involutions are as follows:

$$\begin{aligned} \begin{aligned} w_0\tau&= (a\,\,\,i)(b\,\,\,i+1)(c\,\,\,i+2)\cdots ,\\ w_0v&= (a\,\,\,i)(b\,\,\,i+2)(c\,\,\,i+1)\cdots ,\\ w_0w&= (a\,\,\,i+1)(b\,\,\,i)(c\,\,\,i+2)\cdots ,\\ w_0(v\underline{s})&= (a\,\,\,i+1)(b\,\,\,i+2)(c\,\,\,i)\cdots ,\\ w_0(w\underline{s}')&= (a\,\,\,i+2)(b\,\,\,i)(c\,\,\,i+1)\cdots ,\\ w_0(\tau \underline{s}\underline{s}'\underline{s})&= (a\,\,\,i+2)(b\,\,\,i+1)(c\,\,\,i)\cdots ,\\ \end{aligned} \end{aligned}$$

for some $a<b<c$; here the trailing dots indicate the remaining two-cycles that all six elements have in common. Since conjugation by a transposition alters either zero or two of the two-cycles of a fixed point free involution, it follows at once from this description that (i) neither v nor w covers any element except $v\underline{s}$ and $w\underline{s}'$, and (ii) $v\underline{s}$ and $w\underline{s}'$ cover no common element except $\tau \underline{s}\underline{s}'\underline{s}$. Lemma 3.1 then implies that $v\underline{s}$ and $w\underline{s}'$ can cover no element at all (common or not) except $\tau \underline{s}\underline{s}'\underline{s}$. By Lemma 3.2, $\rho (v\underline{s}) = \rho (w\underline{s}') = 1$ as desired.

It remains to consider the case $v\underline{s}= w\underline{s}' = x$. Since this was not possible to avoid, no descent of x commutes with either s or $s'$. If $x\ne e$, this implies $D_{\mathrm {R}}(x) = \{s_i\}$ and $\{s,s'\}=\{s_{i-1},s_{i+1}\}$ for some i. If in addition $x\underline{s}_i$ has a descent, say $s_j$, it cannot commute with $s_i$. Thus, $s_j\in \{s,s'\}$, implying that either v or w has $s_i$ as a descent, a contradiction. Hence $\rho (x) \le 1$. $\square$

4 Special partial matchings

Let $\Pi$ be a finite poset equipped with a unique maximum element $\hat{1}$ and let $\prec$ denote the cover relation.

Definition 4.1

A special partial matching, or SPM, of $\Pi$ is a function $M:\Pi \rightarrow \Pi$ such that

• $M^2 = \mathrm {id}$.

• $M(\hat{1}) \prec \hat{1}$.

• For all $x\in \Pi$, either $M(x)\prec x$, $M(x) = x$ or $x\prec M(x)$.

• If $x\prec y$ and $M(x)\ne y$, then $M(x) < M(y)$.

An SPM without fixed points is nothing but a special matching in the sense of Brenti [3]. Like special matchings, SPMs restrict to principal order ideals:

Proposition 4.2

Suppose M is an SPM of $\Pi$ and that $M(x) \le x$. Then, M preserves the subposet $I_x = \{y\in \Pi \mid y\le x\}$. In particular, M restricts to an SPM of $I_x$ if $M(x) \prec x$.

Proof

We must show $M(y) \le x$ for all $y\le x$. Pick $y < x$ and assume by induction $M(y') \le x$ for all $x\ge y' > y$. Choose $x\ge z\succ y$. Then, either $M(y) = z\le x$ or $M(y) < M(z)\le x$. $\square$

Special matchings were designed to mimic multiplication by a Coxeter generator, i.e. maps of the form $x\mapsto xs$, in $\mathrm {Br}(W)$. Similarly, the idea behind SPMs is to capture the behaviour of the twisted conjugation maps $x\mapsto x*s$ in $\mathrm {Br}(\iota )$.

Theorem 4.3

Let $w\in \iota$ and $s\in D_{\mathrm {R}}(w)$. Then, $x\mapsto x*s$ is an SPM of the lower interval $[e,w]_\iota$.

Proof

The lifting property shows that $[e,w]_\iota$ is preserved by $x\mapsto x*s$. The first three properties required by Definition 4.1 are readily checked. It remains to verify the fourth.

Suppose $x\triangleleft y$ and $x*s \ne y$. We must show $x*s < y*s$. If $x*s \ne x$ and $y*s \ne y$, this is immediate from the lifting property. The nontrivial cases that remain to be considered are $x*s = x$, $y*s < y$ and $x*s > x$, $y*s = y$, respectively. The former case is, however, impossible since it would imply $x\underline{s}> x \ne y\underline{s}< y$ contradicting the lifting property. The latter is in fact also impossible; it implies that $y\underline{s}$ covers the two twisted identities $x\underline{s}$ and y which contradicts Lemma 2.7. $\square$

We shall refer to an SPM of the form described in Theorem 4.3 as a conjugation SPM.

Lemma 4.4

Let $w\in \iota$. Suppose M is an SPM of $[e,w]_\iota$ and $\rho (u)\ge 2$ for $u\in [e,w]_\iota$. Then, $M(u)=u$ if and only if all $v\in \iota$ with $v \triangleleft u$ satisfy either $M(v)\triangleleft v$ or $M(v)=v$.

Proof

Suppose first that $M(u)=u$ and let $v\triangleleft u$. Since M is an SPM, $M(v)< M(u)=u$. Hence, $v\ntriangleleft M(v)$.

Now assume that $v\ntriangleleft M(v)$ holds for every $v\triangleleft u$. In particular, $M(u)\ntriangleleft u$. Suppose next that $M(u)\triangleright u$. By Lemma 3.2, $u' \triangleleft M(u)$ for some $u'\ne u$. Since $M(u') < M(M(u))=u$, we have $v \triangleleft u$ and $M(v) \triangleright v$ for $v = M(u')$, contradicting the hypothesis. We conclude that $M(u)=u.$ $\square$

Taking $w = w_1 = w_2$, the next proposition in particular shows that an SPM of $[e,w]_\iota$ is completely determined by its restriction to the atoms, i.e. the elements that cover the identity.

Proposition 4.5

Let $w_1,w_2\in \iota$ and suppose $M_1$ and $M_2$ are SPMs of $[e,w_1]_\iota$ and $[e,w_2]_\iota$, respectively, such that $M_1(u)=M_2(u)$ for all $u\in [e,w_1]_\iota \cap [e,w_2]_\iota$ with $\rho (u) \le 1$. Then, $M_1(u)=M_2(u)$ for all $u\in [e,w_1]_\iota \cap [e,w_2]_\iota$.

Proof

Let $M_1$ and $M_2$ satisfy the hypotheses of the proposition. Employing induction on the length of u, suppose that $\rho (u)\ge 2$ and that for all v with $\rho (v)<\rho (u)$, $M_1(v)=M_2(v)$. We consider three cases.

Case 1 If $M_1(u)\triangleleft u$, then $u=M_1(M_1(u))=M_2(M_1(u))$ by the induction assumption. Therefore, $M_1(u)=M_2(u)$.

Case 2 Suppose that $M_1(u)=u$. By Lemma 4.4 and the induction hypothesis, every $v\triangleleft u$ satisfies either $M_2(v)=M_1(v)=v$ or $M_2(v)=M_1(v)\triangleleft v$. Using Lemma 4.4 again, we conclude $M_2(u)=u=M_1(u)$.

Case 3 Assume now $M_1(u)\triangleright u$ and $M_2(u)\triangleright u$; interchanging the roles of $M_1$ and $M_2$ if necessary, this is the only remaining case. Let $A_1 = \{v \in \iota {\setminus }\{u\}\ | \ v\triangleleft M_1(u) \}$ and $A_2 = \{v \in \iota {\setminus }\{u\}\ | \ v\triangleleft M_2(u) \}$. It follows immediately from Definition 4.1 that $A_i=\{M_i(x)\mid M_i(x) \triangleright x\triangleleft u\}$. Thus, $A_1=A_2$ is implied by the induction assumption, so $M_1(u)$ and $M_2(u)$ cover the same set of elements. Since $\rho (M_1(u))=\rho (M_2(u))=\rho (u)+1\ge 3$, $M_1(u) = M_2(u)$ follows from Proposition 3.5. $\square$

Corollary 4.6

Suppose M is an SPM of $[e,w]_\iota$ for some $w\in \iota$. If there exists an $s\in S$ such that $M(x) = x*s$ for all $x\in [e,w]_\iota$ with $\rho (x) \le 1$, then $M(x) = x*s$ for all $x\in [e,w]_\iota$.

Proof

The result follows from Proposition 4.5 if we are able to construct $w_2\in \iota$ with $s\in D_{\mathrm {R}}(w_2)$ such that $w_2 \ge w_1 = w$. Observe that $s_i\in D_{\mathrm {R}}(\hat{w})$ if and only if i is even, where $\hat{w} = w_0s_1s_3\cdots s_{2n-1}$ denotes the maximum of $\mathrm {Br}(\iota )$.

We may consider W to be embedded in the symmetric group of permutations of $\{0,1,\ldots ,2n+1\}$ with generators $S' = S\cup \{s_0 = (0\,\,\,1),s_{2n}=(2n\,\,\,2n+1)\}$ on which we have the automorphism $\theta '$ given by $s_i \mapsto s_{2n-i}$. Then $\theta '$ restricts to $\theta$ on W and $\iota$ embeds in $\iota (\theta ')$. Moreover, the maximum of $\iota (\theta ')$, call it $\hat{w}'$, has $s_i$ as descent if and only if i is odd. Hence, either $w_2 = \hat{w}$ or $w_2= \hat{w}'$ does the job. $\square$

The recurrence relation in Proposition 2.8 relies on a conjugation SPM. Our goal is to replace it with an arbitrary SPM in order to arrive at a combinatorially defined recurrence for the Q-polynomials. In order to do so, we need a good understanding of non-conjugation SPM behaviour. The next lemma imposes strong restrictions on such partial matchings.

Lemma 4.7

Suppose M is an SPM of $[e,w]_\iota$ for $w\in \iota$. If M is not a conjugation SPM, then $M(e)=\underline{s}_i$ for some $2\le i\le n-2$ and one of the following two sets of conditions holds:

• (1) $M(\underline{s}_{i-1}) = \underline{s}_{i-1}\underline{s}_i$, $M(\underline{s}_{i+1}) = \underline{s}_i\underline{s}_{i+1}$ and $\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1} \not \le w$.

• (2) $M(\underline{s}_{i-1}) = \underline{s}_i\underline{s}_{i-1}$, $M(\underline{s}_{i+1}) = \underline{s}_{i+1}\underline{s}_i$ and $\underline{s}_{i-1}\underline{s}_i\underline{s}_{i+1} \not \le w$.

Proof

Let M be an SPM of $[e,w]_\iota$.

First, consider the case $M(e)=e$. We cannot have $M(\underline{s}_i)=\underline{s}_i$ for every $\underline{s}_i\le w$ because Lemma 4.4 would then imply that $M(u) = u$ for all $u\le w$ contradicting that M is an SPM. Hence $M(\underline{s}_i)=\underline{s}_i\underline{s}_j$ for some i and j. Then $x\triangleleft \underline{s}_i\underline{s}_j$, $x\in \iota$, can only happen if $x = \underline{s}_i$; otherwise $M(x)\triangleleft x$ which is impossible. By Lemma 3.2, this means $\underline{s}_i = \underline{s}_{n-1} = \underline{s}_{n+1}$ and $j=n$. In other words, $M(u) = u*s_n$ for all $u\in [e,w]_\iota$ with $\rho (u)\le 1$, whence M is a conjugation SPM by Corollary 4.6.

Second, suppose $M(e) = \underline{s}_i$, $i<n$. For $i\ne j<n$, the only elements which cover both $\underline{s}_i$ and $\underline{s}_j$ are $\underline{s}_i\underline{s}_j = \underline{s}_j\underline{s}_{2n-i}$ and $\underline{s}_j\underline{s}_i = \underline{s}_i\underline{s}_{2n-j}$; they coincide if and only if $i\ne j\pm 1$. If M is neither twisted conjugation by $s_i$ nor by $s_{2n-i}$ we must therefore have $M(\underline{s}_j) = \underline{s}_i\underline{s}_j \ne \underline{s}_j\underline{s}_i$ and $M(\underline{s}_k) = \underline{s}_k\underline{s}_i \ne \underline{s}_i\underline{s}_k$ for some $j,k<n$, $\underline{s}_j,\underline{s}_k\le w$. This is only possible if $\{j,k\} = \{i-1,i+1\}$. In particular, $2\le i\le n-2$. Assume $M(\underline{s}_{i-1})=\underline{s}_{i-1}\underline{s}_i$ and $M(\underline{s}_{i+1})=\underline{s}_i\underline{s}_{i+1}$, the other case being entirely similar. Suppose in order to obtain a contradiction $\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1}\le w$. By the subword property, $\underline{s}_{i+1}\underline{s}_i\le w$ and $\underline{s}_i\underline{s}_{i-1}\le w$. Since $M(\underline{s}_{i+1}\underline{s}_i)$ covers both $\underline{s}_{i+1}\underline{s}_i$ and $\underline{s}_i\underline{s}_{i+1}$, $M(\underline{s}_{i+1}\underline{s}_i)=\underline{s}_i\underline{s}_{i+1}\underline{s}_i$. Similarly, $M(\underline{s}_i\underline{s}_{i-1})=\underline{s}_i\underline{s}_{i-1}\underline{s}_i$. Now, $M(\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1})$ covers $\underline{s}_i\underline{s}_{i+1}\underline{s}_i$ and $\underline{s}_i\underline{s}_{i-1}\underline{s}_i$, so $M(\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1}) = \underline{s}_i\underline{s}_{i-1}\underline{s}_{i+1}\underline{s}_i$ by Lemma 3.4. This is however impossible since $\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1}\nleq \underline{s}_i\underline{s}_{i-1}\underline{s}_{i+1}\underline{s}_i$. $\square$

A conjugation SPM may have fixed points. The upcoming proposition, however, states that any non-conjugation SPM is fixed point free and commutes with some fixed point free conjugation SPM.

Proposition 4.8

Let $w\in \iota$ and assume M is an SPM of $[e,w]_\iota$ which is not a conjugation SPM. Then M has no fixed point. Moreover, there exists $s\in D_{R}(w)$ such that $w*s \ne M(w)$ and, furthermore, $u*s\ne u$ and $M(u*s) = M(u)*s$ for all $u\in [e,w]_\iota$.

Proof

Lemma 4.7 shows that if M is a non-conjugation SPM of $[e,w]_\iota$, $M(e) = \underline{s}_i$ for some $2\le i \le n-2$, and either $M(\underline{s}_{i+1}) = \underline{s}_i\underline{s}_{i+1}$ and $M(\underline{s}_{i-1}) = \underline{s}_{i-1}\underline{s}_i$ or else $M(\underline{s}_{i+1}) = \underline{s}_{i+1}\underline{s}_i$ and $M(\underline{s}_{i-1}) = \underline{s}_i\underline{s}_{i-1}$. Replacing w with $w^{-1}$ if necessary, we may assume the former situation is at hand. It follows that $\underline{s}_{i+1}\underline{s}_i\underline{s}_{i-1} \not \le w$. Hence, Lemma 3.3 implies that every element in $[e,w]_\iota$ has a permutation diagram of the form illustrated in Fig. 3.

Fig. 3

Illustration for the proof of Proposition 4.8. Permutation diagrams of elements in $[e,w]_\iota$ have the depicted form. Shaded regions are empty. Region C has $i-1$ columns and $i+1$ rows, and it contains $i-1$ dots

For any $u\in [e,w]_\iota$, its diagram either contains two dots in each of A and $A'$, and B is empty, or else B contains two dots and both A and $A'$ are empty. Say u is of type 4 in the former case and type 2 in the latter; i.e. the type indicates the total number of dots in $A\cup A'\cup B$.

Recall the description of $\triangleleft$ from Fig. 1. Let us say that a covering of the form depicted in the lower left picture is produced by a box cover transformation which involves the dots which are indicated in the picture, i.e. those not shared by the two diagrams.

Claim If u is of type 4, M(u) is obtained from u by a box cover transformation which involves the four dots in $A\cup A'$, whereas $M(u) = u$ if u is of type 2.

The claim is readily verified if $\rho (u)\le 1$. In order to prove it in general, we assume $\rho (u)\ge 2$ and induct on $\rho (u)$.

Suppose first that u is of type 2. Recalling from Fig. 1 the description of the cover relation in $\iota$, it is clear that $v\triangleleft u$ implies v is of type 2 or of type 4 with the dots in $A'$ forming a fall. The induction assumption shows that $M(v) = v$ (in the former case) or $M(v) \triangleleft v$ (in the latter). By Lemma 4.4, $M(u) = u$ as desired.

Now assume u is of type 4. Let b denote the operator which acts on elements of type 4 by applying a box cover transformation involving the dots in A and $A'$. The induction assumption implies $b(v)=M(v)$ for all $u\ne v \in [e,u]_\iota$ since all such v are of type 4 by Theorem 2.4. It must be shown that $b(u)=M(u)$. If $b(u)<u$ or $M(u) < u$ we are done by induction, so suppose $b(u) > u$ and $M(u) \ge u$. In order to obtain a contradiction, assume $M(u) \ne b(u)$. It suffices to find $x\triangleleft M(u)$, $x\ne u$, such that $b(x)> x$; since M is an SPM it would satisfy $M(x)\triangleleft x$ (if $M(u) \triangleright u$) or $M(x) \le x \triangleleft u$ (if $M(u) = u$), so that the induction assumption implies $b(x) = M(x)$ which is the needed contradiction.

Consider the diagram of M(u) as depicted in Fig. 3. If $b(M(u)) < M(u)$, $x=b(M(u))$ has the desired properties. Hence, we may assume the dots in A form a rise, as do those in $A'$. By Proposition 4.2, $M(u)\ge \underline{s}_i = M(e)$. This implies $\underline{s}_{i-1}\le M(u)$ or $\underline{s}_{i+1}\le M(u)$, since otherwise $s_i$ would be a descent of M(u) corresponding to a fall in A.

First, if $\underline{s}_{i-1}\le M(u)$, the dots in $A'$ are not in the two leftmost columns by Theorem 2.4. Therefore, there exists $k\in [i]$ such that $\theta (s_k)\in D_{\mathrm {R}}(M(u))$, and this descent involves exactly one dot in $A'$ (by which we mean $M(u)(2n-k)>2n+1-i$ and $M(u)(2n+1-k)\le 2n+1-i$). It is clear that $b(M(u)*\theta (s_k)) > M(u)*\theta (s_k)$.

Second, if $\underline{s}_{i+1}\le M(u)$, the dots in A are not in the two leftmost columns. Then, $s_j\in D_{\mathrm {R}}(M(u))$ for some $i\le j \le 2n-i-2$ with this descent involving exactly one dot in A (i.e. $M(u)(j)>i+1$ and $M(u)(j+1)\le i+1$), implying $b(M(u)*s_j) > M(u)*s_j$.

Now, if both $\underline{s}_{i-1}\le M(u)$ and $\underline{s}_{i+1}\le M(u)$, we note $M(u)*\theta (s_k) \ne M(u)*s_j$ e.g. since the latter element coincides with M(u) on $[i-1]$ whereas the former does not. Thus, at least one of them is not equal to u; let x be this element.

Finally, let us consider the case $\underline{s}_{i+1}\le M(u)$, $\underline{s}_{i-1}\not \le M(u)$ (the situation $\underline{s}_{i+1}\not \le M(u)$, $\underline{s}_{i-1}\le M(u)$ being completely analogous). Let $x=M(u)*s_j$. If $M(u) = u$, $x\ne u$ and we are done. If $u < M(u)$, M restricts to an SPM of $[e,M(u)]_\iota$ by Proposition 4.2. Since $\underline{s}_{i-1}\not \le M(u)$, Lemma 4.7 implies that the restriction is a conjugation SPM. Examining M(e) and $M(s_{i+1})$, we conclude $M(v) = v*\theta (s_i)$ for all $v\in [e,M(u)]_\iota$. Hence, $u = M(u) *\theta (s_i) \ne x$. The claim is established.

Now, Theorem 2.4 implies that w is of type 2 whenever u is of type 2 for some $u\le w$. Since $M(w) \ne w$ it follows from the claim that every element in $[e,w]_\iota$ must in fact be of type 4. In particular, M coincides with b which has no fixed point.

Just as in the proof of the claim, the fact that $\underline{s}_{i-1} \le w$ implies $\theta (s_k)\in D_{\mathrm {R}}(w)$ for some $k\in [i]$ with $w*\theta (s_k) \ne b(w)$. Moreover, for $u \in [e,w]_\iota$, $u*\theta (s_k) = u$ would imply u is of type 2 which we have just seen is impossible. Finally, it is not hard to see that $b(u)*s = b(u*s)$ for any $s\in S$. In particular, $s=\theta (s_k)$ has all the asserted properties. $\square$

5 KLV polynomials

Finally, we have gathered all ingredients that are necessary in order to prove the main result which asserts that any SPM of $[e,w]_\iota$ can be used in the recurrence relation for the Q-polynomials of the intervals $[u,w]_\iota$. With the key SPM properties from the previous section under the belt, the arguments that remain are essentially identical to those employed by Brenti in his proof of [3, Theorem 5.2].

Theorem 5.1

Let M be an SPM of $[e,w]_\iota$. Then, for any $u\in [e,w]_\iota$,

$$\begin{aligned} Q_{u,w}(q)= {\left\{ \begin{array}{ll} Q_{M(u),M(w)}(q) &{} \text { if } M(u)\triangleleft u, \\ qQ_{M(u),M(w)}(q)+(q-1)Q_{u,M(w)}(q) &{} \text { if } M(u)\triangleright u, \\ qQ_{u,M(w)}(q) &{} \text { if } M(u)= u. \end{array}\right. } \end{aligned}$$

Proof

This is just Proposition 2.8 if M is a conjugation SPM, so suppose it is not; in particular $\rho (w)\ge 3$ by Lemma 4.7. We induct on $\rho (w)$. By Proposition 4.8, there exists $s\in D_{\mathrm {R}}(w)$, $M(w)\ne w*s$, such that the conjugation SPM given by s commutes with M and fixes no element in $[e,w]_\iota$. Let $u\in [e,w]_\iota$. Proposition 4.8 shows $M(u)\ne u$, so we consider two cases:

Case 1 $M(u)\triangleleft u$. We need to show that $Q_{u,w}(q)=Q_{M(u),M(w)}(q)$.

Suppose first that $s\in D_{\mathrm {R}}(u)$. Then, either $s\in D_{\mathrm {R}}(M(u))$ or $M(u)=u*s$. If $s\in D_{\mathrm {R}}(M(u))$, $M(u*s)=M(u)*s\triangleleft u*s$. Therefore,

$$\begin{aligned}&Q_{u,w}(q)=Q_{u*s,w*s}(q)=Q_{M(u*s),M(w*s)}(q)\\&=Q_{M(u)*s,M(w)*s}(q)=Q_{M(u),M(w)}(q), \end{aligned}$$

where the second equality (as is the case in all subsequent computations of this kind throughout the proof) follows from the inductive hypothesis and the fact, provided by Proposition 4.2, that M is an SPM of $[e,w*s]_\iota$. If $M(u)=u*s$, then

$$\begin{aligned} Q_{u,w}(q)= & {} Q_{u*s,w*s}(q)\\= & {} qQ_{M(u*s),M(w*s)}(q)+(q-1)Q_{u*s,M(w*s)}(q)\\= & {} qQ_{M(u)*s,M(w)*s}(q)+(q-1)Q_{M(u),M(w)*s}(q)\\= & {} Q_{M(u),M(w)}(q). \end{aligned}$$

Suppose now that $s\notin D_{\mathrm {R}}(u)$. Since twisted conjugation by s does not fix any element in $[e,w]_\iota$, $M(u) \triangleleft u \triangleleft u*s$. We also have $M(u) \triangleleft M(u)*s = M(u*s) \triangleleft u*s$ because $\rho (u*s) = \rho (M(u))+2$. Therefore,

$$\begin{aligned} Q_{u,w}(q)= & {} qQ_{u*s,w*s}(q)+(q-1)Q_{u,w*s}(q)\\= & {} qQ_{M(u*s),M(w*s)}(q)+(q-1)Q_{M(u),M(w*s)}(q)\\= & {} qQ_{M(u)*s,M(w)*s}(q)+(q-1)Q_{M(u),M(w)*s}(q)\\= & {} Q_{M(u),M(w)}(q). \end{aligned}$$

Case 2 $M(u)\triangleright u$. We must prove that $Q_{u,w}(q)=qQ_{M(u),M(w)}(q)+(q-1)Q_{u,M(w)}(q)$.

First, assume that $s\in D_{\mathrm {R}}(u)$. Then we have $u*s \triangleleft u \triangleleft M(u)$, and therefore also $u*s\triangleleft M(u*s) = M(u)*s \triangleleft M(u)$. Hence,

$$\begin{aligned} Q_{u,w}(q)= & {} Q_{u *s,w*s}(q)\\= & {} qQ_{M(u*s),M(w*s)}(q)+(q-1)Q_{u*s,M(w*s)}(q)\\= & {} qQ_{M(u)*s,M(w)*s}(q)+(q-1)Q_{u*s,M(w)*s}(q)\\= & {} qQ_{M(u),M(w)}(q)+(q-1)Q_{u,M(w)}(q). \end{aligned}$$

Suppose now that $s\notin D_{\mathrm {R}}(u)$. Again, this means $u\triangleleft u*s$. If $M(u)\ne u*s$, then $u\triangleleft M(u) \triangleleft M(u)*s=M(u*s)$. Hence, $u*s \triangleleft M(u*s)$. We obtain

$$\begin{aligned} Q_{u,w}(q)= & {} qQ_{u*s,w*s}(q)+(q-1)Q_{u,w*s}(q)\\= & {} q(qQ_{M(u*s),M(w*s)}(q)+(q-1)Q_{u*s,M(w*s)}(q))\\&+(q-1)(qQ_{M(u),M(w*s)}(q) +(q-1)Q_{u,M(w*s)}(q))\\= & {} q(qQ_{M(u)*s,M(w)*s}(q)+(q-1)Q_{M(u),M(w)*s}(q))\\&+(q-1)(qQ_{u*s,M(w)*s}(q) +(q-1)Q_{u,M(w)*s}(q))\\= & {} qQ_{M(u),M(w)}(q)+(q-1)Q_{u,M(w)}(q).\\ \end{aligned}$$

Finally, if $M(u)=u*s$, then,

$$\begin{aligned} Q_{u,w}(q)= & {} qQ_{u*s,w*s}(q)+(q-1)Q_{u,w*s}(q)\\= & {} qQ_{M(u*s),M(w*s)}(q)+(q-1)(qQ_{M(u),M(w*s)}(q)\\&+(q-1)Q_{u,M(w*s)}(q))\\= & {} qQ_{M(u)*s,M(w)*s}(q)+(q-1)(qQ_{u*s,M(w)*s}(q)\\&+(q-1)Q_{u,M(w)*s}(q))\\= & {} qQ_{M(u),M(w)}(q)+(q-1)Q_{u,M(w)}(q).\\ \end{aligned}$$

$\square$

Since $Q_{u,w}$ is determined by the SPMs of the intervals $[e,v]_\iota$ for $v\in [e,w]_\iota$, this also holds for the KLV R-polynomials and the KLV polynomials themselves. Since an SPM is a poset invariant, the next corollary follows.

Corollary 5.2

If $f:[e,w]_\iota \rightarrow [e,w']_\iota$ is a poset isomorphism, then for all $v\in [e,w]_\iota$, $Q_{v,w}= Q_{f(v),w'},$ $R_{v,w}= R_{f(v),w'}$ and $P^\iota _{v,w}= P^\iota _{f(v),w'}$.

In particular, Theorem 1.2 is established.