Shellability of the higher pinched Veronese posets

Abstract

The pinched Veronese poset ${\mathcal {V}}^{\bullet }_n$ is the poset with ground set consisting of all nonnegative integer vectors of length $n$ such that the sum of their coordinates is divisible by $n$ with exception of the vector $(1,\ldots ,1)$. For two vectors $\mathbf {a}$ and $\mathbf {b}$ in ${\mathcal {V}}^{\bullet }_n$, we have $\mathbf {a}\preceq \mathbf {b}$ if and only if $\mathbf {b}- \mathbf {a}$ belongs to the ground set of ${\mathcal {V}}^{\bullet }_n$. We show that every interval in ${\mathcal {V}}^{\bullet }_n$ is shellable for $n \ge 4$. In order to obtain the result, we develop a new method for showing that a poset is shellable. This method differs from classical lexicographic shellability. Shellability of intervals in ${\mathcal {V}}^{\bullet }_n$ has consequences in commutative algebra. As a corollary, we obtain a combinatorial proof of the fact that the pinched Veronese ring is Koszul for $n \ge 4$. (This also follows from a result by Conca, Herzog, Trung, and Valla.)

1 Introduction

In this paper, we focus on the following question: Is every interval in the pinched Veronese poset shellable? (Cohen-Macaulay?) Let us explain this question and its background in detail.

By the $m$-th Veronese poset on $n$ generators, denoted as $({\mathcal {V}}_{m,n}, \le )$, we mean the following poset. Its ground set consists of nonnegative integer vectors of length $n$ such that the sum of their coordinates is divisible by $m$. The partial order on ${\mathcal {V}}_{m,n}$ is given so that $\mathbf {a}\le \mathbf {b}$ if and only if $\mathbf {a}$ is less or equal to $\mathbf {b}$ in each coordinate. It is not hard to see that every interval in ${\mathcal {V}}_{m,n}$ is shellable and, therefore, Cohen-Macaulay.

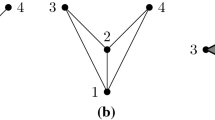
If we set $m = n$, we just speak of the $n$-th Veronese poset ${\mathcal {V}}_{n} := {\mathcal {V}}_{n,n}$. We can pinch this poset in the following way. We remove the distinguished vector $\mathbf {j}$ which contains $1$ in each coordinate. We also remove order relations between vectors that differ exactly by $\mathbf {j}$ (making them incomparable). In this way, we thus obtain the $n$-th pinched Veronese poset $({\mathcal {V}}^{\bullet }_n,\preceq )$; see Fig. 1. (More details on this poset are discussed in Sect. 4.) It is very interesting that removing this single element $\mathbf {j}$ (and the corresponding order relations) strongly influences understanding the properties of the poset.

Fig. 1

An example of an interval in ${\mathcal {V}}_3$ and ${\mathcal {V}}^{\bullet }_3$. The edges that have to be removed from ${\mathcal {V}}_3$ in order to obtain ${\mathcal {V}}^{\bullet }_3$ are emphasized on the left

On the algebraic side, it follows that the $n$-th pinched Veronese ring is Koszul for $n \ge 4$ from a result by Conca et al. [9] (we will discuss this in more detail below). This is equivalent to stating that every interval in ${\mathcal {V}}^{\bullet }_n$ is Cohen-Macaulay; see [16, Corollary 2.2]. Later on, Caviglia [7] showed that the third pinched Veronese ring is Koszul. The methods used in [7] are based on computer calculations. Recently, a more general result was found by Caviglia and Conca [8] without the use of computer.

Our task is to focus on the combinatorial side of this question. That is, we focus on shellability of intervals in the pinched Veronese poset remarking that shellability implies Cohen-Macaulayness. We also remark that Cohen-Macaulayness of a poset implies several deep intrinsic properties of the poset, for example certain enumerative properties. The reader is referred, for example, to [1] for more details on Cohen-Macaulayness.

We develop a new method for showing that a certain poset is shellable. Using this method, we are able to prove the following theorem.

Theorem 1.1

Let $n \ge 4$. For any $\mathbf {z}\in {\mathcal {V}}^{\bullet }_n$, the interval $[\mathbf {0},\mathbf {z}]$ in ${\mathcal {V}}^{\bullet }_n$ is a shellable poset, where $\mathbf {0}$ is the zero vector of length $n$.

Note that we do not lose anything by considering intervals $[\mathbf {0}, \mathbf {z}]$ only, since an interval $[\mathbf {a},\mathbf {b}]$ is isomorphic to $[\mathbf {0}, \mathbf {b}- \mathbf {a}]$.

Our motivation for proving Theorem 1.1 can be seen from two sides. On one hand, the pinched Veronese poset is an interesting poset from a combinatorial point of view and it is interesting to understand its combinatorial properties, especially, if its combinatorial properties have further consequences in commutative algebra (see the text at the end of this section).

On the other hand, Theorem 1.1 can be seen as a testing example for a new method for showing that a certain poset is shellable. We establish inductive criteria showing that a certain poset $P$ is shellable assuming that several subposets of $P$ are shellable and that $P$ satisfies few other properties. Let us remark that, in general, our method differs from a very standard tool which is lexicographic shellability.

A small drawback of our method is that it requires quite technical case analysis checking that all inductive criteria are satisfied. In this part, the main message for the reader is that the analysis can be done (still, it is fully included in the paper).

1.1 The third pinched Veronese poset

The reader might wonder what is the importance of our assumption $n \ge 4$ in Theorem 1.1. The case $n=1$ does not make sense. The case $n= 2$ makes the most sense (in relation to the algebraic side of the question) if the elements $(\alpha _1,\alpha _2)$ are further removed from the poset whenever $\alpha _1$ and $\alpha _2$ are odd. However, in this case, ${\mathcal {V}}^{\bullet }_2$ is isomorphic to ${\mathcal {V}}_{1,2}$.

The only real issue occurs when $n = 3$. In this case, our method, as stated in Sect. 2, does not suffice to prove shellability of ${\mathcal {V}}^{\bullet }_3$. In fact, it is possible to show that some intervals in ${\mathcal {V}}^{\bullet }_3$ are not lexicographically shellable. It turns out that the reason why some intervals in ${\mathcal {V}}^{\bullet }_3$ are not lexicographically shellable also implies limitations for our method. Maybe a further improvement of our method might yield a solution for $n = 3$.

1.2 More detailed relation to commutative algebra

Let us fix an integer $n$ and consider a subset ${\mathcal {A}}$ of ${\mathbb {N}}_0^n$. For simplicity we assume that the sum of the coordinates of all vectors in ${\mathcal {A}}$ equals a fixed integer $m$. Given a commutative field , we consider the ring as a subring of generated by all monomials $x^{\mathbf {a}}$ for $\mathbf {a}\in {\mathcal {A}}$ where $x_1^{a_1} \cdots x_n^{a_n}$ if $\mathbf {a}= (a_1, \ldots , a_n)$.

We can also associate a poset $P({\mathcal {A}})$ to ${\mathcal {A}}$ in the following way. We let $\varLambda$ consist of those vectors in ${\mathbb {N}}_0^n$ that are nonnegative integer combinations of vectors from ${\mathcal {A}}$ (including zero). Then, we set $P({\mathcal {A}}) = (\varLambda , \le _{{\mathcal {A}}})$ where $\mathbf {a}\le _{{\mathcal {A}}} \mathbf {b}$ if and only if $\mathbf {b}- \mathbf {a}\in \varLambda$.

Cohen-Macaulayness of intervals in $P({\mathcal {A}})$ is related to the Koszul property of in the following way.

Proposition 1.2

([16, Corollary 2.2]) The ring is Koszul if and only if every interval in $P({\mathcal {A}})$ is Cohen-Macaulay over .

The reader is referred, for example, to [11] for more information about the importance of the Koszul property.

If we set ${\mathcal {A}}_{m,n}$ to consist of all vectors in ${\mathbb {N}}^n_0$ whose coordinates sum to $m$, we get $P({\mathcal {A}}_{m,n}) = {\mathcal {V}}_{m,n}$. Similarly, if we set ${\mathcal {A}}^\bullet _n$ to ${\mathcal {A}}_{n,n} {\setminus } \{\mathbf {j}\}$, we get $P({\mathcal {A}}^\bullet _n) = {\mathcal {V}}^{\bullet }_n$. Thus, we have the following corollary of Theorem 1.1 and Proposition 1.2.

Corollary 1.3

The ring is Koszul for any $n \ge 4$.

As we mentioned above, Corollary 1.3 also follows from the result of Conca et al. [9], and thus our contribution for the algebraic side is a combinatorial proof of this corollary.

For completeness, we explain how to derive Corollary 1.3 from Corollary 6.10 (2) in [9]. We set $I$ to be the ideal $(x_1^2, \ldots , x_n^2)$ in . It is generated by a regular sequence since $x_i^2$ is a nonzero divisor in . Setting $d = 2$, $e = 1$, $c = n-2$, and $r = n$ in Corollary 6.10 (2) from [9], we get that is Koszul where is generated by all monomials of degree $n$ belonging to $I$; that is, .

Very recently, Vu [17] proved a general result that for $m,n \ge 2$ and $\mathbf {x}\in {\mathcal {A}}_{m,n}$, the ring is Koszul unless $m \ge 3$ and $\mathbf {x}$ is $(0,\ldots ,0,2,m-2)$ or one of its permutations (this result also includes Corollary 1.3).

1.3 Further related work

Here, we very briefly mention further related work. We keep several terms undefined in this paragraph. The reader is welcome to consult the cited sources for more details. Eisenbud et al. [10] showed that the $m$-th Veronese subrings of are Koszul where $I$ is a homogeneous ideal and $m$ is large enough (more precisely when $m \ge {{\mathrm{reg}}}(I)/2$ where ${{\mathrm{reg}}}(I)$ is Castelnuovo-Mumford regularity of $I$). Further investigation of Koszulness of can be found in [6, 12, 13, 16] in the context where the generators $z_i$ correspond to monomials $x^{\mathbf {a}}$ as above and $I$ records the syzygies between the monomials (and then ).

1.4 Structure

In Sect. 2, we explain our new method for showing shellability. In Sect. 3, we prove the correctness of the method. Section 4 serves as a preliminary section on properties of the (pinched) Veronese posets. In Sect. 5, we prove Theorem 1.1. Finally, in Sect. 6, we compare the strength of our shellability method (mainly) with standard chain-lexicographic shellability of Björner and Wachs [4]. If the reader is more interested in the shellability criteria rather than Theorem 1.1, we highly recommend to read Sect. 6 right after Sect. 2. Here, we offer the graph of the dependency of the sections:

The dashed arrow between Sects. 3 and 5 means that Sect. 3 is not necessary for understanding Sect. 5; however, the correctness of the proof in Sect. 5 is based on Sect. 3.

2 Method for showing shellability

In this section, we describe our main tools for the proof of Theorem 1.1. We need to set up some preliminaries first.

2.1 Poset preliminaries

Let $P = (P,\le )$ be a graded poset with rank function ${{\mathrm{rk}}}$. By $\hat{0}$ we mean the unique minimal element of $P$ (if it exists), and similarly, by $\hat{1}$ we mean the unique maximal element (if it exists). For $a, b \in P$, we say that $a$ covers $b$, $a {\ > \cdot \ }b$, if $a > b$ and there is no $c$ with $a > c > b$. Equivalently, $a > b$ and ${{\mathrm{rk}}}(a) = {{\mathrm{rk}}}(b) + 1$. Pairs of elements $a, b$ with $a {\ > \cdot \ }b$ are also known as edges in the Hasse diagram of $P$. Atoms are elements that cover $\hat{0}$. That is, atoms are elements of rank $1$ in a poset that contains $\hat{0}$.

From now on, let us assume that $P$ contains a unique minimal element. Let $A$ be a set of some atoms in $P$. By $P\langle A \rangle = (P\langle A \rangle , \le )$ we mean the induced subposet of $P$ with the ground set

$$\begin{aligned} P\langle A \rangle = \{\hat{0}\} \cup \{b \in P:b \ge a \hbox { for some }a \in A\}. \end{aligned}$$

2.2 Shellability

Now, we assume that $P$ contains both a unique minimal and a unique maximal element. Let $C(P)$ be the set of maximal chains of $P$. A shelling order is an order of chains from $C(P)$ satisfying the following condition.

• (Sh) If $c'$ and $c$ are two chains from $C(P)$ such that $c'$ appears before $c$, then there is a chain $c^*$ from $C(P)$ appearing before $c$ such that $c \cap c^* \supseteq c \cap c'$ and also $c$ and $c^*$ differ in one level only (that is, $|c \Delta c^*| = 2$ where $\Delta$ denotes the symmetric difference).

A poset $P$ is shellable if it admits a shelling order. This is equivalent with saying that the order complex of $P$ is shellable (as a simplicial complex).

2.3 A-shellability

Now, let us assume that $A = (A, \le ^\circ )$ is a partially ordered set of some atoms in $P$. We say that $P\langle A \rangle$ is $A$ -shellable if $P\langle A \rangle$ is shellable with a shelling order respecting the order on $A$. That is, if $c$ and $c'$ are two maximal chains on $P\langle A \rangle$ and the unique atom of $c'$ appears before the unique atom of $c$ in the $\le ^\circ$ order, then $c'$ appears before $c$ in the shelling.¹

2.4 Using A-shellability

Let $P$ be a poset for which we aim to show that $P$ is shellable (in our application $P = {\mathcal {V}}^{\bullet }_n$). Let us order all the atoms of $P$ into a sequence $a_1, \ldots , a_t$. For $k \in [t]$, let us set $A_k := \{a_1, \ldots , a_k\}$ and consider $A_k$ as a partially ordered set with the order $a_1 \le ^\circ a_2 \le ^\circ \cdots \le ^\circ a_k$. We would like to prove inductively that $P\langle A_k \rangle$ is $A_k$-shellable. Let us assume that we are able to perform the first induction step, that is, to show $A_1$-shellability of $P\langle A_1 \rangle$, and let us focus on the second induction step. We will provide two criteria, Theorems 2.1 and 2.2 below, how to prove $A_{k+1}$-shellability of $P\langle A_{k+1} \rangle$ assuming $A_{k}$-shellability of $P\langle A_k \rangle$.

This technique is quite similar to the technique using recursive atom orderings defined by Björner and Wachs [5] and a comparison of these two techniques is discussed in Sect. 6. In particular, the second criterion (Theorem 2.2) is set up in such a way that it covers the case of recursive atom orderings. However, the technique presented here allows more freedom. In particular, it allows to combine different criteria to achieve the task.

One technical issue is the following. In our application for the pinched Veronese posets, it is not enough to consider the induction steps along a single ordering $a_1 \le ^\circ a_2 \le ^\circ \cdots \le ^\circ a_t$ of the atoms of $P$. If we aimed on a single ordering only, we would not have strong enough induction assumption to achieve the task. Thus, we will rather focus on many orderings of the atoms. For considering more orderings simultaneously, it pays off to set up a third criterion, Theorem 2.3, which allows to “restrict” an $A$-shelling of $P\langle A \rangle$ to an $A'$-shelling of $P\langle A' \rangle$ where $A'$ is a subset of $A$.

2.5 Necessity of the criteria

In our approach, the first criterion, Theorem 2.1, seems to be the most important. The remaining two theorems could, perhaps, be circumvented; however, they will simplify our analysis.

2.6 Setting up the criteria

To set up conditions in the criteria, we need some additional notation. We fix some partially ordered set $A = (A, \le ^\circ )$ of atoms of $P$ and a further atom $a^+$ which is not in $A$. Think of $A = A_k$ and $a^+ = a_{k+1}$ when comparing with the sketch above (it is more convenient to use a notation independent of the index $k$).

We set $A^+ := A \cup \{a^+\}$ and $Q := P\langle A^+ \rangle {\setminus } P\langle A \rangle$. The partial order on $A^+$, which we again denote by $\le ^\circ$, extends $\le ^\circ$ on $A$ so that $a^+ \ge ^\circ a$ for any $a \in A$. We also consider $Q = (Q, \le )$ as a subposet of $P$ with the unique minimal element $a^+$ (it does not need to have a unique maximal element).

For $q \in Q$, we set $I(q)$ to be the interval $[q, \hat{1}]$. Elements of $P$ that cover $q$ are atoms of $I(q)$. By $A(q)$ we denote the set of (all) atoms of $I(q)$ which simultaneously belong to $P\langle A \rangle$. By $A^\mathrm{all}(q)$ we denote the set of all atoms of $I(q)$. In particular, note that the poset $I(q)\langle A(q) \rangle$ is well defined (we will need this poset later on).

2.7 Edge falling property

Let $q \in Q$. We say that $q$ has the edge falling property if for every $p \in P\langle A \rangle$ with $p {\ > \cdot \ }q$ and every $q' \in Q \cup \{\hat{0} \}$ with $q {\ > \cdot \ }q'$ there is $p' \in P\langle A \rangle$ such that $p {\ > \cdot \ }p' {\ > \cdot \ }q'$. See Fig. 2.

Fig. 2

The edge falling property. The $P\langle A \rangle$–$Q$ edge $pq$ falls by one level to $p'q'$

2.8 Shellability criteria

Now, we can state our first criterion; see also Fig. 3.

Theorem 2.1

(Criterion I) The poset $P\langle A^+ \rangle$ is $A^+$-shellable if the following conditions are satisfied.

• (i) $P\langle A \rangle$ is $A$-shellable;

• (ii) for every $q \in Q$ the interval $[a^+,q]$ is shellable;

• (iii) every $q \in Q$ has the edge falling property; and

• (iv) for every $q \in Q$ the poset $I(q)\langle A(q) \rangle$ is shellable.

Fig. 3

Important subposets appearing in the conditions of Theorem 2.1. We also recall the edge falling property by a little diamond between $P\langle A \rangle$ and $Q$

The second criterion is similar to the first one; however, it focuses more on the structure of the interval $I(a^+)$ rather than on the structure of $Q$. See also Fig. 4.

Theorem 2.2

(Criterion II) The poset $P\langle A^+ \rangle$ is $A^+$-shellable if the following conditions are satisfied.

• (i) $P\langle A \rangle$ is $A$-shellable;

• (ii) there is a linear order on $A^\mathrm{all}(a^+)$ such that the elements of $A(a^+)$ appear before other elements in this order and such that $I(a^+) = I\langle A^\mathrm{all}(a^+) \rangle$ is $A^\mathrm{all}(a^+)$-shellable (with respect to this order); and

• (iii) for every $q \in Q$ and for every $p \in P\langle A \rangle$ if $p {\ > \cdot \ }q$, then $p \in I(a^+)\langle A(a^+) \rangle$.

Fig. 4

Schematic drawing of the conditions of Theorem 2.2

The third criterion that we provide below differs from the previous two. In this case, we rather reduce $A$ to $A'$ instead of enlarging it.

Theorem 2.3

(Criterion III) Let $A'$ be a subset of $A$, linearly ordered with the order inherited from $A$. The poset $P\langle A' \rangle$ is $A'$-shellable if the following conditions are satisfied.

• (i) $P\langle A \rangle$ is $A$-shellable; and

• (ii) for every $b \in A {\setminus } A'$ and for every $p \in P\langle A' \rangle$ with $p {\ > \cdot \ }b$, there is $b'$ appearing before $b$ in $A$ such that $b' \in A'$ and $p {\ > \cdot \ }b'$ (see Fig. 5).

Fig. 5

Schematic drawing of condition (ii) of Theorem 2.3

The proofs of all three criteria are given in Sect. 3.

We conclude this section by remarks about the differences in the criteria above and their comparison to lexicographic shellability.

2.9 Relation between Criterion I and Criterion II

A reader might check that Theorem 2.1 “almost” follows from Theorem 2.2. More precisely, it is not hard to see that conditions (i) and (iii) of Theorem 2.2 easily follow from the assumptions of Theorem 2.1. The main difference is that condition (ii) of Theorem 2.2 does not immediately follow from the assumptions of Theorem 2.1. (Assuming that the conditions of Theorem 2.1 are satisfied, we can immediately deduce that $I(a^+)\langle A(a^+) \rangle$ is shellable by setting $q = a^+$ in condition (iv) of Theorem 2.1; however, we do not have shelling of whole $I(a^+)$ yet).

Actually, the essence of the proof of Theorem 2.1 can be seen as verifying condition (ii) of Theorem 2.2 from conditions (ii), (iii) and (iv) of Theorem 2.1, which is solely a property of a certain decomposition of the interval $I(a^+)$. The interested reader is welcome to formulate the criteria on extension of a shelling of $I(a^+)\langle A(a^+) \rangle$ to a shelling of whole $I(a^+)$ separately, following the proof of Theorem 2.1.

2.10 Relation of lexicographic shellability and $A$-shellability

A very standard notion for showing that a certain poset is shellable is the so-called (chain lexicographic) CL-shellability, introduced by Björner and Wachs [4], or even a further generalization, the so-called (chain compatible) CC-shellability introduced by Kozlov [14], still induced by a lexicographic order on chains. It is natural to ask what is the relation between $A$-shellability introduced here and lexicographic shellability (we will focus on CL-shellability only; some ideas can be carried for CC-shellability as well). We discuss this relation in more detail separately in Sect. 6, and the reader interested in these details is encouraged to read Sect. 6 immediately (perhaps after finishing this section). Questions addressed in Sect. 6 have arisen in discussions with Anders Björner and Afshin Goodarzi. Here, we briefly survey these questions.

It is not hard to see that every lexicographically shellable poset is $A$-shellable where $A$ is the set of all atoms equipped with an appropriate linear order. On the other hand, it is not hard to find an $A$-shellable poset (again with $A$ consisting of all atoms) which is not lexicographically shellable.

We can also ask more subtle questions about the relative power of Theorems 2.1 and 2.2 compared with lexicographic shellability. (We skip Theorem 2.3 since it is of a different spirit.)

The conditions of Theorem 2.2 are analogous to the conditions on recursive atom orderings from [5], and in particular, Theorem 2.2 preserves lexicographic shellability (if the “shellable” assumptions are changed into “lexicographically shellable”) as well as lexicographically shellable posets satisfy the conditions of Theorem 2.2. The added value of Theorem 2.2 appears when we use it with nonlexicographic assumptions.

Regarding Theorem 2.1, let us (again) consider the following two questions: whether a lexicographically shellable poset satisfies the criteria of Theorem 2.1; and whether lexicographic shellability is kept by the criteria of Theorem 2.1 (for linearly ordered $A$).

The answer to the first question is no. The answer to the second question is not known to the author. We just remark that the proof of Theorem 2.1 might produce nonlexicographic shelling even if all posets in the conditions of Theorem 2.1 are assumed to be lexicographically shellable (not even a CC-shelling). We again refer to Sect. 6 for more details.

The above-mentioned remarks suggest that $A$-shellability using Theorem 2.1 and lexicographic shellability are perhaps in “generic position” regarding applicability in various situations.

3 Proofs of shellability criteria

Here, we prove Theorems 2.1, 2.2, and 2.3. We keep the notation introduced in the previous section.

Below, we also set up an additional notation common to proofs of Theorems 2.1 and 2.2. Let $C := C(P\langle A \rangle )$ and $C^+ = C(P\langle A^+ \rangle )$ be the sets of maximal chains in $P\langle A \rangle$ and $P\langle A^+ \rangle$. We know that $P\langle A \rangle$ is shellable; therefore, there is some shelling order $c_1, c_2, \ldots , c_t$ of all chains from $C$ (note that $P\langle A \rangle$ contains both $\hat{0}$ and $\hat{1}$). We are going to describe a shelling order on $C^+$. In both cases, we start with $c_1, \ldots , c_t$ and then we continue with chains containing $a^+$. This way, if we show that we have a shelling order, it will immediately be an $A^+$-shelling.

3.1 Proof of Theorem 2.1

We choose some order $q_1, \ldots , q_u$ of elements of $Q$ such that $i \le j$ if ${{\mathrm{rk}}}(q_i) \le {{\mathrm{rk}}}(q_j)$. In particular, $q_1 = a^+$. For every $q_i \in Q$, we have an order of maximal chains in the interval $[a^+,q_i]$ inducing a shelling of this interval, by condition (ii).

Now, we describe a shelling order of all maximal chains from $C^+{\setminus } C$. (We already have an order on $C$.) Let $c$ be a chain from $C^+ {\setminus } C$, and the index $i(c)$ is denoted in such a way that $q_{i(c)}$ is the element of $c \cap Q$ with the largest rank. Note that if $r \in c$, $r \ne \hat{0}$, and ${{\mathrm{rk}}}(r) < {{\mathrm{rk}}}(q_{i(c)})$, then $r \in Q$.

Now, let $c$ and $c'$ be two different chains from $C^+ {\setminus } C$ and we want to describe when $c'$ is before $c$.

The first criterion is whether $i(c') < i(c)$. That is, if $i(c') < i(c)$, then $c'$ is sooner in the order than $c$ (and symmetrically $c'$ is later if $i(c')>i(c)$); see Fig. 6, on the left.

Fig. 6

Three cases when $c'$ appears before $c$

If $i(c) = i(c')$, then we have the following second criterion. Let $q = q_{i(c)} = q_{i(c')}$. We look at the two maximal chains $\underline{c} = c \cap [a^+,q]$ and $\underline{c}' = c' \cap [a^+,q]$ in the interval $[a^+,q]$. As we sooner realized, if $\underline{c} \ne \underline{c}'$, then there is order of these chains inducing a shelling on $[a^+,q]$. This induces the order of $c$ and $c'$; see Fig. 6, in the middle. If $\underline{c} = \underline{c}'$, we need a third criterion.

Now, we assume that $i(c) = i(c')$ and $\underline{c} = \underline{c}'$. The element $q$ is defined as above. We set $\bar{c} = c \cap I(q)$ and $\bar{c}' = c' \cap I(q)$ recalling that $I(q)$ is the interval $[q, \hat{1}]$. Both chains $\bar{c}$ and $\bar{c}'$ are maximal chains in $I(q)\langle A(q) \rangle$ due to the choice of $q = q_{i(c)} = q_{i(c')}$. The condition (iv) in the statement of the theorem implies that $I(q)\langle A(q) \rangle$ is shellable. We set that $c'$ appears before $c$ in our shelling if and only if $\bar{c}'$ appears before $\bar{c}$ in the shelling of $I(q)\langle A(q) \rangle$; see Fig. 6, on the right.

We have described an order of chains in $C^+$. Now, we have to prove that it is indeed a shelling order. That is, we have to prove condition (Sh). In the sequel, we, therefore, assume that $c$ and $c'$ are given, as in (Sh), and we seek for $c^*$.

If $c \in C$, then we find required $c^*$ immediately from shellability of $P\langle A \rangle$. In the sequel, we assume $c \in C^+ {\setminus } C$ and we set $q = q_{i(c)}$. We distinguish several cases.

• 1. $q \not \in c'$. In this case we use the edge falling property. Let $q'$ be the element of $c$ such that $q {\ > \cdot \ }q'$ and $p$ be the element of $c$ such that $p {\ > \cdot \ }q$. The edge falling property implies that there is $p' \in P\langle A \rangle$ such that $p {\ > \cdot \ }p' {\ > \cdot \ }q'$. We set up $c^* = (c \cup \{p'\}) {\setminus } \{q\}$. Obviously, $c^*$ satisfies the required properties.

• 2. $q \in c'$, and $\underline{c} \ne \underline{c}'$ (where $\underline{c} = c \cap [a^+,q]$ and $\underline{c}' = c' \cap [a^+,q]$). By their definition, $c'$ appears before $c$, and thus due to the first criterion we have that $i(c') \le i(c)$. Now, since $q \in c'$, it follows that $i(c') = i(c)$ and, therefore, $q = q_{i(c')}$ (that is, $q$ is the element of $c' \cap Q$ of the highest rank). In addition, due to the second criterion, we know that $\underline{c}'$ appears before $\underline{c}$ in the shelling of $[a^+,q]$. Therefore, there is a maximal chain $\underline{c}^*$ in $[a^+,q]$ appearing before $\underline{c}$ which coincides with $\underline{c}$ with exception of one level and such that $\underline{c} \cap \underline{c}^* \supseteq \underline{c} \cap \underline{c}'$. We set $c^*$ so that it coincides with $\underline{c}^*$ on $Q$ and with $c$ on $P\langle A \rangle$.

• 3. $q \in c'$, and $\underline{c} = \underline{c}'$. We again have $q = q_{i(c')}$. Hence, the third criterion on comparison of $c$ and $c'$ applies. That is, $\bar{c}'$ appears before $\bar{c}$ in the shelling of $I(q)\langle A(q) \rangle$. Similarly, as in the previous case, there is, therefore, a maximal chain $\bar{c}^*$ in $I(q)\langle A(q) \rangle$ appearing before $\bar{c}$ which coincides with $\bar{c}$ with exception of one level and such that $\bar{c} \cap \bar{c}^* \supseteq \bar{c} \cap \bar{c}'$ (recall that $\bar{c} = c \cap I(q)$ and $\bar{c}' = c' \cap I(q)$). We set $c^*$ so that it coincides with $c$ on $Q$ and with $\bar{c}^*$ on $P\langle A \rangle$.

We have verified condition (Sh) in all cases. This concludes the proof of Theorem 2.1.

3.2 Proof of Theorem 2.2

In this case, it is easier to set up the order of shelling $C^+{\setminus } C$. (Let us recall that the order on $C$ is already set up and that the chains from $C^+ {\setminus } C$ will follow after the chains from $C$.)

Every chain $c \in C^+ {\setminus } C$ contains $a^+$. Let $\bar{c}$ be in this case $c \cap I(a^+)$. We set that $c'$ precedes $c$ if and only if $\bar{c}'$ precedes $\bar{c}$ in the shelling from condition (ii) of the statement of the theorem.

Now, we need to verify condition (Sh) to be sure that we have indeed a shelling order. Similarly, as in the proof of previous theorem, we assume that $c$ and $c'$ are given, as in (Sh), and we seek for $c^*$. We distinguish several cases.

• 1. $c \in C$. In this case, we know that $c'$ appears before $c$ and thus $c' \in C$. Therefore, we can find suitable $c^*$ from the shellability of $P\langle A \rangle$.

• 2. $c \in C^+ {\setminus } C$ and $c' \in C^+ {\setminus } C$. In this case, $\bar{c}'$ appears before $\bar{c}$; therefore, there is $\bar{c}^*$ from shelling of $I(a^+)$ such that $\bar{c}$ and $\bar{c}^*$ differ in one level only and that $\bar{c}^* \cap \bar{c} \supseteq \bar{c}' \cap \bar{c}$. We set $c^* = \bar{c}^* \cup \{\hat{0}\}$. This choice of $c^*$ obviously satisfies the required properties.

• 3. $c \in C^+ {\setminus } C$, $c' \in C$, and $c \cap A(a^+) \ne \emptyset$. Let $b \in c \cap A(a^+)$. Then, there is $a \in A$ such that $b {\ > \cdot \ }a$ due to the definition of $A(a^+)$. Let us set $c^* := (c {\setminus } \{a^+\}) \cup \{a\}$. Then, $c^* \cap c \supseteq c' \cap c$ since $c'$ misses $a^+$. See Fig. 7, on the left.

• 4. $c \in C^+ {\setminus } C$, $c' \in C$, and $c \cap A(a^+) = \emptyset$. As usual, let $q$ be the largest element of $c \cap Q$. Let $p$ be the element of $c \cap P\langle A \rangle$ such that $p {\ > \cdot \ }q$. See Fig. 7, on the right. Condition (iii) in the statement of the theorem implies that there is a maximal chain $c'_2$ in the interval $[a^+,p]$ such that $c'_2 \cap A(a^+) \ne \emptyset$. Let $\bar{c}'_2$ be the maximal chain in $I(a^+)$ which agrees with $c'_2$ on $[a^+,p]$ and which agrees with $c$ on $[p,\hat{1}]$. Note that $\bar{c}'_2$ precedes $\bar{c}$ in the shelling of $I(a^+)$ since $\bar{c}'_2 \cap A(a^+) \ne \emptyset$ whereas $c \cap A(a^+) = \emptyset$. Therefore, by (Sh), there is a chain $\bar{c}^*$ in $I(a^+)$ which agrees with $\bar{c}$ in all levels but one and which satisfies $\bar{c}^* \cap \bar{c} \supseteq \bar{c}'_2 \cap c$. In particular, $\bar{c}^*$ agrees with $\bar{c}$ on $p$ and all elements above $p$. Now, we set $c^* := \bar{c}^* \cup \{\hat{0}\}$. We have that $c^* \cap c \supseteq c' \cap c$ since $c' \cap c \subseteq P\langle A \rangle$.

Fig. 7

Cases 3 and 4 in the proof of Theorem 2.2

This finishes the proof of Theorem 2.2.

3.3 Proof of Theorem 2.3

Let $C = C(P\langle A \rangle )$ and $C' = C(P\langle A' \rangle )$ be the sets of maximal chains of $P\langle A \rangle$ and $P\langle A' \rangle$. We have that $C' \subset C$. Since $P\langle A \rangle$ is $A$-shellable, we have a shelling order on $C$ respecting $A$. We simply inherit this order on $C'$. It respects $A'$; however, we have to show that it is indeed a shelling order.

Let $c$ and $c'$ be chains in $P\langle A' \rangle$ as in condition (Sh). We look for a suitable $c^*$ from (Sh).

Chains $c$ and $c'$ also belong to $P\langle A \rangle$. Since we started with a shelling on $C$, there is $c^{**} \in C$ such that $c^{**} \cap c \supseteq c' \cap c$ and $c^{**}$ differs from $c$ in one level. If $c^{**}$ belongs to $C'$, we set $c^* := c^{**}$ and we are done.

Now, let us assume that $c^{**} \not \in C'$. Let $b$ and $p$ be the elements of $c^{**}$ of rank 1 and 2, respectively, in particular $p {\ > \cdot \ }b$. Since $c^{**} \notin C'$, it follows from the definition of $C'$ that $b \in A {\setminus } A'$. Moreover, $c$ and $c^{**}$ differ in only one level. Therefore, they differ in level 1 and $p \in c$. This implies that $p \in P\langle A' \rangle$. By applying now assumption (ii) of the theorem for elements $b$ and $p$, we conclude that there is $b' \in A'$ appearing before $b$ in $A$ such that $p {\ > \cdot \ }b'$. Let us set $c^* := (c^{**} {\setminus } \{b\}) \cup \{b'\}$. Then, $c^*$ appears before $c^{**}$ in the shelling of $C$ and hence also before $c$. In addition, $c^{*}$ and $c$ have to differ in level $1$ (only) by definition of $c^*$. Thus, we obtain $c^* \cap c = c^{**} \cap c \supseteq c' \cap c$ as required.

This finishes the proof of Theorem 2.3.

4 Preliminaries on the (pinched) Veronese poset

The $n$-th Veronese poset $({\mathcal {V}}_n, \le )$ is given by

$$\begin{aligned} {\mathcal {V}}_n = \{(\alpha _1, \ldots , \alpha _n) \in {\mathbb {N}_0}^n :\alpha _1 + \cdots + \alpha _n \equiv 0 \pmod n\} \end{aligned}$$

and $\mathbf {a}\le \mathbf {b}$ for $\mathbf {a}= (\alpha _1, \ldots , \alpha _n)$, $\mathbf {b}= (\beta _1, \ldots , \beta _n)$ if and only if $\alpha _i \le \beta _i$ for $i \in [n]$. In the sequel, we often write $\mathbf {a}= \alpha _1\alpha _2\alpha _3$ instead of $\mathbf {a}= (\alpha _1, \alpha _2, \alpha _3)$ and so on for higher $n$. We can also use brackets to separate coordinates in expressions such as $(\alpha _1 + 1)01\alpha _4$ instead of $(\alpha _1 + 1, 0, 1, \alpha _4)$.

In slightly more general setting, for positive integers $m$ and $n$ we also define

$$\begin{aligned} {\mathcal {V}}_{m,n} = \{(\alpha _1, \ldots , \alpha _n) \in {\mathbb {N}_0}^n :\alpha _1 + \cdots + \alpha _n \equiv 0 \pmod m\}. \end{aligned}$$

We again have that $\mathbf {a}\le \mathbf {b}$ if $\mathbf {a}$ is less than or equal to $\mathbf {b}$ in every coordinate. In particular, we have ${\mathcal {V}}_n = {\mathcal {V}}_{n,n}$.

The $n$-th pinched Veronese poset $({\mathcal {V}}^{\bullet }_n, \preceq )$ is a (noninduced) subposet of ${\mathcal {V}}_n$ given by the following data.

$$\begin{aligned} {\mathcal {V}}^{\bullet }_n = \{\mathbf {a}\in {\mathcal {V}}_n :\mathbf {a}\ne \mathbf {j}\}. \end{aligned}$$

Here, $\mathbf {j}= 1\cdots 1$. The partial order on ${\mathcal {V}}^{\bullet }_n$ is given by $\mathbf {a}\preceq \mathbf {b}$ if $\mathbf {a}\le \mathbf {b}$ and $\mathbf {b}- \mathbf {a}\ne \mathbf {j}$.

We also define $\mathbf {0}= 0\cdots 0$ to be the minimal element of ${\mathcal {V}}^{\bullet }_n$.

4.1 Arithmetic operations on ${\mathcal {V}}_n$ and ${\mathcal {V}}^{\bullet }_n$

We consider elements of ${\mathcal {V}}_n$ and ${\mathcal {V}}^{\bullet }_n$ as vectors in ${\mathbb {Z}}^n$. We can then sum and subtract these vectors. For a set $X \subseteq {\mathbb {Z}}^n$ and vector $\mathbf {v}\in {\mathbb {Z}}^n$, we let $X \oplus \mathbf {v}$ to be the set $\{\mathbf {x}+ \mathbf {v}:\mathbf {x}\in X\}$. Similarly, $X \ominus \mathbf {v}:= \{\mathbf {x}- \mathbf {v}:\mathbf {x}\in X\}$. Let $[\mathbf {0},\mathbf {z}]$ be an interval in ${\mathcal {V}}^{\bullet }_n$ and $\mathbf {x}\in [\mathbf {0},\mathbf {z}]$. In our considerations, we will often use the fact that $[\mathbf {x}, \mathbf {z}]$ and $[\mathbf {0},\mathbf {z}- \mathbf {x}]$ are isomorphic; more precisely, $[\mathbf {0},\mathbf {z}- \mathbf {x}] = [\mathbf {x},\mathbf {z}] \ominus \mathbf {x}$.

4.2 Shellability of intervals in ${\mathcal {V}}_{m,n}$

It is not hard to observe, using known results, that every interval in ${\mathcal {V}}_{m,n}$ is shellable. We will actually need this for considering the pinched version, and thus we provide full details.

Proposition 4.1

Let $m$ and $n$ be positive integers. For any $\mathbf {z}\in {\mathcal {V}}_{m,n}$, the interval $[\mathbf {0},\mathbf {z}]$ in ${\mathcal {V}}_{m,n}$ is a shellable poset.

Proof

We have that ${\mathcal {V}}_{m,n}$ is a subposet of ${\mathcal {V}}_{1,n}$. We first observe that $[\mathbf {0}, \mathbf {z}]$ is shellable as an interval in ${\mathcal {V}}_{1,n}$ and then we deduce that $[\mathbf {0}, \mathbf {z}]$ is shellable as an interval in ${\mathcal {V}}_{m,n}$ as well.

It is not hard to observe that $[\mathbf {0}, \mathbf {z}]$ as an interval in ${\mathcal {V}}_{1,n}$ is a graded modular lattice: By modular we mean that

$$\begin{aligned} {{\mathrm{rk}}}(\mathbf {a}) + {{\mathrm{rk}}}(\mathbf {b}) = {{\mathrm{rk}}}(\mathbf {a}\vee \mathbf {b}) + {{\mathrm{rk}}}(\mathbf {a}\wedge \mathbf {b}). \end{aligned}$$

If $\mathbf {a}= \alpha _1\cdots \alpha _n$ and $\mathbf {b}= \beta _1\cdots \beta _n$, then

$$\begin{aligned} \mathbf {a}\vee \mathbf {b}= \max (\alpha _1,\beta _1)\cdots \max (\alpha _n,\beta _n) \end{aligned}$$

and

$$\begin{aligned} \mathbf {a}\wedge \mathbf {b}= \min (\alpha _1,\beta _1)\cdots \min (\alpha _n,\beta _n). \end{aligned}$$

These relations easily imply modularity of ${\mathcal {V}}_{1,n}$. Therefore, ${\mathcal {V}}_{1,n}$ is shellable by [2, Theorem 3.7] (semimodular would be sufficient).

The fact that ${\mathcal {V}}_{m,n}$ is shellable follows from the fact that the shellability is preserved by rank selections. Indeed, if we start with $[\mathbf {0}, \mathbf {z}]$ as an interval in ${\mathcal {V}}_{1,n}$, we remove elements exactly in levels not divisible by $m$ in order to turn it into an interval in ${\mathcal {V}}_{m,n}$. This means that we remove the same number of elements from every maximal chain. Therefore, ${\mathcal {V}}_{m,n}$ is shellable by [3, Theorem 11.13]. $\square$

5 Proof of Theorem 1.1

The task of this section is to prove Theorem 1.1. Throughout this section, we assume that $n \ge 4$ is fixed.

5.1 The induction mechanism

Let $A^\mathrm{all}$ be the set of all atoms of ${\mathcal {V}}^{\bullet }_n$.² We will consider several linear orders on $A^\mathrm{all}$ and some of its subsets. Let $\mathbf {x}= \xi _1\cdots \xi _n \in {\mathbb {Z}}^n$. For $\ell \in [n]$ we set $\mathbf {x}^{(\ell )} = \xi _{\ell } \cdots \xi _n$. We also set $A^{(\ell )}$ to be the subset of $A^\mathrm{all}$ made of all $\mathbf {x}\in A^\mathrm{all}$ such that $\mathbf {x}^{(\ell )} \ne 0\cdots 0$. We consider two linear orders, $<^L$ and $<^S$ on $A^\mathrm{all}$.

The first order is the lexicographic order given in the following way. Let $\mathbf {s}= \sigma _1\cdots \sigma _n$ and $\mathbf {t}= \tau _1\cdots \tau _n$. We set $\mathbf {s}<^L \mathbf {t}$ if and only if there is $j \in [n]$ such that $\sigma _i = \tau _i$ for $i < j$ and $\sigma _j < \tau _j$.

The second order is a $specific$ order which we describe now. We set $A^S := A^{(n)} {\setminus } \{1\cdots 102\}$. The smallest elements in $<^S$ order are the elements of $A^S$ sorted lexicographically by the $<^L$ order. Then, the element $1\cdots 102$ follows. Finally, the elements of $A^\mathrm{all}{\setminus } A^{(n)}$ follow sorted again by the $<^L$ order. The reader is referred to Table 1 for more concrete comparison of these orders (for $n = 4$).

Table 1 Atoms of $A^\mathrm{all}$ and $A^{(4)}$ sorted by the $<^L$ order and atoms of $A^\mathrm{all}$ sorted by the $<^S$ order for $n= 4$

We will need to work with the following ordered sets. Let $\mathbf {a}^L_i$ be the $i$th smallest element of $A^\mathrm{all}$ in the $<^L$ order and similarly $\mathbf {a}^S_i$ be the $i$th smallest element in the $<^S$ order. We then set $A^L_k := \{\mathbf {a}_1^L,\ldots ,\mathbf {a}_k^L\}$ and $A^S_k := \{\mathbf {a}_1^S,\ldots ,\mathbf {a}_k^S\}$. We also set $A^{(\ell )}_k$ to be the set of the first $k$ elements of $A^{(\ell )}$ in the $<^L$ order (this time, we omit the superscript $L$ for simpler notation).

Now, let $I = [\mathbf {0},\mathbf {z}]$ be any interval in ${\mathcal {V}}^{\bullet }_n$. Our task is to show that $I$ is shellable. In order to explain our next step, let us use the following simplification of notation. Let $A$ be some set of atoms of $I$ equipped with the $<^L$ order (resp. with the $<^S$ order). Instead of saying that $I\langle A \rangle$ is $A$-shellable we say that $I\langle A \rangle$ is $(L)$-shellable (resp. $I\langle A \rangle$ is $(S)$-shellable). This simplifies the notation when our typical $A$ will be of form $A^{(\ell )}_k \cap I$. In addition, it also explicitly emphasizes whether $A$ is equipped with the $<^L$ order or the $<^S$ order.

Our task will be to prove the assertions below. The first two assertions depend on $k \le |A^\mathrm{all}|$. The third assertion depends on $\ell \in [n-1]$ and $k \le |A^{(\ell + 1)}|$.

$$\begin{aligned} \begin{array}{cl} ({\mathbf {A}}^L_{k}) &{} \hbox {The poset}\;I\langle A^L_k \cap I \rangle \; \hbox {is}\; (L)\hbox {-shellable (if nonempty)}.\\ ({\mathbf {A}}^S_{k}) &{} \hbox {The poset}\;I\langle A^S_k \cap I \rangle \; \hbox {is}\; (S)\hbox {-shellable (if nonempty)}.\\ ({\mathbf {A}}^{(\ell + 1)}_k) &{} \hbox {The poset}\;I\langle A^{(\ell + 1)}_k \cap I \rangle \;\hbox {is}\;(L)\hbox {-shellable}.\\ \end{array} \end{aligned}$$

Proposition 5.1

Let $I = [\mathbf {0},\mathbf {z}]$ be any interval in ${\mathcal {V}}^{\bullet }_n$. Then, assertions $({\mathbf {A}}^L_{k})$ and $({\mathbf {A}}^S_{k})$ are valid for any positive integer $k \le |A^\mathrm{all}|$ and assertion $({\mathbf {A}}^{(\ell + 1)}_k)$ is valid for any $\ell \in [n-1]$ and any positive integer $k \le |A^{(\ell + 1)}|$.

Theorem 1.1 follows from the proposition by setting $k = |A^\mathrm{all}|$ in $({\mathbf {A}}^L_k)$ (or $({\mathbf {A}}^S_k)$).

The task is to prove Proposition 5.1 by a double induction. The first (outer) induction is over ${{\mathrm{rk}}}(\mathbf {z})$. The second (inner) induction is slightly unusual—we first prove $({\mathbf {A}}^L_{k})$ by induction in $k$ (see Lemmas 5.2, 5.3, and 5.4 below), then we prove $({\mathbf {A}}^S_{k})$ by induction in $k$ (see Lemmas 5.2, 5.3, and 5.5 below), and finally, we prove $({\mathbf {A}}^{(\ell + 1)}_k)$ already assuming $({\mathbf {A}}^L_{k})$ directly with no induction (see Lemma 5.6 below). The fact that we use the induction is also the reason why we need to prove all assertions $({\mathbf {A}}^L_{k})$, $({\mathbf {A}}^S_{k})$, and $({\mathbf {A}}^{(\ell + 1)}_k)$, although only $({\mathbf {A}}^L_{k})$ is sufficient for deducing Theorem 1.1. We need the induction assumption strong enough so that the induction works well.

We also remark that $I$ does not need to contain all atoms from $A^\mathrm{all}$ (for example, if the first coordinate of $\mathbf {z}$ is zero). This is why we need to consider, for example, $(L)$-shellability of $I\langle A^L_k \cap I \rangle$ instead of (possibly expected) $(L)$-shellability of $I\langle A^L_k \rangle$.

For improved readability, we decompose the induction step into several lemmas, with different approaches on how to prove them. From now on, we assume that $\mathbf {z}$ and $I = [\mathbf {0},\mathbf {z}]$ are fixed.

Lemma 5.2

Let us assume that Proposition 5.1 is valid for every interval $[\mathbf {0},\mathbf {y}]$ with ${{\mathrm{rk}}}(\mathbf {y}) < {{\mathrm{rk}}}(\mathbf {z})$. Then, $I\langle A^L_1 \cap I \rangle$ is $(L)$-shellable and $I\langle A^S_1 \cap I \rangle$ is $(S)$-shellable (if they are nonempty), that is, $({\mathbf {A}}^L_{1})$ and $({\mathbf {A}}^S_{1})$ are valid.

Lemma 5.3

Let us assume that Proposition 5.1 is valid for every interval $[\mathbf {0},\mathbf {y}]$ with ${{\mathrm{rk}}}(\mathbf {y}) < {{\mathrm{rk}}}(\mathbf {z})$. Then, $I\langle A^L_2 \cap I \rangle$ is $(L)$-shellable and $I\langle A^S_2 \cap I \rangle$ is $(S)$-shellable (if they are nonempty), that is, $({\mathbf {A}}^L_{2})$ and $({\mathbf {A}}^S_{2})$ are valid.

Lemma 5.4

Let $k \in \{3, \ldots , |A^\mathrm{all}|\}$. Let us assume that Proposition 5.1 is valid for every interval $[\mathbf {0},\mathbf {y}]$ with ${{\mathrm{rk}}}(\mathbf {y}) < {{\mathrm{rk}}}(\mathbf {z})$. Let us also assume that $({\mathbf {A}}^L_{k'})$ is valid for the interval $I = [\mathbf {0},\mathbf {z}]$ and for $k' < k$. Then, $I\langle A^L_k \cap I \rangle$ is $(L)$-shellable (if nonempty), that is, $({\mathbf {A}}^L_{k})$ is valid.

Lemma 5.5

Let $k \in \{3, \ldots , |A^\mathrm{all}|\}$. Let us assume that Proposition 5.1 is valid for every interval $[\mathbf {0},\mathbf {y}]$ with ${{\mathrm{rk}}}(\mathbf {y}) < {{\mathrm{rk}}}(\mathbf {z})$. Let us also assume that $({\mathbf {A}}^S_{k'})$ is valid for the interval $[\mathbf {0},\mathbf {z}]$ and for $k' < k$. Then, $I\langle A^S_k \cap I \rangle$ is $(S)$-shellable (if nonempty), that is, $({\mathbf {A}}^S_{k})$ is valid.

Lemma 5.6

Let $\ell \in [n-1]$ and $k \in \{1, \ldots , |A^{(\ell +1)}|\}$. Let us assume that $({\mathbf {A}}^L_{k'})$ is valid for the interval $I = [\mathbf {0},\mathbf {z}]$ and for $k' = |A^\mathrm{all}|$. Then, $I\langle A^{(\ell +1)}_k \cap I \rangle$ is $(L)$-shellable (if nonempty), that is, $({\mathbf {A}}^{(\ell +1)}_{k})$ is valid.

We remark that Lemma 5.3 implies Lemma 5.2. Similarly, Lemmas 5.4 and 5.5 together imply Lemma 5.3. The reason why we state Lemmas 5.2 and 5.3 separately is that Lemma 5.2 is used in the proof of Lemma 5.3, and this one is used in the proofs of Lemmas 5.4 and 5.5.

Assuming the validity of the lemmas, we immediately obtain a proof of Proposition 5.1 as described just below the statement of the proposition. Therefore, it is sufficient to prove the lemmas.

5.2 Proofs of Lemmas 5.2-5.6

Proof of Lemma 5.2

Let $A := A^L_1 = A^S_1 = \{\mathbf {a}^+\}$ where $\mathbf {a}^+ = 0\cdots 0n$. We also assume that $\mathbf {a}^+ \in I$ otherwise we encounter the “empty” case. Thus, $(L)$-shellability of $I\langle A^L_1 \cap I \rangle$ and $(S)$-shellability of $I\langle A^S_1 \cap I \rangle$ coincide with the usual shellability of $I\langle A \rangle$ (since $A$ contains a single atom). We easily observe that the interval $[\mathbf {a}^+,\mathbf {z}]$ is shellable, since it is isomorphic to $[\mathbf {0}, \mathbf {z}- \mathbf {a}^+]$, and $[\mathbf {0},\mathbf {z}- \mathbf {a}^+]$ is shellable by our assumption. It follows that $I\langle A \rangle$ is shellable by extending every maximal chain of $[\mathbf {a}^+,\mathbf {z}]$ by $\{\mathbf {0}\}$ and considering the same order of maximal chains as for shelling $[\mathbf {a}^+,\mathbf {z}]$. $\square$

For the proof of a next lemma, the following claim will be useful.

Claim 5.7

Let $\mathbf {u}= \omega _1 \cdots \omega _{n-1}0$ be a nonzero element of ${\mathcal {V}}^{\bullet }_n$ with the last coordinate $0$, or $\mathbf {u}= 1\cdots 102$. Then, there is $\mathbf {v}\in A^S$ such that $\mathbf {v}\prec \mathbf {u}+ 1\cdots 102$.

Proof

If $\mathbf {u}= 1\cdots 102$, we can set $\mathbf {v}:= 1\cdots 1003$, for example.

Further, we assume $\mathbf {u}\ne 1\cdots 102$. Let $i$ be such that $\omega _i \ge 1$ while we prefer $i \ne n-1$ if possible; and furthermore, if we meet the first preference, we prefer $\omega _i \ne 2$ if possible.

If we meet both preferences, we set $\mathbf {v}:= 1\cdots 121\cdots 101$ where the “2” occurs in the $i$th position. In particular, $\mathbf {v}\in A^S$. We also have $\mathbf {u}+ 1\cdots 102 - \mathbf {v}= \omega _1\cdots \omega _{i-1}(\omega _i + 1)\omega _{i+1}\cdots \omega _{n-1}1$, which is different from $\mathbf {j}$ since $\omega _i \ne 2$. That is, $\mathbf {u}+ 1\cdots 102 \succ \mathbf {v}$.

If we meet the first preference only, then we still set $\mathbf {v}:= 1\cdots 121\cdots 101$ where the “2” occurs on the $i$th position. This time we conclude $\mathbf {u}+ 1\cdots 102 - \mathbf {v}\ne \mathbf {j}$ by realizing that there is $j \ne i,n-1$ such that $\omega _j \ne 1$ (here, we use $n \ge 4$).

Finally, if we meet no preference, then $\mathbf {u}= 0\cdots 0(r\cdot n)0$ for some integer $r$. In this case, we set $\mathbf {v}= 1\cdots 1021$ and we have $\mathbf {u}+ 1\cdots 102 - \mathbf {v}= 0\cdots 01(rn-2)1 \ne \mathbf {j}$. $\square$

Proof of Lemma 5.3

We have $\mathbf {a}^L_1 = \mathbf {a}^S_1 = 0\cdots 0n$ and $\mathbf {a}^L_2 = \mathbf {a}^S_2 = 0\cdots 01(n-1)$. We set $A := \{\mathbf {a}^L_1\}$ and $A^+ := \{\mathbf {a}^L_1,\mathbf {a}^L_2\}$. With this setting, our only task is to show that $I\langle A^+ \cap I \rangle$ is $(L)$-shellable (which coincides with $(S)$-shellability). We can assume that $\mathbf {a}^L_2 \in I$, otherwise $A^+ \cap I$ coincides with $A \cap I$ and we conclude by Lemma 5.2. We can also assume that $\mathbf {a}^L_1 \in I$; otherwise $A^+ \cap I$ contains a single atom only and we obtain $(L)$-shellability of $I\langle A^+ \cap I \rangle$ in the same way as in the proof of Lemma 5.2.

Altogether, we assume $\mathbf {a}^L_1, \mathbf {a}^L_2 \in I$ and, therefore, our task simplifies to showing $(L)$-shellability of $I\langle A^+ \rangle$. We are going to use Theorem 2.2 for this task. For consistent notation, we set $Q := I\langle A^+ \rangle {\setminus } I\langle A \rangle$ and $\mathbf {a}^+ = \mathbf {a}^L_2$ (we prefer using bold $\mathbf {a}^+$ rather than $a^+$ in Theorem 2.2 emphasizing that $\mathbf {a}^+ \in {\mathcal {V}}^{\bullet }_n$). We also recall that $I(\mathbf {a}^+) = [\mathbf {a}^+,\mathbf {z}]$ and $A^\mathrm{all}(\mathbf {a}^+)$ is the set of all atoms of $I(\mathbf {a}^+)$ whereas $A(\mathbf {a}^+)$ is the set of only those atoms of $I(\mathbf {a}^+)$ which belong to $I\langle A \rangle$ as well. We need to check the conditions of Theorem 2.2.

The first condition, $A$-shellability of $I\langle A \rangle$, just follows from Lemma 5.2.

For checking the remaining two conditions, we need more intrinsic description of $Q$. Note that in our notation $(\mathbf {q}- \mathbf {a}^+)^{(n)}$ denotes the last coordinate of $\mathbf {q}- \mathbf {a}^+$. Consult Fig. 8 while following the proof of the next claim and the rest of the proof of the lemma.

Fig. 8

Schematic drawing of $I\langle A^+ \rangle$ in Lemma 5.3

Claim 5.8

We have the following description of $Q$.

$$\begin{aligned} Q = \{\mathbf {q}\in I\langle A^+ \rangle :\mathbf {q}\succeq \mathbf {a}^+, (\mathbf {q}- \mathbf {a}^+)^{(n)} = 0 \hbox { or } \mathbf {q}- \mathbf {a}^+ = 1\cdots 102 \}. \end{aligned}$$

Proof

If $\mathbf {q}\in Q$, then it must satisfy $\mathbf {q}\succeq \mathbf {a}^+$. Therefore, we can consider $\mathbf {q}$ satisfying $\mathbf {q}\succeq \mathbf {a}^+$ and our task is to determine whether $\mathbf {q}\in Q$.

Let us first consider the case $(\mathbf {q}- \mathbf {a}^+)^{(n)} = 0$. Then, $\mathbf {q}^{(n)} = (\mathbf {a}^+)^{(n)} = n - 1$, and, therefore, $\mathbf {q}\not \succeq \mathbf {a}^L_1 = 0\cdots 0n$. We conclude $\mathbf {q}\in Q$ since $\mathbf {q}\notin I\langle A \rangle$.

Now, let us consider the case $(\mathbf {q}- \mathbf {a}^+)^{(n)} \ge 1$. Then, $\mathbf {q}\ge \mathbf {a}^L_1$. We deduce $\mathbf {q}\succeq \mathbf {a}^L_1$ unless $\mathbf {q}= \mathbf {a}^L_1 + \mathbf {j}$. That is, $\mathbf {q}\notin Q$ unless $\mathbf {q}= (0\cdots 0n) + (1\cdots 1)= 1\cdots 1(n+1)$. In this case, $\mathbf {q}- \mathbf {a}^+ = 1\cdots 102$. $\square$

Using Claim 5.8, it is easy to check the second condition in Theorem 2.2.

We first observe that Claim 5.8 implies the following description of $A(\mathbf {a}^+)$:

$$\begin{aligned} A(\mathbf {a}^+) = \{\mathbf {p}' \in I:\mathbf {p}' - \mathbf {a}^+ \in A^S\}. \end{aligned}$$

(1)

Indeed, $A(\mathbf {a}^+)$ consists of those elements in $I$ covering $\mathbf {a}^+$ which do not belong to $Q$. By Claim 5.8 and the definition of $A^S$, we obtain that $A(\mathbf {a}^+)$ consists of those elements $\mathbf {p}' \in I$ covering $\mathbf {a}^+$ such that $\mathbf {p}' - \mathbf {a}^+ \in A^S$. This immediately yields the required description (1) since if $\mathbf {p}' - \mathbf {a}^+ \in A^S$, then $\mathbf {p}' {\ > \cdot \ }\mathbf {a}^+$.

Now, by the assumptions of the lemma, the interval $[\mathbf {0}, \mathbf {z}- \mathbf {a}^+]$ is $(S)$-shellable. This interval is isomorphic to $I(\mathbf {a}^+)$ by adding $\mathbf {a}^+$. Therefore, using (1), this isomorphism induces a shelling of $I(\mathbf {a}^+)$ required by condition (ii) of Theorem 2.2.

Finally, we want to check condition (iii) of Theorem 2.2. Therefore, we are given $\mathbf {q}\in Q$ and $\mathbf {p}\in I\langle A \rangle$ such that $\mathbf {p}$ covers $\mathbf {q}$. Our task is to show that $\mathbf {p}\in I(\mathbf {a}^+)\langle A(\mathbf {a}^+) \rangle$. Recalling (1), our task is to show that there is $\mathbf {p}' \in I$ such that $\mathbf {p}' - \mathbf {a}^+ \in A^S$ and $\mathbf {p}\succeq \mathbf {p}'$. Note that the condition $\mathbf {p}' \in I$ follows from $\mathbf {p}\succeq \mathbf {p}'$, and thus we do not need to check it in the following verification separately.

A natural candidate for $\mathbf {p}'$ is the element $\mathbf {p}'_\mathrm{cand} := \mathbf {a}^+ + (\mathbf {p}- \mathbf {q})$. We have $\mathbf {p}'_\mathrm{cand} \preceq \mathbf {p}$ since $\mathbf {p}- \mathbf {p}'_\mathrm{cand} = \mathbf {q}- \mathbf {a}^+$ and $\mathbf {q}\succeq \mathbf {a}^+$. Furthermore, $\mathbf {p}'_\mathrm{cand} - \mathbf {a}^+ = \mathbf {p}- \mathbf {q}$; therefore, we are done if $\mathbf {p}- \mathbf {q}\in A^S$. See Fig. 9, on the left.

It remains to consider $\mathbf {p}- \mathbf {q}\notin A^S$. In this case, we have to choose $\mathbf {p}'$ different from $\mathbf {p}'_\mathrm{cand}$. We further distinguish two cases whether $\mathbf {q}- \mathbf {a}^+ = 1\cdots 102$ or $(\mathbf {q}- \mathbf {a}^+)^{(n)} = 0$ (which is sufficient due to Claim 5.8 using $\mathbf {q}\in Q$) while we keep in mind that $\mathbf {p}- \mathbf {q}\notin A^S$. See Fig. 9, in the middle and on the right.

• 1. First, let us assume that $\mathbf {q}- \mathbf {a}^+ = 1\cdots 102$. We let $\mathbf {u}:= (\mathbf {p}- \mathbf {q})$. In particular, either $\mathbf {u}= 1\cdots 102$, or $\mathbf {u}^{(n)} = 0$ since $\mathbf {p}- \mathbf {q}\notin A^S$. By Claim 5.7, there is $\mathbf {v}\in A^S$ such that $\mathbf {v}\prec \mathbf {u}+ 1\cdots 102$. Let $\mathbf {p}' := \mathbf {v}+ \mathbf {a}^+$. Then, $\mathbf {p}' - \mathbf {a}^+ \in A^S$ and also $\mathbf {p}' \prec \mathbf {p}$ since $\mathbf {p}- \mathbf {p}' = (\mathbf {p}- \mathbf {q}) + (\mathbf {q}- \mathbf {a}^+) - \mathbf {v}= \mathbf {u}+ 1\cdots 102 - \mathbf {v}$ and $\mathbf {u}+ 1\cdots 102 \succ \mathbf {v}$.

• 2. Now, we assume $(\mathbf {q}- \mathbf {a}^+)^{(n)} = 0$. Since $\mathbf {p}\notin Q$, Claim 5.8 implies that $(\mathbf {p}- \mathbf {a}^+)^{(n)} > 0$ (and $\mathbf {p}- \mathbf {a}^+ \ne 1\cdots 102$). Therefore, $(\mathbf {p}- \mathbf {q})^{(n)} > 0$. Since $\mathbf {p}- \mathbf {q}\notin A^S$, we conclude $\mathbf {p}- \mathbf {q}= 1\cdots 102$. (This also implies that $\mathbf {q}\ne \mathbf {a}^+$.) Now, let $\mathbf {u}:= \mathbf {q}- \mathbf {a}^+$. By Claim 5.7, there is $\mathbf {v}\in A^S$ such that $\mathbf {u}+ 1\cdots 102 \succ \mathbf {v}$. We set $\mathbf {p}' := \mathbf {v}+ \mathbf {a}^+$. Then, $\mathbf {p}' - \mathbf {a}^+ \in A^S$ and also $\mathbf {p}\succ \mathbf {p}'$ since $\mathbf {p}- \mathbf {p}' = (\mathbf {p}- \mathbf {q}) + (\mathbf {q}- \mathbf {a}^+) + \mathbf {v}= 1\cdots 102 + \mathbf {u}- \mathbf {v}\succ 0$.

We have checked all conditions of Theorem 2.2. This concludes the proof of the lemma. $\square$

Fig. 9

Verifying condition (iii) of Theorem 2.2. If $\mathbf {p}- \mathbf {q}$ does not belong to $A^S$ (on the left), then we need to distinguish two further cases (in the middle and on the right). Label of an edge (a path) $\mathbf {s}\mathbf {t}$ is given by $\mathbf {t}- \mathbf {s}$

The following claim will be useful for the proof of the next lemma. Item (ii) of the claim is trivial; however, it will be useful to refer to it as stated in the claim.

Claim 5.9

• (i) Let $\mathbf {a}\in A^\mathrm{all}$ such that $\mathbf {a}\ne \mathbf {a}^L_1$. Then, there is $\mathbf {a}' \in A^\mathrm{all}$ such that $\mathbf {a}' <^L \mathbf {a}$ and $\mathbf {a}' \prec \mathbf {a}+ \mathbf {j}$. In addition, we can require $\mathbf {a}' \ne 1\cdots 102$.

• (ii) Let $\mathbf {a}:= \mathbf {a}^L_1$. Then, $\mathbf {a}' \prec \mathbf {a}+ \mathbf {j}$ for $\mathbf {a}' = \mathbf {a}^L_2$.

Proof

Let us start with item (i). Let $\mathbf {a}= 0\cdots 0\alpha _{\ell } \cdots \alpha _n$ where $\alpha _\ell \ne 0$. That is, we require $\mathbf {a}' \prec 1\cdots 1(\alpha _{\ell } + 1)\cdots (\alpha _n + 1)$. We have $\ell \le n - 1$ since $\mathbf {a}\ne \mathbf {a}^L_1 = 0\cdots 0n$. Let $\mathbf {b}:= 0\cdots 0(\alpha _\ell - 1)\alpha _{\ell + 1}\cdots \alpha _{n - 1}(\alpha _n + 1)$. If $\mathbf {b}\ne \mathbf {j}, 1\cdots 102$, then $\mathbf {b}<^L \mathbf {a}$, and thus we can set $\mathbf {a}' := \mathbf {b}$. (Note that $\mathbf {b}\le \mathbf {a}' + \mathbf {j}$ and $\mathbf {b}+ \mathbf {j}\ne \mathbf {a}+ \mathbf {j}$ implying $\mathbf {b}\prec \mathbf {a}+ \mathbf {j}$.) If $\mathbf {b}= \mathbf {j}$, then $\mathbf {a}= 21\cdots 10$ and we can, for example, set $\mathbf {a}' = 1\cdots 120$. If $\mathbf {b}= 1\cdots 102$, then $\mathbf {a}=21\cdots 101$ and we can set $\mathbf {a}' = 1\cdots 1201$.

Item (ii) is trivial just since by definition of $\mathbf {a}^L_1$ and $\mathbf {a}^L_2$ we have $\mathbf {a}^L_1 = 0\cdots 0n$ and $\mathbf {a}^L_2 = 0\cdots 01(n-1)$.

Proof of Lemma 5.4

We set $A := A^L_{k-1} \cap I$ and $A^+ := A^L_k \cap I$; we also set $\mathbf {a}^+ = \mathbf {a}^L_k$. Our task is to show that if $A^+$ is nonempty, then $I\langle A^+ \rangle$ is $(L)$-shellable.

We can assume that $\mathbf {a}^+ \in I$ otherwise $(L)$-shellability of $I\langle A^+ \rangle$ coincides with $(L)$-shellability of $I\langle A \rangle$ which we conclude from the assumptions of the lemma (if $A^+ \ne \emptyset$).

We can also assume that $A \ne \emptyset$, otherwise $I\langle A^+ \rangle$ has a single atom only and we derive the lemma analogously as Lemma 5.2. In particular, from the assumptions of the lemma, we know that assertion $({\mathbf {A}}_{k-1}^L)$ is valid, and, therefore, we have that $I\langle A \rangle$ is $(L)$-shellable.

Our task is to use Theorem 2.1 for verifying $(L)$-shellability of $I\langle A^+ \rangle$. We set $Q := I\langle A^+ \rangle {\setminus } I\langle A \rangle$. We need to verify assumptions of Theorem 2.1.

We have already observed that item (i) of Theorem 2.1 is satisfied; that is, that $I\langle A \rangle$ is $(L)$-shellable.

For verifying other items, we need more intrinsic definition of $Q$. We will assume that $\mathbf {a}^+ = 0\cdots 0\alpha _{\ell }\alpha _{\ell + 1}\cdots \alpha _n$ where $\ell$ is the smallest integer such that $\alpha _\ell > 0$. Note that $\ell \le n-1$ since $k \ge 3$.

Claim 5.10

We have the following description of $Q$.

• (i) $Q = \{\mathbf {q}\in I\langle A^+ \rangle :\mathbf {q}\succeq \mathbf {a}^+, (\mathbf {q}- \mathbf {a}^+)^{(\ell + 1)} = \underbrace{0\cdots 0}_{n-\ell } \}$ if $\mathbf {a}^+ \ne 201\cdots 1$; and

• (ii) $Q = \{\mathbf {q}\in I\langle A^+ \rangle :\mathbf {q}\succeq \mathbf {a}^+, (\mathbf {q}-\mathbf {a}^+)^{(2)}\in \{\underbrace{0\cdots 0}_{n-1},\underbrace{10\cdots 0}_{n-1} \}\}$ if $\mathbf {a}^+ =201\cdots 1$.

Proof

First, we assume that $\mathbf {a}^+ \ne 201\cdots 1$ and we want to prove item (i). Let $\mathbf {q}\succeq \mathbf {a}^+$. Our task is to determine whether $\mathbf {q}\in Q$. We also let $\mathbf {q}- \mathbf {a}^+ = \kappa _1\cdots \kappa _n$.

We need to show two inclusions.

• For the first one, we assume that $(\mathbf {q}-\mathbf {a}^+)^{(\ell + 1)} \ne \underbrace{0\cdots 0}_{n-\ell }$, and we want to show that $\mathbf {q}\notin Q$. That is, we want to find an atom from $A$ which is below $\mathbf {q}$. In this case, we have $i \in \{\ell +1, \ldots , n\}$ such that $\kappa _i \ne 0$. Let

  $$\begin{aligned} \mathbf {a}:= 0\cdots 0(\alpha _{\ell } - 1)\alpha _{\ell + 1}\cdots \alpha _{i-1}(\alpha _i + 1)\alpha _{i+1}\cdots \alpha _n. \end{aligned}$$

  We have $0 < \mathbf {a}< \mathbf {q}$. If $\mathbf {a}\ne \mathbf {j}$ and $\mathbf {q}- \mathbf {a}\ne \mathbf {j}$, then $0 \prec \mathbf {a}\prec \mathbf {q}$, and thus $\mathbf {a}$ is the required atom of $A$ since $\mathbf {a}$ precedes $\mathbf {a}^+$ in the $<^L$ order. If $\mathbf {a}= \mathbf {j}$, then $\mathbf {a}^+ = 21\cdots 101\cdots 1$ where the “0” appears in the $i$th position ($i \ge 3$ since $\mathbf {a}^+ \ne 201\cdots 1$). In particular, if $\mathbf {a}' = 201\cdots 1$, then $\mathbf {q}\ge \mathbf {a}'$ (since $\kappa _i \ge 1$) and $\mathbf {a}'$ precedes $\mathbf {a}^+$ in the $<^L$ order. Therefore, $\mathbf {a}'$ is the required atom of $A$ unless $\mathbf {q}= \mathbf {a}' + \mathbf {j}= 312\cdots 2$. In this case, we can use $1\cdots 102$ for example. If $\mathbf {q}- \mathbf {a}= \mathbf {j}$ and $\mathbf {a}\ne \mathbf {j}$, we consider $\mathbf {a}' \prec \mathbf {a}+ \mathbf {j}= \mathbf {q}$ obtained from Claim 5.9. We also have $\mathbf {a}' <^L \mathbf {a}^+$. This follows from Claim 5.9 (i) by $\mathbf {a}' <^L \mathbf {a}<^L \mathbf {a}^+$ if $\mathbf {a}\ne \mathbf {a}^L_1$. It follows from Claim 5.9 (ii) if $\mathbf {a}= \mathbf {a}^L_1$ since $\mathbf {a}' <^L \mathbf {a}^L_3 \le ^L \mathbf {a}^+$.

• For the second inclusion, we assume that $(\mathbf {q}-\mathbf {a}^+)^{(\ell + 1)} = \underbrace{0\cdots 0}_{n-\ell }$, and we need to show that $\mathbf {q}\in Q$; that is, we need to show that $\mathbf {a}\not \preceq \mathbf {q}$ for any $\mathbf {a}\in A$. Let $\mathbf {a}= \alpha '_1\cdots \alpha '_n \in A$. Since $\mathbf {a}<^L \mathbf {a}^+$, we have that $\alpha '_1 = \cdots = \alpha '_{\ell - 1} = 0$ and $\alpha '_{\ell } \le \alpha _{\ell }$. This implies that there is $i \in \{\ell + 1, \ldots , n\}$ such that $\alpha '_i > \alpha _i$ (note that $\alpha _1 + \cdots + \alpha _n = n = \alpha '_1 + \cdots + \alpha '_n$ since both $\mathbf {a}^+$ and $\mathbf {a}$ are atoms; note also that we get a strict inequality since $\mathbf {a}^+ \ne \mathbf {a}$). This implies $\mathbf {q}\not \succeq \mathbf {a}$ since $\mathbf {q}$ and $\mathbf {a}^+$ agree in the $i$th position.

Now, we want to prove item (ii). That is, we assume that $\mathbf {a}^+ = 201\cdots 1$. Similarly, as before, let $\mathbf {q}\succeq \mathbf {a}^+$. Our task is to determine whether $\mathbf {q}\in Q$. We also let $\mathbf {q}- \mathbf {a}^+ = \kappa _1\cdots \kappa _n$. We again need to show two inclusions.

• For the first one, we assume that $(\mathbf {q}-\mathbf {a}^+)^{(2)} \notin \{\underbrace{0\cdots 0}_{n-1}, \underbrace{10\cdots 0}_{n-1}\}$, and we want to show that $\mathbf {q}\notin Q$. If we apply the reasoning from item (i), we obtain that $\mathbf {q}\notin Q$ if $\kappa _i > 0$ for some $i \ge 3$. It remains to consider the case $(\mathbf {q}-\mathbf {a}^+)^{(2)} = \kappa _20\cdots 0$ where $\kappa _2 \ge 2$. In this case, we set $\mathbf {a}= 021\cdots 1$. Thus, $\mathbf {q}> \mathbf {a}$. In addition, $\mathbf {q}\ne \mathbf {a}+ \mathbf {j}$ since $(\mathbf {q}-\mathbf {a}^+)^{(2)} = \kappa _20\cdots 0$. Thus, $\mathbf {q}\succ \mathbf {a}$. We also have $\mathbf {a}<^L \mathbf {a}^+$, and, therefore, $\mathbf {q}\notin Q$.

• For the second inclusion, we assume that $(\mathbf {q}-\mathbf {a}^+)^{(2)} \in \{\underbrace{0\cdots 0}_{n-1}, \underbrace{10\cdots 0}_{n-1}\}$ and we need to show that $\mathbf {a}\not \preceq \mathbf {q}$ for any $\mathbf {a}\in A$. Let $\mathbf {a}= \alpha '_1\cdots \alpha '_n \in A$. Since $\mathbf {a}<^L \mathbf {a}^+$, we have that $\alpha '_1 \le 2$. This implies that either is $i \in \{3, \ldots , n\}$ such that $\alpha '_i > \alpha _i = 1$, or $\alpha '_2 > \alpha _2 = 0$ and $\alpha '_i = \alpha _i = 1$ for $i \ge 3$. In the first case, we have $\mathbf {q}\not \succeq \mathbf {a}$ since $\mathbf {q}$ and $\mathbf {a}^+$ agree in the $i$th position. In the second case, we have $\alpha _2 \ge 2$ since $\mathbf {a}\ne \mathbf {j}$. Therefore, again $\mathbf {q}\not \succeq \mathbf {a}$, since $\mathbf {q}$ exceeds $\mathbf {a}^+$ in the second position at most by $1$.

Now, we verify condition (ii) of Theorem 2.1. Let $J = [\mathbf {a}^+,\mathbf {q}]$ be an interval where $\mathbf {q}\in Q$. We recall that $[\mathbf {a}^+,\mathbf {q}]$ is isomorphic to $[\mathbf {0},\mathbf {q}- \mathbf {a}^+]$.

If $\mathbf {a}^+ \ne 201\cdots 1$, then by Claim 5.10, $J$ is isomorphic to an interval in ${\mathcal {V}}_{n,\ell }$ (by forgetting last $n - \ell$ coordinates of $J \ominus \mathbf {a}^+$). Therefore, $J$ is shellable by Proposition 4.1.

If $\mathbf {a}^+ = 201\cdots 1$, then $Q$ has a very simple structure by Claim 5.10; see Fig. 10. We could check that every interval in $Q$ in this case is a modular lattice and deduce shellability of $Q$ in the same way as in Proposition 4.1, using [2, Theorem 3.7]. However, this is perhaps just an overkill in this case and the shelling order of every interval can be easily found explicitly.

Fig. 10

The structure of $Q$ in item (ii) of Claim 5.10 (or Claim 5.12)

We continue with the verification of condition (iii) of Theorem 2.1; that is, we verify the edge falling property. Let $\mathbf {q}\in Q, \mathbf {q}' \in Q \cup \{\mathbf {0}\}$ and $\mathbf {p}\in I\langle A \rangle$ be such that $\mathbf {p}{\ > \cdot \ }\mathbf {q}$ and $\mathbf {q}{\ > \cdot \ }\mathbf {q}'$. Our task is to find $\mathbf {p}' \in I\langle A \rangle$ such that $\mathbf {p}{\ > \cdot \ }\mathbf {p}' {\ > \cdot \ }\mathbf {q}'$.

Natural candidate for $\mathbf {p}'$ is $\mathbf {p}'_\mathrm{cand} := \mathbf {q}' + (\mathbf {p}- \mathbf {q})$. We have $\mathbf {p}{\ > \cdot \ }\mathbf {p}'_\mathrm{cand} {\ > \cdot \ }\mathbf {q}'$. If $\mathbf {a}^+ \ne 201\cdots 1$, we immediately obtain that $\mathbf {p}'_\mathrm{cand} \in I\langle A \rangle$ from Claim 5.10 (i) as follows. We know that $(\mathbf {q}- \mathbf {q}')^{(\ell + 1)} = \underbrace{0\cdots 0}_{n-\ell }$ by Claim 5.10 (i) since $\mathbf {q}- \mathbf {q}' = (\mathbf {q}- \mathbf {a}^+) - (\mathbf {q}' - \mathbf {a}^+)$. Therefore, $\mathbf {p}^{(\ell + 1)} = (\mathbf {p}'_\mathrm{cand})^{(\ell + 1)}$, and it follows by Claim 5.10 (i) that $\mathbf {p}'_\mathrm{cand}$ indeed belongs to $I\langle A \rangle$. Therefore, we can set $\mathbf {p}' := \mathbf {p}'_\mathrm{cand}$.

If $\mathbf {a}^+ = 201\cdots 1$, we need to be more careful. We have $\mathbf {p}^{(2)} - (\mathbf {p}'_\mathrm{cand})^{(2)} = \mathbf {q}^{(2)} - (\mathbf {q}')^{(2)}$. Therefore, if $\mathbf {q}^{(2)} = (\mathbf {q}')^{(2)}$, then we obtain $\mathbf {p}'_\mathrm{cand} \in I\langle A \rangle$ by Claim 5.10 (ii) and we can set $\mathbf {p}' := \mathbf {p}'_\mathrm{cand}$. However, it might also occur that $(\mathbf {q}- \mathbf {a}^+)^{(2)} = 10\cdots 0$ and $(\mathbf {q}' - \mathbf {a}^+)^{(2)} = 0\cdots 0$ by Claim 5.10 (ii). In this case, we focus on $(\mathbf {p}- \mathbf {q})^{(2)}$. Claim 5.10 (ii) implies that $(\mathbf {p}- \mathbf {q})^{(2)} \ne 0\cdots 0$. If $(\mathbf {p}- \mathbf {q})^{(2)} \ne 10\cdots 0$, then $\mathbf {p}'_\mathrm{cand} \in I\langle A \rangle$ again by Claim 5.10 (ii) and we can again set $\mathbf {p}' := \mathbf {p}'_\mathrm{cand}$.

Finally, it remains to consider the case $(\mathbf {p}- \mathbf {q})^{(2)} = 10\cdots 0$. In this case, $\mathbf {p}'_\mathrm{cand} \in Q$ and we have to choose $\mathbf {p}'$ differently. We actually obtain $\mathbf {p}- \mathbf {q}= (n-1)10\cdots 0$ since $\mathbf {p}{\ > \cdot \ }\mathbf {q}$. Similarly, we obtain $\mathbf {q}- \mathbf {q}' = (n-1)10\cdots 0$. We can then choose $\mathbf {p}' := \mathbf {q}' + (n-2)20\cdots 0$. Then, $\mathbf {p}{\ > \cdot \ }\mathbf {p}' {\ > \cdot \ }\mathbf {q}'$ and $\mathbf {p}' \in I\langle A \rangle$ by Claim 5.10. See Fig. 11.

Fig. 11

The last case of the verification of the edge falling property. Similarly as in Fig. 9, the label of an edge $\mathbf {s}\mathbf {t}$ is $\mathbf {t}- \mathbf {s}$

We conclude by verifying condition (iv) of Theorem 2.1. Let $\mathbf {q}\in Q$; we need to show that the poset $I(\mathbf {q})\langle A(\mathbf {q}) \rangle$ is shellable where $A(\mathbf {q})$ is defined as in the statement of the theorem. We observe that this poset is isomorphic with $I(\mathbf {q})\langle A(\mathbf {q}) \rangle \ominus \mathbf {q}$, that is, with $[\mathbf {0},\mathbf {z}-\mathbf {q}]\langle A(\mathbf {q}) \ominus \mathbf {q} \rangle$. Note that ${{\mathrm{rk}}}(\mathbf {z}- \mathbf {q}) < {{\mathrm{rk}}}(\mathbf {z})$. Here, we plan to use our assumption that Proposition 5.1 is valid for intervals $[\mathbf {0},\mathbf {y}]$ with ${{\mathrm{rk}}}(\mathbf {y}) < {{\mathrm{rk}}}(\mathbf {z})$, in particular, for the interval $[\mathbf {0},\mathbf {z}-\mathbf {q}]$. Therefore, we want to determine $A(\mathbf {q}) \ominus \mathbf {q}$.

Let $\mathbf {a}\in A^\mathrm{all}$; we want to determine whether $\mathbf {a}\in A(\mathbf {q}) \ominus \mathbf {q}$. This is equivalent with determining whether $\mathbf {q}+ \mathbf {a}\in A(\mathbf {q})$ and using the definition of $A(\mathbf {q})$ with determining whether $\mathbf {q}+ \mathbf {a}\in I\langle A \rangle$ (assuming that $\mathbf {q}+ \mathbf {a}\in I(\mathbf {q})$, otherwise $\mathbf {a}\notin A(\mathbf {q}) \ominus \mathbf {q}$).

If $\mathbf {a}^+ \ne 201\cdots 1$, we get that $\mathbf {q}+ \mathbf {a}\in I\langle A \rangle$ if and only if $\mathbf {a}\in A^{(\ell + 1)}$ and $\mathbf {q}+ \mathbf {a}\in I(\mathbf {q})$ by Claim 5.10 (i). Therefore, we obtain the required shellability of $[\mathbf {0},\mathbf {z}-\mathbf {q}]\langle A(\mathbf {q}) \ominus \mathbf {q} \rangle$ from assertion $({\mathbf {A}}^{(\ell + 1)}_k)$ (with $k = |{\mathcal {A}}^{(\ell + 1)}|$) for the interval $[\mathbf {0},\mathbf {z}-\mathbf {q}]$.

If $\mathbf {a}^+ = 201\cdots 1$ and $(\mathbf {q}- \mathbf {a}^+)^{(2)} = 1\cdots 0$, then $\mathbf {q}+ \mathbf {a}^+ \in I\langle A \rangle$ if and only if $\mathbf {a}\in A^{(2)}$ and $\mathbf {q}+ \mathbf {a}\in I(\mathbf {q})$ by Claim 5.10 (ii). Therefore, we obtain the required shellability of $[\mathbf {0},\mathbf {z}-\mathbf {q}]\langle A(\mathbf {q}) \ominus \mathbf {q} \rangle$ from assertion $({\mathbf {A}}^{(2)}_k)$ (with $k = |{\mathcal {A}}^{(2)}|$) for the interval $[\mathbf {0},\mathbf {z}-\mathbf {q}]$.

If $\mathbf {a}^+ = 201\cdots 1$ and $(\mathbf {q}- \mathbf {a}^+)^{(2)} = 0\cdots 0$, then $\mathbf {q}+ \mathbf {a}^+ \in I\langle A \rangle$ if and only if $\mathbf {a}\in A^\mathrm{all}{\setminus }\{(n-1)10\cdots 0, n0\cdots 0\}$ and $\mathbf {q}+ \mathbf {a}\in I(\mathbf {q})$ by Claim 5.10 (ii). Luckily, $A^\mathrm{all}{\setminus }\{(n-1)10\cdots 0, n0\cdots 0\}$ is $A^\mathrm{all}$ minus the latest two elements of $A^\mathrm{all}$ in the $<^L$ order. Therefore, we obtain the required shellability of $[\mathbf {0},\mathbf {z}-\mathbf {q}]\langle A(\mathbf {q}) \ominus \mathbf {q} \rangle$ from assertion $({\mathbf {A}}^L_k)$ (with $k = |A^\mathrm{all}| - 2$) for the interval $[\mathbf {0},\mathbf {z}-\mathbf {q}]$.

This covers all cases when $\mathbf {a}^+ = 201\cdots 1$ by Claim 5.10 (ii). Thus, we have verified condition (iv) of Theorem 2.1 which concludes the proof of the lemma. $\square$

For the proof of the next lemma, we need the following extension of Claim 5.9.

Claim 5.11

Let $\ell \in [n-1]$. Let $\mathbf {a}\in A^\mathrm{all}$ such that $\mathbf {a}\ne \mathbf {a}^L_1$. Then, there is $\mathbf {a}' \in A^{(\ell +1)}$ such that $\mathbf {a}' <^L \mathbf {a}$ and $\mathbf {a}' \prec \mathbf {a}+ \mathbf {j}$. In addition, we can assume $\mathbf {a}' \ne 1\cdots 102$.

Proof

By Claim 5.9 (i) we have $\mathbf {b}'' \in A^\mathrm{all}$ (playing the role of $\mathbf {a}'$ in Claim 5.9) such that $\mathbf {b}'' <^L \mathbf {a}$ and $\mathbf {b}'' \prec \mathbf {a}+ \mathbf {j}$ and $\mathbf {b}'' \ne 1\cdots 102$. If $\mathbf {b}'' \in A^{(\ell +1)}$, then we set $\mathbf {a}' := \mathbf {b}''$ and we are done.

If $\mathbf {b}'' \notin A^{(\ell +1)}$, then $\mathbf {b}'' := \beta _1\cdots \beta _{n-1}0$ for some $\beta _1,\ldots ,\beta _{n-1} \ge 0$. Let $i \in [n-1]$ be such that $\beta _i \ne 0$ and $\beta _i$ is as small as possible. We set $\mathbf {a}' := \beta _1\cdots \beta _{i-1}(\beta _i - 1)\beta _{i+1}\cdots \beta _{n-1}1$. We have that $\mathbf {a}' \ne \mathbf {j}$ due to our choice that $\beta _i$ is as small as possible. Thus, $\mathbf {a}' <^L \mathbf {b}'' <^L \mathbf {a}$. In addition, $\mathbf {a}' \prec \mathbf {a}+ \mathbf {j}$ since $\mathbf {a}' \le \mathbf {a}+ \mathbf {j}$ ($\mathbf {a}'$ is dominated by $\mathbf {b}''$ in the first $n-1$ coordinates and dominated by $\mathbf {j}$ in the last coordinate) and $\mathbf {a}' \ne \mathbf {a}$. Finally, $\mathbf {a}' \in A^{(\ell +1)}$ and $\mathbf {a}' \ne 1\cdots 102$ since its last coordinate is $1$.

Proof of Lemma 5.5

The proof is similar to the proof of Lemma 5.4. It is only slightly more technical, since the $<^S$ order is more complicated than the $<^L$ order.

We set $A := A^S_{k-1} \cap I$ and $A^+ := A^S_k \cap I$; we also set $\mathbf {a}^+ = \mathbf {a}^S_k$. Our task is to show that if $A^+$ is nonempty then $I\langle A^+ \rangle$ is $(S)$-shellable.

Similarly, as in the proof of Lemma 5.4, we derive that we can assume $\mathbf {a}^+ \in I$, $A \cap I \ne \emptyset$ and, therefore, $I\langle A \rangle$ is $(S)$-shellable from the assumptions of this lemma.

Our task is to use Theorem 2.1 for verifying $(S)$-shellability of $I\langle A^+ \rangle$. We set $Q := I\langle A^+ \rangle {\setminus } I\langle A \rangle$. We need to verify assumptions of Theorem 2.1.

We have already observed that item (i) of Theorem 2.1 is satisfied; that is, that $I\langle A \rangle$ is $(S)$-shellable.

For verifying other items, we need more intrinsic definition of $Q$. We will assume that $\mathbf {a}^+ = 0\cdots 0\alpha _{\ell }\alpha _{\ell + 1}\cdots \alpha _n$ where $\ell$ is the smallest integer such that $\alpha _\ell > 0$. Note that $\ell \le n-1$ since $k \ge 3$.

Claim 5.12

We have the following description of $Q$.

• (i) $Q = \{\mathbf {q}\in I\langle A^+ \rangle :\mathbf {q}\succeq \mathbf {a}^+, (\mathbf {q}- \mathbf {a}^+)^{(\ell +1)} = \underbrace{0\cdots 0}_{n-\ell } \}$ if $\mathbf {a}^+ \ne 1\cdots 102,201\cdots 1,201\cdots 102$;

• (ii) $Q = \{\mathbf {q}\in I\langle A^+ \rangle :\mathbf {q}\succeq \mathbf {a}^+, (\mathbf {q}-\mathbf {a}^+)^{(2)}\in \{\underbrace{0\cdots 0}_{n-1},\underbrace{10 \cdots 0}_{n-1}\}\}$ if $\mathbf {a}^+ =201\cdots 1$ or $\mathbf {a}^+ = 201 \cdots 102$; and

• (iii) $Q = \{\mathbf {a}^+\}$ if $\mathbf {a}^+ = 1\cdots 102$.

Note that we crucially use that $n \ge 4$ in order that this claim makes sense; that is, we use that $20\underbrace{1\cdots 1}_{n-4}02$ belongs to ${\mathcal {V}}^{\bullet }_n$.

Proof

The proof is similar to the proof of Claim 5.10; however, in this proof, there are more cases to consider. Keeping in mind the number of cases we want to consider, we use slightly different approach how to treat them, compared to Claim 5.10.

We assume that we are given $\mathbf {q}$ such that $\mathbf {q}\succeq \mathbf {a}^+$ (this is a necessary condition for $\mathbf {q}\in Q$). We let $\mathbf {q}- \mathbf {a}^+ = \kappa _1\cdots \kappa _n$. If $\mathbf {a}^+ \notin \{1\cdots 102,201\cdots 1,201\cdots 102\}$, we want to verify that $\mathbf {q}\in Q$ if and only if $\kappa _{\ell +1} = \cdots = \kappa _n = 0$. If $\mathbf {a}^+ \in \{1\cdots 102, 201\cdots 102\}$, we want to verify that $\mathbf {q}\in Q$ if and only if $\kappa _2 \in \{0,1\}$ and $\kappa _3 = \cdots = \kappa _n = 0$. If $\mathbf {a}^+ = 1\cdots 102$, we want to verify that $\mathbf {q}\in Q$ if and only if $\mathbf {q}= \mathbf {a}^+$.

First, we distinguish cases according to whether $\kappa _{\ell +1}\cdots \kappa _{n} = 0\cdots 0$ (note that we also cover $\mathbf {a}^+ \in \{1\cdots 102, 201\cdots 1, 201\cdots 102\}$ by setting $\ell = 1$ in these cases).

• 1. $\kappa _{\ell +1}\cdots \kappa _{n} \ne 0\cdots 0$. In this case, we have $i \in \{\ell + 1, \cdots , n\}$ such that $\kappa _i > 0$. We prefer $i \ne 2$, if possible. We set

  $$\begin{aligned} \mathbf {a}:= 0\cdots 0(\alpha _{\ell } - 1)\alpha _{\ell + 1}\cdots \alpha _{i-1}(\alpha _i + 1)\alpha _{i+1}\cdots \alpha _n. \end{aligned}$$

  Note that if $\mathbf {a}\ne \mathbf {j}$, then $\mathbf {a}$ precedes $\mathbf {a}^+$ in the $<^L$ order. (In fact, $\mathbf {a}$ precedes $\mathbf {a}^+$ in the lexicographic order in any case, but we do not define the $<^L$ order for $\mathbf {j}$.) Note also that $\mathbf {a}^+ < \mathbf {q}$. In some cases, we will manage to show that $\mathbf {a}\ne \mathbf {j}$, $\mathbf {a}<^S \mathbf {a}^+$, and $\mathbf {a}+ \mathbf {j}\ne \mathbf {q}$. This will imply that $\mathbf {a}\in A$ and $\mathbf {a}\prec \mathbf {q}$ and, therefore, $\mathbf {q}\not \in Q$. In some other cases, we will replace $\mathbf {a}$ with another $\mathbf {a}'$ satisfying the above-mentioned conditions still deriving $\mathbf {q}\notin Q$. However, this will be impossible if $\mathbf {a}^+ \in \{1\cdots 102, 201\cdots 102\}$, $i = 2$, and $\kappa _2 = 1$ when we will actually derive that $\mathbf {q}\in Q$. Now, we distinguish several subcases according to $\mathbf {a}^+$.

  • (a) $\mathbf {a}^+ \in A^{(n)} = A^S \cup \{1\cdots 102\}$. Before we start, we remark that all considerations are also valid if $\mathbf {a}^+ = 1\cdots 102$. The atom $1\cdots 102$ is the last atom of $A^{(n)}$ in the $<^S$ order. This will reflect in such a way that in some cases we check for $\mathbf {a}^+ = 1\cdots 102$ more than we need (which is not a big price for a coherent case analysis). We have that $\mathbf {a}$ precedes $\mathbf {a}^+$ in the $<^S$ order unless $\mathbf {a}\in \{\mathbf {j},1\cdots 102\}$. Therefore, for the beginning, we assume that $\mathbf {a}\notin \{\mathbf {j}, 1\cdots 102\}$. If, in addition, $\mathbf {a}+ \mathbf {j}\ne \mathbf {q}$, then we have the required properties of $\mathbf {a}$ deriving $\mathbf {q}\notin Q$. However, if $\mathbf {a}+ \mathbf {j}= \mathbf {q}$, then we obtain $\mathbf {a}' \ne 1\cdots 102$ of required properties by Claim 5.11 (or by Claim 5.9 (ii) if $\mathbf {a}= 0\cdots 0n$). If $\mathbf {a}= \mathbf {j}$, then $\mathbf {a}^+ = 21\cdots 101\cdots 1$ where the “0” appears in the $i$th position. We distinguish subsubcases according to $i$.

    • i. $i \ge 3$. In this situation, we set $\mathbf {a}' = 201\cdots 1$. Then, $\mathbf {q}> \mathbf {a}'$ (since $\kappa _i \ge 1$ and $\mathbf {q}\succ \mathbf {a}^+$) and $\mathbf {a}'$ precedes $\mathbf {a}^+$ in the $<^L$ order and, therefore, in $<^S$ order as well. Therefore, $\mathbf {a}'$ has the required properties unless $\mathbf {q}= \mathbf {a}' + \mathbf {j}= 312\cdots 2$. In this case, we can use $1\cdots 1201 \prec \mathbf {q}$, for example.

    • ii. $i = 2$. In this situation, $\mathbf {a}^+ = 201\cdots 1$. We also have $\kappa _3 = \cdots = \kappa _n = 0$ since we wanted $i \ne 2$ if possible. If $\kappa _2 \ge 2$, implying $\mathbf {q}\ge 221\cdots 1$, we still can set $\mathbf {a}' = 021\cdots 1$ deriving $\mathbf {q}\notin Q$ (note that $\mathbf {q}\ne \mathbf {a}+ \mathbf {j}$ since $\kappa _n = 0$). If $\kappa _2 = 1$, we actually want to derive $\mathbf {q}\in Q$ according to our description. In this case, it is easiest to refer to Claim 5.10 (ii) (since we have already done this analysis). The claim implies that there is no $\mathbf {a}\in A^\mathrm{all}$ such that $\mathbf {a}<^L \mathbf {a}^+$ and $\mathbf {a}\preceq \mathbf {q}$. In particular, there is no such $\mathbf {a}\in A^{(n)}$. Since $\mathbf {a}<^L \mathbf {a}^+$ is equivalent with $\mathbf {a}<^S \mathbf {a}^+$ in this case, we deduce $\mathbf {q}\in Q$.

    If $\mathbf {a}= 1\cdots 102$, then we can perform the same analysis as if $\mathbf {a}= \mathbf {j}$ just replacing the suffix $111$ with $102$. (The only major difference is that we cannot use the shortcut referring to Claim 5.10.) Here, the analysis follows in detail. We have $\mathbf {a}^+ = 21\cdots 101\cdots 102$ where the first “0” appears in the $i$th position or $\mathbf {a}^+ = 21\cdots 101$ if $i = n$. (In particular, $i \ne n-1$.) We distinguish subsubcases according to $i$.

    • i. $i \ge 3$. In this situation, we set $\mathbf {a}' = 201\cdots 102$. Then, $\mathbf {q}> \mathbf {a}'$ (since $\kappa _i \ge 1$ and $\mathbf {q}\succ \mathbf {a}^+$) and $\mathbf {a}'$ precedes $\mathbf {a}^+$ in the $<^L$ order (hence in $<^S$ order as well). Therefore, $\mathbf {a}'$ has the required properties unless $\mathbf {q}= \mathbf {a}' + \mathbf {j}= 312\cdots 213$. In this case, we can use $1\cdots 1201 \prec \mathbf {q}$, for example.

    • ii. $i = 2$. In this situation, $\mathbf {a}^+ = 201\cdots 102$. We also have $\kappa _3 = \cdots = \kappa _n = 0$ since we wanted $i \ne 2$ if possible. If $\kappa _2 \ge 2$, implying $\mathbf {q}\ge 221\cdots 102$, we still can set $\mathbf {a}' = 021\cdots 102$ deriving $\mathbf {q}\notin Q$ (note that $\mathbf {q}\ne \mathbf {a}+ \mathbf {j}$ since $\kappa _n = 0$). If $\kappa _2 = 1$, we actually want to derive $\mathbf {q}\in Q$ according to our description. In this case, $\mathbf {q}= (r\cdot n + 1)1\cdots 102$ for some positive integer $r$. We want to show that there is no $\mathbf {a}\in A^S$ such that $\mathbf {a}<^S \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$. For contradiction, there is such $\mathbf {a}= \alpha '_1\cdots \alpha '_n$. Condition $\mathbf {a}<^S \mathbf {a}^+$ implies $\alpha '_1 \le 2$. Since the sum of the last $(n-1)$ coordinates of $\mathbf {q}$ equals $n - 1$, we derive either that $\alpha '_1 = 1$ and $\mathbf {a}$ agrees with $\mathbf {q}$ on all remaining $n-1$ coordinates or that $\alpha '_1 = 2$ and $\mathbf {a}$ agrees with $\mathbf {q}$ on all remaining $n-1$ coordinates except one coordinate, where it is one less. The first case is excluded since $1\cdots 102 \not <^S \mathbf {a}^+$. The second case is also excluded, since in such a case $\mathbf {a}\not <^L \mathbf {a}^+$, implying $\mathbf {a}\not <^S \mathbf {a}^+$, a contradiction. We conclude that $\mathbf {q}\in Q$ if $\kappa _2 = 1$.

  • (b) $\mathbf {a}^+ \in A^\mathrm{all}{\setminus } A^{(n)}$. In this case, $\alpha _n = 0$. We also emphasize that $\mathbf {a}$ precedes $\mathbf {a}^+$ in the $<^S$ order if $\mathbf {a}\ne \mathbf {j}$. This is simply because $\mathbf {a}$ precedes $\mathbf {a}^+$ in the $<^L$ order and $\mathbf {a}^+ \notin A^{(n)}$ in this case. Therefore, we derive $\mathbf {q}\notin Q$ if $\mathbf {a}\ne \mathbf {j}$ and $\mathbf {a}+ \mathbf {j}\ne \mathbf {q}$. Now, let us consider the case $\mathbf {a}\ne \mathbf {j}$, but $\mathbf {a}+ \mathbf {j}= \mathbf {q}$. Then, there is $\mathbf {a}'$ from Claim 5.9 (i) or (ii) such that $\mathbf {a}' <^L \mathbf {a}^+$, $\mathbf {a}\prec \mathbf {q}$. We derive $\mathbf {a}' <^S \mathbf {a}^+$, and, therefore, $\mathbf {q}\notin Q$. Finally, we consider the case $\mathbf {a}= \mathbf {j}$. We derive $\mathbf {a}^+ = 21\cdots 10$ and $i = n$ (since $\alpha _n = 0$). We set $\mathbf {a}' := 21\cdots 101$ or $\mathbf {a}' := 21\cdots 1011$ so that $\mathbf {a}' + \mathbf {j}\ne \mathbf {q}$. We derive $\mathbf {a}' \prec \mathbf {q}$, $\mathbf {a}' <^S \mathbf {a}^+$, and, therefore, $\mathbf {q}\notin Q$ as desired.

• 2. $\kappa _{\ell +1}\cdots \kappa _{n} = 0\cdots 0$. In this case, we want to derive $\mathbf {q}\in Q$ for all possible choices of $\mathbf {a}^+$ except $\mathbf {a}^+ = 1\cdots 102$ and $\mathbf {q}\succ \mathbf {a}^+$. We distinguish subcases according to $\mathbf {a}^+$.

  • (a) $\mathbf {a}^+ \in A^S$. In this case, we refer to Claim 5.10 which implies that there is no $\mathbf {a}\in A^\mathrm{all}$ such that $\mathbf {a}<^L \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$. Therefore, in particular, there is no $\mathbf {a}\in A^S$ with $\mathbf {a}<^S \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$ which is what we need.

  • (b) $\mathbf {a}^+ = 1\cdots 102$. If $\mathbf {q}= \mathbf {a}^+$, then $\mathbf {q}\in Q$ as desired. If $\mathbf {q}\succ \mathbf {a}^+$, then $\mathbf {q}= (rn+1)1\cdots 102$ for some integer $n$. Setting $\mathbf {a}= 21\cdots 101$, we get $\mathbf {a}\in A^{(n)}$ implying $\mathbf {a}<^S \mathbf {a}^+$ and also $\mathbf {a}\prec \mathbf {q}$. Thus, $\mathbf {q}\notin Q$ as required.

  • (c) $\mathbf {a}^+ \in A^\mathrm{all}{\setminus } A^{(n)}$. By Claim 5.10, there is no $\mathbf {a}\in A^\mathrm{all}$ such that $\mathbf {a}<^L \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$. Therefore, in particular, there is no $\mathbf {a}\in A^\mathrm{all}{\setminus } A^{(n)}$ with $\mathbf {a}<^S \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$. On the other hand, there is no $\mathbf {a}\in A^{(n)}$ with $\mathbf {a}<^S \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$ either, because $\alpha _n = \kappa _n = 0$ implying that the last coordinate of $\mathbf {q}$ is $0$ whereas $\mathbf {a}$ from $A^{(n)}$ has the last coordinate nonzero. Altogether, there is no $\mathbf {a}\in A^\mathrm{all}$ with $\mathbf {a}<^S \mathbf {a}^+$ and $\mathbf {a}\prec \mathbf {q}$ implying $\mathbf {q}\in Q$. $\square$

This finishes the proof of the claim.

Now, we verify condition (ii) of Theorem 2.1. However, the verification is almost the same as in the case of Lemma 5.4 using Claim 5.12 instead of Claim 5.10. This is because of the described structure of $Q$. (Compare with the text below the proof of Claim 5.10.)

If $\mathbf {a}\notin \{1\cdots 102, 201\cdots 1, 201\cdots 102\}$, then we just use Proposition 4.1. If $\mathbf {a}\in \{201\cdots 1, 201\cdots 102\}$, then we obtain shellability of $Q$ referring to Fig. 10. Finally, if $\mathbf {a}= 1\cdots 102$ then the verification is trivial, since a poset with single element is shellable.

We continue with the verification of condition (iii) of Theorem 2.1; that is, we verify the edge falling property. If $\mathbf {a}^+ \ne 1\cdots 102$, then again this verification can be taken in verbatim from the analogous verification in the proof of Lemma 5.4 using Claim 5.12 instead of Claim 5.10, considering cases according to structure of $Q$. We, therefore, do not repeat the relevant text again.

If $\mathbf {a}^+ = 1\cdots 102$, then the verification of the edge falling property is somewhat trivial. In this case, $Q = \{\mathbf {a}^+\}$ by Claim 5.12. Therefore, we are supposed to verify that if $\mathbf {q}= \mathbf {a}^+$, $\mathbf {q}' = \mathbf {0}$, and $\mathbf {p}\in I\langle A \rangle$ is such that $\mathbf {p}{\ > \cdot \ }\mathbf {q}$, then there is $\mathbf {p}' \in A$ covering $\mathbf {0}$ and covered by $\mathbf {p}$. But, this just immediately follows from $\mathbf {p}\in I\langle A \rangle$ since ${{\mathrm{rk}}}(\mathbf {p}) = 2$.

We conclude by verifying condition (iv) of Theorem 2.1. We again refer that if $\mathbf {a}^+ \ne 1\cdots 102$, then this verification is already done in the proof of Lemma 5.4. It again solely depends on the structure of $Q$.

If $\mathbf {a}^+ = 1\cdots 102$, then we are just supposed to check that the interval $[\mathbf {a}^+,\mathbf {z}]$ is shellable. This follows from the assumptions of this lemma, since it is isomorphic to $[\mathbf {0}, \mathbf {z}- \mathbf {a}^+]$. $\square$

Proof

First, we observe that it is sufficient to prove the lemma for case $k = |A^\mathrm{all}|$ since an $(L)$-shelling of $I\langle A_{j+1}^{(\ell + 1)} \cap I \rangle$ restricts to an $(L)$-shelling of $I\langle A_{j}^{(\ell + 1)} \cap I \rangle$. Therefore, in case $k = |A^\mathrm{all}|$, we just aim to show that $I\langle A^\mathrm{all}\cap I \rangle$ is $(L)$-shellable.

We plan to use Theorem 2.3 for the proof of this lemma where we set $A := A^\mathrm{all}\cap I$ and $A' := A^{(\ell + 1)} \cap I$.

Condition (i) of Theorem 2.3 follows from the assumptions of the lemma.

For checking condition (ii), we have $\mathbf {b}\in I \cap (A^\mathrm{all}{\setminus } A^{(\ell +1)})$ and $\mathbf {p}\in I\langle A^{(\ell +1)} \cap I \rangle$ covering $\mathbf {b}$. We need to find $\mathbf {b}' \in A^{(\ell +1)} \cap I$ such that $\mathbf {p}{\ > \cdot \ }\mathbf {b}'$ and $\mathbf {b}' <^L \mathbf {b}$. Actually, we will only check $\mathbf {b}' \in A^{(\ell +1)}$, $\mathbf {p}{\ > \cdot \ }\mathbf {b}'$, and $\mathbf {b}' <^L \mathbf {b}$ since $\mathbf {p}{\ > \cdot \ }\mathbf {b}'$ implies $\mathbf {b}' \in I$.

We have that $\mathbf {b}= \beta _1\cdots \beta _{\ell }0\cdots 0$ since $\mathbf {b}\notin A^{(\ell +1)}$. On the other hand, if we let $\mathbf {p}= \pi _1\cdots \pi _n$, then there is $j \in \{\ell +1,\ldots ,n\}$ such that $\pi _j > 0$ since $\mathbf {p}\in I\langle A^{(\ell +1)} \cap I \rangle$. Let also $i \in [\ell ]$ be such an index that $\beta _i > 0$ and $\beta _i$ is as small as possible. We set the following candidate for $\mathbf {b}'$.

$$\begin{aligned} \mathbf {b}'_\mathrm{cand} := \beta _1\cdots \beta _{i-1}(\beta _i - 1)\beta _{i+1}\cdots \beta _{\ell }0\cdots 010\cdots 0, \end{aligned}$$

where the “1” appears on the $j$th position. We have $\mathbf {b}'_\mathrm{cand} \le \mathbf {p}$. We also have $\mathbf {b}'_\mathrm{cand} \ne \mathbf {j}$; this is obvious if $\ell \ne n-1$, and it follows from our choice of $\beta _i$ if $\ell = n-1$. In particular, $\mathbf {b}'_\mathrm{cand} <^L \mathbf {b}$ and $\mathbf {b}'_\mathrm{cand} \in A^{(\ell +1)}$. If $\mathbf {b}'_\mathrm{cand} + \mathbf {j}\ne \mathbf {p}$, then $\mathbf {b}'_\mathrm{cand} \prec \mathbf {p}$ and consequently $\mathbf {p}{\ > \cdot \ }\mathbf {b}'_\mathrm{cand}$ (by comparing ranks). Thus, we can simply set $\mathbf {b}' := \mathbf {b}'_\mathrm{cand}$ in this case.

If $\mathbf {b}'_\mathrm{cand} + \mathbf {j}= \mathbf {p}$, we think of $\mathbf {b}'_\mathrm{cand}$ as $\mathbf {a}$ from Claim 5.11. We obtain the corresponding $\mathbf {a}'$, and we just set $\mathbf {b}' := \mathbf {a}'$. $\square$

6 Relation of lexicographic shellability and $A$-shellability

6.1 Lexicographic shellability

Here, we briefly recall the definition of lexicographic shellability. The reader interested in more details (including examples) is referred to sources such as [4, 5, 14, 15]. The reader familiar with lexicographic shellability can skip this subsection.

As usual, we let $(P, \le )$ be a graded poset (with a unique minimal and maximal element), using the notation from Sect. 2. Given a maximal chain $c \in C(P)$, we label all of its edges with elements of some poset $\varLambda$ (typically, $\varLambda = {\mathbb {Z}}$). In this way, we label edges of all maximal chains in $C(P)$ (that is, a label of an edge might differ if we start with two different chains). We obtain a chain-edge labeling of $P$ if the following condition is satisfied. Whenever $c, c' \in C(P)$ are two chains sharing first $k$ edges (for some $k$), then the labels of these first $k$ edges have to coincide. Let us assume that $P$ is equipped with a fixed chain-edge labeling.

A rooted interval $[x,y]_r$ is an interval in $P$ where the root $r$ of this interval is a maximal chain in the interval $[\hat{0}, x]$. Given a maximal chain $c_0$ in $C([x,y])$, we obtain (with respect to $r$) a labeling of edges of $c_0$ induced from the labeling of a maximal chain $c' \in C[x,y]$ obtained by composing $r$, $c_0$, and an arbitrary maximal chain in interval $[y, \hat{1}]$. This labeling does not depend on the choice of the chain in $[y,\hat{1}]$ due to the definition of chain-edge labeling. In the sequel, we consider the labeling of $c_0$ as a sequence of ${{\mathrm{rk}}}(y) - {{\mathrm{rk}}}(x)$ elements of $\varLambda$. In particular, we can say that $c_0$ is increasing (in $[x,y]_r$) if its labeling is increasing and $c_0$ is lexicographically smaller than another maximal chain $c_1$ in $C([x,y])$ if the labeling of $c_0$ is lexicographically smaller than the labeling of $c_1$.

We say that a chain-edge labeling is a CL-labeling (chain-lexicographic labeling) if for every rooted interval $[x,y]_r$ in $P$ the following two conditions are satisfied.

• (i) There is a unique maximal increasing chain $c_0$ in $[x,y]_r$; and

• (ii) $c_0$ is lexicographically smaller than any other maximal chain in $[x,y]_r$.

The poset $P$ is (chain-)lexicographically shellable, abbreviated as CL-shellable, if it admits a CL-labeling.

It follows from [4] that every CL-shellable poset is indeed shellable. Actually, the order of shelling is given by the lexicographic order of chains in $C(P)$ (with respect to given CL-labeling). The converse is not true—there are posets which are shellable but not lexicographically shellable; see [18, 19].

6.2 Lexicographic shellability versus $A$-shellability

In this subsection, we want to compare $A$-shellability and lexicographic shellability. This comparison makes sense if $A = A^\mathrm{all}$ is the set of all atoms. In addition, we also assume that $A^\mathrm{all}$ is linearly ordered. (If we allow arbitrary partial order on $A^\mathrm{all}$, then, for example, we can allow all elements incomparable; then, $A^\mathrm{all}$-shellability just coincides with shellability.)

6.3 Lexicographic shelling is an $A^\mathrm{all}$-shelling

Let $P$ be a CL-shellable poset, and let us fix a $CL$-labeling of it. Given an atom $a$ of $P$, we observe that the edge $e_a = \hat{0}a$ is labeled the same way in all maximal chains containing $e_a$ (by the definition of chain-edge labeling). Thus, we can denote by $\varLambda (e_a)$ this label of $e_a$. By condition (ii) of the definition of CL-labeling, we have that $\varLambda (e_a)$ and $\varLambda (e_{a'})$ differ for two different atoms $a$ and $a'$, and in addition, they are comparable with $\varLambda$. Thus, these labels induce a linear ordering $\le _\varLambda$ on $A^\mathrm{all}$. In this setting, the CL-shelling of $P$ is also an $A^\mathrm{all}$-shelling of $P$ (where $A^\mathrm{all}$ is equipped with $\le _\varLambda$).

6.4 $A^\mathrm{all}$-shelling which is not lexicographic shelling

It is not hard to come up with an example of an $A^\mathrm{all}$-shelling which is not a CL-shelling. Let $P'$ be a poset which is shellable but not CL-shellable. Let us consider $k$ copies $\hat{0}_1, \ldots , \hat{0}_k$ of the minimal element in $P'$. The poset $P$ is obtained by replacing the minimal element of $P'$ by these $k$ copies and then adding a new minimal element $\hat{0}_{new}$ smaller than everything else. Note that $A^\mathrm{all}= \{\hat{0}_1, \ldots , \hat{0}_k\}$.

It is not hard to check that $P$ is $A^\mathrm{all}$-shellable where $A^\mathrm{all}$ is equipped with an arbitrary linear order (either by elementary means or using Theorem 2.1). On the other hand, $P$ is not CL-shellable since $P$ contains an interval isomorphic to $P'$ and all intervals in a CL-shellable poset are CL-shellable as well.

6.5 Recursive atom orderings

Björner and Wachs [5] gave an equivalent reformulation of CL-shellability using recursive atom orderings. It is useful to compare $A$-shellability and recursive atom orderings. We first repeat their definition.

A poset $P$ (graded, with a unique minimum and maximum) admits a recursive atom ordering if it has length 1 or if the length of $P$ is greater than 1 and there is an ordering $a_1, \ldots , a_t$ of all the atoms of $P$ which satisfies:

• (R1) For all $k \in [t]$, the interval $[a_k,\hat{1}]$ admits a recursive atom ordering in which the atoms of $[a_k,\hat{1}]$ that come first in the ordering are those that cover some $a_i$ where $i < k$.

• (R2) For all $i < k$, if $a_i, a_k < y$, then there is $j < k$ and an element $z$ such that $a_j,a_k {\ < \cdot \ }z \le y$.

Björner and Wachs [5] proved that a poset is CL-shellable if and only if it admits a recursive atom ordering.

In our notation, a recursive atom ordering induces an ordering of $A^\mathrm{all}$. From this point of view, recursive atom orderings are very strongly related to our second criterion, Theorem 2.2. Let us assume that condition (i) of Theorem 2.2 is satisfied in slightly stronger form, that is, we assume that $P\langle A \rangle$ admits a recursive atom ordering (which induces an $A$-shelling). Similarly, let us assume that we can replace $A^\mathrm{all}(a^+)$-shellability of $I(a^+)$ with a recursive atom ordering on $I(a^+)$ inducing $A^\mathrm{all}(a^+)$-shellability. Then, we can deduce that $P\langle A^+ \rangle$ admits a recursive atom ordering:

Indeed, condition (R1) translates to condition (ii) of Theorem 2.2 (it is sufficient to check (R1) only for $a_k = a^+$ since we already assume that $P\langle A \rangle$ admits a recursive atom ordering). Similarly, we will check that condition (R2) translates to condition (iii) of Theorem 2.2. Given $a_i$, $a_k$, and $y$ from (R2), we can again assume that $a_k = a^+$. We choose a maximal chain $c$ in $[a^+,y]$ and set $p$ to be the smallest element of $c$ belonging to $P\langle A \rangle$ (note that $y \in P\langle A \rangle$ since $a_i < y$); see Fig. 12. Then, we can set $q$ to be the element of $c$ one rank below $p$. Then, by assuming (iii) of Theorem 2.2, $p$ is above some $z \in A(a^+)$. This is the required $z$ since $z \in A(a^+)$ implies that $z$ covers some atom $a_j$ preceding $a_k$.

Fig. 12

Condition (iii) of Theorem 2.2 follows from (R2). We also recommend to compare this picture with Fig. 4

Altogether, we see that the method using $A$-shellability includes the recursive atom ordering method. On the other hand, it is not hard to see, that if we were allowed to use only Theorem 2.2, we would not get more than recursive atom orderings. However, Theorem 2.2 is still more flexible since, for example, it does not need to assume that $P\langle A \rangle$ comes with a recursive atom ordering. This is useful, when it is combined with Theorem 2.1.

6.6 Lexicographic shellability versus Theorem 2.1

Now, we compare our first criterion, Theorem 2.1, to lexicographic shellability (in this case, it is more natural to choose lexicographic shellability rather than recursive atom orderings). In this case, Theorem 2.1 seems to be in more “generic” position in relation with lexicographic shellability.

6.7 CL-shellable poset which does not satisfy assumptions of Theorem 2.1

First, we provide an example of a poset that is CL-shellable, but which does not satisfy assumptions of Theorem 2, with respect to a given CL-shelling. This example arose in discussions with Afshin Goodarzi.

Let $P$ be the poset from Fig. 13. It is lexicographically shellable: we first label edges as on picture; and then we label chains according to labels of edges. The reader is welcome to check that we indeed obtain a CL-labeling. (Actually, we obtain a so-called EL-labeling where, in addition, the label of an edge does not depend on the considered chain.) Note also that chains containing $a$ appear before chains containing $a^+$ in the corresponding lexicographic shelling. In particular, $P$ is $A^+$-shellable where $A^+ := \{a, a^+\}$ and $a$ appears before $a^+$.

Fig. 13

Lexicographically shellable poset which does not satisfy assumptions of Theorem 2.1

On the other hand, if we intend to use Theorem 2.1 for showing $A^+$-shellability of $P$, we will not succeed. The condition (iii) (edge falling property) is not satisfied for the edge $q\hat{1}$.

6.8 Theorem 2.1 does not provide a CL-shelling

Let us imagine that we replace our shellability assumptions in Theorem 2.1 by CL-assumptions. That is, for condition (i), we would assume that $P\langle A \rangle$ is CL-shellable (and the corresponding CL-shelling is $A$-shelling as well); and for condition (iv), we would assume that $I(q)\langle A(q) \rangle$ is CL-shellable. Does it follow that $P\langle A^+ \rangle$ is CL-shellable?

The author does not know the answer to this question; but, it seems that the more probable answer is “no.” If the answer is indeed “no,” then this would mean further difference in applicability of Theorem 2.1 and CL-shellability (or even more general CC-shellability of Kozlov [14] as remarked below). However, even if the answer is “yes,” Theorem 2.1 still provides particular conditions that might possibly be checked in an easier way than establishing CL-labeling (or establishing recursive atom ordering).

Here, we can at least provide a simple example showing that the current proof of Theorem 2.1 does not provide CL-shelling even if we ask CL-shelling assumptions. Let $P$ be the poset on Fig. 14. If we set $a^+$ as in the picture, we can easily check that all assumptions of Theorem 2.1 are satisfied even with lexicographic assumptions. We label elements of $Q$ as $q_1, \ldots , q_5$ consistently with the proof of Theorem 2.1. Then, the proof provides shelling such that the chains $\hat{0}q_1q_2q_4\hat{1}$, $\hat{0}q_1q_3q_4\hat{1}$, $\hat{0}q_1q_2q_5\hat{1}$, and $\hat{0}q_1q_3q_5\hat{1}$ appear in this order; consult also Fig. 6. This cannot be a CL-shelling due to the alternation of edges $q_1q_2$ and $q_1q_3$. (The reader familiar with Kozlov’s CC-shellability [14] is welcome to check that this is not even a CC-shelling.)

Fig. 14

Theorem 2.1 does not produce a lexicographic shelling of this poset