Reward mechanisms for P2P VoIP networks

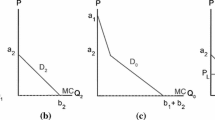
Abstract

As we have seen, P2P VoIP software, such as Skype, has emerged from the current generation of telecommunication systems. However, establishing communication applications based on P2P networks without considering the operational models of the Internet presents potential dangers. In this study, we treat a VoIP telephone conversation as a dynamic game and compare the ex post reward mechanism with the ex ante reward mechanism in forward versus discard and QoS routing. Our simulation results point out that the ex post reward mechanism is better than the ex ante reward mechanism in forward versus discard; however, the opposite holds true in QoS routing when the expected number of periods is sufficiently large. In addition, this study considers the reward mechanisms and the platform provider’s benefit to find the optimal number of supernodes in a transmission path.

Appendix

1.1 Proposition 1

Proof

We first assume all exert high-effort except the supernode $i$. For simplicity, we define $R_{H}$ and $R_{L}$ as follows.

$$ \begin{aligned} R_{H} \equiv & \Pr \left( {\left. {x^{G} } \right|\forall j,a_{j} = 1} \right)s_{i}^{G} + \left( {1 - \Pr \left( {\left. {x^{G} } \right|\forall j,a_{j} = 1} \right)} \right)s_{i}^{B} - c_{i} \\ R_{L} \equiv & \Pr \left( {\left. {x^{G} } \right|\forall j \ne i,a_{j} = 1,a_{i} = 0} \right)s_{i}^{G} + \left( {1 - \Pr \left( {\left. {x^{G} } \right|\forall j \ne i,a_{j} = 1,a_{i} = 0} \right)} \right)s_{i}^{B} + w_{i} \\ \end{aligned} $$

Obviously, when $R_{H} \ge R_{L}$ and $R_{H} \ge w_{i}$ hold, we have the cooperating Nash equilibrium. Moreover, because $q(n)s_{i}^{G} + (1 - q(n))s_{i}^{B}$ is the expected payment by the platform provider, solving $R_{H} = w_{i}$ yields the optimal contract.

Lemma 1

When all supernodes exert high-effort in each period (that is, the cooperation strategy), the expected value of each supernode i’s payoff is given by $\Uppi_{i,t = 0}^{c} = {\frac{{\rho_{i} - c_{i} - \delta (1 - q(n))F_{i} }}{1 - \delta }}$ . Moreover, if the supernode $i$ adopts the fraud strategy, its expected payoff is given by $\Uppi_{i,t = 0}^{s} = {\frac{{\rho_{i} + w_{i} - \delta (1 - \hat{q}(n))F_{i} }}{1 - \delta }}$ .

Proof

Because the liability resulting from bad communication quality at the current period is paid in the next period, the expected value of each supernode’s payoff is: $\Uppi_{i,t = 0}^{c} = (\rho_{i} - c_{i} ) + \delta \left( {\Uppi_{i,t = 0}^{c} - (1 - q(n))F_{i} } \right) = {\frac{{\rho_{i} - c_{i} - \delta (1 - q(n))F_{i} }}{1 - \delta }}$.

If the supernode $i$ adopting the fraud strategy is willing to pay the liability, its payoff is given by$\Uppi_{i,t = 0}^{s} = (\rho_{i} + w_{i} ) + \delta \left( {\Uppi_{i,t = 0}^{s} - (1 - \hat{q}(n))F_{i} } \right) = {\frac{{\rho_{i} + w_{i} - \delta (1 - \hat{q}(n))F_{i} }}{1 - \delta }}$.

Lemma 2

When all supernodes adopt the cooperation strategy, the platform provider’s expected payment to the supernode $i$ in the ex ante reward mechanism is given by ${\frac{{\rho_{i} - \delta (1 - q(n))F_{i} }}{1 - \delta }}$ .

Proof

In the ex ante reward mechanism, the platform provider has to pay the reward $\rho_{i}$ to the supernode $i$ in each period. In addition, it may receive the liability from the supernode $i$ with the probability $\Pr \left( {\left. {x^{B} } \right|\forall j,a_{j} = 1} \right)$. Therefore, its expected payment to the supernode $i$ is given by$\rho_{i} + \sum\limits_{t = 1}^{\infty } {\delta^{t} \left( {\rho_{i} - \Pr \left( {\left. {x^{B} } \right|\forall j,a_{j} = 1} \right)F_{i} } \right)} = {\frac{{\rho_{i} - \Pr \left( {\left. {x^{B} } \right|\forall j,a_{j} = 1} \right)\delta F_{i} }}{1 - \delta }}$.

Lemma 3

When $\rho_{i} \ge (c_{i} + w_{i} ) + (1 - \delta q(n))F_{i}$ holds, the supernode $i$ adopting the cooperation strategy is willing to pay the liability.

Proof

If the supernode i rejects the contract, its reserved payoff is given by ${{w_{i} } \mathord{\left/ {\vphantom {{w_{i} } {(1 - \delta )}}} \right. \kern-\nulldelimiterspace} {(1 - \delta )}}$. Therefore, if $\Uppi_{i,t = 0}^{c} - F_{i} \ge {{w_{i} } \mathord{\left/ {\vphantom {{w_{i} } {(1 - \delta )}}} \right. \kern-\nulldelimiterspace} {(1 - \delta )}}$ holds, the supernode adopting the cooperation strategy is willing to pay the liability in all periods. That is,

$$ \Uppi_{i,t = 0}^{c} - F_{i} \ge {{w_{i} } \mathord{\left/ {\vphantom {{w_{i} } {(1 - \delta )}}} \right. \kern-\nulldelimiterspace} {(1 - \delta )}} \Rightarrow \Uppi_{i,t}^{c} \ge {{w_{i} } \mathord{\left/ {\vphantom {{w_{i} } {(1 - \delta )}}} \right. \kern-\nulldelimiterspace} {(1 - \delta )}},\quad \forall t \Rightarrow \rho_{i} \ge (c_{i} + w_{i} ) + (1 - \delta q(n))F_{i} . $$

1.2 Theorem 1

Proof

Theorem 1 is based on lemma 1 and lemma 3. Because of the constraint $\rho_{i} \ge (c_{i} + w_{i} ) + (1 - \delta q(n))F_{i}$, the supernode adopting the cooperation strategy would pay the liability in the game and any of the subgames. The following inequalities ensure the payoff of the cooperating strategy is better than the fraud strategy.

$$ \begin{aligned} \Uppi_{i,t = 0}^{c} \ge \Uppi_{i,t = 0}^{s} \Rightarrow & \Uppi_{i,t}^{c} \ge \Uppi_{i,t}^{s} ,\forall t \Rightarrow {\frac{{\rho_{i} - c_{i} - \delta (1 - q(n))F_{i} }}{1 - \delta }} \ge {\frac{{\rho_{i} + w_{i} - \delta (1 - \hat{q}(n))F_{i} }}{1 - \delta }} \\ \Rightarrow & F_{i} \ge {\frac{{c_{i} + w_{i} }}{{\delta (q(n) - \hat{q}(n))}}} \\ \end{aligned} $$

(A.1)

1.3 Corollary 1

Proof

The relation between $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F}_{\;i}$ and $F_{i}$ is derived from Eq. A.1 in the proof of Theorem 1, whereas the relation between $\bar{F}_{i}$ and $F_{i}$ is derived from Lemma 3.

1.4 Corollary 2

Proof

To begin with, we can easily derive $\rho_{i}^{\min }$ and $F_{i}^{\min }$ from Theorem 1. Obviously, $\rho_{i}^{\min } < F_{i}^{\min }$. Moreover, the platform provider’s expected payment in Lemma 2 implies that $\rho_{i}^{\min }$ and $F_{i}^{\min }$ are the optimal solution for the platform provider. The reason is as follows. First, from Eq. A.1 we know that the value of $F_{i}$ cannot be affected by $\rho_{i}$; thus, we only consider $\rho_{i}^{\min }$. Second, plugging $\rho_{i}^{\min }$ into the platform provider’s expected payment, we find that the platform provider’s expected payment is given by

$$ {\frac{{\rho_{i}^{\min } - (1 - q(n))\delta F_{i} }}{1 - \delta }} = {\frac{{(c_{i} + w_{i} ) + (1 - \delta )F_{i} }}{1 - \delta }}. $$

Obviously, $\rho_{i}^{\min }$ and $F_{i}^{\min }$ are the optimal solution for the platform provider. Finally, comparing $\rho_{i}^{\min }$ with $s_{i}^{G}$, we have the following result.

$$ \rho_{i}^{\min } \le s_{i}^{G} \Rightarrow {\frac{{(1 - \delta \hat{q}(n))(c_{i} + w_{i} )}}{{\delta (q(n) - \hat{q}(n))}}} \le {\frac{{c_{i} + w_{i} }}{{q(n) - \hat{q}(n)}}} \Rightarrow {{(1 - \delta )} \mathord{\left/ {\vphantom {{(1 - \delta )} \delta }} \right. \kern-\nulldelimiterspace} \delta } \le \hat{q}\left( n \right) $$

1.5 Proposition 2

Proof

Because ${{\partial^{2} P_{4} } \mathord{\left/ {\vphantom {{\partial^{2} P_{4} } {\partial \delta^{2} }}} \right. \kern-\nulldelimiterspace} {\partial \delta^{2} }} > 0$, we can figure out the minimal value of $P_{4}$ by solving ${{\partial P_{4} } \mathord{\left/ {\vphantom {{\partial P_{4} } {\partial \delta }}} \right. \kern-\nulldelimiterspace} {\partial \delta }} = 0$. Because ${{\partial P_{4} } \mathord{\left/ {\vphantom {{\partial P_{4} } {\partial \delta }}} \right. \kern-\nulldelimiterspace} {\partial \delta }} = 0$ implies ${\frac{1}{{(1 - \delta )^{2} }}} - {\frac{1}{{\delta^{2} (1 - \alpha )q(n)}}} = 0$, we can define $J(\delta )$ by $\delta^{2} (1 - \alpha )q(n) - (1 - \delta )^{2}$

1.6 Proposition 3

Proof

The equation ${{\partial P_{4} } \mathord{\left/ {\vphantom {{\partial P_{4} } {\partial n}}} \right. \kern-\nulldelimiterspace} {\partial n}} = 0$ implies $q(n) - nq^{\prime}(n) \le 0$. If ${{\partial P_{4} } \mathord{\left/ {\vphantom {{\partial P_{4} } {\partial n}}} \right. \kern-\nulldelimiterspace} {\partial n}} = 0$ holds for some $n$, we have ${{\partial^{2} P_{4} } \mathord{\left/ {\vphantom {{\partial^{2} P_{4} } {\partial n^{2} }}} \right. \kern-\nulldelimiterspace} {\partial n^{2} }} > 0$ due to $q(n) - nq^{\prime}(n) \le 0$.

1.7 Proposition 4

Proof

We can confirm ${{\lambda_{0} q\left( {n_{2}^{ * } } \right)} \mathord{\left/ {\vphantom {{\lambda_{0} q\left( {n_{2}^{ * } } \right)} n}} \right. \kern-\nulldelimiterspace} n} > c + w$. Otherwise, the platform provider’s expected payoff wouldn’t be positive (i.e., $\pi_{4} < 0$). Subsequently, we claim $q\left( {n_{2}^{ * } } \right) - nq^{\prime}\left( {n_{2}^{ * } } \right) > 0$. Suppose not, we can induce a contrary conclusion by the following inequalities.

$$ \begin{gathered} \because\,\lambda_{0} q^{\prime}\left( {n_{2}^{ * } } \right) - {\frac{(c + w)(1 - \delta )}{\delta (1 - \alpha )}} \cdot {\frac{{q\left( {n_{2}^{ * } } \right) - nq^{\prime}\left( {n_{2}^{ * } } \right)}}{{q\left( {n_{2}^{ * } } \right)^{2} }}} - (c + w) = 0 \hfill \\ \therefore\,\lambda_{0} q^{\prime}\left( {n_{2}^{ * } } \right) - (c + w) < 0 \Rightarrow {{\lambda_{0} q\left( {n_{2}^{ * } } \right)} \mathord{\left/ {\vphantom {{\lambda_{0} q\left( {n_{2}^{ * } } \right)} n}} \right. \kern-\nulldelimiterspace} n} < c + w \hfill \\ \end{gathered} $$

Based on the above result, we can straightforwardly observe the impact of the system parameters on the platform provider’s expected payoff.

1.8 Proposition 5

Proof

First, $\left. {{\frac{{\partial \pi_{4} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }} = 0$ implies ${\frac{{\lambda_{0} q^{\prime}\left( {n_{2}^{ * } } \right)}}{c + w}} = {\frac{(1 - \delta )}{\delta (1 - \alpha )}} \cdot {\frac{{q\left( {n_{2}^{ * } } \right) - nq^{\prime}\left( {n_{2}^{ * } } \right)}}{{q\left( {n_{2}^{ * } } \right)^{2} }}} + 1$. Considering $\left. {{\frac{{\partial \pi_{3} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }}$, we find that the sign of $\left. {{\frac{{\partial \pi_{3} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }}$ is the same as that of ${\frac{{q\left( {n_{2}^{ * } } \right) - nq^{\prime}\left( {n_{2}^{ * } } \right)}}{{q\left( {n_{2}^{ * } } \right)^{2} }}} - {\frac{\alpha \delta }{(1 - \delta )}}$. Because $q\left( {n_{2}^{ * } } \right) - nq^{\prime}\left( {n_{2}^{ * } } \right) > 0$ has been shown in Proposition 4, we can easily confirm $\left. {{\frac{{\partial \pi_{3} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }} > 0$ when $\delta$ approaches zero and $\left. {{\frac{{\partial \pi_{3} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }} < 0$ when $\delta$ approaches one. Because $\pi_{3}$ is a concave function of $n$, we have $n_{1}^{ * } > n_{2}^{ * }$ if $\left. {{\frac{{\partial \pi_{3} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }} > 0$ and $n_{1}^{ * } < n_{2}^{ * }$ if $\left. {{\frac{{\partial \pi_{3} }}{\partial n}}} \right|_{{n = n_{2}^{ * } }} < 0$.

1.9 Proposition 6

Proof

We define $\phi (t)$ by $\phi (t) \equiv \sum\nolimits_{i = t}^{\infty } {\prod\nolimits_{j = t}^{i} {\delta (j)} }$ where $t \ge 1$. In period $t - 1$, the difference between the expected payoffs results from the cooperation strategy and the fraud strategy is given by $\Uppi_{i}^{c} - \Uppi_{i}^{s} = \phi (t)((q(n) - \hat{q}(n))F_{i} - (c_{i} + w_{i} )) - (c_{i} + w_{i} )$. Obviously, the difference decreases with $t$. That is, the incentive for supernodes to cheat increases with time.

1.10 Proposition 7

Proof

Because we have shown the case in which each supernode exerts high effort in the two reward mechanisms, in the following, we only consider partial cooperation and the case in which each supernode exerts low effort. In the ex post reward mechanism, we define the expected payoffs of exerting high effort and low effort by $R^{c} (n,k)$ and $R^{s} (n,k)$, given $k$ supernodes exerting high effort. The condition in which there are k supernodes exerting high effort is:

$$ \begin{aligned} R^{c} (n,k) \ge R^{s} (n,k - 1) \Rightarrow & s_{i}^{G} \ge {\frac{{c_{i} + w_{i} }}{q(n,k) - q(n,k - 1)}} \\ R^{s} (n,k) \ge R^{c} (n,k + 1) \Rightarrow & {\frac{{c_{i} + w_{i} }}{q(n,k + 1) - q(n,k)}} \ge s_{i}^{G} \\ \end{aligned} $$

The condition in which each supernode exerts low effort is given by

$$ R^{s} (n,0) \ge R^{c} (n,1) \Rightarrow {\frac{{c_{i} + w_{i} }}{q(n,1) - q(n,0)}} \ge s_{i}^{G} $$

In the ex ante reward mechanism, we define the expected payoffs of exerting high effort and low effort by $\Uppi_{i}^{c} (n,k)$ and $\Uppi_{i}^{s} (n,k)$, given $k$ supernodes exerting high effort. The condition in which there are k supernodes exerting high effort is:

$$ \Uppi_{i}^{c} (n,k) \ge \Uppi_{i}^{s} (n,k - 1) \Rightarrow F_{i} \ge {\frac{{c_{i} + w_{i} }}{\delta (q(n,k) - q(n,k - 1))}} $$

$$ \Uppi_{i}^{s} (n,k) \ge \Uppi_{i}^{c} (n,k + 1) \Rightarrow {\frac{{c_{i} + w_{i} }}{\delta (q(n,k + 1) - q(n,k))}} \ge F_{i} $$

$$ \Uppi_{i}^{c} (n,k) - F_{i} \ge {\frac{{w_{i} }}{1 - \delta }} \Rightarrow \rho_{i} \ge (c_{i} + w_{i} ) + (1 - \delta q(n,k))F_{i} $$

$$ \Uppi_{i}^{s} (n,k) - F_{i} \ge {\frac{{w_{i} }}{1 - \delta }} \Rightarrow \rho_{i} \ge (1 - \delta q(n,k))F_{i} $$

Obviously, regarding the bound of $\rho_{i}$, we only need $\rho_{i} \ge (c_{i} + w_{i} ) + (1 - \delta q(n,k))F_{i}$. Moreover, the condition in which each supernode exerts low effort is given by

$$ \Uppi_{i}^{s} (n,0) \ge \Uppi_{i}^{c} (n,1) \Rightarrow {\frac{{c_{i} + w_{i} }}{\delta (q(n,1) - q(n,0))}} \ge F_{i} $$

$$ \Uppi_{i}^{s} - F_{i} \ge {\frac{{w_{i} }}{1 - \delta }} \Rightarrow \rho_{i} \ge (1 - \delta q(n,0))F_{i} $$