Modelling forest fire dynamics using conditional variational autoencoders

Abstract

Forest fires have far-reaching consequences, threatening human life, economic stability, and the environment. Understanding the dynamics of forest fires is crucial, especially in high-incidence regions. In this work, we apply deep networks to simulate the spatiotemporal progression of the area burnt in a forest fire. We tackle the region interpolation problem challenge by using a Conditional Variational Autoencoder (CVAE) model and generate in-between representations on the evolution of the burnt area. We also apply a CVAE model to forecast the progression of fire propagation, estimating the burnt area at distinct horizons and propagation stages. We evaluate our approach against other established techniques using real-world data. The results demonstrate that our method is competitive in geometric similarity metrics and exhibits superior temporal consistency for in-between representation generation. In the context of burnt area forecasting, our approach achieves scores of 90% for similarity and 99% for temporal consistency. These findings suggest that CVAE models may be a viable alternative for modeling the spatiotemporal evolution of 2D moving regions of forest fire evolution.

1 Introduction

Forest fires occur hundreds of thousands of times worldwide, burning several million square kilometers annually (Meng et al., 2015). These phenomena have far-reaching consequences, including significant loss of human lives and substantial economic and social impacts (Paveglio et al., 2018). Furthermore, it may also result in disruptions to local ecosystems (Certini, 2005) and contribute to the reduction of biomass and carbon dioxide release to the atmosphere (C3S, 2023).

Most traditional wildfire propagation simulation models and systems (e.g., Rothermel, 1972; Noble et al., 1980;Finney et al., 1998) adopt the fire geometry as a spreading line-fire and require extensive input data related to fuel characteristics, topography, and weather conditions (Zacharakis & Tsihrintzis, 2023). Although such models may achieve reasonable performance in specific areas, spatial heterogeneity makes scaling up them to large areas challenging, limiting their global applicability (McLauchlan et al., 2020; Meng et al., 2015). Over the years, alternative methods have emerged to model fire behavior, including the use of remote sensing, and geographic information systems coupled with machine learning-based fire behavior modeling (Wu et al., 2022; Zacharakis & Tsihrintzis, 2023). Moreover, some recent works (e.g., Duarte et al., 2019; Costa et al., 2020; Costa et al., 2021) used spatiotemporal database and region interpolation techniques to reconstruct the burned area evolution. Such an approach considers the burned area a 2D region and uses region interpolation functions to estimate the region’s (i.e., burned area) shape and position between observations.

Fig. 1

(A) Interpolation and (B) extrapolation of burned area. For continuous representation models, a method is required to recreate the spatiotemporal evolution of a region, such as the progression of the burned area

In this work, we employ deep models based on a Conditional Variational Autoencoder (CVAE) (Sohn et al., 2015) to estimate the past and future shapes of the area burned in a forest fire. Notably, our focus is on the 2D area affected by the fire. Our primary focus is on the 2D regions burned by the fire, rather than the fire’s front line.

Variational Autoencoders (VAE) (Hinton & Zemel, 1993) are generative models composed of encoders and decoders that learn the probabilistic distribution of the latent space (i.e. the low-dimensional representation generated by the encoder). CVAEs are extensions of VAEs that enforce conditioning information on the latent space (Sohn et al., 2015).

We assess our proposals using the BurnedAreaUAV Dataset (Ribeiro et al., 2023a, b), which contains representations of the burned area extracted from a video of a controlled fire acquired by a stationary drone. We train the CVAE model using distinct compression rates and evaluate its capability to generate in-between observations. We compare the performance of our proposal with other interpolation methods from the literature (Schenk et al., 2000; McKenney et al., 2016) in terms of spatial and temporal consistency metrics.

We also evaluate the potential of the CVAE to model the future behaviour of the forest fire, i.e., we forecast the burned area for different horizons and stages of the fire evolution, as outlined in Fig. 1. This work builds upon our previous research (Ribeiro et al., 2023) by modeling the future behavior of forest fires and applying a new model (with improved reproducibility) to generate in-between observations.

The primary contributions of this work include using a CVAE to forecast the size and shape of the area burned at a forest fire at distinct horizons and to simulate in-between observations of the burned area, and an experimental evaluation of our proposals and comparison with other methods from the literature using real-world data, and geometric similarity and temporal consistency metrics.

In the subsequent section, we review background and related work, covering spatiotemporal data representation, moving regions, interpolation methods, and neural networks. In Section 3, we describe the CVAE model, detailing its architecture and the generation of spatiotemporal data. Next, in Section 4, we outline the experimental evaluation and present and discuss the obtained results. Finally, in Section 5, we draw conclusions based on our findings and outline future directions.

2 Background and Related Work

Spatiotemporal data is often discretely encoded, with spatial attributes such as location and shape associated with time instants. A prevalent continuous representation for real-world spatiotemporal phenomena data is through moving regions (Erwig et al., 1999; Forlizzi et al., 2000). Formally, a region is defined as a set of non-intersecting line segments connecting distinct points, forming a closed loop that delineates the external faces of a polygon. A region may contain holes, which are also delimited by line segments in a closed loop and, crucially, do not intersect the external faces (Tøssebro & Güting, 2001).

2.1 Moving Regions and Traditional Interpolation Methods

Moving regions serve as abstract data types used to describe the spatiotemporal evolution of objects of interest, i.e., describing how their shape and position evolve over time. This representation is described as a sequence of sequentially stored regions (interval regions). Each interval region encapsulates the movement of an object over a defined time interval between two instances, called slices (Tøssebro & Güting, 2001).

Tøssebro et al. (2001) proposed a framework in which moving regions can be represented from observations stored in spatiotemporal databases. Subsequent works have extended this framework by various authors using the same principles (Heinz & Güting, 2020; Mckennney & Frye, 2015; Duarte et al., 2023). The primary objective is to produce representations that continuously maintain topological validity while ensuring consistency with the underlying spatiotemporal database systems. The Region Interpolation Problem (RIP) is the challenge of creating a moving region from a set of observations. Specifically, considering two observations at instants $t_1$ and $t_2$, the objective is to identify some interpolating function f capable of generating a valid representation of the moving object, its position and shape at any intermediate time point within the interval between $t_1$ and $t_2$ (Duarte et al., 2019).

Several works have addressed the challenge of moving regions, proposing various strategies to tackle the RIP. For instance, Duarte et al. (2019) presented a qualitative analysis of interpolation methods for deformable moving regions, while Costa et al. (2020) introduced sampling strategies to create moving regions from real-world observations. Moreover, Costa et al. Costa et al. (2021) assessed the quality and improvement of a forest fire dataset, and Duarte et al. (2023) approximated the evolution of rotating moving regions using Bézier curves. These works, among others, have attempted to solve the problem of moving regions using database-based strategies, without the use of machine learning methods.

Other interpolation approaches have also been suggested. For instance, if we regard a moving region as a polyhedron, where time takes the place of a third dimension (height) (Heinz & Güting, 2020), techniques used to interpolate polygons representing sections of a volumetric object, such as human organs in tomographic imaging, may be adapted to generate in-between regions. The so-called Shape-Based interpolation is an example of one such algorithm. Contrary to the abovementioned methods, typically, this algorithm operates with raster data (Schenk et al., 2000; Herman et al., 1992). Its process can be described in a sequence of steps, as follows. Let $x_1$ and $x_2$ be the 2D snapshots that contain the shape of the region at instants $t_1$ and $t_2$. For each selected snapshot, a binary image $y_k, k \in \{1,2\}$ is generated by segmenting the region of interest. Next, a grey-level distance map $z_k, k \in \{1,2\}$ is generated for each binary image $y_k$ by mapping the Euclidean distance to the boundary of the region. The distance values inside the region are set to positive, and the outside ones are set to negative. The maps $z_k$ are then reconstructed by using linear interpolation at the pixel level. The shape of the region at a given point in time $t_i, t_1< t_i < t_2$ is found by identifying the zero-crossings of the interpolated distance maps. Finally, these contours generate the region of interest in $t_i$.

Spatio-temporal Kriging (Snepvangers et al., 2003; Gräler et al., 2016) is another method that can be used for spatiotemporal data interpolation. This technique treats the temporal dimension similarly to the spatial dimensions, modelling the temporal variability of the data. It does this by adding a temporal dimension to the Kriging system, transforming the problem into a four-dimensional Kriging problem.

The spatiotemporal Kriging process involves calculating variograms for both the pure time and space domains, constructing covariance functions for the space and time domains based on these variograms, and combining these functions to create a spatiotemporal covariance function. This function describes the spatial and temporal covariance of the data simultaneously. Next, the algorithm calculates the space-time distances between the point to be predicted and the surrounding points (known points). These distances are used to derive a variogram vector, which is then used in conjunction with the known points and the spatio-temporal variogram to calculate the weight vector. This weight vector is used to calculate the estimation of the unobserved point.

Notably, the method proposed by McKenney (McKenney et al., 2016), a classical spatiotemporal database approach for modeling moving regions, will be used as a baseline for comparison with the proposed CVAE-based machine learning method in this study, as it has been shown to be an effective alternative in the context of burned area evolution (Duarte et al., 2023).

Fig. 2

Artificial Neural Network Architecture. Inputs are processed through weighted connections and activation functions in hidden layers, leading to predictions in the output layer. During Backward Propagation, the weights are adjusted based on the error calculated from comparing the predicted output against the ground truth values

Fig. 3

Basic architecture of a CNN. On top, it is the core process of a 2D convolution on an RGB image using a 3$\times$3 filter, and the resulting feature map is demonstrated. Below, is a simplified CNN featuring 2D convolution and pooling layers

2.2 Neural Networks and Autoencoders

Neural Networks (NNs) are computational models loosely inspired by the biological neural networks present in the human brain (McCulloch & Pitts, 1943). They are composed of interconnected nodes or artificial neurons organized into input, hidden, and output layers. Each node in a neural network computes a weighted sum of its inputs, applies an activation function to the sum, and transmits the resulting output signal to the next layer. The weights are adjusted during training based on the error between the predicted and actual outcomes, aiming to minimize this error, as outlined in Fig. 2. The learning process in NNs is facilitated by optimization algorithms, such as gradient descent, which systematically adjust the weights to enhance the model’s performance (Rumelhart et al., 1988).

The architecture of a NN can vary significantly, depending on the complexity of the problem, the nature of the input data, and the desired output format it is designed to address. Common architectures include Feedforward Neural Networks (FNNs), Recurrent Neural Networks (RNNs), and Deep Neural Networks (DNNs), among others. FNNs propagate information in one direction, from input to output, without loops. RNNs introduce feedback connections, allowing them to maintain internal states and process sequential data efficiently. DNNs consist of multiple layers of neurons, which enables them to learn and represent increasingly complex patterns (Goodfellow et al., 2016).

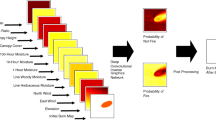
Convolutional Neural Networks (CNNs) are a subclass of FNNs specifically designed for analyzing data that has a grid-like topology, such as images. CNNs are characterized by their convolutional layers, which apply a set of filters to the input data (Lecun et al., 1998).

These filters slide over the input volume, extracting local features at each position (Fig. 3 A)). Following the convolutional layer, pooling layers are typically employed to reduce the spatial size of the representation (Fig. 3 B)), thereby controlling overfitting and reducing computational complexity. The convolutional layers allow CNNs to automatically and adaptively learn spatial hierarchies of features from the input data, capturing both local and global patterns (Simonyan & Zisserman, 2015).

Employed for feature extraction from the input data, convolutional layers enable the utilization of these features for downstream tasks, including image classification, object detection, and segmentation, thus highlighting CNNs’ effectiveness in these domains (Li et al., 2022).

Fig. 4

Autoencoder Architecture. The transformation of an input $\textbf{x}$ into a compressed representation $\textbf{z}$, and then back into a reconstructed output $\hat{\textbf{x}}$, through the use of an encoder function $f_\phi$ and a decoder function $g_\theta$

Fig. 5

Variational Autoencoder Architecture.Inputs, denoted as x, undergo transformation via the encoder function $q_\phi (z|x)$, yielding parameters $\mu _\phi$ and $\sigma _\phi$. These parameters facilitate the sampling of a latent variable z. Then, z and the original input x are processed by the decoder function $p_\theta (x|z)$ to reconstruct the data as $\hat{x}$

In simple terms, Autoencoder (AE) (Hinton & Zemel, 1993) can be seen as a tool that extracts the essence of the most important features of the data, such as an image, generates a compressed representation of that data, and then reconstructs the original input data from this compressed code, albeit with the loss of some details (Fig. 4). During the training process, the autoencoder is forced to learn a compact representation of the input data, as its architecture includes a bottleneck (where the compact representation is stored) through which the essential information must flow. Through this process, the autoencoder aims to replicate the original data as closely as possible, with its training objective being to minimize the reconstruction error, which is some measure of the difference between the input and the output.

The ability of AEs to compress and decompress data has proven valuable in various applications. For instance, they are often employed in denoising tasks, where they are used to remove noise from images or signals (Poole et al., 2014). Additionally, autoencoders are utilized for dimensionality reduction (Wang et al., 2014), simplifying high-dimensional data for improved visualization and analysis.

In more formal terms, an AE is a neural network that takes a high-dimensional input $\textbf{x}\in \mathbb {R}^D$, and maps it to a compact, low-dimensional representation $z \in \mathbb {R}^d$, referred to as the latent space z, which is typically a vector.

A decoder then uses this compressed representation to reconstruct the original input. The structure of an AE can be broken down into three main components: the encoder $f_{\phi }(\cdot )$, which maps the input to the latent space, a decoder $g_{\theta }(\cdot )$, which maps the latent representation back to input space, and a bottleneck z that holds the compressed codes. Both the encoder and decoder are often implemented as neural networks with learnable parameters $\phi$ and $\theta$, respectively.

Fig. 6

Conditional Variational Autoencoder (CVAE) Architecture. The encoder $q_\phi ({z}|{x},{y})$ transforms inputs x and condition $\textbf{y}$ into parameters $\mu _\phi$ and $\sigma _\phi$. These parameters are used to sample a latent variable $\textbf{z}$. The decoder $p_\theta ({x}|{z},{y})$ then receives the sampled z and y to output the reconstructed data $\hat{\textbf{x}}$. This process demonstrates encoding and decoding data into a latent space, conditioned on variable y, enabling the model to generate diverse outputs based on the given condition

2.3 Variational and Conditional Variational Autoencoders

Variational Autoencoders (VAEs) (Kingma & Welling, 2013; Rezende et al., 2014) are a type of neural network that builds upon the concept of AEs. While AEs learn to compress and reconstruct data, VAEs learn to model the underlying probability distribution of the data, as shown in the Fig. 5.

To illustrate the concept, consider the task of generating new handwritten digits that bear resemblance to existing ones. In this scenario, a standard Autoencoder (AE) would learn a lower-dimensional representation of the given digits and subsequently reconstruct them. However, it might not capture the variations and styles present. Consequently, the generated digits would be faithful reconstructions but cannot represent novel variations within the data manifold.

VAEs overcome this by introducing a latent space that explicitly models the probability distribution of the data. During training, the VAE maps input digits to this latent space and vice versa. Crucially, the latent space is imbued with a probabilistic structure, allowing the VAE to not only reconstruct the training data but also sample new data points from the learned distribution. These newly generated digits will inherently resemble the training examples in terms of style and features but can also exhibit novel variations within the confines of the captured probability distribution.

As such, VAEs have found successful applications across several fields. In generative modelling, they enable the creation of new data points that resemble existing ones, for instance, producing novel typography fonts or faces (Parente et al., 2023; Bagautdinov et al., 2018). Additionally, VAEs facilitate unsupervised learning tasks, enabling activities like clustering and dimensionality reduction (Prasad et al., 2020). They also play a role in anomaly detection by learning the underlying probability distribution of normal data, thereby identifying deviations or outliers (Ulger et al., 2021).

Proceeding to a more rigorous exposition, the VAE, a variant of the AE, consists of an encoder $q_{\phi }(z|x)$ and a decoder $p_{\theta }(x|z)$. VAEs are trained to optimize the surrogate objective, which is essentially a lower bound on the log-likelihood of the data. This surrogate objective is composed of two elements: a conditional likelihood term and a negative Kullback-Leibler (KL) divergence term. The conditional likelihood term assesses how effectively the model reproduces the observed data, while the KL divergence term acts as a regularizer, guiding the learned latent distribution to align closely with a prior distribution. The loss function can be formally expressed as:

$$\begin{aligned} \mathcal {L}(\theta , \phi , x) = \mathbb {E}_{q_{\phi }(z|x)}\left[ \log p_{\theta }(x|z)\right] - D_{KL}(q_{\phi }(z|x) || p(z)) \end{aligned}$$

(1)

The initial surrogate objective term, $\mathbb {E}_{q_{\phi }(z|x)}\!\left[ \log p_{\theta }(x|z)\right]$, signifies the expected log-likelihood of the observed data under the approximate posterior distribution $q_{\phi }(z|x)$. It pushes the model to reproduce the observed data accurately, often approximated through reconstruction error computations. The second surrogate objective term, $-D_{KL}(q_{\phi }(z|x) ||$ $p(z))$, represents the KL divergence between the approximate posterior distribution $q_{\phi }(z|x)$ and a prior distribution p(z). It acts as a regularizer, aligning the learned latent distribution with the chosen prior distribution.

In this context, p(z) is a selected prior distribution, such as a multivariate Gaussian distribution. The encoder predicts the mean $\mu _{\phi }(x)$ and standard deviation $\sigma _{\phi }(x)$ for an input x, and a latent sample $\hat{z}$ is drawn using the reparameterization trick: $\hat{z} = \mu _{\phi }(x) + \sigma _{\phi }(x) * \epsilon$, where $\epsilon \sim \mathcal {N}(0,I)$. The KL divergence term can be analytically calculated due to the choice of a multivariate Gaussian prior.

New, previously unseen samples can be generated by drawing latent samples from the prior, $z \sim p(z)$, and then synthesizing data samples from $p_{\theta }(x|z)$ by passing the latent samples through the decoder, $D_{\theta }(z)$. The VAE’s architecture facilitates superior interpolation compared to traditional AEs, thanks to the continuous latent space enabling smooth transitions in generated outputs (Berthelot et al., 2018).

Conditional Variational Autoencoders (CVAEs) (Sohn et al., 2015) extend the functionality of VAEs by allowing them to learn a conditional distribution $p_{\theta }(x|y)$, where y represents some conditioning information, such as class labels. CVAEs consist of an encoder $q_{\phi }(z|x,y)$ and a decoder $p_{\theta }(x|z,y)$, both of which incorporate the conditioning information y, as depicted in Fig. 6. Like VAEs, CVAEs are also trained to optimize the surrogate objective on $\log p_{\theta }(x|y, z)$.

The loss function for CVAEs is similar to that of VAEs, but is conditioned on y:

$$\begin{aligned} \mathcal {L}(\theta , \phi , x, y) =&\mathbb {E}_{q_{\phi }(z|x, y)}\left[ \log p_{\theta }(x|z, y)\right] \nonumber \\&- D_{KL}(q_{\phi }(z|x, y) || p(z|y)) \end{aligned}$$

(2)

where p(z) is a chosen prior distribution. The encoder predicts the mean $\mu _{\phi }(x,y)$ and standard deviation $\sigma _{\phi }(x,y)$ for a given input (x, y), and a latent sample $\hat{z}$ is drawn from $q_{\phi }(z|x,y)$ using the reparameterization trick: $\hat{z} = \mu _{\phi }(x,y) + \sigma _{\phi }(x,y) * \epsilon$, where $\epsilon \sim \mathcal {N}(0,I)$.

The first term in the surrogate objective equation is typically approximated by computing the reconstruction error, such as Mean Squared Error or Binary Cross-Entropy losses, between many samples of x and their corresponding reconstructions $\hat{x}=D_{\theta }(E_{\phi }(x,y))$.

In the context of discrete variables, the conditioning variable can serve as a categorical identifier, signifying the category of the data point. For example, in a collection of images, the conditioning variable might represent the class label assigned to each image. By using the conditioning variable, the CVAE can learn to generate new data points within the same category, thus performing an interpolation operation within the discrete space defined by the categories.

For continuous variables, the conditioning variable can act as a scalar value that modulates the distribution of the latent space. For example, in a time series prediction task, the conditioning variable could represent the time index. By varying the conditioning variable, the CVAE can generate a sequence of predictions that smoothly transition from the initial state to the final state. This property suggests that this model could be an alternative for addressing the region interpolation problem by learning the spatiotemporal representation of phenomena. In Oring et al. (2021), Oring et al. explore interpolation techniques for raster images depicting polyhedra at different angles and other geometric representations with deformable objects, by smoothly interpolating the latent space of Autoencoder models. Similarly, Cristovao et al. and Mi et al. propose equivalent methods for interpolating raster images with three-dimensional objects at various angles, as well as snapshots representing moving objects, using the latent space interpolation of various Generative Latent Variable models (Cristovao et al., 2020; Mi et al., 2021).

In this work, we apply the Conditional Variational Autoencoder (CVAE) model to generate both interpolated and extrapolated representations of the evolution of burned areas in 2D regions.

3 CVAE-based Representation of Spatial Phenomena

The continuous latent space acts as a conduit between high-dimensional data and the low-dimensional representations learned by a VAE. The smoothness and unboundedness of the latent space are inherent properties that ascertain the absence of sudden leaps or discontinuities (Mi et al., 2021). This property enables coherent spatiotemporal data generation and consistent geometric representation of the phenomena being modeled (Chen et al., 2021).

3.1 Spatiotemporal Data Generation

CVAEs can perform conditional image editing in the latent space; given two different conditioning inputs, $x_1$ and $x_2$, one can interpolate in the latent space between the corresponding latent codes $z_1$ and $z_2$ to generate novel images that smoothly blend the two conditioning factors. This capability makes CVAEs suitable to interpolate different discrete or continuous codified representations. Instead of directly interpolating between the initial and final states in the latent space, another approach is to have the CVAE learn a representation of the phenomenon and sample the latent space conditioned to a specific instant.

In this scenario, the CVAE learns to map the conditioning variable y to a specific point in the latent space conditioned on the input. This point can be thought of as a snapshot of the phenomenon at the specified instant. By manipulating the conditioning variable, the CVAE can generate different snapshots of the phenomenon, effectively interpolating between different instants.

Fig. 7

CVAE directed graph representation of the generation process. The solid lines represent the generative model, with $\theta$ being the model weights and $\textbf{y}$ being the condition variable and function of $t$. The latent variable $\textbf{z}$ is sampled from a distribution $q_{\phi }(z|y)$, and the generated output $\textbf{x}$ is sampled from a distribution $p_{\theta }(x|z)$. Figure adapted from Zhang et al. (2016)

In this framework, the conditioning variable y is dependent on the time t. Altering the value of y enables us to navigate through the timeline of the phenomenon, generating new instances of the phenomenon at varying instants. This process facilitates an interpolation operation within the continuous space defined by the time variable, as depicted in Fig. 7.

Our approach involves training a CVAE model on the set of samples meant for interpolation, with each sample being associated with a conditioning temporal information, such as the timestamp or frame number, as shown in Fig. 8. For applications involving discrete variables, i.e., a finite number of classes, it is standard practice to encode these classes using one-hot encoding. The resulting vector is subsequently incorporated into the latent space.

Fig. 8

CVAE Training Process. We use the normalized frame number value as a conditioning variable. Each region stored in WKT format is converted to a raster image to be processed by the model

Given that we’re dealing with continuous phenomena, and considering the conditioning variable, which represents the instant of interpolation, is also continuous, we chose to use the frame number (Label) of the original video, normalize it to a range between 0 and 1, and then concatenate the resulting value y to the latent space z. This conditioning variable is then utilized during the training of the CVAE, enabling the model to learn the relationship between the instant and the evolution of the geometry of the burned area.

During the inference stage, we sample both the latent space variable z and the conditioning variable y to generate new samples from the learned conditional distribution $p_{\theta }(x|y)$. More specifically, we first sample a random vector $\epsilon$ from a standard normal distribution, then use it to compute a sample z from the learned approximate posterior distribution $q_{\phi }(z|x,y)$ using the reparameterization trick. Next, we define a specific conditioning variable $y_i$, representing an arbitrary instant within the length of the video, and concatenate it with the sampled z to the decoder network $p_{\theta }(x|z,y)$ to generate a new sample $\hat{x}_i$, an estimated raster image for the instant i.

The capability to sample from the latent space and the conditioning variable enables the performance of interpolation and extrapolation, with interpolation being the generation of intermediate samples between known samples in our training set, and extrapolation the generation of samples beyond the known data. To a certain extent, this dual functionality allows for the exploration of both historical and out-of-sample, future states (Yoon et al., 2022).

The generated output undergoes a threshold operation, transforming the continuous values into binary masks. Values less than 0 are set to 0, signifying unburnt areas, while values equal to or greater than 0 are set to 1, indicating predicted burned areas. Subsequently, the output is resized to match the original size of the input. Following this, the binary mask is converted into a Well-Known Text (WKT) format for compatibility with spatial databases and mapping tools, as shown in Fig. 9.

Fig. 9

Inference Stage. The model generates a representation of the burned area at an arbitrary instant, either from an intermediate point (interpolation) or from some point in the future (extrapolation). The conditioned output is binarized, resized, and converted to WKT format

Table 1 CVAE Model Architecture. The table illustrates the sequence of layers in the CVAE model and their key parameters. Abbreviations used: K=kernel size, F=filter, P=padding, S=stride, A=activation function. ’same’ padding maintains the spatial dimensions post-convolution

3.2 Model Architecture

The proposed architecture comprises an encoder-decoder structure with convolutional layers, incorporating the conditioning variable during the decoding phase, as described in Table 1.

The encoder starts with the input tensor, which symbolizes the raster image of the continuous phenomenon. The following layers include Separable Convolution (Chollet, 2017) with Leaky ReLU activation functions and MaxPooling layers. These layers enable the encoder to learn hierarchical representations. After this, the encoder flattens the output and feeds it into a fully connected layer with 64 units and a Leaky ReLU activation function. This results in the representation of the mean and log variance of the latent variable distribution. The latent variable is then sampled using the reparameterization trick via a custom sampling layer.

During the decoding phase, the sampled latent variable and the conditioning variable, derived from the normalized frame number of the original video, are merged. The combined tensor undergoes a dense layer with $64\times 64\times 64$ units, followed by a reshaping operation that transforms the data into a 3D tensor again, which the subsequent convolution layers can process. Similar to the encoder, the decoder employs Depthwise Separable Convolution layers followed by Transposed Convolution layers, which restore the feature maps to the input resolution.

Fig. 10

Flowchart outlining the main stages of the experiment

4 Experimental Evaluation

To assess the performance of the proposed model, our experimental approach is structured in a series of stages, as illustrated in the flowchart in Fig. 10, which will be further detailed in the following sections.

We begin with the collection and treatment of polygonal data representing the progression of a forest fire (I). These data are then subject to subsampling, effectively creating datasets with different sampling rates as well as diverse segments of time (II). In stage III, the CVAE model undergoes training using the polygonal data corresponding to the timestamp of the burned area. Following the training phase, the data generation stage (IV) is performed, encompassing both interpolation (generation of polygons between samples) and extrapolation (prediction of the burned area’s evolution to instances in the future where the model lacks training data).

Lastly, in stage V, the CVAE model is evaluated by employing geometric similarity metrics, namely the Jaccard Index and Hausdorff Distance, as well as assessments of temporal consistency (Section 4.1). For benchmarking purposes, we compare the performance of our model with two classical alternatives identified in the literature: the McKenney interpolation method (McKenney et al., 2016) and the Shape-Based interpolation (Schenk et al., 2000).

The experiments were conducted on an HP Victus, 32 GB of RAM, Intel i5-12500Hx16 processor, with Nvidia GeForce RTX 4060 and Pop!_OS 22.04 LTS operating system. We primarily use Python language scripting and Jupyter Notebooks to facilitate data exploration and result visualization. The development of the CVAE model was accomplished using the TensorFlow-Keras framework. For image processing and manipulation, we relied mostly on the OpenCV library. We provide our code and additional documentation on a public GitHub repository: https://github.com/Tiago1Ribeiro/spatiotemporal-vae-reconstruction/.

Fig. 11

Overview of the utilized data sources for the experiment. (A) BurnedAreaUAV Dataset: annotations were conducted for the entire video duration for the burned and unburned classes, (B) Distance-Based Sampled data, (C) Frame-wise U-Net burned area generated polygons

4.1 Performance Metrics

To evaluate the performance of the spatiotemporal representation, we use two similarity metrics between generated images and ground truth data. We also propose a temporal consistency metric that measures the consistency between generated representations considering phenomena-specific features.

Jaccard Index. The Jaccard Index (JI) measures the overlap or similarity between two shapes or polygons (A and B). It returns a value between 0 and 1, where 1 means the shapes are identical and 0 means they have no overlap:

$$\begin{aligned} JI(A,B) = \frac{A\cap B}{A\cup B} \end{aligned}$$

(3)

Hausdorff Distance. The Hausdorff Distance (HD) measures the degree of mismatch between two non-empty sets of points $A = \{a_1,...,a_p\}$ and $B = \{b_1,...,b_p\}$ by measuring the distance of the point A that is farthest from any point of B and vice versa (Huttenlocher et al., 1993). In simpler terms, it measures how far apart two sets are from each other by finding the maximum distance between a point in one set and its closest point in the other set. Formally, it can be denoted as follows:

$$\begin{aligned} HD(A,B) = max(h(A,B), h(B,A)) \end{aligned}$$

(4)

where h(A, B) is the directed HD from shape A to shape B, and h(B, A) is the directed HD from shape B to shape A. The directed HD is defined as:

$$\begin{aligned} h(A,B) = \underset{a \in A}{max}\,\underset{b \in B}{min}|| a - b || \end{aligned}$$

(5)

where a is a point in shape A, b is its closest point in shape B, and $||a - b||$ denotes the Euclidean distance between two points.

Temporal Consistency. Given the nature of fire outbreaks, an area that is established as burned cannot cease to be so at a later stage. Likewise, we know that the burned area never decreases. With these considerations in mind, we apply the temporal consistency TC as a complement of a geometric difference (Ribeiro et al., 2023):

$$\begin{aligned} TC_{stride} = 1 - \frac{A_{t} - A_{t+stride}}{A_{t+stride}}, \forall t \in \{1, 2, ... ,T-stride\} \end{aligned}$$

(6)

where $A_{t}$ and $A_{t+stride}$ represent the burned area region in separated by stride samples. To assess different time scales, we consider various values of stride from a geometric progression $stride_n = ar^{n-1}$, $\forall n \in \{1, 2, ..., N\}$, with N smaller than the total number of polygons in the sequence, a the coefficient of each term and r is the common ratio between adjacent terms. Varying temporal strides facilitate the exploration of the burned area at different temporal resolutions. While larger strides provide a broader view of the burned area over a longer duration, smaller strides capture minute changes over shorter periods. Moreover, varying strides offer an additional reading into the dynamic of the burned area progression. To assess the performance for each stride, we calculate the average of $TC_{stride}$. Finally, we can also estimate the overall Temporal Consistency by computing the mean of all $TC_{stride}$ averages.

4.2 Burned Area Data

This study relies on data captured from a video recorded by a DJI Phantom 4 PRO UAV equipped with an RGB camera, documenting a prescribed fire at Torre do Pinhão in northern Portugal (41$^{\circ }$ 23’ 37.56”, -7$^{\circ }$ 37’ 0.32”). During the data collection, the UAV maintained a nearly stationary position, ensuring that the analysis of the evolution of the burned area and the geometry of the polygons could be conducted as a series of coherent temporal events. The video spans approximately 15 minutes, featuring a frame rate of 25 fps and a resolution of 720$\times$1280, resulting in a total of 22,500 images. This footage has been utilized in previous studies, as cited in Costa et al. (2021); Costa and Moreira (2022).

In a prior study (Ribeiro et al., 2023b), we have outlined a method for manually annotating and validating data on the burned area in forest fires, as depicted in Fig. 11 A.

As a result of this work, a total of 249 annotated frames were obtained, with 226 frames allocated for training and 23 for testing. The sets were constructed with a periodicity of 100 frames, offset by 50 frames between the training and testing subsets. This training subset serves as a reliable representation of the polygon delineating the burnt area, serving as the basis for interpolation with Uniform or Periodic Sampling.

In Periodic Sampling, we consider the regions corresponding to the burned area as a sequence of observations $x_t = \{x_1, x_2, ..., x_n\}$, where n is the length of the sequence, ordered in time with a given sampling frequency $f_s$, corresponding to the video frame rate. Then we sample the sequence periodically using some downsampling factor $d \in \mathbb {N}$. This results in a new sequence of observations $w_t = \{w_1, w_2, ..., w_m\}$, where $m = \lfloor n/d \rfloor$ is the length of the downsampled sequence. Each observation $y_i$ corresponds to the original observation $x_{id}$, where i is the index of the downsampled sequence and d is the downsampling factor. Although this method reduces the size of the sequence by a factor of d, it may also result in the discarding of potentially important samples.

Table 2 Training Parameters. The Scheduler adjusts the learning rate during training based on certain conditions. Patience (P) defines the number of epochs or steps without improvement before the learning rate is reduced or training is halted. Factor (F) determines the amount by which the learning rate is reduced. Monitor (M) refers to the metric being monitored for improvement. The Stopping Criteria determine when to halt training based on the number of epochs or steps without improvement in the monitored metric

Fig. 12

Stem plot depicting the sampling frequencies and sample densities of the three datasets employed in the experiment

The resulting 226-frame set was further subsampled using Distance-Based Sampling (Fig. 11 B). This method downsamples a sequence of observations by selecting representative points that are dissimilar from one other. It takes a set of observations and a distance function that calculates the dissimilarity between two observations, along with a threshold value $\alpha$. The algorithm initializes the downsampled sequence with the first observation and iteratively adds subsequent observations to the sequence only if they are more dissimilar than the threshold value from the last selected observation. This process continues until all observations have been considered, or the sequence length reaches the desired length. The distance function can be any metric that calculates dissimilarity, such as Jaccard distance, HD, or a combination of several metrics. We employed the Jaccard’s distance as a dissimilarity measure with a tolerance threshold of $\alpha = 0.15$, ultimately reducing the number of samples to 13.

Additionally, we trained a segmentation model based on the U-Net architecture (Ronneberger et al., 2015) from scratch on the BurnedAreaUAV training set (Ribeiro et al., 2023b) (Fig. 11 C). This model produced segmentation masks for all video frames, subsequently converted to Well-known Text (WKT) compatible polygons. The polygons derived from the U-Net model achieved an overall JI value exceeding 0.95 on the BurnedAreaUAV dataset’s test set, establishing them as accurate approximations of the actual progression of the burnt area. We denote this set of 22,500 polygons as U-Net Samples.

4.3 Model Training and Inference

This section details the essential parameters and methodologies employed in training the CVAE model. Referencing Table 2, we summarize the key parameters for both interpolation and extrapolation.

For the interpolation task, the model was trained for a maximum of 500 epochs. The learning rate underwent a reduction by a factor of 0.3 every 30 epochs if there was no decrease in the loss function value, monitored by a learning rate adjustment based on plateau detection (ReduceLROnPlateau). Additionally, training ceased after 30 epochs without loss enhancement, guided by a strategy where training halts when no improvement is detected for a certain period (EarlyStopping). The training dataset incorporated both the complete (periodic) and sampled BurnedAreaUAV datasets, as represented by the top two two plots in Fig. 12.

Table 3 Training and Inference Times. CVAE training times for periodic, distance-based and 90% of U-Net samples (maximum number of samples for extrapolation) and Inference times for Shape-Based, McKenney, and CVAE algorithms

In the extrapolation task, the model underwent training for a maximum of 2 epochs. Similar to the interpolation setup, the learning rate experienced a reduction by a factor of 0.3 for every 10,000 steps without loss improvement, leading to training cessation after 10,000 steps without loss enhancement. Frame-wise samples generated by the U-Net model constituted the training data.

A custom data generator facilitated batching and shuffling during training. Post-training, the model-generated frames for a video, are saved as PNG images and converted to WKT polygons.

Table 3 presents the average inference times for the Shape-Based, McKenney, and CVAE algorithms, as well as the CVAE training times for periodic and distance-based sampling. Notably, the training times reported for CVAE take into account the hyperparameters described in Table 2. The inference times were quantified for the generation of individual instances of burned area, and the averages were reported in the table. These averages were calculated from the mean of 10 successive generations to ensure a representative estimate. It is important to note that the training time applies exclusively to the CVAE model, as the Shape-Based and McKenney algorithms do not require a training phase.

4.4 Data Generation and Evaluation

For each algorithm, we generate in-between samples corresponding to the frame timestamps of the original video by employing the 226 samples resulting from Periodic Sampling as well as the subset of 13 Distance-Based samples (Fig. 13, below). The generated polygons were then compared to the U-Net Samples, which were produced by automatic segmentation and validated using the test subset of the BurnedAreaUAV dataset. JI and HD metrics were calculated to evaluate the similarity between the generated and U-Net samples.

We complement the evaluation by accessing the quality of the generated polygons in terms of the Temporal Consistency indicator as formulated in Section 4.1. To calculate the JI and HD, we discarded the samples that supported the calculation of the intermediate regions, both for Periodic Sampling and for Distance-Based sampling. That is, out of a universe of 22,500 observations corresponding to the video frames, we considered 22,274 intermediate regions for the Periodic Sampling and 22,487 for the Distance-Based sampling. All the metrics were calculated considering the resolution of the original footage ($720\times 1280$).

As outlined in Fig. 13, the starting points of our extrapolation experiments, within the video sequence at four unique time stamps: 88, 256, 448, 628, and 810 seconds. These time stamps, represented in red, correspond to approximately 10%, 30%, 50%, 70%, and 90% of the total duration of the original BurnedAreaUAV dataset video, respectively.

Fig. 13

Outline of the Extrapolation Experiment Setup. The figure delineates the video segments utilized for extrapolation and the various testing horizons. Letters A to E indicate the distinct support durations tested

To assess the model’s extrapolation ability, we established four distinct horizons, each representing 20, 40, 60, and 80 seconds, highlighted in yellow. This setup allowed us to evaluate the model’s performance under varying prediction scenarios.

The extrapolation experiments involved training models up to each origin time instant and subsequently evaluating the “future” instant at the designated horizons. We then calculated the average metrics for JI and HD across the evaluated horizons. Finally, we employed the Temporal Consistency indicator to evaluate the generated polygons, spanning from the origin to the horizon, following a similar procedure as in the Interpolation experiment.

Table 4 Similarity Evaluation. Comparison of Jaccard Index and Hausdorff Distance for U-Net Samples and BurnedAreaUAV test set using periodic and distance-based sampling

4.5 Experimental Results

In this section, we present and compare the results of the Shape-Based, CVAE, and McKenney algorithms in interpolation experiments. We also evaluate the performance of the CVAE model, trained on U-Net-generated burned area polygons, in extrapolation experiments using the JI, HD, and Temporal Consistency metrics in both interpolation and extrapolation.

4.5.1 Interpolation Results

Table 4 details the similarity metrics, while Table 5 focuses on temporal consistency. These tables offer a broad view of the algorithms’ performance under different sampling techniques.

Table 5 Temporal Consistency Comparison. Average temporal consistency across different algorithms for periodic and distance-based sampling

The Shape-Based and CVAE interpolation methods outperformed the McKenney interpolation method in both the periodic and distance-based sampling, as shown in Table 4 and Fig. 14 (top). This was particularly evident in the BurnedAreaUAV test set, where the Shape-Based algorithm and the CVAE had similar performance, with the former having a slight advantage. Regarding the HD metric, the Shape-Based algorithm achieved the best performance on both datasets.

The relatively low results on the U-Net dataset can be attributed to the error inherent in the auto-generated segmentation. Notably, reducing the number of support samples for interpolation did not have a significant impact on the JI or HD values. This finding supports the validity of the distance-based compressing algorithm, which reduced the number of samples from 226 to 13, for these particular datasets.

Fig. 14

Boxplots illustrating the comparison of performance metrics, namely the Jaccard Index and Hausdorff Distance, using periodic and distance-based sampling methods. (a) Jaccard Index for periodic sampling, (b) Jaccard Index for distance-based sampling, (c) Hausdorff Distance for periodic sampling, and (d) Hausdorff Distance for distance-based sampling

The Table 5 indicates the average Temporal Consistency across all stride values (1, 10, 100, 1,000 and 10,000) and shows that the CVAE model can produce polygons with higher consistency for the burnt area evolution phenomenon in both datasets. Figure 15 corroborates that by showing the superior monotonicity and smoother evolution of the burned area representations generated by the CVAE model. Analysis of Fig. 16 indicates that the CVAE algorithm is superior for strides up to 1,000 and performs less well for strides of 10,000, implying a reduced capacity to maintain consistency over extended time windows.

Fig. 15

Burned area of the generated polygons by interpolation throughout the entire time of the video

Fig. 16

Results for Periodic Sampling and Distance-Based Sampling, and different temporal strides. Different y-axis scales are used for better visibility

4.5.2 Extrapolation Results

The extrapolation performance of the CVAE model was evaluated through the calculation of JI and HD at the forecast horizon and for the average of the interval extending from the origin to the forecast horizon (Table 6 and Table 7, respectively). This dual approach allows for an overall assessment of the model’s predictive capabilities over time.

Table 6 End-point Jaccard Index and Hausdorff Distance. Values measured at the forecast horizon originating from different starting points (origins) within the video timeline

Analyzing the results from Table 6, it is evident that there is no decrease in the JI as the forecast horizon extends, suggesting a capable extrapolation capability. Simultaneously, it is observed that, on average, the model performs better for origins corresponding to the initial frames of the video.

The HD values, as displayed in the same Table 6, indicate that the model’s extrapolation abilities remain consistent as the forecast horizon extends, albeit with minor fluctuations. A slight uptick in HD values for longer horizons suggests a marginal loss in precision over time. Notably, the model generally performs better for origins closer to the video’s start. This fact may be attributed to the comparatively less volatile dynamics of the fire during its initial stages, which may facilitate more precise extrapolations.

Table 7 provides averaged JI and HD values for the intervals from the origin to the horizon, making it a potentially more comprehensive representation of performance for various horizons. Overall, it becomes apparent that there is a decrease in performance as the horizon extends, in both metrics. However, the performance does not decrease drastically.

Table 7 Average Jaccard Index and Hausdorff Distance. Average metrics from the origin to the horizon of the generated frames

As with the interpolation, we evaluated the temporal consistency for the frames of the considered intervals and found that it was almost perfect ($\approx$ 1.000) for all origins and horizons.

4.6 Discussion

Interpolation Performance. Regarding the performance achieved when using distinct sampling strategies to train the models and generate interpolations, one may note that the strategy with periodic data sampling led to better results. However, using distance-based sampling leads to training the model with only about 5.7% of the volume of data used in the periodic sampling strategy and leads to a performance of about the same order of magnitude as that obtained with the periodic sampling strategy. For instance, when evaluating the CVAE with the BurnedAreaUAV Test set, the performance drop when using distance-based instead of periodic sampling was only 2% but the reduction of the amount of training data was over 96%.

Table 4 presents performance values achieved using the BurnedAreaUAV Test set, which was manually generated and validated, and the U-Net Samples dataset, which was created by a U-Net network. Although the automatic burned area identification process used to create the U-Net Samples data may have added some error to the reference data, the performance achieved when using data from the U-Net Samples and the BurnedAreaUAV Test Set datasets as ground truth is quite similar.

The McKenney method obtained the worst spatial similarity performance (Table 4 and Fig. 14). Local deformations in the polygons generated by the McKenney method cause this method to reach, in some scenarios, an HD value almost three times higher than those obtained by other ones. Such deformations also negatively impacted the values measured for the JI. On the other hand, the CVAE and the Shape-Based method alternated as the best-performing method depending on the scenario.

Temporal Consistency in Interpolation. However, when analyzing the temporal consistency results from Table 5, one may notice that CVAE obtained the best performance for both periodic and distance-based sampling. Also, the graphs in Fig. 15 show how the area of the polygons generated by CVAE evolves much more smoothly and stably than the ones of polygons generated by the other considered methods.

Extrapolation Performance. When analyzing the capacity to predict the future shape of the burned area in terms of spatial similarity metrics (Table 6), one may notice that the CVAE model was able to achieve, in extrapolation, a performance with the same order of magnitude it achieved for interpolation operations, with JI values in the range of 0.9 (small variations depending on the stage of fire evolution and the horizon considered). Such similarity metrics values remained significantly high even when considering a set of predictions (Table 7). Furthermore, the CVAE model reached very high values of temporal consistency while generating future representations (almost near 1).

Temporal Consistency in Extrapolation. Indeed, when analyzing the temporal consistency values obtained while generating intermediate observations and the ones achieved in the extrapolation experiments used to forecast future representations, it is possible to observe that CVAE has a high capacity for creating a series of representations with smooth transitions. On the other hand, this is also somewhat associated with a certain stationarity of the model, conditioned even if at least partially by the relatively slow evolution of the burned area between the observed timestamps.

Limitations. Hence, although we tested and validated the use of CVAE based on different training and validation samples and forecasting horizons, achieving superior performance than other methods in many conditions, one must take into account that the forest fire data we made use of evolved relatively slowly and, thus, it is not possible to assert that the CVAE model used in this work can be directly applied to other scenarios, especially those with a more erratic fire evolution. Therefore, assessing the model generalization capacity is necessary and planned for future work.

5 Conclusions and Future Work

Representing natural phenomena with the support of the continuous spatiotemporal data model has the potential to obtain accurate representations using a smaller number of parameters than traditional simulation models, which usually require much information on the physical characteristics of the events and the environment. However, the continuous spatiotemporal representation model requires methods capable of generating the representation of in-between observations for the modeled entity. Region interpolation methods are commonly used to generate the necessary representations. In this work, we evaluate the use of CVAE models to generate such intermediate representations and make predictions about the evolution of the area burned in forest fires. We use datasets based on an aerial video of a prescribed fire captured by drones and evaluate the quality of the obtained representations in terms of spatial and temporal metrics.

While generating intermediate representations, our CVAE model and the Shape-based method obtained similar performance in terms of spatial metrics. For example, for data periodically sampled from the sequence generated by U-Net, the Shape-based solution was superior in terms of the JI by a difference of just 0.7%. However, our CVAE model achieved better values for HD by a difference of 1% and outperformed the other methods in all configurations when considering the temporal consistency metric. Indeed, the CVAE also achieved high values of temporal consistency in the extrapolation, i.e., forecasting experiments. The experimental results show that our proposal generates realistic and smooth representations of the burned area evolution. Furthermore, our model demonstrated the fastest inference times (25 ms), being significantly faster than our Shape-Based method implementation at 109 ms and almost 70 times faster than the McKenney algorithm (1790 ms). This highlights the practicability of the CVAE model for real-time applications.

Looking ahead, we plan to continue exploring using AE-based models and other latent space representation models to generate the spatiotemporal evolution of natural phenomena. A crucial aspect of our future work will involve evaluating the model’s generalization capacity by testing its performance on diverse datasets with varying fire evolution rates and applying it to a wider range of real-world phenomena to assess the generalizability of the results.

Finally, to enhance the predictive capabilities of the CVAE model, we propose automatically incorporating additional features that capture contextual information, such as terrain characteristics or meteorological data.