Attack and Defense Strategies in Cyber War Involving Production and Stockpiling of Zero-Day Cyber Exploits

Abstract

Two players strike balances between allocating resources for defense and production of zero-day exploits. Production is further allocated into cyberattack or stockpiling. Applying the Cobb Douglas expected utility function for equivalent players, an analytical solution is determined where each player’s expected utility is inverse U shaped in each player’s unit defense cost. More generally, simulations illustrate the impact of varying nine parameter values relative to a benchmark. Increasing a player’s unit costs of defense or development of zero-days benefits the opposing player. Increasing the contest intensities over the two players’ assets causes the players to increase their efforts until their resources are fully exploited and they receive zero expected utility. Decreasing the Cobb Douglas output elasticity for a player’s stockpiling of zero-days causes its attack to increase and its expected utility to eventually reach a maximum, while the opposing player’s expected utility reaches a minimum. Altering the Cobb Douglas output elasticities for a player’s attack or defense contests towards their maxima or minima causes maximum expected utility for both players.

1 Introduction

1.1 Background

In 2010, the Natanz nuclear facility in Iran suffered a series of malfunctions causing significant damage to its nuclear program. The cause was a sophisticated cyber attack, a worm called Stuxnet, that is widely considered one of the first significant acts of cyber war, in large part, due to its use of zero-day vulnerabilities. The zero-day vulnerability gets its name from a vulnerability in a defender’s computer system being known to the defender for zero days before it was discovered through the attack or in some other way. That is, the zero-day was unknown to or unaddressed through public patches or a fix by the defender. Because they are unknown and unpatched, zero-day cyberattacks are highly effective. They are also hard to produce, often requiring a significant allocation of resources by the attacker. As a result, it was noteworthy that the cyberattack on the Natanz facility exploited not one but four zero-day vulnerabilities, a previously unobserved use of cyber firepower. In the new landscape of cyberwar, such zero-day attacks are well-researched and highly prized weapons of cyber armies. The catch? They can only be used once. Cyber armies therefore face the tradeoff between using weapons today or stockpiling them for tomorrow.

1.2 Contribution

The Natanz attack raised the awareness of zero-day vulnerabilities. A facility such as the Natanz nuclear facility is controlled by, or has interests aligned by, a player which in this case is the Iranian government. Such a player has resources to defend against zero-day attacks, and has resources to launch zero-day attacks against an opposing player. In this case the opposing player is widely understood to be the United States and Israel (Nakashima 2012). The research context in this article is zero-day vulnerabilities generally, i.e. whether to produce zero-day capabilities, stockpile the capabilities, launch the capabilities as an attack, and defend against zero-day attacks. The model in this article has applicability beyond zero-day vulnerabilities, assuming two players who attack and defend, and may stockpile their capabilities.

To analyze this research problem, we introduce a two-player game to elucidate potential strategies of cyber armies and the decision to stockpile or use zero-day capabilities to exploit zero-day vulnerabilities. More specifically, each player has cyber resources applicable to produce zero-day exploits or defend against the opposing player’s zero-day attacks. Production of zero-days includes discovery, reconnaissance (research into the opponent’s systems), and weaponization. We, therefore, specify that each player can have zero-day vulnerabilities, which can be attacked by the opposing player, and zero-day exploits, which are produced and are applicable to attack the opposing player. That is, each player’s zero-day exploits can either be used to attack the opposing player or be stockpiled for future use. Since the nature of a zero-day vulnerability is that it has limited or no value after a zero-day attack exploits it and the defender realizes the exploit, the attacker can be expected to have an incentive to use it immediately in some cases, and to stockpile it in other cases. The value of stockpiling is specified in a Cobb Douglas expected utility function. The attacker derives utility from stockpiling zero-day capabilities due to enhanced security, in the knowledge that various uncertain threats posed by the opposing player (and which the attacker may keep secret) can be immediately eliminated or ameliorated. Announcing that a player has zero-day capabilities may also constitute deterrence utility for the player. Hence each player faces a resource allocation decision about how to strike a balance between producing zero-days, storing zero-days, attacking with zero-days, and defense against zero-days, which is explored. The article is to our knowledge the first to assess how a player strikes such a balance. The literature, reviewed below, has a more specific focus not focusing on these balances.

1.3 Literature

No game-theoretic treatment of zero-days have been found in the literature to date. For cyber security more generally, Nagurney and Shukla (2017) compare three models for cybersecurity investment accounting for noncooperation, Nash bargaining theory to facilitate information sharing, and system-optimization through cooperation. Edwards et al. (2017) present a game-theoretic model of blame with an attacker and a defender exploring the asymmetric problem of attribution, the stability of peace, conditions for attack tolerance, and conditions that allow a mistake or third party attacker to undermine peace.

Baliga et al. (2020) expand the treatment of the imperfect attribution in a game-theoretic model with a single defender and multiple attackers in order to identify opportunities for cyber deterrence. They identify conditions for enhancing deterrence through detection while revealing the potential for enhanced attribution to undermine deterrence. Interestingly, Baliga et al. (2020) uncover an endogenous strategic complementarity where increased aggression by one attacker increases the aggression of the other attackers. Welburn et al. (2019) expand on the discussion of cyber deterrence by defining an attribution game between an attacker and a defender and introducing signaling. In their attribution game, following the attacker’s decision to attack or not, the defender receives a (possibly noisy) signal and choses to retaliate or not. Their signaling game randomly assigns the defender a capability to retaliate and allows the defender to signal this capability to the attacker before it decides to attack. While finding that it is never in the best interest of the defender to signal truthfully, they find that the defender can enhance deterrence through signaling and discuss implications for cyber deterrence policy. Trang and Brendel (2019) find through meta-analysis that deterrence theory involving sanctions to enforce information security policies better predicts deviant behavior in cultures with malice, power distance, and uncertainty avoidance.

Regarding strategy and timing of security investments, Xu et al. (2019) find through options theory that reactive investments to improve IT security and proactive investments to exploit commercial opportunities is beneficial. Miaoui and Boudriga (2019) find that optimal information security investment depends on the attitude towards security risk, and increases with the investment horizon for all types of vulnerabilities for located attacks, but not always for distributed attacks. Crossler et al. (2019) study 279 individuals’ computer security behaviors and three security threats, i.e. security related performance degradation, identify theft, and data loss. They find through expert interviews that response efficacy and response cost help explain chosen behaviors, and identify security threat-response pairs, which may aid to obtain multi-layered protection.

Further game theoretic research exists on information security to protect against attacks, accounting for returns on information security investment (Hausken 2006b, 2014), substitution and interdependence (Enders and Sandler 2003; Hausken 2006a; Lakdawalla and Zanjani 2002), data survivability versus security in information systems (Levitin et al. 2012), and information sharing to prevent attacks (Hausken 2007, 2015, 2017a, 2017b, 2018b). For recent reviews of the use of game theoretic models applied to cyber security, see Roy et al. (2010), Hausken and Levitin (2012), and Do et al. (2017).

2 Theoretical Background

Appendix 1 shows the nomenclature. Consider two players in a simultaneous move one-period game. Assume that player i, i = 1, 2, gets cyber resources R_i (capital, manpower, competence, etc.) from a national budget which is allocated to develop zero-day exploits (zero-days, for short) Z_i (intended to exploit zero-day vulnerabilities) at unit cost b_i, and defense with effort F_i at unit cost a_i. Player i’s resource allocation is

$$ {R}_i={a}_i{F}_i+{b}_i{Z}_i $$

(1)

Assume that player i uses z_i of its zero-days, 0 ≤ z_i ≤ Z_i, to attack its opponent’s asset, and stockpiles the remaining Z_i − z_i. In order to enable independence between player i’s effort Z_i to develop zero-day capabilities, and player i’s defense effort F_i, which is necessary for the model to be conceptually consistent, we assume that player i’s effort Z_i confines attention to exploiting the opposing player j’s vulnerabilities, j ≠ i. i = 1, 2, not player i’s own vulnerabilities, which is a means of defense for player i, which we now proceed to elaborate upon.

When player i as a defender and player j as an attacker use the same or similar systems (e.g. produced by the same manufacturer), we assume that player i can defend itself by discovering its own vulnerabilities, and patching them, without informing player j about the patch. If player j discovers the patch (e.g. through leakage or spying), player i’s defense is still intact (since the patch is operational), and player j can be expected to apply the same or a similar patch which means that player i can not exploit this vulnerability to develop zero-day exploits against player j.

When the defending player i and the attacking player j apply different systems, discovering vulnerabilities in one system generally does not mean that the other system has the same vulnerabilities. This article assumes that all kinds of defense, including conventional defense against zero-day attacks, and discovering player i’s own vulnerabilities and patching them, have the same unit effort cost a_i. To the extent different kinds of defense in practice may have different unit effort costs, we assume that some weighted average unit effort cost a_i can be determined. Future research may model different kinds of defense effort which, e.g., may operate additively (Hausken 2020) or multiplicatively (Arbatskaya and Mialon 2010). Such generalization causes various complications. For example, if multiple defense efforts operate additively, player i generally chooses the effort with the lowest unit effort cost. Alternatively, if such multiple efforts operate multiplicatively, e.g. applying the Cobb Douglas function which Arbatskaya and Mialon (2010) do, player i needs to exert all its efforts to ensure impact. The latter is not realistic in the current model since we assume that any defense effort exerted by player i, whether exerted alone or in conjunction with other defense efforts, constitutes defense effort for player i. These considerations are such that we model player i’s defense effort as F_i with an average unit cost a_i, which accounts for all kinds of defense including conventional defense and discovering and patching player i’s own vulnerabilities as a means of defense.

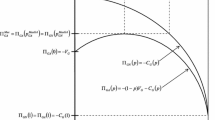
The players fight over two assets as shown in Fig. 1. We may think of player 1 as blue and player 2 as red. An asset has value, which can be, e.g., economic, human, or symbolic (Hausken 2018a). Two players owning one asset each usually value their assets differently, causing four different valuations. For example, the US may value the Statue of Liberty highly, whereas an opposing player may assign a lower value to it. As a second example, Fort Knox which contains the US Bullion Depository has high value to the US, but also has value to an opposing player (which may differ from the US’ value) since destroying it is a way of attacking the US. Player 1 values its own asset as V₁ and player 2’s asset as W₁. Player 2 values its own asset as W₂ and player 1’s asset as V₂. The players attack their opponents’ assets with zero-day attacks z₁ and z₂, and defend their own assets with defenses F₁ and F₂.

Fig. 1

Two players attacking assets with zero-day attacks z₁ and z₂, and defending with defenses F₁ and F₂. Player 1 values its own asset as V₁ and player 2’s asset as W₁. Player 2 values its own asset as W₂ and player 1’s asset as V₂. Player i’s stockpiles Z_i − z_i of its zero-days, i = 1, 2

We first consider player 1’s asset valued as V₁ by player 1 and V₂ by player 2. Player 1 defends with effort F₁, while player 2 attacks with its zero-days z₂. We apply the ratio form contest success function (Tullock 1980), which is a plausible and widely used method for assessing two opposing players’ success. Player 1’s expected contest success is p₁, and player 2’s expected contest success is q₂, i.e.

$$ {p}_1=\frac{F_1^v}{F_1^v+{z}_2^v},{q}_2=\frac{z_2^v}{z_2^v+{F}_1^v} $$

(2)

where the parameter v is the contest intensity over player 1’s asset. In (2) the ratios have a sum of two efforts (each raised to v) in the denominator, and one of the efforts in the numerator. That gives a number between zero and one which specifies contest success. The contest success can express the probability of winning the contest, or the fraction that one receives. In (2), v = 0 means that the players’ efforts have equal impact on the contest success p₁ and q₂, 0 < v < 1 gives disproportional advantage of exerting less effort than one’s opponent. Assuming v = 1 gives proportional advantage, and v > 1 gives disproportional advantage of exerting more effort than one’s opponent. For further interpretations of the contest intensity v in risk analysis see Hausken and Levitin (2008).

We secondly consider player 2’s asset valued as W₁ by player 1 and W₂ by player 2. Player 1 attacks with its zero-days z₁ while player 2 defends with effort F₁. Player 1’s expected contest success is q₁, and player 2’s expected contest success is p₂, i.e.

$$ {q}_1=\frac{z_1^w}{z_1^w+{F}_2^w},{p}_2=\frac{F_2^w}{F_2^w+{z}_1^w} $$

(3)

where the parameter w is the contest intensity over player 2’s asset, with the same interpretation as v in (2).

Finally, we assume that player i earns a benefit from its stockpiled zero-days Z_i − z_i, which are produced but not used in the attack. Assuming a Cobb Douglas expected utility function with these three ingredients, with output elasticities α_i, μ_i, 1 − α_i − μ_i for player i’s stockpiled non-used zero-days Z_i − z_i, 0 ≤ α_i, μ_i, 1−α_i−μ_i≤ 1, player i’s contest success when defending its own asset, and player i’s contest success when attacking its opponent’s asset, respectively, player i’s expected utility is

$$ {\displaystyle \begin{array}{c}{U}_1={\left({Z}_1-{z}_1\right)}^{\alpha_1}{\left({p}_1{V}_1\right)}^{\mu_1}{\left({q}_1{W}_1\right)}^{1-{\alpha}_1-{\mu}_1}\\ {}\begin{array}{c}={\left({Z}_1-{z}_1\right)}^{\alpha_1}{\left(\frac{F_1^v}{F_1^v+{z}_2^v}{V}_1\right)}^{\mu_1}{\left(\frac{z_1^w}{z_1^w+{F}_2^w}{W}_1\right)}^{1-{\alpha}_1-{\mu}_1},\\ {}{U}_2={\left({Z}_2-{z}_2\right)}^{\alpha_2}{\left({p}_2{W}_2\right)}^{\mu_2}{\left({q}_2{V}_2\right)}^{1-{\alpha}_2-{\mu}_2}\\ {}={\left({Z}_2-{z}_2\right)}^{\alpha_2}{\left(\frac{F_2^w}{F_2^w+{z}_1^w}{W}_2\right)}^{\mu_2}{\left(\frac{z_2^v}{z_2^v+{F}_1^v}{V}_2\right)}^{1-{\alpha}_2-{\mu}_2}\end{array}\end{array}} $$

(4)

where (2) and (3) have been inserted. Player 1’s free choice variables are Z₁ and z₁, where F₁ is determined by (1). Player 2’s free choice variables are Z₂ and z₂, where F₂ is determined by (1).

In (4) the term ${\left({Z}_i-{z}_i\right)}^{\alpha_i}$ for player i’s stockpiled zero-days Z_i − z_i requires further interpretation. Especially, the expected utility of stockpiling comprises time discounting of the future expected utility of attack, since that is what stockpiling is for. The future expected utility of attack depends on the players’ time discounting, future available strategies, future cyber resources and budgets, and future asset valuations, contest intensities, and Cobb Douglas output elasticities. Equation (4) makes a first step towards modeling this complex phenomenon of stockpiling by abstracting away and compressing the time considerations and other considerations into one strategic choice and one parameter. The strategic choice is Z_i − z_i, i.e. how much to stockpile. Evidently, more stockpiling enables a larger attack at some future time. The parameter is α_i, i.e. the Cobb Douglas output elasticity for player i’s stockpiled non-used zero-days Z_i − z_i, which contains ample information. First, α_i weighs stockpiling relative to the two other ingredients, μ_i for defending its own asset and 1 − α_i − μ_i for attacking the opponent’s asset, in the Cobb Douglas expected utility. Second, α_i, 0 ≤ α_i ≤ 1, specifies the degree of concavity imposed on Z_i − z_i which implicitly accounts for the plethora of phenomena mentioned above, including time discounting of the future expected utility of attack. Future research may model strategic interaction through time to account for the various aspects of stockpiling. This article confines attention to ${\left({Z}_i-{z}_i\right)}^{\alpha_i}$ for stockpiling, which player i weighs against defending its own asset with defense effort F_i and attacking the opponent’s asset with z_i.

3 Methodology

3.1 First Order Conditions

Differentiating player i’s expected utility in (4) with respect to its two free choice variables Z_i and z_i, and equating with zero, gives the first order conditions

$$ {\displaystyle \begin{array}{c}\frac{{\partial U}_1}{\partial {Z}_1}=\frac{{\left({Z}_1-{z}_1\right)}^{\alpha_1-1}{\left(\frac{F_1^v{V}_1}{F_1^v+{z}_2^v}\right)}^{\mu_1}{\left(\frac{z_1^w{W}_1}{z_1^w+{F}_2^w}\right)}^{1-{\alpha}_1-{\mu}_1}}{\left({R}_1-{b}_1{Z}_1\right)\left({F}_1^v+{z}_2^v\right)}\\ {}\times \left({a}_1{F}_1^{v+1}{\alpha}_1+{z}_2^v\left({R}_1{\alpha}_1-{b}_1\left({Z}_1{\alpha}_1+v\left({Z}_1-{z}_1\right){\mu}_1\right)\right)\right)=0,\\ {}\begin{array}{c}\frac{{\partial U}_2}{\partial {Z}_2}=\frac{{\left({Z}_2-{z}_2\right)}^{\alpha_2-1}{\left(\frac{F_2^w{W}_2}{F_2^w+{z}_1^w}\right)}^{\mu_2}{\left(\frac{z_2^v{V}_2}{z_2^v+{F}_1^v}\right)}^{1-{\alpha}_2-{\mu}_2}}{\left({R}_2-{b}_2{Z}_2\right)\left({F}_2^w+{z}_1^w\right)}\\ {}\times \left({a}_2{F}_2^{w+1}{\alpha}_2+{z}_1^w\left({R}_2{\alpha}_2-{b}_2\left({Z}_2{\alpha}_2+w\left({Z}_2-{z}_2\right){\mu}_2\right)\right)\right)=0,\\ {}\begin{array}{c}\frac{{\partial U}_1}{\partial {z}_1}=\frac{{\left({Z}_1-{z}_1\right)}^{\alpha_1-1}}{z_1^{w+1}{W}_1}{\left(\frac{F_1^v{V}_1}{F_1^v+{z}_2^v}\right)}^{\mu_1}{\left(\frac{z_1^w{W}_1}{z_1^w+{F}_2^w}\right)}^{2-{\alpha}_1-{\mu}_1}\\ {}\times \left({F}_2^w\left(w\left({Z}_1-{z}_1\right)\left(1-{\alpha}_1-{\mu}_1\right)-{z}_1{\alpha}_1\right)-{z}_1^{w+1}{\alpha}_1\right)=0,\\ {}\begin{array}{c}\frac{{\partial U}_2}{\partial {z}_2}=\frac{{\left({Z}_2-{z}_2\right)}^{\alpha_2-1}}{z_2^{v+1}{V}_2}{\left(\frac{F_2^w{W}_2}{F_2^w+{z}_1^w}\right)}^{\mu_2}{\left(\frac{z_2^v{V}_2}{z_2^v+{F}_1^v}\right)}^{2-{\alpha}_2-{\mu}_2}\\ {}\times \left({F}_1^v\left(v\left({Z}_2-{z}_2\right)\left(1-{\alpha}_2-{\mu}_2\right)-{z}_2{\alpha}_2\right)-{z}_2^{v+1}{\alpha}_2\right)=0\end{array}\end{array}\end{array}\end{array}} $$

(5)

3.2 Analytical Solution for Equivalent Players

Equation (5) is analytically solvable for v = w = 1 and equivalent players where R_i = R, a_i = a, b_i = b, α_i = α, μ_i = μ, Z_i = Z, z_i = z, i = 1, 2, which is inserted into (5) to yield the two first order conditions

$$ {\displaystyle \begin{array}{c}\frac{{\left(R- BZ\right)}^2}{a}\alpha +z\left( R\alpha -b\left( Z\alpha +\left(Z-z\right)\mu \right)\right)=0,\\ {}\frac{\left(R- BZ\right)}{a}\left(\left(Z-z\right)\left(1-\alpha -\mu \right)- z\alpha \right)-{z}^2\alpha =0\end{array}} $$

(6)

which are solved to yield the equilibrium strategies and expected utilities

$$ {\displaystyle \begin{array}{c}Z=\frac{R\left(b{\left(1-\mu \right)}^2\mu -\sqrt{a}\sqrt{b}\sqrt{1-\alpha -\mu}\left(1-\mu \right){\mu}^{3/2}- a\alpha \left(1-\alpha -\mu \right)\left(\alpha +\mu \right)\right)}{b\left(b{\left(1-\mu \right)}^2\mu -a\left(1-\alpha -\mu \right){\left(\alpha +\mu \right)}^2\right)},\\ {}z=\frac{R\sqrt{\mu}\left(1-\alpha -\mu \right)\left(\sqrt{b}\left(1-\mu \right)\sqrt{\mu }-\sqrt{a}\sqrt{1-\alpha -\mu}\left(\alpha +\mu \right)\right)}{\sqrt{b}\left(b{\left(1-\mu \right)}^2\mu -a\left(1-\alpha -\mu \right){\left(\alpha +\mu \right)}^2\right)},\\ {}\begin{array}{c}{U}_1=\sqrt{a}{W}_1\left(\frac{\sqrt{b}\sqrt{1-\alpha -\mu}\sqrt{\mu }-\sqrt{a}\left(1-\alpha -\mu \right)}{b\mu -a\left(1-\alpha -\mu \right)}\right)\\ {}\times {\left(\frac{V_1}{1+\frac{\sqrt{a}\sqrt{1-\alpha -\mu }}{\sqrt{b}\sqrt{\mu }}}\right)}^{\mu }{\left(\frac{W_1}{1+\frac{\sqrt{b}\sqrt{\mu }}{\sqrt{a}\sqrt{1-\alpha -\mu }}}\right)}^{-\alpha -\mu}\\ {}\begin{array}{c}\times {\left(\frac{R\alpha \left(b\left(1-\mu \right)\mu -a\left(1-\alpha -\mu \right)\left(\alpha +\mu \right)+\sqrt{a}\sqrt{b}\sqrt{1-\alpha -\mu}\sqrt{\mu}\left(1-\alpha -2\mu \right)\right)}{b\left(b{\left(1-\mu \right)}^2\mu -a\left(1-\alpha -\mu \right){\left(\alpha +\mu \right)}^2\right)}\right)}^{\alpha },\\ {}{U}_2=\sqrt{a}{V}_2\left(\frac{\sqrt{b}\sqrt{1-\alpha -\mu}\sqrt{\mu }-\sqrt{a}\left(1-\alpha -\mu \right)}{b\mu -a\left(1-\alpha -\mu \right)}\right)\\ {}\begin{array}{c}\times {\left(\frac{W_2}{1+\frac{\sqrt{a}\sqrt{1-\alpha -\mu }}{\sqrt{b}\sqrt{\mu }}}\right)}^{\mu }{\left(\frac{V_2}{1+\frac{\sqrt{b}\sqrt{\mu }}{\sqrt{a}\sqrt{1-\alpha -\mu }}}\right)}^{-\alpha -\mu}\\ {}\times {\left(\frac{R\alpha \left(b\left(1-\mu \right)\mu -a\left(1-\alpha -\mu \right)\left(\alpha +\mu \right)+\sqrt{a}\sqrt{b}\sqrt{1-\alpha -\mu}\sqrt{\mu}\left(1-\alpha -2\mu \right)\right)}{b\left(b{\left(1-\mu \right)}^2\mu -a\left(1-\alpha -\mu \right){\left(\alpha +\mu \right)}^2\right)}\right)}^{\alpha}\end{array}\end{array}\end{array}\end{array}} $$

(7)

where F₁ and F₂ are determined by (1).

3.3 Analytical Solution for Equivalent Players when α = μ = 1/3

Inserting α = μ = 1/3 into (6) gives

$$ Z=\frac{R\left(\sqrt{a}+2\sqrt{b}\right)}{2b\left(\sqrt{a}+\sqrt{b}\right)},z=\frac{R}{2\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)},Z-z=\frac{R}{2b},{U}_i={\left(\frac{R\sqrt{a}{V}_i{W}_i}{2\sqrt{b}{\left(\sqrt{a}+\sqrt{b}\right)}^2}\right)}^{1/3} $$

(8)

The Hessian matrix for player 1, inserting (8), is negative semi-definite, i.e.

$$ {\displaystyle \begin{array}{c}\left|{H}_1\right|=\left|\begin{array}{cc}\frac{\partial^2{U}_1}{\partial {Z}_1^2}& \frac{\partial^2{U}_1}{\partial {Z}_1\partial {z}_1}\\ {}\frac{\partial^2{U}_1}{\partial z\partial {Z}_1}& \frac{\partial^2{U}_1}{\partial {z}_1^2}\end{array}\right|\\ {}\begin{array}{c}=\left|\begin{array}{cc}-\frac{4\times {2}^{2/3}{V}_1^{1/3}{W}_1^{1/3}{\left(\sqrt{a}+\sqrt{b}\right)}^{1/3}}{3{a}^{1/3}{b}^{-11/6}{R}^{5/3}}& \frac{2\times {2}^{2/3}{a}^{1/6}{b}^{11/6}{V}_1^{1/3}{W}_1^{1/3}}{3{R}^{5/3}{\left(\sqrt{a}+\sqrt{b}\right)}^{2/3}}\\ {}\frac{2\times {2}^{2/3}{a}^{1/6}{b}^{11/6}{V}_1^{1/3}{W}_1^{1/3}}{3{R}^{5/3}{\left(\sqrt{a}+\sqrt{b}\right)}^{2/3}}& -\frac{4\times {2}^{2/3}{V}_1^{1/3}{W}_1^{1/3}{\left(\sqrt{a}+\sqrt{b}\right)}^{1/3}}{3{a}^{-1/6}{b}^{-4/3}{R}^{5/3}}\end{array}\right|\\ {}=\frac{8\times {2}^{1/3}{b}^{19/6}{V}_1^{2/3}{W}_1^{2/3}\left(4a+7\sqrt{a}\sqrt{b}+4b\right)}{9{a}^{1/6}{R}^{10/3}{\left(\sqrt{a}+\sqrt{b}\right)}^{4/3}}\end{array}\end{array}} $$

(9)

The Hessian matrix for player 2 is equivalent to (9), except that V₁ is replaced with W₂, W₁ is replaced with V₂, Z₁ is replaced with Z₂, z₁ is replaced with z₂, U₁ is replaced with U₂, and H₁ is replaced with H₂.

3.4 Property for Equivalent Players when α = μ = 1/3

• Property 1. For v = w = 1 and the symmetric event in (8) where R_i = R, a_i = a, b_i = b, α_i = α, μ_i = μ, Z_i = Z, z_i = z, i = 1, 2, $\frac{\partial {Z}_i}{\partial {a}_i}\le 0$,$\frac{\partial {Z}_i}{\partial {b}_i}\le 0$, $\frac{\partial {Z}_i}{\partial {R}_i}\ge 0$, $\frac{\partial {Z}_i}{\partial {V}_i}=0$, $\frac{\partial {Z}_i}{\partial {W}_i}=0$, $\frac{\partial {z}_i}{\partial {a}_i}\le 0$,$\frac{\partial {z}_i}{\partial {b}_i}\le 0$, $\frac{\partial {z}_i}{\partial {R}_i}\ge 0$,$\frac{\partial {z}_i}{\partial {V}_i}=0$, $\frac{\partial {z}_i}{\partial {W}_i}=0$, $\frac{\partial \left({Z}_i-{z}_i\right)}{\partial {a}_i}=0$, $\frac{\partial \left({Z}_i-{z}_i\right)}{\partial {b}_i}\le 0$, $\frac{\partial \left({Z}_i-{z}_i\right)}{\partial {R}_i}\ge 0$, $\frac{\partial \left({Z}_i-{z}_i\right)}{\partial {V}_i}=0$, $\frac{\partial \left({Z}_i-{z}_i\right)}{\partial {W}_i}=0$, $\frac{\partial {U}_i}{\partial {a}_i}\le 0$ when a ≥ b, $\frac{\partial {U}_i}{\partial {b}_i}\le 0$, $\frac{\partial {U}_i}{\partial {V}_i}\ge 0$, $\frac{\partial {U}_i}{\partial {W}_i}\ge 0$.

• Proof. Appendix 2. □.

Property 1 states that for v = w = 1 and in the symmetric event in (8) where R_i = R, a_i = a, b_i = b, α_i = α, μ_i = μ, Z_i = Z, z_i = z, i = 1, 2, each equivalent player i’s effort Z_i to develop zero-day capabilities, and each player i’s part z_i of zero-day capabilities used in the attack, decreases as each player’s unit effort cost a_i of defense, and unit effort cost b_i of developing zero-day capabilities, increase. Player i’s allocation Z_i − z_i to stockpiling decreases in b_i and is independent of a_i. Furthermore, Z_i, z_i, and Z_i − z_i increase as player i’s resources R_i increase, and are independent of the asset valuations V_i and W_i.

Player i’s expected utility U_i decreases as each player’s unit effort cost a_i of defense increases, provided that a_i ≥ b_i, and increases when a_i increases provided that a_i < b_i, i.e. is inverse U shaped as a_i varies. This latter result follows since low a_i < b_i means that defense is cheap, which causes more resources R_i to be allocated to exert effort Z_i to develop zero-day capabilities and more effort z_i to attack. Such costly attacks cause low expected utility U_i which increases as a_i increases to a_i = b_i. As a_i increases above a_i = b_i, the opposite impact takes over. That is, although attacks z_i decrease, defense F_i decrease even more, causing each player to suffer from the attacks and receive decreasing expected utility U_i as a_i increases. Finally, player i’s expected utility U_i decreases as each player’s unit effort cost b_i of developing zero-day capabilities increases, and increases as its resources R_i and asset valuations V_i and W_i increase.

4 Analysis and Discussion

Figure 2 illustrates the solution with the benchmark parameter values R_i = a_i = b_i = V_i= W_i = v = w = 1, α_i = μ_i = 1/3, i = 1, 2, which causes the symmetric event in (8) with solution Z₁ = Z₂ = 3/4, z₁ = z₂ = F₁ = F₂ = 1/4, U₁ = U₂ = 1/2. Given that choices have to be made for the parameter values, we believe that e.g. V₁ = V₂ = W₁= W₂ = 1 are the most plausible choices for the four asset valuations. We have chosen unitary parameter values whenever possible. Hence at the benchmark each player i’s allocation Z_i − z_i = 1/2 of zero-day capabilities to stockpiling is twice as large as its allocation z_i = 1/4 to attack. This follows since in (4) allocation Z_i − z_i to stockpiling appears as a proportional term, whereas allocations z_i to attack and F_i to defense appear in the numerator and denominator of two ratio terms. In each of the nine panels one parameter value varies, while the other parameter values are kept at their benchmarks.

Fig. 2

Efforts Z₁,Z₂,z₁,z₂ and expected utilities U₁ and U₂ for players 1 and 2 as functions of R₁, a₁, b₁, V₁, W₁, v, w, α₁, and μ₁ relative to the benchmark parameter values R_i = a_i = b_i = V_i= W_i = v = w = 1, α_i = μ_i = 1/3, i = 1, 2

In Figure 2 panel a, as player 1’s cyber resources R₁ increase from R₁ = 0, intuitively, its effort Z₁ to develop zero-day capabilities, its part z₁ of zero-day capabilities used in the attack, its defense effort F₁, and its expected utility U₁, all increase, $\underset{R_1\longrightarrow \infty }{\lim }{Z}_1=\underset{R_1\longrightarrow \infty }{\lim }{z}_1=$ $\underset{R_1\longrightarrow \infty }{\lim }{F}_1=$ $\underset{R_1\longrightarrow \infty }{\lim }{U}_1=\infty$. The limit values are determined numerically or, in rare instances, analytically. In contrast, player 2’s effort Z₂ to develop zero-day capabilities decreases convexly from Z₂ = 1 when R₁ = 0, and asymptotically towards $\underset{R_1\longrightarrow \infty }{\lim }{Z}_2=2/3$. Player 2’s part z₂ of zero-day capabilities used in the attack, and its defense effort F₂, increase concavely from z₂ = F₂ = 0 when R₁ = 0, and asymptotically towards $\underset{R_1\longrightarrow \infty }{\lim }{z}_2=\underset{R_1\longrightarrow \infty }{\lim }{F}_2=1/3$. When R₁ is negligible, it is sufficient for the superior player 2 to allocate negligibly to defense F₂ and attack z₂. Player 2’s limit values reflect that player 2 allocates its resources R₂ = 1 equally to stockpiling Z₂ − z₂ = 1/3, defense$\underset{R_1\longrightarrow \infty }{\lim }{F}_2=1/3$, and attack $\underset{R_1\longrightarrow \infty }{\lim }{z}_2=1/3$. Consequently, player 2’s expected utility U₂ decreases from U₂ = 1 when R₁ = 0, and asymptotically towards $\underset{R_1\longrightarrow \infty }{\lim }{U}_2=0$, as it becomes increasingly inferior to player 1’s possession of superior cyber resources.

In Figure 2 panel b, as player 1’s unit defense effort a₁ increases from a₁ = 0, its defense effort F₁ decreases convexly from infinity towards the limit $\underset{a_1\longrightarrow \infty }{\lim }{F}_1=0$, as defense becomes more costly. Interestingly, this makes player 2’s part z₂ of zero-day capabilities used in the attack increasingly superior, causing z₂ to decrease convexly from z₂ = 0.389 when a₁ = 0, and asymptotically towards $\underset{a_1\longrightarrow \infty }{\lim }{z}_2=0$, as player 2 does not need to spend excessive resources on the attack. This remarkable de-escalating result for player 1’s asset has implications for external actors and technological and other factors which may somehow impact player 1’s unit defense effort a₁ (which is a parameter in this article). That is, increasing a₁ causes both F₁ and z₂ to decrease. Player 1’s F₁ decreases most as it becomes more inferior. Player 2’s z₂ decreases least as it becomes more superior. A consequence of decreasing z₂ is that player 2’s effort Z₂ to develop zero-day capabilities also decreases convexly from Z₂ = 0.777 when a₁ = 0, and asymptotically towards $\underset{a_1\longrightarrow \infty }{\lim }{Z}_2=0.701$. Player 1’s effort Z₁ to develop zero-day capabilities decreases convexly from Z₁ = 1 when a₁ = 0, and asymptotically towards $\underset{a_1\longrightarrow \infty }{\lim }{Z}_1=0.611$, as it allocates more resources to defense F₁. Similarly, its part z₁ of zero-day capabilities used in the attack also decreases convexly, from z₁ = 0.299 when a₁ = 0, and asymptotically towards $\underset{a_1\longrightarrow \infty }{\lim }{z}_1=0.223$. That is, player 1 attacks less when a₁ increases since defense F₁ becomes more costly. This also remarkable result means that higher a₁ causes player not only to choose lower defense F₁, but also to become so inferior that it attacks less. Player 2 takes advantage of the increasing a₁. Its defense effort F₂ increases slightly and concavely from F₂ = 0.223 when a₁ = 0, and towards $\underset{a_1\longrightarrow \infty }{\lim }{F}_2=0.299$. Hence, out of the four defense and attack variables F₁, z₂, z₁, F₂, increasing player 1’s unit defense effort a₁ causes the three former to decrease, and the latter to increase slightly. Consequently, player 2’s expected utility U₂ increases concavely from U₂ = 0 when a₁ = 0 (and player 1 is superior), and asymptotically towards $\underset{a_1\longrightarrow \infty }{\lim }{U}_2=0.738$, as player 2 becomes increasingly superior to player 1. In contrast, player 1’s expected utility U₁ decreases convexly from U₁ = 0.738 when a₁ = 0, and asymptotically towards $\underset{a_1\longrightarrow \infty }{\lim }{U}_1=0$, as it becomes increasingly inferior to player 2.

In Figure 2 panel c, as player 1’s unit effort cost b₁ of developing zero-day capabilities increases from b₁ = 0, its effort Z₁ to develop zero-day capabilities decreases convexly from infinity towards $\underset{b_1\longrightarrow \infty }{\lim }{Z}_1=0$, as development becomes more costly. Concomitantly, its part z₁ of zero-day capabilities used in the attack also decreases convexly from infinity towards the limit $\underset{b_1\longrightarrow \infty }{\lim }{z}_1=0$, as its attack becomes constrained from above by its decreasing Z₁. This makes player 2’s defense F₂ increasingly superior, causing F₂ to decrease convexly from F₂ = 0.388 when b₁ = 0, and asymptotically towards $\underset{b_1\longrightarrow \infty }{\lim }{F}_2=0$, as player 2 does not need to spend excessive resources on the defense. Decreasing F₂ for player 2 implies increasing Z₂ according to (1). Accordingly, player 2’s effort Z₂ to develop zero-day capabilities increases concavely from Z₂ = 0.612 when b₁ = 0, and asymptotically towards $\underset{b_1\longrightarrow \infty }{\lim }{Z}_2=1$. Concomitantly, its part z₂ of zero-day capabilities used in the attack also increases slightly and concavely, from z₂ = 0.223 when b₁ = 0, towards the limit $\underset{b_1\longrightarrow \infty }{\lim }{z}_2=0.299$, as more zero-day capabilities Z₂ become available. Player 1 does its best to counter the slightly increasing attack z₂, but cannot overcome is inferiority, so that its defense F₁ decreases slightly from F₁ = 0.299 when b₁ = 0, and towards $\underset{b_1\longrightarrow \infty }{\lim }{F}_1=0.223$. Consequently, player 2’s expected utility U₂ increases concavely from U₂ = 0 when b₁ = 0 (and player 1 is superior), and asymptotically towards $\underset{b_1\longrightarrow \infty }{\lim }{U}_2=0.734$ as player 2 becomes increasingly superior to player 1. In contrast, player 1’s expected utility U₁ decreases convexly from infinity, i.e. $\underset{b_1\longrightarrow 0}{\lim }{U}_1=\infty$ when b₁ → 0, and asymptotically towards $\underset{b_1\longrightarrow \infty }{\lim }{U}_1=0$, as it becomes increasingly inferior to player 2.

In Figure 2 panel d, increasing player 1’s valuation V₁ of its own asset causes its own expected utility U₁ to increase concavely from U₁ = 0 when V₁ = 0, towards infinity, $\underset{V_1\longrightarrow \infty }{\lim }{U}_1=\infty$. The other seven variables remain at their benchmarks.

In Figure 2 panel e, increasing player 1’s valuation W₁ of player 2’s asset causes its own expected utility U₁ to increase concavely from U₁ = 0 when W₁ = 0, towards infinity, $\underset{W_1\longrightarrow \infty }{\lim }{U}_1=\infty$. The other seven variables remain at their benchmarks.

In Figure 2 panel f, increasing the contest intensity v over player 1’s asset from zero makes the contest between player 1’s defense F₁ and player 2’s attack z₂ increasingly contested. At the benchmark v = 1, these variables are F₁ = z₂ = 1/4. As v increases above v = 1, the variables F₁ and z₂ increase above their benchmarks, as is commonly the case for increasing contest intensity. Furthermore, F₁ and z₂ increase equivalently since the players are equally advantaged at the benchmark, and also equally advantaged as v varies outside the benchmark. Consequently, $\underset{v\longrightarrow \infty }{\lim }{F}_1=\underset{v\longrightarrow \infty }{\lim }{z}_2=1$, which means that at the limit with infinitely large contest intensity v over player 1’s asset, player 1 allocates all its resources R₁ = 1 to defense F₁, while player 2 allocates all its resources R₂ = 1 to attack z₂. To furnish its attack z₂, player 2 must allocate sufficient resources to its effort Z₂ to develop zero-day capabilities. Hence increasing v causes Z₂ to increase more rapidly than z₂, $\underset{v\longrightarrow \infty }{\lim }{Z}_2=1$. Consequently, at the limit when v approaches infinity, player 1 allocates no resources R₁ to develop zero-day capabilities, $\underset{v\longrightarrow \infty }{\lim }{Z}_1=0$, and player 2 allocates no resources R₂ to defend its asset, $\underset{v\longrightarrow \infty }{\lim }{F}_2=0$. Hence also, $\underset{v\longrightarrow \infty }{\lim }{z}_1=0$, since player 1 at the limit when v approaches infinity cannot attack with zero-day capabilities z₁ when it has not developed zero-day capabilities Z₁. The dismal result at the limit when v approaches infinity is that both players receive zero expected utilities, $\underset{v\longrightarrow \infty }{\lim }{U}_1=\underset{v\longrightarrow \infty }{\lim }{U}_2=0$. This result is consistent with (1) since the results above imply that the first term on the right hand side of both expected utility equations approaches zero, $\underset{v\longrightarrow \infty }{\lim }{\left({Z}_i-{z}_i\right)}^{\alpha_i}=0$, i = 1, 2. As v approaches zero, the limits are different. First, decreasing contest intensity v over player 1’s asset makes that contest more egalitarian so that efforts matter less. Hence the players exert no efforts at the limit when v = 0, i.e. no defense $\underset{v\longrightarrow 0}{\lim }{F}_1=0$ for player 1 and no attack $\underset{v\longrightarrow 0}{\lim }{z}_2=0$ for player 2. In the beginning of this section we observed that at the benchmark when v = 1 each player i’s allocation Z_i − z_i = 1/2 of zero-day capabilities to stockpiling is twice as large as its allocation z_i = 1/4 to attack and F_i = 1/4 to defense. This same ratio 2/1 also occurs when v = 0. Since $\underset{v\longrightarrow 0}{\lim }{F}_1=0$ for player 1, the ratio 2/1 between stockpiling and attack is preserved by allocating $\underset{v\longrightarrow 0}{\lim }{Z}_1-{z}_1=2/3$ to stockpiling and $\underset{v\longrightarrow 0}{\lim }{z}_1=1/3$ to attack, i.e. $\underset{v\longrightarrow 0}{\lim }{Z}_1=1$ since player 1 allocates all its resources R₁ to develop zero-day capabilities. Since $\underset{v\longrightarrow 0}{\lim }{z}_2=0$ for player 2, the ratio 2/1 between stockpiling and defense is preserved by allocating $\underset{v\longrightarrow 0}{\lim }{Z}_2-{z}_2=2/3$ to stockpiling and $\underset{v\longrightarrow 0}{\lim }{F}_2=1/3$ to defense, i.e. $\underset{v\longrightarrow 0}{\lim }{Z}_2=2/3$. This asymmetry between player 1 and player 2 follows since the contest intensity is v = 0 for the asset player 1 defends and player 2 attacks, while w = 1 for the asset player 1 attacks and player 2 defends. The asymmetry does not cause different expected utilities for the players. Inserting the variables above into (4) when v = 0 gives $\underset{v\longrightarrow 0}{\lim }{U}_1=\underset{v\longrightarrow 0}{\lim }{U}_2=1/\sqrt[3]{6}\approx 0.550$. That is, the players’ expected utilities are highest with zero contest intensity v = 0 over player 1’s asset.

In Figure 2 panel g, the results are analogous to panel f, but with interchanged variables since the contest intensity that varies is w over player 2’s asset. Hence, interchanging $\underset{w\longrightarrow \infty }{\lim }{F}_2=\underset{w\longrightarrow \infty }{\lim }{z}_1=\underset{w\longrightarrow \infty }{\lim }{Z}_1=1$, $\underset{w\longrightarrow \infty }{\lim }{Z}_2=\underset{w\longrightarrow \infty }{\lim }{F}_1=\underset{w\longrightarrow \infty }{\lim }{z}_2=\underset{w\longrightarrow \infty }{\lim }{U}_1=\underset{w\longrightarrow \infty }{\lim }{U}_2=\underset{w\longrightarrow \infty }{\lim }{\left({Z}_i-{z}_i\right)}^{\alpha_i}=0$, i = 1, 2, $\underset{w\longrightarrow 0}{\lim }{F}_2=\underset{w\longrightarrow 0}{\lim }{z}_1=0$, $\underset{w\longrightarrow 0}{\lim }{Z}_2=1$, $\underset{w\longrightarrow 0}{\lim }{z}_2=$ $\underset{w\longrightarrow 0}{\lim }{F}_1=1/3$, $\underset{w\longrightarrow 0}{\lim }{Z}_1=\underset{w\longrightarrow 0}{\lim }{\left({Z}_i-{z}_i\right)}^{\alpha_i}=2/3,i=1,2$, $\underset{w\longrightarrow 0}{\lim }{U}_1=\underset{w\longrightarrow 0}{\lim }{U}_2=1/\sqrt[3]{6}\approx 0.550.$

In Figure 2 panel h, decreasing the Cobb Douglas output elasticity α₁ for player 1’s stockpiled non-used zero-days Z₁ − z₁ to zero gives $\underset{\alpha_1\longrightarrow 0}{\lim }{Z}_1=\underset{\alpha_1\longrightarrow 0}{\lim }{z}_1=0.616$. This result follows from the term ${\left({Z}_1-{z}_1\right)}^{\alpha_1}$ in (4) which gives no value to player 1 of storing zero-days when α₁ = 0. As α₁ increases above α₁ = 0, player 1 gets increasing expected utility U₁ from stockpiling, accomplished by increasing its effort Z₁ to develop zero-day capabilities, and decreasing its part z₁ of zero-day capabilities used in the attack. This decrease continues until z₁ = 0 when α₁ = 2/3, which causes 1 − α₁ − μ₁ = 0 (since μ₁ = 1/3), and hence an egalitarian contest over player 2’s asset which causes no need for the players to exert efforts z₁ and F₂ and hence $\underset{\alpha_1\longrightarrow 2/3}{\lim }{F}_2=\underset{\alpha_1\longrightarrow 2/3}{\lim }{z}_1=0$, to the advantage of player 2 who wins the contest. Player 1 eventually earns increased expected utility U₁ from stockpiling as α₁ increases. Hence, as z₁ decreases, player 1 increases its effort Z₁ to develop zero-day capabilities moderately towards a maximum, and thereafter slightly decreases Z₁ due to decreasing return on investment, finally causing $\underset{\alpha_1\longrightarrow 2/3}{\lim }{Z}_1=0.777$. Consistently with concavely increasing (and eventually slightly decreasing) Z₁ is convexly decreasing (and eventually slightly increasing) defense effort F₁ for player 1 of its own asset, from $\underset{\alpha_1\longrightarrow 0}{\lim }{F}_1=0.384$ to $\underset{\alpha_1\longrightarrow 2/3}{\lim }{F}_1=0.223$. The overall result for player 1 is U shaped expected utility U₁ with minimum U₁ = 0.499 for α₁ = 0.294, a maximum $\underset{\alpha_1\longrightarrow 0}{\lim }{U}_1=0.647$ for α₁ = 0, and a high value $\underset{\alpha_1\longrightarrow 2/3}{\lim }{U}_1=0.636$ for α₁ = 2/3. This interesting result means that when player 2 has the Cobb Douglas output elasticities α₁ = μ₁ = 1/3, and player 1 has Cobb Douglas output elasticity μ₁ = 1/3 for when defending its own asset, then player 1 prefers to avoid intermediate Cobb Douglas output elasticity α₁ = 0.294 for storing its zero-days Z₁ − z₁. Player 2’s prefers zero attack z₁ = 0 by player 1, which occurs when α₁ = 2/3. Then player 2 can choose $\underset{\alpha_1\longrightarrow 2/3}{\lim }{F}_2=0$ due to being advantaged with respect to its own asset. That, in turn, enables player 2 to allocate all its resources R₂ to exert effort Z₂ to develop zero-day capabilities, i.e. $\underset{\alpha_1\longrightarrow 2/3}{\lim }{Z}_2=1$, and to attack player 1 with $\underset{\alpha_1\longrightarrow 2/3}{\lim }{z}_2=0.299$, which gives player 2 its highest expected utility $\underset{\alpha_1\longrightarrow 2/3}{\lim }{U}_2=0.738$. That is, player 2 is advantaged with respect to its own asset, and strikes a balance between storing zero-days, Z₂ − z₂, and attacking player 1 with z₂. As α₁ decreases below α₁ = 2/3, player 1’s attack z₁ increases above zero, causing player 2’s defense F₂ to increase above zero, eventually reaching $\underset{\alpha_1\longrightarrow 0}{\lim }{F}_2=0.297$. Consequently, player 2’s effort Z₂ to develop zero-day capabilities decreases, eventually reaching $\underset{\alpha_1\longrightarrow 0}{\lim }{Z}_2=0.703$. Player 2’s attack z₂ is relatively constant (has a very weak U shape), eventually reaching $\underset{\alpha_1\longrightarrow 0}{\lim }{z}_2=0.262$, since it still prefers to attack player 1, and accepts allocating less, Z₂ − z₂, to stockpiling. The overall result for player 2 is decreasing expected utility U₁ as α₁ decreases, eventually causing $\underset{\alpha_1\longrightarrow 0}{\lim }{U}_2=0.388$. In other words, when only α₁ varies from the given benchmark, player 2 prefers not to be attacked, z₁ = 0, which occurs for maximum α₁ = 2/3. This maximum α₁ = 2/3 is also relatively preferable for player 1 which then receives good expected utility U₁ from storing all its produced zero-days, $\underset{\alpha_1\longrightarrow 2/3}{\lim }{z}_1=0$. However, player 1 receives slightly higher expected utility U₁ when α₁ = 0 when the attack $\underset{\alpha_1\longrightarrow 0}{\lim }{Z}_1=\underset{\alpha_1\longrightarrow 0}{\lim }{z}_1=0.616$ is substantial.

In Figure 2 panel i, increasing the Cobb Douglas output elasticity μ₁ for player 1’s contest success when defending its own asset to its maximum μ₁ = 2/3, which causes 1 − α₁ − μ₁ = 0 (since α₁ = 1/3), causes an egalitarian contest over player 2’s asset (as in panel h) which causes no need for the players to exert efforts z₁ and F₂ and hence $\underset{\mu_1\longrightarrow 2/3}{\lim }{F}_2=\underset{\mu_1\longrightarrow 2/3}{\lim }{z}_1=0$, to the advantage of player 2 who wins the contest. Hence also (as in panel h), since player 2 allocates no resources R₂ to defense F₂ when μ₁ = 2/3, it allocates all its resources R₂ to exert effort Z₂ to develop zero-day capabilities, i.e. $\underset{\mu_1\longrightarrow 2/3}{\lim }{Z}_2=1$, and to attack player 1 substantially with $\underset{\mu_1\longrightarrow 2/3}{\lim }{z}_2=0.361$, which gives player 2 its highest expected utility $\underset{\mu_1\longrightarrow 2/3}{\lim }{U}_2=0.653$. Player 1 responds by defending substantially, $\underset{\mu_1\longrightarrow 2/3}{\lim }{F}_1=0.466$. Hence player 1 can allocate less resources R₁ to exert effort Z₁ to develop zero-day capabilities, $\underset{\mu_1\longrightarrow 2/3}{\lim }{Z}_1=0.534$, receiving expected utility $\underset{\mu_1\longrightarrow 2/3}{\lim }{U}_1=0.554$. Decreasing μ₁ below μ₁ = 2/3 causes the contest over player 1’s asset to become more egalitarian so that effort z₂ by player 2 to attack it and effort F₁ by player 1 to defend it have less impact and eventually no impact, i.e. $\underset{\mu_1\longrightarrow 0}{\lim }{z}_2=\underset{\mu_1\longrightarrow 0}{\lim }{F}_1=0$. Thus player 2 also allocates less resources R₂ to exert effort Z₂ to develop zero-day capabilities, which decreases to $\underset{\mu_1\longrightarrow 0}{\lim }{Z}_2=0.639$. In contrast, player 1 increases its effort Z₁ to develop zero-day capabilities, eventually allocating all its resources R₁ to it, i.e. $\underset{\mu_1\longrightarrow 0}{\lim }{Z}_1=1$. Thus player 1 also allocates more resources R₁ to attack player 2 with z₁, which increases to $\underset{\mu_1\longrightarrow 0}{\lim }{z}_1=0.466$. Player 2 responds by defending its asset more with F₂, which increases to $\underset{\mu_1\longrightarrow 0}{\lim }{F}_2=0.361$. Especially interesting in panel i is the symmetry around μ₁ = 1/3 which did not arise around α₁ = 1/3 in panel h for player 1’s stockpiled non-used zero-days Z₁ − z₁. The reason is that increasing (decreasing) the Cobb Douglas output elasticity μ₁ for player 1’s contest success around μ₁ = 1/3 causes equivalent decrease (increase) of the Cobb Douglas output elasticity μ₁ for player 1’s contest success around 1 − α₁ − μ₁ = 0 when α₁ = 1/3. Hence $\underset{\mu_1\longrightarrow 0}{\lim }{z}_1=\underset{\mu_1\longrightarrow 2/3}{\lim }{F}_1=0.466$ and $\underset{\mu_1\longrightarrow 2/3}{\lim }{z}_2=\underset{\mu_1\longrightarrow 0}{\lim }{F}_2=0.361$. The impact on the players’ expected utilities is also symmetric so that each player is indifferent regarding its preference for the extreme values μ₁ = 0 and μ₁ = 2/3, i.e. $\underset{\mu_1\longrightarrow 0}{\lim }{U}_1=\underset{\mu_1\longrightarrow 2/3}{\lim }{U}_1=0.554$ and $\underset{\mu_1\longrightarrow 0}{\lim }{U}_2=\underset{\mu_1\longrightarrow 2/3}{\lim }{U}_2=0.653$. Player 2’s expected utility U₂ is larger than player 1’s expected utility U₁ at μ₁ = 0 and μ₁ = 2/3 since player 1 exerts higher costly efforts $\underset{\mu_1\longrightarrow 0}{\lim }{z}_1=\underset{\mu_1\longrightarrow 2/3}{\lim }{F}_1=0.466$ than $\underset{\mu_1\longrightarrow 2/3}{\lim }{z}_2=\underset{\mu_1\longrightarrow 0}{\lim }{F}_2=0.361$ for player 2. At the midpoint benchmark value μ₁ = 1/3, as we know from the first paragraph of this section, the players receive their equal minimum expected utilities U₁ = U₂ = 1/2.

5 Conclusion

A model is developed for two players (e.g. countries) which allocate resources to defend against zero-day attacks, and to produce zero-day exploits for attack and stockpiling. Each player also defends against zero-day cyber attacks. First, using one part of one’s resources to build up a defense infrastructure to handle attacks or potential attacks is useful. Second, using the remaining part of one’s resources to produce zero-day capabilities is useful. This illustrates a balance or tradeoff that has to be struck between defense and production. Third, the produced zero-day exploits can be stockpiled, or can be used in attacking the opposing player, both of which are useful. This article determines each player’s optimal strategy by applying the common Cobb Douglas expected utility function while accounting for three inputs; the production of zero-day exploits for stockpiling, production for attack, and defense.

For equivalent players an analytical solution is determined. When, additionally, production for attack and stockpiling, and defense, are valued equally in the Cobb Douglas expected utility function, a property is developed showing, for example, that each player’s expected utility is inverse U shaped in each player’s unit effort cost of defense.

For different players the solution is illustrated with simulations where each of nine parameters are varied for player 1, without loss of generality, relative to a plausible benchmark where production for stockpiling and the contests for attack and defense are valued one third each. First, increasing player 1’s resources causes all its efforts (production, attack, defense) and its expected utility to increase towards infinity. In contrast, player 2’s expected utility decreases towards zero, its production decreases convexly towards a constant, and its attack and defense increase concavely towards a constant.

Second, increasing player 1’s unit defense cost causes its defense and expected utility to decrease to zero due to inferiority, while its production and attack decrease towards constants. Player 2 decreases its production and attack somewhat due to superiority, defends marginally more, and receives increasing expected utility. Importantly, both players’ attacks decrease, due to inferiority and superiority, respectively. This counterintuitive result, that making defense more expensive could decrease overall attacks and potentially deescalate conflict, warrants future exploration. For example, it raises the issue of whether the players themselves, external players, or technological innovation, can influence the players’ unit defense costs.

Third, increasing player 1’s unit development cost of zero-day capabilities causes its production, attack, and expected utility to decrease to zero, while its defense increases marginally towards a constant. Player 2 decreases its defense to zero due to superiority, which enables it to increase its production and attack towards constants, causing increasing expected utility towards a constant. This more intuitive result means that increasing a player’s unit development cost causes that player to attack less and the opposing player to attack more.

Fourth and fifth, increasing player 1’s valuation of its own asset, or player 2’s asset, causes its expected utility to increase to infinity, while the other variables remain at their benchmarks.

Sixth, increasing the contest intensity over player 1’s asset causes player 1’s defense and player 2’s attack to increase until all their resources are exploited, eventually approaching zero expected utility to both players. Player 1’s production and attack decrease towards zero, and player 2’s production and attack increase until all its resources are exploited.

Seventh, increasing the contest intensity over player 2’s asset causes the same result as when increasing the contest intensity over player 1’s asset, except that the two players’ roles are interchanged. That is, production and attack for one player is interchanged with defense for the other player, and vice versa.

Eighth, decreasing the Cobb Douglas output elasticity for player 1’s stockpiled zero-days to zero causes its attack to increase to equal its production, since stockpiling is useless. Its defense increases somewhat, and its expected utility reaches its maximum. In contrast, player 2 suffers the attack and receives its minimum expected utility. Increasing the same elasticity to its maximum causes player 1 not to attack, which also gives it high expected utility, compared to intermediate elasticity, while player 2 receives its maximum expected utility due to not being attacked.

Ninth, decreasing the Cobb Douglas output elasticity for player 1’s contest success when defending its own asset to zero eliminates its useless defense, causes intermediate attack, and maximum production and expected utility. Player 2 also receives maximum expected utility for zero elasticity due to not spending resources on attack. Maximum elasticity eliminates player 1’s useless attack, and both players receive their same maximum expected utilities as for zero elasticity.

Future research should incorporate the time dimension and complexity more thoroughly, making stockpiling a time discounted version of the future expected utility of attack and defense. Future research should also include more players and outside regulation, estimate the parameter values, and furnish empirical support from contemporary and historical records.

Appendices

Appendix 1 Nomenclature

1.1 Parameters

R _i :

Player i’s cyber resources, i = 1, 2, R_i ≥ 0.

a _i :

Player i’s unit effort cost of defense, i = 1, 2, a_i ≥ 0

b _i :

Player i’s unit effort cost of developing zero-day capabilities, i = 1, 2, b_i ≥ 0

V ₁ :

Player 1’s valuation of its own asset, V₁ ≥ 0

V ₂ :

Player 2’s valuation of player 1’s asset, V₂ ≥ 0

W ₁ :

Player 1’s valuation of player 2’s asset, W₁ ≥ 0

W ₂ :

Player 2’s valuation of its own asset, W₂ ≥ 0

v :

Contest intensity over player 1’s asset, v ≥ 0

w :

Contest intensity over player 2’s asset, w ≥ 0

α _i :

Cobb Douglas output elasticity for player i’s stockpiled non-used zero-days Z_i − z_i, i = 1, 2, 0 ≤ α_i ≤ 1

μ _i :

Cobb Douglas output elasticity for player i’s contest success when defending its own asset, i = 1, 2, 0 ≤ μ_i ≤ 1

1-α_i -μ_i:

Cobb Douglas output elasticity for player i’s contest success when attacking its opponent’s asset, i = 1, 2, 0 ≤ 1− α_i − μ_i ≤ 1

1.2 Strategic choice variables

Z _i :

Player i’s effort to develop zero-day capabilities, i = 1, 2

z _i :

Player i’s part of zero-day capabilities used in the attack, 0 ≤ z_i ≤ Z_i, i = 1, 2

1.3 Dependent variables

F _i :

Player i’s defense effort, i = 1, 2

p _i :

Player i’s expected contest success over its own asset, i = 1, 2

q _i :

Player i’s expected contest success over its opponent’s asset, i = 1, 2

U _i :

Player i’s expected utility, i = 1, 2

Appendix 2 Proof of Property 1

Differentiating (8) gives

$$ \frac{\partial Z}{\partial a}=\frac{\partial z}{\partial a}=-\frac{R}{4\sqrt{a}\sqrt{b}{\left(\sqrt{a}+\sqrt{b}\right)}^2},\frac{\partial {U}_i}{\partial a}=\frac{R^{1/3}{V}_i^{1/3}{W}_i^{1/3}\left(\sqrt{b}-\sqrt{a}\right)}{6\times {2}^{1/3}{a}^{5/6}{b}^{1/6}{\left(\sqrt{a}+\sqrt{b}\right)}^{5/3}} $$

(10)

$$ {\displaystyle \begin{array}{l}\frac{\partial Z}{\partial b}=-\frac{R\left(2a+5\sqrt{a}\sqrt{b}+4b\right)}{4{b}^2{\left(\sqrt{a}+\sqrt{b}\right)}^2},\frac{\partial z}{\partial b}=-\frac{R\left(\sqrt{a}+2\sqrt{b}\right)}{4{b}^{3/2}{\left(\sqrt{a}+\sqrt{b}\right)}^2},\\ {}\frac{\partial {U}_i}{\partial b}=-\frac{R^{1/3}{a}^{1/6}{V}_i^{1/3}{W}_i^{1/3}\left(\sqrt{a}+3\sqrt{b}\right)}{6\times {2}^{1/3}{b}^{7/6}{\left(\sqrt{a}+\sqrt{b}\right)}^{5/3}}\end{array}} $$

(11)