Skip to main content
SpringerLink
Log in

On stability of parametrically excited linear stochastic systems

  • Published:
International Applied Mechanics Aims and scope

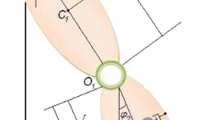
The dynamic stability of a coupled two-degrees-of-freedom system subjected to parametric excitation by a harmonic action superimposed by an ergodic stochastic process is investigated. For the stability analysis, the method of moment functions is used. Explicit expressions for the stability of the second moments are obtained when the frequency of the harmonic excitation lies in the vicinity of the combination sum of the natural frequencies. Good agreement between the analytical and numerical results is obtained. As an application, the example of the flexural-torsional instability of a thin elastic beam under dynamic loading is considered

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. T. Ariaratnam and D. D. F. Tam, “Parametric random excitation of a damped Mathieu oscillator,” ZAMM (J. Appl. Math. Mech.), 56, No. 11, 449–512 (1976).

    Article  ADS  Google Scholar 

  2. S. T. Ariaratnam and Wei-Chau Xie, “Lyapunov exponents and stochastic stability of coupled linear systems under real noise excitations,” ASME J. Appl. Mech., 59, 664–673 (1993).

    Article  MathSciNet  Google Scholar 

  3. R. Bellman, Stability Theory of Differential Equations, Dover, New York (1969).

    Google Scholar 

  4. V. V. Bolotin, The Dynamic Stability of Elastic Systems, Holden-Day, Inc. (1964).

  5. V. V. Bolotin, Random Vibration in Elastic Systems, Martinus Nijhoff, New York (1984).

    Google Scholar 

  6. V. V. Bolotin (ed.), Vibrations in Engineering: Handbook [in Russian], Mashinostroenie, Moscow (1978).

    Google Scholar 

  7. R. V. Bobryk and L. Stettner, “Moment stability for linear systems with a random parametric excitation,” Syst. Contr. Let., 54, No. 8, 791–786 (2005).

    MathSciNet  Google Scholar 

  8. R. V. Bobryk, “Comparison of some approaches to stability of a sdof system under random parametric excitation,” J. Sound Vibr., 305, 317–321 (2007).

    Article  MathSciNet  ADS  Google Scholar 

  9. M. F. Dimentberg, Stochastic Processes in Dynamic Systems with Variable Parameters [in Russian], Nauka, Moscow (1989).

    Google Scholar 

  10. F. C. L. Fu and S. Nemat-Nasser, “On the stability of steady-state response of certain nonlinear dynamic systemes subjected to harmonic excitations,” Arch. Appl. Mech., 41, No. 6, 407–420 (1972).

    MATH  Google Scholar 

  11. R. Z. Khasminskii, Stability of System of Differential Equations with Randomly Disturbed Parameters [in Russian], Nauka, Moscow (1969).

    Google Scholar 

  12. M. M. Klosek-Dygas, B. J. Matkowsky, and Z. Schuss, “Stochastic stability of nonlinear oscillators,” SIAM J. Appl. Math., 48, No. 5, 1115–1127 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  13. F. Kozin, “A survey of stability of stochastic systems,” Automatica, 5, 95–112 (1969).

    Article  MathSciNet  MATH  Google Scholar 

  14. H. J. Kushner, Stochastic Stability and Control, Academic Press, London–New York (1967).

    MATH  Google Scholar 

  15. J. La sale and S. Lefschetz, Stability by Lyapunov’s Direct Method with Applications, Academic Press, New York (1961).

    Google Scholar 

  16. M. Labou, “Stochastic stability of parametrically excited random systems,” Int. Appl. Mech., 40, No. 10, 1175–1183 (2004).

    MathSciNet  ADS  Google Scholar 

  17. M. Labou, “On the stability of parametrically excited random systems,” Int. Appl. Mech., 41, No. 12, 1437–1446 (2005).

    Article  MathSciNet  ADS  Google Scholar 

  18. M. Labou and T-W. Ma, “Lyapunov exponents of coupled two-DOF stochastic linear systems and related stability problems,” J. Sound Vibr., 325, 421–435 (2009).

    Article  ADS  Google Scholar 

  19. D. R. Merkin, Introduction to the Theory of Stability, Spring-Verlag, New York (1996).

    Book  MATH  Google Scholar 

  20. E. Mettler, “Stability and vibration problems of mechanical systems under harmonic excitation,” in: Dynamic Stability of Structures, New York (1967), pp. 169–188.

  21. E. W. Montroll and M. F. Shlesinger, “On the wonderful world of random walks,” in: J. L. Lebowitz and E. W. Montroll (eds.), Nonequilibrium Phenomena II: From Stochastics to Hydrodynamics, Studies in Statistical Mechanics, XI, North-Holland, Amsterdam (1984), pp. 1–121.

    Google Scholar 

  22. R. L. Stratonovich, Topics in the Theory of Random Noise, Gordon and Breach, New York (1963).

    Google Scholar 

  23. Xie Wei-Chau, Dynamic Stability of Structures, Cambridge Univ. Press, New York (2006).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Hawaii at Manoa, 2540 Dole Street, Honolulu, HI, 96822, USA

    M. Labou

Authors
  1. M. Labou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Labou.

Additional information

Published in Prikladnaya Mekhanika, Vol. 46, No. 12, pp. 123–138, December 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Labou, M. On stability of parametrically excited linear stochastic systems. Int Appl Mech 46, 1440–1453 (2011). https://doi.org/10.1007/s10778-011-0438-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-011-0438-1

Keywords

Search

Navigation