Abstract
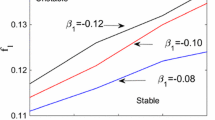
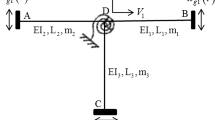
The paper analyzes questions related to the construction of dynamic stability boundaries of elastic systems subjected to stochastic parametric excitation. It is supposed that the parametric action is a combination of a deterministic static component and a stochastic fluctuating component. The fluctuating component is taken to be a stationary ergodic process. The stability boundaries are built in the region of combination resonance using the stochastic averaging method and a probabilistic approach due to Khasminskii. In this connection, the stochastic averaging method based on the Stratonovich-Khasminskii theory is used. The probabilistic approach consists in using explicit asymptotic expressions for the largest Lyapunov exponent, from which the asymptotic stability boundaries are determined. As an application, the stability of a simply supported thin-walled bar subjected to a stochastically varying longitudinal load is investigated
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. T. Ariaratnam and T. K. Srikantaih, “Parametric instabilities in elastic structures under stochastic loading,” J. Struct. Mech., 6, No. 4, 349–365 (1978).
S. T. Ariaratnam and Wei-Chau, “Lyapunov exponents and stochastic stability of two-dimensional parametrically excited random systems,” Trans. ASME, Ser. E, J. Appl. Mech., 60(3), 667–682 (1993).
K. V. Avramov, “Bifurcations at combination resonance and quasiperiodic vibrations of flexible beams,” Int. Appl. Mech., 39, No. 8, 976–982 (2003).
V. A. Bazhenov and E. S. Dekhtyaryuk, “Parametric oscillations in elastic systems excited by random perturbations with a finite correlation radius,” Int. Appl. Mech., 39, No. 12, 1436–1440 (2003).
V. V. Bolotin, The Dynamic Stability of Elastic System, Holden-Day, San Francisco (1964).
M. F. Dimentberg, Stochastic Processes in Dynamic Systems with Variable Parameters [in Russian], Nauka, Moscow (1989).
I. I. Gikhman and A. V. Skorokhod, Introduction to the Theory of Stochastic Processes [in Russian], Nauka, Moscow (1977).
R. Z. Khasminskii, “A limit theorem for the solutions of differential equations with random right-hand sides,” Theory Prob. Appl., 11, 390–406 (1966).
R. Z. Khasminskii, The Stability of System of Differential Equations under Random Disturbance of Its Parameters [in Russian], Nauka, Moscow (1969).
M. Labou, “Stochastic stability of parametrically excited random systems,” Int. Appl. Mech., 40, No. 10, 1175–1183 (2004).
V. V. Bolotin (editor), Vibrations in Engineering: Handbook [in Russian], Mashinostroenie, Moscow (1978).
Author information
Authors and Affiliations
Additional information
Published in Prikladnaya Mekhanika, Vol. 41, No. 12, pp. 128–138, December 2005.
Rights and permissions
About this article
Cite this article
Labou, M. On the stability of systems with stochastically variable parameters. Int Appl Mech 41, 1437–1446 (2005). https://doi.org/10.1007/s10778-006-0053-8
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10778-006-0053-8