Intelligent Reflecting Surface Framework for ED Based Spectrum Sensing

Abstract

According to a recent study, adding intelligent reflecting surfaces (IRS) to propagation environments improves the performance of wireless devices. The capabilities of cognitive radio’s spectrum sensing over environments with assisted wireless propagation via IRS are examined in this research. Taking channel fading effects into consideration, we derive closed-form analytical expressions for the average probability of detection (APD) for single user and cooperative users. Further, the derived APD expression is used to derive the average area under the receiver operating characteristics curve (${\overline{AUC}}$) expression. Monte Carlo simulations are also carried out in order to validate the derived expressions. Results demonstarte the extent of detectability performance in cognitive radio on utilizing the IRS aided wireless propagation environment therefore witnessing its significance for upcoming wireless technological advancement by offering spectrum efficiency with good quality of service (QoS).

1 Introduction

The wireless industry is looking towards technological advancements like 5G, 6G, and beyond services with an aim to enhance the communication capacity and quality of service (QoS) to the users. In response to such rapidly rising demand, we need a system that offers a spectral and energy efficient model while fulfilling the higher rate requirement. Cognitive Radio (CR) is one such system that has been widely studied to offer the spectral efficiency, however due to unpredictable nature of propagation channel behaviour and its unavoidable losses, leads to inaccurate detection performance of CR system that restricts its usage due to negative interference to primary user (PU) and/or low spectral efficiency (SE) for secondary user (SU). Numerous studies have been conducted on the design of various detectors and the algorithms for the spectrum sensing (SS) of CR system including energy detector (ED) [1,2,3], eigenvalue-based detector [4], matched-filter detector [5] and cyclostationary feature detector [6]. Amongst all ED has been widely studied due to its low computational complexity, and fast sensing performance that is a crucial parameter of SS where there is rapid transition from one band to another. However, ED performance is constrained by channel impairment issues like shadowing, multipath reflections, fading, and path losses, that makes the PU signals at the SU so weak for accurate sensing. To overcome this limitation, recent researches have reported the use of digitally controlled and dynamically-tunable meta-surface to improve the network performance. Such smart intelligent reflecting surface (IRS) elements adopt joint phase control and radio propagation environment control to enhance received signal performance [7]. Due to this appealing feature IRS, it has recently emerged as crucial enabler technology to improve signal coverage and enhance spectral efficiency. Additionally, the deployment of IRS in CR network can meet the demand of maximizing SU throughput and mitigate SU interference level at PU [8].

Motivated by the above features, IRS assisted CR-network has recently drawn much research interest [9] [10]. Where, IRS exploits the large aperture and passive beamforming gains to boost the PU signal strength received at the SU. This configuration facilitates the SS in a cost-effective manner and also offers better spectrum sharing [11] and improved spectrum sensing [12] performance. Other related work based on IRS assisted CR network assumes optimization problem for evaluation of performance metrics of the aforementioned system. In [8] IRS is employed to improve the SE of the SU. The formulated problem is non-convex in nature and is solved by alternating optimization (AO) algorithm. AO is further studied in [13] to solve another such nonconvex problem of maximizing SE of the SU by joint optimizing the transmit precoding matrices at SU, the phase shift matrix at IRS, and power-splitting factors at the user. Further, another such optimization problem is dealt in [14] by adopting inexact block coordinate descent (IBCD) optimization algorithm. where the phase matrix at the IRS, the precoding matrix, and the artificial noise covariance at the SU are optimally designed to achieve maximal secrecy performance of the SU assuming imperfect knowledge of the PU channel state information (CSI). Such intractable non-convex optimisation problem constitutes a several design challenges and requires computationally intensive solution. This complexity in design is further escalated by increase in number of IRS elements and hence poses constraint in practical realization of massive scale network. The authors in [15] have carried out statistical analysis and evaluated the average detection probability of IRS assisted CR network but the study is limited to only detection probability evaluation and not considered the average area under curve (AUC) performance parameter. However, the above research, assumes that the SU has statistical/ instantaneous CSI, which is practically difficult to attain. Since, the PU position is random and time variant due to which the channel is uncontrollable and random hence assuming statistical CSI information is impractical.

Motivated, by the above literature study where the prior studies have mainly focussed either on computationally intensive solutions or assumption of CSI which practically waves-off the potential effect of simplicity in design of passive elements of IRS based system on digital communication system performances and a very few have considered the statistical analysis of the detection performance of CR system. Therefore, with a focus on the significance of the issue, this article investigates the ED detection performance in an IRS aided propagation environment. Considering large number of IRS elements and leveraging central limit theorem to characterise PU-IRS-SU SNR statistics we derive various performance measures for the ED based spectrum sensing. The key contributions to this work are summarised as follows:

• Firstly, spectrum sensing performance for the proposed model is examined via deriving closed form expressions for average probability of detection (APD) for single user and cooperative user scenario.

• Secondly, in order to get better understandings on CR operating behaviour we derive closed form analytical expression for average area under the receiver operating characteristics (${\overline{AUC}}$).

• Based on derived performance parameters we analyses ED detection performance for different number of IRS elements, distance between nodes and time bandwidths etc.

Rest of the article is organised as;

Section 2 provided the proposed system model for IRS assisted ED based spectrum sensing and SNR statistics. Derivation of various performance measures is provided in Sect. 3. Related discussions on ED performance through numerical simulation have been presented in Sect. 4. In the end conclusion to important findings in this article are provided in Sect. 5.

2 System Model and SNR Characteristics

2.1 System Model

Fig. 1

System model

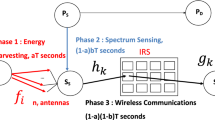
As illustrated in Fig. 1, the conceptual framework of the proposed system comprises a primary user (PU), secondary user (SU), and an intelligent reflecting surface (IRS) that is made up of N reflective elements. The SU is tasked with detecting the existence of an active signal transmitted by the PU, at the presence of the IRS. The signal that the SU receives through the IRS can be represented as follows.

$$\begin{aligned} {y = \left\{ {\begin{array}{*{20}{c}} n&{}{:{H_0}}\\ {{\alpha }.x + n}&{}{:{H_1}} \end{array}} \right. } \end{aligned}$$

(1)

where x, $\alpha$ and n represents transmitted PU signal, PU-IRS-SU channel gain and additive white gaussian noise respectively. The presence (i.e. hypothesis $H_1$) or absence (hypothesis $H_0$) of PU signal is decided by comparing decision threshold $\xi$ with the energy ($\Xi$) of received signal y. The two performance probability are defined as probability of detection as ${P_r}\left( {\Xi > \xi |{H_1}} \right)$ and probability of false alarm as ${P_r}\left( {\Xi > \xi |{H_0}} \right)$. Considering non-faded channel conditions (i.e. $\alpha$ constant), the two probabilities are as follow [16],

$$\begin{aligned} {{p_d}\left( {\left. \gamma \right| \xi } \right) = {Q_d}\left( {\sqrt{2\gamma } ,\sqrt{\xi }} \right) } \end{aligned}$$

(2)

and

$$\begin{aligned} {{p_{fa}}\left( \xi \right) = \frac{1}{{\Gamma \left( d \right) }}\Gamma \left( {d,\frac{\xi }{2}} \right) } \end{aligned}$$

(3)

where, $Q_d(.,.)$ is Marcum-Q function, $\Gamma (.)$ is Gamma function, and $\Gamma (.,.)$ is upper incomplete Gamma function, d is the time-bandwidth product and $\gamma$ represents instantaneous signal-to-noise ratio (SNR) defined as, $\gamma = {\left| \alpha \right| ^2}\frac{{{E_p}}}{{{N_0}}}$ with $E_p$ and $N_0$ representing PU transmitted power and noise power spectral density respectively.

2.2 SNR Characteristics

For the given propagation framework, PU-IRS-SU channel coefficient can be written as follow:

$$\begin{aligned} {\alpha = \sum \limits _{i = 1}^N {{h_i}} {e^{j{\phi _i}}}{g_i}} \end{aligned}$$

(4)

where, N represents number of IRS elements, ${\phi _i}$ is the phase shift induced by $i^{th}$ IRS element. ${h_i}$ and ${g_i}$ denotes channel gains between PU to $i^{th}$ IRS element and $i^{th}$ IRS element to SU such that ${h_i} = d_{pr}^{ - \varsigma /2}{\beta _i}{e^{ - j{\psi _i}}}$ and ${g_i} = d_{rs}^{ - \varsigma /2}{\varepsilon _i}{e^{-j{\varphi _i}}}$. Where ${d_{pr}}$ and ${d_{rs}}$ are link distances between PU to IRS and IRS to SU respectively, $\varsigma$ is path loss exponent, ${\varphi _i}$ and ${\psi _i}$ are associated phases corresponds to channel gains $h_i$ and $g_i$ respectively.

From [17] maximised SNR at SU can be attained by setting up ${\phi _i}={\varphi _i} + {\psi _i}$. Therefore from (1)

$$\begin{aligned} {\alpha = \frac{1}{{\sqrt{d'} }}\sum \limits _{i = 1}^N {{\beta _i}} {\varepsilon _i}} \end{aligned}$$

(5)

where $d' = d_{pr}^\varsigma \times d_{rs}^\varsigma$.Hence received instantaneous snr at SU terminal can be written as;

$$\begin{aligned} {\gamma = \frac{1}{{d'}}{\left( {\sum \limits _{i = 1}^N {{\beta _i}} {\varepsilon _i}} \right) ^2}\frac{{{E_P}}}{{{N_0}}} = \frac{1}{{d'}}{R^2}\,{\bar{\gamma }}} \end{aligned}$$

(6)

where ${\bar{\gamma }}$ denotes average SNR defined as ${\bar{\gamma }} = {E_P}/{N_0}$ and $R = \sum \limits _{i = 1}^N {{\beta _i}{\varepsilon _i}}$.

For a significant number of IRS elements, specifically when $N>>1$ and in accordance with the central limit theorem, the PDF of R can be approximated by Gaussian random distribution with mean and variance as $N\pi /4$ and $N(1 - {(\pi /4)^2})$ respectively [17]. Therefore $R^2$ will be a non-central chi-square RV with one degree of freedom and PDF as given by [18].

$$\begin{aligned} {{f_{{R^2}}}(r) = \frac{1}{{2\sigma _{clt}^2}}{\left( {\frac{r}{{{\lambda _{clt}}}}} \right) ^{ - 1/4}}{e^{ - \,\frac{{r + {\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}{I_{ - 0.5}}\left( {\frac{{\sqrt{r{\lambda _{clt}}} }}{{\sigma _{clt}^2}}} \right) } \end{aligned}$$

(7)

where, ${I_n}(.)$represents modified Bessel function first kind with nth order,${\lambda _{clt}} = {(N\pi /4)^2}$and $\sigma _{clt}^2 = N(1 - {\pi ^2}/16)$. Now from (6) the PDF of instantaneous snr is expressed as:

$$\begin{aligned} {{f_\gamma }(\gamma ) = \frac{{d'}}{{2\sigma _{clt}^2{\bar{\gamma }} }}{\left( {\frac{{d'}}{{{\bar{\gamma }} {\lambda _{clt}}}}} \right) ^{ - 1/4}}{\gamma ^{ - 0.25}}{e^{ - \,\frac{{{\lambda _{clt}}{\bar{\gamma }} + \gamma d'}}{{2{\bar{\gamma }} \sigma _{clt}^2}}}}{I_{ - 0.5}}\left( {\frac{{\sqrt{\gamma d'{\lambda _{clt}}} }}{{\sqrt{{\bar{\gamma }} } \sigma _{clt}^2}}} \right) } \end{aligned}$$

(8)

A more simplified expression for PDF in (8) can be obtained by expanding Bessel function as summation series i.e.

$$\begin{aligned} {{f_\gamma }(\gamma ) = {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\sum \limits _{p = 0}^{\infty } {\frac{1}{{p!\Gamma (p + 0.5)}}{{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) }^p}{\beta ^{p + 0.5}}} {\gamma ^{p - 0.5}}{e^{ - \,\beta \,\gamma }}} \end{aligned}$$

(9)

where, $\beta = \frac{{d'}}{{2{\bar{\gamma }} \sigma _{clt}^2}}$. Observe (9) consist of $\infty$ series and related series truncation terms i.e. P can be obtained by using PDF area property $\int \limits _0^\infty {{f_\gamma }(\gamma )d\gamma } = 1$ , as given by (11).

$$\begin{aligned} {{f_\gamma }(\gamma ) = {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\sum \limits _{p = 0}^P {\frac{1}{{p!\Gamma (p + 0.5)}}{{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) }^p}{\beta ^{p + 0.5}}} {\gamma ^{p - 0.5}}{e^{ - \,\beta \,\gamma }}} \end{aligned}$$

(10)

$$\begin{aligned} {\sum \limits _{p = 0}^P {\frac{{\lambda _{clt}^p}}{{p!{{(2\sigma _{clt}^2)}^p}}}} {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}} \approx 1} \end{aligned}$$

(11)

Table 1 shows, the minimum number of truncation terms (P) for different IRS elements (N) required to satisfy condition (11).

Table 1 Truncation terms for different L values

3 Performance Analysis

3.1 Detection Probability at Stand-Alone SU

Detection probability expressed in (3) considers no fading effects although practical propagation scenario are subjected to fading, therefore channel coefficient is no longer constant, but rather fluctuate randomly. Thus, the determination of the average detection probability can be expressed in the follow:

$$\begin{aligned} {{{{\bar{p}}}_d}\left( \xi \right) = \int \limits _0^\infty {{Q_d}\left( {\sqrt{2\gamma } ,\sqrt{\xi }} \right) } {f_{\gamma }}\left( \gamma \right) d\gamma } \end{aligned}$$

(12)

where, ${f_\gamma }(\gamma )$ represents PDF of instantaneous SNR in fading environment.

Using integral form of Marcum-Q function [19, eq.(1)], in (12) followed by [20, Eq. (8.445)], (12) can be represented as:

$$\begin{aligned} {{{{\bar{p}}}_d}\left( \xi \right) = 1 - \sum \limits _{s = 0}^\infty {\frac{{\Upsilon \left( {d + s,\xi /2} \right) }}{{s!{\hspace{0.55542pt}} \Gamma \left( {d + s} \right) }}} \int \limits _0^\infty {{e^{ - \gamma }}{\gamma ^s}{f_{\gamma }}\left( \gamma \right) d\gamma }} \end{aligned}$$

(13)

with (13) and (10) and [20, eq.(6.643.2 )], the average detection probability is obtained in (14).

$$\begin{aligned}{} & {} {{{\bar{p}}}_d}\left( \xi \right) = 1 - {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\sum \limits _{s = 0}^\infty {\sum \limits _{p = 0}^P {\frac{{\Upsilon \left( {d + s,\xi /2} \right) }}{{s!{\hspace{0.55542pt}} \Gamma \left( {d + s} \right) }}\frac{{\Gamma \left( {s + p + 0.5} \right) }}{{p!\Gamma (p + 0.5)}}} }\nonumber \\{} & {} \quad \,{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) ^p}\frac{{{\beta ^{p + 0.5}}}}{{{{\left( {1 + \beta } \right) }^{s + p + 0.5}}}} \end{aligned}$$

(14)

3.1.1 Proposition A

The truncation error, due to limiting infinite series in (14) to S finite terms, can be expressed as in (15). Where the value of truncation term S depends on the number of IRS elements, and SNR, etc., and it is chosen in such a way that the error is confined within a certain limit.

$$\begin{aligned}{} & {} \left| E \right| \le {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\frac{{\Upsilon \left( {d + S + 1,\xi /2} \right) }}{{\Gamma (S)\Gamma \left( {d + S + 1} \right) }}\sum \limits _{p = 0}^P \frac{{\Gamma \left( {S + p + 1.5} \right) }}{{p!\Gamma (p + 0.5)}}\nonumber \\{} & {} \quad {{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) }^p}\frac{{{\beta ^{p + 0.5}}}}{{{{\left( {1 + \beta } \right) }^{p + S + 1.5}}}} \,{}_2{F_1}\left( {1,S + p + 1.5;S;\frac{1}{{1 + \beta }}} \right) \end{aligned}$$

(15)

Table 2 lists the number of terms S needed to ensure that the error $\left| E\right| \le {10^{-7}}$ with $p_{fs}=0.1$, $d=10$, $d_{pr}=d_{rs}=5$,$\varsigma =2.3$ and different values of SNR and IRS elements.

Table 2 Truncation terms S for $\left| E\right| \le {10^{-7}}$

Proof

See Appendix. A $\square$

3.2 Detection Probability with Collaborative SUs

Numerous research studies have demonstrated that energy detection-based spectrum sensing can be substantially enhanced through the cooperation among the of SU by sharing detection information. When multiple users collaborate, the probability of detection and false alarm can be expressed as ${{\bar{p}}}_d^{css} \buildrel \Delta \over = 1 - {(1 - {{{\bar{p}}}_d}(\xi ))^{{H_c}}}$ and ${{\bar{p}}}_{fa}^{css} \buildrel \Delta \over = 1 - {(1 - {p_{fa}}(\xi ))^{{H_c}}}$ respectively [21]. Utilizing these expressions, the average probability of detection for a collaborative scenario involving $H_c$ users for the given propagation scenario is derived as follows:

$$\begin{aligned}{} & {} {{\bar{p}}}_d^{css} \buildrel \Delta \over = 1 - \left( {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}} \sum \limits _{s = 0}^\infty {\sum \limits _{p = 0}^P {\frac{{\Upsilon \left( {d + s,\xi /2} \right) }}{{s!{\hspace{0.55542pt}} \Gamma \left( {d + s} \right) }}\frac{{\Gamma \left( {s + p + 0.5} \right) }}{{p!\Gamma (p + 0.5)}}} }\right. \nonumber \\{} & {} \quad \left. \,{{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) }^p}\frac{{{\beta ^{p + 0.5}}}}{{{{\left( {1 + \beta } \right) }^{s + p + 0.5}}}} \right) ^{{H_c}} \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \quad {{\bar{p}}}_{fa}^{css} \buildrel \Delta \over = 1 - {\left( {1 - \frac{1}{{\Gamma \left( d \right) }}\Gamma \left( {d,\frac{\xi }{2}} \right) } \right) ^{{H_c}}}\, \nonumber \\{} & {} \quad \buildrel \Delta \over = 1 - \frac{1}{{\Gamma {{\left( d \right) }^{{H_c}}}}}\Upsilon {\left( {d,\frac{\xi }{2}} \right) ^{{H_c}}} \end{aligned}$$

(17)

3.3 AUC Performance

Area under ROC is another performance metric used to assess an energy detector’s effectiveness and have its utility when comparing two systems. AUC computation is independent of decision threshold hence can serve as a single figure to gain better insights on ED receiver performance. Computation of AUC is as follow:

$$\begin{aligned} {\overline{{{AUC}}} = - \int \limits _0^\infty {{{{{\bar{p}}}}_d}\left( \xi \right) \frac{{\partial {p_{fa}}\left( \xi \right) }}{{\partial \xi }}d\xi }} \end{aligned}$$

(18)

where,

$$\begin{aligned} {\frac{{\partial {p_{fa}}\left( \xi \right) }}{{\partial \xi }} = - \frac{{{\xi ^{d - 1}}{e^{ - \xi /2}}}}{{{2^d}\Gamma \left( d \right) }}} \end{aligned}$$

(19)

From (18) ,(19) and (14) we get,

$$\begin{aligned}{} & {} \overline{{{AUC}}} = 1 - {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\nonumber \\{} & {} \quad \sum \limits _{s = 0}^\infty {\sum \limits _{p = 0}^P {\frac{{\Gamma \left( {s + p + 0.5} \right) }}{{s!p!\Gamma (p + 0.5)}}} } \,{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) ^p}\frac{{{\beta ^{p + 0.5}}}}{{{{\left( {1 + \beta } \right) }^{s + p + 0.5}}}}\nonumber \\{} & {} \quad \int \limits _0^\infty {\frac{{\Upsilon \left( {d + s,\xi /2} \right) }}{{{\hspace{0.55542pt}} \Gamma \left( {d + s} \right) }}\frac{{{\xi ^{d - 1}}{e^{ - \xi /2}}}}{{{2^d}\Gamma \left( d \right) }}d\xi } \end{aligned}$$

(20)

with the aid of [20, eq.(6.445.2)] $\overline{{{AUC}}}$ is given as:

$$\begin{aligned} {\begin{array}{l} \overline{{{AUC}}} = 1 - {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\sum \limits _{s = 0}^\infty {\sum \limits _{p = 0}^P {\frac{{\Gamma \left( {2d + s} \right) }}{{\Gamma \left( d \right) \Gamma \left( {d + s + 1} \right) }}\frac{{\Gamma \left( {s + p + 0.5} \right) }}{{s!p!\Gamma (p + 0.5)}}} } \\ \,\,\,\,\,\,\,\,\, \times {\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) ^p}\frac{{{\beta ^{p + 0.5}}}}{{{2^{2d + s}}{{\left( {1 + \beta } \right) }^{s + p + 0.5}}}}\,\,{}_2{F_1}\left( {1,2d + s,d + s + 1,\frac{1}{2}} \right) \end{array}} \end{aligned}$$

(21)

4 Results and Discussion

This section presents an analysis of the performance of ED based spectrum sensing for the introduced IRS assisted system model. The aim is to demonstrate the efficacy of the ED based spectrum sensing, and this is achieved through the use of various curves, including ROC (${{\bar{p}}}_d$ vs $p_{fa}$), ${{\bar{p}}}_d$ vs ${\bar{\gamma }}$ , and ${\overline{AUC}}$. Drawn curves are obtained through the derived analytical expressions and verified with the corresponding Monte Carlo simulations.

Fig. 2

Average probability of detection versus Probability of false alarm (ROC) with $d=1$,$\varsigma =2.1$, $d_{pr}=5$ ,$d_{rs}=4$ and different number of IRS elements (N) and SNR

Figure 2 presents the ED detection performance using the ROC curve for varying numbers of IRS elements (N) and SNR levels. The results obtained demonstrate a significant improvement in the detection capability of ED based spectrum sensing as the number of IRS elements increases, at both 0 dB and 5 dB SNR levels. This can be attributed to the fact that an increase in the number of IRS elements results in better beam-forming at the IRS, leading to a higher SNR at the SU and thereby improving the ED sensing performance. Additionally, it is noteworthy that even at lower SNRs, the performance of the ED detection system is improved with larger numbers of IRS elements. For instance, when N=10 (SNR=+5dB) and N=20 (SNR=0dB), and similarly for N=20 (SNR=+5dB) and N=40 (SNR=0dB), improved ED performance is observed for lower SNRs (due to the presence of a larger number of IRS elements) indicating efficacy of IRS-assisted framework detecting low-powered PUs.

Fig. 3

$P_d$ versus SNR (dB) Plots, with $d=1$, $\varsigma =2.1$, $p_{fa}=0.1$ different number of IRS elements (N) and link distances (i.e. $d_{pr}$ & $d_{rs}$)

Figure 3 illustrates the effects of PU-IRS-SU link distances on the detection performance as a function of the average received SNR. The results demonstrate a significant degradation in the ED detection performance when the PU-SU link distance is increased. However, an improvement in the detection performance is observed with an increase in the IRS elements (N), for instance, the POD increases by $25.4\%$ and $67.88\%$ when N increased to 20 and 30 (from its initial value of 10 at $d_{pr}=d_{rs}=10$ and SNR=+10dB), similarly, an improvement of $142.2\%$ and $234.7\%$ is observed (at $d_{pr}=d_{rs}=5$) indicating that a large aperture IRS can effectively sense PU with low SNR.

Fig. 4

$P_d$ versus SNR(dB) Plots for cooperative detection, with $d=1$, $\varsigma =2.1$, $p_{fa}=0.1$, $d_{pr}=10$ & $d_{rs}=10$ and different number of IRS elements (N)

Figure 4 depicts the ${{\bar{p}}}_d$ versus SNR curve for the cooperative spectrum sensing scenario. The results reveal that the detection capabilities are further improved with the incorporation of cooperation between the SUs. It can be observed that the POD improves by $59.83\%$ and $89.70\%$ (with N=30, SNR=0dB) when considering 2 and 3 cooperative users, respectively. Furthermore, the observed improvement is $200.79\%$ and $298.82\%$ at 30 dB SNR. Hence, the utilization of cooperation among SU, along with a larger size IRS, has the potential to sense a PU located at larger distances or with low transmitted power.

Fig. 5

${\overline{AUC}}$ versus $d_{pr}$ ($d_{pr}+d_{rs}=15$) with $d=1$, $\varsigma =2.5$ and different number of IRS elements (N) and SNR

Figure 5 portrays the ED detection performance in terms of the ${\overline{AUC}}$ characteristics with different $d_{pr}$ values, where $d_{pr}+d_{rp}=15$, at SNRs levels of 5 dB and 15 dB. It can be observed that at lower SNRs and with fewer IRS elements (i.e. SNR=+5 dB, N=10), the receiver performs poorly, and the ${\overline{AUC}}$ lies close to its lower bound, i.e., 0.5. However, for higher SNRs and with more IRS elements (i.e. SNR=+15 dB and N=20 or 30), an improved ${\overline{AUC}}$ performance is observed. Moreover, at N=30, SNR=+5 dB, and N=10, SNR=+15 dB, almost equal ${\overline{AUC}}$ performance is observed, indicating an important outcome that a 10 dB SNR requirement can be met by simply increasing the number of IRS elements. Additionally, an interesting observation is that poor detection performance is observed when the PU or SU is at an equal distance from the IRS. In contrast, for unequal distances from the IRS, the performance is comparatively better.

Fig. 6

${\overline{AUC}}$ versus time-bandwidth product (d) with $d_{pr}=5$, $d_{rs}=5$, SNR=10 dB and different number of IRS elements (N) and $\varsigma$

Figure 6 presents the ${\overline{AUC}}$ vs d curve for different IRS elements and path loss conditions. It is evident that under the given path loss condition, the time-bandwidth product d plays a critical role in determining detector performance. As the value of d increases, the ${\overline{AUC}}$ performance reduces since both APD and PFA increase with an increase in d, but PFA increases at a higher rate leading to an overall reduction in ${\overline{AUC}}$. Additionally, the behaviour is studied at $\varsigma$=2 and $\varsigma$=3, which demonstrates the worst receiver detection performance at $\varsigma$=3, as the ${\overline{AUC}}$ lies near 0.5. However, its performance improves significantly when the number of IRS elements is increased. Conversely, for $\varsigma$=2, a superior receiver performance is observed due to better path loss conditions, which further improves with an increase in the number of IRS elements.

5 Conclusion

The presented research investigates the performance of ED spectrum sensing over of intelligent reflecting surfaces (IRS) assisted communication systems. To this end, Novel expressions for two performance measures i.e. average probability of detection with (i) single user and (ii) cooperative detection and average area under the ROC curve are derived. The results demonstrate an improved detection performance of ED-based spectrum sensing when number of IRS elements are increased which can be further improved by incorporation of cooperation between SUs. Hence enhancing ED capabilities to identify the presence of low-powered PU or operating over larger distances. Therefore, using IRS has the potential to be a highly effective solution for spectrum sensing in future cognitive radio-based wireless communication systems.

Proof: Proposition A

The expression for the truncation error resulting from the truncation of an infinite series into a finite number of terms, can be expressed as:

$$\begin{aligned}{} & {} \left| E \right| = {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\sum \limits _{p = 0}^P {\frac{1}{{p!\Gamma (p + 0.5)}} {{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) }^p}\frac{{{\beta ^{p + 0.5}}}}{{{{\left( {1 + \beta } \right) } ^{p + 0.5}}}}} \nonumber \\{} & {} \quad \sum \limits _{s = S + 1}^\infty {\frac{{\Upsilon \left( {d + s,\xi /2} \right) }}{{\Gamma \left( {d + s} \right) }}} \,\frac{{\Gamma \left( {s + p + 0.5} \right) }}{{s!{\hspace{0.55542pt}} {{\left( {1 + \beta } \right) }^s}}} \end{aligned}$$

(22)

Observe $\frac{{\Upsilon \left( {d + s,\xi /2} \right) }}{{\Gamma \left( {d + s} \right) }}$ represents regularised lower incomplete gamma function and decreases with increase in s , hence maximising right hand side and reordering series from 0 to $\infty$ we get.

$$\begin{aligned}{} & {} \left| E \right| \le {e^{ - \frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}}}\frac{{\Upsilon \left( {d + S + 1,\xi /2} \right) }}{{\Gamma \left( {d + S + 1} \right) }}\sum \limits _{p = 0}^P \frac{1}{{p!\Gamma (p + 0.5)}}\nonumber \\{} & {} \quad {{\left( {\frac{{{\lambda _{clt}}}}{{2\sigma _{clt}^2}}} \right) }^p}\frac{{{\beta ^{p + 0.5}}}}{{{{\left( {1 + \beta } \right) }^{p + S + 1.5}}}} \sum \limits _{t = 0}^\infty {\,\frac{{\Gamma \left( {t + S + p + 1.5} \right) }}{{(t + S + 1)!{\hspace{0.55542pt}} {{\left( {1 + \beta } \right) }^t}}}} \end{aligned}$$

(23)

Again, rearranging infinite series in (23) as hyper geometric function, expression for truncation error bound is given by (15)