1 Introduction

As the 5G wireless technology will be inadequate in the near future due to explosive growth of D2D networks like IoT, IIoT, and IoS. Next generation wireless communication systems, 6G is aimed at supporting communication needs of 2030s. Therefore, 6G wireless technology is essential which uses terahertz (0.1–10 THz) frequencies of EM spectrum and supports 10–100 GHz bandwidths, data rates of Terabits/sec 6G wireless system architecture is an integrated system of different radio access technologies with ultra-massive scales and dynamic network resources to achieve diverse performance improvements. The radio network architecture of 6G cellular systems should make use of cognitive radio, carrier aggregation, THz bands, ultra-mMIMO, and femto cell-based heterogeneous networks to provide maximum capacity [1,2,3]. The main aim of this article is to propose and design a hybrid beamforming system for 6G wireless networks that consist of ultra-mMIMO antenna array configurations of size varies from 64 to 256 at BS and 4–16 at MS of multiple users that operates at 0.14THz frequency band. The performance measurements at 0.14 THz are conducted and feasibility of the proposed system is verified for higher order QAM modulation schemes, also compared with mmWave hybrid beamforming systems that operate at 28–73 GHz bands.

1.1 Applications of mmWave and THz Frequency Bands

6G use applications include autonomous driving, industrial automation, machine-to-machine communications that have hard thresholds in terms of throughput, latency, and reliability. There are challenges in 6G system architecture design, network and resource management.

The mmWave and THz applications mentioned in Fig. 1 and Table 1 demand data rates of the order 100 Gbps and wider bandwidths (in terms of GHz) which can be possible with transmission schemes whose minimum spectral efficiencies are 14bits/sec/Hz. Unavailability of such digital modulation schemes and transceiver components to achieve higher data rates in the current scenarios motivates to explore the frequency spectrum above 100 GHz. “Information showers(IS)” provide extreme data rates (> 1Tbps) for ultra-short range wireless networks at THz frequencies. IS makes massive offloading of heavy traffic (up to 95%) in long-range networks and improves UE’s energy efficiency [5]. In wireless cognition applications, massive computations are conducted on a high capacity remote device like centralized servers. Low power drones (example of resource constrained robots) having limited on-board computing facilities takes advantage of cloud robotics and offload the computations to a cloud server [6]. In drone based cellular networks (3D), BSs and UEs uses drones to ensure full coverage with less number of BSs in the given space. 3D cellular networks achieve up to 46% reduction in average delay at UEs that includes backhaul delay, transmission, computation delays, also improves spectral efficiency [7]. GPS based navigation systems are vulnerable to jamming via RF interference, as an alternate THz signals can be used to have high precision range measurements [8]. Sensing applications mentioned in Table 1 exploit the absorption characteristics of channel materials, frequency-selective channel fading, ultra-mMIMO, and wider bandwidths at THz frequencies. Electronic beam steering techniques and ability of “wireless reality sensing” allows to generate real-time high resolution 3D maps of any given location with less latencies (< 10 nsec). At mmWave and THz frequencies, the effect of ambient light and weather have lesser impact on radar channel than LIDAR. Dual-frequency radars at THz bands give high resolution (similar to high-definition videos) under heavy rain or foggy, cloudy weather conditions whereas LIDAR have very poor performance under such conditions. “Dark vision” is the ability to reconstruct 3D maps of unknown environments at mmWave and THz bands using the combined techniques of sensing, imaging, and position location. Imaging methods at THz bands have less computational complexity in reconstruction of images and less hardware complexity than optical imaging methods even under NLOS channel conditions. THz time-domain high-resolution images can be generated by radar systems for objects irrespective of their shape, size, position and orientation where edges (edge lengths less than 400 µm) are clearly detected [9]. By exploiting mMIMO beam steering, arrival time/angle of uplink pilot signals one can generate the mmWave image of surrounding environment (both LOS and NLOS objects). Presence of ultra-mMIMO antenna arrays and large available bandwidths at mmWave and THz bands made possible to locate both LOS and NLOS users with centimetre precision [10].

Fig. 1
figure 1

EM spectrum and possible Applications [4]

Full size image
Table 1 Potential applications of 5G & 6G wireless technologies
Full size table

Optical wireless communication technologies such as free space optical communication, light fidelity, visible light communication, and optical camera communication can provide effective solutions for deployment of 6G systems and IoT [11]. Combination of free-space optical and mmWave systems provide significantly high data rates in wireless transmissions in spite of rapid variations in channel and environmental conditions. The selection of active link is determined by index modulation that does not need CSI or any feedback at Tx and it provides higher spectral efficiency [12]. The combination of optical and digital system architectures at THz bands provide data rates of Terabits/s, nearly zero latency and bandwidths greater than 50 GHz. The front-end transceivers are designed such that they support higher-order modulation schemes to provide ultra-high spectral efficiency [13].

This paper is organized as follows: Sect. 1 provides insight into mmWave and THz applications. Section 2 explores design challenges, key enabling technologies, role of AI, security aspects in 6G wireless networks. Section 3 describes the wave propagation, channel modelling and measurements at THz bands. Section 4 explores the possibility of using ultra-massive MIMO hybrid beamforming techniques for improved front-end performance at frequencies above 100 GHz. Section 5 discusses the results of ultra-massive MIMO hybrid beamforming system at 140 GHz and compared with the performance at 28 GHz, and 73 GHz mmWave frequencies [14, 136]. Section 6 gives overall observations, conclusions and possible future directions of research that can be carried out towards THz frequency bands.

2 6G Wireless Communication Systems

2.1 Design Challenges and Key Enabling Technologies

The connectivity goals of 6G wireless systems include: usage of THz frequencies to have abundant bandwidths, pervasive AI, cell-free mMIMO, backscatter communication to save energies, massive network automation etc., Beyond 6G, technologies like internet of nano and bionano things, quantum communications are expected to have impact on wireless communication systems [15]. Free-space optical network, wireless optical technology, AI, THz, blockchain, quantum communications, 3D networking, driverless vehicles, integrated sensing and communication, cell-free communications, integration of wireless information and energy transfer, backscatter communication, integrated access-backhaul networks, dynamic network slicing, intelligent reflecting surface, holographic beamforming, big data analytics, and proactive caching are the key enabling technologies to support 6G wireless systems development with guaranteed QoS [16]. In spite of technical challenges, it is possible to implement 6G wireless networks above 100 GHz for the applications shown in Table 1. Using special theory of relativity, computational complexity of signal processing in adaptive antenna arrays can be minimized and improve the performance of digital phased array antennas. The new path loss, partition loss and channel models (that considers correlation over space and minute changes) are defined for frequencies above 100 GHz.

“Unmanned aerial vehicles (UAV)” communication is one of the important components of 6G wireless technologies where flexible deployment, high degree of design freedom with controlled mobility, strong LOS paths are expected [17]. UAV-mounted flying BS allow data transmissions to a number of radio devices spread over the area. Optimized trajectories for high throughput and efficient discovery of channel parameters can be designed in UAV communication systems [18]. UAV communication provides high QoS in deep rural, difficult-to-serve areas, disaster-stricken areas using relay signals. 6G wireless networks are open and intelligent to support dynamic services in IoT which demands for convergence of computing, caching and communicating (3C). 6G wireless technologies support 3C-based spectrum management, wireless distributed computing, delay-aware transmission and network selection [19]. Deployment of smart health-care systems using 5G wireless technologies have challenges in terms of device density, latency, bandwidth, security, and energy efficiencies [20]. It is important to focus on study of channel, devices, and space-based system at mmWave and THz frequencies [21, 22]. 6G wireless technologies are the key for IoE applications that integrates applications ranging from virtual reality to autonomous systems [23]. 6G wireless technologies are expected to have high energy efficiency and technical standard of new spectrum to address the challenges including network designs, testbed developments, physical payer transmissions, and security [24]. High data rates can be achieved at THz bands such as 0.275–3 THz, however there are challenges in designing adaptive transceivers (both RF and digital domain), signal processing algorithms, channel characterization, privacy, and security [25].

6G wireless network features include high-precision 3D localization, ultra-low latency, high reliability, and high bandwidths leads to native applications like distributed, ubiquitous AI, IoT. In 6G wireless networks, the key enabling technologies such as ultra-mMIMO, THz, a tactile internet should address security aspects in 6G [26]. The design and development challenges in high-speed T–R modules, ultra-wideband antennas, channel modelling, higher order modulation schemes at THz bands are the new frontiers of 6G wireless systems [27]. Investigation of nonlinear optical effects and nanoscale phenomena at THz frequencies are essential as THz bands play an important role in 6G wireless networks [28].

2.2 Role of AI in 6G Wireless Networks

AI and machine learning techniques are most important features in making intelligent 6G networking systems [29]. AI plays a crucial role in 6G network designs and protocols to support mobile internet as well as ubiquitous AI services for the users [30]. Next generation driving use cases (vehicular communication: vehicle-to-everything applications) are AI based which is an emerging field in 6G vehicular networks that demands high reliability, ultra-low latency, high data rates, and high security [31, 32]. To address these use cases, mmWave mMIMO beamforming techniques are essential with beam alignment and beam sweeping capabilities. Also, optimal beam sweeping schemes have to be introduced at Tx and Rx to reduce the latency in achieving beam alignment [33]. AI-powered applications demand 6G wireless technologies and motivates to in-depth research possibilities in terms of coverage, spectrum, energy consumption, air interface, and delay [34]. Applications of 6G wireless networks can get potential benefits with the synergies of quantum computing, machine learning and deep learning techniques [35].

AI based architecture for 6G includes flexible radio access network-slicing, mobile edge caching & content delivery, and automated radio access technology selection [36]. Air-interface designs (integration of communication with radio sensing) in 6G wireless technologies are optimized by AI techniques to meet the latency, reliability and synchronization requirements [37]. AI-enabled 5G and 6G cellular networks deployment provides significant improvements in performance and robustness at lower complexity [38]. AI-based adaptive scheme for 6G IoT networks provides security where IoT devices are connected to mobile networks using different THz and mmWave frequency bands. Extended Kalman filtering in 6G networks can estimate future harvesting power and avoid energy exhaustion [39]. Deep learning-based (using a deep neural network structure) mmWave beam selection in 5G NR by exploiting sub-6 GHz channel information minimizes beam sweeping overhead by 79.3% [40]. Heterogeneous multi-layer mobile edge computing in which MSs generate raw data of computing tasks in radio access networks to cloud centre that involves collaborative data processing at various network layers. It is essential to have ultra-low latency service in 6G networks which is possible by reinforcement learning in pricing scheme design, network congestion control, cognitive radio access, and task offloading for volatile wireless environments [41]. 6G mobile network architecture is expected to operate at THz frequencies with high QoS support and energy efficiency. The architectural challenges of 6G networks include 3D coverage, efficient protocol stack, pervasive AI [42]. AI (deep learning methods) techniques optimize the performance of space-air-ground integrated networks by improving traffic balancing [43]. Hybrid beamforming designs for mMIMO with minimum number of RF chains and phase shifters based analog beamforming designs are challenging with imperfect CSI [44]. “Multitask deep learning” techniques are used in hybrid beamforming for MU-mMIMO OFDM systems [45]. Deep learning based beamforming designs maximizes spectral efficiency with imperfect CSI and less hardware.

2.3 Security Aspects in 5G and 6G Wireless Systems

It is challenging to implement security in 5G and 6G wireless networks as they are deployed in decentralized, heterogeneous, and massive ubiquitous devices. Blockchain technology can provide security and privacy for 5G and 6G networks like edge computing, cloud computing and device-to-device communications [46, 47]. 6G applications scenarios demand for high privacy, secrecy, and security [48]. Physical layer level security techniques are essential at THz frequencies to address threats like eavesdropping which is possible by placing an object and intercept the LOS signal to get scatter radiation in the direction of eavesdropper. However, characterization of backscatter in channel addresses the problem of eavesdrop and also detects eavesdropper [49]. Security can be provided in mmWave mMIMO wireless systems using channel sparsity where the data is precoded onto dominant angle components while artificial noise in broadcasted over non-dominant angles which interfere with eavesdropper’s signals. The entropy of channel sparsity (is unknown to eavesdropper) defines secrecy rate and optimal levels of sparsity provides maximum secrete rate [50].

3 Wave Propagation at THz Frequencies

3.1 Wave Propagation Scenarios (Reflections, Diffraction, Scattering)

The radio signal propagation undergoes through three main propagation mechanisms called reflection, diffraction and scattering in multipath channel as shown in the Fig. 2 [51]. At THz carrier frequencies, signal transmissions are highly directive (less angular divergence) and effects of diffraction is minimum. Adaptation of mMIMO, hybrid beamforming or beam steering techniques overcomes the shadowing effects at mmWave frequencies [52].

Fig. 2
figure 2

Wave propagation in a multipath fading channel

Full size image

Scattering is an important propagation mechanism to consider in channel modelling at THz frequencies for 6G wireless systems. The surface scattering at THz frequencies exhibit both diffuse and strong specular reflections. “Directive scattering” and “radar cross section” scattering models support development of ray tracing tool design, imaging, and localization for 6G wireless systems [53]. Characterization of surface scatterers (for both diffused and specular components) at 60 GHz leads to small-scale fading due to rough surface scatterers. The diffused scattering depends on distance from the surface, angle of incidence, and material roughness [54]. The multipath delay spread and path losses of a radio channel are characterized at frequency range 126–156 GHz [55].

Wavelengths of THz frequencies approach the dimensions of dust, snow particles or rain and effects of Mie scattering becomes more significant contribution to link budget. The rain effects do not contribute to additional attenuation losses at THz frequencies (0.1–0.5 THz) [56]. Atmospheric gases like hydrogen, oxygen, and carbon-di-oxide etc., causes significant attenuation at THz bands (183 GHz, 325 GHz, 450 GHz, 550 GHz, 760 GHz) and these frequency bands can be used for secure ultra-short range communications [57, 58].

3.2 Channel Modelling and Measurements

Channel properties define the performance limits in 6G wireless communication system. So, it is very important to explore different 6G channel models, measurement techniques and develop statistical channel impulse response models both in space and time at THz frequencies [59,60,61]. 3GPP defines human blockage, spatial consistency, and outdoor-to-indoor penetration losses as main components of channel modelling for mmWave mMIMO hybrid beamforming system designs. A geometry-based, spatially consistent channels are realized by generating time-variant and spatially correlated channel coefficients. Human blockage shadowing losses are modelled at 73 GHz using four-state Markov model [62,63,64,65,66]. Radio propagation models or channel models (both large-scale, small-scale fading, also MIMO channels) for mmWave 5G wireless systems are defined with hybrid beamforming and coordinated multi-point transmissions at 24 GHz to 86 GHz frequencies. The performance metrics (coverage, spectral efficiency, hardware requirements) are highly dependent on channel models [67]. mmWave technology provides adaptive tuning in military communication networks as per atmospheric variations and high node mobility without compromise for high data rates [68]. Various channel models and propagation parameters of 5G wireless communication systems such as building penetration losses, large-scale path loss, LOS probabilities helps to understand the propagation of mmWave frequencies over 0.5–100 GHz [69].

In the presence of CSIT, antenna array gains and spatial multiplexing gains are fully utilized in mMIMO systems. But, conventional CSIT techniques do not suit FDD mMIMO systems due to their feedback and training overhead. Three pilot training strategies are proposed for acquiring CSI in MU mMIMO mmWave systems using “generalized block OMP algorithm” that performs better than conventional OMP algorithm [70]. Joint optimization technique of communication and computation powers is formulated for MU mMIMO systems with partially-connected RF structures that saves powers up to 76.59% [71]. “Generalized-block compressed sampling matching pursuit algorithm” offers better performance in acquiring CSI and minimizes errors compared to “generalized block OMP algorithm” [72]. Using a distributed compressive sensing CSIT, feedback and training overhead can be minimized in MU mMIMO hybrid beamforming systems [73].

Requirement of high data rates and bandwidths for smart rail mobility motivates to explore high gain mMIMO, advanced handover designs, and dynamic beamforming techniques at mmWave and THz bands [74]. The communication between passengers and rails as well as intra-wagon scenarios are characterized using ultra-wideband channel sounding and ray tracing at 60–300 GHz frequency bands with 8 GHz of bandwidth [75]. The measured propagation losses of a communication link at 350 GHz frequency estimates the data rates of 1Gbps at 8.5 m and 100Gbps for 1 m distances [76]. Channel models and propagation measurements are presented at D-band (110–170 GHz) frequencies. Channel sounder system is designed for 140 GHz and signal attenuation measurements are investigated for indoor models [77, 78]. The large-scale path loss and multipath time dispersion measurements for ultra-dense indoor wireless networks at mmWave bands show that multipath RMS delay spread can be minimized using more directive antennas [79]. Certain mmWave and THz frequency bands exhibit less path loss (< 10 dB/Km) in addition to free-space path loss values. Therefore, these frequencies can be used for 6G cellular and mobile applications (long-range communications) [80].

THz frequencies exhibit a very high signal attenuation or path loss, however, we can overcome this using ultra-mMIMO antenna arrays which compensate increased path loss and provides highly reliable links. Neighbour discovery is challenging in mMIMO systems at THz bands and this process can be made time-efficient by using the complete antenna radiation pattern instead of only main-lobe [77, 81].

3.3 Channel Measurements at 73 GHz

Indoor wave propagation mechanisms (scattering, reflection, path-loss) and channel properties are studied at mmWave and Terahertz (28 GHz, 73 GHz and 140 GHz) frequencies. At these frequencies, reflection coefficient is linearly increasing with increase in angle of incidence and the scattered power is 20 dB less than the reflected power. Also, for a given angle of incidence, path loss is inversely proportional and partition loss (material dependent) is proportional to frequencies [82]. mmWave multipath signal propagation characteristics for indoor communication were measured in terms of power received, path loss and delay spread at 28 GHz, 39 GHz, 60 GHz, and 73 GHz frequencies. The received power and delay spread are inverse in relation to T–R separation, whereas path loss is proportional to T–R distance. The amount of path loss due to multi-floors is very high at 28–39 GHz compared to 60–73 GHz [83]. Coordinated Multipoint and BS diversity measurements of a large-scale mmWave 5G wireless system at 73 GHz shows the improvements in interference suppression where 43% of users overcome interference [84]. Penetration losses, outdoor foliage induced scattering, and ground reflection measurements are conducted at 73 GHz, 81 GHz with both cross-polarized and co-polarized antenna configurations to provide consistency and reliability in measurements at any given frequency [85,86,87,88].

Beam steering capabilities of directional antenna arrays at mmWave bands can overcome the path loss of a multipath channel in a dense urban cellular environment [89]. Large-scale path loss models based on ultra-wideband mmWave propagation measurements at 28–73 GHz offer simplicity in path loss calculations and predictions with high accuracy. 3GPP floating-intercept path loss model needs a simple modification for converting in to the close-in free space reference distance models [90]. Indoor and outdoor channel measurements at 100 GHz, 200 GHz, 300 GHz, and 400 GHz are carried out for a link data rate of 1Gbps. The multi-path channel measurements proved the feasibility of using THz radio links for data transmissions in a highly fading channel environments [91]. The radiation at THz (0.1–10 THz) bands penetrates through materials (indoor office) with minimum penetration losses and loss increases for higher end of THz band [92].

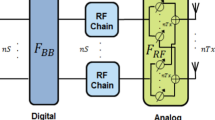
4 Ultra-mMIMO and Hybrid Beamforming Techniques for 6G

mMIMO and ultra-mMIMO are the key enabling technologies in 5G and 6G networks respectively with efficient beam steering capabilities. The important open research challenges in mMIMO system design are channel estimation, pilot contamination, user scheduling, precoding, signal detection, and energy efficiency [93]. The mMIMO and ultra-mMIMO beamforming systems offers huge bandwidths with very high data rates in 5G and 6G cellular mobile systems. They provide maximum antenna array gains by overcoming the high path loss, atmospheric absorption, and rapid channel variations. These designs demand precise alignment of BS and UE beams that increases latency in link establishment, implications of control layer procedures like beam tracking, and handover [94].

6G wireless technologies use ultra-mMIMO antenna arrays and THz frequencies to support AI-infused applications, autonomous driving, IIoT, wireless brain–computer interaction, wireless backhaul, augmented/virtual reality, and holographic applications [95]. Design and development of RF antenna systems for beyond 5G and 6G are very important as the operating frequencies are very high. It is important to focus on breakthrough performance of antenna system with new materials and metamaterials, evolution of propagation channels, and updates in antenna measurement technology [96]. ultra-mMIMO communications can overcome the higher propagation losses at THz bands and increase the communication range. Graphene-based plasmonics allow us to design large antenna array structures within small area (e.g., 144 antenna elements per 1cm2 at 60 GHz, 1024 antenna elements per 1 mm2 at 1 THz) and enables ultra-mMIMO communication in 6G wireless systems [97]. “quantum-inspired social emotional optimization” algorithm achieves optimal power control and QoS in mMIMO UL networks for maximizing spectral efficiency [98]. Accuracy of beam selection, beam pair update delay effects the QoS performance. Best measurement techniques for mobility and beamforming management needs to be followed to have more accuracy in 3GPP NR mmWave systems [99]. In a MU mMIMO systems, low complex solutions are proposed to reduce Tx power based on individual SINR constraints for users less than and greater than the number of RF chains [100]. Low complex inter-user interference reduction algorithms are used in MU mMIMO UL systems to achieve performance close to fully digital beamforming system [101].

To minimize the hardware cost of MU mMIMO systems, “hybrid beamforming with selection” considers instantaneous channel variations using switch bank architecture [102]. Joint user scheduling is proposed for MU mMIMO OFDM systems where users with identical radiation beams are multiplexed using OFDM to improve the system performance [103]. Accuracy of channel estimation in MU mMIMO systems is improved using its continuous representation instead of grid-based as a result there is an improvement in spectral efficiency [104]. A novel hybrid beamforming design is proposed to improve the total sum rate based on “weighed sum mean square error minimization” and “compressed sensing” under perfect CSIT [105]. “Manifold optimization”, “eigenvalue decomposition”, and OMP hybrid beamforming algorithm is proposed for mmWave systems to minimize the computational complexity, mean square error and increase transmission reliability as well as spectral efficiency [106, 107]. Relay assisted MU mMIMO hybrid beamforming mmWave system can overcome the path loss and improves system performance [108]. Splitting of hybrid precoding and combining between Tx and Rx along with OMP algorithm increases the total sum data rates in a MU mMIMO systems [109]. In MU mMIMO hybrid beamforming systems, under imperfect CSI, radiated power of UEs is inversely proportional to square-root of the number of BS antennas whereas with perfect CSI, radiated power is just inversely proportional to number of BS antennas [110]. If the number of BS antennas are minimum, MRC performs better than ZF and as number of BS antennas are increasing, uplink data sum rates for MRC and ZF becomes equal. Total data sum-rate is maximized by minimizing weighted sum MSE (based on block diagonalization in digital beamforming) in DL MU-mMIMO hybrid beamforming systems with perfect CSI. Lower capacity bounds for MRC, ZF and MMSE detection are derived. Generally, ZF and MMSE performs better than MRC Rx due to their ability to cancel intra-cell interference. In multi-cell environment, at lower power levels, cross-talk introduced by inferior MRC falls below the noise level and this Rx becomes a viable option. For example, in a small-scale Rayleigh fading channel, 50 MSs can be served with 100 an antenna array of 100 at BS using same time–frequency resources. Therefore, each MS has 1bits/channel/MS and it leads to a total system throughput of 50bits/channel/MS.

mmWave mMIMO DL hybrid beamforming with geographically distributed cluster antennas over the coverage area (remote antenna arrays) decreases the average distance between UEs and arrays, also provides more spatial diversity. This design has performance same as fully digital beamforming in terms of spectral efficiency per user when the number of RF chains are not less than twice the number of UEs [111]. mmWave mMIMO lens antenna array reduces the number of RF chains considerably in the presence of CSI. “Approximate message passing learned prior-aided Gaussian mixture” beamspace channel estimation algorithm can give more accuracy [112].

4.1 MU-mMIMO Hybrid Beamforming

In a multi-user communication, multiple users share the same channel, therefore communication needs to be coordinated in T–F domains. In MIMO systems, the Tx power is divided and provide both diversity gain as well as antenna array gain. MIMO beamforming improves spectral efficiency and coverage is high in a particular direction. Hybrid beamforming can be categorized depends on average or instantaneous CSI where instantaneous CSI provides better SNIR and average CSI gives lower overhead in CSI acquisition. Therefore, algorithm selection to get best trade-off essentially depends on channel characteristics [113]. CSI availability at Rx (CSIR) is collected using pilot signals and CSI at Tx (CSIT) is collected using feedback channels from Rx to Tx. If we have CSIT, the Tx signal can be precoded to provide diversity gain at the Rx, on the other hand if we have CSIR then it is possible to provide diversity using “space–time coding”. MU-MIMO provides all-to-all communication (between K-access points and K-UEs where each UE has multiple independent data streams) and facilitates higher spectral efficiency (over mMIMO) using an interference cancellation beamforming algorithm. Shannon’s limit for channel capacity is defined with K > 3 under Rayleigh fading channel conditions and defined the upper limit for MIMO antenna array size to have an optimum throughput and overhead [114]. Coordinated multipoint techniques in a multi-cell MU-mMIMO hybrid beamforming system can mitigate intra-cell and inter-cell interference, also achieves high spectral efficiency by maximizing signal-to-leakage-plus-noise ratio [115].

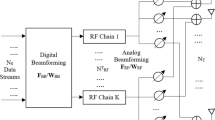
Data processing steps in a MU mMIMO systems are shown in Fig. 3 where the source encoded user’s data symbols are encoded (channel encoding) using convolutional codes at the Tx. The channel encoded bit stream is mapped to QAM symbols and the resultant QAM data of every user is split into multiple independent data streams. Precoding weights (computed using HBPS algorithm) are assigned for each subcarrier of independent data stream at Tx. The same precoding weights are used to derive the corresponding combining weights at Rx. HBPS algorithm provides all digital beamforming weights and recognize peaks to form corresponding analog beamforming weights. The digital precoded signal is modulated using OFDM with pilot mapping followed by analog beamforming process at Tx antennas. The transmitted signal travels through a scatter rich MIMO channel and this signal is demodulated, and decoded at Rx. Channel sounding and estimations processes are performed using JSDM algorithm that permits large scale MIMO antenna arrays at BS with less CSI feedback information from UEs of a mMIMO DL channel.

Fig. 3
figure 3

Data processing steps in a MU-mMIMO hybrid beamforming system

Full size image

4.2 Wideband mMIMO-OFDM Systems

OFDM technique eliminates ISI by distributing high-rate user’s data across many number of narrowband sub-channels (those are closely spaced) to provide reliable broadband communication. When the bandwidth is sufficiently large, the channel between any Tx antenna and Rx antenna will appear dispersive. Because of this, we can combine MIMO with OFDM for frequency selective channels as shown in Fig. 4. We can perform this by connecting OFDM Tx to each transmitting antenna and OFDM Rx to each receiving antenna, and process the signals across different antennas.

Fig. 4
figure 4

mMIMO-OFDM system

Full size image

Using MIMO-OFDM, we can convert wideband mMIMO channel into many parallel narrow band MIMO channels. All practical mMIMO systems operate in a wideband region, therefore, mMIMO can be combined with OFDM for frequency selective channels. The combination of MU mMIMO-OFDM gives extremely high spectral efficiencies even in the absence of CSIT. In the presences of CSIT, channel capacity of MU mMIMO-OFDM systems approach the theoretical limits and these systems are essential for beyond 5G wireless communications.

4.3 Channel Modelling in MU-ultra-mMIMO Systems

The mMIMO channel can be characterized as

$${\mathbf{y}} = {\mathbf{HX}} + {\mathbf{n}}$$
(1)

The channel matrix, \({\mathbf{H}} = \left[ {\begin{array}{*{20}l} {h_{11} } \hfill & {h_{12} } \hfill & \ldots \hfill & {h_{{1{\text{Mt}}}} } \hfill \\ {h_{21} } \hfill & {h_{22} } \hfill & \ldots \hfill & {h_{{2{\text{Mt}}}} } \hfill \\ \ldots \hfill & \ldots \hfill & \ldots \hfill & {h_{{3{\text{Mt}}}} } \hfill \\ {h_{{{\text{Mr}}1}} } \hfill & {h_{{{\text{Mr}}2}} } \hfill & \ldots \hfill & {h_{{{\text{MrMt}}}} } \hfill \\ \end{array} } \right]\).where hij is a gaussian complex random variable which models fading gain between jth Rx antenna and ith Tx antenna.

For any given subcarrier ‘k’, the vector observation is given as,

$${\mathbf{z}}_{k} = {\mathbf{H}}_{k} {\mathbf{X}}_{k} + {\mathbf{n}}_{k}$$
(2)

where y → Rx column vector of size Mr × 1, H → channel matrix of size Mr × Mt, X → Tx column vector of size Mt × 1, n → AWGN noise column vector of size Mr × 1, zk → observation vector of size Mr × 1.

High accurate and low complex channel estimation scheme called “Step-length optimization-based joint iterative scheme” is developed for MU mMIMO system that uses less number of training sequences even for large number of users [116]. Hybrid channel estimation is proposed where the channel matrix is decomposed into an angle matrix and gain matrix. This technique improves channel estimation accuracy with minimum training overhead in a MU mMIMO hybrid beamforming systems [117]. Lens antennas array based MIMO needs less number of RF chains as it exploits the property of angle-dependant energy focus. “Path delay compensation” techniques that exploits multi-path sparsity converts MU MIMO channels that are frequency selective into parallel narrow-band flat fading channels [118]. Optimizing hybrid beamforming design of relay system with full-connected and mixed structures maximizes the sum rate in a mMIMO systems [119].

The changes in angles of arrival/departure (AoAs/AoDs) are less compared to their path gains in a MU mMIMO systems. MSE minimization of received signal using the solution of digital beamforming gives maximum sum rates in a mmWave hybrid beamforming system. The sum rate increases with number of paths (accuracy of AoA/AoD) and number of RF chains [120]. The estimation of AoA/AoD helps in pilot beamforming and maximizes it power to achieve accurate path gains [121].

4.4 Channel Estimation in MU-ultra-mMIMO Systems

Estimation of more channel coefficients in a MU-mMIMO systems and high propagation loss in mmWave transmission give a challenge in channel estimation for DL. The BS antenna array uses imperfect CSI that is derived using transmitted pilots signals to extract individual data streams. The radiated power of MSs is inversely proportional to square-root of number of BS antennas with no reduction in performance. If perfect CSI is available, transmitted power at MSs can be made inversely proportional to number of BS antennas. For complete utilization of spatial multiplexing gains (or antenna array gains) of mMIMO, CSI must be obtained at the Tx side.

Joint design of digital and analog stages overcomes loss of information at each stage and this gives optimal solution for MU-mMIMO hybrid beamforming system whose sum rate approaches channel capacity [122]. The users are grouped into clusters based on feedback and CQI of beams in a mmWave MU mMIMO DL NOMA system which offers maximum sum rates [123]. Angular representation of channel using non-zero sparse matrix to form clusters in a MU-mMIMO systems better than the system without clusters [124]. “compressive sensing” techniques reduce the channel measurement complexity and configure hybrid precoders & combiners in a mmWave MU MIMO system with frequency selective channels [125]. Usage of “penalty dual decomposition” method in hybrid precoding approaches the fully digital precoding performance even in the presence of less number of RF chains at Tx and Rx [126].

Diagonalization of channel matrix provides unconstrained optimal precoding weights by taking the first NTRF dominating modes under known CSI conditions. Most of the time, CSI is at Rx (CSIR) is acquired using pilot signals which carry channel estimation information. Sometimes, using feedback channels from Rx to Tx we can also collect CSI at Tx (CSIT). If we have CSIR, we can provide diversity gain using “space–time coding”, on the other hand, if CSIT is available, we can precode the transmitting signal to provide diversity gain at the Rx. Under the availability of CSI at BS, MU precoding is performed to transmit signals to all users using same T–F resources and UEs can recover signals with minimum complexity [127].

Design of two stage beamformers for FDD MU mMIMO DL hybrid beamforming systems optimizes hybrid precoding to increase sum rates and conditional average signal-to-leakage-plus-noise ratio [128]. Optimal hybrid precoding and combining algorithms based on the principle of basis pursuit demands only low cost RF hardware in mmWave mMIMO systems [129]. Performance of iterative hybrid precoding approaches the capacity of fully digital precoding scheme [130]. “Hybrid regularized channel diagonalization” based hybrid beamforming design uses low-complex non-iterative process in a MU-mMIMO DL mmWave channel [131]. A low-complex hybrid precoding scheme called phased-ZF can approach the performance of full-complexity baseband ZF precoding in a mMIMO systems [132].

Closed-form expressions are defined to configure mobility-aware hybrid precoder for high-speed mobile users in mmWave mMIMO systems with reduced computational complexity. The number of RF chains can be activated adaptively based on channel conditions to maximize energy efficiency and beamforming gains at high SNRs [133]. Transform domain precoder is designed for a mmWave mMIMO hybrid beamforming system that reduces 60–89% of overhead and enhances 2.38–21% of spectral efficiency [134]. Fixed phase shifter implementation in mmWave hybrid precoding is hardware-efficient as it needs only less number of phase shifters with fixed and quantized phase values. A switch network (group-connected mapping) between phase shifters and antennas provides dynamic connections according to channel conditions. This setup maximizes the spectral efficiency with minimum hardware complexity [135].

4.5 CSIR Detection Algorithms in MU-ultra-mMIMO Systems

Lower capacity bounds for MRC, ZF and MMSE detection are derived. ZF and MMSE performs better than MRC Rx due to their ability to cancel intra-cell interference. In multi-cell environment, at lower power levels, cross-talk introduced by inferior MRC falls below the noise level and this Rx becomes a viable option. For example, in a small-scale Rayleigh fading channel, 50 MSs can be served with an antenna array of 100 at BS using same T–F resources. Therefore, each MS has 1bits/channel/MS and it leads to a total system throughput of 50bits/channel/MS. In this case, Tx does not know the channel instead only Rx is assumed to know the channel. Therefore, Tx sense the vector x QAM symbols, and Rx observes y. Here, the objective is to recover x from y as \({\mathbf{y}} = {\mathbf{Hx}} + {\mathbf{n}}\).

4.5.1 ML Detector

It is an optimal detector in terms of error probability in the presence of IID gaussian noise at the Rx. We can find the best possible x by maximizing likelihood from all possible likelihoods as

$${\text{Estimate}}\,{\text{of}}\,{\mathbf{x}} = \arg \,\max \left[ {{\text{p}}\left( {{{\mathbf{y}} \mathord{\left/ {\vphantom {{\mathbf{y}} {{\mathbf{X}},\,{\mathbf{H}}}}} \right. \kern-\nulldelimiterspace} {{\mathbf{X}},\,{\mathbf{H}}}}} \right)} \right]\,{\text{for}}\,{\text{all}}\,{\mathbf{x}}$$
(3)

Since the noise is gaussian, the estimation of x is equal to minimum of Euclidean distance between the observation y and HX for all possible x.

$${\text{Estimate}}\,{\text{of}}\,{\mathbf{x}} = \arg \,\min \left[ {\left\| {{\mathbf{y}} - {\mathbf{HX}}} \right\|^{2} } \right]\,{\text{for}}\,{\text{all}}\,{\mathbf{x}}$$
(4)

However, the complexity of ML detector increases exponentially with number of Tx antennas, Mt.

4.5.2 ZF Detector

ZF equalizer uses inverse of channel frequency response to restore the signal at the Rx and it gives zero ISI in a noise free channel conditions. We can achieve flat fading by combining channel frequency response with ZF equalizer frequency response. This equalizer is essential when ISI is dominating the noise. For mMIMO systems, it is used when Mr ≥ Mt, and there exists at least ‘Mt’ linearly independent columns in channel matrix, H. It has lower complexity than ML detector. ZF detector equalizer is given as,

$${\mathbf{z}} = \left( {{\mathbf{H}}^{{\text{H}}} {\mathbf{H}}} \right)^{ - 1} {\mathbf{H}}^{{\text{H}}} {\mathbf{y}} = {\mathbf{x}} + {\mathbf{w}}$$
(5)

where \(\left( {{\mathbf{H}}^{{\text{H}}} {\mathbf{H}}} \right)^{ - 1} {\mathbf{H}}^{{\text{H}}}\) is a pseudo inverse.

If HHH is a singular matrix, then the noise enhancement w is very high. We can perform element by element detection as z1 = x1 + w1, z2 = x2 + w2, etc., ZF equalizer can provide higher data rate gains at the cost of diversity gain. However, the challenge in ZR detector is that it needs infinitely long impulse response and also, it can amplify the noise if minimum singular value of channel matrix is too small.

4.5.3 MMSE Equalizer

In MMSE equalizer, we do not exactly recover x instead its approximation, and w noise enhancement value less. MMSE relies on Gaussian model of x. In order to avoid the noise enhancements (w), there is a trade-off achieved by MMSE equalizer. MMSE estimate of the transformed symbols x (where x is assumed to be Gaussian) is

$${\mathbf{z}} = \left( {{{{\mathbf{H}}^{{\text{H}}} {\mathbf{H}} + {\mathbf{I}}_{{{\text{Mt}}}} } \mathord{\left/ {\vphantom {{{\mathbf{H}}^{{\text{H}}} {\mathbf{H}} + {\mathbf{I}}_{{{\text{Mt}}}} } \rho }} \right. \kern-\nulldelimiterspace} \rho }} \right)^{ - 1} {\mathbf{H}}^{{\text{H}}} {\mathbf{y}} \approx {\mathbf{x}} + {\mathbf{w}}$$
(6)

where IMt/ρ is a regularization term that depends on SNR, ρ.

If SNR is too high and approaches ‘∞’ or noise approaches zero, then MMSE approaches ZF detector. In MU-mMIMO systems, favorable propagation conditions in NLOS relies on orthogonal columns of UL channel matrix \({\mathbf{H}}^{{\text{H}}} {\mathbf{H}} \approx {\text{M}}{\mathbf{I}}_{{\text{K}}}\), rayleigh fading entries from CN (0,1), and scaling of off-diagonal elements. The condition for LOS orthogonality is given as,

$$\left| {{\text{h}}^{{\text{H}}} {\text{kh}}_{1} } \right|^{2} = \left| {{\text{g}}^{ * } \,_{{\text{k}}} {\text{g}}_{1} } \right|^{2} \left| {\left\| {\sum\limits_{m = 0}^{M - 1} {\exp \left( {{\text{j}}\pi {\text{m}}\left( {\sin \theta_{1} - \sin \theta_{{\text{k}}} } \right)} \right)} } \right.} \right|^{2} \approx 0,\,\Delta_{{{\text{lk}}}} > {2 \mathord{\left/ {\vphantom {2 {\text{M}}}} \right. \kern-\nulldelimiterspace} {\text{M}}}$$
(7)

4.6 CSIT Detection Algorithms in MU-ultra-mMIMO Systems

FDD mode of channel estimation utilizes different spectrum for UL and DL. In FDD mode, the channel estimation time is proportional to number of antennas and makes the time overhead prohibitively expensive for mMIMO systems. Therefore, we have assumed the channel estimation by reciprocity, so the channel is operated in TDD mode where the same spectrum is used for both UL and DL. UL represents a “standard MIMO” communication system, so we can apply standard detection MIMO detection techniques like ZF, MMSE, maximum likelihood etc., For UL, no CSIT is needed at the users (Txs) for BS to recover the data and processing can occur in one coherence interval. UL can be trained using (Bc*Tc) samples with a fixed channel where Bc is coherence bandwidth, Tc is coherence time. If we use a fraction a for pilots, then the rate (1 − a) x maximum rate. We want to have full spatial reuse, so some users will have same pilot. If any two users have same pilot,

$$\overline{h}_{k} = {\mathbf{h}}_{{\text{k}}} + {\mathbf{h}}_{{\text{l}}} + {\mathbf{w}}_{{\text{k}}}$$
(8)

w is noise that depends on length of pilot or power.

Leads to wrong precoder, loss in rate: SINR in UL and DL are interference-limited which is called “pilot contamination”.

4.6.1 Parallel Decomposition

As shown in Fig. 5, any given complex Mr x Mt matrix can be expressed as \({\mathbf{H}} = {\mathbf{U}}\Sigma {\mathbf{V}}^{{\text{H}}}\).where U → unitary matrix of size Mr x Mt, Σ → Diagonal matrix of size Mr x Mt and rank RH ≤ min(Mr, Mt), V → unitary matrix of size Mt x Mt.

Fig. 5
figure 5

Parallel decomposition using SVD

Full size image

RH = min (Mr, Mt) in a rich scattering environment like Rayleigh fading environment, the value of RH is typically small in a LOS channel.

The estimated symbols,

$$\begin{array}{*{20}l} {{\mathbf{y}}^{1} = {\mathbf{U}}^{{\text{H}}} {\mathbf{HV}}{\text{x}}^{1} + {\mathbf{n}}} \hfill \\ {\,\,\,\,\,\, = {\mathbf{U}}^{{\text{H}}} {\mathbf{U}}\Sigma {\mathbf{HV}}^{{\text{H}}} {\mathbf{V}}{\text{x}}^{1} + {\mathbf{n}}\,{\text{as}}\,{\mathbf{U}}^{{\text{H}}} {\mathbf{U}} = {\mathbf{V}}^{{\text{H}}} {\mathbf{V = I}}} \hfill \\ {\,\,\,\,\,\, = {\mathbf{x}}^{1} + {\mathbf{n}}} \hfill \\ \end{array}$$
(9)

where, xl → data symbols, x → transformed symbols, y → received symbols.

It creates RH parallel channels out of which no data is transmitted on Mt–RH channels. It can be combined with rate and power adaption. This is a simple detector and not affected by noise.

4.7 Capacity of MU-ultra-mMIMO Beamforming Channel

In a MIMO system, transmitting one symbol over all Mt antennas leads to high diversity but with low rate. But, in a mMIMO system with beamforming as shown in Fig. 6 gives both diversity gain as well as higher data rates. The received symbols in such systems is given as

$$y = {\mathbf{U}}^{{\text{H}}} {\mathbf{HV}}_{{\text{x}}} + {\text{n}}$$
(10)

where x, y, n are scalars and select U and V along largest singular value.

Fig. 6
figure 6

mMIMO channel with beamforming

Full size image

The narrowband MIMO channel can be represented as,

$${\text{y}} = {\mathbf{Hx}} + {\mathbf{n}}$$
(11)

where \({\text{E}}\left\{ {{\mathbf{xx}}^{{\text{H}}} } \right\} = {\mathbf{R}}_{{\text{x}}} ,\) Rx → input covariance matrix and RxT = ρ.

\({\text{E}}\left\{ {{\mathbf{nn}}^{{\text{H}}} } \right\} = {\mathbf{I}}_{{{\text{Mr}}}}\) where n is zero mean gaussian noise.

The channel matrix, H can be represented as \({\mathbf{H}} = {\mathbf{U}}\Sigma {\mathbf{V}}^{{\text{H}}} \,{\text{with}}\,\Sigma = {\text{diag}}\left( {\sigma_{1}^{2} ,\,\sigma_{2}^{2} ,\, \ldots \sigma_{{{\text{RH}}}}^{2} ,\,0,\, \ldots 0} \right)\).

Channel capacity for fixed channel,

$${\text{C}} = \max \left\{ {{\text{B}}\log_{2} \det \left[ {{\mathbf{I}}_{{{\text{Mr}}}} + {\mathbf{HR}}_{{\text{x}}} {\mathbf{H}}^{{\text{H}}} } \right]} \right\}\,{\text{for}}\,{\text{all}}\,{\mathbf{R}}_{x} = {\mathbf{R}}_{x}^{T} = \rho$$
(12)

The above equation maximizes overall possible covariance matrices that satisfy the total energy constraint. If the channel is unknown at the Tx (no CSIT), then the total energy is spread among all Mt Tx antennas, therefore \({\mathbf{R}}_{{\text{x}}} = \left[ {{\rho \mathord{\left/ {\vphantom {\rho {{\text{Mt}}}}} \right. \kern-\nulldelimiterspace} {{\text{Mt}}}}} \right]{\mathbf{I}}_{{{\text{Mt}}}}\).

Channel capacity,

$${\text{C}} = {\text{B}}\sum\limits_{{{\text{i}} = 1}}^{{{\text{RH}}}} {\log_{2} \left( {{{1 + \left( {\rho \sigma_{i}^{2} } \right)} \mathord{\left/ {\vphantom {{1 + \left( {\rho \sigma_{i}^{2} } \right)} {{\text{M}}_{{\text{t}}} }}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{{\text{t}}} }}} \right)}$$
(13)

On the other hand, if CSIT is available, we can do more sophisticated detection using SVD and exploit power allocation.

Channel capacity,

$${\text{C}} = \sum\limits_{{{\text{i}} = 1}}^{{{\text{RH}}}} {{\text{B}}\log_{2} \left( {1 + \left( {\rho_{{\text{i}}} \sigma_{{\text{i}}}^{2} } \right)} \right)} \,{\text{for}}\,{\text{all}}\,\rho_{{\text{i}}} :\sum\limits_{{{\text{i}} = 1}} {\rho_{{\text{i}}} \le \rho }$$
(14)

In MU-mMIMO systems users are always orthogonal and favourable propagation conditions in LOS relies on geometry of the array and far field conditions. If ‘M’ antenna elements spaced at d = λ/2 and incoming signal from angle ‘θ’, then the path difference \(\delta = {\text{d}}\sin \left( \theta \right)\). Therefore, the received passband signals are given as follows:

$${\text{r}}_{0} \left( {\text{t}} \right) = {\text{Re}} \left\{ {{\text{As}}\left( {{\text{t}} - \tau } \right)\exp \left( {{\text{j}}2\pi {\text{f}}_{{\text{c}}} \left( {{\text{t}} - \tau } \right)} \right)} \right\} = {\text{Re}} \left\{ {{\text{gs}}\left( {\text{t}} \right)\exp \left( {{\text{j}}2\pi {\text{f}}_{{\text{c}}} {\text{t}}} \right)} \right\}$$
$${\text{r}}_{1} \left( {\text{t}} \right) = {\text{Re}} \left\{ {{\text{gs}}\left( {{\text{t}} - {\delta \mathord{\left/ {\vphantom {\delta {\text{c}}}} \right. \kern-\nulldelimiterspace} {\text{c}}}} \right)\exp \left( {{\text{j}}2\pi {\text{f}}_{{\text{c}}} \left( {{\text{t}} - {\delta \mathord{\left/ {\vphantom {\delta {\text{c}}}} \right. \kern-\nulldelimiterspace} {\text{c}}}} \right)} \right)} \right\} = {\text{Re}} \left\{ {{\text{g}}_{{\text{s}}} \left( {\text{t}} \right)\exp \left( {{\text{j}}2\pi {\text{f}}_{{\text{c}}} {\text{t}}} \right)\exp \left( { - j2\pi {\text{f}}_{{\text{c}}} {\delta \mathord{\left/ {\vphantom {\delta {\text{c}}}} \right. \kern-\nulldelimiterspace} {\text{c}}}} \right)} \right\}$$

and the corresponding received baseband signals:

$${\text{y}}_{{\text{m}}} \left( {\text{t}} \right) = {\text{gs}}\left( {\text{t}} \right)\exp \left( {{{ - {\text{j}}2\pi \delta {\text{m}}} \mathord{\left/ {\vphantom {{ - {\text{j}}2\pi \delta {\text{m}}} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} \right),\,{\text{m}} = 0,\, \ldots {\text{M}} - 1\,{\text{and}}\,{\mathbf{y}} = {\mathbf{h}}{\text{s}} + {\mathbf{n}}$$
(15)

Channel (with gk being a complex number, same for all antenna elements)

$${\text{h}}_{{\text{k}}} = {\text{g}}_{{\text{k}}} \left[ {1\exp^{{{{ - {\text{j}}2\pi {\text{d}}\sin \left( {\theta {\text{k}}} \right)} \mathord{\left/ {\vphantom {{ - {\text{j}}2\pi {\text{d}}\sin \left( {\theta {\text{k}}} \right)} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \exp^{{{{ - {\text{j}}4\pi {\text{d}}\sin \left( {\theta {\text{k}}} \right)} \mathord{\left/ {\vphantom {{ - {\text{j}}4\pi {\text{d}}\sin \left( {\theta {\text{k}}} \right)} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \exp^{{{{ - {\text{j}}2\left( {{\text{M}} - 1} \right)\pi {\text{d}}\sin \left( {\theta {\text{k}}} \right)} \mathord{\left/ {\vphantom {{ - {\text{j}}2\left( {{\text{M}} - 1} \right)\pi {\text{d}}\sin \left( {\theta {\text{k}}} \right)} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} } \right]\theta_{1} \ne \theta_{{\text{k}}} \to {\text{h}}_{{\text{k}}}^{{\text{H}}} {\text{h}}_{1} \approx 0$$

This allows beamforming in specific directions (d = λ/2).

5 Results and Discussions

3GPP recommends 28 GHz, 73 GHz, and 140 GHz frequency bands for future MU-ultra-mMIMO mmWave and THz wireless communication systems [136, 137]. Therefore, system performance is verified at these frequencies using the simulation parameters shown in Tables 2 and 3 for a maximum of 256 × 16 MIMO order with 4 users and 8 users. At the BS, rectangular antennas array is used of size 256 (64 rows and 4 columns) is connected with 4-RF chains and at MS, 16-element (4 rows and 4 columns) square array antenna is used with 4-RF chains. With this design, every antenna element is connected to four phase shifters and radiation patterns of antenna arrays becomes isotropic with linear or rectangular geometry. In order to have peak spectral efficiencies, independent channels are assigned for each user and independent data streams are transmitted through each RF chain that leads to maximum of four data streams per user. The channel between UEs and BS is modeled as well as validated through “scattering-based MIMO spatial channel with single-bounce ray tracing” model. This model assumes the randomly placed scatters and presence of UEs at various T–R spatial locations. The MSs of each user is modeled by compensating thermal noise and path loss. Common channel is used for path loss modelling for both LOS, non-LOS scenarios, data transmissions as well as for channel sounding. The periodic updates of channel matrix at regular intervals are essential to mimic the channel variations.

Table 2 System parameters for MU-ultra-mMIMO hybrid beamforming system
Full size table
Table 3 Configure OFDM system parameters
Full size table

From Table 4, it is very clear that the RMS EVM values are minimum when the number of independent data streams per user are high. However, for user 1 (who has four data streams which is maximum), error values are increasing with increasing mMIMO system configurations from 64 × 16 to 256 × 16. When the number of independent data streams per user are minimum (1data stream/user, 2data stream/user), the error values are higher at lower configurations of mMIMO size, however, the RMS EVM values are reducing at higher mMIMO size configurations. From the above simulation results, we can conclude that 256 × 8, 128 × 16, and 64 × 16 mMIMO configurations are optimum for 4-user mMIMO hybrid beamforming systems when the number of independent data streams per user are 2, 4, and 4 respectively.

Table 4 RMS EVM values in an ultra-mMIMO systems for different QAM schemes at 140 GHz frequencies for four Users with multiple data streams per user
Full size table

From Table 5, the optimum RMS EVM values are achieved for 256 × 16 mMIMO antenna configurations where users maintain 4 independent data streams/user, and error values are highest for 64 × 4 mMIMO configuration with one independent data stream/user. For a given BS antenna arrays and modulation scheme, it is clear that RMS EVM values are decreasing when the users maintain higher number of independent data streams. For the given modulation scheme, the increasing size of BS antenna array leads to decrease in RMS EVM values. However, there are a few cases where there is a little increase RMS EVM values for increasing BS antenna array size. For users 3, 4, and 7 there is little increase in EVM values when the BS antennas are increased from 128 to 256. For user 5 there is a significant increase in EVM values when the BS antennas are increased from 64 to 256. If the user data has divided into multiple number of independent parallel data streams, then it needs less number of active antenna elements to transmit signals. Therefore, it gives trade-off between multiple independent data streams per user and size of T–R antenna arrays.

Table 5 RMS EVM values in an ultra-mMIMO systems for different QAM schemes at 140 GHz frequencies for eight users with multiple data streams per user
Full size table

5.1 Performance of MU-mMIMO Systems for Four Users

Figures 7 and 8 represent the performance in terms of RMS EVM values in a MU-mMIMO hybrid beamforming system for four users at 140 GHz and compared with performance at 28 GHz, 73 GHz (Dilli R). Users 1,2,3, and 4 transmit their data using 4, 1, 2, and 1 number of independent data streams respectively. From the Figs. 7 and 8, it is observed that RMS EVM values are minimum for users 1 and 3 as they maintain more number of data streams for transmission. Interestingly, for user 4, the error values are lowest at 140 GHz as compared to 28 GHz, and 73 GHz frequencies. It justifies the use of THz frequencies and higher order modulation schemes to achieve higher bandwidths, data rates and spectral efficiencies. For user 3 that maintain two independent data streams, the error values are minimum at 73 GHz and it motivates to study the performance of MU-mMIMO hybrid beamforming at these frequencies. For user 1 which has highest number of data streams, the error values are slightly increasing at 140 GHz compared to 73 GHz, and 28 GHz frequency bands, however the errors are within the acceptable limits. Also for a given order of QAM modulation scheme and carrier frequencies that are considered in this paper, the error values are slightly increasing even at higher order mMIMO antenna array configurations for the users who maintain large number of independent data streams and it needs more explorations to minimize the errors in spite that they are within limits.

Fig. 7
figure 7

Representation of RMS EVM values using 256-QAM scheme with 64 BS Antennas for four users at 28 GHz, 73 GHz, and 140 GHz frequencies

Full size image
Fig. 8
figure 8

Representation of RMS EVM values using 256-QAM scheme with multiple BS Antennas for four users at 28 GHz, 73 GHz, and 140 GHz frequencies

Full size image

The signal 3D-radiation patterns in MU-mMIMO hybrid beamforming systems with multiple BS antennas array sizes for 4 users are shown in Fig. 9. The stronger lobes represent distinct data streams of users and these lobes indicate the spread achieved by hybrid beamforming. From the Fig. 9, the observation is that radiation beams are becoming more focused for increasing antennas array size at BS and MS that enhances the reliability of signal reception there by throughput.

Fig. 9
figure 9

Signal 3D-Radiation pattern of 256-QAM with multiple BS Antennas for four users at 140 GHz

Full size image

Figures 10 and 11 represent the equalized symbol constellation per data stream with various combinations of QAM modulation schemes and antennas array sizes for 4 users. From the received symbol constellation diagrams of all combinations shown, it is evident that the users with minimum number of independent data streams have higher variance in recovered symbols because of dominant modes are not present in channel and it leads to poor SNR. For the users with multiple data streams, variance of recovered data streams is very minimum as the symbol points are located with minimum dispersion in symbol constellation diagram. Fact is that the data streams use most dominant mode of scattering MIMO channel have maximum SNR values. On the other hand, symbol points in constellation diagrams of users with single data stream are highly dispersed and they have minimum SNR values.

Fig. 10
figure 10

Equalized symbol constellation per data stream of 16-QAM with 64 BS Antennas for four users at 140 GHz

Full size image
Fig. 11
figure 11

Equalized symbol constellation per data stream of 16-QAM with multiple BS Antennas for four users at 140 GHz

Full size image

5.2 Performance of MU-mMIMO systems for Eight Users

Figures 12 and 13 represent the performance in terms of RMS EVM values in a MU-mMIMO hybrid beamforming system for eight users at 140 GHz and compared with performance at 28 GHz, 73 GHz (Dilli R et al.,). Users 1,2,3, 4, 5, 6, 7, and 8 transmit their data using 4, 1, 3, 1, 2, 1, 3, and 1 number of independent data streams respectively. From the Figs. 12 and 13, it is observed that RMS EVM values are minimum for users 1, 3, 5, and 7 as they maintain higher number of data streams for transmission. Interestingly, for user 1, the error values are lowest at all the frequencies as it maintains four independent data streams and the errors are further reduced at 140 GHz as compared to 28 GHz, and 73 GHz frequencies. Users who maintain three or two number of data streams have minimum errors in data transmissions at 140 GHz compared to 28GH, and 73 GHz. It justifies the use of THz frequencies and higher order modulation schemes to achieve higher bandwidths, data rates and spectral efficiencies. User 2 that maintains only one data stream has highest errors in transmission, however the alternate users who have same number of independent data streams leads to lower error values. The common observation is that alternate users with same number of independent data streams undergoes through higher transmission errors. From the overall results at 140 GHz comparing with mmWave frequencies of 28 GHz, and 73 GHz strongly recommends to explore and use the frequencies beyond 100 GHz for next-generation wireless systems.

Fig. 12
figure 12

Representation of RMS EVM values using 256-QAM scheme with 64 BS Antennas for eight users

Full size image
Fig. 13
figure 13

Representation of RMS EVM values using 256-QAM scheme with multiple BS Antennas for eight users

Full size image

The signal 3D-radiation patterns in MU-mMIMO hybrid beamforming systems with multiple BS antennas array sizes for 8 users are shown in Fig. 14. The stronger lobes represent distinct data streams of users and these radiation lobes indicate the spread achieved due to hybrid beamforming. From the Fig. 14, the observation is that radiation beams are becoming more focused for increasing antennas array size at BS and MS which leads to increase in signal reliability there by throughput.

Fig. 14
figure 14

Signal 3D-Radiation pattern of 256-QAM scheme with multiple BS Antennas for eight users at 140 GHz

Full size image

Figures 15 and 16 represent the equalized symbol constellation per data stream with various combinations of QAM modulation schemes and antennas array sizes for 8 users mMIMO hybrid beamforming system. From the received symbol constellation diagrams of all combinations shown, it is evident that the variance of recovered data streams is minimum for the users with more number of independent data streams as symbol points are located with less dispersion in symbol constellation diagram. Fact is that the data streams use most dominant mode of scattering MIMO channel have maximum SNR values. But, the users with only one independent data stream have highly dispersed received symbols and it is very difficult to estimate the actual transmitted symbols. This higher variance in the received symbols is due to the fact that the absence of dominant modes in channel leads to poor SNR. However, the dispersion is very much reduced with increasing size of antenna arrays at BS and MS as shown in Figs. 15 and 16. Therefore, it is essential to use higher order antenna arrays to achieve higher spectral efficiency.

Fig. 15
figure 15

Equalized symbol constellation per data stream of 16-QAM with 64 BS Antennas for eight users at 140 GHz

Full size image
Fig. 16
figure 16

Equalized symbol constellation per data stream of 16-QAM with multiple BS Antennas for eight users at 140 GHz

Full size image

6 Conclusions and Future scope

In this paper, MU-ultra-mMIMO hybrid beamforming system is designed for THz frequencies with many independent data streams per user. Rigorous analysis is performed with different QAM modulation orders as well as antenna array configurations at Tx and Rx. The results of MU-ultra-mMIMO hybrid beamforming system at THz and mmWave frequencies [136] are compared to prove the feasibility of using THz frequencies for next-generation wireless communication systems. For a 4-user mMIMO hybrid beamforming systems, it is suggested to use 256 × 8, 128 × 16, and 64 × 16 mMIMO system configurations where the number of independent data streams per user are 2,4, and 4 respectively. At the same time, for 8-user mMIMO hybrid beamforming systems, it is suggested to use 256 × 16 mMIMO antenna array configurations where users maintain four independent data streams/user. In both four-user mMIMO and eight-user mMIMO hybrid beamforming, if the user has only one independent data stream then it is essential to have higher order mMIMO antenna arrays at BS and MS in which case 256 × 4 mMIMO configuration is suitable. From the overall results of research work carried at 140 GHz, the main observation is that for users with less number of independent data streams, their RMS EVM values are higher whereas for users with more number of independent data streams, the RMS EVM values are minimum. Therefore, it is strongly recommended to maintain higher number of independent data streams per user to minimize the RMS EVM values and achieve higher order throughputs. However, hybrid beamforming designs with an objective of minimizing RMS EVM values for users with single (or less) number of independent data streams and achieve higher throughput needs to be carried out as a future research direction. Future work also includes performance analysis of the proposed MU-mMIMO hybrid beamforming system for ultra-mMIMO antenna array configurations of order 1024 × 1024 at 0.2THz, 0.34THz, and 0.4THz frequency bands as the atmospheric absorption loss beyond Frii’s free space path loss of the signal is minimum.