Performance Evaluation of NL-BMD Precoding over Analog-Digital Hybrid Beamforming for High SHF Wide-Band Massive MIMO in 5G

Abstract

Massive multiple-input multiple-output (MIMO) technology is a key enabler in 5G. A configuration combining analog beamforming and digital MIMO signal processing for multi-beam multiplexing, i.e. analog-digital hybrid beamforming, is one of the promising approaches of massive MIMO. With the configuration, we can mitigate the problems of complexity and power consumption, which are serious in higher super high frequency and extremely high frequency bands. In this paper, we evaluate the performance of nonlinear block multi-diagonalization (NL-BMD) precoding, an intermediate solution between the conventional linear precoder (LP) and nonlinear precoder (NLP), over an analog-digital hybrid beamforming constitution. Through numerical evaluation assuming indoor hotspot scenarios, it is clarified that, NL-BMD yields up to 18.8% improvement and 5.1 dB gain in average sum-rate spectral efficiency performance, compared with block diagonalization (BD), which is one of the typical schemes of conventional LP, while reducing the complexity to 1/2 of the conventional NLP. In addition, even under a dynamic fading condition, NL-BMD shows tolerance for channel transitions and still better performance than BD: NL-BMD suppresses performance loss in sum-rate spectral efficiency due to channel transitions to 18.3%, whereas BD shows over 20% loss.

1 Introduction

With the mobile traffic in the early 2020’s being predicted to be 1000 times greater than that of 2010, the fifth generation mobile communications (5G) system is expected to accommodate the forthcoming huge traffic demands [1, 2]. 5G will be used for events with heavy traffic demand such as multi-angle/real-time video transmission, 4K/8K digital signage, automated vehicle driving, etc. Therefore, we will inevitably require large capacity as well as low latency. 5G small cells will use higher frequency bands, such as super high frequency (SHF) or extremely high frequency (EHF), than ultra high frequency (UHF) bands used in the conventional macro cells. They will offer larger capacity and denser deployment of base stations (BSs), yielding its peak data rate of over 20 Gbps [1, 3, 4].

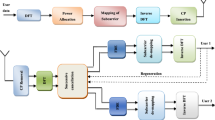
Massive multiple-input multiple-output (MIMO) technology utilizing hundreds of antenna elements has drawn attention as a key antenna configuration for 5G [5,6,7]. It enables us to drastically earn antenna beam gain and spatial multiplexing capability, and its benefit is of significance especially in high SHF/EHF bands to combat severe propagation loss. To realize massive MIMO, its configurations have been widely studied [7]. The fully-digital massive MIMO configuration requires a large-scale digital signal processing unit and digital-to-analog converters (DACs) corresponding to all the antenna elements. While it yields excellent transmission performance thanks to a number of degrees of freedom, implementation and computational costs are relatively higher. On the other hand, the analog-digital hybrid massive MIMO configuration, which is realized by combining analog beamforming and digital MIMO signal processing, has been proposed [8, 9]. For the hybrid beamformer, full-array and subarray configurations are proposed. The latter one can reduce the complexity of RF circuits while reasonably maintaining the performance similar to the former one. Figure 1 briefly shows its block configuration, where $N_{\text {st}}$ downlink (DL) substreams are transmitted from $N_e$ antenna elements via $N_{\text {tx}}$ transmit (TX) baseband ports. A TX baseband port is associated with a massive-element subarray, of which the number of antenna elements is $N_{e,\text {sub}}$. That is, we have $N_e= N_{e,\text {sub}}\times N_{\text {tx}}$. The digital processing unit here controls analog beams from massive-element subarrays, in addition to digital precoding. Use of an active phased array antennas (APAA) as a massive-element subarray is a promising solution for realizing massive MIMO for high SHF/EHF bands in practice.

Fig. 1

Block configuration of an analog-digital hybrid massive MIMO DL architecture

Multiuser-MIMO (MU-MIMO) must be a spatially-efficient wireless access system exploiting the benefit of massive MIMO, where a BS equipped with multiple antennas simultaneously makes co-channel communications with multiple users having multiple antennas. In MU-MIMO DL, inter-user interference (IUI) observed at each user is an essential issue due to the broadcasting from BS even if using sharp analog beams. It is desirable to mitigate IUI at BS in advance because there is a more computational room at BS. Therefore, studies on digital precoding for IUI reduction have been reported in the past literature [10,11,12,13,14,15,16].

Approaches of digital precoding for MU-MIMO DL can be roughly classified into linear precoding (LP) and nonlinear precoding (NLP) approaches. Block diagonalization (BD) is well known as a typical case of LP accomplishing perfect nulling, where we direct prescribed nulls to users except for the target user [10,11,12,13]. BD enables us to realize IUI-free DL situation in a spatially-uncorrelated scenario and to ease receiver designing. However, since most of the spatial resources at BS are consumed to direct nulls in the BD system, we cannot expect extra TX diversity gain so that the performance of BD may deteriorate considerably in ill-conditioned or spatially-correlated channels. Alternatively, NLP provides near-capacity performance and establishes spatially-robust DL transmission, by canceling IUI observed at users in advance, i.e. IUI pre-cancellation (IUI-PC). Nonlinear block triangulation (NL-BT)¹ is a sub-optimal NLP method composed of LP for achieving block triangulation (BT) and IUI-PC with modulo operation for limiting signal distortion [14,15,16]. Although NL-BT brings high system throughput in principle, we have to solve the critical issue of high complexity for IUI-PC.

Based on these studies, in [17], nonlinear block multi-diagonalization (NL-BMD) precoding has been proposed as an intermediate precoding approach between BD and NL-BT. It is composed of BMD [18] and adjacent IUI-PC. The BMD precoder for the desired user is computed to incorporate a predetermined number of interfered users (hereafter referred to as IUI users) with fixed complexity comparable to the conventional BD. So, it enables us to ensure extra degrees of freedom at the TX array even after null steering. In the adjacent IUI-PC we can limit IUI to be pre-canceled to the adjacent users allowed in BMD computation. Therefore NL-BMD precoding offers advantages in numerical complexity in IUI-PC. It has been reported in [17] that, NL-BMD provides higher throughput over BD with reasonable complexity less than NL-BT, through numerical evaluation assuming narrow-band single-carrier transmission and Rician fading.

In this paper, through orthogonal frequency division multiplexing (OFDM) simulations over an analog-digital hybrid massive MIMO configuration, we reveal the capability of NL-BMD precoding in realistic indoor hotspot scenarios: a densely-populated environment and dynamic fading condition assuming pedestrians. We hereinafter handle nonlinear block bi-diagonalization (NL-BBD) precoding, which allows one IUI user in the BMD computation, as a typical strategy in the NL-BMD family.

The rest of the paper is organized as follows. First the handled MU-MIMO DL system model is defined in Sect. 2. Then, Sect. 3 reviews BD, NL-BT, and NL-BBD schemes, and in Sect. 4 user ordering algorithm adopted in the paper is described. To numerically evaluate the performance of the precoding schemes, Sect. 5 explains simulation setup, and then Sect. 6 demonstrates the spectral efficiency performance in both the quasi-static and dynamic fading conditions. Finally, Sect. 7 concludes the paper.

2 System Model

The scope of this paper is digital baseband architecture. We assume a mobile cellular system where all the equipment is under synchronous control, and the issue we handle is to spatially multiplex signals to the users determined by a scheduler in BS. Also BS is assumed to have DL channel state information of all users, exploiting channel reciprocity in time division duplex (TDD). Let us consider the MU-MIMO DL system where BS has $N_{\text {tx}}$ TX digital baseband ports, user ${\#}i$ has $N_{\text {rx},i}$ receive (RX) digital baseband ports, and the number of existing users is $N_{\text {usr}}$. We define the number of system RX digital ports, namely total RX digital baseband ports of all users, as $N_{\text {rx}}= \sum _{i=1}^{N_{\text {usr}}} N_{\text {rx},i}$. Also, we assume that $N_{\text {st},i}$ ($1 \le N_{\text {st},i}\le N_{\text {rx},i}$) substreams are transmitted to user ${\#}i$. Note that the number of total substreams transmitted from BS is denoted as $N_{\text {st}}= \sum _{i=1}^{N_{\text {usr}}} N_{\text {st},i}$, and in the following formulation let us assume that the number of digital baseband ports satisfies the condition of $N_{\text {tx}}\ge N_{\text {rx}}$ for the sake of simplicity².

Although we deal with MU-MIMO over OFDM transmission in the paper, hereinafter let us simplify the discussion by focusing on a subcarrier. Note that the following procedure is common to all the subcarriers. Assuming transmission at a certain subcarrier, for user ${\#}i$ we here define: an $N_{\text {st},i}$-dimensional TX signal vector $\varvec{s}_i (t)$, an $N_{\text {tx}}\times N_{\text {st},i}$ TX precoding (beamforming) matrix $\varvec{B}_i$, an $N_{\text {rx},i}\times N_{\text {tx}}$ channel matrix $\varvec{H}_i$, an $N_{\text {rx},i}$-dimensional RX signal vector $\varvec{r}_i (t)$, and an $N_{\text {rx},i}$-dimensional additive white Gaussian noise (AWGN) vector $\varvec{n}_i (t)$. Then the system can be briefly modeled as follows:

$$\begin{aligned} \bar{\varvec{r}}(t) = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}\bar{\varvec{s}}(t) + \bar{\varvec{n}}(t) , \end{aligned}$$

(1)

where,

$$\begin{aligned} \bar{\varvec{r}}(t) = \left[ \varvec{r}_1^T(t) \quad \varvec{r}_2^T(t) \quad \ldots \quad \varvec{r}_{N_{\text {usr}}}^T(t) \right] ^{T} , \end{aligned}$$

(2)

$$\begin{aligned} {\varvec{\mathcal {H}}}= \left[ \varvec{H}_1^T \quad \varvec{H}_2^T \quad \ldots \quad \varvec{H}_{N_{\text {usr}}}^T\right] ^{T} , \end{aligned}$$

(3)

$$\begin{aligned} {\varvec{\mathcal {B}}}= \left[ \varvec{B}_1 \quad \varvec{B}_2 \quad \ldots \quad \varvec{B}_{N_{\text {usr}}}\right] , \end{aligned}$$

(4)

$$\begin{aligned} \bar{\varvec{s}}(t) = \left[ \varvec{s}_1^T(t) \quad \varvec{s}_2^T(t) \quad \ldots \quad \varvec{s}_{N_{\text {usr}}}^T(t) \right] ^{T}, \text {and} \end{aligned}$$

(5)

$$\begin{aligned} \bar{\varvec{n}}(t) = \left[ \varvec{n}_1^T(t) \quad \varvec{n}_2^T(t) \quad \ldots \quad \varvec{n}_{N_{\text {usr}}}^T(t) \right] ^{T} , \end{aligned}$$

(6)

respectively. Note that the matrices ${\varvec{\mathcal {H}}}$ and ${\varvec{\mathcal {B}}}$ denote $N_{\text {rx}}\times N_{\text {tx}}$ system channel matrix and $N_{\text {tx}}\times N_{\text {st}}$ system precoding matrix, respectively. Hence the product of ${\varvec{\mathcal {H}}}$ and ${\varvec{\mathcal {B}}}$, namely ${\varvec{\mathcal {H}}}_e = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}$, can be regarded as an effective system channel matrix:

$$\begin{aligned} {\varvec{\mathcal {H}}}_e = \begin{bmatrix} \varvec{H}_1 \varvec{B}_1&\varvec{H}_1 \varvec{B}_2&\cdots&\varvec{H}_1 \varvec{B}_{N_{\text {usr}}} \\\varvec{H}_2 \varvec{B}_1&\varvec{H}_2 \varvec{B}_2&\cdots&\varvec{H}_2 \varvec{B}_{N_{\text {usr}}} \\\vdots&\vdots&\ddots&\vdots \\\varvec{H}_{N_{\text {usr}}} \varvec{B}_1&\varvec{H}_{N_{\text {usr}}} \varvec{B}_2&\cdots&\varvec{H}_{N_{\text {usr}}} \varvec{B}_{N_{\text {usr}}} \end{bmatrix} . \end{aligned}$$

(7)

Among submatrices (block entries) in the matrix ${\varvec{\mathcal {H}}}_e$, the block diagonal entries $\varvec{H}_i \varvec{B}_i$ ($i = 1, \ldots , N_{\text {usr}}$) mean the desired effective channel components for users, and the other entries (block off-diagonal entries) $\varvec{H}_i \varvec{B}_j$ ($i \ne j$) represent IUI channel components. LP is to spatially reduce IUI channel components by the precoder ${\varvec{\mathcal {B}}}$, and NLP is to pre-cancel IUI signal observed at users in addition to LP.

3 MU-MIMO Precoding Schemes

Figure 2 illustrates TX and RX block diagrams in an NLP system with OFDM. At the transmitter, a per-substream data sequence is encoded and interleaved before quadrature amplitude modulation (QAM) mapping. Through serial-to-parallel conversion (S/P), at each subcarrier NL operation (IUI-PC) and LP (feedforward spatial filter) are applied to all users’ QAM-modulated substreams, yielding MU-MIMO multiplexing. After inverse fast Fourier transform (IFFT), parallel-to-serial conversion (P/S), and addition of cyclic prefix (CP), OFDM signal chains are fed to TX ports. At each user (receiver), removal of CP, S/P, and fast Fourier transform (FFT) are applied to received signal chains. In the frequency domain, the receiver performs demultiplexing and detection of the desired substreams, and then computes modulo operation and demapping at each subcarrier. Through P/S, each of estimated sequences is fed to subsequent decoding process.

Fig. 2

Block diagrams of NLP over OFDM (equivalent baseband system). a Transmitter and b receiver (user $\#i$)

In the following, we review BD and NL-BT as the conventional LP and NLP schemes, respectively, and then introduce NL-BBD as an intermediate approach between them. Note that, the NL operation block at TX and modulo operation blocks at RX shown in Fig. 2 are not necessary in LP schemes.

3.1 Block Diagonalization (BD)

This subsection explains the BD scheme, which is the typical LP, by showing how to compute the user ${\#}i$’s precoding matrix $\varvec{B}_{\text {bd},i}$.

We first consider an $(N_{\text {rx}}- N_{\text {rx},i}) \times N_{\text {tx}}$ channel matrix ${\varvec{\mathcal {H}}}^{(i)}_{\text {bd}}$ composed of user channel matrices except for user $\# i$’s one, and its singular value decomposition (SVD) can be expressed as

$$\begin{aligned} {\varvec{\mathcal {H}}}^{(i)}_{\text {bd}}= \left[ \varvec{H}_1^T \quad \ldots \quad \varvec{H}_{i-1}^T \quad \varvec{H}_{i+1}^T \quad \ldots \quad \varvec{H}_{N_{\text {usr}}}^T \right] ^{T} \end{aligned}$$

(8)

$$\begin{aligned} = \varvec{U}^{(i)}_{\text {bd}}\begin{bmatrix} {\varvec{\varSigma }}^{(i)}_{\text {bd[s]}}&\varvec{O} \end{bmatrix} \begin{bmatrix} \varvec{V}_{\text {bd[s]}}^{(i)H} \\\varvec{V}_{\text {bd[n]}}^{(i)H} \end{bmatrix} , \end{aligned}$$

(9)

where $\varvec{U}^{(i)}_{\text {bd}}$ is an $(N_{\text {rx}}- N_{\text {rx},i})$-dimensional unitary matrix composed of left singular vectors, and an $(N_{\text {rx}}-N_{\text {rx},i})\times N_{\text {tx}}$ singular value matrix consists of an $(N_{\text {rx}}- N_{\text {rx},i})$-dimensional diagonal submatrix ${\varvec{\varSigma }}^{(i)}_{\text {bd[s]}}$, of which diagonal entries are non-negative singular values, and a zero matrix $\varvec{O}$. Also, an $N_{\text {tx}}$-dimensional matrix composed of right singular vectors can be classified into submatrices $\varvec{V}^{(i)}_{\text {bd[s]}}$ and $\varvec{V}^{(i)}_{\text {bd[n]}}$, which correspond to the signal space ${\varvec{\varSigma }}^{(i)}_{\text {bd[s]}}$ and the kernel space $\varvec{O}$, respectively. When $\varvec{V}^{(i)}_{\text {bd[n]}}$ is set to a TX precoder $\varvec{B}_{\text {bd},i}$, we can direct perfect nulls to all users except for user ${\#}i$ because the vector space spanned by $\varvec{V}^{(i)}_{\text {bd[n]}}$ is the mapper to the kernel. Consequently, the precoder $\varvec{B}_{\text {bd},i}$ ($i = 1, \ldots , N_{\text {usr}}$) achieves block diagonalization of the effective system channel matrix as below:

$$\begin{aligned} {\varvec{\mathcal {H}}}_{e,\text {bd}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bd}} \end{aligned}$$

(10)

$$\begin{aligned} = \begin{bmatrix} \varvec{H}_1 \varvec{B}_{\text {bd},1}&\varvec{O}&\cdots&\varvec{O} \\\varvec{O}&\varvec{H}_2 \varvec{B}_{\text {bd},2}&\cdots&\varvec{O} \\\vdots&\vdots&\ddots&\vdots \\\varvec{O}&\varvec{O}&\cdots&\varvec{H}_{N_{\text {usr}}} \varvec{B}_{\text {bd},N_{\text {usr}}} \end{bmatrix} . \end{aligned}$$

(11)

Over the block-diagonalized channel ${\varvec{\mathcal {H}}}_{e,\text {bd}}$, we can subsequently apply any kind of single-user (SU) MIMO precoding per user, i.e. intra-user precoding.

Although the BD scheme eliminates IUI, we cannot avoid spending degrees of freedom at the TX array upon the perfect nulling. So, it is not necessarily the case that the obtained TX beams can improve SNR at each user. In particular, assuming correlated or densely-populated scenarios, many users may be located in a certain direction area when viewed from BS. Therefore, lots of degrees of freedom at the TX array would be consumed to direct nulls to similar directions, so that we cannot expect residual TX array gain to the desired user.

3.2 Nonlinear Block Triangulation (NL-BT)

In NLP, user hierarchization is mandatory for practical IUI-PC. When BT computation is applied onto the system channel matrix ${\varvec{\mathcal {H}}}$, the obtained unitary matrix ${\varvec{\mathcal {B}}}_{\text {bt}}$ enables us to successively pre-cancel IUI [19] (see Appendix in [17]). Using the system precoding matrix ${\varvec{\mathcal {B}}}_{\text {bt}}$ yielding BT, we can obtain the effective system channel matrix as

$$\begin{aligned} {\varvec{\mathcal {H}}}_{e,\text {bt}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bt}} \end{aligned}$$

(12)

$$\begin{aligned} = \begin{bmatrix} \varvec{H}_1 \varvec{B}_{\text {bt},1}&\varvec{O}&\cdots&\varvec{O} \\ \varvec{H}_2 \varvec{B}_{\text {bt},1}&\varvec{H}_2 \varvec{B}_{\text {bt},2}&\cdots&\varvec{O} \\ \vdots&\vdots&\ddots&\vdots \\ \varvec{H}_{N_{\text {usr}}} \varvec{B}_{\text {bt},1}&\varvec{H}_{N_{\text {usr}}} \varvec{B}_{\text {bt},2}&\cdots&\varvec{H}_{N_{\text {usr}}} \varvec{B}_{\text {bt},N_{\text {usr}}} \end{bmatrix} . \end{aligned}$$

(13)

Since ${\varvec{\mathcal {B}}}_{\text {bt}}$ obtained by any approaches of block LQ factorization is a unitary matrix, it can maintain the property of the given channel nature. In other words, it accomplishes lossless linear mapping from TX-port space to user space.

Fig. 3

TX processing circuit diagram in NL-BT

Joint precoding of BT and IUI-PC, namely NL-BT, can release MU-MIMO’s potential. However, since IUI-PC causes a significant increase in TX signal amplitude, introduction of THP, where modulo operation limits the amplitude to a required threshold, would be a practical manner. Although use of a modulo operator at TX obliges all users to have the same modulo operator, its impact on hardware implementation can be kept low. Figure 3 illustrates TX processing circuit diagram in NL-BT precoding. In [16], IUI-PC with modulo operation for the case of single-stream transmission per user is formulated. We extend the formulation to the case of multi-stream transmission per user in the same manner. When applying BT, the TX signal vector for user $\# i$ preprocessed by THP can be written as

$$\begin{aligned}&\text {NL-BT}: \\&\quad \varvec{s}'_{i}(t) = \text {modulo}_{\tau } \left[ \varvec{s}_i(t) - \left( \varvec{H}_i \varvec{B}_{\text {bt},i} \right) ^{+} \sum _{j=1}^{i-1} \varvec{H}_i \varvec{B}_{\text {bt},j} \varvec{s}'_{j}(t)\right] , \end{aligned}$$

(14)

where $\varvec{s}'_1(t) = \varvec{s}_1(t)$, and $\left( \cdot \right) ^{+}$ denotes Moore–Penrose (MP) pseudo inverse. Also, $\text {modulo}_{\tau }\left( \cdot \right)$ means substream-wise modulo operation with modulo boundary $\tau$ defined as follows:

$$\begin{aligned} \text {modulo}_{\tau } (x)&= \left( x_i - \left\lfloor \frac{x_i}{2 \tau } + \frac{1}{2} \right\rfloor \cdot 2 \tau \right) + j \left( x_q - \left\lfloor \frac{x_q}{2 \tau } + \frac{1}{2} \right\rfloor \cdot 2 \tau \right) , \end{aligned}$$

(15)

here $x = x_i + j x_q$ is a complex value. Unfortunately, for the desired user ${\#}i$, IUI-PC utilized together with BT needs removal of IUI signals from all the upper-layer users ${\#}1$, $\cdots$, ${\#}(i-1)$, resulting in higher computational load in proportion to the number of users $N_{\text {usr}}$. In NL-BT, the order of numerical complexity in IUI-PC is $\mathcal {O} \left( N_{\text {usr}}^2\right)$ [17].

When applying IUI-PC, implementation of modulo operation can significantly reduce TX power while reasonably maintaining spectral efficiency performance [17]. So, modulo operation is important for practical use of IUI-PC. Note that hereinafter we proceed to a discussion assuming that IUI-PC includes modulo operation.

3.3 Nonlinear Block Bi-Diagonalization (NL-BBD)

The NL-BBD method is composed of two essential techniques: (i) BBD which can provide extra TX diversity by allowing adjacent IUI, and (ii) adjacent IUI-PC which cancels adjacent users’ IUI only with effectively-reduced computational load compared with that in NL-BT. Figure 4 shows a conceptual image of NL-BBD.

Fig. 4

An image of NL-BBD, composed of BBD precoding and adjacent IUI-PC

In the following each technique is described.

3.3.1 Block Bi-Diagonalization (BBD)

While the conventional BD scheme enables per-user spatially-closed signal transmission, it is difficult to ensure extra degrees of freedom at the TX array due to perfect nulling. Also, the BT scheme, with which the whole system space can be losslessly hierarchized per user, is effective for NLP whereas the cascaded IUI-PC process suffers from computational load in proportion to the number of users. Considering massive MIMO with subarray-type analog-digital hybrid beamforming configuration, beams directed to users from BS may be overlapped especially in a dense scenario. In this case we have severe IUI, and conventional LP schemes may sacrifice beam gains to mitigate the IUI.

Extending the BD approach, the BMD concept proposed in [18] is to partially allow IUI in the LP computation process for each desired user. Partial IUI allowance brings residual degrees of freedom at the TX array even after nulling. Also, for NLP, the concept enables us to reduce the number of IUI signals to be pre-canceled to the order of $\mathcal {O} (N_{\text {usr}})$. In this paper, we focus on a valid approach in the BMD family: BBD, allowing one IUI user, from an implementational viewpoint. Actually premising the aforementioned massive MIMO, dominant IUI would arise in a limited area close to the desired user due to overlapping beams.

In the BBD computation, user ${\#}(i+1)$ is set to the IUI user corresponding to the desired user ${\#}i$. Next, we define ${\varvec{\mathcal {H}}}^{(i)}_{\text {bbd}}$ by eliminating the channel components of users ${\#}i$ and ${\#}(i+1)$ from the system channel matrix ${\varvec{\mathcal {H}}}$, and its SVD can be expressed as

$$\begin{aligned} {\varvec{\mathcal {H}}}^{(i)}_{\text {bbd}}= \left[ \varvec{H}_{1}^T \quad \ldots \quad \varvec{H}_{i-1}^T \quad \varvec{H}_{i+2}^T \quad \ldots \quad \varvec{H}_{N_{\text {usr}}}^T \right] ^{T} \end{aligned}$$

(16)

$$\begin{aligned} = \varvec{U}^{(i)}_{\text {bbd}}\begin{bmatrix} {\varvec{\varSigma }}^{(i)}_{\text {bbd[s]}}&\varvec{O} \end{bmatrix} \begin{bmatrix} \varvec{V}_{\text {bbd[s]}}^{(i)H} \\\varvec{V}_{\text {bbd[n]}}^{(i)H} \end{bmatrix} . \end{aligned}$$

(17)

Here the submatrix ${\varvec{\varSigma }}^{(i)}_{\text {bbd[s]}}$ in Eq. (17) indicates the user space except for users ${\#}i$ and ${\#}(i+1)$, and the zero matrix indicates the kernel space. Therefore, when we use $\varvec{V}^{(i)}_{\text {bbd[n]}}$, corresponding to the kernel, as a virtual TX weight, we obtain the presumed effective channel matrix as

$$\begin{aligned} {\varvec{\mathcal {H}}}\varvec{V}^{(i)}_{\text {bbd[n]}}= \begin{bmatrix} \vdots \\\varvec{O} \\\varvec{H}_{i} \varvec{V}^{(i)}_{\text {bbd[n]}}\\\varvec{H}_{i+1} \varvec{V}^{(i)}_{\text {bbd[n]}}\\\varvec{O} \\\vdots \end{bmatrix} . \end{aligned}$$

(18)

That is, $\varvec{V}^{(i)}_{\text {bbd[n]}}$ achieves perfect null steering to all the users except for users ${\#}i$ and ${\#}(i+1)$. The above procedure is basic computation of BBD as inter-user precoding.

Moreover, based on the channel component of the desired user ${\#}i$, $\varvec{H}_{i} \varvec{V}^{(i)}_{\text {bbd[n]}}$, noted in Eq. (18), we try to direct suitable beam to user ${\#}i$, namely intra-user precoding. We here presume an eigenvector matrix $\varvec{V}^{(i)}_{\text {bbd[e]}}$ corresponding to the larger singular values of $\varvec{H}_{i} \varvec{V}^{(i)}_{\text {bbd[n]}}$. Multiplying $\varvec{V}^{(i)}_{\text {bbd[n]}}$ by $\varvec{V}^{(i)}_{\text {bbd[e]}}$ from right side gives desirable beamforming to improve SNR for user ${\#}i$, i.e. eigenmode transmission, over determinate signal space of only users ${\#}i$ and ${\#}(i+1)$, exploiting the residual degrees of freedom at the TX array.

Hence the precoding matrix for user ${\#}i$ in the BBD scheme is computed by $\varvec{B}_{\text {bbd},i} = \varvec{V}^{(i)}_{\text {bbd[n]}}\varvec{V}^{(i)}_{\text {bbd[e]}}$, and the system precoding matrix ${\varvec{\mathcal {B}}}_{\text {bbd}}$ can be obtained by applying the above procedure to all the desired users. We here note that the last user $\#N_{\text {usr}}$ should be handled in a different manner for NLP. User $\#N_{\text {usr}}$ must not have its IUI user when we apply IUI-PC requiring user hierarchization. Therefore, the precoder for user $\#N_{\text {usr}}$ is computed via the same processing of the BD scheme. Consequently, we obtain a purely block bi-diagonalized matrix:

$$\begin{aligned} {\varvec{\mathcal {H}}}_{e,\text {bbd}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bbd}} \end{aligned}$$

(19)

$$\begin{aligned} = \begin{bmatrix} \varvec{H}_1 \varvec{B}_{\text {bbd},1}&\varvec{O}&\cdots&\varvec{O} \\\varvec{H}_2 \varvec{B}_{\text {bbd},1}&\varvec{H}_2 \varvec{B}_{\text {bbd},2}&\cdots&\varvec{O} \\\vdots&\vdots&\ddots&\vdots \\\varvec{O}&\varvec{O}&\cdots&\varvec{H}_{N_{\text {usr}}} \varvec{B}_{\text {bbd},N_{\text {usr}}} \end{bmatrix} . \end{aligned}$$

(20)

Table 1 overviews effective system channel matrices mapped by the three LP schemes: (a) BD, (b) BT, and (c) BBD.

Table 1 Effective system channel matrix, ${\varvec{\mathcal {H}}}_e$ ($N_{\mathrm {usr}}=4$)

3.3.2 Adjacent IUI-PC

Although BBD brings higher beam gain than BD due to extra diversity effect, we additionally need countermeasure for the allowed IUI.

In NL-BBD [17], IUI-PC is adopted at BS, as well as NL-BT. TX signal vectors after applying IUI-PC prior to BBD can be expressed as

$$\begin{aligned}&\text {NL-BBD}: \\&\quad \varvec{s}'_{i}(t) = \text {modulo}_{\tau } \left[ \varvec{s}_i(t) - \left( \varvec{H}_i \varvec{B}_{\text {bbd},i} \right) ^{+} \varvec{H}_i \varvec{B}_{\text {bbd},i-1} \varvec{s}'_{i-1}(t) \right] . \end{aligned}$$

(21)

Figure 5 illustrates a TX processing circuit diagram in NL-BBD. As noticed by Fig. 5 and Eq. (21), in IUI-PC cascaded to BBD the required cancellation is only for adjacent users’ substreams corresponding to the allowed IUI in BBD, unlike that with BT shown in Fig. 3 and Eq. (14). Therefore, in [17] IUI-PC in NL-BBD is referred to as adjacent IUI-PC. As discussed in [17], the complexity in NL-BBD can be reduced to $2 / N_{\text {usr}}$ of that in NL-BT, e.g. 1/2 in the case of $N_{\text {usr}}= 4$ and 1/4 in the case of $N_{\text {usr}}= 8$.

Fig. 5

TX processing circuit diagram in NL-BBD

4 User Ordering

Although user ordering does not make sense in the conventional BD scheme achieving uniform user orthogonalization, in NLP schemes it plays an important role affecting the performance. User ordering is jointly composed of two factors: pairing of the desired and IUI users, and ordering of precoder computation. Examples of criteria of user pairing (IUI user selection) include: combination using channel correlation, selection based on geometric user location relationship, etc. Also, ordering of precoder computation is related to IUI-PC, so examples of the ordering criteria include: channel gain of users, eigenvalues of users, diversity gains of substreams, channel capacity assuming SU-MIMO, etc. However, these issues are not independent and can be regarded as a joint optimization problem, where resource allocation to users also has to be taken into account. Additional study is needed for them, and detailed discussion is beyond the scope of this paper.

In this paper, the authors adopt a simple user ordering algorithm based on azimuth angles of users viewed from BS, exploiting a massive MIMO property. As will be discussed later, in the performance evaluation we assume that BS covered a sectoral service area, and that the TX array at BS was composed of multiple subarrays. Assuming that BS could grasp information on user locations through a beam search procedure, an analog beam from a subarray was directed to the associated user. In the ordering algorithm, we first searched the user having the maximum azimuth angle, namely the angle closest to the sector-edge direction, out of the given users, and set the user as the first user. Then the subsequent users were determined by sorting the rest of users in descending order of their azimuth angles. With the ordering scheme, we can expect diversity effect between adjacent users even using sharp analog beams. Note that we should take zenith angles of user directions into account for more accurate ordering. However, for the sake of simplicity, we hereafter deal with the simple algorithm based on azimuth angles only as an initial study.

In the subsequent sections, the user ordering algorithm explained here was uniformly adopted irrespective of the precoding schemes.

5 Simulation Setup

To evaluate the performance of NL-BBD over an analog-digital hybrid beamforming system, we conducted link-level simulations. Prior to showing the results, in this section we explain the setup for the computer simulations.

Fig. 6

Scenario setup

5.1 Scenario Setup

Figure 6 illustrates the scenario setup in this paper. We assumed MU-MIMO DL transmission to user equipment (UE) at radio frequency of 28 GHz, of which wavelength is $\lambda = 10.7\,\text {mm}$. Here we define $\phi$ and $\theta$ as azimuth and zenith angles, respectively. We assumed an indoor hotspot area [20] where BS mainly serves a communication area of $20\,\text {m} \times 20\,\text {m}$. BS (TX) was installed at 3m height, and its frontface direction was fixed to $\phi = -45^{\circ }$ and $\theta = 90^{\circ }$. Note that we did not give tilt angle to the TX array in installation. UEs (RXs) with 1 m height were located within a horizontal distance of 2–28.3 m ($=\sqrt{2} \times 20\,\text {m}$) and an azimuth angle range of $-90^{\circ } \le \phi \le 0^{\circ }$ from BS. The numbers of TX&RX baseband ports and UEs were set to $N_{\text {tx}}= 16$, $N_{\text {rx}}= 32$, and $N_{\text {usr}}= 4$, respectively, where the number of RX ports per UE was fixed to $N_{\text {rx},i}= 8$ irrespective of UEs.

Figure 7 shows two scenarios evaluated in this paper. Scenario A is a configuration where UEs were randomly distributed within the area, equivalently assuming a non-correlated case. Since each of beams from BS can be directed to different directions, this scenario is favorable for the system to spatially multiplex UEs. Scenario B, on the other hand, is a configuration where all UEs were located within a circular spot of which radius was 3 m, assuming a densely-populated indoor environment. Although for stable system operation a scheduler would generally tend to group relatively-distant UEs for space division multiple access (SDMA), this scenario is to evaluate an extreme case that it cannot avoid unfavorable scheduling. Note that the circular spot for geometrically constraining all UEs was randomly dropped so as not to exceed the area. In both the scenarios, we examined two fading conditions: a quasi-static fading condition where all UEs were static after being dropped per trial, and a dynamic fading condition where each UE randomly walked as a pedestrian at velocity of 3 km/h.

Fig. 7

Evaluation scenarios (top view). a Scenario A (random) and b Scenario B (dense)

The employed channel model for link-level simulations was clustered delay line model type-D (CDL-D) specified in [20], which models line-of-sight (LOS) channels in indoor hotspot cells for above 6 GHz frequencies. We note that the LOS angular values defined in the first cluster (see Table 7.7.1-4 in [20]) were replaced by instantaneous LOS angular values between BS subarrays and UE antennas depending on the given geometric condition, in order to simulate the aforementioned MU-MIMO DL scenarios. Cross-polarization power ratio (XPR) in CDL-D is 11 dB except LOS rays [20]. Root mean square (RMS) delay spread was set at 16ns as a 28GHz short-delay profile for indoor office prescribed in Table 7.7.3-2 in [20].

5.2 Antenna Configuration

Targeting the analog-digital hybrid configuration with multiple subarrays as massive MIMO [21, 22], an antenna corresponding to a TX port at BS was assumed to be a planar APAA, so the TX array was composed of 16 APAA subarrays arranged in a plane, where we exactly had $2 \times 4 = 8$ pairs of ideally-isolated cross-polarized ($45^{\circ }$-slanted V/H) subarrays as shown in Fig. 8. Each subarray had $\lambda /2$-spaced $8 \times 8 = 64$ single-polarized antenna elements, of which radiation pattern was based on the prescription in Table 7.3-1 in [20], namely maximum directional gain of 8 dBi and angular full width at half maximum (FWHM) of $65^{\circ }$ for both azimuth and elevation planes. Therefore a subarray pair had $64 \times 2 = 128$ antenna elements, and the entire TX array had $64 \times 16 = 1024$ antenna elements in total. A signal from a TX port was fed to a subarray and divided into 64 antenna elements via phase shifters, controlled so as to direct an analog beam to the target UE. Note that the power of an amplifier at each antenna element was common to the whole antenna elements and among subarrays. TX subarray spacing between adjacent pairs was set to $8 \lambda$, and two out of eight pairs were associated with a target UE, as shown in Fig. 8, to configure four TX analog beams per UE.

Fig. 8

Configurations of BS antenna array and each V/H subarray pair

Also, we assumed that each UE had four ideally-isolated cross-polarized antenna pairs with adjacent inter-pair spacing of $5 \lambda$ as illustrated in Fig. 6, where each element pattern was assumed to be ideally isotropic with gain of 0 dBi, for the sake of simplicity. Array orientation of each UE was randomly set in horizontal plane.

5.3 Simulation Conditions

Table 2 lists simulation parameters, and Fig. 9 illustrates the frame format assumed in the simulations. We conducted OFDM simulations to evaluate wide-band MU-MIMO DL transmission, where the number of subcarriers and subcarrier spacing were set at $N_{\text {sc}}= {1200}$ and 60 kHz, respectively. In order to solve computation of linear precoders at BS in the system antenna configuration of $N_{\text {tx}}= 16$ and $N_{\text {rx}}= 32$, we first degenerated the per-user RX antenna domain from eight physical antenna ports to four beam-space antennas, by using four major eigenvectors maximizing effective channel gain as postcoders at all the subcarriers. Exploiting time reciprocity, BS acquired channel state information at TX (CSIT) for all UEs through uplink (UL) and then computed a linear precoder from a $16 \times 16$ beam-space system channel matrix at each subcarrier, where we assumed that CSIT was perfectly acquired. The time interval from CSIT acquisition and actual DL transmission using the updated precoders was assumed to be 1 ms. So, in a dynamic fading condition, the computed precoders and the up-to-date channels should be mismatched, resulting in unmanaged IUI at UEs. When UEs move at velocity of 3 km/h, the maximum phase rotation due to the maximum Doppler frequency over the time interval of 1ms is $28.0^{\circ }$ at the 28 GHz band, whereas that within an FFT period (16.67 $\upmu$s) is just $0.47^{\circ }$. Note that, in performance measurement, we observed only the first DL OFDM symbol per subframe for simple evaluation of the mismatch.

Fig. 9

Frame format

Table 2 Simulation parameters

Table 3 Per-substream MCS table

BS transmitted $N_{\text {st},i}= 4$ substreams per UE. Therefore 16-substream transmission over 4-user multiplexing was performed. Turbo coding was applied to each substream independently, where each codeword was closed within each OFDM symbol. As listed in Table 3, we prepared 19 patterns of modulation and coding schemes (MCSs) in total from combinations of modulation schemes and coding rates in order to evaluate achievable spectral efficiency for every substream. Here, per-substream spectral efficiency for MCS index ${\#}i$ is derived from

$$\begin{aligned} \eta _i = \frac{\left( \log _2 M_i \right) \times R_i \times N_{\text {sc}}}{T_s \times \text {BW}_{\text {ch}}} \quad \text {[bps/Hz]}, \end{aligned}$$

(22)

where $M_i$ is modulation order of index ${\#}i$ ($M_i = 4, 16, 64, 256$ for QPSK, 16QAM, 64QAM, and 256QAM, respectively), $R_i$ is coding rate of index ${\#}i$, $T_s$ is OFDM symbol time length, and $\text {BW}_{\text {ch}}$ is channel bandwidth, as specified in Table 2. The maximum sum-rate spectral efficiency in 16-substream transmission is, therefore, $16 \eta _{19} = {99.7}$ bps/Hz. When we tried MCS index ${\#}i$ upon a substream and found no bit errors after turbo decoding, we could count $\eta _i$ as an instantaneous spectral efficiency of the substream. Note that, for the sake of simplicity, equal power allocation over substreams was adopted, and simple UE ordering based on azimuth angles discussed in Sect. 4 was applied. In NL-BBD and NL-BT, modulo boundary in modulo operation was set to $\tau = \sqrt{3/2} = 1.225$ (see Appendix in [17]). In this case, TX power in NLP is almost the same as that in BD, of which precoders are normalized vectors. At UEs, MIMO demultiplexing was performed by minimum mean square error (MMSE) spatial filtering based on precoded channel estimates for the desired UE, where we employed amplitude correction of spatial filter outputs so that the subsequent modulo operation works well (see Appendix C in [23]). We assumed that each UE could ideally estimate the latest precoded channel at all the subcarriers. In demapping after modulo operation in NLP schemes, bit log-likelihood ratios (LLRs) were computed by expanding the replica signal constellation on the basis of modulo boundary [16].

6 Simulation Results

Based on the setup explained in the previous section, we here show the simulation results.

Fig. 10

Sum-rate spectral efficiency performance in Scenario A. a Average sum-rate spectral efficiency versus average TX SNR and b CDF of instantaneous spectral efficiency at average TX SNR of 25 dB

Fig. 11

Sum-rate spectral efficiency performance in Scenario B. a Average sum-rate spectral efficiency versus average TX SNR and b CDF of instantaneous spectral efficiency at average TX SNR of 25 dB

Figures 10 and 11 demonstrate sum-rate spectral efficiency performance in Scenarios A and B, respectively. Each figure shows (a) average sum-rate spectral efficiency vs. average TX SNR, and (b) CDF of instantaneous sum-rate spectral efficiency at average TX SNR of 25 dB. Here, average TX SNR is defined on the basis of power sum of all UEs’ QAM-mapped signals, $E \left[ \Vert \bar{\varvec{s}}(t) \Vert ^2 \right]$. It is also equivalent to the SNR observed in open-loop (non-precoded) transmission, where received gain by analog beamforming from BS is included in the SNR definition.

6.1 Spectral Efficiency Performance in Quasi-Static Fading Condition

Here, we evaluate the performance under the quasi-static fading condition. We first summarize the observation in this condition. In Scenario B, where we have dense user distribution, NL-BBD yields up to 18.8% performance improvement and 5.1 dB gain in sum-rate spectral efficiency on average, compared with the conventional BD. The difference in behavior between the scenarios is analyzed by properties of analog-beamformed channels. In addition, at 10th percentile of CDF of sum-rate spectral efficiency, NL-BBD outperforms BD by 40% thanks to extra diversity gain. Although NL-BT gives the best spectral efficiency, we can say that NL-BBD has higher implementability with valid performance when considering computational load required in IUI-PC.

Now let us take a close look at the performance in this condition. From Figs. 10 and 11, we notice that NL-BBD yields higher spectral efficiencies than BD. However, the improvement gain in Scenario A is marginal and limited at a high SNR region of over 20 dB. In comparison with BD at average TX SNR of 25 dB, in Scenario A, NL-BBD gives 69.3 bps/Hz (2.8% improvement over BD), whereas BD achieves 67.5 bps/Hz. This implies that, when users are randomly distributed and illuminated by custom-tailored beams from massive-element antennas, in general the given system channel tends to naturally become semi-diagonal across UEs so that the conventional BD is sufficient to mitigate IUI. On the other hand, improvement by NL-BBD is visibly significant in Scenario B, where UEs are densely located: NL-BBD gives 60.1 bps/Hz (18.8% improvement over BD) whereas BD shows 50.6 bps/Hz. This is because BBD ensures beam gain by partially allowing IUI even if UEs are in proximity, and then adjacent IUI-PC compensates the residual IUI, resulting in the equivalent of flexible beamforming.

Fig. 12

Average element-wise channel gain with and without precoding in Scenario A under the quasi-static fading condition. a ${\varvec{\mathcal {H}}}$ (without precoding), b ${\varvec{\mathcal {H}}}_{e,\text {bd}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bd}}$, c ${\varvec{\mathcal {H}}}_{e,\text {bt}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bt}}$ and d ${\varvec{\mathcal {H}}}_{e,\text {bbd}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bbd}}$

Fig. 13

Average element-wise channel gain with and without precoding in Scenario B under the quasi-static fading condition. a ${\varvec{\mathcal {H}}}$ (without precoding), b ${\varvec{\mathcal {H}}}_{e,\text {bd}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bd}}$, c ${\varvec{\mathcal {H}}}_{e,\text {bt}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bt}}$ and d ${\varvec{\mathcal {H}}}_{e,\text {bbd}} = {\varvec{\mathcal {H}}}{\varvec{\mathcal {B}}}_{\text {bbd}}$

To investigate the phenomena aforementioned in detail, we check analog-beamformed channel gain with and without LP. Figures 12 and 13 visually show element-wise channel gain in channel matrices averaged over subcarriers and trials. In each figure, (a) shows average element-wise gain of the $16 \times 16$ postcoded beam-space system channel matrix ${\varvec{\mathcal {H}}}$, and (b), (c), and (d) show that of the $16 \times 16$ effective system channel matrix ${\varvec{\mathcal {H}}}_e$ when applying BD, BT, and BBD, respectively, as LP. All the values of channel gain are normalized by the average gain of analog-beamformed channels associated with the desired UEs. We notice that the substreams #3 and #4 per UE have significantly low gain less than $-10$ dB, compared with the substreams #1 and #2. The assumed environment was LOS, and analog beams from subarrays were steered to corresponding UEs. Therefore, the first two substreams per UE, mainly associated with V and H polarizations of the direct path, were dominant.

In Scenario A, thanks to analog beams directed to distant UEs, the channel ${\varvec{\mathcal {H}}}$ can be roughly block-diagonalized even without precoding, where undesired power (IUI power) is reduced to less than $-10$ dB compared to desired power (channel gain of the first two substreams per UE in block-diagonal entries). So, with the conventional BD we can obtain relatively good effective channels without losing gain for the desired UEs, whereas the other LP schemes provide marginal gain. On the other hand, in Scenario B, we have high gain at block off-diagonal entries, i.e. IUI components, in the channel ${\varvec{\mathcal {H}}}$ due to overlapping of analog beams directed to similar directions. As shown in Fig. 13b, thus, BD sacrifices channel gain for the desired UEs in order to reduce the IUI components. Meanwhile, we see that BBD yields better channel gain for the desired UEs by the benefit of the extra degrees of freedom after partial nulling. Since IUI caused by the residual block off-diagonal entries can be canceled by IUI-PC, NL-BBD consequently provides better performance than the conventional BD, especially in Scenario B.

We see that NL-BT provides excellent performance. As discussed in Sect. 3.2, BT achieves lossless spatial conversion of the given MU-MIMO channel, and in the study here we assume quasi-static fading and ideal IUI-PC. Therefore, NL-BT performance in Figs. 10 and 11 can be regarded as nearly optimal upper bound of sum-rate spectral efficiency under our simulation conditions. In the meantime, when considering numerical complexity in IUI-PC, while NL-BT requires removal of 24 substreams per symbol per subcarrier, NL-BBD takes removal of just 12 substreams (1/2 complexity of NL-BT). The fact indicates that NL-BBD has higher implementability.

Let us set the target sum-rate spectral efficiency at 80 bps/Hz, which can be reached by transmitting fully four substreams per UE. When comparing average spectral efficiency performance under the quasi-static fading condition with BD, NL-BBD provides significant gain of 5.1 dB in Scenario B while giving 1.9 dB gain in Scenario A. Also, CDF performance shows that NL-BBD provides remarkable gain at lower probabilities, thanks to successful diversity effect, compared with BD. Especially in Scenario B, at 10th percentile, NL-BBD gives 47.7 bps/Hz (40.2% improvement over BD) whereas BD shows 34.0 bps/Hz. In addition to improvement in user experience, such stability in the performance is expected to relax complexity in scheduling computation in an actual operational system.

6.2 Spectral Efficiency Performance in Dynamic Fading Condition

Next, we evaluate an influence of channel transitions between CSIT acquisition and DL transmission, where we may face mismatch between the computed precoder and the up-to-date channel. We first note a summary of this subsection. Even under dynamic fading, NL-BBD has more tolerance for channel transitions and gives still better performance than BD: performance loss due to channel transitions in average sum-rate spectral efficiency is 18.3% in NL-BBD whereas that in BD is over 20%, in Scenario B.

Let us see in detail the performance in this condition. Comparing the quasi-static fading and dynamic fading conditions, degradation due to channel transitions is remarkable at a high TX SNR region over 25 dB. We consider that IUI due to out-dated precoding is more significant at substreams corresponding to lower eigenvalues, i.e. substreams #3 and #4 per UE. At the average sum-rate spectral efficiency of 80 bps/Hz, in Scenario A, degradation due to the mismatch is 3.8, 2.9, and 3.0 dB in BD, NL-BT, and NL-BBD, respectively. In Scenario B, furthermore, BD and NL-BT cannot reach 80 bps/Hz even under a noise-free assumption. We figure out that, channel transitions due to just walking speed of 3 km/h bring unignorable degradation in a high frequency band, and that nulling in a dense scenario is more sensitive to the channel transitions. However, it should be noted that only NL-BBD achieves 80 bps/Hz in Scenario B and shows the best performance under the dynamic fading condition.

At saturation levels in the average sum-rate spectral efficiency performance which are obtained under a noise-free assumption, performance losses due to channel transitions in Scenario A are 14.3, 12.9, and 12.7% in BD, NL-BT, and NL-BBD, respectively, compared with the quasi-static fading condition. In addition, performance losses at saturation levels in Scenario B are 20.3, 20.1, and 18.3% in BD, NL-BT, and NL-BBD, respectively. As discussed above, in Scenario A the channel matrix is already semi-block-diagonalized by sharp analog beamforming, so that IUI due to out-dated precoding is not so serious. In Scenario B, on the other hand, since block off-diagonal entries in the channel matrix have larger gain as shown in Fig. 13, they lead to severe IUI when channels are time-varying. Meanwhile, we find less degradation when employing NLP schemes. Although NLP tends to be regarded as sensitive to dynamic fading due to symbol-by-symbol pre-cancellation with estimated CSIT, diversity effect yielded by partial nulling in BT and BBD precoding gives tolerance for channel transitions, and such a phenomenon appears more visible in a densely-populated scenario. In particular, the fact that IUI-PC in NL-BBD is applied only to adjacent UEs contributes to less degradation than NL-BT.

Consequently, the authors clarified that NL-BBD provides better performance than BD and less complexity than NL-BT irrespective of the scenario and fading condition.

7 Conclusions

In this paper, the authors discussed the performance of NL-BMD precoding for MU-MIMO DL transmission over an analog-digital hybrid massive MIMO configuration. The NL-BMD concept provides an intermediate precoder between the conventional LP and NLP, to overcome the weak points of both the approaches. The authors picked out the NL-BBD scheme typifying the NL-BMD family. Through numerical evaluation over OFDM, it has been clarified that, NL-BBD yields up to 18.8% performance improvement and 5.1 dB gain in sum-rate spectral efficiency on average, compared with the conventional BD. Moreover, we have verified that, at 10th percentile of CDF of sum-rate spectral efficiency, NL-BBD outperforms BD by 40% thanks to extra diversity gain. Even under dynamic fading, NL-BBD has shown more tolerance for channel transitions and still better performance than BD: performance loss due to channel transitions in average sum-rate spectral efficiency is 18.3% in NL-BBD whereas that in BD is over 20%, in a densely-populated scenario.