Fractional Analysis of Magnetohydrodynamics Maxwell Flow Over an Inclined Plate with the Effect of Thermal Radiation

Abstract

This current study provides a comprehensive examination of a novel method for studying the dynamics of a fractionalized Maxwell flow near an inclined plate, considering non-uniform mass transfer through a permeable media. Through the use of partial differential equations, incorporating heat and mass movement effects, the study employs a combination of generalized Fick’s and Fourier’s law with the Caputo operator. Transforming the fractionalized model into dimensionless form using appropriate dimensionless values, semi-analytical solutions for the non-dimensional transmitted fractional model are obtained via the Laplace transformation method. Through graphical analysis, the precise contributions of key parameters such as heat generation, radiation, and chemical reactions are elucidated, including their impacts on the calculated heat generation parameter (Qo), radiation parameter (Nr), and others. The study’s significance lies in its implications for the design of efficient heat exchangers, fluid flow systems, and cooling components in complex engineering systems, including nuclear reactors and power generation plants. Furthermore, the fractional derivative approach offers a more accurate representation of the viscoelastic behavior of materials like polymers, crucial for optimizing fabrication processes such as extrusion and molding. The insights gained from this study extend to the realm of miniaturized fluidic devices, including bio-analysis tools, lab-on-a-chip technology, and microfluidic drug delivery systems, where improved performance and control need a grasp of Maxwell fluid dynamics. The physical outcome of this research lays the groundwork for future investigations that will maximize heat transfer efficiency in real-world systems and give insightful information on the behavior of complicated fluids. We compute and display the skin friction, mass and heat transfer rate in tabular form.

Nomenclature

Symbol	Name	Unit	Symbol	Name	Unit
U	Velocity of fluid	$[ms^{-1}]$	u	Velocity of fluid	$[ms^{-1}]$
T	Fluid temperature	[K]	C	Fluid Concentration	$[Kgs^{-3}]$
$C_w$	Concentration level at the plate	$[Kgm^{-3}]$	$C_{\infty }$	Concentration flow far from the plate	$[Kgm^{-3}]$
$T_{w}$	Temperature of fluid at the plate	[K]	$T_{\infty }$	Temperature flow far away from plate	[K]
$C_{P}$	specific heat under constant pressure	$[Jkg^{-1}K^{-1}]$	D	Mass diffusivity	$[m^{2}s^{-1}]$
g	Acceleration due to gravity	$[ms^{-2}]$	k	Thermal conductivity of fluid	$[Wm^{-2}K^{-1}]$
$\nu$	Kinematic viscosity of fluid	$[m^{2}s^{-1}]$	$\mu$	dynamic viscosity	$[Kgm^{-1}s^{-1}]$
$\rho$	Fluid density	$[Kgm^{-3}]$	t	Time	[s]
$\beta _{T}$	Volumetric coefficient of thermal expansion	$[K^{-1}]$	$\beta _{C}$	Volumetric coefficient of mass expansion	$[m^{3}Kg^{-1}]$
$\alpha$	Fractional parameters	(-)	Ha	Magnetic parameter	(-)
s	Laplace transform variables	(-)	$B_{o}$	Uniform applied magnetic field	(-)
$\lambda$	Maxwell fluid parameter	(-)	Kr	Dimensional chemical reaction parameter	(-)
Q	Heat generation	(-)	M	Chemical reaction	(-)

1 Introduction

Scientists have shown a significant deal of interest in non-Newtonian fluids because of their many classical features. Their nature is quite different from that of viscous liquids. Non-Newtonian fluids are useful in various chemical processing, manufacturing, and engineering industries. Some of their applications include starch suspension, molten, blood, medicine, cosmetics, and paints. The fluid types that they belong to are differential, integral, and rate types. One useful rate-type model for precisely predicting the classical features of relaxations is the Maxwell model. It is effective in predicting elastic and viscous properties, as well as the effects of tensile and denser perspectives. Furthermore, the Maxwell model does not have shear-dependent viscosity to dedicate the study to understanding the interplay between fluid elasticity and the boundary layer. This model can be applied to many materials, such as polymeric solutions, crude oil, glycerin, and toluene.

Yang et al. [1] discussed the heat transfer technique to examine the slippage flow of a Maxwell medium. Khan et al. [2] looked at the fluid properties of a Maxwell flow on two parallel plates with periodically accelerating walls concerning the heat transfer phenomenon. Ali et al. [3] created a special Maxwell fluid numerical model by accounting for buoyant forces and activation energy. Next, Khan et al. [4] concentrated on the isothermal Maxwell fluid flow with mixed convection brought on by a revolving disk. Finally, for the Maxwell material, Khan et al. [5] investigated the Forchheimer medium flow quantitatively. Ramesh et al. [6] used numerical methods to explore the impact of bio-convection on Maxwell nanoparticle surface flow in the Riga plate. A vertical exploration of the elastic characteristics of rate-dependent materials using the Maxwell fractional model, which includes memory effects was conducted by Moosavi et al. [7]. Kumar et al. [8] used thermophoretic decomposition to study the dipole magnetized properties of Maxwell material. The Marangoni thermal significance in a Maxwell fluid with a thermal transfer mechanism was evaluated by Zhang et al. [9]. In addition, Shah et al. [10] provided an illustration of the viscosity of Maxwell fluid with memory impacts under pressure.

Because of its applications in solar physics, chemical engineering, and aeronautics, MHD free convection flow has drawn the attention of several researchers. Stars and planets are often composed of free convection flow, as is the coolant in nuclear reactors. Alim et al. [11] investigated the effects of Joule heating and heat transfer on MHD free convection flow on a vertical plate. For the boundary layer equations, the authors employed non-dimensionalization, and then used the Keller box scheme and the procedure of implicit finite difference to solve the resulting non-linear system of PDEs numerically. Chemical engineering, aeronautics, and planetary magnetosphere all heavily rely on MHD free convection fluxes.

The issues of mass and heat transport in MHD free convective flows over numerous domains with varying boundary conditions have drawn much interest from researchers. Samiulhaq et al. [12] analyzed the impact of magnetized area on the unsteady natural convection second-grade fluid on an infinitely vertical plate with a ramping wall temperature contained within a porous material. They discovered that, compared to an isothermal temperature, the amount of skin friction and velocity in the case of a ramping temperature is substantially smaller. Their analysis yielded two cases: a Newtonian fluid executing the same motion in the occurrence of an electromagnetic field and a second-grade fluid when both a magnetic field and porous material are present. Siddique et al. [13] analyzed the free convectional flow with the transfer of mass and heat of an electrically conductive viscous flow across a permeable material with variable permeability was examined. The movement of a flow domain half space was limited by a vertical permeable plate with constant heat flux, constant concentration, and constant linear movement in its plane at a constant velocity. Mjankwi et al. [14] explored the intriguing dynamics of unstable MHD nanofluid flows by introducing complexities like variable fluid properties, an inclined sheet geometry, heat radiation, and chemical reactions.

Recently, engineering and geographic applications have shown interest in the MHD transfer of mass and heat from various geometries implanted in a permeable media. Swain et al. [15] aimed to advance our understanding of fluid flow in real-world scenarios by analyzing the intricate interplay of heat radiation, magnetic forces, and the influence of porous material on a viscous, fluid that conducts electricity across a stretched surface, relevant to applications in various fields like manufacturing and energy extraction. Raju et al. [16] investigated how heat generated by friction and electrical resistance affects the consistent viscous flow across a porous channel, considering a fixed temperature at the bottom. The MHD and radiation impacts of irregular MHD natural convection flow in a permeable media over an infinite plate with ramping wall fluid temperature were studied by Ismail et al. [17].

Today, a wide range of physical and natural phenomena are modeled using the fractional calculus technique, including fluid mechanics, biosciences, engineering, economics, geophysics, petroleum, the food and food industries, oceanology, meteorology, the ship and aviation industry, etc. To solve fractional (IEs), PDEs, and ODEs, analytical techniques including the Laplace transform [18], Fourier transforms, variational iteration and Green function approaches have been well investigated. Additionally, coupled systems of ODEs have been created from boundary-layer equations by several authors using similarity transforms ([19], and references therein).

Other techniques to offer analytical approximation results for linear and nonlinear fractional differential equations were Homotopy Perturbation [22], Differential Transform [21], Adomian Decomposition [20], and Homotopy Analysis. Due to their non-linearity, the majority of fractional differential equations lack accurate analytical solutions; hence, numerical techniques are often utilized to approximate the solution. Rehman et al. [23] described the Prabhakar fractional derivative technique for generalized Mittag-Leffler kernel form problems of convection-free mass and heat flow of Maxwell liquid with Newtonian heating. Rehman et al. [24] examined the MHD free convective Casson flow with an emphasis on utilizing the Yang–Abdel–Aty–Cattani (YAC) operator, a non-integer-order derivative, to achieve analytical solutions. The consequences of second-grade flow due to thermal diffusion under exponential heating were discussed by Rehman et al. [25] with the use of (ABC), (CF), and (CPC). Riaz et al. [26] studied the solutions of the unsteady convection of an MHD Maxwell flow with ramping velocity and wall temperature with concentration utilizing specific functions. The fractional order bio-heat model, which is susceptible to thermal memory shocks, is a multi-parameter-modified Mittag-Leffler kernel-based model with unique function form solutions, according to Riaz et al. [27]. A Newtonian heating effect was reported by Rehman et al. [28] in a fractional study on heat-absorbing MHD radiation flow of rate-type fluid using a specific hybrid fractional derivative operator. Some results are helpful [29,30,31,32,33,34].

In this study, we investigated the impacts of heat radiation, uniform density unstable Maxwell flow caused by impulsive surface stretching, and a constant magnetic field and chemical reaction. In the design of furnaces, metal rolling, fins, casting, and levitation, thermal radiation is a basic idea. To achieve the extremely high temperatures needed for engineering procedures, nuclear power plants, spacecraft, gas turbines, and satellites, radiant heat transfer is employed. Key components also include mass transfer procedures such as fractional distillation, liquid extraction, drying, adsorption, distillation, and absorption. Zafar et al. [35] previously reported their model for an unsteady Maxwell fluid free convection flow on a porous multilayer inclined plate and used the classical derivative to find their results. This work uses Laplace transform methods to manage the momentum, temperature, and mass boundary surface of an inclined surface by studying the Caputo fractional model of Maxwell fluid using modified Fourier and Fick’s laws. The Maxwell fluid governing equations are discovered in this study by applying constitutive rules to the dimensionless non-Newtonian fluid governing equations. Additionally, the Laplace transform technique is used to provide analytical solutions for the fluid parameters of temperature, velocity, and concentration. Plotting of several graphs in the graphical section provides insight into the behavior of flow particles. Comparing the current fractional model to the classical model, it is more appropriate for displaying memory since the fractional derivative shows the function’s memory at the selected time. When fitting real data, such results might be helpful. For velocity, in the limiting situation, we derive the answers using ordinary derivatives from the literature, provided that fractional parameters are chosen, $\alpha = 1$.

2 Problem Formulation

Assumptions of the present Casson fluid model:

• The flow has one dimension and is unidirectional.

• The heat dissipation is ignored.

• The flow is compressible.

• Plate is considered of infinite length.

• Strong magnetic field $B_o$ operates in a transverse direction to the direction of flow.

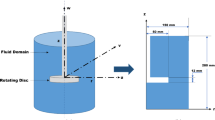
Consider a fluid enriched with mass and heat transfer capabilities (Maxwell flow) flowing through a permeable media past an inclined vertical plate. Initially, at time $t = 0$, the surrounding environment maintains a uniform concentration level of $C_\infty$, and both the plate walls and fluid remain stationary with a fixed temperature fluid $T_\infty$. As shown in Fig. 1, at time $t > 0$, the scenario undergoes a change: the temperature transfer from the plate to the flow intensifies, raising the temperature fluid to $T_w$. Additionally, the concentration level near the plate starts to increase from its initial value $C_w$.

Fig. 1

Flow geometry

Equation of momentum:

$$\begin{aligned} \rho \left( 1+ \lambda _o\frac{\partial }{\partial t}\right) \frac{\partial U}{\partial t}\!\!\!{} & {} =\mu \frac{\partial ^2 U}{\partial \xi ^2}+\rho g \beta _T \left( 1+ \lambda _o\frac{\partial }{\partial t}\right) (T-T_\infty )\cos \gamma +\rho g \beta _C \left( 1+ \lambda _o\frac{\partial }{\partial t}\right) (C-C_\infty )\cos \gamma \nonumber \\{} & {} -\left( 1+ \lambda _o\frac{\partial }{\partial t}\right) \sigma B^2_o U -\frac{\mu \phi }{k}U. \end{aligned}$$

(1)

Temperature equation:

$$\begin{aligned} \rho C_p \frac{\partial T}{\partial t} - \text {Q}(T-T_\infty )= - \frac{\partial q(\xi ,t)}{\partial \xi }+\frac{16 \sigma T^3_\infty }{3K}\frac{\partial ^2 T}{\partial \xi ^2}, \end{aligned}$$

(2)

with

$$\begin{aligned} q(\xi ,t) =-k \frac{\partial T}{\partial \xi }. \end{aligned}$$

(3)

Concentration equation:

$$\begin{aligned} \frac{\partial C}{\partial t}= - \frac{\partial J(\xi ,t)}{\partial \xi }-\text {K}_r(C-C_\infty ), \end{aligned}$$

(4)

with

$$\begin{aligned} J(y,t) = -D\frac{\partial C(\xi ,t)}{\partial \xi }. \end{aligned}$$

(5)

Where $u(\xi ,t)$ is the velocity fluid, $C(\xi ,t)$ and $T(\xi ,t)$ are the flow concentration and temperature, respectively, and $\lambda _o$ is a Maxwell fluid parameter. The symbol $\mu$ denotes the dynamic viscosity of a fluid, and $\beta _T$ and $\beta _C$ indicate the heat and mass expansion coefficient, respectively. The fluid electrical conductivity is denoted by $\sigma$, whereas $B_0$ represents the magnetic field. $C_p$ is a symbol for the fluid particular heat capacity. $D_n$ is a representation of mass diffusivity, whereas k indicates thermal conductivity.

This introduces the subsequent non-dimensional variables

$$\begin{aligned} \text {for} \,\,\,\, t = 0, \,\,\, u(\xi ,t)=0,\,\,\,\,\,\,\,C(\xi ,t)=C_\infty , \,\,\,\,\,\,\,T(\xi ,t)=T_\infty , \end{aligned}$$

(6)

$$\begin{aligned} \text {for }\,\,\, \xi = 0, \,\,\, u(\xi ,t)=0,\,\,\,\,\,\,\,C(\xi ,t)=C_w,\,\,\,\,\,\,\, T(\xi ,t)=T_w, \end{aligned}$$

(7)

$$\begin{aligned} \text {for}\,\,\,\,\xi \rightarrow \infty , \,\,\, u(\xi ,t)\rightarrow 0,\,\,\,\,\,\,\,C(\xi ,t)=C_\infty ,\,\,\,\,\,\,\, T(\xi ,t)=T_\infty . \end{aligned}$$

(8)

Introducing the dimensionless variables as follow

$$\begin{aligned}{} & {} u=\frac{U}{u_o},\,\,\,\,\,\,\,\,\,\,\,\, \tau =\frac{tu^2_o}{\nu }, \,\,\,\,\,\,\,\,\,\,\,\, y=\frac{u_o \xi }{\nu },\,\,\,\,\,\,\,\,\,\,\,\, \lambda = \frac{\nu }{u^2_o}\lambda _o, \,\,\,\,\,\,\,\,\,\,\,\,\phi =\frac{C-C_\infty }{C_w-C_\infty },\nonumber \\{} & {} \theta = \frac{T-T_\infty }{T_w-T_\infty },\,\,\,\,\,\,\,\,\,\,\,\, \delta _1 =\frac{J\nu }{Du_o ( C_w -C_\infty )}, \,\,\,\,\,\,\,\,\,\,\,\, \delta = \frac{q\nu }{ku_o (T_w - T_\infty )}. \end{aligned}$$

(9)

Using dimensionaless variables from (9), we obtain dimensionless model of (1)-(8) as follows

$$\begin{aligned} (1+ \lambda \frac{\partial }{\partial \tau })\frac{\partial u}{\partial \tau }= \frac{\partial ^2 u}{\partial y^2}+(1+ \lambda \frac{\partial }{\partial \tau })\text {Gr}\theta \cos \gamma +(1+ \lambda \frac{\partial }{\partial \tau })\text {Gm}\phi \cos \gamma -(1+ \lambda \frac{\partial }{\partial \tau })\sigma H_a u-\frac{1}{W}u, \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial \theta }{\partial \tau }=-\frac{1}{\text {Pr}}(1+\frac{4}{3}\text {Nr})\frac{\partial \delta (y,\tau )}{\partial y} + Q_o\theta , \end{aligned}$$

(11)

$$\begin{aligned} \delta (y,\tau ) = - \frac{\partial \theta }{\partial y}. \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial \phi }{\partial \tau } = -\frac{1}{\text {Sc}}\frac{\partial \delta _1(y,\tau )}{\partial y}-\text {M}\phi (y,\tau ), \end{aligned}$$

(13)

$$\begin{aligned} \delta _1(y,\tau ) = - \frac{\partial \phi }{\partial y}. \end{aligned}$$

(14)

The dimensionless IBCs now become

$$\begin{aligned} u(y,0)=0,\,\,\,\,\,\,\,\phi (y,0)=0,\,\,\,\,\,\,\, \theta (y,0)=0, \end{aligned}$$

(15)

$$\begin{aligned} u(y,0)=0,\,\,\,\,\,\,\,\phi (y,0)=1,\,\,\,\,\,\,\, \theta (y,0)=1, \end{aligned}$$

(16)

$$\begin{aligned} \text {for}\,\,\,\,y \rightarrow \infty , \,\,\, u(y,\tau )\rightarrow 0,\,\,\,\,\,\,\,\phi (y,\tau )=0,\,\,\,\,\,\,\, \theta (y,\tau )\rightarrow 0, \end{aligned}$$

(17)

here Grashof number is $\text {Gr}=\frac{\nu g \beta _T(T_w-T_\infty )}{u_o},$ mass Grashof is $\text {Gm}=\frac{\nu g \beta _T(C_w-C_\infty )}{u_o},$ Hartmann number is $H_a=\frac{\nu B^2_o \sigma }{\rho u^2_o},$ Prandtl number is $\text {Pr}=\frac{\mu C_p}{k},$ radiation parameter is $\text {Nr}=\frac{4\sigma T^3_\infty }{kK},$ Stephan-Boltzmann constant is $\sigma$, heat generation parameter is $\text {Q}_o=\frac{Q\nu }{u^2_o \rho C_p},$ Schmidt number is $\text {Sc}=\frac{\nu }{D}$ and Porosity parameter is $\text {W}=\frac{k u^2_o}{\nu ^2}$.

3 Generalized Model

Generalized Fourier’s and Fick’s laws are applied to build the fractional model that follows [36,37,38].

$$\begin{aligned} \delta (y,\tau ) = -\,\, ^{C}D^{1-\alpha }_\tau \frac{\partial \theta }{\partial y} \,\,\,\,\,\,\,\,\,\, 0 < \alpha \le 1, \end{aligned}$$

(18)

$$\begin{aligned} \delta _1(y,\tau ) = -\,\, ^{C}D^{1-\alpha }_\tau \frac{\partial \phi }{\partial y} \,\,\,\,\,\,\,\,\,\, 0 < \alpha \le 1, \end{aligned}$$

(19)

Equations (11), (13), (18), and (19) were used to arrive at the following result in simplex form

$$\begin{aligned} \frac{\partial \theta }{\partial \tau }=\frac{1}{\text {Pr}}(1+\frac{4}{3}\text {Nr}) ^{C}D^{1-\alpha }_\tau \frac{\partial \theta ^2(y,\tau )}{\partial y^2} + Q_o\theta (y,t), \end{aligned}$$

(20)

$$\begin{aligned} \frac{\partial \phi }{\partial \tau } = \frac{1}{\text {Sc}} \,\,^C D^{1-\alpha }_\tau \frac{\partial \phi ^2(y,\tau )}{\partial y^2}-\text {M}\phi (y,\tau ), \end{aligned}$$

(21)

where $^{C}D^{1-\alpha }_t(\cdot )$ represent the time fractional Caputo operator and its define as

$$\begin{aligned} \,\,^{C}D^{\alpha }_{t} R(t) = \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-\tau )^{-\alpha }R'(\tau )d\tau . \end{aligned}$$

(22)

Moreover, its Laplace form

$$\begin{aligned} L\{\,\,^{C}D^{\alpha }_{t} R(t)\}= s^{\alpha }L[R(t)]-s^{\alpha -1}R(0). \end{aligned}$$

(23)

We return to the time-fractional integral function to generate the more suitable version of (20) and (21).

$$\begin{aligned} \,\,I^{\alpha }_{t} R(t) = (K_{1-\alpha }*R)(t) = \frac{1}{\Gamma (\alpha )}\int _{0}^{t}R(s)(t-s)^{\alpha -1}ds. \end{aligned}$$

(24)

The fractional derivative described in (22) has an inverse operator in (24). The following may be used to write the (20) and (21) using the characteristics given in [39]:

$$\begin{aligned} ^{C}D^{\alpha }_\tau \theta (y,\tau ) =\frac{1}{\text {Pr}}(1+\frac{4}{3}\text {Nr}) \frac{\partial \theta ^2(y,\tau )}{\partial y^2} + Q_o\theta (y,t), \end{aligned}$$

(25)

$$\begin{aligned} ^{C}D^{\alpha }_\tau \phi (y,\tau ) = \frac{1}{\text {Sc}} \frac{\partial \phi ^2(y,\tau )}{\partial y^2}-\text {M}\phi . \end{aligned}$$

(26)

4 Solution of the Problem

In this section Laplace transform is applied on concentration, temperature and velocity equation and solution is obtained.

4.1 Calculation of Temperature

Recalling the initial condition (15), we obtain, after simplifying and using the Laplace transform to (16) and (25).

$$\begin{aligned} \frac{d^2 \bar{\theta }(y,s)}{d y^2} - \frac{\text {Pr} (s^\alpha -Q_o)}{1+\frac{4}{3}\text {Nr}} \bar{\theta }(y,s)=0, \end{aligned}$$

(27)

$$\begin{aligned} \bar{\theta }(0,s)=\frac{1}{s},\,\,\,\,\,\,\,\, \text {and}\,\,\,\,\,\,\,\, \bar{\theta }(\infty ,s)=0, \end{aligned}$$

(28)

where the Laplace parameter is represented by s.

The Laplace transformation formulation for any function X(y, t) is represented as $\bar{X}(y,s)$, which may be mathematically defined as

$$\begin{aligned} \bar{X}(y,s) = \int _{0}^{\infty }X(y,t)e^{-st}dt. \end{aligned}$$

Regarding the boundary conditions (28) the solution provided by differential equation (27) is

$$\begin{aligned} \bar{\theta }(y,s)=\frac{1}{s}\exp \left( -y\sqrt{{\frac{\text {Pr} (s^\alpha -Q_o)}{1+\frac{4}{3}\text {Nr}}}}\right) . \end{aligned}$$

(29)

4.2 Calculation of Concentration

By adopting starting condition (15) and using the Laplace transform to (16) and (26), we get

$$\begin{aligned} \frac{d^2 \bar{\phi }(y,s)}{d y^2}-\text {Sc}(s^\alpha +M)\bar{\phi }(y,s)=0, \end{aligned}$$

(30)

$$\begin{aligned} \bar{\phi }(0,s)=\frac{1}{s},\,\,\,\,\,\,\,\, \text {and}\,\,\,\,\,\,\,\, \bar{\phi }(\infty ,s)=0, \end{aligned}$$

(31)

The solution provided by differential equation (30) with conditions (31) is

$$\begin{aligned} \bar{\phi }(y,s)=\frac{1}{s}\exp \left( {-y\sqrt{\text {Sc}(M+s^\alpha )}}\right) . \end{aligned}$$

(32)

4.3 Calculation of Velocity

We have obtained the momentum solution and related conditions stated in (15)-(17) by utilizing the Laplace integral transformation on (10)

$$\begin{aligned} \frac{d^2 \bar{u}(y,s)}{d y^2}-\left[ (1+\lambda s)H_a+\frac{1}{W}+s(1+\lambda s) \right] \bar{u}(y,s) = -(1+\lambda s)\cos \gamma [\text {Gr}\theta (y,s) + \text {Gm} \phi (y,s)], \end{aligned}$$

(33)

subject to satisfy

$$\begin{aligned} \bar{u}(0,s)=0,\,\,\,\,\,\,\,\, \text {and}\,\,\,\,\,\,\,\, \bar{u}(\infty ,s)=0. \end{aligned}$$

(34)

After substituting the calculated concentration and temperature solutions, i.e., the values from (32) and (29) into (33), the modified velocity solution is expressed

$$\begin{aligned} \begin{aligned} \bar{u}(y,s) = c_1e^{-y\sqrt{(1+\lambda s)H_a+\frac{1}{W}+s(1+\lambda s)}}+c_2e^{-y\sqrt{(1+\lambda s)H_a+\frac{1}{W}+s(1+\lambda s)}} \\ -\text {Gr}(1+\lambda s)\cos \gamma \left[ \frac{1}{s}\exp \left( -y\sqrt{{\frac{\text {Pr} (s^\alpha -Q_o)}{1+\frac{4}{3}\text {Nr}}}}\right) \right] \\ - \text {Gm} (1+\lambda s)\cos \gamma \left[ \frac{1}{s}\exp \left( {-y\sqrt{\text {Sc}(s^\alpha +M)}}\right) \right] . \end{aligned} \end{aligned}$$

(35)

When we compute the values of constants $c_1$ and $c_2$ using the velocity beginning and boundary conditions as in (35), we obtain

$$\begin{aligned} \bar{u}(y,s)\!\!{} & {} =\frac{\text {Gr}(1+\lambda s)\cos \gamma }{s\left[ \frac{\text {Pr}(s^\alpha -Q_o)}{1+\frac{4}{3}\text {Nr}}-[(1+\lambda s)(s+H_a)+\frac{1}{W}]\right] }\left[ e^{-y\sqrt{(1+\lambda s)(s+H_a)+\frac{1}{W}}}-e^{-y\sqrt{\frac{\text {Pr} (s^\alpha -\text {Q}_o)}{1+\frac{4}{3}\text {Nr}}}}\right] \nonumber \\{} & {} +\frac{\text {Gm}(1+\lambda s)\cos \gamma }{s\left[ \text {Sc}(s^\alpha +M)-[(1+\lambda s)(s+H_a)+\frac{1}{W}]\right] }\left[ e^{-y\sqrt{(1+\lambda s)(s+H_a)+\frac{1}{W}}} - e^{-y\sqrt{\text {Sc}(s^\alpha +M)}}\right] . \end{aligned}$$

(36)

4.3.1 Classical Maxwell Fluid

In this instance, the velocity solution becomes $\alpha$ = 0 to provide the Ordinary Maxwell model in (36).

$$\begin{aligned} \bar{u}(y,s)\!\!{} & {} =\frac{\text {Gr}(1+\lambda s)\cos \gamma }{s\left[ \frac{\text {Pr}(1-Q_o)}{1+\frac{4}{3}\text {Nr}}-[(1+\lambda s)(s+H_a)+\frac{1}{W}]\right] }\left[ e^{-y\sqrt{(1+\lambda s)(s+H_a)+\frac{1}{W}}-e^{-y\sqrt{\frac{\text {Pr} (1-\text {Q}_o)}{1+\frac{4}{3}\text {Nr}}}}}\right] \nonumber \\{} & {} +\frac{\text {Gm}(1+\lambda s)\cos \gamma }{s\left[ \text {Sc}(1+M)-[(1+\lambda s)(s+H_a)+\frac{1}{W}]\right] }\left[ e^{-y\sqrt{(1+\lambda s)(s+H_a)+\frac{1}{W}}-e^{-y\sqrt{\text {Sc}(1+M)}}}\right] . \end{aligned}$$

(37)

4.3.2 Ordinary Newtonian Fluid

For the viscous fluid (classical) case, in this case, the velocity result becomes $\lambda$ = 0 in (37).

$$\begin{aligned} \bar{u}(y,s)\!\!{} & {} =\frac{\text {Gr}\cos \gamma }{s\left[ \frac{\text {Pr}(1-Q_o)}{1+\frac{4}{3}\text {Nr}}-[s+H_a+\frac{1}{W}]\right] }\left[ e^{-\xi \sqrt{s+H_a+\frac{1}{W}}-e^{-\xi \sqrt{\frac{\text {Pr} (1-\text {Q}_o)}{1+\frac{4}{3}\text {Nr}}}}}\right] \nonumber \\{} & {} +\frac{\text {Gm}\cos \gamma }{s\left[ \text {Sc}(1+M)-[s+H_a+\frac{1}{W}]\right] }\left[ e^{-y\sqrt{s+H_a+\frac{1}{W}}-e^{-y\sqrt{\text {Sc}(1+M)}}}\right] . \end{aligned}$$

(38)

4.3.3 Fractionalized Newtonian Fluid

In the case of the viscous fluid (fractional) situation, the velocity solution becomes if $\lambda$ = 0 in (36).

$$\begin{aligned} \bar{u}(y,s)\!\!{} & {} =\frac{\text {Gr}\cos \gamma }{s\left[ \frac{\text {Pr}(s^\alpha -Q_o)}{1+\frac{4}{3}\text {Nr}}-[s+H_a+\frac{1}{W}]\right] } \left[ e^{-y\sqrt{s+H_a+\frac{1}{W}}-e^{-y\sqrt{\frac{\text {Pr} (s^\alpha -\text {Q}_o)}{1+\frac{4}{3}\text {Nr}}}}}\right] \nonumber \\{} & {} +\frac{\text {Gm}\cos \gamma }{s\left[ \text {Sc}(s^\alpha +M)-[s+H_a+\frac{1}{W}]\right] }\left[ e^{-y\sqrt{s+H_a+\frac{1}{W}}-e^{-y\sqrt{\text {Sc}(s^\alpha +M)}}}\right] . \end{aligned}$$

(39)

5 Comparison and Analysis of Results

For instance, Fig. 22 displayed the classical Maxwell and fractional Maxwell models of fluids side by side. The fractional fluid instance travels more slowly than the typical Maxwell fluid example, which is an important point to remember. These figures also demonstrate that the velocity of fractional Maxwell flow is significantly smaller than that of regular Maxwell flow. Notably, for both fractional and ordinary models, the velocity field exhibits the same behavior for $\alpha \rightarrow 1$. The validity and accuracy of temperature are shown in Fig. 23, which is provided. Figures that contrasted the current results with fractional parameters $\alpha = 1$ and $Q_o = 0$ demonstrated the variations from the conventional solutions generated by Zafar et al. [35]. Our overall findings are confirmed to be accurate and valid in the limited form.

As we can see from Table 1, there is no difference in the velocity between the current and published values. Table 2 presents a quantitative assessment of the fractional parameter $\alpha$ impact on skin friction. In terms of $\alpha$, skin friction decreases. Table 3 quantitatively examines the influence of the fractional parameter $\alpha$ on the Nusselt number. Given $\alpha$, the Nusselt number decreases with it. Table 4 presents a numerical investigation of the influence of the $\alpha$ on the Sherwood number. Given a $\alpha$, the Sherwood number decreases.

5.1 Skin Friction

For a Maxwell fluid, the skin friction in dimensionless form is given by

$$\begin{aligned} S_k = \frac{\partial u(0,\tau )}{\partial y}. \end{aligned}$$

(40)

5.2 Nusselt Number

For a Maxwell fluid, the Nusselt number in dimensionless form

$$\begin{aligned} N_u = -\frac{\partial \theta (0,\tau )}{\partial y}. \end{aligned}$$

(41)

Table 1 Comparisons of dimensionless velocity

Table 2 Effect of fractional parameter

Table 3 Effect of fractional parameter

5.3 Sherwood Number

For a Maxwell fluid, the Sherwood number in dimensionless form

$$\begin{aligned} Sh = - \frac{\partial \phi (0,\tau )}{\partial y}. \end{aligned}$$

(42)

Table 4 Effect of fractional parameter

6 Discussion of Results

This article examines the effect of numerous physical parameters, including mass and heat Grashof numbers (Gm and Gr), Schmidt and Prandtl numbers (Sc and Pr), the Maxwell fluid parameter ($\lambda$), and the porosity parameter (W) on the Caputo operator of a Maxwell fluid flowing over a porous media. Once the fractional model is formed using modified Fick’s and Fouier’s Laws, it may be solved applying the Laplace transform. Furthermore, an evaluation and tabulation of the impacts of the aforementioned factors on Sherwood and Nusselt numbers, and skin friction are performed. Figures 2-14 shows how physical characteristics affect the profiles of temperature, velocity, and mass equations.

Fig. 2

Impact of Gr on the distribution of velocity

Fig. 3

Impact of Gm on the distribution of velocity

Fig. 4

Impact of Pr on the distribution of velocity

Fig. 5

Impact of Sc on the distribution of velocity

Fig. 6

Impact of $Q_o$ on the distribution of velocity

The influence of Gr and Gm on the Maxwell flow is seen in Figs. 2 and 3. As we raise the values of these parameters, the flow is accelerated by both Gr and Gm. The basic theory underlying this is the augmentation of thermal buoyant force. The rise in Gr and Gm signifies the attenuation of viscous forces by buoyancy forces, which in turn lowers resistance and increases fluid velocity. This is because the two quantities are inversely connected with viscous force and directly correlate with buoyant forces. The main distinction is that in Gm, buoyant forces rise as a result of solutal volumetric expansion, whereas in Gr, buoyant forces rise as a result of thermal volumetric expansion. Figure 4 illustrates how the Pr affects velocity. Physically speaking, this means that when the Pr rises, the velocity distribution contracts. Since the Pr is inversely correlated with thermal diffusivity and directly correlated with kinematic viscosity, a higher Prandtl number means the fluid’s internal resistance rises faster than its ability to conduct heat. This results in increased friction and decreased flow speed. Figure 5 shows the impact of Sc on the Maxwell velocity distribution. Physically speaking, the image accurately depicts the velocity profile as a diminishing function of the Schmidt number. Mass diffusion has an inverse relationship with Sc, while viscous forces have a direct connection with Sc. The velocity fluid decreases as a result of viscous forces predominating mass diffusion when Sc values rise.

Figure 6 was created to investigate the influence of Q on the temperature distribution. Q has a pronounced trend. The temperature distributions rise as a result of the system producing more heat as Q increases. Figure 7 illustrates how $\gamma$ affects the velocity distribution. As $\gamma$ grows, the velocity decreases, as the illustration makes clear. Figure 8 provides an explanation of the Hartmann number Ha’s impact. The velocity fluid drops with an increasing Hartmann number t value, while the boundary layer’s thickness rises. The cause of the fluid’s tendency to slow down at increasing magnetic field parameter values was that the Lorentz force opposed the flow motion more forcefully. The effect of porosity W is discussed in Fig. 9, where it is apparent from the profile pattern that as W develops, the fluid’s velocity slows down. This outcome is physically possible when the permeable medium’s spaces are extremely tiny, which can provide a significant amount of flow resistance.

Fig. 7

Impact of $\gamma$ on the distribution of velocity

Fig. 8

Impact of Ha on the distribution of velocity

Fig. 9

Impact of W on the distribution of velocity

Fig. 10

Impact of $\lambda$ on the distribution of velocity

Fig. 11

Impact of Pr on the distribution of temperature

Fig. 12

Impact of Nr on the distribution of temperature

Fig. 13

Impact of $Q_o$ on the distribution of temperature

Fig. 14

Impact of Sc on the distribution of concentration

Fig. 15

Impact of M on the distribution of concentration

Since $\lambda$ has an inverse connection with viscous forces and an exact correlation with inertial forces, rising $\lambda$ indicates that inertial forces would predominate over viscous forces, resulting in the velocity fluid is reduce as shown in Fig. 10. Figure 11 illustrates how Pr affects the distribution of temperature. The illustration shows a decay in the temperature distribution as Pr rises. This is true from a physical standpoint as rising Pr causes the thermal forces to weaken, which lowers the temperature. Figure 12 shows how the fractional Maxwell fluid’s capacity for heat transport is affected by the heat radiation parameter Nr. The application of thermal radiation raises the fluid particle’s temperature. The result is an increase in the kinetic energy of the particles and a high rate of collision between the fluid’s particles, which raises the temperature profile. As a result, the fluid’s temperature rises as Nr is increased. Figure 13 was created in order to examine Q influence on the temperature profile. Q follows a straightforward pattern. The temperature distribution rises as Q rises because the system generates more heat.

Fig. 16

Impact of $\alpha$ on the distribution of velocity

Fig. 17

Impact of $\alpha$ on the distribution of temperature

Fig. 18

Impact of $\alpha$ on the distribution of concentration

Fig. 19

Inverse of velocity distribution

Fig. 20

Inverse of temperature distribution

Fig. 21

Inverse of temperature distribution

Fig. 22

Comparison of velocity distribution

Fig. 23

Comparison of temperature distribution

A decrease in rising levels of Sc is seen in Fig. 14, which shows the concentration profile for a range of Sc values. Over time, the concentration profile stays constant. Considering that Sc is inversely correlated with mass diffusion and directly correlated with viscous forces. As a result of the fluid’s viscous forces increasing, the concentration profile decreases as Sc values rise. Figure 15 looks at how the fluid flow in the mass profile is affected by the chemical parameter. As M is raised, which corresponds to $\alpha$ = 0.3, these numbers demonstrate how the concentration of fluid increases. The concentration, temperature, and velocity profiles decrease if the fractional parameters increase for a large time as shown in Figs. 16, 17, 18. Lastly, Figs. 19, 20, 21 illustrate Graeve Stehfest’s and Tzou’s numerical approaches are compared, for temperature, concentration, and velocity profiles, respectively (Figs. 22 and 23). In these situations, Tzou’s and Stehfest’s algorithm curves coincide, proving the validity of the current findings.

7 Conclusion

This paper presents an analytical result of Maxwell flow over an inclined porous infinite plate. The analysis incorporates critical factors such as the Prandtl number (viscosity to diffusivity ratio), Maxwell fluid parameter (elasticity), Hartmann number (magnetic influence), inclination angle, chemical reaction parameter, Grashof number (buoyancy), radiation parameter, and internal heat generation parameter. The following are the most important results drawn from the study.

• Large values of Pr, Nr, Sc, and M, respectively, are observed to coincide with a fall in temperature and concentration graphs.

• It has been seen that the temperature, velocity, and concentration profile decrease as the fractional parameter values rise.

• The parameters Pr, Sc, $\gamma$, Ha, W, and $\lambda$ all have decreasing cumulative values when analyzing the velocity field.

• Gr, Gm, and $Q_o$ parameter values are increased to increase the velocity fluid.

• The ordinary Maxwell fluid is shown to have a comparatively higher velocity than the fractional Maxwell fluid.