1 Unraveling the Conundrum of the Einstein-Podolsky-Rosen (EPR) Paradox

In order to fully grasp the distinction between quantum entanglement and classical correlations, we will construct classical states that exhibit certain characteristics of quantum entangled states. These classical states possess indefinite values for individual outcomes, yet they are correlated or relationally encoded in such a way that measurement of a particular outcome on one side guarantees the outcome of the same experiment on the other side with certainty. The key difference between quantum and classical systems lies in the ontology of the microstates. While classical physical states are statistical and have completely specified individual value-definite properties, such value definiteness in quantum mechanics is postulated to hold true only for a specific context or a “star-shaped” multiplicity of contexts (as proposed in [1]), corresponding to the particular pure state in which the particle was prepared (preselected).

2 Enhancing Understanding of EPR-Type Configurations with Classical Shares

In this section, we investigate classical models of singlet states. While a deterministic outcome is obtained by considering individual micro-states, bundling these micro-states effectively leads to value indefiniteness in the macro-states.

The distinction between micro- and macro-states, rooted in the philosophical concepts of ontology and epistemology, respectively, finds parallels in classical statistical mechanics [2]. In Maxwell’s own words [3, p. 442], “I carefully abstain from asking the molecules which enter where they last started from. I only count them and register their mean velocities, avoiding all personal inquiries which would only get me into trouble.” Hence [4, p. 279], “The truth of the second law is, therefore, a statistical, not a mathematical, truth, for it depends on the fact that the bodies we deal with consist of millions of molecules, and that we never can get hold of single molecules.”

2.1 Peres’ Bomb Fragment Model: A Classical Mechanics Analog for the Quantum Mechanical ’Singlet’ State

To establish a concrete classical simulacrum, we begin by reviewing the explanatory model introduced by Peres in [5]. Peres proposed a system consisting of a bomb that is initially at rest, with zero angular momentum, which subsequently explodes into two fragments carrying opposite angular momenta. Dichotomic, that is, binary, observables of those individual fragments are then defined by \(\textbf{r}_{\varvec{\alpha }} = \textrm{sign} \left( \varvec{\alpha } \cdot \textbf{J} \right) \), where \(\varvec{\alpha }\) is a unit vector in an arbitrary direction, chosen by the observer, and \(\textbf{J}\) is that individual particle’s angular momentum.

Disregarding other physical categories and features, we can denote \(\textbf{J}\) as the “micro-state” of the explosion fragments. Ontological realism posits that \(\textbf{J}\) exists independently of any (finite) observing mind, as suggested by Stace [6]. However, a precise specification of \(\textbf{J}\) may require an infinite amount of information, such as specifying an orthonormal basis and its respective three real-valued coordinates.

The epistemology of the classical configuration in question requires further clarification. On one hand, it is theoretically possible to measure and operationalize \(\textbf{J}\) with arbitrary precision, for example, by probing it with dichotomic observables \(\textbf{r}_{\varvec{\alpha }}\) at any arbitrary angle \(\varvec{\alpha }\). The level of precision achieved depends on the specific choices made by the experimenter, including the means invested and the measurement setup. In classical systems, it may even be claimed that, at least in principle, the outcome of any stochastic process such as a coin toss an explosion, can be controlled, allowing for the production of a precisely specified state at will, rather than being purely random [7].

In contrast, to maintain analogy with quantum EPR configurations, and for practical considerations, it is assumed that the parameter \(\textbf{J}\) remains effectively hidden and unknown to the experimenter until the observable \(\textbf{r}_{\varvec{\alpha }}\) is measured. Additionally, the experimenter is assumed to have no effective control or choice over the individual particle’s angular momentum \(\textbf{J}\) due to the supposed uncontrollable detonation of the bomb in the environment, even if ontological realism suggests otherwise. Therefore, for practical purposes, by Jaynes’ principle [8] \(\textbf{J}\) is assumed to be equidistributed over all spatial directions, following Peres’ characterization of it as “unpredictable and randomly distributed.”

Note that, as per the construction of the experiment, two experimenters share individual fragments of the bomb. Due to the conservation of angular momentum (and the initial angular momentum being zero), each fragment carries the same absolute but opposing amount of angular momentum, expressed as “opposing” states denoted as \(\textbf{J}\) and \(-\textbf{J}\).

Due to the inherent and subjective nature of each experimenter \(\textbf{A}\) and \(\textbf{B}\), as well as the prevailing circumstances, the observed outcome \(\textbf{r}_{\varvec{\alpha }}\) or \(\textbf{r}_{\varvec{\beta }}\) of any single observation appears to be uncontrollable and unpredictable. This is a consequence of the effective concealment of the parameter \(\textbf{J}\) relative to the available means of \(\textbf{A}\) and \(\textbf{B}\).

It appears, albeit erroneously, that the outcomes on each side of the system occur in an irreducibly random manner. These outcomes seem to be spontaneously and continuously created—in theological terms, creatio continua—as if by a mysterious process, in relation to the measurement apparatus and the environment of sides \(\textbf{A}\) and \(\textbf{B}\), which may be spatially separated. This phenomenon is reminiscent of Bohr’s [9,10,11] concept of conditionality of phenomena [9,10,11], a contingency due to “the impossibility of any sharp separation between the behavior of atomic objects and the interaction with the measuring instruments which serve to define the conditions under which the phenomena appear.”

Despite this, joint outcomes from the same explosion exhibit correlations, which are observed statistically over many experimental runs and through averaging over multiple outcomes. A compelling geometric argument [5] establishes the existence of these correlations \(\langle \textbf{r}_{\varvec{\alpha }} \textbf{r}_{\varvec{\beta }}\rangle = 2 \theta / \pi - 1\) which are linear in the angle \(\theta = \angle { \varvec{\alpha } \varvec{\beta } }\) between \(\varvec{\alpha }\) and \(\varvec{\beta }\).

For pairs of outcomes associated with two fragments of the same bomb, it is always observed that when both experimenters \(\textbf{A}\) and \(\textbf{B}\) measure the same observable \(\textbf{r}_{\varvec{\alpha }}\), that is, \(\varvec{\beta }=\varvec{\alpha }\), they end up with exactly inverse events. Specifically, if \(\textbf{A}\) obtains outcome \(\textbf{r}_{\varvec{\alpha }} = \pm 1\), then \(\textbf{B}\) obtains outcome \(-\textbf{r}_{\varvec{\alpha }} = \mp 1\) along the same direction \(\varvec{\alpha }\), and vice versa. This phenomenon arises from the configuration of the original angular momentum being zero and the conservation of momentum, where if \(\textbf{A}\) measures the shares \({\pm }\) J, then \(\textbf{B}\) measures the (opposite) shares \({\mp }\) J, and vice versa.

The relational property described above is shown to be independent of the spatio-temporal distance between events. Even under strict Einstein locality conditions, where events are spatially separated such that no causal communication can occur between observers \(\textbf{A}\) and \(\textbf{B}\), this property holds. It may seem astonishing to these observers that despite being “far away” and causally (relativistically) separated, and despite each event appearing irreducibly random on their respective sides, the state is encoded in such a way that every random outcome on one side necessarily corresponds to the exact opposite outcome on the other side.

This seemingly perplexing aspect can be resolved by recognizing that the apparent randomness is an inherent illusion, as it is intrinsically determined by a shared state \(\textbf{J}\) that both spatially separated observers work on, from an ontological perspective. This unknown shared state serves as both the source of intrinsic randomness and the relational encoding. Importantly, in this case, the share and the two fragments representing it are value definite and precisely defined, rendering the randomness epistemic in nature. This is in contrast to Bohr’s suggestion of contextuality, as neither the environment nor any nesting of Wigner’s friend contributes to the outcome. One may also consider that the interface or Heisenberg cut is located at the share, that is, the individual fragments themselves. These fragments, as a reminder, carry the share \(\textbf{J}\) and possess definite values.

2.2 Finite Set Partitions in the Formation of Analogues to Singlet Quantum States

One feature of Peres’ model discussed earlier is the infinite amount of information necessary to specify the “hidden parameter” share \(\textbf{J}\). In what follows a finite quasi-classical set representable partition model will be presented that allows similar EPR-type considerations but delineates the basic assumptions even further. It is based on partition logics [12,13,14] that are pasting of blocks [15] many allowing a faithful orthogonal representation [16] by a vertex labeling of vectors that are mutually orthogonal within blocks [17, 18]. For the sake of comparison to the Clauser-Horne-Shimony-Holt (CHSH) configuration, consider again pairs of particles with four potential observables \(\textbf{a} , \textbf{a}' , \textbf{b} , \textbf{b}'\). Suppose that \(\textbf{a} , \textbf{a}\) are measured on experimenter \(\textbf{A}\)’s side, and \(\textbf{b} , \textbf{b}\) are measured on experimenter \(\textbf{B}\)’s side, respectively.

For the convenience of comparison with the CHSH configuration we again suppose that these observables are dichotomic, with outcomes \(+1\) or \(-1\); that is, more explicitly, \(\textbf{a} , \textbf{a}' , \textbf{b} , \textbf{b}' \in \{-1,+1\}\). Suppose further that we are forming “singlets” by “bundling opposite-valued” particle pairs, represented as ordered pairs \(\textbf{H}=\big [ \{\textbf{a} , \textbf{a}' , \textbf{b} , \textbf{b}' \} , \{-\textbf{a} , -\textbf{a}' , \) \( -\textbf{b} , -\textbf{b}' \} \big ]\) of two four-tuples per singlet state, forming the singlet states. There are \(2^4=16\) different types of pairs or singlet states, namely, in lexicoraphic order (\(-1 < +1\)),

$$\begin{aligned}{} & {} \big [ \{-1 , -1 , -1 , -1 \} , \{1,1,1,1, \} \big ],\\{} & {} \big [ \{-1 , -1 , -1 , 1 \} , \{1,1,1,-1, \} \big ],\\{} & {} \qquad \ldots \\{} & {} \big [ \{1,1,1,-1\} , \{-1 , -1 , -1 , 1 \} \big ], \text {and}\\{} & {} \big [ \{1,1,1,1, \} , \{-1 , -1 , -1 , -1 \} \big ]. \end{aligned}$$

A generalization to more observables is straightforward.

Suppose further that we are filling a generalized urn [19] with such ordered pairs, and draw (choose) them “at random”. We might imagine these ordered pairs as two balls painted uniformly black; printed on this black background are the symbols “−” (for value \(-1\)) or “\(+\)” (for value \(+1\)) in exactly four mutually different colors—one color for each one of the four observables \(\textbf{a} , \textbf{a}' , \textbf{b} , \textbf{b}'\). Suppose that experimenter \(\textbf{A}\) wears two types of eye-glasses, making visible either observable \(\textbf{a}\) or observable \(\textbf{a}'\); likewise, experimenter \(\textbf{B}\) wears two other types of eye-glasses, making visible either observable \(\textbf{b}\) or observable \(\textbf{b}'\). Suppose that, in this subtractive color scheme, all other three colors appear black. Each one of the two observers sees exactly one of the four observables. (More economically, only two colors could be used, assuming that the two experimenters are isolated from each other. In such a case, the same two colors can be used on both sides.)

The “hidden parameters” in this case are the values of \(\textbf{a} , \textbf{a}' , \textbf{b} , \textbf{b}'\) in the state or share \(\textbf{H}\); and yet the way this model or game is constructed, every single experimental run accesses only two of them, corresponding to the choices \(\textbf{a}\) versus \(\textbf{a}'\), and \(\textbf{b}\) versus \(\textbf{b}'\). (Of course, experimenters may cheat and put off their eyeglasses, thereby seeing the full state with all variations.)

Classical probabilities and expectations of such models can be obtained by forming the convex sum over all extreme cases or states. In particular, the CHSH bounds to these probabilities and expectations are obtained by (i) first interpreting the tuples codifying these 16 extreme cases or two-valued states as vector coordinates (with respect to an orthonormal basis such as the Cartesian standard basis), (ii) then consider the convex polytope defined by identifying these 16 vectors as vertices of the polytope (in four-dimensional vector space \(\mathbb {R}^4\)), and (iii) finally solving the hull problem, yielding the hull inequalities characterizing the “inside-outside” borders of this convex polytope [20,21,22,23].

As mentioned earlier, we must make a distinction between ontology versus epistemology, or, in another conceptualization, extrinsic versus intrinsic, operational observables. In this case, it is transparent that the seemingly random occurrence of outcomes originated in the choice or draw of the pair from the (generalized) urn. There is no influence of the environment on the outcome, and thus contextuality in the way possibly imagined by Bohr appears to be absent.

2.3 Microstates Versus Macrostates

The inherent uncertainty of experimental outcomes in classical cases arises from the lack of knowledge in the specific selection of certain elements: in the Peres model, it is the angular momentum vectors of the fragments denoted as \(\textbf{J}\), and in the discrete generalized urn model described earlier, it is the random selection of particular elements \(\textbf{H}\) from the set of ball pairs. Since we are either unwilling or unable or limited in directly observing these individual micro-states, we refer to the resulting outcomes as exhibiting ‘irreducible randomness’. This irreducibility is rooted in our epistemic limitations in capturing and comprehending the individual share as a microstate.

When the microstate is specified, the correlation for identical measurements becomes perfect. However, for non-identical measurements, the share \(\textbf{J}\) produces linear correlations given by the equation: \(\langle \textbf{r}_{\varvec{\alpha }} \textbf{r}_{\varvec{\beta }}\rangle = 2 \theta / \pi - 1\) where \(\theta \) represents the relative angle in the plane perpendicular to the fragment’s velocity. The correlations in the discrete urn case are bound by linear constraints

$$\begin{aligned} -1\le & {} E_{13}, E_{14}, E_{23}, E_{24} \le 1, \nonumber \\ -2\le & {} -E_{13} +E_{14} +E_{23} +E_{24} \le 2,\nonumber \\ -2\le & {} E_{13} -E_{14} +E_{23} +E_{24} \le 2,\nonumber \\ -2\le & {} E_{13} +E_{14} -E_{23} +E_{24} \le 2,\nonumber \\ -2\le & {} E_{13} +E_{14} +E_{23} -E_{24} \le 2, \end{aligned}$$
(1)

called the “conditions of possibly experience” by Boole, who encountered the following challenge [22, 24, 25]: When provided with (rational) numbers representing the relative frequencies (or reals representing the probabilities of expectation) of specific events, and these events exhibit logical interconnections, a new layer of constraints emerges beyond the basic requirements of non-negativity and being less than one for each number. In instances where events are intricately linked by logical relations, additional equalities or inequalities arise among these numerical values. Consequently, the central issue is to ascertain the precise numerical relationships—expressed through a combination of equalities and inequalities—arising from a defined set of logical relations among the events. The task involves unraveling the intricate numerical fabric woven by the interplay of logic and frequency, thereby elucidating the underlying structure of these interconnected events.

A systematic way of deriving Boole’s “conditions of possibly experience” is by enumerating all possible “extremal” configurations—formalized by the two-valued states supported by the logic of events—and interpreting them as vertices of a convex polytope, whose equivalent representation is in terms of its hull, thereby solving the hull problem [20, 21, 26]. Some of Boole’s conditions have been rediscovered by physicists in recent years, such as Bell-type or inequalities. Indeed, the last four of these linear constraints in (1) are called CHSH inequalities for historical reasons. Relative to the assumptions, such as value definiteness of all hypothetical (counterfactual) observables and strict Einstein locality, As they are violated by quantum events, Boole’s “conditions of possibly experience” pose a challenge for the classical interpretation of quantum mechanics.

3 Value (in)Definiteness in EPR Type Configurations with Quantum Shares

Quantum mechanics postulates that a pure state, such as the entangled singlet Bell state \(\vert \Psi \rangle = \frac{1}{2}\left( \vert +- \rangle - \vert -+ \rangle \right) \), provides the most comprehensive representation of a quantized system. Any entangled state, including \(\vert \Psi \rangle \), encodes a certain degree of value indefiniteness in its individual constituents [27, 28, 29, §10]. Due to the unitarity of quantum mechanics, if a state specification is shifted or rescrambled to relational properties, it results in a tradeoff or a zero-sum game of information: any increase in relational information encoded into a quantum system must be compensated by a decrease in individual value definiteness of the components of the composite system involved [30]. In the case of \(\vert \Psi \rangle \), the value indefiniteness of each component is maximal, as there is a 50:50 chance of finding the respective particles in the single-particle states \(\vert - \rangle \) and \(\vert + \rangle \) individually, respectively.

We may hypothesize that \(\vert \Psi \rangle \) could potentially be considered as a macro-state, similar to classical examples mentioned earlier, while there might be microstates analogous to \(\textbf{J}\) or \(\textbf{H}\). This hypothesis can be ruled out either through statistical analysis [5], or by employing proof by contradiction [31,32,33,34,35]. It is important to note that these theorems are contingent upon the assumptions made, particularly the existence of definite values that reflect potential but counterfactual experimental outcomes, and their independence from the measurement context or type.

However, when considering Einstein’s original motivation for the EPR paper as explained to Schrödinger [36,37,38], the ontological irreducible randomness (or contextual behavior) exhibited by both ends of the entangled pair, along with the perfect singlet correlation, presents a perplexing and seemingly contradictory phenomenon. How does the second constituent of the pair “know” the outcome produced by the first constituent, possibly influenced by its local measurement context and the disposition of the measurement instrument? Unlike in the (quasi-)classical cases discussed in earlier sections, there is no discernible, albeit potentially hidden, information or share that corresponds to or determines the single outcomes encoded in the quantum share.

This challenge is particularly pronounced when the events or outcomes, along with their local measurement contexts, are spatially separated under strict Einstein locality conditions [39]. Moreover, in such cases, the temporal succession of events or outcomes becomes a matter of conventions determined by observational means, as this depends on the reference frame, and could occur simultaneously or sequentially. In Einstein’s terms [37], “The real state of \(\textbf{B}\) thus cannot depend upon the kind of measurement I carry out on \(\textbf{A}\).” (German original: “Der wirkliche Zustand von B kann nun nicht davon abbhängen, was für eine Messung ich an A vornehme.”)

In the quantum case, it is not primarily the correlation function that is of significance, which in this case is described by \(\cos \theta \) (in contrast to the linear classical correlation \(2 \theta / \pi - 1\) mentioned earlier). Rather, it is the inherent and irreducible (by whatever quantum means) ambiguity or indefiniteness in the values of the apparently “isolated” constituents of the Bell singlet state \(\vert \Psi \rangle \) in all spatial directions that plays a crucial role. I purposely used the term ’isolated’ in quotations, because the concept of isolation may be a fallacy, an illusion, a fantasy. In the realm of quantum theory, the constituents of an entangled multi-partite state lack operational and theoretical separateness.

For instance, if we were to measure a pair of such particles that are separated by a significant distance (e.g., lightyears) apart from each other in space-like fashion, regardless of the measurement direction chosen (as long as the directions at both ends are identical), we would obtain

  1. (i)

    value indefiniteness: any individual outcome on each of the two ends occurs randomly, reflecting value indefiniteness of individual observables; and yet,

  2. (ii)

    relational encoding: those outcomes are the exact opposite of each other, reflecting the relational encoding of the particle pair.

It is important to highlight that local contextuality, as described by Bohr, cannot be at play on either side of the measurement in question. In the case of the singlet state, where the individual state of any of the two constituents is indefinite, the outcome of the measurement would only be influenced by the local environment, as it provides the sole source of information. This would result in maximal or total contextuality, where the outcome conveys no information about the state, but only reflects the measurement environment. However, the question arises: how can two seemingly uncorrelated and spatially separated environments, potentially light years apart, produce perfect (anti-)correlations in individual outcomes of joint measurements for each pair with a share devoid of any local (possibly hidden) information?

Einstein proposed a solution to the challenges of quantum entanglement by rejecting the idea of wave function completeness and embracing the concept of hidden parameters. For example, a wave function such as \(\vert \Psi \rangle = \frac{1}{2}\left( \vert +- \rangle - \vert -+ \rangle \right) \) could correspond to a macrostate that groups or bundles together \(\vert +- \rangle \) and \(\vert -+ \rangle \). The microstate, for a specific measurement direction \(\varvec{\alpha }\) on both sides, could then be either \(\vert +- \rangle \) or \(\vert -+ \rangle \).

An objection to this proposal is that it seems ad hoc, as it would require choosing between \(\vert +- \rangle \) or \(\vert -+ \rangle \) for every direction \(\varvec{\alpha }\), resulting in an infinite amount of information in the microstate. However, a response to this objection is that even in the classical case, a precise choice of \(\textbf{J}\) would also require an infinite amount of information. This infinite amount of information or specification may even be true for the specification of any quantum observable or state, thereby challenging the alleged finiteness of information encoded in a quantum state of finite particles [30].

An alternative approach to consider is the hypothesis altogether of discarding the notion of spatio-temporal distinctness among the elements of an entangled state, which would challenge the principle of Einstein locality. This paradigm shift would necessitate a comprehensive reevaluation of how space-time categories are formed. We plan to address this intriguing question in a forthcoming publication, where we will delve deeper into this concept.

4 Elastic Band Toy Model for Classical Local Simulation Value Indefiniteness and Relational Encoding

The following should not be interpreted as a claim about the fundamental nature of reality, but rather as a conceptual framework for constructing classical local model analogues that can provide a basis for understanding capacities of quantized systems. For the purpose of demonstration, we propose a modified and “inverted” elastic sphere model, inspired by the work of Aerts and de Bianchi [40,41,42,43,44], that may be considered “local” under certain circumstances, and satisfies the criteria of value indefiniteness and relational encoding mentioned earlier.

In this model, depicted in Fig. 1(a), the dichotomic observable \(\textbf{A}\) is characterized by the angle \(\varvec{\alpha }\) relative to the angle of the state \(\textbf{J}\). The state is represented as an elastic string \(\textbf{J}\), and is further characterized by a single, unique breaking point x. In each experiment, the breaking point is pre-determined, and for multiple experiments, the breaking points are evenly distributed along the entire length of the elastic string. Thus, effectively,

$$\begin{aligned} A = \textrm{sgn} \big ( \textbf{J} \cdot \textbf{A} - x \big ). \end{aligned}$$
(2)
Fig. 1
figure 1

(a) “Inverted” elastic string model of Aerts and de Bianchi [40, 42, 43]: A stands for the observable located on the unit circle. The state J is characterized by its angle (aka position of the sphere, in this drawing it is at angle zero), as well as its single, unique breaking point x. \(\varvec{\alpha }\) is the angle between J and A. The “quantum-type” cosine law results from the orthogonal projection of A onto J at point \(\textbf{A}_\textbf{J}\), as well as from the assumption that the breaking point x is equidistributed along the line segment \(\overline{\textbf{J}_+ \textbf{J}_-}\). Whenever x lies within \(\overline{\textbf{J}_+ \textbf{A}_\textbf{J}}\) the observable \(\textbf{r}_{\varvec{\alpha }}\) is associated with \(+1\); otherwise it is \(-1\). (b) The same elastic string model with two observables A and B

Full size image

4.1 Single Observable Probabilities and Expectations

The angle between the observable vector \(\textbf{A}\) and the elastic string vector \(\textbf{J}\) is denoted as \(\varvec{\alpha }\). It is assumed that the breaking point x of the elastic string is uniformly distributed along the line segment \(\overline{\textbf{J}_+ \textbf{J}_-}\), where \(\textbf{J}_+\) and \(\textbf{J}_-\) are the endpoints of the segment. The radius of the unit circle is given as 1.

The probability that the breaking point will be observed as lying between \(\textbf{J}_+\) and the projection of \(\textbf{A}\) onto \(\textbf{J}\), denoted as \(\textbf{A}\textbf{J}\), can be calculated as the length of the line segment \(\overline{\textbf{J}_+ \textbf{A}\textbf{J}}\), which is equal to \(1 + \cos \varvec{\alpha }\), divided by the length of the diameter of the circle; that is, \(P_+(\varvec{\alpha })= \frac{1}{2}\left( 1 + \cos \varvec{\alpha } \right) =\cos ^2(\varvec{\alpha }/2)\). Likewise, \(P_-(\varvec{\alpha })=1-P_+(\varvec{\alpha })= \frac{1}{2}\left( 1 - \cos \varvec{\alpha } \right) =\sin ^2(\varvec{\alpha }/2)\). The expectation is an affine transformation of the probabilities; that is, \(E(\varvec{\alpha })=P_+(\varvec{\alpha })-P_-(\varvec{\alpha })= 1 - 2 P_-(\varvec{\alpha })= -1 + 2 P_+(\varvec{\alpha })= \cos \varvec{\alpha }\).

4.2 Joint Probabilities and Correlations

EPR-type configurations involving elastic band models can be conceptualized by considering pairs of identical elastic bands that share the same initial states. This means that both bands need to be aligned along the same ray, and their breaking points should be inversely identical.

In the case of a “singlet” configuration, the orientation of the elastic bands should be relatively inverse. This can be visualized by imagining two initially identical bands, with one of the bands rotated by 180 degrees around its midpoint, so that the directions of the bands are essentially opposite to each other.

For two observables \(\textbf{A}\) and \(\textbf{B}\) in a configuration depicted in Fig. 1(b) with the relative angle \(\varvec{\theta } = \varvec{\beta } - \varvec{\alpha }\) between the measurement directions \(0\le \varvec{\alpha } \le \pi \) and \(0\le \varvec{\beta } \le \varvec{\alpha }\) associated with \(\textbf{A}\) and \(\textbf{B}\), respectively, an analog argument counting the length of the respective line segments on \(\textbf{J}\) yields

$$\begin{aligned} P_+( \varvec{\alpha }, \varvec{\beta } )= & {} \frac{1}{2}\big [ \left( 1 - \cos \varvec{\beta } \right) + \left( 1 + \cos \varvec{\alpha } \right) \big ] \nonumber \\= & {} 1+ \frac{1}{2} \left( \cos \varvec{\alpha } - \cos \varvec{\beta } \right) ,\nonumber \\ P_-( \varvec{\alpha }, \varvec{\beta } )= & {} \frac{1}{2} \left( \cos \varvec{\beta } - \cos \varvec{\alpha } \right) ,\nonumber \\ E( \varvec{\alpha }, \varvec{\beta } )= & {} P_+( \varvec{\alpha }, \varvec{\beta } ) - P_-( \varvec{\alpha }, \varvec{\beta } ) \nonumber \\= & {} 1+ \cos \varvec{\alpha } - \cos \varvec{\beta } \nonumber \\= & {} 1+ \cos \varvec{\alpha } - \cos \left( \varvec{\alpha } + \varvec{\theta } \right) . \end{aligned}$$
(3)

A plausibility check indicates that this correlation function lies in-between \(-1\) and \(+1\): for \(\varvec{\alpha } = - \varvec{\theta } =\pi \) and \(\varvec{\beta } = 0\), \(E( \pi , 0 ) = -1\); likewise, for \(\varvec{\alpha } = \varvec{\beta }\) and thus \(\varvec{\theta } = 0\), \(E( \pi , 0 )= +1\).

A similar calculation for \(\varvec{\beta } \ge \varvec{\alpha }\) yields the general form for \(0 \le \varvec{\alpha }, \varvec{\beta } \le \pi \):

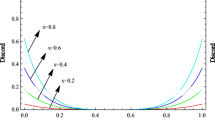
$$\begin{aligned} E( \varvec{\alpha }, \varvec{\beta })= & {} 1+ \big ( \cos \varvec{\alpha } - \cos \varvec{\beta } \big ) \textrm{sgn} \big (\varvec{\alpha } - \varvec{\beta } \big ) \nonumber \\= & {} E( \varvec{\alpha }, \varvec{\alpha } + \varvec{\theta })= 1- \big [ \cos \varvec{\alpha } - \cos \left( \varvec{\alpha } + \varvec{\theta } \right) \big ] \textrm{sgn} \varvec{\theta } , \end{aligned}$$
(4)

as depicted in Fig. 2.

Fig. 2
figure 2

Correlation function of the elastic band model

Full size image

Suppose now a protocol in which \(\varvec{\alpha }\) is always aligned along with the share \(\textbf{J}\), such that \(\varvec{\alpha }=0\). Then the correlation in (4) reduces to

$$\begin{aligned} E( \varvec{\alpha }=0, \varvec{\beta } = \varvec{\theta } ) \equiv E( \varvec{\theta } ) = \cos \varvec{\theta }. \end{aligned}$$
(5)

Another option would be to assume that the direction of \(\textbf{J}\) is uniformly distributed in the interval \([0, \pi ]\), resulting in

$$\begin{aligned} E( \varvec{\theta } )= & {} \frac{1}{\pi } \int _0^\pi \big [ 1+ \cos \varvec{\alpha } - \cos \left( \varvec{\alpha } - \varvec{\theta } \right) \big ] d \varvec{\alpha } \nonumber \\= & {} 1 - \frac{2}{\pi } \sin \varvec{\theta } . \end{aligned}$$
(6)

4.3 Locality and Contextuality

The quantum-type cosine form of the two-particle expectation function \(E(\textbf{A},\textbf{B})\) should give rise to violations of classical Boolean “conditions of possible experience” [20, 22], in particular, the CHSH inequality \(-2 \le E(\varvec{\alpha },\varvec{\beta }) + E(\varvec{\alpha },\varvec{\beta }') + E(\varvec{\alpha }',\varvec{\beta }) - E(\varvec{\alpha }',\varvec{\beta }') \le 2\). It is maximally violated [45, 46] by quantum mechanics at, for instance, \(\varvec{\alpha }= 0\), \(\varvec{\alpha }'= \pi / 2\), \(\varvec{\beta } = \pi / 4\), \(\varvec{\beta }' = -\pi /4\). This can be readily verified by inserting into the quantum expectation functions \(E(\varvec{\alpha },\varvec{\beta }) = \cos ( \varvec{\beta } - \varvec{\alpha } )\), cosine of the (relative) angles, so that \( E(0,\pi / 4) + E(0,-\pi /4) + E(\pi / 2,\pi / 4) - E(\pi / 2,-\pi /4) = \cos (-\pi /4)+ \cos (\pi /4)+ \cos (\pi /4)- \cos (3\pi /4) = 2\sqrt{2}\).

The elastic band model, when analyzed using a specific protocol, exhibits a correlation pattern that is similar to quantum mechanics, as shown by the expectation function (5). This suggests that, for one particular context (but not for other contexts, as discussed later), like quantum mechanics, the elastic band model may also allow for violations of the CHSH inequality.

However, this hypothesis is challenged by Peres’ argument [5], who thoroughly examined all classically possible configurations and demonstrated that the convex sum of their entries never violates the CHSH inequality. This raises the question of how violations of the CHSH inequality could occur in the elastic band model, despite Peres’ findings.

In the following sections, we will present arguments in favor of an adaptive protocol that adjusts \(\varvec{\alpha }\) and \(\varvec{\alpha }'\) to align with the direction of the share \(\textbf{J}\), as an approach capable of violating the CHSH inequality. This particular type of adaptation refers to adapting or changing the relative positioning of the pairs of observables \({\varvec{\alpha },\varvec{\beta }}\), \({\varvec{\alpha },\varvec{\beta }}\), \({\varvec{\alpha }',\varvec{\beta }}\), and \({\varvec{\alpha }',\varvec{\beta }'}\) defining the four contexts containing \(\varvec{\alpha }\) or \(\varvec{\alpha }'\) on one side of the EPR arrangements relative to the direction of the shared \(\textbf{J}\). This (re)alignment, which also affects the position of \(\varvec{\beta }\) or \(\varvec{\beta }'\) relative to \(\textbf{J}\) on the other side of the EPR arrangements, effectively resets those contexts in terms of \(\textbf{J}\) and thereby allows a reshaping or rescrambling of the correlation function to a uniform cosine form that is instrumental for violations of a CHSH inequality.

Without these (re)alignments, the correlation function would not maintain its uniform quantum-type cosine form. This absence of (re)alignments would enable a context-independent assignment of (counterfactual) observables in a Peres-type valuation table, consequently preventing any violation of the CHSH inequalities imposed by classical value definiteness. Conversely, the adaptive protocol results in a nonlocal, context-dependent assignment of (counterfactual) observables in a Peres-type valuation table, thereby allowing for violations of the CHSH inequalities.

It is worth noting that delayed choice protocols pose limitations on adaptation. Therefore, under strict Einstein locality conditions, as enforced in studies [39, 47], non-adaptive protocols can be employed, but adaptive protocols are not feasible.

First, let us observe that a non-adaptive protocol allowing delayed choice under strict Einstein locality conditions yielding a correlation function of the type of (4) does not violate the CHSH inequality, say, for \(\varvec{\alpha }= 0\), \(\varvec{\alpha }= \pi / 2\), \(\varvec{\beta } = \pi / 4\), \(\varvec{\beta }' = -\pi /4\); indeed it renders the value \(\sqrt{2}\) for the CHSH sum \(E(\varvec{\alpha },\varvec{\beta }) + E(\varvec{\alpha },\varvec{\beta }') + E(\varvec{\alpha }',\varvec{\beta }) - E(\varvec{\alpha }',\varvec{\beta }')\). Indeed, for \(\varvec{\beta },\varvec{\beta }' \le \varvec{\alpha },\varvec{\alpha }'\) the CHSH sum reduces to \(2 \big ( 1 + \cos \varvec{\alpha } - \cos \varvec{\beta } \big ) \le 2\) which, as per assumption, \(\varvec{\alpha } \ge \varvec{\beta }\), is bounded from above and below by the classical bounds. The second to fifth colums of Table 1 enumerate a simulation (similar to Peres’ Table 1[5]) of all four terms of the CHSH inequality in a non-adaptive setting.

However, when utilizing an adaptive protocol, such as the one resulting in (5), it is possible for the absolute value of the CHSH (Clauser-Horne-Shimony-Holt) sum to surpass the maximal classical value of 2. This occurs due to the significance of the complete context, including the need to discern between either \(\textbf{A}\) or \(\textbf{A}'\) in order to unambiguously define \(\textbf{B}\) and \(\textbf{B}'\). In Table 1, columns seven to ten present a simulation of all four terms of the CHSH inequality in an adaptive setting, employing the same configurations as the simulation for the non-adaptive protocol mentioned previously.

Table 1 Peres-type valuation table for 20 runs of the elastic string model: the first number indicates the position of the breaking point x, the following group of four numbers enumerates instances of single outcomes of the observables \(\textbf{A}\), \(\textbf{A}'\), \(\textbf{B}\), and \(\textbf{B}'\), the second group of five numbers enumerates the respective expectations \(\textbf{A}\textbf{B}\), \(\textbf{A}\textbf{B}'\), \(\textbf{A}'\textbf{B}\), and \(\textbf{A}'\textbf{B}'\) and the resulting CHSH sum for the non-adaptive protocol, and the second group of five numbers enumerates these expectations and the resulting CHSH sum for the adaptive protocol
Full size table

The evaluation of correlation functions in the CHSH sum necessitates knowledge not only of the share but also of the specific context selected, which includes the choice between \(\textbf{A}\) or \(\textbf{A}'\), as well as between \(\textbf{B}\) or \(\textbf{B}'\). In order for violations of the CHSH inequality to occur, there must be uniformity, which implies that the form of the correlation function must remain invariant across all variations of the (classical) share. It is insufficient to render, say, the classical cosine form of the quantum correlation function for a particular configuration, such as setting \(\varvec{\alpha } = 0\) in the general correlation function \( 1+ \cos \varvec{\alpha } - \cos \left( \varvec{\alpha } + \varvec{\theta } \right) \) of (3), thereby obtaining the quantum \(\cos \varvec{\theta }\) form. Because any other configuration \(\varvec{\alpha } \ne 0\) involving shares \(\textbf{J}\) not aligned with \(\varvec{\alpha }0\) yields correlations that may “compensate” and “regularize” the CHSH form to its classical bounds.

5 Plasticity of the Elastic Band Model

The elastic band model exhibits a degree of plasticity, allowing for the deformation of the circumference of a circle, as illustrated in Fig. 1. In particular, by applying pressure or other forms of distortion to the outer circle, elliptic shapes, as depicted in Fig. 3, can be obtained while maintaining a constant length of the elastic band. However, this deformation results in changes to the length of the convex shape, necessitating compensation and renormalization in terms of the parametrization based on the length of the outer shape.

The model indicates the existence of two limits in this process. The first limit corresponds to a classical scenario achieved by decreasing the minor axis in Fig. 3(a), which increases the eccentricity. The second limit yields a unit step function centered around the mid-point of the elastic band, as described in a previous work by Krenn and the author [48], by increasing the eccentricity through increasing the major axis in Fig. 3(b). It is worth noting that similar distortion transformations have been discussed previously [26], albeit without a concrete model.

Fig. 3
figure 3

“squeezed” elastic band models, whereby the length of the elastic band is kept constant but the circumference is distorted: (a) towards weaker-than-quantum correlations; (b) towards stronger-than-quantum, classical type correlations

Full size image

6 Discussion and Outlook

The general goal of this paper was twofold. First, to point out that it is not sufficient to recover, by classical means, a quantum-type correlation function or some non-linear, trigonometric form (such as cosine) of probability for elementary propositions in order to fully reconstruct quantum predictions. And second, and more importantly, it has been argued that the mind-boggling features of quantum mechanics reveal themselves only through delayed choice measurements under strict Einstein locality conditions.

Without the enforcement of delayed choice under strict Einstein locality conditions, we can still simulate epistemic randomness using classical means and the communication of the context. Epistemic randomness is a type of randomness that arises due to our limited knowledge about the system, rather than inherent properties of the system itself. Despite the limitations associated with epistemic versus ontic randomness, we can observe total relational dependence between pairs of observables. In other words, these models yield observed quantum phenomena that, for all practical purposes (as referenced in [49]), are consistent with quantum predictions within our operational means and practical purposes.

To gain a deeper understanding of these phenomena, we have constructed a classical model based on Aerts’ elastic band model, with certain modifications. We computed the corresponding quantum-type probabilities and correlation functions for “singlet” states using this classical model, while making certain assumptions, particularly regarding (non-)adaptive measurements.

This model incorporates the communication of context information, rather than the outcome, and has the potential to accurately replicate quantum predictions in the standard experimental setup. For instance, if the four terms in the CHSH (Clauser-Horne-Shimony-Holt) sum are sequentially measured in a coordinated fashion, such that the respective contexts are well known to the two observers and allow for communication about which context is used; or alternatively, if the terms entering the CHSH sum are measured consecutively, one after the other, this model could yield results that closely resemble quantum predictions. For instance, by performing observations “\(\textbf{A}\textbf{B}\) after breakfast, \(\textbf{A}\textbf{B}'\) after lunch, \(\textbf{A}'\textbf{B}\) after teatime, and \(\textbf{A}'\textbf{B}'\) after supper”—the elastic band model can deliver quantum performance. Indeed, by deforming the circumference of the elastic band we obtain a wide variety of correlation functions; and even stronger-than-classical correlations such as approximations to the unit step function [48].

At first glance, this may seem similar to protocols that involve the transfer of a single bit, as discussed in previous studies [50, 51]. However, there is one crucial difference: while the previously quoted protocols necessitate direct communication of actual measurement outcomes between the parties, the adaptive protocol introduced in this study for the elastic band model only requires communication of the context. In the CHSH simulation case, this is a single bit. (In that aspect, our protocol is not dissimilar to the Wiesner [52] and BB84 [53] schemes requiring classically communicating the choice of basis.) If this bit is denoted by \(1 \text { co-bit}\) then it may be compared to \(1 \text { bit}\) exchanging outcomes, and considered to be a “weaker” form of communication—that is, \(1 \text { co-bit} \prec 1 \text { bit}\)—because it would be possible to simulate quantum correlations without revealing the actual outcomes. Moreover, a \(1 \text { co-bit}\) can be used to simulate a (Popescu-Rohrlich) non-local machine [54] and the associated \(1 \text { nl-bit}\) by identifying it with the hidden variable \(\lambda \) transferred [55].

While it has been pointed out that the direct communication of actual respective measurement outcomes can be replaced by the invocation of a non-local resource [55], one may still ask whether the only way to realize such a non-local resource is by means of a concealed internal signal between its ports [56]. The protocol introduced by Cerf, Gisin, Massar, and Popescu [55], which invokes a generic (Popescu-Rohrlich) non-local machine, in combination with the realization of such a non-local machine that uses non-local rubber band shares and pulls and remains causal such that no superluminal signalling occurs by Sven Aerts [56], is capable of delivering a violation of the CHSH inequality by classical means, similar to the direct communication of the context discussed earlier. We conjecture that the protocol introduced by Cerf, Gisin, Massar, and Popescu, augmented by Aerts’ non-local resources, can be generalized to render stronger-than-classical violations of the CHSH inequality.

Furthermore, we postulate that, similar to the elastic band model previously discussed, the non-local resource would need to perform uniformly across all possible variations of legal states of the share. In light of this conjecture, it is concluded that achieving this goal would be impossible through strictly local means.

The analogy between the phenomenon of “non-local” signaling and the cloning (also known as copying) of bits is intriguing. Just as this type of signaling appears to be allowed for only one specific parameter setting [56] and a single context, the copying of a fixed single bit is similarly possible but strictly limited to a single context [57, Eq.(2.12), page 40].

It could be argued that the information encoded in an entangled state of two constituents, such as a singlet state, appears to be purely relational sampling [30, 58], and therefore quantum entanglement may not provide any means to encode any potential hidden internal share \(\textbf{J}\). This is consistent with relativity theory, as the respective outcomes are uncontrollable and faster-than-light signaling is not achievable.

The implications of these findings have far-reaching consequences for various forms of “quantum certifications” in security applications, such as the generation of random bits certified by value indefiniteness [59,60,61,62], or EPR-based quantum cryptography [63]. The implementations of these protocols can be considered “good” only with respect to the means—in particular, strict Einstein locality—highlighting the importance of this factor in evaluating their effectiveness.

Let us revisit the broader perspective and review the strategy adopted in this study. One approach to explain the singlet-type behavior observed in both sides of the EPR-type (Einstein-Podolsky-Rosen) configuration is to hypothesize that the constituent particles of a pair possess a common share that determines their outcomes. The apparent randomness of these outcomes is attributed to the random sampling of these shared properties. According to this conception, randomness does not arise from the measurement process itself, which is often seen as revealing aspects or properties of the share as well as of the (supposedly macroscopic) measurement context, but rather from the inherent randomness of the shared properties.

One direct approach to achieving this goal is through Peres’ bomb model, as previously mentioned. However, this model is incapable of violating inequalities such as the CHSH inequality. To explain a violation of Bell-type inequalities, which are based on Boole’s conditions of possible experience, a cost must be incurred. This cost could be in the form of one or more bits of communication between the parties at both ends of the EPR configuration, either by informing the other side of one’s outcome(s) [50, 51], or by revealing (part of) the measurement context, as proposed in this study. Alternatively, another option could be to provide the parties with a non-local machine [55, 56].

My current perspective, though highly speculative and hypothetical, is that we inhabit a vector-based realm where entangled quantum states are not truly separated in space and time. Rather, a pure state represented by a vector is the complete and sole share, without any hidden elements that trigger outcomes, as discussed previously. Both observers have access to and share the same vector, which formalizes a pure entangled state. This concept does not necessarily require a revision of the construction of space-time coordinate frames, as long as peaceful coexistence is maintained. In another part of this series, we will further explore this scenario.