A Unified Explanation of Some Quantum Phenomena

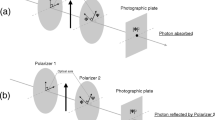
Abstract

There has been wide interest in beam splitter, quantum tunneling, and double-slit experiments for a long time. The states of single material particles are typically explained as being independent of other objects (and/or electromagnetic fields) and interactions. We argue that this independence causes counterintuitive explanations. By analyzing the research conducted separately by Wineland’s group and Haroche’s group, we naturally deduced that the states are dependent on other objects. Based on this dependence, our unified explanation is more intuitive. We design a double-slit thought experiment that can solve the center problem, i.e., which-path information. The dependence can also work for qubits in quantum information. To emphasize and use the dependence in the future, we propose a fundamental postulate that no material particle is free as the zeroth postulate of quantum mechanics.

Appendices

Appendix A: Explanations of the interference patterns of $N=0.31, 2, 12.8;$ 0

We explain the four interference patterns of $N=0.31, 2, 12.8, 0$ in Figure 2 in the paper published by Haroche’s group [3]. This figure is redrawn in Fig. 5. An atom initially in $\left|e\right.\rangle$ enters one input of $BS1$. After exiting from $BS1$, the atom and $BS1$ are still in an entangled state $\frac{1}{\sqrt{2}}\left(\left|g\right.\rangle |1\rangle |{\gamma }_{g}\rangle +{e}^{i\theta }\left|e\right.\rangle |2\rangle |{\gamma }_{e}\rangle \right)$, where $|1\rangle$ and $|2\rangle$ represent the atom’s two path states, and $\theta$ is the adjustable relative phase. An interference pattern that varies with $\theta$ can be obtained at one output of $BS2$. The atom stays in a mixed state. We note the coherent state of $BS1$ by the mean photon number, $|{\gamma }_{g}\rangle \equiv |N+1\rangle$ and $|{\gamma }_{e}\rangle \equiv |N\rangle$, which is different from the photon number state. When just entering $BS2$ (initially in state $|{N}^{^{\prime}}\rangle$) and omitting a global phase, the total state of the atom and the two beam splitters can be expressed as

$$\frac{1}{\sqrt{2}}\left(\left|g\right.\rangle |1\rangle |N+1\rangle +{e}^{i\theta }|e \rangle |2\rangle |N\rangle \right)|{N}^{^{\prime}}\rangle$$

(A1)

Fig. 5

Atoms in state $\left|{\varvec{e}}\right.\rangle$ enter an input of the first beam splitter ${\varvec{B}}{\varvec{S}}1$ one by one, and the relative phase ${\varvec{\theta}}$ is adjusted in path 2. After exiting from ${\varvec{B}}{\varvec{S}}1$, each atom enters the second beam splitter ${\varvec{B}}{\varvec{S}}2$. By detecting the atomic probability, which varies with ${\varvec{\theta}}$ at output 3, an interference pattern varying with ${\varvec{\theta}}$ can be obtained

Upon exiting from $BS2$, the total state of the atom and the two beam splitters is

$$\begin{array}{c}\frac{1}{2}(\left|g\right.\rangle |3\rangle \left|N+1\rangle \right|{N}^{\mathrm{^{\prime}}}\rangle -\left|e\right.\rangle |4\rangle \left|N+1\rangle \right|{N}^{\mathrm{^{\prime}}}-1\rangle \\ +{e}^{i\theta }\left|g\right.\rangle |3\rangle \left|N\rangle \right|{N}^{\mathrm{^{\prime}}}+1\rangle +{e}^{i\theta }\left|e\right.\rangle |4\rangle |N\rangle |{N}^{\mathrm{^{\prime}}}\rangle )\end{array}$$

(A2)

The atom stays in state $\left|g\right.\rangle |3\rangle$ at output 3 of $BS2$, and its appearance probability is

$$\begin{array}{c}P=\frac{1}{4}(2+{e}^{-i\theta }\langle N |N+1\rangle \langle {N}^{\mathrm{^{\prime}}}+1|{N}^{\mathrm{^{\prime}}}\rangle +\\ {e}^{i\theta }\langle N+1 | N\rangle \langle {N}^{^{\prime}} | {N}^{^{\prime}}+1\rangle )\end{array}$$

(A3)

When $BS2$ stays in the classical limit state, ${N}^{^{\prime}}\gg 1$ and $|{N}^{^{\prime}}\rangle \approx |{N}^{^{\prime}}+1\rangle$, so

$$P=\frac{1}{2}(1+Re\left(\langle N+1|N\rangle {e}^{i\theta }\right))$$

(A4)

When $N=0.31, 2, 12.8$ in $BS1$, all of the experiment results obtain interference patterns. The larger $N$ is, the larger the fringe visibility is, or the clearer the fringe is. This indirectly reflects the degree of coherence of states $\left|g\right.\rangle |1\rangle |N+1\rangle$ and $\left|e\right.\rangle |2\rangle |N\rangle$ in the entangled state and reflects the coherence of $\left|g\right.\rangle |1\rangle$ and $\left|e\right.\rangle |2\rangle$ in the atomic mixed state. Theoretically, the larger $N$ is, the closer the entangled state of the atom and $BS1$ is to the product state, and the closer the atomic mixed state is to the pure state. All coherent mixed states of such an atom are dependent on $BS1$. Since the coherent superposed pure state is approximated from a mixed state, the pure state is naturally dependent on $BS1$. When $N=0$ in $BS1$, it stays in the quantum limit state, so $|{\gamma }_{e}\rangle =|0\rangle$, $|{\gamma }_{g}\rangle =|1\rangle$, and $\langle {\gamma }_{g}|{\gamma }_{e}\rangle =0$. The atom and $BS1$ stay in the entangled state

$$\frac{1}{\sqrt{2}}\left(\left|g\right.\rangle |1\rangle |1\rangle +\left|e\right.\rangle |2\rangle |0\rangle \right)$$

(A5)

As can be seen from Equation (S4), $P=\frac{1}{2}$, which is a constant, and there is no interference fringe. This also indirectly reflects that the degree of coherence of $\left|g\right.\rangle |1\rangle$ and $\left|e\right.\rangle |2\rangle$ in the atomic mixed state is zero.

The two beam splitters are set in the same cavity, i.e., $BS1$ and $BS2$ can correspond to two pulses with a short interval time in the same cavity. When both $BS1$ and $BS2$ remain in the quantum limit state, i.e., $N={N}^{^{\prime}}=0$, an interference fringe is reobtained in the experiment. Since

$$\left|N+1\rangle \right|{N}^{^{\prime}}\rangle =\left|1\rangle \right|0\rangle =|one\rangle$$

(A6)

and

$$\left|N\rangle \right|{N}^{^{\prime}}+1\rangle =\left|0\rangle \right|1\rangle =|one\rangle$$

(A7)

if an atom is detected at output 3 of $BS2$, then the states of the cavity make no difference. If an atom is detected at output 4 of $BS2$, then

$$\left|N+1\rangle \right|{N}^{^{\prime}}-1\rangle =\left|1\rangle \right|-1\rangle =|zero\rangle$$

(A8)

and

$$\left|N\rangle \right|{N}^{^{\prime}}\rangle =\left|0\rangle \right|0\rangle =|zero\rangle$$

(A9)

A photon is left after the pulse corresponding to $BS1$ has acted on the atom, and the state $|-1\rangle$ of $BS2$ actually expresses that the atom absorbs the photon from the cavity. Thus, the mean photon number in $\left|1\rangle \right|-1\rangle$ in the cavity expresses zero. Upon exiting from $BS2$, the total state of the atom and cavity can be expressed as

$$\frac{1}{2}\left(\left|g\right.\rangle |3\rangle |one\rangle +{e}^{i\theta }\left|g\right.\rangle |3\rangle |one\rangle -\left|e\right.\rangle |4\rangle |zero\rangle +{e}^{i\theta }\left|e\right.\rangle |4\rangle |zero\rangle \right)$$

(A10)

At output 3 of $BS2$, the probability of detecting an atom is

$$P=\frac{1}{2}(1+Re\left({e}^{i\theta }\right))$$

(A11)

and an interference fringe may be detected. This also indicates that the atom’s state is dependent on the two beam splitters.

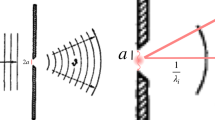
Appendix B: Additional details of the explanations of the double-slit experiment

If a particle is measured by one of the detectors placed just in front of the slits, for example, its which-path information (passing through slit 1) is read out, then its state at slit 1 will be one of the different momenta (continuous variable) states $|{\sigma }_{i}\rangle$. This is because the interaction between the detector and the particle drives them to evolve into the entangled state. This is expressed in discrete form for simplicity:

$$|{\sigma }_{1}\rangle |{D}_{10}\rangle +|{\sigma }_{2}\rangle |{D}_{20}\rangle +\cdots +|{\sigma }_{n}\rangle |{D}_{n0}\rangle$$

(B1)

where $n$ is a very large number. After the particle’s state is detected and read out, one of the states is $|{\sigma }_{i}\rangle$. Therefore, one of the evolutions is from the initial state $|{\sigma }_{i}\rangle |{S}_{10}\rangle$ to the entangled state,

$${\alpha }_{1i}|{\psi }_{1i}\rangle |{S}_{1i}\rangle +{\alpha }_{2i}|{\psi }_{2i}\rangle |{S}_{2i}\rangle$$

(B2)

Similarly, the entangled states approximate product states. The particle is in one of the states,

$$({\alpha }_{1i}|{\psi }_{1i}\rangle +{\alpha }_{2i}|{\psi }_{2i}\rangle )\equiv |{\Phi }_{1i}(t)\rangle$$

(B3)

which form one of the interference patterns. In the symmetric case, the phenomenon is the same for slit 2, and the dual states of $|{\Phi }_{1i}(t)\rangle$ are represented as $|{\Phi }_{2i}(t)\rangle$. The interference pattern on the screen is the sum of all 2n interference patterns. Near the slits, the interference pattern on the screen still exhibits two large wave peaks. As the distance between the slits and the screen increases, the interference pattern becomes vague because it is the sum of all 2n patterns. Similarly, if a particle is measured by detectors just behind the slits and its which-path information can be read out, then the interference pattern becomes vague for the same reason. This is why knowing the which-path information causes the interference pattern to become vague.

Scully et al. [15] used two extreme detection methods to explain whether or not the which-path information can be obtained before an atom enters the two slits. The first detection method they used involves the use of two vacuum cavities, and the second detection method they used involves the use of two coherent fields with large mean photon numbers (${N}_{1},{N}_{2}\gg 1$) in the two cavities or classical microwave radiation. The interaction between an atom and the light fields in the two cavities drives them to evolve into an entangled state,

$$|{\varphi }_{1}\rangle |{N}_{1}+1\rangle |{N}_{2}\rangle +|{\varphi }_{2}\rangle |{N}_{1}\rangle |{N}_{2}+1\rangle$$

(B4)

where $|{\varphi }_{1,2}\rangle$ are the two path states to slits 1 and 2, and $|{N}_{1,2}\rangle$ are the coherent states in the two cavities with mean photon numbers ${N}_{1}$ and ${N}_{2}$. When the fields are quantum fields with ${N}_{1}={N}_{2}=0$, a photon emitted by an atom in one vacuum cavity can be detected, and then, the interference pattern becomes very vague or disappears. Scully et al. explained this as the which-path information being obtainable by detecting the photon number in the cavities. If an atom is detected using classical microwave radiation in the two cavities, then the interference pattern appears. This is because an atom emits a photon into the two cavities, and this change cannot be detected. Thus, the which-path information cannot be obtained.

Here, we offer a different explanation. The atom interacts with the photon field (quantum or classical), and the AICQS evolves into an entangled state. The detection using a quantum field forces the atomic state to become a mixed state before it enters a slit, and then, the atom, which is in different states with different probabilities, interacts with the double-slit object. This is similar to the above case of the measurement before the atom enters a slit, in which the interference pattern disappears. In the case of detection using a classical field, the fields in the two cavities remain approximately unchanged, the entangled state approximates a product state, and the atomic state approximately remains in a pure state. Thus, the interference pattern will appear. If ${N}_{1}$ and ${N}_{2}$ change from small to large numbers, then the atomic mixed state tends to the pure state, and the contrast of the interference pattern increases. In addition, after detecting the path state of an atom approaching the slits using a quantum field and obtaining the which-way information, Scully et al. re-obtained the interference pattern by the eraser and explained that the pattern’s reappearance is due to the which-way information deletion. We have explained pattern reappearance in another way in the experiment in Appendix A.