1 Introduction

Modeling various physical events that occur in several fields of physics, engineering, and applied mathematics is done using nonlinear evolution equations (NLEEs). In order to better comprehend the phenomena that these NLEEs mimic, it is crucial to look at the precise explicit solutions of NLEEs [1,2,3,4,5,6]. Recently one type NLEE is the Burgers-type equation [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] that arises in different field of science such as in plasma astrophysics, ocean dynamics, atmospheric science, computational fluid mechanics, cosmology, condensed matter physics, statistical physics and so forth. In this paper, we investigate the following extended (2 + 1)-dimensional coupled Burgers system in fluid mechanics [24]

$$ \begin{array}{@{}rcl@{}} &&u_t + \alpha (u_{xx} + u_{yy}) + \beta(u u_x + u_y v) + \gamma (u u_x + u v_y) = 0, \end{array} $$
(1.1a)
$$ \begin{array}{@{}rcl@{}} &&v_t + \alpha (v_{xx} + v_{yy}) + \beta (u v_x + v v_y) + \gamma (u_x v + v v_y) = 0, \end{array} $$
(1.1b)

where u(x,y,t) and v(x,y,t) are the velocity components in fluid related problems and α,β,γ are real constants. In [24] with the aid of symbolic computation constructed a hetero-B\(\ddot { a}\)cklund transformation and a similarity reduction for (1.1a).

An exceptional case of (1.1a)

$$ \begin{array}{@{}rcl@{}} &&u_t - \frac{1}{R_{e}} \left( u_{xx} + u_{yy}\right) + u u_x + u_y v=0, \end{array} $$
(1.2a)
$$ \begin{array}{@{}rcl@{}} &&v_t - \frac{1}{R_{e}} \left( v_{xx} + v_{yy}\right) + u v_x + v v_y=0. \end{array} $$
(1.2b)

which is similar to the incompressible Navier-Stokes equations without the pressure and continuity considerations [18]. It is said to constitute an appropriate model for developing computational algorithms for solving the incompressible Navier-Stokes equations [23], to be a suitable test case because the equation structure is similar to that of the incompressible fluid flow momentum equations [19] and to be used in models for the study of hydrodynamical turbulence and wave processes in nonlinear media [19]. Note that u(x,y,t) and v(x,y,t) are the velocity components in fluid-related problems [14, 18], Re is the Reynolds number. In contrast, \(\frac {1}{R_{e}}\) represents the viscosity [14], the total or material derivative including the convective term is used while the diffusive and convective terms are linked with Re [18].

2 Symmetry Reductions (1.1a)

The symmetry generator of an extended (2 + 1)-dimensional coupled Burgers system in fluid mechanics (1.1a) will be generated by the vector field

$$ \begin{array}{@{}rcl@{}} X &=& \xi^{1} (t, x, y, u, v) \frac{\partial }{\partial t} + \xi^{2} (t, x, y, u, v) \frac{\partial }{\partial x} + \xi^{3} (t, x, y, u, v) \frac{\partial }{\partial y} + \eta^{1} (t, x, y, u, v) \frac{\partial }{\partial u}\\ && + \eta^{2} (t, x, y, u, v) \frac{\partial }{\partial v} . \end{array} $$
(2.1)

where

$$ \left. \textbf{X}^{[\textbf{2}]} \left\{\begin{array}{l} {u_{t} + \alpha (u_{xx} + u_{yy}) + \beta(u u_{x} + u_{y} v) + \gamma (u u_{x} + u v_{y})}, \\ {v_{t} + \alpha (v_{xx} + v_{yy}) + \beta (u v_{x} + v v_{y}) + \gamma (u_{x} v + v v_{y}) } \end{array}\right\}\right|_{(1.1)} = 0 $$
(2.2)

Expanding the above equation and splitting on the derivatives of u and v, where X[2] is the second prolongation, leads to the following linear overdetermined system of partial differential equations.

$$ \begin{array}{@{}rcl@{}} &&{\xi_{t}^{1}} \left( t, x, y, u, v \right) = - 2 t C_{4} + C_{3},\\ &&{\xi_{x}^{2}} \left( t, x, y, u, v \right) = -y C_{1} - x C_{4} + C_{2},\\ &&{\xi_{y}^{3}} \left( t, x, y, u, v \right) = x C_{1} - y C_{4} + C_{5},\\ &&{\eta_{u}^{1}} \left( t, x, y, u, v \right) = - v C_{1} + u C_{4}, \\ &&{\eta_{v}^{2}} \left( t, x, y, u, v \right) = u C_{1} + v C_{4}. \end{array} $$
(2.3)

Solving the above system of partial differential equations with the aid of Maple program the above general solution contains five arbitrary constants. Thus, the infinitesimal symmetries of system (1.1a) form the five-dimensional Lie algebra spanned by the following linearly independent generators:

$$ \begin{array}{@{}rcl@{}} &&X_{1} = \frac{\partial}{\partial x},\\ &&X_{2}= \frac{\partial}{\partial y},\\ &&X_{3}= \frac{\partial}{\partial t},\\ &&X_{4}=- y \frac{\partial}{\partial x} + x \frac{\partial}{\partial y} - v \frac{\partial}{\partial u} + u \frac{\partial}{\partial v},\\ &&X_{5}= - 2 t \frac{\partial}{\partial t} - x \frac{\partial}{\partial x} - y \frac{\partial}{\partial y} + u \frac{\partial}{\partial u} + v \frac{\partial}{\partial v}. \end{array} $$

2.1 Symmetry Reductions of (1.1a)

In order to construct symmetry reductions and exact solutions, we need to implement the associated Lagrange equations

$$ \begin{array}{@{}rcl@{}} \frac{dt}{\xi^{1}(t,x,y,u,v)}&=&\frac{dx}{\xi^{2}(t,x,y,u,v)}=\frac{dy}{\xi^{3}(t,x,y,u,v)}=\frac{du}{\eta^{1}(t,x,y,u,v)}\\ &=& \frac{dv}{\eta^{2}(t,x,y,u,v)} . \end{array} $$
(2.4)

The linear combination of the translation symmetries Γ = a1X1 + a2X2 + a3X3, where a1,a2,a3 are constants reduces (1.1a) to a partial differential equation (PDE). The symmetry Γ yields the following four invariants

$$ f = a_{2} x - a_{1} y, \quad g = a_{3} x - a_{1} t, \quad h = u \quad \phi = v $$

Hence (1.1a) reduces to a PDE in two independent variables given below

$$ \left\{\begin{array}{l} { - a_1 \phi_g + \alpha \left( a_2 \left( a_2 \phi_{ff} + a_3 \phi_{fg} \right) + a_3 \left( a_2 \phi_{fg} + a_3 \phi_{gg} \right) + a_1^2 \phi_{ff} \right) + \beta a_2 \phi \left( \phi_f + a_3 \phi_g \right)} \\ {- \beta a_1 \psi \phi_f + \gamma \left( \phi \left( a_2 \phi_f + a_3 \phi_g \right) - a_1 \phi \psi_f \right) = 0 }, \\ { - a_1 \psi_g + \alpha \left( a_2 \left( a_2 \psi_{ff} + a_3 \psi_{fg} \right) + a_3 \left( a_2 \psi_{fg} + a_3 \psi_{gg} \right) + a_1^2 \psi_{ff} \right) + \beta a_2 \phi \left( \psi_f + a_3 \psi_g \right)} \\ {- \beta a_1 \psi \phi_f + \gamma \left( \psi \left( a_2 \phi_f + a_3 \phi_g \right) - a_1 \psi \psi_f \right) = 0 } \end{array}\right. $$
(2.5)

which is a nonlinear PDE in two independent variables f and g. We now further reduce this equation using its symmetries. The above equation has the two translation symmetries, namely

$$ {\Upsilon}_{1} = \frac{\partial}{\partial f}, \quad {\Upsilon}_{2} = \frac{\partial}{\partial g}. $$

By taking a linear combination b1Υ1 + b2Υ2 of the above symmetries, we see that it yields the invariants

$$ z = b_{2} f - b_{1} g, \quad \phi = E, \quad \psi = F $$

Now treating E and F as new dependent variables, z as the new independent variable then the system (1.1a) reduces to the second order ordinary differential equations

$$ \left\{\begin{array}{l} { a_1 b_1 F^{\prime} + \left( \left( a_2 b_2^2 - a_3 b_1 b_2 \right) a_2 - \left( a_2 b_1 b_2 - a_3 b_1^2 \right) a_3 + a_1^2 b_2^2 \right) \alpha F^{\prime \prime} + \left( a_2 b_2 F - a_3 b_1 \right) \beta F^{\prime} } \\ { - \beta a_1 b_2 G F^{\prime} + \left( a_2 b_2 F - a_3 b_1 \right) \gamma F^{\prime} - a_1 b_2 F G^{\prime} = 0 }, \\ \\ { a_1 b_1 G^{\prime} + \left( \left( a_2 b_2^2 - a_3 b_1 b_2 \right) a_2 - \left( a_2 b_1 b_2 - a_3 b_1^2 \right) a_3 + a_1^2 b_2^2 \right) \alpha G^{\prime \prime} + \left( a_2 b_2 F - a_3 b_1 \right) \beta G^{\prime} } \\ { - \beta a_1 b_2 G G^{\prime} + \left( a_2 b_2 G - a_3 b_1 \right) \gamma F^{\prime} - a_1 b_2 G G^{\prime} = 0 } \end{array}\right. $$
(2.6)

3 Exact Solutions Using Kudryashov Method

The intention of this segment is to introduce the algorithm of the Kudryashov method for finding exact solutions of the nonlinear evolution equations. The Kudryashov method was one of the original procedures for acquiring exact solutions of nonlinear partial differential equations. Let us briefly recall the basic steps of the Kudryashov method. Consider for instance a scalar nonlinear partial differential equation in the form

$$ E_{1}[u_{t},u_{x},u_{y},\cdots]=0. $$
(3.1)

We use the following ansatz

$$ u(x,y,t)=F(z), z=k_{1} x+k_{2} y+k_{3} t+k_{4}. $$
(3.2)

From (3.1) we obtain the nonlinear ordinary differential equation

$$ E_{2}[k_{1}F^{\prime}(z),k_{2}F^{\prime}(z),k_{3}F^{\prime}(z),{k_{1}^{2}}F^{\prime\prime}(z),{k_{2}^{2}}F^{\prime\prime}(z),{k_{3}^{2}}F^{\prime\prime}(z),\cdots]=0, $$
(3.3)

which has a solution of the form

$$ F(z)=\sum\limits_{i=0}^{M} A_{i} (H(z))^{i}, $$
(3.4)

where

$$ \begin{array}{@{}rcl@{}} H(z)=a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \end{array} $$

satisfies the equation

$$ H^{\prime}(z)=aH(z)+bH^{2}(z) $$
(3.5)

M is a positive integer and A0,⋯ ,AM are parameters to be determined.

3.1 Application of the Kudryashov Method

The solutions of (2.6) are of the form

$$ \begin{array}{@{}rcl@{}} F(z)&=&\sum\limits_{i=0}^M A_{i} H(z)^{i}, \end{array} $$
(3.6a)
$$ \begin{array}{@{}rcl@{}} G(z)&=&\sum\limits_{i=0}^M B_{i} H(z)^{i}. \end{array} $$
(3.6b)

Reverting back to our underlying system (1.1a), the solution structure takes the form

$$ \begin{array}{@{}rcl@{}} u(x,y,t)&=&\sum\limits_{i=0}^M A_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right)^{i}, \end{array} $$
(3.7a)
$$ \begin{array}{@{}rcl@{}} v(x,y,t)&=&\sum\limits_{i=0}^M B_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right )^{i}, \end{array} $$
(3.7b)
$$ z = b_{2} \left( a_{2} x -a_{1} y \right)-b_{1} \left( -a_{1} t +a_{3} x \right). $$

The above solution structure is attained by beplacing (3.7a) into (2.6) and making use of (3.5), and then equating all coefficients of the functions Hi to zero, to obtain an overdetermined system of algebraic equations. Solving the resultant system leads to following possible solutions with its associated cases.

3.1.1 M = 1

Considering M = 1 the desired solution take the form below.

$$ \begin{array}{@{}rcl@{}} u(x,y,t)&=&\sum\limits_{i=0}^1 A_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right)^{i}, \end{array} $$
(3.8a)
$$ \begin{array}{@{}rcl@{}} v(x,y,t)&=&\sum\limits_{i=0}^1 B_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right )^{i} \end{array} $$
(3.8b)
$$ z = b_{2} \left( a_{2} x -a_{1} y \right)-b_{1} \left( -a_{1} t +a_{3} x \right). $$

Case 1

$$ \begin{array}{@{}rcl@{}} &&\beta = -\frac{2 \alpha b {a_{1}^{2}} {b_{2}^{2}}+2 \alpha b {a_{2}^{2}} {b_{2}^{2}}-4 \alpha b a_{2} a_{3} b_{1} b_{2}+2 \alpha b {a_{3}^{2}} {b_{1}^{2}}+\gamma A_{1} a_{2} b_{2}-\gamma A_{1} a_{3} b_{1}}{A_{1} \left( a_{2} b_{2}-a_{3} b_{1}\right)},\\ &&A_{0} = \frac{A_{1} \left( a \alpha {a_{1}^{2}} {b_{2}^{2}}+a \alpha {a_{2}^{2}} {b_{2}^{2}}-2 a \alpha a_{2} a_{3} b_{1} b_{2}+a \alpha {a_{3}^{2}} {b_{1}^{2}}+a_{1} b_{1}\right)}{2 \alpha b \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)}, B_{0} = 0, B_{1} = 0 \end{array} $$

Case 2

$$ \begin{array}{@{}rcl@{}} &&b = \frac{A_{1} \left( a \alpha {a_{1}^{2}} {b_{2}^{2}}+a \alpha {a_{2}^{2}} {b_{2}^{2}}-2 a \alpha a_{2} a_{3} b_{1} b_{2}+a \alpha {a_{3}^{2}} {b_{1}^{2}}+a_{1} b_{1}\right)}{2 \alpha A_{0} \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)},\\ &&B_{0} = \frac{a \alpha {a_{1}^{2}} {b_{2}^{2}}+a \alpha {a_{2}^{2}} {b_{2}^{2}}-2 a \alpha a_{2} a_{3} b_{1} b_{2}+a \alpha {a_{3}^{2}} {b_{1}^{2}}+\beta A_{0} a_{2} b_{2}-\beta A_{0} a_{3} b_{1}+\gamma A_{0} a_{2} b_{2}-\gamma A_{0} a_{3} b_{1}+a_{1} b_{1}}{\left( \gamma +\beta \right) a_{1} b_{2}},\\ &&B_{1} = \frac{A_{1} \left( a \alpha {a_{1}^{2}} {b_{2}^{2}}+a \alpha {a_{2}^{2}} {b_{2}^{2}}-2 a \alpha a_{2} a_{3} b_{1} b_{2}+a \alpha {a_{3}^{2}} {b_{1}^{2}}+\beta A_{0} a_{2} b_{2}-\beta A_{0} a_{3} b_{1}+\gamma A_{0} a_{2} b_{2}-\gamma A_{0} a_{3} b_{1}+a_{1} b_{1}\right)}{A_{0} a_{1} b_{2} \left( \gamma +\beta \right)}, \end{array} $$

Case 3

$$ \begin{array}{@{}rcl@{}} && \alpha = -\frac{a_{1} b_{1}}{a \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)}, A_{0} = 0, B_{0} = 0,\\ && B_{1} = \frac{a \beta A_{1} a_{2} b_{2}-a \beta A_{1} a_{3} b_{1}+a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}-2 b a_{1} b_{1}}{a a_{1} b_{2} \left( \gamma +\beta \right)}, \end{array} $$

3.1.2 M = 3

Upon setting M = 3 the desired solutions take the form below.

$$ \begin{array}{@{}rcl@{}} u(x,y,t)&=&\sum\limits_{i=0}^3 A_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right)^{i}, \end{array} $$
(3.9a)
$$ \begin{array}{@{}rcl@{}} v(x,y,t)&=&\sum\limits_{i=0}^3 B_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right )^{i} \end{array} $$
(3.9b)
$$ z = b_{2} \left( a_{2} x -a_{1} y \right)-b_{1} \left( -a_{1} t +a_{3} x \right). $$

Case 1

$$ \begin{array}{@{}rcl@{}} \beta &=& -\frac{5 \gamma}{3}, A_{0} = \frac{a A_{1}}{3 b}, A_{2}= \frac{3 a A_{3}}{b}, B_{0} = \frac{a B_{1}}{3 b}, B_{2} = 0, B_{3} = 0, a_{1} = -\frac{B_{1} \gamma}{3 \alpha b b_{2}}, \\ a_{2} &=& \frac{a_{3} a \gamma B_{1}}{9 b}, b_{1} = \frac{a \gamma B_{1} b_{2}}{9 b} \end{array} $$

Case 2

$$ \begin{array}{@{}rcl@{}} &&\alpha = -\frac{3 a_{1} b_{1}}{a \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)}, \beta = -\frac{5 \gamma}{3}, A_{0} = \frac{a A_{1}}{3 b}, A_{2} = \frac{3 a A_{3}}{b},\\ &&B_{0} = \frac{a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}+9 b a_{1} b_{1}}{3 b_{2} a_{1} \gamma b}, B_{1} = \frac{a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}+9 b a_{1} b_{1}}{\gamma a_{1} a b_{2}},\\ &&B_{2} = \frac{3 a A_{3} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{b a_{1} b_{2}}, B_{3} = \frac{A_{3} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{a_{1} b_{2}}. \end{array} $$

3.1.3 M = 4

Considering M = 4 the desired solutions take the form below.

$$ \begin{array}{@{}rcl@{}} u(x,y,t)&=&\sum\limits_{i=0}^4 A_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1 - b\cosh [a (z + C)] - b \sinh [a (z + C)]} \bigg\} \right)^{i}\!, \end{array} $$
(3.10a)
$$ \begin{array}{@{}rcl@{}} v(x,y,t)&=&\sum\limits_{i=0}^4 B_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1 - b\cosh [a (z + C)] - b \sinh [a (z + C)]} \bigg\} \right )^{i} \end{array} $$
(3.10b)
$$ z = b_{2} \left( a_{2} x -a_{1} y \right)-b_{1} \left( -a_{1} t +a_{3} x \right). $$

Case 1

$$ \begin{array}{@{}rcl@{}} \beta &=& -\frac{3 \gamma}{2}, A_{0} = \frac{a A_{1}}{4 b}, A_{2}= \frac{6 a^{2} A_{4}}{b^{2}}, A_{3} = \frac{4 a A_{4}}{b}, B_{0} = \frac{a B_{1}}{4 b}, B_{2} = 0, B_{3} = 0, \\ B_{4} &=& 0, a_{1} = -\frac{B_{1} \gamma}{4 \alpha b b_{2}},a_{2} = \frac{a_{3} a \gamma B_{1}}{8 b}, b_{1} = \frac{a \gamma B_{1} b_{2}}{8 b}. \end{array} $$

Case 2

$$ \begin{array}{@{}rcl@{}} &&\alpha = -\frac{2 a_{1} b_{1}}{a \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)}, \beta = -\frac{3 \gamma}{2}, A_{0} = \frac{a A_{1}}{4 b}, A_{3} = \frac{2 A_{2} b}{3 a},\\ &&A_{4} = \frac{b^{2} A_{2}}{6 a^{2}},B_{0} = \frac{a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}+8 b a_{1} b_{1}}{4 b_{2} a_{1} \gamma b},\\ && B_{1} = \frac{a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}+8 b a_{1} b_{1}}{\gamma b_{2} a_{1} a}, B_{2} = \frac{A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{a_{1} b_{2}},\\ &&B_{3}= \frac{2 A_{2} b \left( a_{2} b_{2}-a_{3} b_{1}\right)}{3 a a_{1} b_{2}}, B_{4} = \frac{b^{2} A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{6 a^{2} a_{1} b_{2}}. \end{array} $$

3.1.4 M = 5

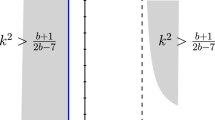
Setting M = 5 the solutions of (1.1a) take the form outlined below (Fig. 1).

$$ \begin{array}{@{}rcl@{}} u(x,y,t)&=&\sum\limits_{i=0}^5 A_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right)^{i}, \end{array} $$
(3.11a)
$$ \begin{array}{@{}rcl@{}} v(x,y,t)&=&\sum\limits_{i=0}^5 B_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right )^{i} \end{array} $$
(3.11b)
$$ z = b_{2} \left( a_{2} x -a_{1} y \right)-b_{1} \left( -a_{1} t +a_{3} x \right). $$

Case 1

$$ \begin{array}{@{}rcl@{}} \beta &=& -\frac{7 \gamma}{5}, A_{1} = \frac{5 A_{0} b}{a}, A_{2} = \frac{2 a^{2} A_{4}}{b^{2}}, A_{3} = \frac{2 a A_{4}}{b}, A_{5} = \frac{b A_{4}}{5 a}, B_{0} = -\frac{\alpha a_{1} b_{2} a}{\gamma}, \\ B_{1} &=& -\frac{5 \alpha b a_{1} b_{2}}{\gamma},B_{2} = 0, B_{3} = 0, B_{4} = 0, B_{5} = 0, a_{2} = -\frac{3 a_{3} a_{1} \alpha a b_{2}}{5}, b_{1} = -\frac{3 a_{1} \alpha a {b_{2}^{2}}}{5}. \end{array} $$
Fig. 1
figure 1

Evolution of the travelling wave solutions (3.10a)

Full size image

Case 2

$$ \begin{array}{@{}rcl@{}} \beta &=& -\frac{7 \gamma}{5}, A_{0} = \frac{a A_{1}}{5 b}, A_{1} = A_{1}, A_{2} = \frac{10 a^{3} A_{5}}{b^{3}}, A_{3} = \frac{10 a^{2} A_{5}}{b^{2}}, A_{4} = \frac{5 a A_{5}}{b}, A_{5} = A_{5}, \\ B_{0} &=& \frac{a B_{1}}{5 b},B_{2} = 0, B_{3} = 0, B_{4} = 0, B_{5} = 0, a_{1} = -\frac{B_{1} \gamma}{5 \alpha b b_{2}}, a_{2} = \frac{3 a_{3} a \gamma B_{1}}{25 b}, a_{3} = a_{3},\\ b_{1} &=& \frac{3 a \gamma B_{1} b_{2}}{25 b}, b_{2} = b_{2}. \end{array} $$

Case 3

$$ \begin{array}{@{}rcl@{}} \alpha &=& -\frac{5 a_{1} b_{1}}{3 a \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)}, \beta = -\frac{7 \gamma}{5}, A_{0} = \frac{a A_{1}}{5 b}, A_{3} = \frac{b A_{2}}{a}, \\ A_{4} &=& \frac{b^{2} A_{2}}{2 a^{2}}, A_{5} = \frac{A_{2} b^{3}}{10 a^{3}},B_{0} = \frac{3 a \gamma A_{1} a_{2} b_{2}-3 a \gamma A_{1} a_{3} b_{1}+25 b a_{1} b_{1}}{15 b_{2} a_{1} b \gamma} , \\B_{1} &=& \frac{3 a \gamma A_{1} a_{2} b_{2}-3 a \gamma A_{1} a_{3} b_{1}+25 b a_{1} b_{1}}{3 \gamma b_{2} a_{1} a} , B_{2} = \frac{A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{a_{1} b_{2}},\\ B_{3} &=& \frac{b A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{a a_{1} b_{2}} , B_{4} = \frac{b^{2} A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{2 a^{2} a_{1} b_{2}} , B_{5} = \frac{A_{2} b^{3} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{10 a^{3} a_{1} b_{2}}. \end{array} $$

3.1.5 M = 6

Finally upon letting M = 6 the solutions of (1.1a) take the form below.

$$ \begin{array}{@{}rcl@{}} u(x,y,t)&=&\sum\limits_{i=0}^6 A_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right)^{i}, \end{array} $$
(3.12a)
$$ \begin{array}{@{}rcl@{}} v(x,y,t)&=&\sum\limits_{i=0}^6 B_{i} \left( a\bigg\{ \frac{\cosh [a (z+C)]+\sinh [a (z+C)]}{1-b\cosh [a (z+C)]-b \sinh [a (z+C)]} \bigg\} \right )^{i} \end{array} $$
(3.12b)
$$ z = b_{2} \left( a_{2} x -a_{1} y \right)-b_{1} \left( -a_{1} t +a_{3} x \right). $$

Case 1

$$ \begin{array}{@{}rcl@{}} \beta &=& -\frac{4 \gamma}{3}, A_{0} = \frac{a A_{1}}{6 b}, A_{2} = \frac{15 a^{4} A_{6}}{b^{4}}, A_{3} = \frac{20 a^{3} A_{6}}{b^{3}} , A_{4} = \frac{15 a^{2} A_{6}}{b^{2}}, A_{5} = \frac{6 a A_{6}}{b},\\ B_{0} &=& \frac{a B_{1}}{6 b}, B_{2} = 0, B_{3} = 0, B_{4} = 0, B_{5} = 0, B_{6} = 0, a_{1} = -\frac{B_{1} \gamma}{6 \alpha b b_{2}}, a_{2} = \frac{a_{3} \gamma B_{1} a}{9 b},\\ b_{1} &=& \frac{\gamma B_{1} b_{2} a}{9 b}. \end{array} $$

Case 2

$$ \begin{array}{@{}rcl@{}} \alpha &=& -\frac{3 a_{1} b_{1}}{2 a \left( {a_{1}^{2}} {b_{2}^{2}}+{a_{2}^{2}} {b_{2}^{2}}-2 a_{2} a_{3} b_{1} b_{2}+{a_{3}^{2}} {b_{1}^{2}}\right)} , \beta = -\frac{4 \gamma}{3}, A_{0} = \frac{a A_{1}}{6 b}, , A_{3} = \frac{4 b A_{2}}{3 a}, \\ A_{4} &=& \frac{b^{2} A_{2}}{a^{2}}, A_{5} = \frac{2 A_{2} b^{3}}{5 a^{3}}, A_{6} = \frac{b^{4} A_{2}}{15 a^{4}}, B_{0} = \frac{a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}+9 b a_{1} b_{1}}{6 b_{2} a_{1} b \gamma},\\ B_{1} &=& \frac{a \gamma A_{1} a_{2} b_{2}-a \gamma A_{1} a_{3} b_{1}+9 b a_{1} b_{1}}{\gamma b_{2} a_{1} a} , B_{2} = \frac{A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{a_{1} b_{2}}, \\ B_{3} &=& \frac{4 b A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{3 a a_{1} b_{2}},B_{4} = \frac{b^{2} A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{a^{2} a_{1} b_{2}} , B_{5} = \frac{2 A_{2} b^{3} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{5 a^{3} a_{1} b_{2}} , \\ B_{6} &=& \frac{b^{4} A_{2} \left( a_{2} b_{2}-a_{3} b_{1}\right)}{15 a^{4} a_{1} b_{2}}. \end{array} $$

4 Conservation Laws

A conservation law of system (1.1a) is a total space-time divergence expression that vanishes on the solution space ε of system (1.1a),

$$ \begin{array}{@{}rcl@{}} D_{t}T^{t} + D_{x}T^{x} + D_{y} T^{y}|_{\varepsilon}=0, \end{array} $$
(4.1)

where Dt, Dx and Dy are the total derivative operators while Tt is a conserved density and Tx, Ty a spatial flux. To determine the conservation law for system (1.1a), we will implement the multiplier method. Since the joint Euler operator annihilates the total divergence, we get

$$ \begin{array}{@{}rcl@{}} &&\frac{\delta}{\delta u}\bigg((u_{t} + \alpha (u_{xx} + u_{yy}) + \beta(u u_{x} + u_{y} v) + \gamma (u u_{x} + u v_{y}) ) {\Lambda}_{1}\\ && + (v_{t} + \alpha (v_{xx} + v_{yy}) + \beta (u v_{x} + v v_{y}) + \gamma (u_{x} v + v v_{y})){\Lambda}_{2} \bigg)=0, \end{array} $$
(4.2)
$$ \begin{array}{@{}rcl@{}} &&\frac{\delta}{\delta v}\bigg((u_{t} + \alpha (u_{xx} + u_{yy}) + \beta(u u_{x} + u_{y} v) + \gamma (u u_{x} + u v_{y}) ) {\Lambda}_{1}\\ && + (v_{t} + \alpha (v_{xx} + v_{yy}) + \beta (u v_{x} + v v_{y}) + \gamma (u_{x} v + v v_{y})){\Lambda}_{2} \bigg)=0, \end{array} $$
(4.3)

where Λ1 and Λ2 are the second-order multipliers to be determined. The expansion of (4.2) and (4.3) where β = γ, split and simplify yields the following multipliers

$$ \begin{array}{@{}rcl@{}} {{\Lambda}_{1}}&=& y c_{1} + c_{2}, \end{array} $$
(4.4)
$$ \begin{array}{@{}rcl@{}} {{\Lambda}_{2}}&=& - x c_{1} + c_{3}, \end{array} $$
(4.5)

where ci, i = 1,2,3 are arbitrary constants. The multipliers Λ1 and Λ2 of system (1.1a) has the property

$$ \begin{array}{@{}rcl@{}} D_{t}T^{t} + D_{x}T^{x} + D_{y} T^{y} &=& (u_{t} + \alpha (u_{xx} + u_{yy}) + \beta(u u_{x} + u_{y} v) + \gamma (u u_{x} + u v_{y}) ) {\Lambda}_{1}\\ && + (v_{t} + \alpha (v_{xx} + v_{yy}) + \beta (u v_{x} + v v_{y}) + \gamma (u_{x} v + v v_{y})){\Lambda}_{2} ,\\ \end{array} $$
(4.6)

for the arbitrary functions u(t,x,y) and v(t,x,y), where the predetermined arguments of Tt, Tx and Ty are of some order in derivatives of the field variables u, v and w. The computations for Tt, Tx and Ty from equation (4.6) reveal that corresponding to the above multipliers we have the following conserved vectors for system (1.1a):

$$ \begin{array}{@{}rcl@{}} {T_{1}^{t}} &=& u y - v x,\\ {T_{1}^{x}} &=& \gamma u^{2} y - \gamma u v x + \alpha u_{x} y - \alpha v_{x} x + \alpha v, \\ {T_{1}^{y}} &=& \gamma u v y - \gamma v^{2} x + \alpha u_{y} y - \alpha v_{y} x - \alpha u ;\\ {T_{2}^{t}} &=& u ,\\ {T_{2}^{x}} &=& \gamma u^{2} + \alpha u_{x}, \\ {T_{2}^{y}} &=& \gamma u v + \alpha u_{y} ;\\ {T_{3}^{t}} &=& v,\\ {T_{3}^{x}} &=& \gamma u v + \alpha v_{x}, \\ {T_{3}^{x}} &=& \gamma v^{2} + \alpha v_{y}. \end{array} $$

We succinctly discuss the significance and physical illumination that ascend from the computed conservation laws. Conservation laws reside in enormously crucial areas both at the foundations of nonlinear science and in its applications. Mathematical expressions of physical laws, such as conservation of energy, momentum and mass are fundamentally conservation laws. Imperative physical information about the complex behaviour in non-linear systems is confined in conservation laws.

5 Concluding Remarks

Today’s work was concerned with a Burgers-type equations that are noticed in plasma astrophysics, ocean dynamics, atmospheric science, computational fluid mechanics, cosmology, condensed matter physics, statistical physics, nonlinear acoustics, vehicular traffic, electronic transport, etc. We determined novel type exact solutions by the Lie symmetry method in conjunction with Kurdyshov method. Finally, conservation laws of the abovementioned system were generated. These new research findings can well mimic complex waves and their dealing dynamics in fluids. Some diverse interaction phenomenon shown graphically have great implication to the nonlinear waves in fluid mechanics. In this paper, the methods used to obtain new exact solutions also can be extended to solve other nonlinear partial different equation of physical interest. For some important classical mathematical and physical models, the techniques shown in this work are of great importance. The precise solutions that were discovered in this study may be utilized as comparison points with numerical simulations in theoretical physics and fluid mechanics, and the conservation laws that were discovered can be used to create numerical integrators for the underlying system.