Brownian-Huygens Propagation: Modeling Wave Functions with Discrete Particle-Antiparticle Random Walks

Abstract

We present a simple method of discretely modeling solutions of the classical wave and Klein-Gordon equations using variations of random walks on a graph. Consider a collection of particles executing random walks on an undirected bipartite graph embedded in $\mathbb {R}^{D}$ at discrete times $\mathbb {Z}$, and assume those walks are “heat-like”, in the sense that a (conserved) density of particles obeys the heat equation in the continuum limit. If the particles possess a binary degree of freedom (so that they may be said to be either particles or “antiparticles”, i.e., “positive” or “negative), then there exist closely related branching random walks on the same graph that are “wave-like”, in the sense that their (also conserved) net density obeys the D-dimensional classical wave equation. Such wave-like paths can be generated even on random graphs. The transformation by which the heat-like random walks become wave-like branching random walks is as follows: at every time step, any “incoming” particle arriving at any node X of the graph along some edge e_X creates a particle-antiparticle pair at that node, with the stipulation that the newly created particle with the opposite sign of the incoming particle must initially step (in “Huygens” back-propagation fashion) along e_X in the reverse direction, while the other two take a step (in “Brownian” fashion) along any edge of X (including possibly e_X) with equal likelihood, and chosen independently. An additional degree of freedom (resulting in “bra” and “ket” particles) leads to quasi-probability densities proportional to the square of the wave functions.

1 Introduction: Heat-Like and Wave-Like Walks

Consider a collection of particles executing random walks on an undirected bipartite graph embedded in $\mathbb {R}^{D}$. In other words, at any integer time t, every particle is located on some node of the graph, and then, in the subsequent time step, it is located at some neighbor of that node. For the purposes of this paper, we shall assume henceforth that unless otherwise specified, any edge of a node where a particle is located is equally likely to be chosen for the subsequent step (and note that there may be more than one edge connecting any two nodes – i.e., the graphs may be multigraphs). We shall say that particles operating under these simple dynamics are executing Brownian motion. (We shall also implicitly assume all particles are initially on the same part of this bipartite graph, and on the other one in the next time step, and so on.) The random walks of such particles are said to be “heat-like” if, in the continuum limit, the expected density ρ(x,t) of the particles obeys the D-dimensional heat equation [1, Chapter 1.3]

$$\frac{\partial}{\partial t} \rho = k \nabla^{2} \rho$$

(1)

for some positive constant k. Equivalently, a distribution is heat-like if the expected location of a particle that is located at x₀ at time t₀ has, at some later time, t₀ + t, the following Gaussian distribution centered on x₀ with a variance proportional to t:

$$\begin{array}{@{}rcl@{}} K(t, x, x_{0}) &=& \frac{1}{(4\pi k t)^{D/2}} e^{-\frac{r^{2}}{4\pi kt}} \\ \textrm{ where } r^{2} &= \|&x - x_{0}\|^{2} \textrm{ and } (t>0) . \end{array}$$

(2)

Throughout this discussion, we shall restrict ourselves to solutions of the heat equation whose integral over $\mathbb {R}^{D}$ is conserved, except where otherwise noted. Assume next that these particles are endowed with an extra binary degree of freedom so that they may be said to be either “positive” or “negative” (or equivalently, can exist either as “particles” or “antiparticles”). The particles and their associated walks are “wave-like” if the expected net density $\tilde {\rho }(\textbf {x}, t)$ (i.e., density differential of positive and negative particles) satisfies the classical wave equation

$$\frac{\partial^{2}}{\partial t^{2}} \tilde{\rho} = c^{2} \nabla^{2} \tilde{\rho} .$$

(3)

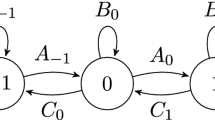
We shall prove that any set of heat-like paths on a stationary graph becomes a wave-like set of (two-state) particles and paths if, at every node to which a particle travels, it spawns a particle-antiparticle pair (i.e., a pair of particles in opposite states) and if, furthermore, the new particle that has the opposite state of the original incoming particle always initially steps along the edge the incoming particle just traversed, in the reverse direction (Fig. 1).

Fig. 1

Brownian-Huygens propagation: any incoming particle (or antiparticle) at a graph node spawns a particle-antiparticle pair, and the newly-created particle that is in the opposite state of the incoming particle must initially step in the opposite direction of the incoming particle, while the other two outgoing particles randomly and independently choose to traverse any edge of the node. Upon reaching their respective neighboring nodes in the subsequent time step, all outgoing particles become incoming particles

In other words, for any graph, including random ones, on which the endpoints of random walks have a probability distribution that is a Gaussian centered on the starting point of that walk with a variance proportional to time (and given the Central Limit Theorem, the variety of graphs and walks which satisfy that requirement is wide), there is a related set of “mostly” random walks of particles (and antiparticles) on the same graph whose distribution satisfies the classical wave equation. (We say “mostly” only to account for the sign- and direction-changing backpropagation steps whose initial post-creation step is therefore not random). As long as the earlier Brownian motion particles and their implied paths are “heat-like”, these modified particles and their paths are assuredly “wave-like”. That being the case, collections of particles that exhibit wave-like properties are no more paradoxical than, say, particles that exhibit diffusion-like properties. All that is needed to transform the latter into the former is the ability of particles to be in one of two states on walks that are reversible.

Note that it is only for ease of visualization that we say the incoming particle has spawned an anti-particle pair. We could equivalently say that it is the incoming particle that always changes state (i.e., that it reverses its sign) and also reverses its direction, while also spawning two other particles with the opposite sign. We prefer the former memory-aid only because physicists will likely regard it as more familiar and evocative, though in analyzing amplitudes or expected particle counts in terms of summations over paths, the latter approach will prove to be more useful. But in either case, note that the net particle count is strictly conserved.

The first part of the proof will show that the above-defined particle-antiparticle dynamics do indeed lead to wave-like distributions in the specific case of regular lattices $\mathbb {Z}^{D}$ (for which the associated regular random walks are indeed heat-like).

Thereafter, we shall show that the normalized net count of the branching random walks in question can be expressed solely as a linear combination of values of the kernel of the heat equation – in other words, the expression does not depend on the particulars of the underlying graph on which the random walks take place (as long as the starting walks are heat-like). Therefore, what was shown to hold for walks on a regular D-dimensional lattice must be true for any graph configuration on which random walks of T steps have endpoints that are Gaussianly distributed in the continuum limit, with variances proportional to T.

In other words, classical wave motion is compatible with a surprisingly wide variety of structures and media.

2 Regular Lattices in D Dimensions

We shall first consider Brownian particles walking randomly along points of $\mathbb {Z}^{D}$ so that a step is always of length 1. Random walks that always traverse a unit distance along any axis have the property that the sums of the components at two successive times alternate in parity (and in this case, the parity of a point’s components distinguishes the two parts of the bipartite graph). For convenience, we shall restrict ourselves to the part of the graph consisting of nodes whose integer components have a sum that is even whenever the time t is even.

The transition matrix that gives the conditional probability that a particle at some point X will in the subsequent time be found at some nearest neighbor of X, call it “HeatMatrix”, is an N × N matrix of the form

$$\textrm{HeatMatrix} = \frac{1}{N} \times \left[\begin{array}{ccc} 1 & 1 & {\dots} \\ {\vdots} & {\ddots} & \\ 1 & & 1 \end{array}\right]$$

(4)

where N is the number of neighbors at a given node (i.e., the degree). For the regular lattice in $\mathbb {Z}^{D}$ we are considering, the degree of any node is 2D, but so as to keep our notation general, we shall continue to use N to signify the number of nearest neighbors at a node.

Note that HeatMatrix is idempotent and that its rows and columns sum to 1. As noted earlier, we shall refer to random walks whose expected values satisfy the above matrix as Brownian motion, regardless of the lattice in which they propagate.

We can also consider branching random walks [2, Chapter 1.1] for which any incoming particle produces a number of “descendant” particles at any step. For example, a particle that always produces another particle upon arriving at any node will have a related transition matrix, HeatMatrix₂ that is twice the value of HeatMatrix.

$$\textrm{HeatMatrix}_{2} = 2 \times \textrm{HeatMatrix}$$

(5)

In that case, the number of particles will of course double at each time. We shall refer to this type of dynamics as Double Branching Brownian motion regardless of the graph in which it takes place. Note that if we choose to count paths, we will typically assume that a particle that was created at some time inherits the past locations of the particle that spawned it, so that every particle’s path, regardless of when that particle was created, has a history with the same number of steps.

We can also choose to give every particle a degree of freedom so that it can be either “positive” or “negative”, in which case, particles in the negative state will be referred to as “antiparticles”. We can likewise define net particle counts on any set of points as the difference between the count of positive and negative particles, and likewise we can define the net particle density. We can even choose to have particles and antiparticles traveling along the same edge at any time annihilate each other, though we will forego doing this whenever we wish to consider the set of all possible paths a particle might take.

Consider also the trivial dynamics wherein every particle always reverses direction and sign at every step. We shall refer to that dynamics as Huygens (back)propagation. In that case, the transition matrix that gives the expected net count of particles on an outgoing edge of some node in terms of the expected particle count along some “incoming” edge of that same node is

$$\textrm{HuygensMatrix} = -I$$

(6)

where I is the N × N identity matrix.

To reiterate, due to the systolic nature of random walks on bipartite graphs on which a node cannot be its own neighbor (in other words, cycles of length 1 are forbidden), the diagonal matrix elements in the above equation relate motions that are oppositely directed (and, due to the negation, of opposite sign) even though they refer to the same edge – in other words, they are a dynamics exclusively of back-and-forth path (and sign) reversal.

If we define the “momentum” of any particle at any time (on any arbitrary graph embedded in $\mathbb {R}^{D}$) as a unit vector in the direction of the propagation of a particle traversing across an edge in a single time step, multiplied by the speed required to traverse an edge along with some unit mass (i.e., ignoring any relativistic corrections merely for the sake of simplicity), we see that the momentum is exactly conserved for particles exhibiting Huygens behavior, whereas in the case of Brownian motion, or the doubled branching thereof, the expected value of the momentum is zero on any graph where the expected vector distance (as determined from a graph’s embedding in $\mathbb {R}^{D}$) from a node to its nearest neighbors has zero magnitude.

And as noted earlier, we can endow the particles with a sign and then calculate the expected net particle count (or net particle density). Using such two-state particles, we can consider a dynamical process that combines Double Branching Brownian motion and Huygens backpropagation, so that any incoming particle at a given node (being in either a positive or negative incoming state) results in an outgoing configuration of two other particles in the same incoming state (in other words a branching random process) and also an additional particle having the opposite sign, and that latter particle must travel in the opposite direction of the incoming particle. Each of the three outgoing particles will in the subsequent step likewise lead to three other outgoing particles in the same manner. (Note, however, that if we allow oppositely signed particles traveling along the same edge to annihilate, then it is possible for one or both of the particles with the same sign as the incoming particle to choose the reverse direction as well, in which case there will only be one outgoing particle in that step).

This particular kind of propagation – as previously noted, we shall refer to it as “Brownian-Huygens propagation”, regardless of the of graph in which the particles travel – is of special interest, since it conserves the particle count and has numerous other interesting properties; for example, it can be shown that if the associated Brownian motion paths on the same graph are heat-like (so that their continuum limit distributions are rotationally invariant Gaussians) then the expected momentum for Brownian-Huygens propagation is also conserved.

Note that as was the case with Double Branching Brownian motion, every particle we create through Brownian-Huygens propagation has, in terms of its ancestry, a well-defined “wave path” that extends all the way back to some initial configuration. However, there is additional structure to consider than was the case with Brownian motion, given that an ancestor might have traveled in the reverse direction of a previous step and changed sign. But purely in terms of a sequence of locations, that takes no account of whether a step was Huygens or Brownian, a given wave path has an obvious correspondence to a specific element in the set of all possible Brownian motion paths. We shall call that element the “Brownian shadow” of that wave path, and because of the multiplicity inherent in any branching process, many wave paths will have the same Brownian shadow.

The matrix that gives the expected net particle count at an outgoing edge, given the presence of an incoming particle along some other edge, which we shall call WaveMatrix, is as follows:

$$\textrm{WaveMatrix} = \left[\begin{array}{cccc} (\frac{2}{N} - 1) & \frac{2}{N} & \frac{2}{N} & {\dots} \\ \frac{2}{N} & (\frac{2}{N} - 1) & \frac{2}{N}& {\dots} \\ \frac{2}{N} & \frac{2}{N} & (\frac{2}{N} - 1) & \\ {\vdots} & {\vdots} & {\ddots} & \\ \frac{2}{N} & \frac{2}{N} & & (\frac{2}{N} - 1) \end{array}\right] .$$

(7)

Which may be expressed more compactly as

$$\textrm{WaveMatrix} = - I + 2 \times \textrm{HeatMatrix} .$$

(8)

Note that WaveMatrix is a relation between the edges of a graph (so that it relates particle propagations on time intervals between two pairs of successive integer times, as opposed to a relationship among function values at nodes at two specific times), so that the resultant value of the expected number of particles at any point is just the sum of the incoming or outgoing expected particle counts along the edges (or “flows”) of that node. (We shall regard HeatMatrix in the same way, even though, as we shall see, the underlying difference equation is first-order, which means that a particle’s contribution to the overall amplitude at a given node can be determined without reference to the edge along which it arrived.)

As was the case with HeatMatrix, WaveMatrix has rows and columns whose sum is 1, so that the sum of flows along any incoming edges converging on some node is the same as the sum of the particle counts in the node’s outgoing flows. And since HeatMatrix is idempotent, it is easy to prove from the previous relation between WaveMatrix and HeatMatrix that the former is involutory. Therefore, for a collection of particles obeying Brownian-Huygens propagation, the sum of the squares of the expected incoming particle counts or flows along any incoming edges to a node is the same as the sum of the squares of the expected outgoing particle counts (we stress that this equality, as was the case with momentum, only applies to the squares of the expected particle counts).

In the case of regular Brownian motion, since a particle has an equal likelihood of traversing to any of its neighbors (and likewise, the expected number of particles at any node is just the average of the expected particle count at its neighbors in the previous step), then considering again a regular lattice $\mathbb {Z}^{D}$, the expected particle count at any time, ψ(x,y,z,…,t), is related to the previous neighboring particle counts according to the following difference equation

$$\begin{array}{@{}rcl@{}} \psi(t+1) &= & \frac{1}{N} (\psi(x+1) + \psi(x-1) \\ && +\psi(y+1) + \psi(y-1) \\ && + \psi(z+1) + \psi(z-1) \dots) . \end{array}$$

(9)

In all of the partial difference equations we present here, we will, for simplicity, usually specify only the coordinate of a function that deviates from x and t, or else omit arguments altogether, e.g.:

$$\psi(x) = \psi(y) = \psi(t) = \psi = \psi(x,y,z,\ldots,t) .$$

(10)

The expected particle count associated with Huygens propagation also follows a trivial difference equation due to the fact that particles reverse direction at every subsequent time step:

$$\psi(t+1) = -\psi(t-1)$$

(11)

In this case, the difference equation applies not just to the expected value of the particle count at t + 1, but the actual particle count, since Huygens dynamics are deterministic.

If we choose to visualize a particle as traveling along an edge from one node of an edge to another before being transformed into some other particle(s), we shall assume that the change-of-state (or particle creation) occurs just before the particle arrives at a neighbor node, and that will specify a particle’s contribution to any count taken along the nodes. (Moreover, in this paper we shall primarily be concerned with dynamics for which the net count is conserved at any node, so that whether particles change state just before or just after arriving at a node is irrelevant, as long as the convention is consistent for any changes of state.)

Given that the RHS in (9) and (11) refer to different times than those in their LHS, the partial difference equation in the case of Brownian-Huygens propagation is easily seen to be (after rearranging so that the temporally displaced coefficients are all on the LHS)

$$\begin{array}{@{}rcl@{}} \psi(t+1) + \psi(t-1) &= & \frac{2}{N} (\psi(x+1) + \psi(x-1) \\ &&+ \psi(y+1) + \psi(y-1) \\ && +\psi(z+1) + \psi(z-1) \dots) . \end{array}$$

(12)

By subtracting the “central” term $2\psi (x,y,z {\dots } t)$ from both the LHS and RHS of eqs (9) and (12) (and in the case of each RHS, apportioning that central term equally to each pair of terms inside the parentheses), i.e.,

$$\begin{array}{@{}rcl@{}} \psi(t+1) - 2\psi + \psi(t-1) &= & \frac{2}{N} (\psi(x+1) - 2\psi + \psi(x-1) \\ & &+\psi(y+1) - 2\psi + \psi(y-1) \\ &&+ \psi(z+1) - 2\psi + \psi(z-1) \dots) . \end{array}$$

(13)

and taking the continuum limit, we see that (9) converges to the familiar heat (1), with k = 1/N, whereas (12) converges to the D-dimensional wave (3) with c² = 2/N (or, in the case of the regular lattices considered here, c² = 1/D).

Given the scaling we have chosen, note that the coefficients of HeatMatrix are all equal to k whereas the off-diagonal and diagonal elements of WaveMatrix are equal to c² and (c² − 1) respectively. And even though the particles in this space move one lattice length per time interval, the speed of any wave pulse is $\sqrt {2/N}$, just as with lattice gases [3] (Fig. 2).

Fig. 2

Contour plots exhibiting nearly circular wave-fronts (at time t = 64) of a wave pulse on a regular lattice whose boundary conditions at t=-1 and t = 0 are respectively Dirac Delta functions at two neighboring nodes with the t = 0 node displaced in the direction of the large arrows. On the left is a two-dimensional pulse; on the right is a two-dimensional slice of a three-dimensional pulse. The respective diameters of the wave fronts, as measured from the peaks of their outer ripples (and as indicated by the notches on the right edge of either graph) are 91 and 75, which even at this relatively granular level are close to what is predicted from their respective continuous-case wave speeds of $128/\sqrt {2}=90.51$ and $128/\sqrt {3}=73.90$

As noted earlier, since the heat equation is first-order, calculating the likelihood that a particle at some node will be at a specific neighboring node in the subsequent step requires no earlier knowledge of where the particle had previously been. This is not the case with Brownian-Huygens propagation and the related second-order wave equation. In that case, we must know both the arrival point of a given particle, and also the edge from which the particle came in the prior step, so that we know along which edge the Huygens backpropagation particle must travel.

Given the nature of HeatMatrix, any sequence of nodes such that each successive member of the sequence is a neighbor of the preceding member constitutes an acceptable path, and has the same probability of being traversed as does any other path of equal length. It is a well-known property of random walks on a square lattice [4] that for any two points X₀ and X₁, and any corresponding times T₀ and T₁ with T₁ > T₀, the value K(T,X₁,X₀) of the kernel of the heat equation (where T = T₁ − T₀) is equal, in the continuum limit, to the number of all paths of length T that begin at X₀ and end at X₁, divided by the number of all paths of length T.

We shall refer to the set of all such paths as HeatPaths(T), and for convenience, we shall omit mention of X₀ and X₁. We can similarly define WavePaths(T), though as mentioned before, in order to fully specify an element of the latter set, we must specify which of its steps were sign-changing Huygens steps (and these can only happen for path steps that are reversals of the prior step); moreover, as noted earlier, given that two Brownian particles are generated at every time step, then even after fully specifying which step of a path, if any, was a Huygens step, there will be multiple identical paths in WavePaths(T) having the same Brownian shadow in HeatPaths(T), the specific number of which shall be calculated below.

Let us similarly define all the paths generated by particles obeying the rules of Double Branching Random motion as HeatPaths₂(T). Clearly, given that the number of particles doubles at each node, the count of HeatPaths₂(T) is 2^T times the count of HeatPaths(T).

In the case of WavePaths(T), in order to be able to precisely determine which of the initial steps of any element can be Huygens steps (so that they are the reversal of their previous step), we shall assume that all the paths in WavePaths(T) arrived at X₀ from the same neighbor X_nbr, though that, too, will be suppressed for ease of notation. That being the case, if a path begins with a Hyugens step, it must, by the rules of Brownian-Huygan propagation, traverse back to that neighbor X_nbr at t = 1.

Finally, note that in the rest of this paper, any reference to the continuum limit in the case of distributions that are unbounded or ill-defined in that limit (e.g., Double Branching Brownian motion and Huygens propagation) will be taken to mean some quasi-continuum regime in which the discreteness of the underlying dynamics is unobservable, though for convenience, we shall continue to refer to that regime as the continuum limit.

3 Graph-Invariance

A relationship associated with a set of heat-like walks on a particular graph, and whose endpoint distributions therefore obey the kernel of the heat equation as in (2), is kD-graph-invariant if, in the continuum limit, that relationship remains true for any other graph whose random walk distributions obey a kernel having the same k and D (and note that regardless of the graph we are considering, we can always alter the time scale and thereby vary k as we please, so that it is essentially a free parameter). For simplicity, we shall henceforth drop the kD prefix and simply speak of graph-invariance.

We have already shown in the last section that heat-like paths, when transformed into the paths associated with Brownian-Huygens propagation, become wave-like if the underlying graph is a regular lattice.

The purpose of this section is to show that this relationship between heat-like paths and the transformed Brownian-Huygens paths is graph-invariant. In other words, distributions of heat-like paths on any graph, not just regular D-dimensional lattices, produce distributions that are wave-like when the associated walks are transformed so as to follow the rules Brownian-Huygens propagation. It should be noted that with regard to all the formulas that are presented in this section, the sole purpose in deriving them is to show that they exhibit graph-invariance.

Given that we are considering branching processes, as well as particles that can be positive or negative, we shall also typically make reference to expected particle counts in what follows rather than probabilities, or more specifically, summations over all possible (possibly signed) paths of the dynamics under consideration.

For example, consider a particle that was initially located at X₀ at T₀, and that undergoes Brownian motion thereafter. The expected particle count EPC(X₁) at X₁ and t = T is then equal to the number of paths in HeatPaths(T), divided by the total number of Brownian motion paths of length T, which we shall designate by η_B(T). In other words, given our initial assumptions about how Brownian motion walks are heat-like, then in the continuum limit

$$\textrm{EPC}(X_{1}) = \frac{1}{\eta_{B}(T)}\textrm{Count[HeatPaths}(T)] = K(T, X_{1}, X_{0})$$

(14)

(Again, the dependence of HeatPaths(T₁) on the boundary conditions X₀ and T₀ is being suppressed, for convenience, and henceforth, we shall likewise typically omit the X₁ argument of the expected particle count.)

With regard to what was said earlier about Double Branching Random motion and the corresponding set of paths HeatPaths₂(T), the expected particle count in that case, designated as EPC_DBRM, in the continuum limit (or quasi-continuum limit, given what was earlier said about the continuum limit of Double Branching Random motion), satisfies the following relation

$$\textrm{EPC}_{\textrm{DBRM}}(T) = 2^{T} * K(T, X_{1}, X_{0})$$

(15)

which follows directly from the definition of Double Branching Random motion, but can also be proved formally by way of induction. Note that even though the count of paths will vary depending on which graph the propagation takes place, as will the sum over all paths, the RHS of the above equation, and therefore the equality itself, is graph-invariant, so that the above relationship therefore holds for any graphs on which Brownian motion is heat-like.

Even in the case of pure Huygens propagation, the very fact that it consists simply of back-and-forth motion between nearest neighboring nodes, with a sign change at each time step, means that however pathological its continuum limit may be, the associated expected particle counts do not depend on the particulars of a given graph and are therefore also graph-invariant.

Given that Brownian-Huygens propagation is in some sense a combination of Double Branching Random motion and Huygens propagation, both of which produce particle distributions that are graph-invariant, it should not be altogether surprising if the same were true for Brownian-Huygens propagation. We at least know that the net count of all paths of a given length T (not just those paths that terminate at X₁) is the same as for Brownian motion, i.e. it is equal to η_B(T), since any branching of paths occurs by way of particle-antiparticle creation, which does not alter the net particle count, and therefore, the net count of signed paths.

But even though there is, unfortunately, no similarly obvious graph-invariant relationship between WavePaths(T) and the kernel of the heat equation, we will show that we can partition WavePaths(T) so that expected particle counts for any of the resultant subsets can indeed be similarly related to kernels of the heat equation in a graph-invariant manner, so the same must therefore be true of WavePaths(T) itself.

With that in mind, let us partition WavePaths(T) into 2^T subsets, with each subset uniquely specified by a binary string composed of B’s and H’s that indicates which steps of the paths in a given subset are Huygens backpropagation steps (i.e., consisting of a step reversal and sign change) or else Brownian steps (the latter having a multiplicity of two since there are two Brownian particles created for any incoming particle). Note that since all the paths in any subset of this binary partition take their Huygens steps (and incur their sign-changes) at the exact same times, all particles traversing a path in that subset will have the same final sign once they reach X₁ at T₁. Moreover, since the number of Brownian steps is likewise the same for all paths in the subset, the multiplicity – i.e., the number of paths within that subset that have the same Brownian shadow in HeatPaths(T) – is likewise identical. We can combine these into a single multiplicity-and-sign factor MultSgn(n_B,n_H) as follows

$$\textrm{MultSgn}(n_{B}, n_{H}) = 2^{n_{B}}*(-1)^{n_{H}} ,$$

(16)

where n_B and n_H are the respective numbers of Brownian and Huygens steps in any path of the subset in question (so that their sum is equal to T).

Note that the count of paths for different subsets varies greatly. For example, there is at most one element in the subset whose corresponding string consists entirely of H’s (i.e. the single path in WavePaths(T) that also happens to satisfy the rules of Huygens propagation for the entire duration of its path), and its contribution to the expected particle count at X₁ is positive or negative depending on whether T is even or odd, though unless X₁ is equal to X₀ (or X_nbr), and T is even (or odd), the subset will be empty (and that may be true for various other subsets as well, but we will continue to refer to the 2^T-fold splitting as a partition). Whereas subsets whose corresponding strings have progressively larger numbers of B’s will have larger and larger counts, since each Brownian step increases the overall multiplicity by a factor of 2, though once again, their contribution to the overall expected particle count at X₁ will be positive or negative depending on whether the number of H’s in the associated string is even or odd.

Given that every element of WavePaths(T) implicitly includes the same “starter step” from some specific neighbor X_nbr to X₀, let us also agree to preface any if its associated binary B-H strings with an S as a placeholder for this starter step immediately preceding T₀.

3.1 A Specific 1-Dimensional Example

To give a specific example, consider a solution of the one-dimensional wave equation whose boundary conditions at t = − 1 and t = 0 are zero except at the point -1 at t = − 1 and 0 at t = T₀ = 0, where the value at both points is one; in other words, a delta-function traveling wave moving along the positive direction with a speed of 1. The solution to the heat equation for boundary conditions that are zero everywhere at t = 0 except at 0, where the value of the solution is 1, is just Pascal’s triangle, up to a normalization constant, with the value at any time T₁ and node X₁ equal to the count of paths of length T₁ whose final value is X₁, divided by $2^{T_{1}}$.

Therefore, if we were to generate 1-dimensional paths as part of a Monte Carlo simulation, then the fraction of runs for which the path endpoint at T₁ is X₁ will approach the heat equation at those endpoint coordinates. Likewise, if we consider Double Branching Random motion, the expected particle count in that case would be $2^{T_{1}}$ times that expected value.

Likewise, if we generate a very large number of simulations of Brownian-Huygens propagation starting with a particle that arrives at the origin at t = 0, having in the prior step been at x = − 1, and consider not only the full path of each particle (that as noted before, includes ancestral steps prior to its generation, so that all paths similarly start with a step to the origin at t = T₀), but also the string that rerecords at which step of a path a particle is in a Huygens state (so that it therefore changed sign and reversed its previous step), then the observed count of particles at any point, divided by the number of simulations, will approach the wave equation at that point.

Observe that for T₁ = 4, the nonzero values of Pascal’s triangle are (1,4,6,4,1) all divided by 16, where x is respectively (− 4,− 2,0,2,4). Let us consider paths of length 4 (plus a starter step) for which the associated strings all have a single H at the step corresponding at T^∗ = 3, i.e., SBBHB, and set X₁ to -2. In that case, there are just two paths to consider, with the coordinates (0,− 1,− 2,− 1,− 2) and (0,− 1,0,− 1,− 2). The value of the heat kernel needed to calculate the contribution for this subset is two steps earlier, and for this value of X₁ it is 1/4 whereas the multiplicity and sign factor is -8, so that the resultant value for this subset is their product, -2. Later on, we shall calculate the rest of the subsets and verify that it gives us the correct value for the wave equation at x = − 2 and t = 4, which is zero.

3.2 Expected Particle Counts for Specific Subsets

As stated earlier, our goal in this section is to show that for any subset of this partition of WavePaths(T) into 2^T subsets, the expected particle count can be expressed in terms of the kernel of the heat equation, so that the relationship between the two is graph-invariant.

For some subsets, this is already obvious. For example, consider the subset of the partition that has absolutely no Huygens steps and is composed simply of Brownian steps. In other words, this single subset of WavePaths(T) is identical to HeatPaths₂(T), and as was already noted in (15), has an expected particle count that is graph-invariant. Likewise, as noted, there is the subset corresponding to the path composed purely of Huygens steps. As noted, its contribution to the expected particle count is positive or negative depending on whether T is even or odd, and in the latter case, the path in the subset will by necessity terminate at X_nbr instead of X₀. Nonetheless, that path is likewise graph-invariant.

Finally, consider the more general case of subsets of WavePaths(T) that are composites of the above two cases; i.e., they consist of some number n_H of Huygens steps followed by n_B strictly Brownian steps (and by setting n_B or n_H to zero, we see that the previous two cases are just special cases of this category). For any such set of composite paths, we can determine the expected particle count of the Brownian (i.e., the non-trivial) portion from (15) simply by making the substitution T = n_B. However, given what we just said about pure Huygens steps, then if n_H is odd, the overall expected particle count will be negative. Moreover, the final argument of the heat kernel (i.e. the node at which the Brownian portion of the path begins) will have to be X_nbr instead of X₀ since Huygens paths of odd length terminate at the former node, which is therefore where the Brownian portion will begin. Regardless, the expected particle counts for all these subsets will therefore be graph-invariant as well.

In fact, as we shall see, for any i, where 1 ≤ i ≤ 2^T, the expected particle count EPC_i (again assuming an initial location of X₀ with the same starter step) of subset i of this binary partition of WavePaths(T) can, in the continuum limit, be expressed as follows

$$\textrm{EPC}_{i} = \textrm{MultSgn}(n_{B}, n_{H}) * K(T-T_{i}, X_{1}, X_{\text{start}})$$

(17)

for some X_start near X₀ (the details will be specified below) and for T_i such that 0 ≤ T_i ≤ T, where n_B and n_H are again the respective number of Brownian and Huygens steps in the i^th subset, i.e., the respective number of B’s and H’s in the associated string. Moreover, T_i (and X_start) may be determined solely by way of that same string, so that the expected particle count of the subset is graph-invariant.

First, let us consider what would happen to the expected particle counts of the paths in HeatPaths₂(T) if every path in the set was extended by m pairs of successive Huygens steps, in any combination. Given the behavior of Huygens steps, the answer is easily seen to be absolutely nothing, apart from delaying the arrival time of each path from T₁ to T₁ + 2m, though, as trivial as that observation may be, let us formalize it into a theorem.

Theorem 1 (Adding paired Huygens steps)

Let {m_i} be an arbitrary finite set of m integers such that 0 ≤ m_i ≤ T; for convenience, assume the integers are in reverse order. For each m_i and for each path in HeatPaths₂(T) – in other words, Double Branching Random motion paths – enlarge it with two successive Huygens path steps immediately after step m_i (thereby violating the rules of pure Double Branching Brownian motion). The expected particle count of the enlarged paths, whose length is now T + 2m, is then unchanged,

$$\textrm{EPC}_{\textrm{mAddedHHPairs}}(T+2m) = 2^{T} * K(T, X_{1}, X_{0})$$

(18)

i.e., exactly as in the RHS of (15).

Proof

By the rules of Brownian-Huygens propagation, a pair of two successive Huygens steps inserted at time T^∗, where the latter is some member of {m_i}, into any Double Branching Random motion path (let us assume that at T^∗, a given DBRM path is at the node X^∗, having just traversed the edge e^∗) must with probability 1 reverse-step twice (i.e., back-and-forth) along e^∗, whereupon it then proceeds exactly as before. Since every added step is part of a deterministic 2-cycle, the associated expected values at any subsequent time are unchanged (other than being delayed by precisely 2 time steps). □

To take a specific example, assume T = 5, and let {m_i} be the set {3,5}. In that case, every single path in HeatPaths₂(T) will, after taking its third step, reverse that third step and then repeat it, and the same goes for the fifth step. Therefore all paths will now have a duration of 9 steps rather than the original 5, but otherwise, nothing about the expected particle count at the destination of the paths has changed.

While the above theorem concerns paths in HeatPaths₂(T), it can also be applied to any of the subsets of our 2^T-fold partition of WavePaths($T^{\prime }$) whose Huygens steps are clustered in pairs, except the relation between the expected particle count (call it EPC_{mExcisedHHPairs}) and the kernel of the heat equation is then as follows:

$$\textrm{EPC}_{\textrm{mExcisedHHPairs}}(T^{\prime}) = \textrm{MultSgn}(n_{B}, n_{H}) * K(T^{\prime} - 2m, X_{1}, X_{0})$$

(19)

where n_H = 2m and MultSgn$=2^{(T^{\prime }-2m)}$. Moreover, $T^{\prime }$ in the above equation equals T + 2m in (18). In other words, instead of starting with Double Branching Random motion and adding Huygens pairs to it, here we are instead excising pairs of Huygens steps from some subset of WavePaths($T^{\prime }$) whose Huygens steps are arranged in pairs so as to create a set of paths identical to HeatPaths₂(T).

We shall leave to the reader the proof for the following corollary of the above theorem: instead of enlarging HeatPaths₂(T) with pairs of Huygens steps, we could have instead chosen to enlarge any other subset of WavePaths(T) in the same manner. The proof is nearly identical, and the only effect to the expected particle count of these Huygens pair insertions is likewise a delay of two time steps for every added pair.

Next, let us consider a slightly different way of starting with HeatPaths₂(T) and then expanding each path so as to be more like an element of WavePaths(T). We will expand each path by pairs of path steps as before, but this time, the first member of any added pair of steps will be another Double Branching Random motion step (so that it has a multiplicity of 2). In other words, in terms of the strings we introduced earlier, we are now adding BH pairs instead of HH pairs. Admittedly, the (doubled branching) Brownian step that begins each added pair manifestly depends on the particulars of whatever lattice node at which the insertion takes place, since Brownian steps, unlike Huygens steps, can traverse to any nearest neighbor node without restriction. Even so, with regard to the resultant expected particle counts at X₁ (call that EPC_{mAddedBHpairs}), the Huygens step that follows the Brownian step effectively undoes whatever the latter might add to the sum over all distinct paths (apart from adding an extra factor of negative two due to the branching that took place, and the sign change of the Huygens step, though that, too, is graph-invariant).

Theorem 2 (Adding Brownian and Huygens step pairs)

Let {m_j} be an arbitrary finite set of m integers such that 0 ≤ m_j ≤ T that are, again, in reverse order. For each m_j and for each path in HeatPaths₂(T), enlarge the path with an arbitrary Brownian step (i.e., a step along any edge leading from the node where the path is situated at t = m_j) followed by a Huygens step. The expected particle count for the enlarged paths (whose length is now T + 2m) is multiplied by a factor of 2^m ∗ (− 1)^m with respect to (15), i.e.,

$$\textrm{EPC}_{\textrm{mAddedBHpairs}}(T+2m) = 2^{T + m} * (-1)^{m} * K(T, X_{1}, X_{0})$$

(20)

Note that this conforms to our earlier derivation of MultSign(n_B,n_H) given that for the resultant enlarged paths, n_B = T + m and n_H = m.

Proof

As before, by the definition of Huygens step, whatever edge the added Brownian step (which due to the branching, has a multiplicity of 2) traverses, the subsequent Huygens step will with probability 1 reverse it (and also change the sign of the path), so that apart from that factor of negative two (leading to an overall multiplier of (− 2)^m when accrued over the entirety of {m_j}), the value of the heat kernel that determines the expected particle count is otherwise exactly as before. □

Again, the fact that Huygens steps are deterministic and also reversals of a prior step means that however many neighbors are at the node at which a new (branching) Brownian step has been inserted, and whatever (possibly random) set of directions they involve, none of that can affect the expected particle count, given that the following Huygens step will with probability 1 undo it.

As with the case of adding pairs of Huygens steps, this result for Double Branching Random motion can instead be applied to subsets of the WavePaths($T^{\prime }$) partition so as to excise any Huygens steps that are preceded by a Brownian step. In that case, the equivalence is

$$\textrm{EPC}_{\textrm{mExcisedBHpairs}}(T^{\prime}) = \textrm{MultSgn}(n_{B}, n_{H}) * K(T^{\prime} - 2m, X_{1}, X_{0})$$

(21)

where $n_{B}=T^{\prime }-m$ and n_H = m and where, as before, $T^{\prime }=T+2m$.

And as before, the proof of the following corollary to the above theorem is nearly identical to the one above: instead of enlarging HeatPaths₂(T) with BH pairs, we can likewise add BH pairs to any subset of WavePaths(T). In either case, the only effect of these insertions will likewise be a delay of two time steps for every added pair, along with an added factor of -2 to the expected particle count.

We have one remaining theorem before we can (by iteratively combining the above theorems – or more specifically, their corollaries) prove that every single subset of our WavePaths(T) partitions can be expressed in terms of the kernel of the heat equation in a graph-invariant manner, and it is related to the earlier observation that a Huygens propagation path of odd length terminates at x_nbr, not at X₀, so that the distribution of any remaining portion of the path has a shifted origin node regarding any kernel of the heat equation.

Let us therefore consider the subsets of the binary partition of WavePaths(T) – i.e., this time, we shall not start with HeatPaths₂(T) and then use that to back out a result for WavePaths(T), but shall instead focus directly on the subset of WavePaths(T) that interests us – the partition subset which has only one Huygens step that occurs at the very beginning of the path. In other words, we are now considering the case of a Huygens step that is not preceded by a Brownian step, as was true with regard to the previous theorem.

Theorem 3 (Single-initial-Huygens-step)

For the expected particle count EPC_{SingleInitialHuygens} of the subset of WavePaths(T) that has a single Huygens step starting at T₀,

$$\textrm{EPC}_{\textrm{SingleInitialHuygens}}(T) = \textrm{MultSgn}(n_{B}, n_{H}) * K(T - 1, X_{1}, X_{\text{nbr}})$$

(22)

where X_nbr is the neighboring node of X₀ at which the starter step originated (i.e., the node of the path at t = − 1), and where n_B = T − 1 and n_H = 1.

Proof

In this case, we choose to excise each path’s initial Huygens step along with the prior starter step (comprising a 2-cycle that with probability 1 began and terminated at X_nbr). Subsequently, the paths (whose length has been reduced by 1, given that the starter step was only a placeholder) now originate at X_nbr instead of X₀; otherwise, given the lack of Huygens steps, the earlier results for Double Branching Random motion still apply, leading to the expression shown. □

Note that the formulas in all three of these theorems are graph-invariant. Also note that whereas for the first two theorems, the displacement to the arguments of the kernel of the heat equation was some even number of time steps, in the final theorem we instead shift both the time coordinate and a spatial coordinate by one step. That means we thereby always relate spacetime points that are on the same part (parity-wise) of our bipartite graph.

To completely extend these theorems and their corollaries to all the 2^T subsets of our partition, we only need to combine them, along with the observations that every single subset of the partition can be iteratively constructed from HeatPaths₂(T^∗) for some T^∗ such that 0 ≤ T^∗≤ T, or else a subset of WavePaths(T^∗) where 1 ≤ T^∗≤ T which has only one Huygens step starting at T₀, and then adding (or excising) HH or BH pairs until the subset with the desired corresponding string is obtained. In all cases, the contributions to the expected particle count are expressible in terms of the kernel of the heat equation and are therefore graph-invariant.

The general formula can then be stated as follows (and again, it is presented in the interest of completeness, given that demonstrating graph-invariance is the primary objective.) For any subset i of the 2^T subsets in the binary partition of WavePaths(T), we must first determine whether the associated string for that subset begins with an odd number of H’s after the starter step (followed either by one or more B’s, or else continuing until the end of the string). If so, let us define X_start to be X_nbr, and if not, then let it be X₀.

Also, define n_odd to be the number of any additional (i.e., not at the start) odd clusters of H’s within the associated string of the subset – in other words, any odd clusters of H’s preceded by one or more B’s.

The expected particle count for that subset is then

$$\textrm{EPC}_{i}(T) = \textrm{MultSgn}(n_{B}, n_{H}) * K(T-T_{i}, X_{1}, X_{\text{start}} )$$

(23)

where T_i = T − n_H − n_odd.

This formula for T_i accounts for the fact that in addition to all the H’s that will be excised from the path, every odd cluster of H’s not immediately after the starter step will require any preceding Brownian step to be excised as well.

As an example, consider the string SHHHBBHHBHHHHHBBHHHHBH, which, in terms of its clusters of B’s and H’s, may be more legibly expressed as (S + 3H + 2B + 2H + B + 5H + 2B + 4H + B + H). It consists of an initial odd grouping of 3 H’s, so that X_start in the above equation for the corresponding subset equals X_nbr. There are also two other odd groupings (a cluster of 5 H’s, and a single H at the end of the string), so that n_odd = 2. Also, N_H = 3 + 2 + 5 + 4 + 1 = 15. Therefore, T_i = T − 15 − 2 = T − 17.

In other words, if there is an initial odd grouping of H’s in the string corresponding to a given subset, then the T_i that must be decremented from T, so as to obtain effective time in the kernel of the heat equation that dictates that subset’s evolution, will be an odd number, and X_start = X_nbr; otherwise, T_i will be even and X_start = X₀.

More importantly, for any subset of this partition of WavePaths(T), the expected particle count has no dependence on the specifics of any underlying graph, and that graph-invariance therefore extends to the expected particle count of their union, i.e., to WavePaths(T) itself.

And having established what was needed in the way of graph-invariance, as given in (17), we are ready to proceed to our main theorem:

Theorem 4

For any graph on which the expected particle counts of Brownian motion are heat-like (so that in the continuum limit, they can be expressed via kernels of the heat equation), the corresponding expected particle counts of Brownian-Huygens propagation are wave-like.

Proof

We have just presented a graph-invariant decomposition of the expected particle counts associated with Brownian-Huygens propagation, which applies to any graph where the expected particle counts associated with Brownian motion are heat-like.

But we also know from the previous section that if the graph in question is a D-dimensional regular lattice, then those Brownian-Huygens walk distributions and their associated expected particle counts are wave-like.

Therefore, given the graph-invariance, they must be wave-like for any graph whose expected particle counts associated with Brownian motion are heat-like. □

In other words, we know from the earlier section that the endpoint distributions of Brownian-Huygens paths on a regular lattice are wave-like. We also know, by way of graph-invariance, that the expected particle counts and therefore the densities are the same for any graph on which Brownian motion distributions obey the kernel of the heat equation having the same k and D. Therefore the Brownian-Huygens path distributions and densities associated with any such graph are wave-like, not just those that are regular lattices.

That means that even if the graph in question is random, and has varying neighbors, as long as the graph is homogenous enough so that at some magnification its random walk endpoints are Gaussianly distributed with a variance proportional to the elapsed time of the walk, then we know that Brownian-Huygens propagation on that same graph will result in wave-like distributions.

3.3 Return to the 1-Dimensional Example

Now we can consider the heat kernel weights for the rest of the 1-dimensional paths considered in the earlier example we noted, wherein a solution of the wave equation at x = − 2 and t = 4 is calculated directly in terms of values of the heat kernel, as derived by way of Pascal’s triangle.

Table 1 displays the 22 distinct paths (and 12 distinct strings) leading from 0 to -2 in four steps that produce non-zero contributions, i.e., weights, to the solution of the wave equation. The remaining 4 possible strings (for a total of 2⁴ = 16) have zero weights and so have been ignored; for example, the string SHHBH, after excising both the initial pair of H’s as well as the remaining BH string, is just the empty string (apart from the starter step), and that means that the relevant value of the heat kernel is at t = 0 and x = − 2, where it is zero. Some strings (e.g., SHBBH) have multiple paths, and though these are both displayed, the weight is specified only for the first instance (and accounts for the entire set of paths corresponding to that string) and is left blank for any subsequent listings of the same string. In each case, the magnitude of the weight (apart from the factor of − 1 to the power of the number of Huygens steps) is simply of the product of the heat kernel at some (possibly earlier) coordinates (those x and t coordinates are listed in the final column) times two to the power of the number of Brownian steps in the corresponding path.

Table 1 Calculating the 1-dimensional wave equation at x = − 2 and t = 4 by tabulating all paths of length 4 (plus an implicit starter step to the origin beginning at x=-1) that begin at zero and terminate at x = − 2

As can be seen by inspection, the sum of the weights in this case is indeed zero at x = − 2, as it should be.

Since we have assumed a starter step that arrives at the origin from the point x = − 1, a similar tabulation for all space and time produces non-zero values only for the values x = t, where the value of the specified traveling wave is 1. For example, at the wave-front value x = t = 4, only the SBBBB string produces a non-zero value, and the value there is simply the multiplicity-and-sign factor, 2⁴. times the value of Pascal’s triangle there, i.e., 1, times the overall normalization constant which is the inverse of the first term, for a result of 1. (Any other strings would, according to the formalism laid out here, involve values of the heat kernel at some earlier space-time coordinates that lie outside the reach of any paths with duration less than 4 – i.e., at earlier times the destination is outside the light cone – and so their weight must be zero.)

This can be directly applied to higher dimensions as well (including, for example, hexagonal or triangular regular lattices in two dimensions, arguably the easiest configurations to consider after the two-dimensional square lattice). As noted in the earlier section, any heat-like walks can be modified in such a way, though in cases of irregular lattices, closed form solutions of the heat equation (apart from the continuum limit case of a Gaussian) will be harder to obtain.

4 Additional Degrees of Freedom, Anisotropy, and Mass

Note that, as mentioned before, there can be multiple edges connecting two nodes. For example, consider a regular D-dimensional lattice where the number of edges connecting any two nearest neighbors is some integer m > 1 (Fig. 3). In that case, HeatMatrix and WaveMatrix have the same general form as before, but N, and therefore the size of the matrices, is now multiplied by m; otherwise, the idempotency and involutority remain unchanged. Such multi-edge variations are useful if we desire our particles to have additional states – for example, charge. And if we choose, for any reason, to impose a “Pauli exclusion principle” on the particles – in other words, mandate that only particle in a given state can travel along an edge at any time – then if we apply that exclusion only to particles that are in identical states, such multi-channel graphs can ensure that annihilation or exclusion only involves particles that have identical states.

Fig. 3

(L) A graph with one edge connecting each neighbor along which oppositely signed particles annihilate. (R) A graph (i.e., a multigraph) with three edges connecting any nearest neighbor, suitable for particles with three binary degrees of freedom

Note that the formalism developed here can also be applied to anisotropic graphs and lattices that require a scale transformation in one or more dimensions in order for the random walks on the graph to become heat-like (Fig. 4). Also, the discreteness, and the manner in which the density of particles scales in one dimension or another can be used to our advantage.

Fig. 4

A case where a graph’s anisotropy can be compensated with a scale transformation (in this case, stretching along the y axis or compressing along the x axis), thereby making the associated random walks heat-like

In particular, consider a graph where a random subset of particles (such that their density is constant throughout the space) has an added dimension. For convenience, we may assume the new dimension is minimally small, i.e., isomorphic to $\mathbb {Z}/2\mathbb {Z}$). To visualize this in two dimensions, imagine that a random graph in the xy plane is duplicated and then stacked along the z axis, and some subset of points (for now, assume they have a uniform density) have pairs of edges leading up and down the z axis to a node’s stacked duplicate (Fig. 5). The evenness of the extra dimension ensures that the graph’s two parts can still be distinguished simply according to the parity of the components of this added dimension (and the same holds true for any regular graphs that are toroidal in one or more dimensions, so that we shall stipulate that for any such $\mathbb {Z}/m\mathbb {Z}$ dimension, that m must likewise be even). In any graph where the edges do not all lie along coordinate axis of $\mathbb {R}^{D}$, say a hexagonal two-dimensional lattice, or some irregular D-dimensional graph, the correspondence between a given particle motion and an axis is not well-defined as it is in the case of the regular D-dimensional lattices we began with. But the fact that this added dimension, by construction, has a distinct axis and a uniform size means that movement in an edge along that dimension – let us refer to it henceforth as a “mass dimension” – is distinct from movement along any of the remaining “spatial” edges. Moreover, there is now an eigenvector in our space of functions corresponding to phase rotation along the axis of that new dimension. Let us isolate that mode and impose it onto the dynamics itself, by demanding that any particle that has taken a Brownian-Huygens propagation step along a spatial edge that then takes a step on an edge along the mass dimension (which means it appears to remains stationary with regard to the remaining dimensions, in the same way that a particle in a regular lattice is stationary with respect to any set of axes other than the one it is propagating along) incurs a factor of -1, just as with a Huygens backpropagation step, and likewise, another sign change when it chooses to take a step along a spatial edge after having traversed some non-zero number of steps along the mass dimension – in other words, any transition into or out of motion along the mass dimension involves a change of sign. We shall call this modified Brownian-Huygens propagation. The length of a step along this mass dimension is also arbitrary, apart from inducing a scale factor α corresponding to that dimension length. (We shall further assume that the length is uniform throughout the space.)

Fig. 5

Adding a “small dimension”, isomorphic to $\mathbb {Z}/2\mathbb {Z}$, along the z axis, by doubling a two-dimensional xy graph. Note that not all the nodes on the graph are required to possess edges leading along the added dimension

Note that on this added dimension, the 2^nd-order partial derivative of any function f, i.e.,

$$\frac{f(x, i+1, t) - 2 f(x, i, t) + f(x, i-1, t)}{\epsilon^{2}} ,$$

(24)

where 𝜖 approaches zero in the continuum limit, has a related function differing only in the sign of the second summand of the numerator and a normalization factor of 1/4:

$$\frac{f(x, i+1, t) + 2 f(x, i, t) + f(x, i-1, t)}{4\epsilon^{2}} ,$$

(25)

which we shall call, for obvious reasons, a 2^nd-order partial smoothing of f. Even though f(x,i + 1,t) and f(x,i − 1,t) are the same point (since the added dimension is isomorphic to $\mathbb {Z}/2\mathbb {Z}$), expressing them in more familiar form will make what follows easier to recognize. We shall also use the flexibility afforded to us by our discrete space to consider for the duration of this section only those expected particle counts that are so small in magnitude that the 2^nd-order partial smoothing remains bounded even when 𝜖 is close enough to zero for our space to be indistinguishable from the continuum (or else, ensure the smoothing term stays bounded in this quasi-continuum limit by a compensating scaling of the mass dimension, since that, too, is essentially a free parameter). We shall further limit ourselves to functions that are already smooth enough so that the above smoothing is arbitrarily close to the continuum value of the function at x (at which point i is assumed to be either 0 or 1 so as to properly specify the non-zero part of the bipartite graph).

Assuming that Brownian walks in this expanded graph are heat-like (up to the aforementioned scale transformation along the mass dimension), then Brownian-Huygens propagation in the graph will create walks that are wave-like. As for the modified Brownian-Huygens propagation with the added sign change incurred when switching between a step along some spatial edge and one that is aligned along the mass dimension, and vice versa, we have the following related equation

$$\frac{\partial^{2}}{\partial t^{2}} \psi = \frac{2 }{N^{\prime}}\left(\nabla^{2}_{N^{\prime}} \psi - \frac{\alpha_{c}}{4} \left(\psi(i+1) +2\psi + \psi(i-1)\right)\right) ,$$

(26)

where ψ(i ± 1) signifies the nearest neighbor locations along the newly added dimension (again, given the isomorphism to $\mathbb {Z}/2\mathbb {Z}$, both refer to the same node) and $N^{\prime }=N+2$, and α_c is the resultant value of the scale factor α in the quasi-continuum limit, and where the discrete Laplacian operator $\nabla ^{2}_{N^{\prime }}$ conforms to the number of neighbors $N^{\prime }$ of the node in question (and where the discreteness of the 2^nd-order time derivative is understood). Given the smoothing operator we have chosen, the central term ψ(x,i,t) in all the respective 2^nd-order derivatives or smoothings in (24) and (25) still cancels on both sides of the above equation (though $2/N^{\prime }$ is of course smaller in magnitude than 2/N). Therefore, in the near-continuum limit we are considering, the above equation reduces to the familiar Klein-Gordon equation with α_c proportional to the square of the associated mass, justifying our usage of “mass dimension”.

If we consider the previous graph’s WaveMatrix to have been expanded by two columns and rows (representing forward and reverse step-wise movement along the added “mass dimension”) the coefficients there are negated relative to the rest of the matrix, except for the 2 × 2 submatrix at the very bottom of the diagonal, where the coefficients retain the same sign. (All of the coefficients, however will change in the sense that N has now increased to N + 2.) We shall call this modified matrix KGMatrix.

Although KGMatrix is still involutory, so that the sum of the expected squares of the amplitude in the edges is conserved under this kind of propagation, the sum of the components along any row or column is no longer unity as before, so that the sum of the amplitudes is no longer strictly conserved. However, given that a particle always incurs a change of sign with every transition from a step along the mass dimension to a step along some spatial edge (or vice versa), it is easy to see, even in the case where the length of the mass dimension is some larger even number than 2, that the sum of the amplitudes in the even-indexed slices along the mass dimension axis minus the sum of the amplitudes in the odd-indexed slices is the same absolutely conserved quantity that would be the sum of the amplitudes if the particle were following the usual Brownian-Huygens propagation rules we defined earlier, instead of the modified version. So in that sense, the conservation of amplitudes still holds.

If we consider any paths in this expanded space, we can easily excise any steps taken along the mass dimension (which will always occur in even numbered groups) by repeating the approach described in the previous section (that was used to progressively excise Huygens steps from a set of paths) and use that to expand any values of the wave functions for a massive particle into either a sum of terms consisting of factors of the regular wave equation, or else, a sum of terms of the propagator of the heat equation (with the excised walks taking place on a graph without any added mass dimension).

Depending on the equation we are interested in modeling, we could introduce still other kinds of alternate small dimensions (with possibly longer lengths), and specify more complicated phase factor transitions, rather than the single mass dimension and the simple negation that will suffice for the purpose of this paper, and in that way account for more complicated particle symmetries. In other words, we did not need to actually double and stack the graph – the extra dimensionality is just a way to incorporate an internal structure to the particles. For that matter, we did not need to introduce signs or antiparticles, and could have continued with scalar particles, and instead, accommodated that two-state degree of freedom by similarly modifying the graph.

The approach here is in some ways a discrete and very rudimentary analog of string theory, and the manner in which dimension is treated there, but the goal of this section is simply to demonstrate that the approach we have chosen is not limited to the wave equation, and that discreteness, far from being a disadvantage, allows for a flexibility that is peculiarly well-suited for the path-integral equations of modern physics.

Moreover, the discussion on anisotropic graphs applies to the mass dimension as well. It is not necessary that every node of the graph contain an edge leading along the mass dimension. A graph that is “sparse” in such nodes would require a scale transformation, relative to one that is not, in order for the generated waves to have identical densities and properly Gaussian evolution distributions, and in this case, that would mean changing the magnitude of the mass term (Fig. 6). Moreover, if the density of such mass dimension edges were different in one region of the space than another, the mass parameter would likewise vary, so that this formalism easily accommodates the curved spacetimes of general relativity in which mass varies. If we admit exogenous forces and interactions (and any such deviation from our rules that that entails), then any edges along the mass dimension can be conditioned on some exogenous variable or coupled to the presence of another kind of particle in the space; and given that all this can be accomplished with even a random arrangement of nodes and edges, spacetime can expand or shrink more easily than would be the case if the ability to model wave equations required the pristine symmetry of a regular lattice.

Fig. 6

Two graphs, each consisting of an irregular 1-dimensional graph along with a mass dimension isomorphic to $\mathbb {Z}/2\mathbb {Z}$. Due to the differences in the density of edges along the mass dimension, the associated mass parameter of the associated Klein-Gordon differs between the two graphs. (Note also that the left-hand side of the top graph has a different density of such edges, so that even within that graph, assuming the density differentials of such edges within different regions persists even in the continuum limit, the mass would then vary across those differing regions)

Therefore, this Brownian-Huygens approach is suitable not just the classical wave equation, but also quantum mechanical wavefunctions for particles with a mass. Since the transfer matrix approach already suffices to transform the second-order wave equations into first-order (a discrete analog of Hamilton’s transformation of second-order Lagrangian mechanics into a system of first-order equations), there is no need to further pursue Dirac’s approach of “taking the square root of the d’Alembertian operator”.

5 Quasi-Probability Particle Densities

In the rest of the paper, we shall for simplicity’s sake ignore mass and return to simple Brownian-Huygens propagation. In addition to endowing particles with a sign, let us expand the universe to two distinct types of particles propagating on the same graph, whose randomly chosen path steps are completely independent. (Note that even with this two-fold expansion of particles, the added degrees of freedom still amount to far less complexity than is contained in, say, a complex-valued 4-vector solution of the Dirac equation). Following Dirac’s nomenclature, we shall refer to this expanded universe of particles as being either “bra” or “ket”, respectively. Let us assume that the net density of both types of particles at t = 0 is equal to some function ψ(x,0), for which the integral of the square of the function is unity. Then, as has previously been noted [5], at any subsequent time $t^{\prime }$, the product at some point x of the net particle count of the bra particles times the net particle count of the ket particles has a positive expected value that is everywhere equal to the square of the expected value of the wave equation $\psi (\textbf {x}, t^{\prime })$. (Recall that since WaveMatrix was previously shown to be involutory, then the expected sum of the squares propagating along the edges of the graph is conserved, as is the sum.) By the law of large numbers, for a sufficiently fine-grained graph, and a sufficiently large region of that graph, the expected value of this count can be made so that the likelihood of it being negative when summed over this region is arbitrarily small, even if this region is itself a very small region of the entire graph. Admittedly, since Brownian-Huygens is a branching process, so that there is no single particle trajectory to speak of, the resultant wave dynamics here is more closely related to that of a quantum field than a wave-function for a single particle, but given the latter is only a non-relativistic limiting case, that is more a problem for the notion of single-particle wavefunctions than this model.

Such generalized densities have similarities to quasi-probability distributions by Wigner and Moyal [6,7,8]. Given the fact that they can be negative, such quasi-probabilities do not violate Bell’s theorem ([9], despite their being local, and the same holds true of this approach.

Let us define a measurement as the operation of integrating any such bra-ket product count over some space-time path, so as to include whatever is on (or sufficiently close to) that path. Note that the presence of a negative bra-ket summand reduces the count, and different sequences of measurements along different paths will lead to different perceptions (or “worlds”), similar in some respects to how the distributions of electrons on an antenna can yield distinctly different programs depending on the frequency with which it is sampled; cf. the Wigner-von Neumann interpretation of quantum mechanics [10, 11] in which the subjective perception of an observer depends on, and is intrinsic to, a quantum mechanical measurement. Assuming all observers in such a space are of a sufficiently large macroscopic size, and only capable of registering macroscopic counts (even if those are taken over, say, the retina of an eye that is focused on a photoelectric cell that is designed to register the presence of a quantum event), then most any measurement would inherently involve nonnegative counts, to the extent that exceptions would be so rare as to be regarded as inconceivable.

6 Discussion

Surprisingly, the fundamental equations of quantum field theory can be modeled to arbitrary precision by extensions of random walks on a random graph, generated with rules so simple that any child who is familiar with the concept of negative numbers can follow and understand them.

The path-integral approach to quantum field theory by Dirac [12], and Feynman [13] is elegant and intuitively appealing; however, it has left physicists – and in particular, those holding to the notion that physics should be fundamentally simple at some basic level – with the philosophical quandary of assuming that any subatomic particles, created and annihilated in vast numbers even in tiny regions of the spacetime vacuum, are each able to traverse all possible paths to a given destination in the course of their propagation, including paths implying arbitrarily superluminal speeds, and integrate at each instant of these paths a Lagrangian. It is a task that the smartest minds could not accomplish, and yet every single field particle is somehow able to execute it. (Admittedly, it was not much better during the reign of Newtonian mechanics, wherein even the tiniest particles were implicitly assumed to have sufficient expertise in vector addition and trigonometry to the extent that they are capable of retaining and transferring energy, momentum, and angular momentum in any collision or interaction, with seemingly infinite precision [14, Note 5].)

Numerous physicists have voiced the notion, in the words of Anthony Zee, that at sufficiently small time scales “new physics must appear” [15, p. 172], and various proposals have been offered in anticipation of a need for a more generalized (and ultimately simpler) paradigm of motion. For example, cellular automata have for decades been regarded by some as conceptually a simpler and more plausible foundation for subatomic behavior [16,17,18,19,20,21], but there has been little effort devoted to the specifics of how the rules that govern cellular automata could recreate the fundamental and well-established equations of modern physics.

With regard to the heat equation, and the summation of paths implicit in its kernel, there is, on the contrary, no particular mystery or vagueness as to how particles acting with simple rules suffice to explain that equation and its many variations, in ways that are accessible to anyone familiar with Pascal’s triangle and its continuum limit. This is in sharp contrast to the Schrödinger equation, which is often characterized as formally being simply a heat equation with an imaginary scale factor k, without any elaboration as to what, if anything, that might mean in a physical sense. That being said, there is also a growing body of research devoted to quantum mechanics with discrete time on quantum graphs that does frequently makes use of that formal diffusion-Schrödinger relationship [22,23,24]. These quantum walk approaches are essentially discrete extensions of the aforementioned path-integral formulation of Feynman, Dirac, et al., so that along these discrete quantum-walk steps, a Lagrangian or Hamiltonian is integrated, so as to derive the particle’s complex-valued phase factor (or alternatively, the overall phase evolution occurs by way of discrete phase shifts obtained by flipping a “quantum coin”).

Here, the dynamics is radically simpler and the only allowed phase factors are 1 and -1, and the transition from one to the other derives not from any evolution operator, but rather, the simple mechanics of particle-antiparticle creation (and the only other mathematical operation, so to speak, consists of choosing a nearest neighbor from among all those available to a given node so as to traverse a random walk). Remarkably, this very restricted range of discrete values and motions nonetheless leads to relativistically invariant wave and Klein-Gordon equations.

The formalism presented here builds on that clear connection between what is fundamentally simple and discrete, and the collective phenomena that emerge therefrom, and extends it to the wave equation and other relativistic quantum wavefunctions of field theory, and thereby simplifies Dirac’s and Feynman’s path-integral formulation (cf. [25]). And unlike the continuous-case propagators first derived by Hadamard [26, Chapter 4.4] which have distinctly different solutions according to the dimension of the space, the propagators shown here are easily generalized to any number of dimensions, as is true of the kernel of the heat equation to which they are related. Moreover, the simplified approach explains how the interactions between fields – which, as Feynman diagrammatically demonstrated, can be expanded in graph-theoretic terms – are similar in nature to the interactions within a single field that govern its internal propagation even in the absence of outside interactions. And all this without so much as a single complex or floating-point number. Granted, the introduction of quasi-probabilities – even those that converge to Newtonian values at sufficiently macroscopic scales – is something that will always be difficult to understand for macroscopic creatures living in a visibly Newtonian world, but there is nothing particularly surprising or unfathomable in recognizing that those who live in a macroscopic realm have powers of perception that conform to those scales.

The formalism presented here, while poorly suited as a computational scheme (though that may change with the emergence of quantum computing or massively parallel computation), clearly demonstrates how radically simple particles motions can, not by complexity, but by sheer number, recreate the fundamental wave equations of modern physics.

7 Conclusion

Not applicable