1 Introduction

The standard Hamiltonian of solid-state theory considers a system of electrons and ions interacting only through Coulomb forces. Magnetic interaction between the moving charges is not included. Only the spin-spin and spin-orbit magnetic interactions may be considered. The former is needed for the explanation of ferromagnetism, whereas the later for the valence-band-splitting in semiconductors is important. However, the non-relativistic magnetic interactions between the moving charges of order 1/c2 responsible for diamagnetism are ignored.

Already 100 years ago Darwin [1] has argued in the frame of the classical electrodynamics of point-like particles, that up to order 1/c2 one might separate the motion of the particles from that of the electromagnetic field. From this separation besides the usual Coulomb also a magnetic current-current interaction should emerge. Since the classical electrodynamics of point-like charged particles is a vicious theory having neither Lagrangian, nor Hamiltonian formulation, his derivation lacked any rigor and cold not be quantized, nevertheless it contains a grain of truth and was considered later also by Landau and Lifshitz [2], as well as by Jackson [3].

Actually, one needs a new analysis of the problem in the frame of the non-relativistic QED of electrons we describe in Section 2. By restricting the discussion to the states without photons and neglecting the retardation in the photon propagator we give in Section 3 a derivation of the electronic Hamiltonian containing the diamagnetic interaction between the transverse currents (microscopic Biot-Savart law !). This proof (stimulated by the classical paper of Holstein, Norton and Pincus [4] on diamagnetism) was first published in a preprint [5] and included in a recent book [6]. A short exposure is contained also in [7]. We try here a better presentation for a wider public, taking into account also discussions, with emphasis on the general problem of diamagnetism.

Our Hamiltonian in its mean field version [7] leads to the same linear linear response to an external magnetic field as the standard mean field BCS [8] theories of superconductivity (see [9,10,11]), predicting [12] ideal diamagnetism in the bulk, whereas being essentially different beyond this reduced frame.

Thereafter, in Section 4 we discuss the derivations of the classical Darwin Hamiltonian [1] by Refs. [2] and [3]. We show, that both reach Darwin’s result in the Coulomb gauge under the assumption of a finite distance between the particles. From the same assumption follows that Darwin’s Hamiltonian coincides with the classical version of the Hamiltonian we derived in Section 3 from the non-relativistic QED.

2 Non-Relativistic QED

The basic idea underlying the solid state theory is that one may describe solids as a system of interacting electrons and ions. These charged particles should obey the rules of the electromagnetic theory. Since these are not the ultimate elementary particles one cannot resort directly to the relativistic quantum field theory. One has to build up a non-relativistic Quantum Electrodynamics for arbitrary charged non-relativistic particles (fermions and bosons). Such a theory may be constructed following the scheme of the relativistic QED, starting form the classical field theory based on the coupled Maxwell and the Schrödinger equations (instead Dirac’s) followed by the quantization of the fields. Such an approach was described recently [13, 14]. The standard presentation however starts from the Hamiltonian of a quantum mechanical charged particle in external electromagnetic field, quantizes both the wave function and the vector potential in the Coulomb gauge, while replacing the scalar potential with the standard quantized Coulomb interaction. Thereafter one has still to add the Hamiltonian of the radiation field. Both ways have to be formulated in the Coulomb gauge, the only one without spurious degrees of freedom for the photons. The two ways lead to the same result however the field-theoretical one omits several sharp jumps by avoiding the inconsistent classical electromagnetic theory of charged point-like particles.

This non-relativistic QED is defined by the Hamiltonian (here just for electrons and photons) in the presence of time-dependent external electric and magnetic potentials

$$ \begin{array}{@{}rcl@{}} H^{QED}(t) = \sum\limits_{\mathbf{q},\lambda}\hbar\omega_{q}b_{\mathbf{q},\lambda}^{+}b_{\mathbf{q},\lambda} \end{array} $$
(1)
$$ \begin{array}{@{}rcl@{}} &&+ d{\mathbf x} {\mathcal N}\!\left[\frac{1}{2m}\!\left( \imath \hbar\nabla \psi^{+}({\mathbf x}) +\frac{e}{c}({\mathbf A}_{\bot}({\mathbf x}) + {\mathbf A}_{ext}({\mathbf x},t))\psi^{+}({\mathbf x})\right)\right. \\ &&\left. \times\left( -\imath \hbar\nabla\psi({\mathbf x}, t) +\frac{e}{c}({\mathbf A}_{\bot}({\mathbf x})+{\mathbf A}_{ext}({\mathbf x},t)))\psi({\mathbf x})\right)\right] \\ &&+ \frac{1}{2}\int \!\! d\mathbf{x}\int \!\! d{\mathbf x}^{\prime}\psi^{+}(\mathbf{x})\psi^{+}(\mathbf{x}^{\prime})\frac{e^{2}}{|\mathbf{x}-\mathbf{x}^{\prime}|}\psi(\mathbf{x}^{\prime})\psi(\mathbf{x}) + e\int \!\! d\mathbf{x} V_{ext}(\mathbf{x},t)\psi^{+}(\mathbf{x})\psi(\mathbf{x}) \enspace . \end{array} $$
(2)

with the transverse radiation field being (Ω is the volume of the system)

$$ \mathbf{A}_{\bot}(\mathbf{x})=\sum\limits_{\lambda=1,2}\sqrt{\frac{\hbar c}{\Omega}}\sum\limits_{\mathbf{q}}\frac{1}{\sqrt{|\mathbf{q}|}}\mathbf{e}_{\mathbf{q}}^{(\lambda)} e^{-\imath\mathbf{q}\mathbf{x}}\left( b_{\mathbf{q},\lambda}+ b_{-\mathbf{q},\lambda}^{+}\right)\enspace, $$
(3)

while Aext(x,t) and Vext(x,t) are classical external vector and scalar potentials. The unit vectors \(\mathbf {e}_{\mathbf {q}}^{(\lambda )}\) are orthogonal to the wave vector q as well as to each other and according to the general recipe of second quantization a normal ordering \({\mathcal N}[... ]\) has to be introduced also with respect to the photon creation and annihilation operators \(b_{\mathbf {q},\lambda }^{+} \), bq,λ in the Hamiltonian and the photon frequency is ωq = c|q|.

One may check, that the equations of motion derived from this Hamiltonian lead to the coupled Maxwell and Schrödinger operator equations.

As usual in many body theories of solid-state, the non-relativistic QED, contrary to the fundamental relativistic QED, is understood as a cut-off theory, where the bare parameters coincide with the physical ones. This eliminates also the divergence of the self-energy.

This non-relativistic QED has been widely and successfully used since the mid of the last century in the quantum optics of atoms and solids. See a recent book [15] about.

Although in their basic paper “de Haas-van Alphen Effect and the Specific Heat of an Electron Gas”, T. Holstein, R. E. Norton and P. Pincus [4] already have shown, that the current-current interaction in the non-relativistic QED is the basic piece for understanding diamagnetism, their ideas and proofs are ignored up to date. Its essence is that (virtual) transverse photons transmit the diamagnetic interaction!

3 The Restricted Electronic Hamiltonian

In order to obtain a pure electronic Hamiltonian suitable for solid state theory one must restrict the discussion to the subspace of states without photons. (To simplify the discussion we omit here the external fields and reintroduce them again at the end according to the “minimal rule”). This task cannot be done without neglecting at least terms of higher order than 1/c2. First of all, the normal ordered “seagull” term \(\frac {e^{2}}{2mc^{2}}\psi ^{+} \psi A^{2}\) being already of order 1/c2 may be ignored. Being itself of order 1/c2 it may have only higher order non-vanishing matrix elements in this subspace.

The next step has to be neglecting any retardation in time induced by the photon propagator [4]. Otherwise one cannot obtain a Hamilton operator local in time. In the 4-dimensional Fourier space it amounts to neglect the term − ω2/c2 in the denominator of the photon propagator

$$ \frac{1}{\omega^{2} /c^{2}-q^{2}+\imath 0}\left( \delta_{\mu,\nu}-\frac{q_{\mu} q_{\nu} }{q^{2}}\right); \qquad (\mu,\nu=1,2,3) $$
(4)

thus retaining only

$$ -\frac{1 }{q^{2}}\left( \delta_{\mu,\nu}-\frac{q_{\mu} q_{\nu} }{q^{2}}\right); \qquad (\mu,\nu=1,2,3) $$
(5)

Since no pole survived, the infinitesimal ı0 term could have been also ignored and 4π/q2 is just the Fourier transform of the Coulomb potential.

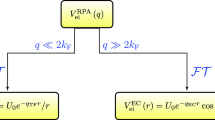
To proceed further one may consider either the S-matrix, or the theory of Green functions in terms of the Feynman diagrams [5, 6] built with the standard Coulomb term and the photon-current interaction \(- \frac {1}{c}{\int \limits } i_{\bot }A_{\bot }\). (We denoted here by i⊥ the transverse current density in the absence of any external field.) It is easy to see that after the previous steps all the Feyman diagrams of the reduced S-matrix (having only external electron legs) may be constructed from the two basic graphs shown in the Fig. 1 having four electron legs, where in both cases now the wavy line represents the Coulomb potential. The vertex “ρ” is a scalar, while the vertex “\(j_{\bot }^{\mu }\)” is a vector one.

Fig. 1
figure 1

The basic four-leg graphs in the reduced S-matrix

Full size image

Therefore, we may conclude that after reintroducing the external fields according to the minimal principle of Yang-Mills theories, the quantum mechanical 1/c2 electron Hamiltonian that generates these diagrams is just

$$ \begin{array}{@{}rcl@{}} \textbf{H}(t)\!\! &=&\!\!\-\!\!\int\!\! d{\mathbf{x}} \psi^{+}(\mathbf{x})\left[\frac{1}{2m} \left( \frac{\hbar}{\imath}\nabla-\frac{e}{c}\mathbf{A}_{ext}(\mathbf{x},t)\right)^{2} \! + \! eV_{ext}(\mathbf{x},t) \right]\psi(\mathbf{x}) \\ &&+ \frac{1}{2} \int d\mathbf{x} \int d\mathbf{x} \frac{{\mathcal N}\left[\rho(\mathbf{x})\rho(\mathbf{x})\right]}{|\mathbf{x}-\mathbf{x}|} -\frac{1}{2} \int d\mathbf{x}\int d\mathbf{x} \frac{{\mathcal N}\left[\mathbf{j}_{\bot}(\mathbf{x},t)\mathbf{j}_{\bot}(\mathbf{x},t)\right]} {c^{2}|\mathbf{x}-\mathbf{x}|} \enspace . \end{array} $$
(6)

Here ρ(x) denotes the charge density operator

$$ \rho(\mathbf{x})=e\psi^{+} (\mathbf{x})\psi(\mathbf{x}),\enspace $$
(7)

while j⊥(x,t) denotes the transverse part of the current density operator

$$ \mathbf{j}(\mathbf{x},t) = \frac{e}{2m}\left( \!\psi^{+}(\mathbf{x}) \left( \frac{\hbar}{\imath}\nabla - \frac{e}{c}\mathbf{A}_{ext}(\mathbf{x},t)\!\!\right)\psi(\mathbf{x}) + h.c.\right) . $$
(8)

The generalization of these results for a system of electrons and ions as constituents of the solid state is obvious.

The current-current term is nothing else but the well-known Biot-Savart law resulting from the exchange of transverse photons responsible for diamagnetic forces. One may argue that due to the smallness of the velocities in the condensed matter such an 1/c2 term may be neglected. This is obviously false. Our everyday experience teaches us, that a macroscopic number of slow electrons may create enormous magnetic fields.

It is worth to mention here that the Feynman diagram technique in the momentum space with the transverse currents introduces no difficulties at all.

For a better understanding of the underlying physics, let us consider now the Hartree approximation of this Hamiltonian. It looks as

$$ \begin{array}{@{}rcl@{}} \textbf{H}_{Hartree}(t)\!\! &=&\!\!\-\!\!\int\!\! d{\mathbf{x}} \psi^{+}(\mathbf{x})\left[\frac{1}{2m} \left( \frac{\hbar}{\imath}\nabla-\frac{e}{c}\mathbf{A}_{ext}(\mathbf{x},t)\right)^{2} \! + \!e V_{ext}(\mathbf{x},t) \right]\psi(\mathbf{x}) \\ &&+ \int d\mathbf{x} \int d\mathbf{x} \frac{\rho(\mathbf{x})\langle\rho(\mathbf{x},t)\rangle}{|\mathbf{x}-\mathbf{x}|} -\int d\mathbf{x}\int d\mathbf{x} \frac{\mathbf{j}_{\bot}(\mathbf{x},t)\langle\mathbf{j}_{\bot}(\mathbf{x},t)\rangle} {c^{2}|\mathbf{x}-\mathbf{x}|} \enspace . \end{array} $$
(9)

where 〈ρ(x,t)〉 and 〈j⊥(x,t)〉 are the (chosen) ensemble averages of the charge and transverse current densities.

One may here identify the s.c. internal scalar and vector potentials

$$ V_{int}(\mathbf{x},t) =\int d\mathbf{x}\frac{\langle \rho(\mathbf{x},t)\rangle}{|\mathbf{x} -\mathbf{x}|}; \qquad \mathbf{A}_{int}(\mathbf{x},t)=\int d\mathbf{x}\frac{\langle j_{\bot}(\mathbf{x},t)\rangle}{|\mathbf{x} -\mathbf{x}|}\enspace . $$
(10)

Of course, here in the definition of the internal vector potential the retardation is missing!

Equations (6) and (9) together with the identifications of (10) show, that the average Coulomb field created by the electron results from the charge-charge interaction and the average (dia-) magnetic field created by the velocity of the electron results from the current-current interactions. This is analogous to the (ferro-) magnetic field of localized spins resulting from their mutual interaction in the Heisenberg spin model.

It is important also to remark, that this mean-field Hamiltonian resulting from the non-relativistic QED differs from the electromagnetic part of the mean-field Hamiltonian used in the equilibrium theories of the BCS superconductivity [9,10,11]

$$ {\mathcal H}=\int\!\! d{\mathbf{x}} \psi^{+}(\mathbf{x})\left[\frac{1}{2m} \left( \frac{\hbar}{\imath}\nabla-\frac{e}{c}\mathbf{A}(\mathbf{x})\right)^{2} \! + \! eV(\mathbf{x}) \right]\psi(\mathbf{x}) \enspace , $$
(11)

where the time independent potentials are interpreted [12] as being the total ones

$$ V(\mathbf{x})=V_{ext}(\mathbf{x})+V_{int}(\mathbf{x}); \qquad {\mathbf A}(\mathbf{x})={\mathbf A}_{ext}(\mathbf{x})+ {\mathbf A}_{int}(\mathbf{x})\enspace . $$
(12)

Though, the terms linear in the vector potentials are correct and therefore the equilibrium linear responses of the two Hamiltonians to an external magnetic field are also identical [7].

4 Darwin’s Classical Approach Revisited

In this Section we show that Darwin’s reasoning within the classical electromagnetic theory of point-like charges, if properly formulated in the Coulomb gauge i.e. considering only the true physical degrees of freedom of the magnetic field, leads to a classical Hamiltonian analogous to the one we got in the previous Section.

As it is well-known, one can not formulate a Lagrangian theory of classical point-like charged particles interacting with the electromagnetic field due to the divergent self-interaction. (From the Lorentz force one has to omit the action of the field created by each charged particle on itself!) This impedes also a proper derivation of an 1/c2 Hamiltonian.

Almost one hundred years ago Darwin [1] proposed nevertheless a closed classical Lagrangian for N point-like charges ei and mass mi (i,j = 1,…N) including terms up to order 1/c2 avoiding self-interaction and constructed the following Hamiltonian

$$ \begin{array}{@{}rcl@{}} {\mathcal H}&=&\sum\limits_{i}\frac{1}{2m_{i}}\mathbf{p_{i}}^{2}+\sum\limits_{i>j}\frac{e_{i} e_{j}}{|\mathbf{r_{i}}-\mathbf{r}_{j}|} \\ & &-\sum\limits_{i>j}\frac{e_{i} e_{j}}{2c^{2}m_{i} m_{j}|\mathbf{r}_{i}-\mathbf{r}_{j}|}\left[\mathbf{p}_{i}\cdot\mathbf{p}_{j}+(\mathbf{p}_{i}\cdot\mathbf{n}_{ij})(\mathbf{p}_{j}\cdot\mathbf{n}_{ij})\right] , \end{array} $$
(13)

where \(\mathbf {n}_{ij}\equiv \frac {\mathbf {r}_{i} -\mathbf {r}_{j}}{|\mathbf {r}_{i} -\mathbf {r}_{j}| }\). His derivation is based on the expansion of the Liénard-Wiechert potentials to second order in \(\frac {1}{c}\).

The reasoning of Refs. [2] and [3] starts from the discussion of the potentials felt by one point-like particle in the field of another one at a finite distance. Landau and Lifshitz [2] use the Lorentz gauge, perform an expansion of the scalar potential up to second order in the finite distance between two particles divided by the light velocity (R/c) and later perform a gauge transformation turning to the Coulomb gauge, without stating it explicitly.

Jackson [3] starts in the Coulomb gauge, gets the transverse current - transverse current Lagrange function for two particles however performs an integration by parts of the vector potential of the two particles at a finite distance leaving aside the vanishing surface contribution and gets Darwin’s Hamiltonian.

Thus the two approaches are similar and their results are identical. Moreover, from Jackson’s derivation results that the transverse current - transverse current version is equivalent to Darwin’s version whenever the distances between the particles are finite.

Without the mentioned partial integration Jackson’s Hamiltonian [3] looks as

$$ \begin{array}{@{}rcl@{}} H &=&\sum\limits_{i}\frac{\mathbf{p_{i}}^{2}}{2m_{i}}+\sum\limits_{i>j}\frac{e_{i} e_{j}}{|\mathbf{r_{i}}-\mathbf{r}_{j}|} \\ & &-\sum\limits_{i>j}\frac{e_{i} e_{j}}{c^{2}m_{i} m_{j}}\mathbf{p}_{i}\left[ \frac{\mathbf{p}_{j} }{|\mathbf{r}_{i}-\mathbf{r}_{j}|}-\frac{1}{4\pi} \int d\mathbf{x}\frac{1}{|\mathbf{r}_{i}-\mathbf{x}|}\nabla \left( \mathbf{p}_{j} \nabla \frac{1}{|\mathbf{x}-\mathbf{r}_{j}|}\right)\right] \end{array} $$
(14)

and consists of transverse current - transverse current terms for i≠j.

By introducing the charge and current densities:

$$ \rho(\mathbf{x})=\sum\limits_{i} e_{i}\delta(\mathbf{x}-\mathbf{r}_{i}); \qquad \mathbf{i}(\mathbf{x})=\sum\limits_{i} \frac{e_{i}}{m_{i}}\mathbf{p}_{i}\delta(\mathbf{x}-\mathbf{r}_{i}) $$
(15)

Ignoring the missing i = j terms one might rewrite this classical Hamiltonia (14) as

$$ \sum\limits_{i}\frac{1}{2m_{i}}\mathbf{p_{i}}^{2}+\frac{1}{2} \int d\mathbf{x}\int d\mathbf{x}^{\prime} \frac{\rho(\mathbf{x})\rho(\mathbf{x}^{\prime})}{|\mathbf{x}-\mathbf{x}^{\prime})|} -\frac{1}{2} \int d\mathbf{x}\int d\mathbf{x^{\prime}} \frac{\mathbf{i}_{\bot}(\mathbf{x})\mathbf{i}_{\bot}(\mathbf{x}^{\prime})} {c^{2}|\mathbf{x}-\mathbf{x}^{\prime}|}\enspace , $$
(16)

where i⊥(x) is the transverse part of the current density

$$ \mathbf{i}_{\bot}(\mathbf{r},t)\equiv\mathbf{i}(\mathbf{r},t)+\frac{1}{4\pi}\nabla\int d\mathbf{r}^{\prime}\frac{\nabla^{\prime}\mathbf{i}(\mathbf{r}^{\prime},t)}{|\mathbf{r}-\mathbf{r}^{\prime}|} \enspace . $$
(17)

Under this form it looks similar to the result we obtained before (in the absence of other external fields) and a quantization of the classical Hamiltonian of the point-like charged particles (14) is then immediate by second quantization of (16) as it was done in Ref. [5] and one may omit the configuration space quantization either of (14) or (13). This leads to the same Hamiltonian (6) as we deduced from the non-relativistic QED.

5 Conclusions

We derived from the non-relativistic QED the (transverse) current-current interaction term to be included in the solid state Hamiltonian in order to take into account the diamagnetic field created by the moving charges. We have shown also, that the classical reasoning of Darwin [1] in Jackson’s version [3] leads to a similar result.

Our Hamiltonian contains explicitly the well-known attraction of two parallel current flows in the same direction as well their repulsion in the opposite case.

The mean-field version of this 1/c2 Hamiltonian differs from the electromagnetic part of the Hamiltonian used in the mean field theory of superconductivity, based just on physical intuition [12]. However, the difference occurs only in the terms non-linear in the vector potential. The correct variant may have important implications for higher magnetic fields, as well as beyond the mean-field approximation.