Quantum-Memory-Assisted Entropic Uncertainty Relation and Quantum Coherence in Structured Reservoir

Abstract

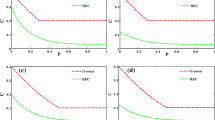
The uncertainty principle is regarded as one of basics in quantum mechanics, which sets up a strict lower bound to quantify the prediction on the outcome concerning a set of incompatible measurements. In this paper, we investigate the dynamic behaviors of quantum-memory-assisted entropic uncertainty relation (EUR), and quantum coherence in structured reservoir. The results shown that the EUR is smallest in the vanishing limit of noise regardless of the forms of the initial sate we considered, while the coherence keeps the maximal value. During the time-evolution process, the uncertainty bound is lifted and the coherence damps monotonously. Subsequently, the EUR converges to an asymptotic nonzero constant in the long-time limit, yet the coherence asymptotically decays to zero. Moreover, the initial state purity plays a deterministic role in the initial amounts of EUR and coherence, i.e. the larger purity the less EUR and larger coherence. As an application, we employ the EUR to witness the coherence, and prove that the corresponding witnessing efficiencies are only depended on the version of coherence, while are insensitive to the reservoir.

Appendix

Here, we revisit the physical model with the interaction of single qubit+reservoir system and the global evolution of composite system. The physical model is that the single qubit is locally interacted with a multimode reservoir, and the corresponding Hamiltonian is (ℏ = 1) [27, 28].

$$ {H}_{Xx}={\omega}_0{\sigma}_{+}^X{\sigma}_{-}^X+\sum \limits_j{\omega}_j{x}_j^{\dagger }{x}_j+\sum \limits_j\left({g}_j{\sigma}_{+}^X{x}_j+{g}_j^{\ast }{\sigma}_{-}^X{x}_j^{\dagger}\right), $$

(6)

where g_j is coupling constant between the qubit and reservoir mode j, x^†(x) is the creation (annihilation) operator of the reservoir with frequency ω_j, ${\sigma}_{+}^X=\left|1\right\rangle \left\langle 0\right|$ and ${\sigma}_{-}^X=\left|0\right\rangle \left\langle 1\right|$ are the qubit rising operator and lowering operator acting on the Xth qubit with transition frequency ω₀ in the orthogonal computational basis {|0〉, |1〉}. The evolution of single qubit+reservoir subsystem depends on the choice of Lorentzian spectral density of the reservoir. To do it, the Lorentzian spectral distribution we taken is of the following form

$$ J\left(\omega \right)=\frac{R^2}{\pi}\frac{\varGamma }{{\left(\omega -{\omega}_c\right)}^2+{\varGamma}^2}. $$

(7)

The parameter R is connected to the qubit+cavity coupling strength and Γ denotes the half-width at half-maximum of the intracavity field spectrum profile. Moreover, their relative magnitudes determine the Markovian (Γ > 2R) and the non-Markovian (Γ < 2R) regimes, respectively.

In terms of the reservoir Hamiltonian (6) and Lorentzian spectral distribution (7), the interaction of single qubit+reservoir can be computationally formulated, which are

$$ {\left|0\right\rangle}_X{\left|\overline{0}\right\rangle}_x\to {\left|0\right\rangle}_X{\left|\overline{0}\right\rangle}_x, $$

(8)

$$ {\left|1\right\rangle}_X{\left|\overline{0}\right\rangle}_x\to \xi (t){\left|1\right\rangle}_X{\left|\overline{0}\right\rangle}_x+\sqrt{1-\xi {(t)}^2}{\left|0\right\rangle}_X{\left|\overline{1}\right\rangle}_x, $$

(9)

where $\xi (t)={e}^{-\varGamma t/2}\left[\cosh \left(\frac{dt}{2}\right)+\frac{\varGamma }{d}\sinh \left(\frac{dt}{2}\right)\right]$ with $d=\sqrt{\varGamma^2-4{R}^2}$. Here, we point out that form the independent qubit+reservoir system the analytical solutions of quantum states can be derived for arbitrary initial states.

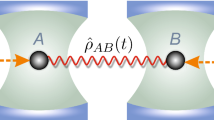
When qubits A and B are initially prepared in the EWL state and reservoirs a and b are initially in the vacuum states ${\left|\overline{0}\overline{0}\right\rangle}_{ab}$, the initial density matrix of the total qubit+reservoir system thus reads

$$ {\rho}_{AB ab}(0)={\rho}_{AB}(0)\otimes {\left|\overline{0}\overline{0}\right\rangle}_{ab}\left\langle \overline{0}\overline{0}\right|, $$

(10)

which will evolve to

$$ {\rho}_{ABab}(t)=\frac{1-p}{16}{I}_{ABab}+p{\left|\phi (t)\right\rangle}_{ABab}\left\langle \phi (t)\right|, $$

(11)

with

$$ {\displaystyle \begin{array}{l}{\left|\phi (t)\right\rangle}_{ABab}=\alpha \left|00\overline{0}\overline{0}\right\rangle +\beta \left[{\left|{\xi}_0(t)\right|}^2\left|11\overline{0}\overline{0}\right\rangle +\left|{\xi}_0(t)\right|\left|{\xi}_1(t)\right|\left|10\overline{0}\overline{1}\right\rangle \right]\\ {}\kern3.75em +\beta \left[\left|{\xi}_0(t)\right|\left|{\xi}_1(t)\right|\left|01\overline{1}\overline{0}\right\rangle \left|11\overline{0}\overline{0}\right\rangle +{\left|{\xi}_1(t)\right|}^2\left|00\overline{1}\overline{1}\right\rangle \right]\end{array}} $$

(12)

where ξ₀(t) = ξ(t) and ${\xi}_1(t)=\sqrt{1-\xi {(t)}^2}$. By tracing over the reservoir freedom, we can obtain the reduced density matrix for the qubit subsystem ρ_AB(t), yielding

$$ {\displaystyle \begin{array}{l}{\rho}_{AB}(t)=\frac{1-p}{4}{I}_{AB}+p\left({\alpha}^2+{\beta}^2{\left|{\xi}_1(t)\right|}^4\right)\left|00\right\rangle \left\langle 00\right|\\ {}\kern2.5em +p{\beta}^2{\left|{\xi}_0(t)\right|}^2{\left|{\xi}_1(t)\right|}^2\left(\left|01\right\rangle \left\langle 01\right|+\left|10\right\rangle \left\langle 10\right|\right)\\ {}\kern2.5em +p{\beta}^2{\left|{\xi}_0(t)\right|}^4\left|11\right\rangle \left\langle 11\right|+ p\alpha \beta {\left|{\xi}_0(t)\right|}^2\left(\left|00\right\rangle \left\langle 11\right|+\left|11\right\rangle \left\langle 00\right|\right)\end{array}} $$

(13)