Abstract
The collection of one-dimensional subspaces of an anisotropic Hermitian space is naturally endowed with an orthogonality relation and represents the typical example of what is called an orthogonality space: a set endowed with a symmetric, irreflexive binary relation. We investigate in this paper symmetry properties of orthogonality spaces. We show that two conditions concerning the existence of automorphisms of orthogonality spaces are essentially sufficient to characterise the basic model of quantum physics, the countably infinite dimensional complex Hilbert space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To characterise the basic quantum-physical model by algebraic means has been a major topic in the discussions around the foundations of quantum mechanics, in particular in the framework of the approach that goes back to the seminal work of Birkhoff and von Neumann [2]. In the centre of interest, we find the complex Hilbert space and the collection of those entities that correspond to the outcomes of quantum physical measurements. Investigations have especially focused on the inner structure of the set of closed subspaces, which correspond to the (crisp) two-valued observables. This set gives rise to an ortholattice and the question is natural whether it can be characterised in purely lattice-theoretic terms. In the infinite-dimensional case, an affirmative answer has been given, e.g., by Wilbur in his 1977 paper [17]. For an overview of the various further aspects and results regarding the algebraic reconstruction of the Hilbert space, we may refer, e.g., to [5, 6].
The present work should be seen in this context. But let us outline the considerations that have led to the particular topic that we have chosen for investigation. We understand the quantum logic approach as an attempt to reduce the Hilbert space model to a simpler and more transparent structure. The aim is, so to say, to increase the degree of abstraction. Dealing with a structure that can hardly be reduced any further, the present work can be understood as a contribution to the question how far one can go. Namely, David Foulis and his collaborators have once proposed the notion of an orthogonality space, the one-dimensional subspaces of a Hilbert space together with the usual orthogonality relation being the prototypical example. The term reflects the idea of distinctness of outcomes of a quantum-physical experiment – and not more. Orthogonality spaces might actually be seen as a generalisation of most structures that have been considered in the context of (sharp) quantum logic.
Accordingly, our interest focuses on orthogonality spaces, which were once studied by Foulis’s Ph.D. student James C. Dacey [3]. Our aim is to characterise those among them that arise from complex Hilbert spaces. To tackle this problem on the basis of principles that are typical for lattice-theoretic approaches seems to be hardly possible though. Indeed, we deal with relational rather than algebraic structures, thus the issue of purely algebraic hypotheses is not relevant. We have to search for conditions of a different kind and we actually do not really mind; lattice-theoretic properties are often technically involved and hard to interpret. Instead, we focus on symmetries; we postulate the existence of certain automorphisms of orthogonality spaces. As we will see, this approach turns out to be remarkably efficient and leads to intuitively comprehensible conditions. Needless to add, lattice theory will in what follows still play a central role.
In the lattice-theoretic framework, conditions involving automorphisms were actually already discovered by several authors as a useful tool. We may mention, for instance, [1, 7, 9, 4]. Compared with these works, we may say that our own approach differs with regard to the extent that postulates involving symmetries occur; we do not use them in addition, but we put the focus on them. We note that we have followed a similar approach in [15], where we characterised complex Hilbert spaces as partial Boolean algebras. The latter structures are based on a concept that resembles in some respects orthogonality spaces. According to our experience, however, partial Boolean algebras are comparably cumbersome to deal with; the present work gets along with a significantly lower degree of technicality.
The two conditions that we will introduce in the sequel can roughly be described as follows. Given a subset A of our orthogonality space and an element e that is incompatible with (the closure of) A, we require that there is an automorphism mapping e to an element orthogonal to A. Moreover, each automorphism (provided that it leaves the closure of two distinct elements fixed) possesses roots of all orders. In both cases, the automorphisms are requested to leave the “uninvolved” elements fixed, like those that are orthogonal to the elements under consideration. Intuitively, both conditions might be seen as an expression of the flexibility inherent to the model. Provided that the rank is at least 4, they imply, e.g., the following: for each pair e, f of incompatible elements, there is a symmetry transformation mapping e optionally either to f or to an element orthogonal to f; this transformation can be chosen to act only locally, in the sense that all elements orthogonal to e and f are left fixed; and we can speak of a gradual transition, because the transformation is, for any n ≥ 1, the n-th power of another transformation that leaves the same elements fixed.
The present work elaborates on, and in fact complements, our recent work [16]. In that paper, we made the additional assumption that dimensions are finite. We described finite-dimensional orthomodular spaces over dense subfields of ℂ on the basis of five conditions; four of them concerned the existence of automorphisms and a further one excluded the existence of non-trivial quotients. In contrast, we deal here exclusively with infinite dimensions. The division of the work into two parts should not surprise and the overlap is in fact insignificant. Recall that lattice-theoretic approaches, like Wilbur’s, have been successful basically only under the assumption of infinite dimensions. The reason can be given a name: Solèr’s Theorem. It tells us that an infinite-dimensional orthomodular space possessing an orthonormal basis is a classical Hilbert space. The key of our arguments lies likewise in this fact, which has no analogue in the finite-dimensional case. We may say that we get along with fewer conditions than in [16] and yet arrive at a more satisfactory result.
We proceed as follows. We introduce in Section 2 orthogonality spaces and we see how they give rise to complete ortholattices. We moreover introduce our first symmetry postulate, which we show to imply that these ortholattices are atomistic, orthomodular, and fulfil the covering property. In Section 3, we recall the lattice-theoretic characterisation of Hermitian spaces. We then apply our results to show a representation theorem for orthogonality spaces of infinite rank by means of classical Hilbert spaces. Our second symmetry postulate finally reduces the choice of the division ring to the field of complex numbers. We review the situation once again and point out open issues in the concluding Section 4.
2 Orthogonality Spaces
The central notion with which we deal in this paper is the following.
Definition 2.1
An orthogonality space is a set X endowed with a symmetric, irreflexive binary relation ⊥, called the orthogonality relation.
Orthogonality spaces were investigated in [3]. For further information, see also Wilce’s overview paper on test spaces [18].
Example 2.2
Let E be a linear space endowed with an orthosymmetric, anisotropic sesquilinear form. Then the orthogonality relation ⊥ between non-zero vectors is symmetric and irreflexive and hence makes E ∖{0} into an orthogonality space.
A slight modification leads to our actual guiding example. Namely, we consider P(E), the collection of one-dimensional subspaces of E, endowed with the induced orthogonality relation. Obviously, (P(E), ⊥) is an orthogonality space as well.
With respect to the notation of Example 2.2, we are especially interested in orthogonality spaces of the form (P(H), ⊥), where H is a complex Hilbert space.
Orthogonality spaces lead directly into the realm of lattice theory. We recall that an ortholattice is a bounded lattice L equipped with an involutorial, order-reversing unary operation ⊥ such that, for each a ∈ L, a⊥ is a complement of a. For lattice-theoretical notions and facts used in the sequel, the reader is referred, e.g., to [8].
For the remainder of the section, let us fix an orthogonality space (X, ⊥). For any \(A \subseteq X\), we put A⊥ = {x ∈ X : x ⊥ a for all a ∈ A}. Then the operation \({\mathcal {P}}(X) \to \mathcal {P}(X), A \mapsto A^{\perp \perp }\) is a closure operator. A set A such that A⊥⊥ = A is called orthoclosed and we denote the set of all orthoclosed subsets by \({\mathcal {C}}(X, \perp )\).
Lemma 2.3
Let \({\mathcal {C}}(X, \perp )\) be partially ordered by set-theoretical inclusion and endowed with the unary operation ⊥. Then \({\mathcal {C}}(X, \perp )\) is a complete ortholattice.
We will call (X, ⊥) irredundant if, for any two distinct elements x, y ∈ X, there is a z ∈ X that is orthogonal to exactly one of x and y. Evidently, this property holds if and only if, for any x, y ∈ X, {x}⊥ = {y}⊥ implies x = y. For instance, let E be as in Example 2.2; then (P(E), ⊥) is irredundant, but (E ∖{0}, ⊥) is not unless E is a space over the two-element field.
Assume that (X, ⊥) is not irredundant. Then there are pairs of distinct elements that are not distinguishable by their orthogonality relation to the remaining elements. Putting \(x \sim y\) if {x}⊥ = {y}⊥, we may in this case switch to the quotient space \(X/{\sim }\), endowed with the induced orthogonality relation. We may say that \(({X/{\sim }}, \perp )\) is an orthogonality space with essentially the same structure as (X, ⊥). Although not much of what follows really depends on irredundancy, this property facilitates the presentation. Hence we will from now on tacitly assume that orthogonality spaces are irredundant.
An automorphism of (X, ⊥) is a bijection φ: X → X such that, for any x, y ∈ X, we have x ⊥ y if and only if φ(x) ⊥ φ(y). Note that each automorphism of (X, ⊥) induces an automorphism of the ortholattice \({\mathcal {C}}(X, \perp )\).
We now introduce a first condition prescribing the existence of certain automorphisms of X. Namely, let us consider the following property of (X, ⊥).
-
(F1)
Let \(A \subseteq X\) and let e ∈ X be such that e ∉ A⊥⊥. Then there is an automorphism φ: X → X such that
-
(i)
φ(e) ⊥ A,
-
(ii)
φ(x) = x for any x ∈ X such that x ⊥ A, e or x ⊥ A, φ(e).
-
(i)
We note that (F1) is distinct from the equally denoted condition in [16]. A basic difference is that we quantify here over all subsets rather than single elements of X.
We draw a first conclusion from (F1).
Lemma 2.4
Let (X, ⊥) fulfil (F1). Then \({\mathcal {C}}(X, \perp )\) is atomistic, the atoms being the singletons {x}, x ∈ X.
Proof
Let e ∈ X. We first show that {e}⊥⊥ is an atom of \({\mathcal {C}}(X, \perp )\).
Assume that {e}⊥⊥ is not an atom. Then there is an f ∈ X such that \(\{f\}^{\perp \perp } \subsetneq \{e\}^{\perp \perp }\). In particular, e ∉ {f}⊥⊥. Consequently, we may apply property (F1) to {f} and e: there is an automorphism φ of X such that φ(e) ⊥ f and φ(x) = x if x ⊥ e, f. We actually have φ(x) = x if x ⊥ e, because \(\{e\}^{\perp } \subseteq \{f\}^{\perp }\). Moreover, we have f ∈{e}⊥⊥, thus f ⊥{e}⊥. It follows φ− 1(f) ⊥{e}⊥, in contradiction to φ− 1(f) ⊥ e.
For any \(A \in {\mathcal {C}}(X, \perp )\), we have \(A = \bigvee _{x \in A} \{x\}^{\perp \perp }\), hence \({\mathcal {C}}(X, \perp )\) is atomistic.
It remains to show that {x}⊥⊥ = {x}, where x ∈ X. Assume y ∈{x}⊥⊥. Then \(\{y\}^{\perp \perp } \subseteq \{x\}^{\perp \perp }\) and hence {y}⊥⊥ = {x}⊥⊥. It follows {y}⊥ = {x}⊥ and as we have assumed X to be irredundant, we conclude y = x. □
Recall that any ortholattice L is endowed with a natural orthogonality relation ⊥, which, when restricted to the non-zero elements, is symmetric and irreflexive. Thus (A, ⊥), where A is any subset of L ∖{0}, is an orthogonality space. We observe from Lemma 2.4 that (F1) implies (X, ⊥) to be isomorphic to the set of atoms of \({\mathcal {C}}(X, \perp )\), endowed with the orthogonality relation; the isomorphism is given by the assignment x↦{x}, x ∈ X.
A further consequence of (F1) is the following. We call a subset A of X orthogonal if any pair of distinct elements of A is orthogonal.
Lemma 2.5
Let (X, ⊥) fulfil (F1). Let \(D \subseteq X\) be orthogonal and let e ∈ X be such that e ∉ D⊥⊥. Then there is an f ⊥ D such that (D ∪ {e})⊥⊥ = (D ∪ {f})⊥⊥.
Proof
By (F1), there is an automorphism φ such that φ(e) ⊥ D and φ(x) = x if x ⊥ D, e or x ⊥ D, φ(e). Put f = φ(e). We claim that (D ∪ {e})⊥ = (D ∪ {f})⊥, then the assertion will follow. Indeed, if x ⊥ D, e, then φ(x) = x and hence x ⊥ φ(e) = f. Conversely, if x ⊥ D, f, then again φ(x) = x and hence x ⊥ φ− 1(f) = e. □
The following criterion for \({\mathcal {C}}(X, \perp )\) to be an orthomodular lattice (OML, for short) is due to Dacey [3], cf. also [18, Thm. 35].
Lemma 2.6
\({\mathcal {C}}(X, \perp )\) is an OML if and only if, for any \(A \in {\mathcal {C}}(X, \perp )\) and any maximal orthogonal subset D of A, we have that A = D⊥⊥.
Let L be a lattice with 0. We recall that, given a, b ∈ L, we say that bcovers a if a < b and there is no c ∈ L such that a < c < b. Furthermore, we say that L has the covering property if, for any a ∈ L and atom p of L such that a ∧ p = 0, we have that a ∨ p covers a. Following [8], we call L AC if it is atomistic and fulfils the covering property.
Proposition 2.7
Let (X, ⊥) fulfil (F1). Then \({\mathcal {C}}(X, \perp )\) is a complete AC OML.
Proof
By Lemmas 2.3 and 2.4, \(({\mathcal {C}}(X, \perp )\) is a complete, atomistic ortholattice.
Furthermore, from Lemma 2.5 and Dacey’s criterion (Lemma 2.6), it follows that \({\mathcal {C}}(X, \perp )\) is orthomodular.
It remains to show that \({\mathcal {C}}(X, \perp )\) fulfils the covering property. Let \(A \in {\mathcal {C}}(X, \perp )\) and e ∉ A. By Lemma 2.5, there is an f ⊥ A such that A ∨{e} = (A ∪ {e})⊥⊥ = (A ∪ {f})⊥⊥ = A ∨{f}. Since {f} is an atom orthogonal to A, it follows by the orthomodularity of \({\mathcal {C}}(X, \perp )\) that A ∨{e} covers A. □
We next show that (F1) implies a weak form of transitivity of (X, ⊥). Condition (F1) ensures that, for any two distinct element e and f of X, there is an automorphism mapping e to an element orthogonal to f. The question seems natural whether there is also an automorphism mapping e to f. We note that Holland’s Ample Unitary Group Axiom [7] as well as Aerts and Van Steirteghem’s plane transitivity [1] are conditions closely related to this issue.
Lemma 2.8
Let (X, ⊥) fulfil (F1) and let e, f ∈ X such that  . Then there is an automorphism φ such that (i) φ(e) = f and (ii) φ(x) = x if x ⊥ e, f.
. Then there is an automorphism φ such that (i) φ(e) = f and (ii) φ(x) = x if x ⊥ e, f.
Proof
The assertion is trivial if e = f. Let us assume e ≠ f.
By Lemmas 2.5, there is a g ⊥ f such that {e, f}⊥⊥ = {f, g}⊥⊥. By assumption, e ≠ g. Furthermore, we have \(\{e\} \subsetneq \{e,g\}^{\perp \perp } \subseteq \{f,g\}^{\perp \perp }\) and thus, by the covering property, {e, g}⊥⊥ = {f, g}⊥⊥.
(F1) implies that there is an automorphism φ such that φ(e) ⊥ g and φ(x) = x if x ⊥ e, g or x ⊥ φ(e), g. We conclude {φ(e), g}⊥ = {e, g}⊥ and hence {φ(e)}∨{g} = {φ(e), g}⊥⊥ = {e, g}⊥⊥ = {f, g}⊥⊥ = {f}∨{g}. By orthomodularity, we further conclude φ(e) = f. Finally, φ(x) = x if x ⊥ e, g, and this is the case iff x ⊥ f, g iff x ⊥ e, f. The lemma follows. □
Note that Lemma 2.8 does not entail the existence of automorphisms mapping a given element e of X to a given element f orthogonal to e. A more general version of transitivity will only be the consequence of a further basic property of orthogonality spaces, to which we turn now. We say that (X, ⊥) is reducible if X is the disjoint union of non-empty subsets \(A, B \subseteq X\) such that x ⊥ y for any x ∈ A and y ∈ B. Otherwise, we call (X, ⊥) irreducible.
We have the following characterisation of the irreducibility of (X, ⊥).
Lemma 2.9
Let (X, ⊥) fulfil (F1). Then (X, ⊥) is irreducible if and only if, for any distinct elements e, f ∈ X, {e, f}⊥⊥ possesses more than two elements.
Proof
Assume that X is reducible. Then X is the disjoint union of non-empty sets A and B such that x ⊥ y for any x ∈ A and y ∈ B. Let e ∈ A and f ∈ B and g ∈{e, f}⊥⊥. As g ∈ A or g ∈ B, it follows that g ⊥ e or g ⊥ f. If g ⊥ e, we have that \(\{g\} \subseteq \{e,f\}^{\perp \perp } \cap \{e\}^{\perp } = (\{e\} \vee \{f\}) \cap \{e\}^{\perp } = \{f\}\) and hence g = f. Similarly, g ⊥ f implies g = e. We conclude that {e, f}⊥⊥ contains no element apart from e and f.
Assume now that X is irreducible. Let e, f ∈ X be distinct elements and assume that {e, f}⊥⊥ = {e, f}. Let A = {x ∈ X : x ≠ e and {e, x}⊥⊥ = {e, x}} and B = X ∖ A. Then e ∈ B and f ∈ A. By irreducibility, there is an x ∈ A and a y ∈ B such that
 . Then {e, x}⊥⊥ is a two-element set and we conclude from Lemma 2.5 that x ⊥ e. In particular, we have y ≠ e. Again by Lemma 2.5, there is a z ⊥ e such that {e, y}⊥⊥ = {e, z}⊥⊥. We distinguish two cases:
. Then {e, x}⊥⊥ is a two-element set and we conclude from Lemma 2.5 that x ⊥ e. In particular, we have y ≠ e. Again by Lemma 2.5, there is a z ⊥ e such that {e, y}⊥⊥ = {e, z}⊥⊥. We distinguish two cases:
- Case 1.:
-
Let z ⊥ x. We then have x ∈{e, z}⊥ and hence x ⊥{e, z}⊥⊥ = {e, y}⊥⊥. This means x ⊥ y, contrary to our assumption.
- Case 2.:
-
Let
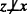 . Then Lemma 2.8 implies that there is an automorphism φ such that φ(z) = x and φ(e) = e. But then {e, y}⊥⊥ = {e, z}⊥⊥ is mapped to {e, x}⊥⊥ = {e, x} and thus has only two elements, again a contradiction.
. Then Lemma 2.8 implies that there is an automorphism φ such that φ(z) = x and φ(e) = e. But then {e, y}⊥⊥ = {e, z}⊥⊥ is mapped to {e, x}⊥⊥ = {e, x} and thus has only two elements, again a contradiction.
We conclude that {e, f}⊥⊥ possesses an element distinct from e and f. □
The irreducibility of (X, ⊥) corresponds to an analogous property of OMLs. We call an OML L reducible if L is isomorphic to the direct product of two at least two-element OMLs, otherwise L is called irreducible.
Lemma 2.10
Let (X, ⊥) fulfil (F1). Then (X, ⊥) is irreducible if and only if \({\mathcal {C}}(X, \perp )\) is irreducible.
Proof
Assume that the OML \({\mathcal {C}}(X, \perp )\) is reducible. Then there is a central element A distinct from the bottom element ∅ and the top element X. It follows that any atom is either below A or below A⊥, that is, any x ∈ X is either in A or in A⊥. Hence (X, ⊥) is reducible.
Conversely, assume that (X, ⊥) is reducible. Then there is a non-empty \(A \in {\mathcal {C}}(X, \perp )\) such that A⊥ is non-empty as well and X = A ∪ A⊥. It follows that, for any \(B \in {\mathcal {C}}(X, \perp )\), B = (B ∩ A) ∪ (B ∩ A⊥) and hence B = (B ∩ A) ∨ (B ∩ A⊥). Hence A is a central element of \({\mathcal {C}}(X, \perp )\) distinct from ∅ and X, that is, \({\mathcal {C}}(X, \perp )\) is reducible. □
As announced above, irreducibility ensures that the conclusion of Lemma 2.8 can be drawn even for pairs of orthogonal elements.
Proposition 2.11
Let (X, ⊥) be irreducible and fulfil (F1). Then there is, for each e, f ∈ X, an automorphism φ: X → X such that (i) φ(e) = f and (ii) φ(x) = x if x ⊥ e, f.
Proof
If  , the assertion holds by Lemma 2.8.
, the assertion holds by Lemma 2.8.
Assume that e ⊥ f. By Lemma 2.9, {e, f}⊥⊥ contains an element g ≠ e, f. Then g ⊥ e would imply \(\{g\} \subseteq (\{e\} \vee \{f\}) \cap \{e\}^{\perp } = \{f\}\) and hence g = f; similarly, g ⊥ f would imply g = e. We conclude
 . Furthermore, similarly as in the proof of Lemma 2.8, we derive from the covering property that {e, g}⊥ = {f, g}⊥ = {e, f}⊥. Hence the assertion follows by twice applying Lemma 2.8. □
. Furthermore, similarly as in the proof of Lemma 2.8, we derive from the covering property that {e, g}⊥ = {f, g}⊥ = {e, f}⊥. Hence the assertion follows by twice applying Lemma 2.8. □
By a Hilbert lattice, we mean a complete, irreducible AC OML. We may summarise as follows what we have shown so far.
Theorem 2.12
Let (X, ⊥) be irreducible and fulfil (F1). Then \({\mathcal {C}}(X, \perp )\) is a Hilbert lattice.
There is still one further property of orthogonality spaces that we need to address. The rank of the orthogonality space (X, ⊥) is the supremum of the cardinalities of the sets consisting of mutually orthogonal elements of X. Likewise, by the rank of an atomistic OML, we will mean the supremum of the cardinalities of the sets of mutually orthogonal atoms.
Lemma 2.13
Let (X, ⊥) fulfil (F1). Then (X, ⊥) has countably infinite rank if and only if \({\mathcal {C}}(X, \perp )\) has countably infinite rank. In this case, there is a countably infinite orthogonal set D such that X = D⊥⊥.
Proof
The first equivalence is clear from the remark after Lemma 2.4.
Assume that (X, ⊥) has countably infinite rank and let D be a maximal orthogonal subset of X. By Lemma 2.6, we then have X = D⊥⊥. If D contains n < ω elements, then the covering property implies that the size of a set of independent atoms of \({\mathcal {C}}(X, \perp )\) (meaning that none is below the supremum of the other ones) is bounded above by n [8, Theorem (8.4)], a contradiction. Hence D is infinite, that is, countably infinite. □
3 Hermitian Spaces
In this section, we will apply our results to the representation of orthogonality spaces by means of inner-product spaces.
We begin by compiling some basic facts. For further information, we refer, e.g., to [8] or to [12].
By a ⋆-sfield, we will mean a skew field (i.e., a division ring), equipped with an involutorial anti-automorphism ⋆.
Definition 3.1
Let E be a linear space over a ⋆-sfield K. Then a map (⋅,⋅): E × E → K is called an (anisotropic) Hermitian form on E if, for any x, y, z ∈ E and α, β ∈ K, we have
In this case, E together with (⋅,⋅) is called an (anisotropic) Hermitian space.
We write [x1, … , xk] for the subspace generated by vectors x1, … , xk of a Hermitian space E. In accordance with Example 2.2, we put P(E) = {[x]: x ∈ E ∖{0}}, and for x, y ∈ E ∖{0}, we set [x] ⊥ [y] if x ⊥ y, the latter relation meaning that (x, y) = 0. Then (P(E), ⊥) is an orthogonality space. It gives rise to the complete ortholattice \({\mathcal {C}}(P(E), \perp )\).
We readily check that for any x, y ∈ E ∖{0} such that y ∉ [x] there is a z ⊥ x such that [x, y] = [x, z]. We conclude that {[x]}⊥⊥ = {[x]} for any [x] ∈ P(E). In particular, it follows that (P(E), ⊥) is irredundant.
For a linear subspace M of E, we likewise define M⊥ = {x ∈ E : x ⊥ y for all y ∈ M}. We call Mclosed if M = M⊥⊥, and we denote the set of all closed subspaces of E by \({\mathcal {C}}(E)\). It is clear that \({\mathcal {C}}(P(E), \perp )\) and \({\mathcal {C}}(E)\) can be identified with each other.
We have the following characterisation of Hermitian spaces [8, Theorems (34.2) and (34.5)].
Theorem 3.2
Let E be a Hermitian space. Then \({\mathcal {C}}(E)\) is a complete, irreducible, AC ortholattice.
Conversely, let L be complete, irreducible, AC ortholattice of height ≥ 4. Then there is a ⋆-sfield K and a Hermitian space E over K such that L is isomorphic to \({\mathcal {C}}(E)\).
The orthomodularity of the ortholattice of closed subspaces of a Hermitian space is characterised as follows; see, e.g., [12, Theorem (2.8)].
Definition 3.3
A Hermitian space E is called an orthomodular space if, for any closed subspace M, we have E = M + M⊥.
Lemma 3.4
A Hermitian space E is an orthomodular space if and only if \({\mathcal {C}}(E)\) is orthomodular.
The standard examples of orthomodular spaces are the Hilbert spaces over \(\mathbb {R}\), \(\mathbb {C}\), or \(\mathbb {H}\), the so-called classical Hilbert spaces. These are, according to Solèr’s Theorem, in the infinite-dimensional case characterised as follows; see [14], cf. also [13].
Here, two vectors u, v of an orthomodular space are said to be of the same length if (u, u) = (v, v).
Theorem 3.5
Let E be an orthomodular space containing an infinite set of mutually orthogonal vectors of the same length. Then E is a classical Hilbert space.
By the dimension of an orthomodular space E, we mean the supremum of the cardinalities of the sets consisting of mutually orthogonal non-zero vectors of E. Understood in this way, a finite dimension of E coincides with the dimension of E as a linear space (i.e., with its Hamel dimension). Moreover, if E is a classical Hilbert space, the dimension of E is the usual one (i.e., its Hilbert dimension).
The automorphisms of the ortholattice of closed subspaces of an orthomodular space are described by Wigner’s Theorem. The following version of it is due to Piron [11, Thm. 3.28], see also [9, Lem. 1].
Theorem 3.6
Let E be a orthomodular space of dimension \(\geqslant 3\) and let φ be an automorphism of the ortholattice \({\mathcal {C}}(E)\). Assume that there is an at least two-dimensional subspace F such that φ|[0, F] is the identity. Then there is a unique unitary operator U on E such that
and such that U|F is the identity.
With respect to Theorem 3.6 and its notation, we will say that the automorphism φ of \({\mathcal {C}}(E)\) is induced by the unitary operator U.
We now return to orthogonality spaces and their representation. We begin by convincing ourselves that the conditions introduced in Section 2 actually hold in the cases of our primary interest.
Proposition 3.7
Let H be an ℵ0-dimensional classical Hilbert space. Then (P(H), ⊥) is an irreducible orthogonality space of rank ℵ0 that fulfils (F1).
Proof
Let [x], [y] ∈ P(H) be distinct. Then [x] ∨ [y] = {[x], [y]}⊥⊥ is, under the identification of \({\mathcal {C}}(P(H), \perp )\) with \({\mathcal {C}}(H)\), the two-dimensional subspace [x, y] spanned by x and y. As {[x], [y]}⊥⊥ contains one-dimensional subspaces distinct from [x] and [y], (P(H), ⊥) is irreducible by Lemma 2.9.
The supremum of the number of mutually orthogonal vectors in H is ℵ0. Hence P(H) has rank ℵ0.
It remains to show (F1). Let \(A \subseteq H\) and [e] ∉ A⊥⊥, e ∈ H ∖{0}. If e ⊥ A, there is nothing to show, hence assume that
 . By the orthomodularity of \({\mathcal {C}}(H)\), there are vectors x ∈ A⊥⊥ and y ∈ A⊥ such that e = x + y. Let U be a unitary operator that maps [e] to [y] and is the identity on [x, y]⊥. Then the automorphism of (P(H), ⊥) induced by U has the desired properties. □
. By the orthomodularity of \({\mathcal {C}}(H)\), there are vectors x ∈ A⊥⊥ and y ∈ A⊥ such that e = x + y. Let U be a unitary operator that maps [e] to [y] and is the identity on [x, y]⊥. Then the automorphism of (P(H), ⊥) induced by U has the desired properties. □
We now formulate a first representation theorem for orthogonality spaces.
Theorem 3.8
Let (X, ⊥) be an irreducible orthogonality space of rank \(\geqslant 4\) that fulfils (F1). Then there is a ⋆-sfield K and an orthomodular space E over K such that \({\mathcal {C}}(X, \perp )\) is isomorphic to \({\mathcal {C}}(E)\). In particular, (X, ⊥) is then isomorphic to (P(E), ⊥). The dimension of E coincides with the rank of X.
Proof
By Theorem 2.12, \({\mathcal {C}}(X, \perp )\) is a Hilbert lattice. By Theorem 3.2, there is a Hermitian space E such that \({\mathcal {C}}(X, \perp )\) is isomorphic to \({\mathcal {C}}(E)\). By Lemma 3.4, E is orthomodular. The first assertion follows; the remaining statements are clear. □
We proceed with a converse of Proposition 3.7.
Theorem 3.9
Let (X, ⊥) be an irreducible orthogonality space of rank ℵ0 that fulfils (F1). Then \({\mathcal {C}}(X, \perp )\) is isomorphic to the ortholattice of closed subspaces of an ℵ0-dimensional classical Hilbert space H. In particular, (X, ⊥) is then isomorphic to (P(H), ⊥).
Proof
By Theorem 3.8, \({\mathcal {C}}(X, \perp )\) is isomorphic to \({\mathcal {C}}(H)\) for an ℵ0-dimensional orthomodular space H over a ⋆-sfield K.
Let y, z ∈ H ∖{0} be orthogonal. By Proposition 2.11, there is an automorphism φ of (P(H), ⊥), and consequently of \({\mathcal {C}}(H)\), such that φ([y]) = [z] and φ([x]) = [x] for any x ∈ H ∖{0} such that x ⊥ y, z. By Wigner’s Theorem 3.6, φ is induced by a unitary map U on H. We conclude that [z] contains a vector of the same length as y.
As H is infinite-dimensional, we further conclude that there exists a countably infinite set of mutually orthogonal vectors of the same length. By Solèr’s Theorem 3.5, H is a classical Hilbert space. □
It remains to single out the field of complex numbers among the three classical ⋆-sfields. The following condition on an orthogonality space (X, ⊥) is inspired by Mayet’s paper [9]. For an automorphism φ of X and \(k \geqslant 1\), we write φk for φ ∘… ∘ φ (k times).
-
(F2)
Let e, f ∈ X be distinct and let φ: X → X be an automorphism such that φ is the identity on {e, f}⊥⊥. Then, for any \(k \geqslant 1\), there is an automorphism ψ: X → X such that
-
(i)
ψk = φ,
-
(ii)
for any x ∈ X, ψ(x) = x whenever φ(x) = x.
-
(i)
Proposition 3.10
Let H be a classical Hilbert space of dimension ≥ 4. Then (P(H), ⊥) fulfils (F2) if and only if the ⋆-sfield of scalars is \(\mathbb {C}\).
Proof
Assume that (P(H), ⊥) fulfils (F2). Choose a two-dimensional subspace M of H. Let U be the unitary operator such that U(x) = x if x ∈ M and U(x) = −x if x ∈ M⊥. Let φ be the automorphism of (P(H), ⊥) induced by U. Then φ([x]) = [x] for any x ∈ M and any x ∈ M⊥. By (F2), there is an automorphism ψ of (P(H), ⊥) such that ψ2 = φ and ψ([x]) = [x] for any x ∈ M and any x ∈ M⊥. Furthermore, ψ extends to an automorphism of \({\mathcal {C}}(H)\) and thus, by Wigner’s Theorem, ψ is induced by a unitary operator V such that V |M is the identity. Note that V leaves every subspace of M⊥ fixed. Moreover, V2 and U induce the same automorphism of \({\mathcal {C}}(H)\) and their restriction to M is the identity, hence the uniqueness part of Theorem 3.6 implies that V2 = U.
Let K be the ⋆-sfield of scalars. If \(K = \mathbb {R}\) or \(K = \mathbb {H}\), the only unitary operators that are the identity on M and leave every subspace of M⊥ fixed are the identity and U [9, Theorem 2]. We conclude that \(K = \mathbb {C}\).
For the converse direction, assume that H is a complex Hilbert space. Let φ be an automorphism of (P(H), ⊥) as specified in condition (F2), and let k ≥ 1. By Wigner’s Theorem, φ is induced by a unitary operator U.
We may assume that H = L2(X) for some compact Hausdorff space X endowed with a Borel measure, and that, for some measurable function u ∈ X → [0,2π), U(v) = eiu(⋅)v(⋅), v ∈ H; see, e.g., [10]. Then, for any non-zero v ∈ H, v and U(v) span the same one-dimensional subspace iff there is a λ ∈ [0,2π) such that v = e−iλU(v) iff, for some λ ∈ [0, 2π), v(x) = ei(u(x)−λ)v(x) for almost all x iff, for some λ ∈ [0,2π), either v(x) = 0 or u(x) = λ for almost all x. Define \(V(v) = e^{\frac {i u(\cdot )}k}v(\cdot )\), v ∈ H. Then Vk = U, and [U(v)] = [v] implies [V (v)] = [v].
Let ψ be the automorphism of (P(H), ⊥) induced by V. Then ψ fulfils the requirements of (F2). □
Combining all that we have shown, we arrive at our main result.
Theorem 3.11
Let (X, ⊥) be an irreducible orthogonality space of rank ℵ0 that fulfils (F1) and (F2). Then \({\mathcal {C}}(X, \perp )\) is isomorphic to the ortholattice of closed subspaces of an ℵ0-dimensional complex Hilbert space H. In particular, (X, ⊥) is then isomorphic to (P(H), ⊥).
Proof
This is a consequence of Theorem 3.9 and Proposition 3.10. □
4 Conclusion
We have proposed in this paper a characterisation of the infinite-dimensional complex Hilbert space by means of structures of a particularly simple type: Foulis’s orthogonality spaces. We have seen that, apart from requirements like an infinite rank and irreducibility, a single postulate concerning the existence of symmetries suffices to be led to the classical Hilbert spaces. Moreover, by means of one additional such postulate we may single out the field of complex numbers.
We made use of Solèr’s Theorem, which is available in infinite dimensions only. In the finite-dimensional case, we chose in our previous work a different and significantly more involved procedure [16]. Further work on the present topic could aim at establishing a theory that is independent of the dimension. In this was, we might also hope to improve our understanding of Solèr’s Theorem, finding what actually makes the decisive difference between finite and infinite dimensionality.
The most interesting issue, however, concerns the possibility of developing an alternative point of view on the presented results. Although our work is rooted in the lattice-theoretic approach to the characterisation of Hilbert space, the conditions that we have actually employed are of a group-theoretic nature. This aspect could be elaborated more explicitly. Moreover, in the complex Hilbert space, each one-dimensional subspace gives rise to a homomorphism of the multiplicative group of complex units to the unitary group. Thus one could replace the elements of the orthogonality space by certain families of transformations. An investigation of the potential of the theory of (Lie) transformation groups in the present context might be worthwhile.
References
Aerts, D., Van Steirteghem, B.: Quantum axiomatics and a theorem of M. P Solèr. Int. J. Theor. Phys. 39, 497–502 (2000)
Birkhoff, G., von Neumann, J.: The logic of quantum mechanics. Ann. Math. 37, 823–843 (1936)
Dacey, J.R.: Orthomodular spaces, Ph.D. thesis, University of Massachusetts, Amherst (1968)
Engesser, K., Gabbay, D.M., Lehmann, D.: A New Approach to Quantum Logic. Kings College Publications, London (2007)
Handbook of Quantum Logic and Quantum Structures – Quantum Structures. In: Engesser, K., Gabbay, D.M., Lehmann, D. (eds.) Elsevier, Amsterdam (2007)
Handbook of Quantum Logic and Quantum Structures – Quantum Logic. In: Engesser, K., Gabbay, D.M., Lehmann, D. (eds.) Elsevier, Amsterdam (2009)
Holland, S.S.: Orthomodularity in infinite dimensions; a theorem of M. Solèr. Bull. Am. M.th. Soc., New Ser. 32, 205–234 (1995)
Maeda, F., Maeda, S.: Theory of Symmetric Lattices. Springer, Berlin (1970)
Mayet, R.: Some characterizations of the underlying division ring of a Hilbert lattice by automorphisms. Int. J. Theor. Phys. 37, 109–114 (1998)
Pedersen, G.K.: Analysis Now. Springer, New York (1989)
Piron, C.: Foundations of Quantum Physics, W.A. Benjamin, Reading (1976)
Piziak, R.: Orthomodular lattices and quadratic spaces: a survey. Rocky Mt. J. Math. 21, 951–992 (1991)
Prestel, A.: On Solèr’s characterization of Hilbert spaces. Manuscr. Math. 86, 225–238 (1995)
Solèr, M.P.: Characterization of Hilbert spaces by orthomodular spaces. Commun. Algebra 23, 219–243 (1995)
Vetterlein, Th.: Partial quantum logics revisited. Int. J. Gen. Syst. 40, 23–38 (2011)
Vetterlein, Th.: Orthogonality spaces of finite rank and the complex Hilbert spaces. Int. J. Geom. Methods Mod. Phys. 16, 1950080 (2019)
Wilbur, W.J.: On characterizing the standard quantum logics. Trans. Am. Math. Soc. 233, 265–282 (1977)
Wilce, A.: Test spaces. In: Engesser, K., Gabbay, D.M., Lehmann, D. (eds.) Handbook of Quantum Logic and Quantum Structures. Quantum Logic, pp 443–549. Elsevier, North-Holland (2009)
Funding
Open access funding provided by Johannes Kepler University Linz.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Vetterlein, T. Orthogonality Spaces Arising from Infinite-Dimensional Complex Hilbert Spaces. Int J Theor Phys 60, 727–738 (2021). https://doi.org/10.1007/s10773-019-04230-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-019-04230-4



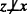 . Then Lemma 2.8 implies that there is an automorphism φ such that φ(z) = x and φ(e) = e. But then {e, y}⊥⊥ = {e, z}⊥⊥ is mapped to {e, x}⊥⊥ = {e, x} and thus has only two elements, again a contradiction.
. Then Lemma 2.8 implies that there is an automorphism φ such that φ(z) = x and φ(e) = e. But then {e, y}⊥⊥ = {e, z}⊥⊥ is mapped to {e, x}⊥⊥ = {e, x} and thus has only two elements, again a contradiction.