Towards Loophole-Free Optical Bell Test of CHSH Inequality

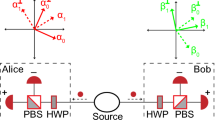
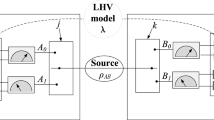
Abstract

Bell test had been suggested to end the long-standing debate on the EPR paradox, while the imperfections of experimental devices induce some loopholes in Bell test experiments and hence the assumption of local reality by EPR cannot be excluded with current experimental results. In optical Bell test experiments, the locality loophole can be closed easily, while the attempt of closing detection loophole requires very high efficiency of single photon detectors. Previous studies showed that the violation of Clauser-Horne-Shimony-Holt (CHSH) inequality with maximally entangled states requires the detection efficiency to be higher than 82.8 %. In this paper, we raise a modified CHSH inequality that covers all measurement events including the efficient and inefficient detections in the Bell test and prove that all local hidden models can be excluded when the inequality is violated. We find that, when non-maximally entangled states are applied to the Bell test, the lowest detection efficiency for violation of the present inequality is 66.7 %. This makes it feasible to close the detection loophole and the locality loophole simultaneously in optical Bell test of CHSH inequality.

Appendices

Appendix A: CH Inequality and CHSH Inequality

The CH inequality was first raised by Clauser and Horne in 1974 [3]. They assume there are six numbers satisfying the relationships

$$ \begin{array}{lll} 0\le&{x_{1}}&\le{X},\\ 0\le&{x_{2}}&\le{X},\\ 0\le&{y_{1}}&\le{Y},\\ 0\le&{y_{2}}&\le{Y}. \end{array} $$

(A1)

By constructing the function U≡x ₁ y ₁ − x ₁ y ₂ + x ₂ y ₁ + x ₂ y ₂ − Y x ₂ − X y ₁, mathematically, one can obtain

$$ -XY\le{U}\le0. $$

(A2)

Let X = 1 and Y = 1, one can then have the CH inequality. Though their procedure of obtaining the CH inequality is mathematically strict, it cannot embody the relationship between the realism and locality in quantum mechanics and the violation of the CH inequality.

In order to exploit the physical meanings of the CH inequality, Clauser and Horne derived the CH inequality from the CHSH inequality. Using the relationships 〈A _i 〉 = P ⁺(a _i ) − P ⁻(a _i ) and P ⁺(a _i ) + P ⁺(a _i ) + P ⁰(a _i ) = 1, they obtained

$$ -1-Q_{1}\le\text{CH}\le-Q_{1}, $$

(A3)

where 〈A _i 〉 is the average value of basis A _i at side A, and P ⁺(a _i ), P ⁻(a _i ) and P ⁰(a _i ) are the the probabilities of the detections on +1, −1 and the missed photons, respectively. When the value of Q ₁ is 0, the CH inequality can be obtained. Because Q ₁ is expanded to be

$$ \begin{array}{lll} Q_{1}&=&\frac{1}{2}\left[P^{+0}(a_{1},b_{1})+P^{0+}(a_{1},b_{1})+\frac{1}{2}P^{00}(a_{1},b_{1})\right.\\ &&+P^{+0}(a_{1},b_{2})+P^{0+}(a_{1},b_{2})+\frac{1}{2}P^{00}(a_{1},b_{2})\\ &&+P^{+0}(a_{2},b_{1})+P^{0+}(a_{2},b_{1})+\frac{1}{2}P^{00}(a_{2},b_{1})\\ &&-P^{+0}(a_{2},b_{2})-P^{0+}(a_{2},b_{2})-\frac{1}{2}P^{00}(a_{2},b_{2})\\ &&\left.-P^{0}(a_{1})-P^{0}(b_{1}){\vphantom{\frac{1}{2}P^{00}(a_{2},b_{2})}}\right], \end{array} $$

(A4)

its value is not to be 0 usually. Accordingly, the CHSH inequality and the CH inequality are not equivalent.

To obtain the CH inequality from the CHSH inequality, Clauser and Horne assumed that

$$ \begin{array}{lll} \langle{A_{i}}\rangle&=&2P^{+}(a_{i})-1,\\ \langle{B_{j}}\rangle&=&2P^{+}(b_{j})-1,\\ \langle{A_{i}B_{j}}\rangle&=&4P^{++}(a_{i},b_{j})-2P^{+}(a_{i})-2P^{+}(b_{j})+1. \end{array} $$

(A5)

If these relationships can be obtained, it means that the nondetection events are absorbed into the −1 detections. With this assumption, the CH inequality can still be obtained.

Appendix B: The relation between $S^{\text {All}}_{\text {CHSH}}\le 2$ and S _CH ≤ 0

The more nonlocality with less entanglement phenomenon observed in Bell test with CH inequality is attractive for realizing detection loophole-free Bell test. From the discussion above, it seems that Bell test with CHSH inequality may be more suitable to judge the completeness of quantum physics. It is interesting whether the more nonlocality with less entanglement phenomenon exists in Bell test with CHSH inequality. In Bell test with CHSH inequality, one can categorize the detection events as both-side detections, one-side detections and the non-detections. The both-side detections mean that both Alice and Bob have efficient detections. The one-side detections mean that either side of Alice and Bob has an efficient detection while the other side has not. The non-detections mean that neither side has efficient detection.

When Alice and Bob miss their photons, it means that the incoming photons do not interact with the measurement devices, alternatively, the measurement devices interact the incoming photons with identity operator, $\hat {I}$. If the detection efficiencies at both sides are η, the events that both Alice and Bob have efficient registers are then characterized to be η ²〈A _i B _j 〉_ideal. The events that Alice has an efficient detection while Bob misses the photon is described as η(1 − η)〈A _i I _B 〉_ideal. The events that Alice misses her photon but Bob has a register reads η(1 − η)〈I _A B _j 〉_ideal. The event that both Alice and Bob miss their photons is calculated to be (1 − η)²〈I _A I _B 〉_ideal. Considering all the detection and the non-detection events, we construct the CHSH polynomial to be

$$ \begin{array}{lll} S^{\text{All}}_{\text{ CHSH}}&=&\eta^{2}\langle{A_{1}B_{1}+A_{1}B_{2}+A_{2}B_{1}-A_{2}B_{2}}\rangle_{\text{ideal}}\\ &&+2\eta(1-\eta)(\langle{A_{1}I_{B}}\rangle_{\text{ideal}}+\langle I_{A}B_{1} \rangle_{\text{ideal}})\\ &&+2(1-\eta)^{2}\langle{I_{A}{I_{B}}}\rangle_{\text{ideal}}. \end{array} $$

(B1)

In local hidden variable model, it is proven that 〈A ₁ B ₁ + A ₁ B ₂ + A ₂ B ₁ − A ₂ B ₂〉_ideal ≤ 2. Thus one can obtain $S^{\text {All}}_{\text { CHSH}}\le 2\eta ^{2}+4\eta (1-\eta )+2(1-\eta )^{2}=2$.

In ideal detection condition, define that P ⁺(a _i ) and P ⁻(a _i ) are the probabilities that Alice obtains measurement outcomes +1 and −1 in direction $\vec {n}_{a_{i}}$. Similarly, one can define P ⁺(b _j ) and P ⁻(b _j ) the probabilities of Bob’s measurement outcomes +1 and −1 in direction $\vec {n}_{b_{j}}$. Thus, one can obtain 〈A _i 〉_ideal = P ⁺(a _i ) − P ⁻(a _i ), 〈B _j 〉_ideal = P ⁺(b _j ) − P ⁻(b _j ), and 〈A _i B _j 〉_ideal = P ⁺⁺(a _i b _j ) − P ⁺⁻(a _i b _j ) − P ⁻⁺(a _i ,b _j ) + P ⁻⁻(a _i ,b _j ). Using the relationships P ⁺(a _i ) + P ⁻(a _i ) = 1, and P ⁺(b _j ) + P ⁻(b _j ), one can obtain

$$ \begin{array}{lll} \langle A_{i}\rangle&=&2P^{+}(a_{i})-1,\\ \langle B_{j}\rangle&=&2P^{+}(b_{j})-1,\\ \langle A_{i}B_{j}\rangle&=&4P^{++}(a_{i},b_{j})-2P^{+}(a_{i})-2P^{+}(b_{j})+1. \end{array} $$

(B2)

Substituting these expressions into (B1), one can thus have

$$ \begin{array}{lll} S^{\text{All}}_{\text{ CHSH}}&=&\eta^{2}\{4[P^{++}(a_{1},b_{1})+P^{++}(a_{1},b_{2})+P^{++}(a_{2},b_{1})\\ &&-P^{++}(a_{2},b_{2})]-4[P^{+}(a_{1})+P^{+}(b_{1})]+2\}\\ &&+4\eta(1-\eta)[P^{+}(a_{1})+P^{+}(b_{1})-1]\\ &&+2(1-\eta)^{2}. \end{array} $$

(B3)

After rearrangement, this equation reads

$$ \begin{array}{lll} S^{\text{All}}_{\text{CHSH}}&=&4\{\eta^{2}[P^{++}(a_{1},b_{1})+P^{++}(a_{1},b_{2})+P^{++}(a_{2},b_{1})\\ &&-P^{++}(a_{2},b_{2})]-\eta[P^{+}(a_{1})+P^{+}(b_{1})]\}\\ &&+8\eta(1-\eta)[P^{+}(a_{1})+P^{+}(b_{1})]\\ &&+2(1-2\eta)^{2}. \end{array} $$

(B4)

We define that $S^{\text {All}}_{\text {CHSH}}=4\left (S_{\text {CH}}^{++}+Q\right )$, where $S_{\text { CH}}^{++}=\eta ^{2}[P^{++}(a_{1},b_{1})+P^{++}(a_{1},b_{2})+P^{++}(a_{2},b_{1}) -P^{++}(a_{2},b_{2})]-\eta [P^{+}(a_{1})+P^{+}(b_{1})]$ and $Q=2\eta (1-\eta )[P^{+}(a_{1})+P^{+}(b_{1})]+\frac {1}{2}(1-2\eta )^{2}$. It is apparent that $S_{\text {CH}}^{++}$ has the same definition as the CH polynomial in lossy condition. To exclude the hidden variable, $S^{\text {All}}_{\text {CHSH}}>2$ should be satisfied. It means that $4\left (S_{\text {CH}}^{++}+Q-\frac {1}{2}\right )>0$ should be founded. If $Q-\frac {1}{2}=0$, one can obtain the condition for excluding the hiden variable in the CH inequality: S _CH>0. Apparently, $Q-\frac {1}{2}=0$ is always satisfied when η = 1. When η ≠ 1, P ⁺(a ₁) + P ⁺(b ₁) is calculated to be 1 to meet the condition of $Q-\frac {1}{2}=0$. For symmetric entangled states, such as

$$ \begin{array}{lll} |{\Psi}^{-}\rangle&=&\frac{1}{\sqrt{2}}\left( |01\rangle-|10\rangle\right),\\ |{\Phi}^{+}\rangle&=&\frac{1}{\sqrt{2}}\left( |00\rangle+|11\rangle\right), \end{array} $$

(B5)

one can obtain $P(a_{1})=P(b_{1})=\frac {1}{2}$. It means that P(a ₁) + P(b ₁) = 1 is satisfied if symmetric entangled states are used. Generally, when the quantum channel is lossy and the quantum state is not well deviced, these two inequalities cannot be equivalent.