1 Introduction

After the pioneering work of Bennett et al. [1] (BB84), quantum key distribution (QKD) has progressed rapidly, and become one of the most important branch of quantum information [2]. The most advantage of QKD is its unconditional security, which is guaranteed by the principle of quantum mechanics, instead of computational complexity. Besides QKD, some other cryptographic tasks can be realized with quantum mechanics, such as quantum teleportation (QT) [3], quantum secret sharing (QSS) [4] and so on.

Classical secret sharing is a cryptographic task aiming to distribute a secret among a group of parties, and classical secret sharing protocol [5] have been proposed, where classical information is encoded by a mathematical transformation. The protocol can be proven to be information-theoretically secure, i.e., no information about the secret can be obtained by those adversaries even when they have unlimited computational power, if the communication channels between the dealer and the parties are secure.

Following the rapid development of quantum information, the extension of secret sharing to the quantum regime has received much theoretical attention. The objective of QSS is to use the quantum correlations in well-constructed entangled states to securely transmit a set of classical or quantum information to only the access structures. In 1999, Hillery et al. [4] proposed the pioneering QSS scheme for sharing a classical secret among three parties with a three-particle entangled GHZ state. Later, their scheme was generalized by Xiao et al. [6] to many parties. Since then, QSS was attracted widespread attention and there were lots of researches in both its theoretical [7–9] and experimental [10].

Generally speaking, the idea of QSS, in the literature, has been developed to the following three tasks: CC [11] (classical information is shared among parties by distributing QSS states through private secure channels, which are invulnerable to eavesdropping), CQ [9](classical information is shared among parties by distributing QSS states through public insecure channels, which are open for eavesdropping) and QQ [12–18](known as quantum state sharing or quantum information splitting, a secret quantum state is shared among parties by distributing QSS states through public channels). We consider the latter approach in the current paper. The three tasks form a hierarchy of the required resources; i.e., a QQ quantum state can perform all three tasks, and a CQ state can be used for CC, while the reverse is not always true.

To date, lots of QIS schemes have been proposed. Hillery et al.’ scheme [4] can be viewed as a typical QIS. Soon later, Cleve and Gottesman et al. [7] have perfectly integrated quantum error correcting code technique for investigating a more general quantum (k,n) threshold QIS. Deng et al. [12] have presented a an arbitrary two-qubit QIS with four sets of EPR pairs as quantum information carrier. And then, instead of EPR pairs, Muralidharan et al. [13] have proposed another QIS via five-qubit Brown state, it have enormously reduced the cost of quantum resource. Yang et al. [14] have found a novel three-qubit GHZ-like state in experimental and demonstrated an arbitrary single-qubit state QIS based on Z basis measurement via it among three-party. Meanwhile, Zhang et al. [15] have also designed a similar three-party QIS of an arbitrary n-qubit state by using n sets of GHZ-like states as quantum information carrier. Recently, many-party QIS schemes of an arbitrary unknown quantum states have been investigated [16–18].

Inspired by some ideas of Refs. [14, 15, 22, 23], in this manuscript we firstly investigate the AQIS scheme of an arbitrary two-qubit state among three participants by using the maximally entangled states, which are made up of a three-qubit entangled GHZ-like state and a Bell state, as quantum information carrier, instead of multi-qubit entangled states. Different from most previous QIS ones, our scheme is claimed an asymmetrical quantum information splitting since that the number of the particles owned by each agent in the secure quantum channel is not necessarily equal except that the quantum information of the receiver is designated in advance. And then, it is generalized to N-qubit scenario. Through deep analysis and research, it can be found that some previous QIS ones exist severely redundancy for the controller to own more than one particle compared with this AQIS scheme. Moreover, the intrinsic efficiency for qubits of the AIQS scheme approaches 100% by reducing the redundant information, and the total efficiency really approaches the maximal value, which is higher than those of some previous QIS schemes [15].

The rest of this manuscript is organized as follows. In Sect. 2, we briefly introduce the preparation of GHZ-like state and then explicitly illustrate the AQIS scheme of an arbitrary two-qubit state. In Sect. 3 we generalize it to N-qubit scenario. In Sect. 4 we analyze the security from the views of participant attack and outside attack in detail. Some discussions and conclusions are given in Sect. 5.

2 AQIS of an Arbitrary Two-Qubit State

In this section, we will briefly introduce the preparation and quantum circuit of the GHZ-like state, then explicitly illustrate an economical and efficient AQIS scheme of an arbitrary two-qubit state by using a maximally entangled state, which is made up of the three-qubit GHZ-like entangled state and a Bell state, as quantum information carrier.

2.1 Preparation of GHZ-like State

As we all known, three-qubit entangled states have been classified into two classes [19]: GHZ-class and W-class. Any one of the two classes cannot be obtained from the other using local operations and classical communication. In accordance with this concept of classification, the GHZ-like state

$$\begin{aligned} |G\rangle =&\frac{1}{2}\bigl(|001\rangle+|010\rangle+|100\rangle+|111\rangle\bigr) \\ &{}=\frac{\sqrt{2}}{2}\bigl(|0\rangle\big|\psi^{+}\big\rangle +|1\rangle\big|\phi^{+}\big\rangle \bigr) \end{aligned}$$
(1)

where Bell states

$$ \big|\phi^{\pm}\big\rangle =\frac{1}{\sqrt{2}}\bigl(|00\rangle \pm|11\rangle\bigr), \qquad \big|\psi^{\pm}\big\rangle = \frac{1}{\sqrt{2}}\bigl(|01\rangle\pm|10\rangle\bigr) $$
(2)

is quite like the W state. However, it belongs to GHZ-class state rather than W-class state and it exists a potential symmetry. This state can be generated by a single photon and an EPR pair as follows [15]:

I.:

One prepares a single photon \(|+\rangle_{1}=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)_{1}\) and an EPR pair \(|\psi^{+}\rangle_{23}=\frac{1}{\sqrt{2}}(|01\rangle+ |10\rangle)_{23}\). The composite system is formed

$$\begin{aligned} |G_{0}\rangle_{123} =&|+\rangle_1\otimes\big|\psi^{+}\big\rangle _{23} \\ =&\displaystyle\frac{1}{\sqrt{2}} \bigl(|0\rangle+|1\rangle\bigr)_1\otimes\frac{1}{\sqrt{2}}\bigl(|01\rangle+|10\rangle\bigr)_{23} \\ =&\frac{1}{2}\bigl(|001\rangle+|010\rangle+|101\rangle+|110\rangle\bigr)_{123} \end{aligned}$$
(3)

where the subscript i (i=1,2,3) denotes different particles of |G 0〉123.

II.:

One can carry out a control-not (C-NOT) gate operation on |G 0〉123 with the first particle as the control qubit and the third particle as the target qubit. Then the GHZ-like can be generated successfully.

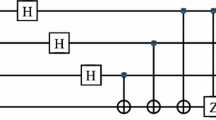
In fact, C-NOT gate operation [20], the generations of single photon and Bell state [21] have already been well demonstrated experimentally. Thus, the preparation of GHZ-like state is also feasible and it can be well demonstrated experimentally within the present technology. The quantum circuit for the preparation of GHZ-like state is shown in Fig. 1.

Fig. 1
figure 1

The quantum circuit for the preparation of GHZ-like state

Full size image

2.2 AQIS of an Arbitrary Two-Qubit State

Recently, Yang et al. [14] have devised a symmetric three-party QIS scheme of an arbitrary single-qubit by using only a GHZ-like state in Eq. (1) as quantum information carrier. Meanwhile, Zhang et al. [15] have also designed a similar symmetric three-party QIS one via another three-qubit GHZ-like state

$$ |G\rangle^{\prime}=\frac{1}{2}\bigl(|000\rangle+|110\rangle+|101 \rangle+|011\rangle\bigr) $$
(4)

In fact, the mentioned above two GHZ-like state are the same contrast of the form dissimilarity but essences.

In this manuscript,we wish to construct a QQ scheme by mainly using the GHZ-like state as quantum information carrier. In principle, constructing a QQ state is versatile, but the amount of resources can be optimized according to the properties of the shared information and the channels. Moreover, according to Ref. [22] it is shown that using only a GHZ-like entangled state can’t be utilized for any QIS task of an arbitrary more than two-qubit state. Inspired by some ideas of Refs. [14, 15, 22], we expect to generalize Yang et al.’ scheme [4] and research into the AQIS scheme of an arbitrary two-qubit state by using a GHZ-like state and a Bell state. Like that in Ref. [14], assume that there are three parties, the boss Alice and two subordinates Bob and Charlie, where Bob is designated as the recover quantum information and Charlie is the controller, as shown in Fig. 2. In other words, Alice wants to transmit the arbitrary unknown quantum information to Bob who is designated to reconstruct it under Charlie’s help.

Fig. 2
figure 2

AQIS of an arbitrary two-qubit state

Full size image

Assume that Alice possesses an arbitrary unknown two-qubit state

$$ |\psi\rangle_{xy}=\bigl(a_0|00\rangle+a_1|01 \rangle+a_2|10\rangle+a_3|11\rangle\bigr)_{xy} $$
(5)

where a i (i=0,1,2,3) are complex numbers that satisfy the normalization condition \(\sum_{i=0}^{3}|a_{i}|^{2}=1\). The quantum information carrier is the product of a GHZ-like state and a Bell state |ϕ +〉, i.e., it can be described as

$$\begin{aligned} |\varOmega\rangle_{12345} =&|G\rangle_{123}\otimes\big|\phi^{+}\big\rangle _{45} \\ =&\frac{1}{2\sqrt{2}} \bigl(|001\rangle+|010\rangle+|100\rangle+|111\rangle\bigr) \otimes\bigl(|00\rangle+|11\rangle\bigr) \end{aligned}$$
(6)

In this scheme, Alice holds the particles {x,y,1,4}, while particles {3,5} and {2} belong to Bob and Charlie, respectively. The basic idea of this QIS scheme is shown in Fig. 2, where the solid lines connect qubits and the dashed lines connect qubits where a BSM is performed.

At the beginning, the whole system

$$\begin{aligned} |Q_{2}\rangle_{total} =&|\psi\rangle_{xy}\otimes|\varOmega\rangle_{12345} =|\psi\rangle_{xy}\otimes|G\rangle_{123}\otimes\big|\phi^{+}\big\rangle _{45} \\ =&\frac{1}{2\sqrt{2}}\bigl(a_0|00\rangle+a_1|01\rangle+a_2|10\rangle+a_3|11\rangle\bigr)_{xy} \\ &{} \otimes\bigl(|001\rangle+|010\rangle+|100\rangle+|111\rangle\bigr)_{123} \otimes\bigl(|00\rangle+|11\rangle\bigr)_{45} \end{aligned}$$
(7)

is prepared by Alice. The procedure of the AQIS proceeds as follows: Alice initially performs two BSMs on her qubit pairs {x,1} and {y,4} under the orthogonal basis {|ϕ ±〉,|ψ ±〉}, respectively. It is clear that Alice may acquire one of 16 types of possible measurement results with equal probability and the remaining qubits may collapse into one of the 16 states |ϕ〉235 after the Bell state measurement. We summarize the possible measurement results and the corresponding states obtained by Bob and Charlie in Table 1, where AMR denotes Alice’s measurement result and the normalization factors are omitted for convenience.

Table 1 The correlations between AMR and the corresponding states |ϕ〉235
Full size table

Depending on AMR, the state of particles {2,3,5} obtained by Bob and Charlie evolves to a pure three-particle entangled state. One can see that neither Bob nor Charlie can reconstruct |ψ〉 xy by performing any general operations on their respective particles without communicating with each other. Whether it is possible for Bob to reconstruct the original state with LUOs on the state |ϕ〉235 depends on Charlie. If Charlie allows Bob to reconstruct |ψ〉 xy , he needs to carry out a SM on his qubit under the Z basis {|+z〉=|0〉,|−z〉=|1〉} and then informs Bob of his measurement results (CMR) via a classical channel. Having obtained both AMR and CMR, Bob can recover |ψ〉 xy by carrying out an appropriate local unitary operation on his particles. The correlations among AMR, CMR, the corresponding state |ϕ〉35 of Bob’s particles and LUOs are shown in Table 2.

Table 2 the correlations among AMR, CMR, |ϕ〉35 and LUOs
Full size table

Now we can take an example in order to explicitly illustrate this AQIS principle. WLG, suppose that AMR is |ϕ +〉 x1|ψ −〉 y4 on her qubit pairs {x,1} and {y,4}, then the remaining qubits {2,3,5} would collapse into the state

$$\begin{aligned} |\phi\rangle_{235} =&a_0\bigl(|011\rangle+|101\rangle\bigr) +a_1\bigl(|010\rangle-|100\rangle\bigr) \\ &{} + a_2\bigl(|001\rangle+|111\rangle\bigr) +a_3\bigl(-|000\rangle+|110\rangle\bigr) \end{aligned}$$
(8)

Then Charlie can do a SM on his particle under the basis Z and send CMR to Bob via a classical channel. If it is |0〉, then Bob needs to perform the LUOs \(\sigma_{x}^{3}\otimes (-i\sigma_{y})^{5}\) on his own qubits; otherwise I 3⊗ (−iσ y )5. Here the LUOs I, σ x , −iσ y and σ z are four different Pauli operations and described as

$$ \begin{array}{l@{\qquad}l} I=|0\rangle\langle0|+|1\rangle\langle1|, & \sigma_{x}=|0\rangle\langle1|+|1\rangle\langle0|\\ -i\sigma_{y}=|1\rangle\langle0|-|0\rangle\langle1|, & \sigma_{z}=|0\rangle\langle0|-|1\rangle\langle1| \end{array} $$
(9)

3 Generalized AQIS of an Arbitrary N-qubit State

Next, the above-mentioned scheme can be generalized to N-qubit scenario. Firstly, assume that Alice possesses an arbitrary unknown N-qubit entangled state

$$ |\phi\rangle_{j_1, j_2, \ldots, j_N}=\sum_{{j_1,j_2, \ldots,j_N}\in\{0,1\}} {a_{j_1, j_2, \ldots, j_N}|j_1, j_2, \ldots, j_N \rangle_{j_1, j_2, \ldots, j_N}} $$
(10)

where \(\sum_{{j_{1},j_{2}, \ldots,j_{N}}\in\{0,1\}}{|a_{j_{1}, j_{2}, \ldots, j_{N}}|^{2}}=1\).

In this scheme, the quantum carrier is composed of (N−1) sets of Bell states |ϕ +〉 i,i+1(i=1,3,…,2N−3) and a GHZ-like state |G〉2N−1,2N,2N+1. Alice holds n pairs of particles {j 1,1},{j 2,3},…,{j N ,2N−1}, while particles {2,4,…,2N} and {2N+1} belong to Bob and Charlie, respectively. The basic idea of this QIS scheme is shown in Fig. 3.

Fig. 3
figure 3

AQIS of an arbitrary N-qubit state

Full size image

At the beginning, the whole system

$$ |Q_{n}\rangle_{total}=|\phi\rangle_{j_1,j_2, \ldots,j_N}\otimes| \phi^{+}\rangle_{1,2}\otimes\cdots\otimes\big|\phi^{+} \big\rangle _{2N-3,2N-2}\otimes|G\rangle_{2N-1,2N,2N+1} $$
(11)

is prepared by Alice. The procedure proceeds as follows: Firstly, Alice makes n BSMs on her qubit pairs {j 1,1},{j 2,3},…,{j N ,2N−1} under the basis {|ϕ ±〉,|ψ ±〉}, respectively. It is clear that Alice may acquire one of 4n kinds of possible measurement results with equal probability, and then Alice publicly informs her measurement results of Charlie. Whether it is possible to reconstruct the initial unknown state for Bob with local operations depends on Charlie. If Charlie cooperates with Bob, he carries out a SM on his qubit {2N+1} under the Z basis and then conveys his measurement results to Bob. Consequently, Bob’s particles will collapse into

$$ |\phi\rangle_{2, 4, \ldots, 2N}=\sum_{{j_1,j_2, \ldots,j_N}\in\{0,1\}} {b_{j_1,j_2, \ldots, j_N}|j_1,j_2, \ldots,j_N \rangle_{2,4, \ldots,2N}} $$
(12)

where every coefficient \(b_{j_{1}, j_{2}, \ldots, j_{N}}\) must be one of the rearrangements of those \(a_{j_{1},j_{2}, \ldots,j_{N}}\), and its value is depended on AMR and CMR. Then Bob can successfully translate |ϕ〉2,4,…,2N to the original state \(|\phi\rangle_{j_{1},j_{2}, \ldots,j_{N}}\) by performing suitable LUOs on his particles according to AMR and CMR. Consequently, we perfectly design the AQIS scheme of an arbitrary N-qubit state.

4 Security Analysis

Now we will analyze the security of our scheme in detail and expect our methods could be also utilized for security analysis of other quantum communication schemes. For simplicity, we only consider two-qubit case. Notice that there are two kinds of eavesdropping. The first is that one dishonest participant (Bob or Charlie) try to obtain Alice’s secret without cooperating with the other. The second is that a fourth eavesdropper Eve attempts to find Alice’s secret without being detected.

Case I Participant attack

Firstly we consider the case of the dishonest participant Charlie, since the participant attack is always more powerful than outsider attack, thus the eavesdropper in this case can obtain more information than a fourth eavesdropper Eve. In the following, we will discuss the participant attack and show that Charlie cannot obtain information on the secret bits without being detectable.

As discussed in Ref. [23], supposed that participant Charlie performs unitary operators attack (P,Q) on the qubits sent from Alice to him and Bob. WLG, P and Q are assumed to share a common probe space \(\mathcal{H}_{E}\). We have the following theorem.

Theorem 1

For Charlie’s attack inducing no error, the final state of Bob’s probe should be independent of Charlie’s measurement result and therefore Charlie gets no information.

Proof

Denote the qubits sent from Alice to Bob and Charlie by B and C, respectively, and denote Charlie’s probe by E. Let us have a look at the evolution of the system B+C+E.

  1. 1.

    After Alice’s BSMs, the remaining particle become a three-qubit state, denoted by |φ〉 BC . Then before Charlie’s attack, the state is |φ〉 BC |0〉 E .

  2. 2.

    After Charlie has performed P, the state evolves to

    $$ |\varphi\rangle_{BCE}=\sum_{i=0}^{7}\big| \varphi^{(i)}\big\rangle _{BC}|E_{i}\rangle $$
    (13)

    where |E i 〉 are un-normalized states of Charlie’s probe. In particular, if Charlie does nothing, then \(|E_{i}\rangle=\frac{1}{2\sqrt{2}}|0\rangle\).

  3. 3.

    After Charlie has performed Q. We want to show that after Q having been performed the state of E is independent of Charlie’s measurement. For Charlie not being detectable, Q must satisfy the following conditions: for ∀i,

    $$ Q\big|\varphi^{(i)}\big\rangle _{BC}|E_{i}\rangle=\big| \varphi^{(i)}\big\rangle _{BC}|F_{i}\rangle $$
    (14)

    It is a key point that Q can not change the state of B+C. Otherwise, Alice will detect Charlie’s attack with a non-zero probability. For example, suppose that Q changes |φ (0)〉 BC |E 0〉 to \(\sum_{i=0}^{7}|\varphi^{(i)}\rangle_{BC}|F'_{i}\rangle\). Then, when Bob have made the recover operator on his qubits, Charlie will be brought some errors with probability \(\sum_{i\neq 0}|\|F'_{i}\rangle\|^{2}\).

We can see that, for Charlie’s attack inducing no errors, the final state of Charlie’s probe is independent of Bob’s recover operation (but dependent on his own measurement result). Therefore, we have proved Theorem 1. □

Of course, In the above proof, if the entangling attack (P,Q) was performed by a fourth eavesdropper Eve, Bob and Charlie’s measurement results should be strongly correlated since the entanglement is monogamous [24]. We can further show that all |F i 〉 are equal, which means that the state of outside eavesdropping Eve’s probe is independent of Bob and Charlie’s measurement results. What’s more, we can mainly use the decoy photons technique and the estimation of mutual information, respectively, to prevent from the outsider attack.

Case II Outsider attack

Next we consider the case of outside attacker Eve, who wants to eavesdrop the secret state. Eve intercepts all the participants’ photons during the particle distribution process and entangles ancillary particles in order to get the information. If she does obtain Alice’s secret information, in the procedure she must inevitably introduce extra error rate which makes her be detected in the process of security checking [1]. In the following, we will provide a more reasonable explanation by means of the decoy photons technique. According to Stingspring dilation theorem [25], Eve’s eavesdropping can be described by a unitary operation \(\hat{U}_{E}\) on a larger Hilbert space \(\mathit{Hom}(\mathcal{H}_{A}, \mathcal{H}_{E} )\). After Eve’s eavesdropping, we have the following equations:

$$ \begin{array}{rcl} \hat{U}_{E}|0\rangle|\varepsilon\rangle_{E} &=&|0\rangle|\varepsilon_{0}\rangle_{E}+|1\rangle|\varepsilon_{1}\rangle_{E}\\ \hat{U}_{E}|1\rangle|\varepsilon\rangle_{E} &=&|0\rangle|\varepsilon^{\prime}_{0}\rangle_{E}+|1\rangle|\varepsilon^{\prime}_{1}\rangle_{E} \end{array} $$
(15)

where |ε〉 E is the initial state of Eve’s ancilla. Since \(\hat{U}_{E}\) is a unitary operation, these pure ancilla’s states \(|\varepsilon_{0}\rangle, |\varepsilon_{1}\rangle, |\varepsilon^{\prime}_{0}\rangle, |\varepsilon^{\prime}_{1}\rangle\), thus, must satisfy

$$ \begin{array}{l} \langle\varepsilon_{0}|\varepsilon_{0}\rangle+\langle\varepsilon_{1}|\varepsilon_{1}\rangle=1, \qquad \big\langle \varepsilon^{\prime}_{0}\big|\varepsilon^{\prime}_{0}\big\rangle +\big\langle \varepsilon^{\prime}_{1}\big|\varepsilon^{\prime}_{1}\big\rangle =1\\ \langle\varepsilon_{1}|\varepsilon_{0}\rangle +\langle\varepsilon^{\prime}_{1}|\varepsilon^{\prime}_{0}\rangle=0,\qquad \big\langle \varepsilon_{0}\big|\varepsilon_{1}\big\rangle +\big\langle \varepsilon^{\prime}_{0}\big|\varepsilon^{\prime}_{1}\big\rangle =0 \end{array} $$
(16)

For the decoy photons |+〉,|−〉, we can rewrite Eq. (15) into

$$ \begin{array}{l} \hat{U}_{E}|+\rangle|\varepsilon\rangle_{E}= \displaystyle\frac{1}{2}\bigl[|+\rangle\bigl(|\varepsilon_{0}\rangle +|\varepsilon_{1}\rangle+\big|\varepsilon^{\prime}_{0}\rangle +\big|\varepsilon^{\prime}_{1}\big\rangle \bigr)\\ \hphantom{\hat{U}_{E}|+\rangle|\varepsilon\rangle_{E}=} {}+|-\rangle\bigl(|\varepsilon_{0}\rangle-|\varepsilon_{1}\rangle +\big|\varepsilon^{\prime}_{0}\big\rangle -\big|\varepsilon^{\prime}_{1}\big\rangle \bigr)\bigr]\\ \hat{U}_{E}|-\rangle|\varepsilon\rangle_{E}= \displaystyle\frac{1}{2}\bigl[|+\rangle\bigl(|\varepsilon_{0}\rangle +|\varepsilon_{1}\rangle-\big|\varepsilon^{\prime}_{0}\big\rangle -\big|\varepsilon^{\prime}_{1}\big\rangle \bigr)\\ \hphantom{\hat{U}_{E}|-\rangle|\varepsilon\rangle_{E}=} {} +|-\rangle\bigl(|\varepsilon_{0}\rangle-|\varepsilon_{1}\rangle -\big|\varepsilon^{\prime}_{0}\big\rangle +\big|\varepsilon^{\prime}_{1}\big\rangle \bigr)\bigr] \end{array} $$
(17)

When the pre-shared decoy state is |0〉 or |1〉, the action of Eve’s eavesdropping will introduce an error rate

$$ P_{e}=\frac{1}{2}\bigl(\langle\varepsilon_{1}| \varepsilon_{1}\rangle+\bigl\langle \varepsilon^{\prime}_{0}\big| \varepsilon^{\prime}_{0}\bigr\rangle \bigr) $$
(18)

Similarly, for the decoy state is |+〉 or |−〉, the introduced error rate is

$$ P^{\prime}_{e}=\frac{1}{2}\bigl[2-\bigl(\bigl\langle \varepsilon_{1}\big|\varepsilon^{\prime}_{0}\bigr\rangle + \bigl\langle \varepsilon_{0}\big|\varepsilon^{\prime}_{1} \bigr\rangle \bigr)\bigr] $$
(19)

Supposed that Eve is clever enough to prevent all participants from detecting her eavesdropping by finding the discrepancy in the error rates of quantum states. Eve tries to achieve the eavesdropping without being detected, if and only if both the error rates P e and \(P^{\prime}_{e}\) equal 0 in the ideal environment, which means that the quantum channels are noiseless. Thus, according to Eqs. (13), (18), (19) we can get the following equation

$$ \begin{array}{l} \langle\varepsilon_{1}|\varepsilon_{1}\rangle =\big\langle \varepsilon^{\prime}_{0}\big|\varepsilon^{\prime}_{0}\big\rangle =0\\ \langle\varepsilon_{0}|\varepsilon_{0}\rangle =\big\langle \varepsilon^{\prime}_{1}\big|\varepsilon^{\prime}_{1}\big\rangle =1\\ \langle\varepsilon_{1}|\varepsilon^{\prime}_{0}\rangle =\big\langle \varepsilon_{0}\big|\varepsilon^{\prime}_{1}\big\rangle =1 \end{array} $$
(20)

Then, in essence, If the entanglement of Eve’s ancilla with the quantum channel does not introduce any errors into the procedure, then the state of the system is a product of the state and the ancillary particles. It means that Eve gain no information about Alice’s original quantum state.

Certainly, except the above decoy photons technique we can also adopt other strategies. Here, we will design an equivalent strategy for the security checking and give the estimation of mutual information. Sender can randomly prepare a Bell state |ϕ +〉 instead of the decoy photons. Then, she distributes one of the entangled particles to receiver, while keeping the other particle herself. Sender randomly measures each qubit in the mutually unbiased basis X or Z after receiving the confirmation. We can note that this model is originated from the celebrated E91 QKD [26]. It is equivalent to the decoy photons method used in our scheme, and more suitable for the following security proof.

At first, we will introduce the entropic uncertainty principle [27, 28] in order to give a more rigorous proof by estimating the mutual information between Alice and Eve. For POVM measurements X and Z and any density operator \(\rho_{ABE}\in End(\mathcal{H}_{A}\otimes\mathcal{H}_{B}\otimes\mathcal{H}_{E})\), the inequality

$$ H(X|B)+H(Z|E)\geq\log\frac{1}{c(X,Z)} $$
(21)

holds, where, \(c(X,Z)=\max_{jk}\parallel\sqrt{X_{j}}\sqrt{Z_{k}}\parallel_{\infty}^{2}\), and {X j } and {Z k } are the elements of corresponding POVM measurements. Moreover, for the mutually unbiased basis X and Z, the Eq. (21) equation can be simplified into

$$ H(X|B)+H(Z|E)\geq1 $$
(22)

Eve’s attack has no effect on the local measurement performed by Alice because of the no-signaling theorem. Thus, the equality

$$ H(Z)=1 $$
(23)

holds. Combining both Eq. (22) and Eq. (23), we can compute an upper bound for the mutual information between Alice and Eve

$$ I(Z; E)=H(Z)-H(Z|E)\leq H(X|B) $$
(24)

It is shown that the above mutual information I(Z;E) will vanish when the uncertainty H(X|B) approaches zero. Thus, what Eve has got is totally disentangled from Bob’s system. In a word, any outside attack will be detected with a non-zero probability.

In addition, for a practical quantum channel, there are noise and loss which will threaten the security of quantum communication since Eve can hide her eavesdropping in the noise. Therefore, a security problem for this scheme implementing in an imperfect quantum channel seems to arise. Fortunately, even for a noise channel, with the help of quantum error correction [29–31], and a quantum repeater technique containing entanglement purification [32], and quantum privacy amplification [33, 34], our scheme can also be acted securely. Of course, this methods of security analysis can be also utilized for security analysis of other quantum communication schemes.

The security of AQIS of an arbitrary N-qubit state is the same as the two-qubit case. In a word, our scheme is secure against participant attack and outside attack.

5 Conclusion and Discussion

In this manuscript, a novel scheme is investigated for AQIS of an arbitrary N-qubit state. Instead of multi-qubit entangled states, the maximally entangled states, which are made up of a three-qubit GHZ-like entangled state and (N−1) sets of Bell states, are used as quantum carrier. Same as most existing symmetric QIS schemes, without the help of Charlie, Bob cannot recover the unknown state even though he obtains the measurement results published by Alice, because Bob does not know whether Charlie measure their particles with the Z basis or not. That means, Bob does not know whether his particles still entangle with those controlled by Charlie or not. Thus, the designated recover Bob can reconstruct the unknown N-qubit state with the probability 100 % in principle if he cooperates with the controller Charlie. It is shown that AQIS of an arbitrary N-qubit state can be faithfully realized by performing appropriate BSMs, SMs and LUOs.

For the security of this AQIS scheme, it depends on the process of the secure quantum channel, which is introduced in Ref. [1], by means of the decoy photons technique. However, the ratio of the decoy photons is small and can be ignored in theory. Thus, the intrinsic efficiency for qubits \(\eta_{q}=\frac{q_{u}}{q_{t}}\) in our AQIS scheme approaches 100%, where q u is the number of the useful qubits in AQIS and q t is the number of qubits transmitted.

In addition, from the point of view of information theory, Cabello [35] proposed a definition of efficiency of a QKD scheme,

$$ \eta=\frac{b_s}{q_t+b_t} $$
(25)

where b s , q t and b t are the number of bits in the raw key, the qubits transmitted, and the total classical bits exchanged between the participants in the quantum communication, respectively. Here we exploited the definition, and the total efficiency for AQIS can be calculated as follows,

$$ \eta_t=\frac{q_s}{q_t+b_t} $$
(26)

where q s is the number of qubits in an unknown quantum state (the secret), q t and b t are described as the above. In our AQIS scheme for sharing an arbitrary N-qubit state with two agents, q s =N, q t =N+1, and b t =2N+1, so \(\eta_{t}=\frac{q_{s}}{q_{t}+b_{t}}=\frac{N}{3N+2}\), which is the maximal value for AQIS theoretically. However, in Ref. [15], for sharing an arbitrary N-qubit state with two agents, q s =N, q t =2N, and b t =3N, so \(\eta_{t}=\frac{q_{s}}{q_{t}+b_{t}}=\frac{1}{5}\), which is lower than that of our scheme (N≥2). Moreover, in our scheme, when finishing one qubit state the principle is the same as Yang et al.’ scheme [14], in other words, we perfectly generalizes Yang et al.’ scheme by asymmetrically distributing the particles among those participants.

In summary, we have presented an asymmetric QIS scheme of an arbitrary N-qubit state with the maximally entangled states, which are made up of a three-qubit entangled GHZ-like state and (N−1) sets of Bell states. It is shown that the proposed AQIS scheme can be faithfully realized by performing appropriate BSMs, Z basis measurement and LUOs, rather than multi-qubit entanglement or multi-particle joint measurements, which make it more convenient in a practical application than some previous schemes. Furthermore, its intrinsic efficiency for qubits approaches 100 %, and the total efficiency really approaches the maximal value, which is higher than those of some previous symmetric quantum information splitting schemes. Finally, the proposed AQIS scheme can be proven information-theoretically secure from the views of participant attack and outside attack in detail. We mainly adopt the following two strategies: the decoy photons technique and estimating the mutual information via entropic uncertainty principle.

Finally we hope that our scheme can be realized experimentally for the N-qubit case. Working along an arbitrary multi-qubit by using other typical states as quantum information carrier is under way.