Abstract
Two qubits coupled by integral spin object are studied in the semi-classical limit of interaction intermediary. It is shown that initial entanglement of qubits becomes more robust when mediated by semi-classical interaction and does not decay below certain value at a given time. The statements are supported by numerical averaging with respect to a set of randomly chosen initial preparations. There are evidences that such a robustness holds true also for different types of quantum correlations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Entanglement [1] is one of these phenomena which are peculiar for quantum world and seem to be absent in classical limit. There are various, often highly sophisticated, techniques of producing entangled states of bi-partite systems. Entanglement can be created via non-local interaction of two parties. Such interaction can be direct, typically described by suitable tensor product term of operators acting on states of parties incorporated in Hamiltonian. Such a modelling is suitable for systems which are ‘not very far away’ from each other. In the case when entanglement of separate (non-proximal) parties is desired one can adapt indirect interaction, caused e.g. by an environment mediating information between parties or by other systems such as cavity mode or wave guide in quantum optics [2–6]. Here we focus our attention on a case of indirect interaction via quantum object (agent) which serves as a intermediary.
We consider here tri-partite setting: two qubits, which entanglement is going to be studied, coupled via intermediary which properties affect entanglement of qubits. It seems to be intuitively clear, that in the classical limit of an intermediary, the qubits in initially separable state are less likely to entangle in time in comparison with deeply quantum regime of the intermediary. In this paper we analyze opposite and probably less intuitive problem: does initial entanglement become more robust against interaction caused by semi-classical intermediary? We present affirmative answer to that question. Entangled systems, when coupled via semi-classical agent, disentangle less likely in comparison with the case of deeply quantum interaction. We show that entanglement of two qubits does not decay below certain value for a given time of running evolution provided that the intermediary is ‘sufficiently classical’. In other words the qubits does not disentangle via semi-classical interaction. We also present evidences that such a property holds true for different types of quantum correlations. Results of this paper shed light on the general properties of quantum-classical hybrid systems [7–12] which has recently been studied also in the context of quantum correlations [13, 14].
The paper is organized as follows: first two section we devote to the entanglement dynamics in (semi) classical limit of interaction mediating agent. Next we consider different type of correlations qualified by quantum discord. We attempt to unify and generalize the results based upon numerical evidences in conjectural statements concerning properties of quantum correlations in classical regime of interaction.
2 Entanglement Dynamics
Time evolution of the qubit–agent–qubit system, in the assumed absence of dissipation, is unitary (ħ=1)
with the Hamiltonian
describing two identical qubits A,B interacting via quantum agent labelled by M. In this work we also assume that the intermediary is given by integral j-spin system:
This choice is motivated by well established ‘classical limit’ j→∞ of such systems studied e.g. in the context of quantum chaos [15, 16] or kicked entanglement dynamics [17]. It is known that in the limit of large (integral) j dynamics of spin systems can be effectively described by classical maps and hence observables of such systems become classical [15]. In that sense large j spins, although described in fully quantum mechanical fashion, can mimic behavior of classical system and hence become natural candidates for components of composites mimicking quantum-classical hybrids.
Qubit–qubit state is obtained by partial tracing of ϱ(t) with respect to intermediary i.e. ρ AB (t)=Tr M ϱ(t). Its entanglement can be quantified by the concurrence [1]
where λ i are eigenvalues (λ 1 is the largest) of a matrix
Quantum entanglement of two qubits is in general a non-monotonic function of time unless the qubit–qubit interaction is a local operation and the time evolution remains Markovian [18]. It is well known that neither Local Operations nor Classical Communication can increase quantum entanglement [1]. However, the interaction modeled in Eq. (2) is clearly non-local and gives no obvious limitation for entanglement behavior.
A natural starting point is to consider how, and if, entanglement of two qubits appears when the interaction mediating agent approaches its semi-classical limit. We start with a qubit–agent–qubit system prepared in separable state:
This choice seems to be arbitrary but it exhibits generic features of qubit–qubit entanglement. For initial preparation (6) we evolve qubit–agent–qubit system according to Eq. (1) with the Hamiltonian (2). At given time instant we calculate qubit–qubit reduced density matrix and qualify its entanglement in terms of the concurrence (4). Numerical calculations are performed with help of QuTip, Python-based computational toolbox [19, 20]. The results are presented in Fig. 1. With increasing j (what corresponds to classical limit [16, 17]) entanglement of qubits appears less likely. This result is intuitively acceptable: quantum entanglement does not emerge in quantum objects placed in (coupled by) classical world.
Entanglement, quantified by the concurrence, of two qubits coupled by integral spin j intermediary. Initial state of the tri-partite system is separable Eq. (6)
However, the aim of our work is to consider a problem which is less intuitive: what happens if the qubits are initially entangled and the intermediary becomes (semi) classical? Does quantum entanglement decay more or less likely for the interaction mediating agent with larger j? A motivation for our work is the following: we investigate how the ‘classicality’ of the mediating agent affects the drain of correlations shared by composite systems.
Let us consider the following preparation:
with maximally entangled qubit–qubit part of the state separated from the intermediary. At the beginning we assume two specific examples of |E i 〉 AB :
Again, this choice exhibits generic features of the model. All the results are qualitatively independent on the particular choice of maximally entangled qubit–qubit state and the state of the intermediary. The results presented in Fig. 2 exhibit the ‘stabilizing character’ of the semi-classical interaction: the larger j the more entangled remain the qubits. Let us notice that for sufficiently large j characteristics of the concurrence corresponding to different j become ‘ordered’ with respect to increasing j and the entanglement does not decay below certain value for a given time of evolution. Let us notice that this time increases with increasing j. The time of evolution in all figures is chosen approximately an order of magnitude larger than characteristic time related to qubit energy in Eq. (2). Let us also notice that as long as the time evolution of the total system is unitary one expects periodic behavior typical for finite quantum systems. However, one can also expect that with increasing j periodicity occurs for larger and larger time scales. Qubit–qubit A−B system given by Eq. (2) can formally be considered as an open system coupled to (non-thermal) ‘environment’ M. As this environment is finite it cannot cause truly irreversible properties of qubits’ pair. Nevertheless, for sufficiently large M (with j→∞) one can consider certain qubit–qubit characteristics, inferred form A−B reduced dynamics, as effectively decaying.
Entanglement, quantified by the concurrence, of two qubits coupled by integral spin j intermediary. Initial state of the tri-partite system is given by Eq. (7) with qubit–qubit part |E 1〉 AB (upper panel) and |E 2〉 AB (lower panel)
One can obviously doubt if the results presented in Fig. 2 are independent on the specific choice of the initial state (7). However, there is natural evidence confirming generic character of entanglement behavior presented in Fig. 2. In the following we present entanglement dynamics averaged with respect to 103 randomly chosen initial states of the form:
where the qubit–qubit part of the initial preparation (10) reads as follows [21, 22]:
where ξ∈[0,π/2] and ϵ 1,2∈[0,2π) are independent uniformly distributed random numbers. In other words concurrence becomes a (classical) random variable with a given uniform probability distribution. In Fig. 3 we present two quantifiers of this random variable: mean (expected) value \(\langle\!\langle\mathcal{C}\rangle\!\rangle\) (upper panel) and its variance \(\langle\!\langle\mathcal{C}^{2}\rangle\!\rangle-\langle\!\langle\mathcal{C}\rangle\!\rangle^{2}\) (lower panel) indicating relation of exceptional to typical states. All the features of ‘expected value’ of the entanglement in Fig. 3 qualitatively agree with these presented in Fig. 2.
Upper panel: Entanglement, quantified by the concurrence, of two qubits coupled by integral spin j intermediary averaged with respect to 103 initial states of the tri-partite system given by Eq. (10). Lower panel: Variance of the quantity presented in the upper panel
3 Dissipation
Environment can change significantly properties of open quantum systems. In this section we check if the entanglement robustness reported in previous section is also present in quantum systems weakly disturbed by the environment. There are various inequivalent ways of describing open quantum systems [23, 24]. Here we consider the simplest case: Markovian dissipation expressed in terms of Lindblad dissipators in the equation of motion [23, 25]. Such description is reliable for quantum systems weakly coupled to the environment [25]. As our further discussion is of qualitative character, instead of rigorous Davies-type treatment [25], we adapt simple phenomenological modelling [23]. Let us consider the simplest case of quantum evolution governed by Lindblad master equation [25] with a single ‘collapse operator’ C and the damping amplitude ε:
We consider two separate cases. In the first case collapse operator C=C 1 acts on the intermediary M, in the second case (for C=C 2) dissipation affects directly one of the qubits:
Assumed form of dissipation is not only simple but also local i.e. it cannot increase entanglement of any parties of the A−M−B triple. Such a dissipation, contrary to many known examples [26–28], does not play any constructive role in entanglement dynamics. The model of dissipation considered here is general enough to incorporate energy exchange between A−M−B system and the environment and hence, contrary to e.g. pure dephasing [18] or driven non-equilibrium systems, entanglement disappears for asymptotically large time. Although physical origin for C 1 and C 2 can be different an impact of both types of dissipation on entanglement of qubits A,B is, as presented in Fig. 4, qualitatively the same. For weak dissipation conclusions of previous section remain valid. In the presence of Markovian dissipation entanglement of qubits becomes more robust with increasing j but the time scale when the concurrence does not decay below certain value becomes shorter for ε>0. Let us notice that, as presented in Fig. 5, qualitatively similar behavior occurs when the single-qubit terms in the system Hamiltonian Eq. (2) are different e.g. when we replace σ z→σ x for either A or B. As an example we consider Hamiltonian
which breaks additional symmetry present imposed in the original system Eq. (2) which, due to ‘dynamical decoupling’ of qubits in the absence of their interaction is responsible for deceleration of the entanglement decay. In the presence of this decoupling, i.e. for the system described by Eq. (2), it is easier to identify the term responsible for changes in initial entanglement in the qubit–qubit subsystem.
Entanglement, quantified by the concurrence, of two qubits coupled by integral spin j intermediary in the presence of Markovian dissipation Eq. (12). Initial state of the tri-partite system is given by Eq. (7) with qubit–qubit part |E 2〉 AB . The dissipator (13) given by C 1 (upper panel) and C 2 (lower panel) and ε=1/50
4 Beyond Entanglement: Quantum Discord
Quantum entanglement, although best known, is not the only (effective for applications) quantifier of quantum correlations. There are other types of correlations which are essentially non-classical and which can exist even in the absence of entanglement [29]. It is natural to ask if robustness of the entanglement in the classical limit of intermediary reported here holds also for other types of quantum correlation between qubits. Unfortunately, mathematical setting for entanglement (incorporating e.g. tensor products of state spaces) has not been uniquely established so far for general quantum correlations which remain, to some extent, ‘definition-dependent’. We limit our consideration to a single type of correlation: the one qualified by quantum discord. It is a very specific but also very popular measure of correlations. Its properties are summarized in the review paper [29] (equipped there with a comprehensive list of references). Let us stress that, in general, quantum discord is neither the only nor always the best quantifier of quantum correlation [29]. Nevertheless, quantum correlations quantified by the quantum discord can open new avenues for quantum computations and quantum communication schemes [30–33].
For a sake of completeness let us briefly review the simplest case: the bi-qubit system. We consider a composite system consisting of two qubits: A and B. Total correlation, encoded in mutual entropy of A and B, is formulated in terms of a difference between entropies:
where ρ A =Tr B ρ AB and ρ B =Tr A ρ AB . That what is known about A, under the condition that on B was performed a measurement \(\varPi_{j}^{B}\), can be quantified in terms of conditional entropy
which, extremized with respect to all measurements, leads to classical part of total correlations
Remaining part
is the quantum discord [29]. Fortunately, for two qubit systems it is enough to consider in Eq. (19) only projective measurements [29, 34]:
where θ,ϕ is a standard parameterization of a single qubit Bloch sphere.
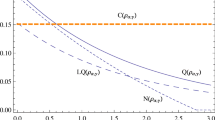
The results presented in Fig. 6 confirm qualitative similarity between time evolution of entanglement quantified by the concurrence and quantum correlations quantified by the discord. The more classical the intermediary is the less likely correlations are formed (upper panel of Fig. 6 and the more robust are the initial correlations (lower panel of Fig. 6. Again, for sufficiently large j quantum discord never decays below certain value for a given time of evolution. We can only conjecture that such a characteristics hold true for any ‘reasonable choice’ of quantum correlation quantifier. Let us notice that such a direct relation between different types of quantum correlations is not always generic even is a simplest case of quantum entanglement and quantum discord [35, 36].
5 Summary
In this paper we analyze entanglement dynamics of qubits coupled via integral j-spin intermediary. We confirm an intuitive expectation that for large j, corresponding to interaction agent operating in semi-classical regime, the concurrence of initially non-entangled qubits remains small in time. We also consider less intuitive problem of initially maximally entangled qubits. We show that initial entanglement is more robust for intermediaries with large j. For sufficiently large j entanglement never decays below certain value for a given time of evolution i.e. the qubits does not disentangle via semi-classical interaction. This is central result of present work. Such behavior is typical in the sense that it holds true for the ‘expected value’ of the concurrence obtained by averaging with respect to a set of randomly chosen initial preparations. It also holds true in the presence of weak Markovian dissipation locally affecting any of the components of the system. Numerical studies of quantum discord suggest a conclusion that this feature is generic for a broad class of different and non-equivalent types of quantum correlations.
In other words, one can say that quantum information qualified here by two types of quantum correlations, shared initially by qubits A and B drain into the system M coupled to qubits slower provided that M is (semi)classical. The coupling via classical mediating agent causes not only slower correlation but also slower discorrelation of the qubits in comparison to the case when the mediating agent is fully quantum mechanical.
Finally, let us mention that results of this paper not only touch general properties of quantum-classical hybrid systems [7–14] but also can be of potential practical value for nanoscience operating on the border of classical and quantum world [37–39] motivated by the role played by quantum entanglement in quantum information processing [40].
References
Horodecki, R., et al.: Rev. Mod. Phys. 81, 565 (2009)
Zheng, H., Baranger, H.U.: Phys. Rev. Lett. 110, 113601 (2013)
Gonzalez-Tudela, A., et al.: Phys. Rev. Lett. 106, 020501 (2011)
Seok, H., et al.: Phys. Rev. A 86, 063829 (2012)
Fei, J., et al.: Phys. Rev. A 86, 062328 (2012)
Zipper, E., et al.: J. Phys. Condens. Matter 20, 275219 (2008)
Peres, A., Terno, D.R.: Phys. Rev. A 63, 022101 (2001)
Chua, A.J.K., et al.: Phys. Rev. A 85, 022110 (2012)
Elze, H.-.-T.: Phys. Rev. A 85, 052109 (2012)
Buric, N., et al.: Phys. Rev. A 86, 034104 (2012)
Radonjic, M., et al.: Phys. Rev. A 85, 064101 (2012)
Barceló, C., et al.: Phys. Rev. A 86, 042120 (2012)
Matzkin, A.: Phys. Rev. A 84, 022111 (2011)
Durt, T., Debierre, V.: Int. J. Mod. Phys. B 27, 1345014 (2013)
Haake, F.: Quantum Signatures of Chaos. Springer, Berlin (1991)
Haake, F., et al.: Z. Phys. B 65, 381 (1987)
Demkowicz–Dobrzeński, R., Kuś, M.: Phys. Rev. E 70, 066216 (2004)
Dajka, J., et al.: Phys. Rev. A 77, 042316 (2008)
Johansson, J.R., et al.: Comput. Phys. Commun. 183, 1760 (2012)
Johansson, J.R., et al.: Comput. Phys. Commun. 184, 1234 (2013)
Kuś, M., Życzkowski, K.: Phys. Rev. A 63, 032307 (2001)
Życzkowski, K., et al.: Phys. Rev. A 65, 012101 (2001)
Breuer, H.-.-P., Pertuccione, F.: The Theory of Open Quantum Systems. Oxford University Press, Oxford (2003)
Weiss, U.: Quantum Dissipative Systems. World Scientific, Singapore (1999)
Alicki, R., Lendi, K.: Quantum Dynamical Semigroups and Applications. Lect. Notes Phys., vol. 717. Springer, Berlin (2007)
Benatti, F., et al.: Phys. Rev. Lett. 91, 070402 (2003)
Benatti, F., Floreanini, R.: J. Phys. A, Math. Gen. 39, 2689 (2006)
Lendi, K., van Wonderen, A.J.: J. Phys. A, Math. Gen. 40, 279 (2007)
Modi, K., et al.: Rev. Mod. Phys. 84, 1655 (2012)
Datta, A., et al.: Phys. Rev. A 72, 042316 (2005)
Madhok, V., Datta, A.: Phys. Rev. A 83, 032323 (2011)
Piani, M., et al.: Phys. Rev. Lett. 100, 090502 (2008)
Dakic, B., et al.: Nat. Phys. 8, 666 (2012)
Hamieh, S., et al.: Phys. Rev. A 70, 052325 (2004)
Dajka, J., et al.: J. Phys. A, Math. Theor. 45, 485306 (2012)
Dajka, J., Łuczka, J.: Phys. Rev. A 87, 022301 (2013)
Kim, H., Kapral, R.: J. Chem. Phys. 122, 214105 (2005)
Bugajski, S.: Mol. Phys. Rep. 11, 161 (1995)
Abdallah, N.B., Tang, S.: Math. Methods Appl. Sci. 27, 643 (2004)
Audretsch, J.: Entangled Systems. New Directions in Quantum Physics. Wiley, Weinheim (2007)
Acknowledgements
The work has been supported by the NCN Grant N202 052940.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Dajka, J. Disentanglement of Qubits in Classical Limit of Interaction. Int J Theor Phys 53, 870–880 (2014). https://doi.org/10.1007/s10773-013-1876-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-013-1876-9