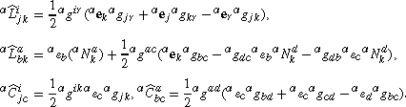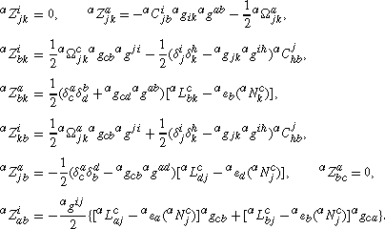Skip to main content
SpringerLink
Log in

Fractional Dynamics from Einstein Gravity, General Solutions, and Black Holes

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

We study the fractional gravity for spacetimes with non-integer fractional derivatives. Our constructions are based on a formalism with the fractional Caputo derivative and integral calculus adapted to nonholonomic distributions. This allows us to define a fractional spacetime geometry with fundamental geometric/physical objects and a generalized tensor calculus all being similar to respective integer dimension constructions. Such models of fractional gravity mimic the Einstein gravity theory and various Lagrange–Finsler and Hamilton–Cartan generalizations in nonholonomic variables. The approach suggests a number of new implications for gravity and matter field theories with singular, stochastic, kinetic, fractal, memory etc processes. We prove that the fractional gravitational field equations can be integrated in very general forms following the anholonomic deformation method for constructing exact solutions. Finally, we study some examples of fractional black hole solutions, ellipsoid gravitational configurations and imbedding of such objects in solitonic backgrounds.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. We follow the system of notations with left abstract labels explained in Refs. [45, 52], see also next section.

  2. In “integer” differential geometry, there are used also equivalent terms like anholonomic and non-integrable manifolds. A nonholonomic manifold of integer dimension is defined by a pair \((\mathbf{V},\mathcal{N})\), where V is a manifold and \(\mathcal{N}\) is a nonintegrable distribution on V, see the next section for a generalization to non-integer dimensions.

  3. The left Riemann–Liouville (RL) derivative is

    $${}_{_{1}x}\overset{\alpha}{\partial}_{x}f(x):=\frac{1}{\Gamma (s-\alpha)}\biggl( \frac{\partial}{\partial x}\biggr) ^{s}\int_{_{1}x}^{x}(x-x^{\prime})^{s-\alpha-1}f(x^{\prime})\,dx^{\prime},$$

    where Γ is the Euler’s gamma function. The left fractional Liouville derivative of order α, where s−1<α<s, with respect to coordinate x is \(\overset{\alpha }{\partial }_{x}f(x):=\lim_{_{1}x\rightarrow -\infty }{}_{\ _{1}x}\overset{\alpha }{\partial }_{x}f(x)\).

    The right RL derivative is \({}_{x}\overset{\alpha }{\partial }_{_{2}x}f(x):=\frac{1}{\Gamma (s-\alpha )}( -\frac{\partial }{\partial x}) ^{s}\int_{x}^{_{2}x}(x^{\prime }-x)^{s-\alpha -1}f(x^{\prime })\,dx^{\prime }\). The right fractional Liouville derivative is \({}_{x}\overset{\alpha }{\partial }f(x^{k}):=\lim_{_{2}x\rightarrow \infty }{}_{\ x}\overset{\alpha }{\partial }_{_{2}x}f(x)\).

    The fractional RL derivative of a constant C is not zero but, for instance, \({}_{_{1}x}\overset{\alpha}{\partial}_{x}C=C\frac{(x-_{1}x)^{-\alpha}}{\Gamma(1-\alpha)}\). Integro-differential constructions based only on such derivatives seem to be very cumbersome and has a number of properties which are very different from similar ones for the integer calculus.

  4. This follows from the fundamental theorem of fractional calculus [35]

  5. For the “integer” calculus, we use as local coordinate co-bases/-frames the differentials dx j=(dx j)α=1. For 0<α<1 we have dx=(dx)1−α(dx)α. The “fractional” symbol (dx j)α, related to \(\overset{\alpha}{d}x^{j}\), is used instead of dx i for elaborating a co-vector/differential form calculus, see below the formula (6).

  6. We to not follow alternative constructions with RL fractional derivative [1, 17] because in that direction it is not clear how to prove integrability of the RL-fractional Einstein equations.

  7. The N-adapted coefficients are explicitly determined by the (13),

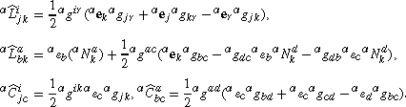
    We can verify that introducing above formulas into (15) we obtain that \(\widehat{T}_{\ jk}^{i}=0\) and \(\widehat{T}_{\ bc}^{a}=0\), but \(\widehat{T}_{\ ja}^{i},\widehat{T}_{\ ji}^{a}\) and \(\widehat{T}_{\ bi}^{a}\) are not zero, and that the metricity conditions are satisfied in component form.

  8. The N-adapted coefficients of distortion tensor \(Z_{\ \alpha\beta }^{\gamma}\) are computed

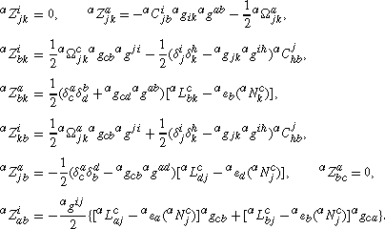
  9. Such transforms of geometric objects (with deformations of the frame, metric, connections and other fundamental geometric structures) are more general than those considered for the Cartan’s moving frame method, when the geometric objects are re-defined equivalently with respect to necessary systems of reference.

  10. ε is an eccentricity because, for integer configurations, the coefficient \(h_{4}=b^{2}=\eta_{4}(\xi,\vartheta ,\varphi,\bar{\theta})\varpi^{2}(\xi)\) becomes zero for data (53) if \(r_{+}\simeq{2\mu_{0}}/[{1+\varepsilon\frac {q_{0}(r)}{4\mu ^{2}}\sin(\omega_{0}\varphi+\varphi_{0})}]\); this is the “parametric” equation for an ellipse r +(φ) for any fixed values \(\frac{q_{0}(r)}{4\mu^{2}},\omega_{0},\varphi_{0}\) and μ 0.

  11. A function η can be a solution of any three dimensional solitonic and/or other nonlinear wave equations

References

  1. Albu, I.D., Neamţu, M., Opriş, D.: The geometry of fractional osculator bundle of higher order and applications. arXiv:0709.2000

  2. Baleanu, D.: Fractional Hamilton formalism with Caputo’s derivative. arXiv:math-ph/0612025

  3. Baleanu, D., Muslih, S.: Phys. Scr. 72, 119 (2005)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  4. Baleanu, D., Trujillo, J.J.: Nonlinear Dyn. 52, 331 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Baleanu, D., Vacaru, S.: J. Math. Phys. 52, 053514 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  6. Baleanu, D., Vacaru, S.: Nonlinear Dyn. 64, 365 (2011)

    Article  MathSciNet  Google Scholar 

  7. Baleanu, D., Vacaru, S.: Int. J. Theor. Phys. 50, 233 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Boleantu, M., Opris, D.: Fractional dynamical systems and applications in mechanics and economics. arXiv:0709.1681 [math.DS]

  9. Carreras, B.A., Lynch, V.E., Zaslavsky, G.M.: Phys. Plasmas 8, 5096 (2001)

    Article  ADS  Google Scholar 

  10. Carpinteri, A., Mainardi, F.: Fractals and Fractional Calculus in Continuous Mechanics. Springer, New York (1997)

    Google Scholar 

  11. Herrmann, R.: Gauge invariance in fractional field theories. arXiv:0708.2262

  12. Hilfer, R. (ed.): Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    MATH  Google Scholar 

  13. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    Google Scholar 

  14. Laskin, N.: Phys. Lett. A 268, 298 (2000)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  15. Laskin, N.: Phys. Rev. E 66, 056108 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  16. Li, M.-F., Ren, J.-R., Zhu, T.: Series expansion in fractional calculus and fractional differential equations. arXiv:0910.4819

  17. Munkhammar, J.: Riemann–Liouville fractional Einstein field equations. arXiv:1003.4981

  18. Muslih, S.: A formulation of Noether’s theorem for fractional classical fields. arXiv:1003.0653

  19. Muslich, S., Agrawal, O., Baleanu, D.: J. Phys. A, Math. Theor. 43, 055203 (2010)

    Article  ADS  Google Scholar 

  20. Naber, M.: J. Math. Phys. 45, 3339 (2004)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  21. El-Naulsi, A.: Chaos, Solitons and. Fractals 42, 2924 (2009)

    Google Scholar 

  22. El-Nabulsi, A.: Rom. Rep. Phys. 59, 763 (2007)

    Google Scholar 

  23. Nishimoto, K.: Fractional Calculus: Integrations and Differentiations of Arbitrary Order. University of New Haven Press, New Haven (1989)

    MATH  Google Scholar 

  24. Oldham, K.B., Spanier, J.: The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Academic Press, San Diego (1974)

    MATH  Google Scholar 

  25. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  26. Raspini, A.: Phys. Scr. 64, 202 (2001)

    Article  Google Scholar 

  27. Riewe, F.: Phys. Rev. E 55, 3581 (1997)

    Article  MathSciNet  ADS  Google Scholar 

  28. Ren, F.-Y., Qiu, W.-Y., Liang, J.-R., Wang, X.-T.: Phys. Lett. A 288, 79 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  29. Roberts, M.D.: Fractional derivative cosmology. arXiv:0909.1171

  30. Ross, B.: Lect. Notes Math. 457, 1 (1975)

    Article  Google Scholar 

  31. Tarasov, V.E.: Chaos 15, 023102 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  32. Tarasov, V.E.: Phys. Plasmas 13, 052107 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  33. Tarasov, V.E.: Celest. Mech. Dyn. Astron. 19, 1 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  34. Tarasov, V.E.: J. Phys. A 39, 8409 (2006)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  35. Tarasov, V.E.: Ann. Phys. 323, 2756 (2008)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  36. Tarasov, V.E., Zaslavsky, G.M.: Physica A 368, 399 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  37. Vacaru, S.: J. Math. Phys. 37, 508 (1996)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  38. Vacaru, S.: Ann. Phys. 256, 39 (1997)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  39. Vacaru, S.: Ann. Phys. 290, 83 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  40. Vacaru, S.: Int. J. Mod. Phys. D 12, 461 (2003)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  41. Vacaru, S.: J. Math. Phys. 46, 042503 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  42. Vacaru, S.: J. Math. Phys. 47, 093504 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  43. Vacaru, S.: J. Math. Phys. 48, 123509 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  44. Vacaru, S.: Phys. Lett. A 372, 2949 (2008)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  45. Vacaru, S.: Int. J. Geom. Methods. Mod. Phys. 5, 473 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  46. Vacaru, S.: J. Math. Phys. 49, 043504 (2008)

    Article  MathSciNet  ADS  Google Scholar 

  47. Vacaru, S.: Int. J. Geom. Methods. Mod. Phys. 6, 873 (2009)

    MathSciNet  MATH  Google Scholar 

  48. Vacaru, S.: J. Math. Phys. 50, 073503 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  49. Vacaru, S.: Acta Appl. Math. 110, 73 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  50. Vacaru, S.: Int. J. Theor. Phys. 49, 884 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  51. Vacaru, S.: Class. Quantum Gravity 27, 105003 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  52. Vacaru, S.: Fractional Nonholonomic Ricci Flows. arXiv:1004.0628

  53. Vacaru, S., Dehnen, H.: Gen. Relativ. Gravit. 35, 209 (2003)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  54. Vacaru, S., Popa, F.C.: Class. Quantum Gravity 18, 4921 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  55. Vacaru, S., Singleton, D.: Class. Quantum Gravity 19, 3583 (2002)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  56. Vacaru, S., Tintareanu-Mircea, O.: Nucl. Phys. B 626, 239 (2002)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  57. Zaslavsky, G.M.: Hamiltonian Chaos and Fractional Dynamics. Oxford University Press, Oxford (2005)

    MATH  Google Scholar 

  58. Zaslavsky, G.M., Edelman, M.A.: Physica D 193, 128 (2004)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  59. Zavada, P.: J. Appl. Math. 2, 163 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Science Department, University “Al. I. Cuza” Iaşi, 54 Lascar Catargi Street, Iaşi, 700107, Romania

    Sergiu I. Vacaru

Authors
  1. Sergiu I. Vacaru
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sergiu I. Vacaru.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vacaru, S.I. Fractional Dynamics from Einstein Gravity, General Solutions, and Black Holes. Int J Theor Phys 51, 1338–1359 (2012). https://doi.org/10.1007/s10773-011-1010-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-011-1010-9

Keywords

Search

Navigation