Skip to main content
SpringerLink
Log in

Hamiltonian Structure of Fractional First Order Lagrangian

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

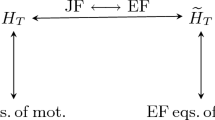
In this paper, we show that the fractional constraint Hamiltonian formulation, using Dirac brackets, leads to the same equations as those obtained from fractional Euler-Lagrange equations. Furthermore, the fractional Faddeev-Jackiw formalism was constructed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Agrawal, O.P.: Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 272, 368–379 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  2. Atanackovic, T.M., Konjik, S., Pilipovic, S., et al.: Variational problems with fractional derivatives: Invariance conditions and Nother’s theorem. Nonlinear Anal. 71, 1504–1517 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  3. Baleanu, D.: Fractional Hamiltonian analysis of irregular systems. Signal Process. 86, 2632–2636 (2006)

    Article  MATH  Google Scholar 

  4. Baleanu, D., Avkar, T.: Lagrangians with linear velocities within Riemann-Liouville fractional derivatives. Il Nuovo Cimento B 119, 73–79 (2004)

    ADS  Google Scholar 

  5. Baleanu, D., Agrawal, O.P.: Fractional Hamilton formalism within Caputo’s derivative. Czech. J. Phys. 56, 1087–1092 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  6. Baleanu, D., Muslih, S.I.: Lagrangian formulation of classical fields within Riemann-Liouville fractional derivatives. Phys. Scr. 72, 119–121 (2005)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  7. Baleanu, D., Muslih, S., Tas, K.: Fractional Hamiltonian analysis of higher order derivatives systems. J. Math. Phys. 47, 103503 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  8. Baleanu, D., Golmankhaneh, K.A., Golmankhaneh, K.A.: The dual action of fractional multi time Hamilton equations. Int. J. Theor. Phys. 48, 2558–2569 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  9. Baleanu, D., Golmankhaneh, K.A., Golmankhaneh, K.A., Nigmatullin, R.R.: Newtonian law with memory. Nonlinear Dyn. (2009). doi:10.1007/s11071-009-9581-1

    Google Scholar 

  10. Baleanu, D., Golmankhaneh, K.A., Nigmatullin, R.R., Golmankhaneh, K.A.: Fractional Newtonian mechanics. Cent. Eur. J. Phys. (2009). doi:10.2478/s11534-009-0085-x

    Google Scholar 

  11. Baleanu, D., Golmankhaneh, A.K., Golmankhaneh, A.K.: Fractional Nambu mechanics. Int. J. Theor. Phys. 48, 1044 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  12. Faddeev, L., Jackiw, R.: Hamiltonian reduction of unconstrained and constrained systems. Phys. Rev. Lett. 60, 1692–1694 (1988)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  13. Golmankhaneh, K.A.: Relativistic scalar fields for non-conservative system. Phys. Scr. (2009). doi:10.1088/0031-8949/2009/T136/014008

    Google Scholar 

  14. Gorenflo, R., Mainardi, F.: Fractional Calculus: Integral and Differential Equations of Fractional Orders, Fractals and Fractional Calculus in Continuum Mechanics. Springer, New York (1997)

    Google Scholar 

  15. Gastao, S.F.F., Delfim, F.M.T.: A formulation of Noether’s theorem for fractional problems of calculus of variations. J. Math. Anal. Appl. 334, 834–846 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  16. Henneaux, M., Teitelboim, C.: Quantization of Gauge Systems. Princeton University Press, Princeton (1992)

    MATH  Google Scholar 

  17. Hilfer, R.: Application of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Google Scholar 

  18. Kilbas, A.A., Srivastava, H.H., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  19. Kishore, B.: Lecture Notes in Physics. Springer, Berlin (1983)

    Google Scholar 

  20. Klimek, K.: Fractional sequential mechanics-models with symmetric fractional derivative. Czech. J. Phys. 51, 1348–1354 (2001)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  21. Klimek, K.: Lagrangean and Hamiltonian fractional sequential mechanics. Czech. J. Phys. 52, 1247–1253 (2002)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  22. Kulshreshtha, D.S., Müller-Kirsten, H.J.W.: Faddeev-Jackiw quantization of self-dual fields. Phys. Rev. D 45, 393–397 (1992)

    Article  MathSciNet  ADS  Google Scholar 

  23. Laskin, N.: Fractional quantum mechanics. Phys. Rev. E 62, 3135–3145 (2000)

    Article  ADS  Google Scholar 

  24. Miller, K.S., Ross, B.: An Introduction to the Fractional Integrals and Derivatives-Theory and Application. Wiley, New York (1993)

    Google Scholar 

  25. Muslih, S.I., Baleanu, D.: Formulation of Hamiltonian Equations for Fractional Variational Problems. Czech. J. Phys. 55, 633–642 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  26. Muslih, S.I., Baleanu, D.: Hamiltonian formulation of systems with linear velocities within Riemann-Liouville fractional derivatives. J. Math. Anal. Appl. 304, 599–606 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  27. Muslih, S.I., El-Zalan, H.A., Rabei, E.M.: Hamilton-Jacobi quantization of singular Lagrangians with linear velocities. Int. J. Theor. Phys. 44, 1271–1279 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  28. Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)

    MATH  Google Scholar 

  29. Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)

    MATH  Google Scholar 

  30. Riewe, F.: Nonconservative Lagrangian and Hamiltonian mechanics. Phys. Rev. E 53, 1890–1899 (1996)

    Article  MathSciNet  ADS  Google Scholar 

  31. Riewe, F.: Mechanics with fractional derivatives. Phys. Rev. E 55, 3581–3592 (1997)

    Article  MathSciNet  ADS  Google Scholar 

  32. Rabei, E.M., Nawafleh, K.I., Hiijawi, R.S., Muslih, S.I., Baleanu, D.: The Hamilton formalism with fractional derivatives. J. Math. Anal. Appl. 327, 891–897 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  33. Rabei, E.M., Almayteh, I., Muslih, S.I., Baleanu, D.: Hamilton-Jacobi formulation of systems with Caputo’s fractional derivative. Phys. Scr. 77, 015101 (2007)

    Article  Google Scholar 

  34. Rabei, E., Tarawneh, D.M., Muslih, S.I., Baleanu, D.: Heisenberg’s equations of motion with fractional derivatives. J. Vibr. Control 13, 239–247 (2007)

    MathSciNet  Google Scholar 

  35. Rabei, E.M., Altarazi, I.M.A., Muslih, S.I., Baleanu, D.: Fractional WKB approximation. Nonlinear Dyn. 57(1–2), 171–175 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  36. Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives Theory and Applications. Gordon and Breach, New York (1993)

    MATH  Google Scholar 

  37. Sundermeyer, K.: Constrained Dynamics. Lecture Notes in Physics, vol. 169. Springer, New York (1982)

    MATH  Google Scholar 

  38. Tarasov, V.E.: Fractional variation for dynamical systems: Hamilton and Lagrange approaches. J. Phys. 39(26), 8409–8425 (2006)

    MATH  MathSciNet  ADS  Google Scholar 

  39. Tarasov, V.E., Zaslavsky, G.M.: Fractional Ginzburg-Landau equation for fractal media. Physica A 354 (2005)

  40. West, B.J., Bologna, M., Grigolini, P.: Physics of Fractal Operators. Springer, New York (2003)

    Google Scholar 

  41. Zaslavsky, G.M.: Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 371, 461–580 (2002)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  42. Zaslavsky, G.M.: Hamiltonian Chaos and Fractional Dynamics. Oxford University Press, Oxford (2005)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Physics, Islamic Azad University-Uromia Branch, P.O. Box 969, Uromia, Iran

    Ali Khalili Golmankhaneh & Alireza Khalili Golmankhaneh

  2. Department of Physics, University of Pune, Pune, 411007, India

    Alireza Khalili Golmankhaneh

  3. Department of Mathematics and Computer Science, Çankaya University, 06530, Ankara, Turkey

    Dumitru Baleanu

  4. Institute of Space Sciences, P.O. Box MG-23, 76900, Magurele-Bucharest, Romania

    Dumitru Baleanu

  5. Faculty of Physics, University of Bucharest, Bucharest, Romania

    Mihaela Cristina Baleanu

  6. National Mihail Sadoveanu High School, District 2, Bucharest, Romania

    Mihaela Cristina Baleanu

Authors
  1. Ali Khalili Golmankhaneh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alireza Khalili Golmankhaneh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dumitru Baleanu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mihaela Cristina Baleanu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dumitru Baleanu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Golmankhaneh, A.K., Golmankhaneh, A.K., Baleanu, D. et al. Hamiltonian Structure of Fractional First Order Lagrangian. Int J Theor Phys 49, 365–375 (2010). https://doi.org/10.1007/s10773-009-0209-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-009-0209-5

Search

Navigation