Topos-Theoretic Extension of a Modal Interpretation of Quantum Mechanics

Abstract

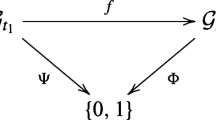
This paper deals with topos-theoretic truth-value valuations of quantum propositions. Concretely, a mathematical framework of a specific type of modal approach is extended to the topos theory, and further, structures of the obtained truth-value valuations are investigated. What is taken up is the modal approach based on a determinate lattice ${\mathfrak{D}}(e,R)$ , which is a sublattice of the lattice ${\mathfrak{L}}$ of all quantum propositions and is determined by a quantum state e and a preferred determinate observable R. Topos-theoretic extension is made in the functor category $\mathbf{Sets}^{\mathcal{C}_{R}}$ of which base category ${\mathcal{C}_{R}}$ is determined by R. Each true atom, which determines truth values, true or false, of all propositions in ${\mathfrak{D}}(e,R)$ , generates also a multi-valued valuation function of which domain and range are ${\mathfrak{L}}$ and a Heyting algebra given by the subobject classifier in $\mathbf{Sets}^{\mathcal{C}_{R}}$ , respectively. All true propositions in ${\mathfrak{D}}(e,R)$ are assigned the top element of the Heyting algebra by the valuation function. False propositions including the null proposition are, however, assigned values larger than the bottom element. This defect can be removed by use of a subobject semi-classifier. Furthermore, in order to treat all possible determinate observables in a unified framework, another valuations are constructed in the functor category $\mathbf{Sets}^{\mathcal{C}}$ . Here, the base category $\mathcal{C}$ includes all ${\mathcal{C}_{R}}$ ’s as subcategories. Although $\mathbf{Sets}^{\mathcal{C}}$ has a structure apparently different from $\mathbf{Sets}^{\mathcal{C}_{R}}$ , a subobject semi-classifier of $\mathbf{Sets}^{\mathcal{C}}$ gives valuations completely equivalent to those in $\mathbf{Sets}^{\mathcal{C}_{R}}$ ’s.