Translation from Three-Valued Quantum Logic to Modal Logic

Abstract

We translate the three-valued quantum logic into modal logic, and prove 3-equivalence between the valuation of the three-valued logic and a kind of Kripke model in regard to this translation. To prove 3-equivalence, we introduce an observable-dependent logic, which is a fragment of the many-valued quantum logic. Compared to the Birkhoff and von Neumann’s quantum logic, some notions about observables, the completeness relation for example, in quantum mechanics can be utilized if the observable-dependent logic is employed.

1 Introduction

It has long been asserted that quantum logic is non-classical since Birkhoff and von Neumann’s memorable paper [2], where the distributive law of logical connectives is no more valid (see [4] for example) and thus we have needed to redefine the negation and the disjunction.

Such non-classical aspects of quantum logic appear in the translation into modal logic. As the intuitionistic logic, another non-classical logic, was translated into the modal system S4 by Gödel-McKinsey-Tarski [7, 11], the quantum logic was translated into the modal system B by Goldblatt [8] and thus found to be non-classical.

By the way, in quantum mechanics, a physical property can be decided to be satisfied or not only after observation. Since the Birkhoff and von Neumann’s quantum logic is non-classical but remain two-valued, we could only represent the physical situations of post-observation [15, Section 7.2].

On the other hand, Pykacz [15] described unobserved physical properties by extending the Birkhoff and von Neumann’s two-valued quantum logic to a many-valued logic. In the (Pykacz’s) many-valued quantum logic, the truth value was regarded as the transition probability in quantum mechanics. In particular, since only the probabilities 1 and 0 represent certainty unlike other probabilities in the open interval (0,1), a three-valued quantum logic with truth values T (certainly true), F (certainly false), and I (indeterminate) is worth considering.

In this paper, we translate the three-valued quantum logic to modal logic. Just as the Goldblatt translation [8] helps to understand the Birkhoff and von Neumann’s quantum logic in the language of modal logic, our translation helps to understand the three-valued quantum logic in it: the truth values T, F, I of a formula α are translated into $\Box \alpha$ (α is necessary true), ♢α ∧♢¬α (α is coincidentally true), and $\Box \neg \alpha$ (α is necessary false) respectively. Although this kind of translation from three-valued logic to modal logic is already known as 3-equivalence in [9], it was not known whether 3-equivalence holds in the three-valued “quantum” logic as well.

The translation from the three-valued quantum logic to modal logic distinguishes ontic truth (i.e. truth independent of an observer) and epistemic truth. That is, ⊧α represents ontic truth of α but $\models \Box \alpha$ or ⊧♢α represents epistemic truth of α. Since epistemic logic is formulated as a kind of modal logic with the modal operators, this translation helps to understand and describe the epistemic aspect of quantum mechanics.

The distinction between ontic and epistemic truth is needed in light of epistemic nature of quantum mechanics. As some no-go theorems such as the Bell’s theorem and the Kochen–Specker theorem assert, a kind of realistic interpretations of quantum mechanics have been failed. That is, quantum objects cannot exist completely independent of or irrelevant from an observer: the measured value of a quantum object is not determined before it is measured by an observer. Accordingly, truth in quantum mechanics should be expressed with the modal operators.¹

To construct the translation and prove its 3-equivalence, we first introduce new quantum logic which can express statements about an observable in quantum mechanics. We call this logic observable-dependent logic. Unlike the traditional or many-valued quantum logic, each formula in the observable-dependent logic represents a physical property α of an observable corresponding to the self-adjoint operator A in a pure |ψ〉. The observable-dependent logic is preferable from the perspective of physics, because quantum observation is executed only when it is specified what observable is going to be observed. In quantum mechanics, a target observable must be determined before executing the observation, and then an observer can confirm whether the physical property is true or not.

This paper is organized as follows: In Section 2, we review some basic notions about the many-valued quantum logic. In Section 3, we extend the definition of 3-equivalence for S5 to that of any modal system not restricted to S5. In Sections 4 and 5, we define a kind of many-valued logic called observable-dependent logic and prove some properties of it. This logic is utilized to prove our main theorem (Theorem 5), namely 3-equivalence (in a broad sense defined in Section 3) between the valuation of the three-valued quantum logic and a kind of Kripke model in Section 6. Finally, we conclude our paper in Section 7.

2 Many-Valued Quantum Logic

Quantum logic is the logic of quantum mechanics originated from Birkhoff and von Neumann’s paper [2]. The Birkhoff and von Neumann’s quantum logic is formulated as a kind of orthomodular lattice called Hilbert lattice [18]. This lattice consists of all the closed subspaces M of a Hilbert space ${\mathscr{H}}$, or equivalently (self-adjoint) projections onto M by the projection theorem. Different from a Boolean lattice (i.e. classical logic), a Hilbert lattice does not satisfy the distributive law in general. Roughly speaking, this is the difference between quantum and classical mechanics from the logical viewpoint.

By the projection theorem in Hilbert space theory, any $x\in {\mathscr{H}}$ is uniquely decomposed into x in the given closed subspace $M\subseteq {\mathscr{H}}$ and y in its orthogonal complement $M^{\perp }\subseteq {\mathscr{H}}$, that is,

$$ x=y+z,\qquad y\in M, z\in M^{\perp}. $$

Thus, there is the one-to-one correspondence between M and the projection P_M onto M.

The notion of projections is significant in quantum mechanics, because projective measurement causes the state transition from a pure state |ψ〉 to the other pure state P_M|ψ〉/∥P_M|ψ〉∥. More precisely, if the physical property α is observed in |ψ〉, the state |ψ〉 is transitioned into $P_{\overline {[\![\alpha ]\!]}}$, where $\overline {[\![\alpha ]\!]}:=([\![\alpha ]\!]^{\perp })^{\perp }$ denotes the closure² of the set $[\![\alpha ]\!]\subseteq {\mathscr{H}}$ of all the (pure) states satisfying α. According to quantum mechanics, the probability of observing α in |ψ〉 is the inner product $\langle \psi |P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$ of |ψ〉 and $P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$. This probability $\langle \psi |P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$ is called the transition probability. However, measurement in classical mechanics do not change a state. Thus, the notion of transition probability is meaningful only in quantum mechanics.

Since the Birkhoff and von Neumann’s quantum logic is not classical (because of invalidity of the distributive law) but two-valued, it cannot describe the probabilistic behavior of quantum phenomena quantitatively. Thus, it is reasonable to assign a [0,1]-truth value to such kind of statement. For example, consider the sentence “There will be a sea battle tomorrow.” This sentence is neither true nor false at the present time. Likewise, the sentence “A photon will pass through a filter” is also neither true nor false. Instead of true or false, the truth value of this kind of statements should be interpreted as probability. Along this line of thought, Pykacz suggested and developed a many-valued quantum logic [15].

Let L^q be the set of all the formulas of the many-valued quantum logic.³ It consists of the propositional function α(|ψ〉), which stands for the statement “The physical property α is observed in a pure state |ψ〉.” The definition of the logical connectives in the many-valued quantum logic does not play an essential role in this paper. Thus, we omit it, and see [16] for a more detailed explanation about this topic instead. The valuation v^q(α(|ψ〉)) of α(|ψ〉) is defined as the probability of observing the physical property α in |ψ〉 [14], namely

$$ v^{q}(\alpha(|\psi\rangle)):=\langle \psi|P_{\overline{[\![\alpha]\!]}}|\psi \rangle. $$

That is, v^q is the function from L^q to the closed interval [0,1].

We emphasize that the Birkhoff and von Neumann’s quantum logic is not [0,1] but two-valued, because it can only deal with α in a post-measurement state. By the projection theorem mentioned above, the property α was either observed or not when the observation is done. (I) If α was observed in |ψ〉, the state was transitioned into $P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$. The probability $v^{q}(\alpha (P_{\overline {[\![\alpha ]\!]}}|\psi \rangle ))$ of observing α again in the state is the inner product of $P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$ and $P_{\overline {[\![\alpha ]\!]}}P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$. Since $P_{\overline {[\![\alpha ]\!]}}$ is a projection, $v^{q}(\alpha (P_{\overline {[\![\alpha ]\!]}}|\psi \rangle ))=1$. (II) If α was not observed in |ψ〉, the state was transitioned into $P_{\overline {[\![\alpha ]\!]}^{\perp }}|\psi \rangle =P_{[\![\alpha ]\!]^{\perp }}|\psi \rangle$. The probability $v^{q}(\alpha (P_{[\![\alpha ]\!]^{\perp }}|\psi \rangle ))$ of observing α in $P_{[\![\alpha ]\!]^{\perp }}|\psi \rangle$ is 0, because

$$ P_{\overline{[\![\alpha]\!]}}P_{[\![\alpha]\!]^{\perp}}|\psi\rangle=P_{\overline{[\![\alpha]\!]}}(I-P_{\overline{[\![\alpha]\!]}})|\psi\rangle=\mathbf{0}, $$

where I stands for the identity operator and 0 stands for the zero vector. Thus, $v^{q}(\alpha ,P_{[\![\alpha ]\!]^{\perp }}|\psi \rangle )=0$. As a result, the truth value is either 1 or 0 when the observation is done.

3 The Definition of 3-Equivalence for Quantum Logic

Let {T, I, F} be the set of all the truth values of a three-valued logic, which intended to be “True”, “Indeterminate” and “False” respectively. The valuation v₃ from the set L₃ of all the formulas of a three-valued logic to {T, I, F} is given by some truth tables. v₃ and an S5-model M^S5 = (W, E, V ), namely a Kripke model which consists of an equivalence relation E, are said to be 3-equivalent [9] if there exist functions τ_T, τ_F, τ_I from L₃ to the set L_ML of all the formulas of modal logic such that

$$ v_{3}(\alpha)=X\Leftrightarrow M^{\mathbf{S5}}\models\tau_{X}(\alpha),\quad X\in\{T,I,F\} $$

for any α ∈ L₃. Here, M^S5⊧τ_X(α) means that τ_X(α) is valid on M^S5 as usual. The existence of 3-equivalent v₃ for each S5-model and the existence of S5-model for each 3-equivalent v₃ was proved [9] by the translation rules

$$ \tau_{T}(\alpha)=\Box\alpha,\quad\tau_{I}(\alpha)=\Diamond\alpha\land\Diamond\neg\alpha,\quad\tau_{F}(\alpha)=\Box\neg\alpha. $$

Unfortunately, this result of [9] fails to make the best use of the expressive power of modal logic, because there are various modal systems such as T, S4, B, D and so on. However, there seems to be a legitimate reason to assume to be S5. Since every α ∈ L₃ is defined independently of any states in W, the distinction between states must be disappeared in the modal system. Thus, a Kripke model M must satisfy the condition

$$ (\text{S5})\left\{\begin{array}{l} M\models\Box\alpha\Leftrightarrow(M,w)\models\Box\alpha, \\ M\models\Diamond\alpha\Leftrightarrow(M,w)\models\Diamond\alpha \end{array}\right. $$

for any α ∈ L_ML, that is, any formula which consists of the modal operator(s) $\Box$ or ♢ holds in some state if and only if it also holds in all states. Since this condition (S5) is satisfied if M is an S5-model, the notion of 3-equivalence was defined only for S5-model in [9].

In fact, if each formula depends on a state, it is no longer necessary to assume to be S5. Thus, we redefine the notion of 3-equivalence by removing the assumption that the model must be S5. Let α(w) be a formula of a so-called state-dependent three-valued logic for any w ∈ W. Instead of L₃, we use the symbol $\check {L}_{3}$ as the set of all the formulas of this logic, because $\alpha (w)\in \check {L}_{3}$ depends on w unlike α ∈ L₃. The valuation $\check {v}_{3}$ of this logic and an Kripke model M = (W, R, V ) are said to be 3-equivalent if there exist functions $\check {\tau }_{T}$, $\check {\tau }_{F}$, $\check {\tau }_{I}:\check {L}_{3}\to L_{\text {ML}}$ such that

$$ \check{v}_{3}(\alpha(w))=X\Leftrightarrow(M,w)\models\check{\tau}_{X}(\alpha(w)),\quad X\in\{T,I,F\} $$

for any $\alpha (w)\in \check {L}_{3}$.

One of the most typical examples of the state-dependent three-valued logic is the three-valued quantum logic. From the perspective of the Pykacz’s many-valued quantum logic reviewed in Section 2, the three-valued quantum logic is just a fragment of it: the set of the formulas of the three-valued quantum logic is the same as that of many-valued quantum logic (i.e. it is L^q) but the number of truth values is different. The valuation ${v_{3}^{q}}:L^{q}\to \{T,I,F\}$ of the three-valued quantum logic is defined by

$$ {v_{3}^{q}}(\alpha(|\psi\rangle))= \begin{cases} T & (v^{q}(\alpha(|\psi\rangle))=1), \\ I & (v^{q}(\alpha(|\psi\rangle))\neq 1,0), \\ F & (v^{q}(\alpha(|\psi\rangle))=0). \end{cases} $$

That is, the range [0,1] of probability value is divided into three parts: the singletons {0},{1}, and the open interval (0,1).

Historically, perhaps the Reichenbach’s three-valued logic [19] with the third truth value “Indeterminate” is the most famous as many-valued interpretation of a quantum logic, because it causes controversy in the field of philosophy mainly by Putnam [13]. The Reichenbach’s three-valued logic is well-motivated in terms of quantum mechanics: Reichenbach had the uncertainty relation in mind, and he assigns the third truth value to a physical property that has not yet been observed.

Although we agree with the Pykacz’s opinion [15, Chapter 5] that the conventional three-valued quantum logic (including Reichenbach’s one) is not rich enough in truth values compared to the [0,1]-valued quantum logic, we confine our attention to the three-valued quantum logic to make the story easier. As suggested in [9] for the non-quantum three-valued logic, the result can extend to n-valued logics. In particular, a translation from the four-valued logic to a kind of modal logic was studied in detail by [10].

4 Observables in Quantum Logic

In order to prove our main theorem, we first prove the lemma for a certain fragment of the three-valued quantum logic called observable-dependent (three-valued) quantum logic in Section 6 (see Lemma 1). For this purpose, we introduce an observable-dependent logic in this section.

Recall that the truth value v(α(|ψ〉)) is defined as the probability $\langle \psi |P_{\overline {[\![\alpha ]\!]}}|\psi \rangle$ in Section 2. However, there is a gap between the conventional (three-valued) quantum logic and quantum mechanics: usually, the transition probability is determined depending on a self-adjoint operator A corresponding to some observable in quantum mechanics (see [12, Section 2.2.5] for example). To be more precise, when projective measurement of A is executed in |ψ〉,

• (P1) the measured value m must be one of the eigenvalues of A;

• (P2) if m is obtained, |ψ〉 is transitioned into the unit eigenvector⁴m of A corresponding to m;

• (P3) the probability of obtaining the measured value m is |〈m|ψ〉|², namely the square of the inner product of |ψ〉 and m.

Since quantum logics are strongly motivated by quantum mechanics, we believe that quantum logics should not be developed without various notions of quantum mechanics. For this purpose, we incorporate the notion of observables into the many-valued quantum logic⁵.

Based on these conditions (P1), (P2) and (P3), we introduce an observable-dependent logic which is a kind of many-valued logic. As with the three-valued quantum logic, the set of the formulas is L^q but the valuation is different from v^q. The valuation ${v_{A}^{q}}:L^{q}\to [0,1]$ of the observable-dependent logic is the probability of observing the physical property α of A in |ψ〉, namely

$$ {v_{A}^{q}}(\alpha(|\psi\rangle)):=\sum\limits_{|\psi^{\prime\rangle}\in E_{A}\cap\overline{[\![\alpha]\!]}}|{\langle\psi^{\prime}|\psi\rangle}|^{2}, $$

where E_A denotes the set of all unit eigenvectors of A. In other words, ${v_{A}^{q}}(\alpha (|\psi \rangle ))$ is the sum of the transition probability from |ψ〉 to each transitionable state (by observing A) which satisfies α.

The valuation $v_{3,A}^{q}:L^{q}\to \{T,I,F\}$ of the three-valued fragment of the observable-dependent logic is defined in the same way as the three-valued quantum logic in Section 3. That is,

$$ v_{3,A}^{q}(\alpha(|\psi\rangle))= \begin{cases} T & ({v_{A}^{q}}(\alpha(|\psi\rangle))=1), \\ I & ({v_{A}^{q}}(\alpha(|\psi\rangle))\neq 1,0), \\ F & ({v_{A}^{q}}(\alpha(|\psi\rangle))=0). \end{cases} $$

To define the functions $\tau _{T,A}^{q},\tau _{I,A}^{q},\tau _{F,A}^{q}:L^{q}\to L_{\text {ML}}$, we first define the components of a Kripke model $M_{A}=(\varSigma ({\mathscr{H}}),\mathcal {P}_{A},V)$ called observable-dependent Kripke model as follows:

• $\varSigma ({\mathscr{H}})$ is a non-empty set of all the pure (normalized) states of a Hilbert space ${\mathscr{H}}$: a pure state $|\psi \rangle \in \varSigma ({\mathscr{H}})$ is the element which norm (induced by the inner product defined on ${\mathscr{H}}$) is 1 of the equivalence class [|ψ〉] in the quotient set $({\mathscr{H}}\setminus \{\mathbf {0}\})/{\equiv }$, where ${\mathscr{H}}\setminus \{\mathbf {0}\}$ represents ${\mathscr{H}}$ without the zero vector 0.⁶ Here, the equivalence relation ≡ is defined by

  $$ |\psi_{1\rangle}\equiv|\psi_{2}\rangle\Leftrightarrow|\psi_{1}\rangle=e^{i\theta}|\psi_{2}\rangle $$

  for some complex number $e^{i\theta }=\cos \limits \theta +i\sin \limits \theta$.

• $\mathcal {P}_{A}$ is an accessibility relation on $\varSigma ({\mathscr{H}})$ defined by

  $$ (|\psi_{1}\rangle,|\psi_{2}\rangle)\in\mathcal{P}_{A}\Leftrightarrow|{\langle\psi_{2}|\psi_{1}\rangle}|^{2}>0\text{ and }|\psi_{2}\rangle\in E_{A}, $$

  where 〈ψ₂|ψ₁〉 denotes the inner product of |ψ₁〉 and |ψ₂〉. In other words, |ψ₂〉 is accessible from |ψ₁〉 if and only if there is a possibility of obtaining an eigenvalue of A as a measured value.

• V is a valuation function from an atomic formula in L_ML to a subset of $\varSigma ({\mathscr{H}})$.

Note that $\mathcal {P}_{A}$ is a restriction of the non-orthogonality relation to E_A, because |〈ψ₂|ψ₁〉|² = 0 if and only if |ψ₁〉 is orthogonal to |ψ₂〉. The idea of regarding (non)-orthogonality relation as the accessibility relation of a Kripke model was suggested by [5] and [8] independently.

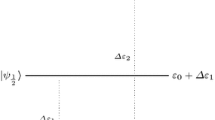
We give an example of the observable-dependent Kripke model. Let σ_x (σ_y) be the self-adjoint operator which corresponds to spin along x-axis (y-axis). That is, σ_x and σ_y are the Pauli matricies

$$ \sigma_{x}=\begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix},\qquad\sigma_{y}=\begin{pmatrix}0 & -i \\ i & 0\end{pmatrix}. $$

For every n ∈ {x, y} and i ∈ {− 1, + 1}, the normalized eigenvectors $|{{\psi _{n}^{i}}}\rangle$ of σ_n corresponding to the eigenvalue i are

$$ |{\psi_{x}^{+1}}\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix}1 \\ 1\end{pmatrix}, |{\psi_{x}^{-1}}\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix}1 \\ -1\end{pmatrix}, |{\psi_{y}^{+1}}\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix}1 \\ i\end{pmatrix}, |{\psi_{y}^{-1}}\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix}1 \\ -i\end{pmatrix}. $$

Fix $\varSigma ({\mathscr{H}})$ as $\{|{\psi _{x}^{-1}}\rangle ,|{\psi _{x}^{+1}}\rangle ,|{\psi _{y}^{-1}}\rangle ,|{\psi _{y}^{+1}}\rangle \}$. Then, the two relations $\mathcal {P}_{\sigma _{x}}$ and $\mathcal {P}_{\sigma _{y}}$ are depicted by Figs. 1 and 2 respectively.⁷

Fig. 1

The diagram of $\mathcal {P}_{\sigma _{x}}$

Fig. 2

The diagram of $\mathcal {P}_{\sigma _{y}}$

In addition, we define the valuations $V_{\sigma _{n}}$ as the function $V_{\sigma _{n}}(p)=\{|{\psi _{n}^{+1}}\rangle , |{\psi _{n}^{-1}}\rangle \}$ for each n ∈ {x, y} for an atomic formula p. These symbols constitute two distinct observable-dependent Kripke models $M_{\sigma _{x}}=(\varSigma ({\mathscr{H}}),\mathcal {P}_{\sigma _{x}},V_{\sigma _{x}})$ and $M_{\sigma _{y}}=(\varSigma ({\mathscr{H}}),\mathcal {P}_{\sigma _{y}},V_{\sigma _{y}})$. Evidently, the truth value of a formula (even if in the same state) depends on the model on one’s mind. For example, $(M_{\sigma _{x}},|{\psi _{x}^{+1}}\rangle )\models p$ but $(M_{\sigma _{y}},|{\psi _{x}^{+1}}\rangle )\not \models p$.

5 Some Properties of $\mathcal {P}_{A}$

In this section, we introduce a new property of a relation on $\varSigma ({\mathscr{H}})$ called idempotency, and prove that $\mathcal {P}_{A}$ satisfies it. After that we discuss other distinguished features of $\mathcal {P}_{A}$.

Theorem 1

$\mathcal {P}_{A}$ is idempotent: $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$ and $(|\psi _{2}\rangle , |{\psi _{3}}\rangle )\in \mathcal {P}_{A}$ jointly imply that |ψ₂〉 = |ψ₃〉 for any $|\psi _{1}\rangle ,|\psi _{2}\rangle ,|{\psi _{3}}\rangle \in \varSigma ({\mathscr{H}})$.

Proof

By the definition of $\mathcal {P}_{A}$, if $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$, then |ψ₂〉,|ψ₃〉∈ E_A. Suppose |ψ₂〉≠|ψ₃〉. Then, since all the eigenvectors of a self-adjoint operator (in this case, A) form an orthonormal basis of ${\mathscr{H}}$, |〈ψ₃|ψ₂〉|² = 0. However, it contradicts the assumption $(|\psi _{2}\rangle ,|{\psi _{3}}\rangle )\in \mathcal {P}_{A}$. On the other hand, |〈ψ₂|ψ₂〉|² = 1 > 0. Therefore, |ψ₂〉 must be identical to |ψ₃〉. □

Theorem 1 means that projective measurement is idempotent. In quantum mechanics, any state will be changed by projective measurement but there is in fact one exception. If the state is an eigenvector of A, no matter how many times projective measurement is repeated, this state will not be changed anymore.

Just as reflexivity, transitivity, symmetry and so on corresponds to the validity of $\Box \alpha \to \alpha$, $\Box \alpha \to \Box \Box \alpha$, $\alpha \to \Box \Diamond \alpha$, $\dots$ respectively, idempotency corresponds to $\Box (\Diamond \alpha \to \alpha )$.

Theorem 2

$\Box (\Diamond \alpha \to \alpha )$ is valid in an observable-dependent Kripke frame $F_{A}=(\varSigma ({\mathscr{H}}),\mathcal {P}_{A})$ if and only if $\mathcal {P}_{A}$ is idempotent.

Proof

(⇒) We prove the contraposition. Suppose $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$. If $\mathcal {P}_{A}$ is not idempotent, there exists $|{\psi _{3}}\rangle \in \varSigma ({\mathscr{H}})$ such that $(|\psi _{2}\rangle ,|{\psi _{3}}\rangle )\in \mathcal {P}_{A}$ and |ψ₂〉≠|ψ₃〉. Fix the valuation V so that it satisfies V (p) = {|ψ₃〉} for some atomic formula p. Then, $(M_{A},|\psi _{1}\rangle )\not \models \Box (\Diamond p\to p)$ for the model $M_{A}=(\varSigma ({\mathscr{H}}),\mathcal {P}_{A},V)$, thus F_A does not validate $\Box (\Diamond p\to p)$.

(⇐) Let M_A be any model $(\varSigma ({\mathscr{H}}),\mathcal {P}_{A},V)$. We have to show (M_A,|ψ₂〉)⊧♢α → α for any |ψ₂〉 satisfying $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$. If (M_A,|ψ₂〉)⊧♢α, there exists $|{\psi _{3}}\rangle \in \varSigma ({\mathscr{H}})$ such that $(|\psi _{2}\rangle ,|{\psi _{3}}\rangle )\in \mathcal {P}_{A}$ and (M,|ψ₃〉)⊧α. Since $\mathcal {P}_{A}$ is idempotent, |ψ₃〉 must be |ψ₂〉. Thus, (M_A,|ψ₂〉)⊧α. As a result, we conclude that (M_A,|ψ₂〉)⊧♢α → α. □

Theorem 3

$\mathcal {P}_{A}$ is serial: for any $|\psi _{1}\rangle \in \varSigma ({\mathscr{H}})$, there exists $|\psi _{2}\rangle \in \varSigma ({\mathscr{H}})$ such that $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$.

Proof

It follows from the fact that all the eigenvectors of a self-adjoint operator form an orthonormal basis of ${\mathscr{H}}$. That is, each |ψ₂〉∈ E_A satisfies $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$ for any $|\psi _{1}\rangle \in \varSigma ({\mathscr{H}})$. □

Theorem 4

$\mathcal {P}_{A}$ is shift-reflexive: $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$ implies $(|\psi _{2}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$ for any $|\psi _{1}\rangle ,|\psi _{2}\rangle \in \varSigma ({\mathscr{H}})$.

Proof

By using the rule of necessitation,⁸$\mathcal {P}_{A}$ is not only serial but also (so-called) shift-serial, namely for any $|\psi _{1}\rangle ,|\psi _{2}\rangle \in \varSigma ({\mathscr{H}})$ satisfying $(|\psi _{1}\rangle ,|\psi _{2}\rangle )\in \mathcal {P}_{A}$, there exists $|{\psi _{3}}\rangle \in \varSigma ({\mathscr{H}})$ such that $(|\psi _{2}\rangle ,|{\psi _{3}}\rangle )\in \mathcal {P}_{A}$. Thus, $\mathcal {P}_{A}$ is shift-reflexive by Theorem 1. □

Shift reflexivity has been discussed in deontic logic, because shift reflexivity is sometimes preferred to mere reflexivity when the necessity operator $\Box$ is interpreted as “it is obligatory that” [6, Section 5.4]. The fact that $\mathcal {P}_{A}$ is shift-reflexive may arouse further attention to shift reflexivity itself in the future.

Note that $\mathcal {P}_{A}$ is neither reflexive nor symmetric, because Figs. 1 and 2 in Section 4 are two counterexamples for it. On the other hand, the non-orthogonality relation $\mathcal {P}$ defined by

$$ (|\psi_{1}\rangle,|\psi_{2}\rangle)\in\mathcal{P}\Leftrightarrow|{\langle\psi_{2}|\psi_{1}\rangle}|^{2}>0 $$

is reflexive and symmetric (see the proof of Lemma 2). Traditionally, the non-orthogonality relation $\mathcal {P}$ (or equivalently the orthogonality relation) is utilized as an accessibility relation of the Kripke frame for quantum logic [5, 8, 17]. This traditional relation $\mathcal {P}$ is replaced with $\mathcal {P}_{A}$ in the observable-dependent Kripke model M_A.

6 Main Theorem

Now we prove our main theorem by using the observable-dependent logic introduced in Section 4.

Lemma 1

M_A and $v_{3,A}^{q}$ are 3-equivalent by the functions $\tau _{T,A}^{q},\tau _{I,A}^{q},\tau _{F,A}^{q}$ such that

$$ \begin{array}{@{}rcl@{}} \tau_{T,A}^{q}(\alpha(|\psi\rangle))&=&\Box\alpha, \\ \tau_{I,A}^{q}(\alpha(|\psi\rangle))&=&\Diamond\alpha\land\Diamond\neg\alpha, \\ \tau_{F,A}^{q}(\alpha(|\psi\rangle))&=&\Box\neg\alpha. \end{array} $$

Proof

Let P_λ be the projection onto the set of the eigenspace of A with eigenvalue λ in the spectrum Spec(A) of A, and I be the identity operator. It follows from the completeness relation

$$ \sum\limits_{\lambda\in\text{Spec}(A)}P_{\lambda}=I, $$

that the following equation holds (see [1, Section 9.3] for example):

$$ \sum\limits_{|{\psi^{\prime}}\rangle\in E_{A}}|{\langle\psi^{\prime}|\psi\rangle}|^{2}=\sum\limits_{\lambda\in\text{Spec}(A)}{\langle\psi|P_{\lambda}|\psi\rangle}={\langle\psi|\psi\rangle}=1. $$

Thus,

$$ \begin{array}{@{}rcl@{}} v_{3,A}^{q}(\alpha(|\psi\rangle))=T&\Leftrightarrow {v_{A}^{q}}(\alpha(|\psi\rangle))=1\Leftrightarrow \sum\limits_{|{\psi^{\prime}}\rangle\in E_{A}\cap\overline{[\![\alpha]\!]}}|{\langle\psi^{\prime}|\psi\rangle}|^{2}=1 \\ &\Leftrightarrow E_{A}\cap\overline{[\![\alpha]\!]}=E_{A}\Leftrightarrow E_{A}\subseteq\overline{[\![\alpha]\!]}. \end{array} $$

Moreover, it follows from $\{|{\psi ^{\prime }}\rangle :(|\psi \rangle ,|\psi ^{\prime }\rangle )\in \mathcal {P}_{A}\}=E_{A}$ that the condition $E_{A}\subseteq \overline {[\![\alpha ]\!]}$ is equivalent to $(M_{A},|\psi \rangle )\models \Box \alpha$. In summary,

$$ v_{3,A}^{q}(\alpha(|\psi\rangle))=T\Leftrightarrow(M_{A},|\psi\rangle)\models\Box\alpha\Leftrightarrow(M_{A},|\psi\rangle)\models\tau_{T,A}^{q}(\alpha(|\psi\rangle)). $$

Likewise, $v_{3,A}^{q}(\alpha (|\psi \rangle ))=F$ if and only if $E_{A}\cap \overline {[\![\alpha ]\!]}=\emptyset$. It follows from $\{|\psi ^{\prime }\rangle :(|\psi \rangle ,|\psi ^{\prime }\rangle )\in \mathcal {P}_{A}\}=E_{A}$ again that

$$ v_{3,A}^{q}(\alpha(|\psi\rangle))=F\Leftrightarrow(M_{A},|\psi\rangle)\models\Box\neg\alpha\Leftrightarrow(M_{A},|\psi\rangle)\models\tau_{F,A}^{q}(\alpha(|\psi\rangle)). $$

Therefore,

$$ v_{3,A}^{q}(\alpha(|\psi\rangle))=X\Leftrightarrow(M_{A},|\psi\rangle)\models\tau_{X,A}^{q}(\alpha(|\psi\rangle)),\quad X\in\{T,I,F\} $$

for any (α(|ψ〉)) ∈ L^q. □

Suppose that there exists the set of self-adjoint operators on ${\mathscr{H}}$ which satisfies the following two conditions.

• (O1) An observer can only observe an observable represented by one of the element of $\mathcal {O}$;

• (O2) $\bigcup \limits _{A\in \mathcal {O}}E_{A}={\mathscr{H}}$.

Then, the following theorem holds by (O2) and (O1) respectively.

Lemma 2

Let M^B be a B-model (W, R^B, V ), namely a Kripke model which consists of a reflexive and symmetric accessibility relation R^B. There exists M^B such that

$$ (M^{\mathbf{B}},|\psi\rangle)\models\Box\alpha\Leftrightarrow(M_{A},|\psi\rangle)\models\Box\alpha\text{ for any }A\in\mathcal{O}. $$

Proof

Consider an accessibility relation $\mathcal {P}\subseteq \varSigma ({\mathscr{H}})\times \varSigma ({\mathscr{H}})$ defined by

$$ (|\psi_{1}\rangle,|\psi_{2}\rangle)\in\mathcal{P}\Leftrightarrow|{\langle\psi_{2}|\psi_{1}\rangle}|^{2}>0. $$

$\mathcal {P}$ is reflexive and symmetric, because |〈ψ₁|ψ₁〉|² > 0 and |〈ψ₁|ψ₂〉|² = |〈ψ₂|ψ₁〉|² for any $|\psi _{1}\rangle ,|\psi _{2}\rangle \in \varSigma ({\mathscr{H}})$ by the definition of the inner product. Moreover, $\mathcal {P}$ is constructed by $\{\mathcal {P}_{A}\}_{A\in \mathcal {O}}$:

$$ \{|\psi_{2}\rangle:(|\psi_{1}\rangle,|\psi_{2}\rangle)\in\mathcal{P}\}=\bigcup\limits_{A\in\mathcal{O}}\{|\psi_{2}\rangle:(|\psi_{1}\rangle,|\psi_{2}\rangle)\in\mathcal{P}_{A}\} $$

because of the above supposition (O2). Therefore, if we choose M^B as $M^{\mathbf {B},q}=(\varSigma ({\mathscr{H}}),\mathcal {P},V)$, then $(M^{\mathbf {B}},|\psi \rangle )\models \Box \alpha$ if and only if $(M_{A},|\psi \rangle )\models \Box \alpha$ for any $A\in \mathcal {O}$. □

Theorem 5

M^{B, q} and ${v_{3}^{q}}$ are 3-equivalent by the functions ${\tau _{T}^{q}},{\tau _{I}^{q}},{\tau _{F}^{q}}:{L_{3}^{q}}\to L_{\text {ML}}$ such that

$$ \begin{array}{@{}rcl@{}} {\tau_{T}^{q}}(\alpha(|\psi\rangle))&=&\Box\alpha, \\ {\tau_{I}^{q}}(\alpha(|\psi\rangle))&=&\Diamond\alpha\land\Diamond\neg\alpha, \\ {\tau_{F}^{q}}(\alpha(|\psi\rangle))&=&\Box\neg\alpha. \end{array} $$

Proof

Let O_A be the event that A is observed, and P(α(|ψ〉)∣O_A) be the conditional probability of α(|ψ〉) given O_A, namely ${v_{A}^{q}}(\alpha (|\psi \rangle ))$. Then, the probability P(α(|ψ〉)) of α(|ψ〉), namely v^q(α(|ψ〉)), is

$$ \sum\limits_{A\in\mathcal{O}}[\mathbf{P}(\alpha(|\psi\rangle)\mid O_{A})\mathbf{P}(O_{A})] $$

by the law of total probability.

Consider the condition ${v_{3}^{q}}(\alpha (|\psi \rangle ))=T$, that is, v^q(α(|ψ〉)) = 1. It follows from

$$ v^{q}(\alpha(|\psi\rangle))=\mathbf{P}(\alpha(|\psi\rangle))=\sum\limits_{A\in\mathcal{O}}[\mathbf{P}(\alpha(|\psi\rangle)\mid O_{A})\mathbf{P}(O_{A})] $$

and ${\sum }_{A\in \mathcal {O}}\mathbf {P}(O_{A})=1$ by the above supposition (O1) that v^q(α(|ψ〉)) = 1 if and only if

• (∗) P(α(|ψ〉)∣O_A) = 1 for any $A\in \mathcal {O}$.⁹

Moreover,

$$\begin{array}{llr} (\ast)&\Leftrightarrow {v_{A}^{q}}(\alpha(|\psi\rangle))=1\text{ for any }A\in\mathcal{O} &(\text{by the definition of } {v_{A}^{q}}) \\ &\Leftrightarrow v_{3,A}^{q}(\alpha(|\psi\rangle))=T\text{ for any }A\in\mathcal{O} &(\text{by the definition of } v_{3,A}^{q}) \\ &\Leftrightarrow (M_{A},|\psi\rangle)\models\Box\alpha\text{ for any }A\in\mathcal{O} &(\text{by Lemma~1}) \\ &\Leftrightarrow (M^{\mathbf{B},q},|\psi\rangle)\models\Box\alpha&(\text{by the proof of Lemma~2}.) \end{array}$$

As a result,

$$ {v_{3}^{q}}(\alpha(|\psi\rangle))=T\Leftrightarrow(M^{\mathbf{B},q},|\psi\rangle)\models\Box\alpha $$

is obtained. The other cases, that is,

$$ \begin{array}{@{}rcl@{}} {v_{3}^{q}}(\alpha(|\psi\rangle))=I&\Leftrightarrow(M^{\mathbf{B},q},|\psi\rangle)\models\Diamond\alpha\land\Diamond\neg\alpha \\ {v_{3}^{q}}(\alpha(|\psi\rangle))=F&\Leftrightarrow(M^{\mathbf{B},q},|\psi\rangle)\models\Box\neg\alpha \end{array} $$

are proved in the same way. □

The intuitive meaning of Theorem 5 is that each necessity ($\Box \alpha$), contingency (♢α ∧♢¬α) and impossibility ($\Box \neg \alpha$) corresponds to the probability 1 (i.e. certainly true), neither 1 nor 0 (i.e. indeterminate), and 0 (certainly false) respectively in the context of quantum logic.

7 Conclusion

We clarified the relationship between three-valued and modal logic from a quantum logical perspective by our main theorem (Theorem 5). Since this theorem relates the three-valued quantum logic to a kind of modal system B, it provides a new example of the relationship between three-valued logic and modal system other than S5 discussed by [9].

To prove Theorem 5, we introduced an observable-dependent logic. This logic is preferable from the perspective of quantum mechanics, because quantum observation is executable only when what an observable would be measured is determined. That is, the observable-dependent logic fills a gap between logic and quantum mechanics. In addition, from a logical viewpoint, we can utilize some notions of quantum mechanics for proving logical property¹⁰ if the observable-dependent logic is employed.

By the translation which consists of ${\tau _{T}^{q}}$, ${\tau _{I}^{q}}$, ${\tau _{F}^{q}}$ from the three-valued quantum logic to modal logic, ontic truth (⊧α) and epistemic truth ($\models \Box \alpha$ or ⊧♢α) were distinguished. According to some no-go theorems such as Bell’s theorem and Kochen-Specker theorem, truth in quantum mechanics should not be interpreted as ontic (i.e. independent of an observer) but epistemic. Thus, this translation clarifies such epistemic aspect of quantum mechanics by the modal operators.