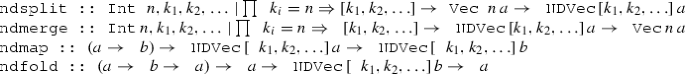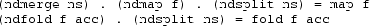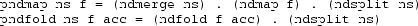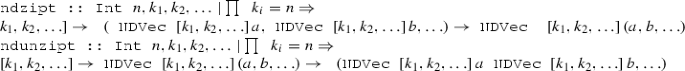Abstract
In this paper we present a novel approach to program optimisation based on compiler-based type-driven program transformations and a fast and accurate cost/performance model for the target architecture. We target streaming programs for the problem domain of scientific computing, such as numerical weather prediction. We present our theoretical framework for type-driven program transformation, our target high-level language and intermediate representation languages and the cost model and demonstrate the effectiveness of our approach by comparison with a commercial toolchain.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The promise of energy efficiency combined with higher logic capacity and maturing high-level synthesis (HLS) tools are pushing FPGAs into the mainstream of heterogeneous high-performance computing (HPC) and big data. FPGAs allow configuration to a custom design at fine granularity. The advantage of being able to customize the circuit for the application comes with the challenge of finding and programming the best possible implementation.
HLS tools such as Maxeler [23], Altera-OpenCL [7] and Xilinx SDAccel [28] have raised the abstraction of design entry considerably. However, even with such tools, parallel programmers with highly specialised expertise are still needed to fine-tune the application for performance and efficiency on the target FPGA device.
We contend that the design flow for HPC needs to evolve beyond current HLS approaches to address this productivity gap. Our proposition is that the design entry should be at a higher abstraction, preferably that of the legacy CPU code, and the task of generating architecture-specific parallel code should be done by the compilers. Such a design-entry point will be truly performance-portable, and accessible to programmers who do not have FPGA and parallel programming expertise.
The FPGA implements a program as a synchronously clocked logic circuit. The resources used by the program are therefore limited by the amount of space available on the chip for each type of resource (logic gates, flip-flops, memory cells, routing). Furthermore, FPGAs excel at operation-level parallelism, i.e. the optimal programming model is a deep pipeline working on a stream of data (as opposed to data parallelism in e.g. a GPU). This is a consequence of the relatively low clock speed of the FPGA. The implication is that for use in HPC, where high throughput is key, the target programs to be deployed on FPGAs are ideally static in terms of memory allocation and are data flow dominated (as opposed to control flow dominated). With that assumption, the optimal deployment of a program onto an FPGA translates to the optimal spatial layout of the data flow pipeline, and determining this optimal layout is our aim.
This work is part of the EPSRC TyTra project,Footnote 1 which aims to address the wider challenge of programming heterogeneous HPC platforms through a type-driven program transformation approach. However, our particular focus in this paper is on the compiler-based program transformations required to optimise performance of scientific, array-based programs on FPGAs. Our proposed approach is inspired by functional languages with expressive type systems such as HaskellFootnote 2 and IdrisFootnote 3 and based on type-driven program transformations and analytical cost models, both implemented in the TyTra compilation toolchain.
The ultimate aim of our work is to compile HPC applications such as climate and weather simulators, written typically in Fortran, to FPGAs.
The focus of this paper is the language and compilation framework for type-driven program transformation. This framework allows us to create very large numbers of variants of a given program with provably identical functionality but different performance and resource utilisation. We combine this program transformation framework with a fast and accurate analytical cost/performance model for the target FPGA architecture to obtain the performance and resource utilisation for each variant. In this way we can obtain the optimal program variant by exploring the program search space. Because of the size of the search space, fast cost/performance calculation is essential. Using a normal commercial toolchain for FPGA programming, it takes several minutes to obtain a performance estimate and several hours to obtain the final resource cost for a single variant.
We show in this paper that the parallelisation of the dataflow graph (netlist) of the FPGA implementation of a program can be expressed through the types of functions in a functional program, while the operations at the nodes of the graph are expressed through the definition of the functions. We show that there is an equivalence between our proposed high-level functional coordination language and the dataflow graph on the FPGA, so that we can reshape the dataflow graph in terms of the parallelism that it exposes by transforming the program. Furthermore, crucially, we show that the transformation of the program is automatically derived from the type transformation.
2 Related Work
The related work is best discussed from three different vantage points: raising the design-entry abstraction above conventional high-level languages in general, high-level programming approaches specific to FPGAs, and cost/performance models developed for FPGAs.
Others have also observed the need for a higher abstraction design entry. For example, researchers have proposed algorithmic skeletons to separate algorithm from architecture-specific parallel programming [6], and a thread pool abstraction framework for accelerator programming [15]. SparkCL [25] can be used to program diverse architectures, including FPGAs, into the familiar Apache Spark framework. Using DSLs (Domain-specific languages) is another route to raising the design abstraction, and numerous examples can be found for FPGAs [1, 16].
Programming FPGAs using conventional high-level programming has seen considerable effort across the academia and industry. They raise the abstraction of the design-entry from HDL to a high-level language, and various optimizations are applied to generate the FPGA solutions. In our view, most solutions have one or more of these limitations that distinguish our work from them: (1) compiler optimizations are limited to incremental improvements in the architecture already specified by the programmer, with no real architectural exploration [2, 7, 12, 23], (2) design entry is in a custom high-level language [7, 12, 23], (3) the flow is limited to very specific application domain e.g. for image processing or DSP applications [11], (4) the design-space exploration takes a prohibitively long amount of time [12], or (5) soft microprocessors based solutions are created which are not optimized for HPC [2, 14]. A flow with high-level, pure software design entry in the functional paradigm, that can apply safe transformations to generate variants automatically, and quickly evaluate them to achieve architectural optimizations, is to the best of our knowledge an entirely novel proposition.
From the perspective of developing a cost model, Kerr et al. [13] have developed a performance model for CUDA kernels on GPUs based on empirical evaluation of a number of existing applications. Park et al. [22] create a performance model for estimating the effects of loop transformation on FPGA designs, and there is a strong parallel between their work and ours. However, their work focuses on loop-unrolling, and is fundamentally different in terms of design entry and variant generation. Deng et al. [10] present cost models based on the MATLAB-based FANTOM tool, for area, time and power. Their estimation model works on generated HDL whereas we make estimates at a higher abstraction, and our approach of generating and evaluating variants is fundamentally different. Reference [17] presents another cost estimation approach comparable to ours, but their work does not estimate performance, and the overall context is very different from the TyTra flow. Reference [18] presents an analytical model, with focus on estimating dynamic and static power of various architectures.
3 Expressing Spatial Layouts Through Types
3.1 Netlists
At the lowest level of abstraction using in digital circuit design, a program is a directed graph (called netlist) where every edge is a wire and every node a logic gate, a memory element (e.g. flip-flop, SRAM cell) or an I/O pin. In practice, netlists are hierarchical. For our purpose, the building blocks of the netlists correspond to functions in the original program. More specifically, each node in our netlists processes finite streams (vectors). Simplifying, each node corresponds to a nested loop in the original program, working on a static array.
3.2 Transforming Netlist Nodes Through Type Transformations
Our aim is to transform the nodes in the dataflow graph spatially to obtain higher throughput for the overall program. Essentially, this means replicating nodes to achieve a degree of data parallelism. As we discuss in more detail in Sect. 4, the nodes in our programs process vectors by application of map or fold on pure functions. We will discuss the limitations of this assumption in Sect. 8.1.
However, our fundamental observation is that, because of this assumption on the nature of the nodes, we only need to know their types in order to perform the parallelism transformations: the type is the communication interface of the node, and the parallelization is only affected by the communication, not by the actual computation performed by the node. Similarly, we do not need to know the actual data that is processed by the odes, only its type. In the rest of this Section we formalise this concept.
3.3 Vector Types and Transformations
-
We define following type variables and sizes:
-
a is an atomic type variable, i.e. representing a nullary type constructor. In practice, this means a is not a vector.
-
b,c are general type variables, not necessarily atomic, i.e. they can be vectors.
-
k,l,m,n are sizes, so \(k,m,n\in \mathbb {N}_{>0}\)
-
-
Let \(\hbox {Vec}\,k\,b\) be a vector type, i.e. it represents a vector of length k containing values of type b as a simple dependent type (cf the vector type in Idris).
-
The total size of a nested vector type is defined as the product of all sizes: \(\mathcal {N}(\hbox {Vec}\,n_{1}\,\hbox {Vec}\,n_{2}\ldots \hbox {Vec}\ldots \hbox {Vec}\,n_{k}\;b)\overset{{\scriptscriptstyle \triangle }}{=}\prod _{i=1}^{k}n_{i}\overset{{\scriptscriptstyle \triangle }}{=}n\)
-
Given an atomic type a, we can generate the set of all vector types V(a, n) for a with total size n:
$$\begin{aligned} {\left\{ \begin{array}{ll} a\notin V(a,n)\\ \forall \,b\,\in \,V(a,n),\forall \,k\,\in \,[0,n]\,|\,\hbox {Vec}\,k\,b\in V(a,n) \end{array}\right. } \end{aligned}$$In other words, this set V(a,n) is formed of all possible types resulting from reshaping a vector \(\hbox {Vec}\,n\,b\) through nesting.
We now introduce transformations of vector types that will allow us to create any element of V(a,n). Functions operating on types start with an uppercase letter, e.g. F,G. They are general, right-associative functions operating on a single type. So we can write e.g. G F b.
We posit two fundamental transformations on vector types, Split and Merge. These correspond to the familiar transformation used in the algorithmic skeleton literature [5, 6, 9], but operate on on types rather than on values.
Note that a transformation on vector types does not have any effect on atomic types:
It is easy to show that V(a, n) is closed under Split and Merge. Furthermore, it should be obvious that application of Split and Merge preserves the total size of a vector type.
Essentially, what these operations describe is a mechanism to partition vectors so that the total size and ordering are conserved.
For convenience, we write a multi-dimensional vector as:
-
The Split reshaping operation splits a vector into multiple vectors, which corresponds to a demultiplexer
-
The Merge reshaping operation combines multiple vectors into one, which corresponds to a multiplexer
-
As shown if Fig. 1, the process of demultiplexing requires replication of the node. We will explain in Sect. 4.1 how this replication can be derived from the transformations.
We should note that the interpretation of split and merge in this way is just one possible interpretation of the effect of splitting and merging vectors; it is however the most common one. We will see in Sect. 5 that the actual parallelism depends on the chosen implementation.
3.4 Tuple Types
Let \( Tup \,b_1\,b_2 \ldots \,b_m\overset{not.}{=}(b_1,b_2,\ldots ,b_m)\) be a tuple type, i.e. it represents a record containing values of different types.
By definition, applying a vector type transformation F to a tuple of vectors results in application to every element in the tuple:
Tuple types are used to describe computations with multiple return values. We will further define functions to represent fan-in to a node (zipping) and fan-out from a node (unzipping).
3.5 Function Types
Function types are types of the form \(b_1\rightarrow b_2\rightarrow \ldots \rightarrow b_m\) representing the type of all arguments and the return value. As in Haskell the arrow is right-associative, and partial application is possible.
By definition, applying a vector type transformation F to a function type results in application to every vector type. For example, applying a type transformation F to the type of the map function gives:
4 TyTra-CL: A Functional Coordination Language for Streaming Programming
With the above definitions of vector types and their transformations, we can now show how the actual program transformation can be derived from the type transformations.
To describe the program netlists, we will use TyTra-CLFootnote 4 “Coordination Language”, a very simple statically typed functional language with dependent types. It is in fact a subset of Haskell, except for the use of dependent vector types. Furthermore, as it is a coordination language—in the sense of S-Net [24]—, functions and input vectors only have a type declaration but no implementation.
The core language consists of:
-
vector and tuple types (dependent types) as defined above;
-
function composition (\(\circ \)) and lambda functions;
-
let-bindings (assignment);
-
a set of opaque functions on atomic types \(f_{j}\,{:}:\,a_{i}\rightarrow a_{k}\), i.e. the implementation of the function is not part of the language;
-
the following primitive higher-order functions, with semantics defined in terms of Haskell Prelude functions:

-
primitive in this context means that e.g. map is not defined in terms of any other lower-level language construct.
-
map and fold apply the opaque functions to vectors;
-
zipt and unzipt convert between tuples of vectors and vectors of tuples.
-
In the remainder we will normalise the shape of the program somewhat: for the sake of simplicity and clarity, every program will be written as a series of let bindings. This is not a limitation as let-bindings are syntactic sugar for lambda expressions. However, a program written in this shape makes the edges and nodes in the graph explicit. For example, consider the program in Listing 1 and the corresponding graph representation in Fig. 2. The correspondence between the variables and function applications in the code and the edges and nodes in the graphs is quite clear.

4.1 Deriving Program Transformations from Type Transformations
Given a type transformation on a vector type and the the language as defined above, it is straightforward to derive the transformed program:
-
The Split and Merge type transformations have corresponding split and merge functions that operate on the vector values:
$$\begin{aligned}&split {:}: (k{:}:Int) \rightarrow \hbox {Vec}\, k.m\, b \rightarrow \hbox {Vec} \, k\, \hbox {Vec} \, m \, b&\qquad \qquad&\qquad \qquad&\qquad \qquad \\&merge {:}: \hbox {Vec}\, k\, \hbox {Vec}\, m\, b \rightarrow \hbox {Vec} \, k.m\, b&\qquad \qquad&\qquad \qquad&\qquad \qquad \end{aligned}$$-
The identity \(\mathtt {merge}\, (\mathtt {split}\, k\, v) = v\) holds iff \(v{:}:\hbox {Vec}\;k.m\;b\);
-
the inverse \(\mathtt {split}\, k\, (\mathtt {merge}\, v) = v\) holds iff \(v{:}:\hbox {Vec}\;k\;\hbox {Vec}\;m\;b\).
-
Note that these functions are not exposed to the programmer.
-
-
The program transformations derived from the Split are:

-
The program transformations derived from Merge are:

4.2 Generalising the Primitive Functions
In general, every vector can be split in many different ways. We therefore generalise the functions split, merge, map, fold, zipt and unzipt into n-dimensional versions ndsplit, ndmerge, ndmap, ndfold, ndzipt and ndunzipt:
-
Definitions:
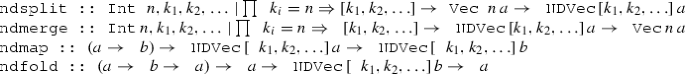
-
We can show that for every valid list of factors ns (i.e. :
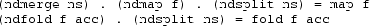
-
We can redefine the LHS as a function of ns:
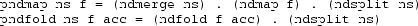
-
For completeness we also define ndzipt and ndunzipt:
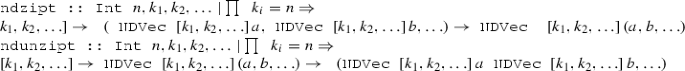
-
Again, we can show that for every valid list of factors ns:

and we can redefine the LHS to pndzipt and pndunzipt
-
In conclusion, we have shown that for every valid list of factors ns:

Thus we have shown that in order to transform the actual netlist (dataflow graph) of the program to optimize its throughput, we do not actually need to transform the program at all! The trivial operation of substitution of the primitive functions with their pnd* counterparts is all that is required.
5 Transforming the TyTra-CL AST
In practice, we do not transform programs in the TyTra-CL. Instead, we transform the Abstract Syntax Tree (AST) of the program.
5.1 Abstract Syntax for the TyTra-CL
The definition of the core of the TyTra-CL abstract syntax in Haskell is given in Listing 2.

The TyTra-CL program is parsed, normalised to a list of assignments and transformed into the actual AST.
The key points to note about this AST are the following:
-
The opaque function nodes MOpaque and FOpaque, which represent functions \(a\rightarrow b\) and \(b\rightarrow a\rightarrow b\) respectively, have an associated PerfCost field which holds the performance and cost figures bases on the TyTraIR implementation (see Sect. 6). The FOpaque node also has an attribute Assoc to indicate if the operation is associative or not. The [Expr] field is used for extra arguments, see the example.
-
The NDMap node takes a list of tuples [(Integer, MVariant)], and similar for NDFold. The variant indicates how the map or fold is implemented. A map can be implemented purely sequentially, as a streaming pipeline or in parallel; a fold (reduction) can be implemented purely sequentially or as a tree if the operation is associative.
For example for a 2-D vector of size 1024, [(1024,Seq)] would mean process 1024 elements sequentially; [(8,Par),(128,Pipe)] means that there will be 8 parallel pipelines that each process 128 scalar elements; [(128,Pipe),(8,Par)] would mean that there is a single pipeline which processes 128 elements as vectors of size 8.
Each of these choices comes with a different cost in terms of requirements for logic gates and buffers, and also a different performance in terms of latency and throughput.
-
As pointed out earlier, NDSplit, NDMerge and NDDistr represent (de-) multiplexing operations, and as such the incur a cost and impact on the performance, so they also carry the (performance, cost) tuple.
-
Initially, the partitioning lists for the various node types, e.g. the [Int] in PNDMap, are empty, which means that no vectors have been transformed.
5.2 AST Transformations and Cost/Performance Calculations
The AST is transformed in three steps:
-
Decompose PND* nodes:
This step is performed only once. The PNDMap and PNDFold operations are replaced by their definitions in terms of NDMerge, NDSplit and NDMap or NDFold and similar for PNDZipT and PNDUnzipT .
-
Combine NDMerge/NDSplit pairs into NDDistr:
Consecutive NDMerge/NDSplit pairs are replaced by NDDistr. This step is also performed only once, and is essential because NDMerge will always return a 1-D vector (i.e. a sequential stream), which is then split by a subsequent NDSplit. This is a potential bottleneck. Instead, NDDistr will generate the most efficient \(n\times m\) multiplexer.
-
Partitioning and Variants:
The AST in this form can be used for obtaining cost/performance estimates simply by populating the partitioning lists (the list describing the nesting of a vector) and variants (i.e. sequential, parallel or pipelined) and generating the TyTraIR. This means that the actual program transformation are essentially expressed as lists of numbers, which makes it possible to use a variety of optimisation and machine learning approaches to find the optimal variant.
6 The TyTra Intermediate Representation Language
Programs written in the TyTra-CL are not directly costable. One option to obtain costs is to emit HDL and perform synthesis and place and route, but that is not practical for exploring a large design-space. We tackled this problem by defining an intermediate abstraction for describing different design variants. This Intermediate Representation (IR) language, which we call the TyTra-IR, serves the additional purpose of providing a hand-off point between the front-end (parsing legacy code, and generating architectural variants through type-transformations) and back-end (evaluating variants, applying low-level back-end optimizations, and generating FPGA solution) of our flow.
We obtain design variants by transforming the AST as discussed earlier, and they are then converted to TyTra-IR. Estimates of performance and resources are made by parsing and analysing the IR, which is also used to generate the final HDL for synthesis and execution on the FPGA.
The TyTra-IR is loosely based on the LLVM-IR, but models the computations on an abstract dataflow machine rather than a Von-Neumann machine. It represents the device-side functionality, and access to host and main memory is over APIs from commercial HLS solutions like Altera-OpenCL or Maxeler. We wrap the TyTra-generated HDL code inside high-level device-side code and that allows us to work with the APIs of these frameworks.
The IR language itself is strongly and statically typed, and uses static single assignments (SSA) to express computations. The compute language component and syntax are based on the LLVM-IR [4], with extensions for coordination, memory access and parallelism. The key semantic differences between Tytra-IR and LLVM-IR are: first, Tytra-IR targets a streaming data-flow architecture, whereas LLVM-IR is designed to be a neutral representation for microprocessor targets; and second, Tytra-IR has functions with added semantics to describe parallelism.
The TyTra-IR instantiates arrays in global memories, and streams which connect to them. This forms the interface to the host, and the compute kernels are expressed using LLVM-IR style SSA expressions. The IR program is then mapped to the shell logic expressed in the HLS framework, and custom HDL pipelines for the required computations (the kernel), which is then integrated with the HLS framework.
The Processing Elements (PEs) of the kernel are described using a hierarchy of functions. They are different from LLVM functions, and can be better related to modules in HDLs like Verilog. They are described at a higher abstraction than HDLs though. Keywords associated with each function express parallelism patterns like pipeline parallelism, thread parallelism, and sequential execution. Using functions with these keywords in various patterns allows us to express the dataflow architecture on the FPGA for a given kernel. There are some restrictions on what type of function combinations we can use in the TyTra-flow, which leads to a limited set of valid configurations that is appropriate in the context of the scientific-computing target domain. We assume that we would want to create deep and custom pipelines on the FPGA for the kernel we wish to accelerate, and additionally we would want to replicate these pipelines when resources allow. The allowed set of configurations follows from these assumptions.
7 The TyTra Cost Model
The TyTra cost model is an analytical model that uses parameters obtained from data sheets as well as synthetic test benches. We make use of the roofline analysis [27], which is a model for estimating the performance, and has been adapted for FPGAs [8]. The constraints to performance are represented by two rooflines, one for the maximum Computational Performance (CP) of the device, and another for the maximum Bandwidth (BW) to the main memory. They are placed on a performance (FLOPS/s) versus operational (or computational) intensity (CI) plane, where CI is defined as the number of word operations performed per word accessed to/from main memory. The performance of a kernel is defined in the model as follows (shown visually in Fig. 3):
\( Attainable~Performance (FLOPS/sec) = min (CP, BW \cdot CI) \)
The original roofline model [27], showing a memory-bound and a compute-bound kernel
We have developed a prototype compilerFootnote 5 that accepts a design variant in TyTra-IR, estimates its cost and performance and plots it on the roofline model, and if needed, generates the HDL code for it. The details of the flow and the cost-model are outside the scope of this paper. Figure 4 is a high-level view of the flow and there is some background in [19, 20] on how we make estimates of performance, memory bandwidth, as well as FPGA-resource utilization. In this section we focus on illustrating the use of this cost model rather than its implementation details.
The TyTra back-end compiler flow, showing the estimation (blue/first three stages), HDL code generation (yellow/next three stages), and OpenCL shell code generation (pink/last stage) flow. The starting point for this subset of the entire TyTra flow is the TyTra-IR description representing a particular design variant (Color figure online)
7.1 An Illustration of Using the Roofline Cost Model in the TyTra Compiler
As discussed earlier, we can use the type transformations to generate variants of the program by reshaping the data, which means we can take a single stream of size N and transform it into L streams of size \({N}\over {L}\), where L is the number of concurrent lanes of execution in the corresponding design variant. This high level translation transforms to scaling the number of PEs.
We show the roofline analysis of the variants thus generated in Fig. 5. The first variant (top-left) with a single PE intersects the computational roof of the design. So this variant is compute-bound. With the performance well below the peak computational capacity of the device for this algorithm (the blue dotted line), there is clearly room for improvement. This improvement can be seen in the next variant, where splitting the PE into two copies raises the computational roof, with a corresponding increase in performance. Similarly, the next variant shows improved performance for 4 PEs. However any further splitting and replication does not yield performance dividends as we hit the memory bandwidth which is independent of the number of PEs.
The TyTra backend that estimates these costs is very fast, even though it is currently implemented in Perl. It takes a mere 0.3 s to evaluate one variant, which is more than 200\(\times \) faster than e.g. the preliminary estimates generated by Xilinx’s SDAccel which takes close to 70 s.
7.2 Accuracy of the Cost Model
Investigating the accuracy of our cost model based on preliminary experiments on small but realistic scientific kernels has yielded very promising results. We evaluated the estimated versus actualFootnote 6 utilization of resources for the kernel pipelines, and throughput measured in terms of cycles-per-kernel-instance.
The evaluation was done on the integer version of kernels from three HPC scientific applications: The successive over-relaxation kernel from the LES weather model that has been discussed earlier; the hotspot benchmark from the Rodinia HPC benchmark suite [3], used to estimate processor temperature based on an architectural floorplan and simulated power measurements; the lavaMD molecular dynamics application also from Rodinia, which calculates particle potential and relocation due to mutual forces between particles within a large 3D space. Our observation, that a constrained IR at the suitable abstraction will let us make quick and accurate estimates, is confirmed by these results as shown in Table 1
8 Exemplar: Successive Over-Relaxation (SOR)
We consider an SOR kernel (Listing 3), taken from the code for the Large Eddy Simulator for Urban Flows, an experimental weather simulator [21]. The kernel iteratively solves the Poisson equation for the atmospheric pressure and is the most time-consuming part of the simulator. The main computation is a stencil over the neighbouring cells (which is inherently parallel).

8.1 The Route from Fortran
In practice, most scientific code in the field of numerical weather prediction and climate simulation is written in Fortran, and still for the largest part effectively in FORTRAN 77. It might therefore seem that our functional language based approach is impractical. In this section we explain the route from Fortran to the TyTra-CL and TyTra-IR.
Because of its age, FORTRAN 77 has many issues, especially in terms of maintainability and correctness. As a first step we therefore refactor FORTRAN 77 into Fortran 95 which features a.o. a module system with qualified imports and much better type checking. The compiler we developed for this purposeFootnote 7 also replaces all global variables with function arguments, allowing easy offloading of portions of the code to accelerators.
Our observation has been that programs in our application domain are typically using loops to operate on static arrays. The SOR kernel above is a good example. We have created a separateFootnote 8 compilerFootnote 9 which analyses Fortran code in terms of map and fold and generates a subroutine corresponding to the body of every loop nest. The code in this form is not only ready for parallelisation with e.g. OpenCL, but effectively consists of sequences of applications of maps and folds applied to opaque functions, so that we can convert it directly into a TyTra-CL program.
Our compiler transforms the complete Large Eddy Simulator main loop code (i.e. everything except file I/O) into 33 kernels, 29 of which are maps and 4 folds. This code is representative for many computational fluid dynamics codes and illustrates the validity of our approach.
A discussion of this source-to-source compilation toolchain, including performance results on the LES, can be found in [26].
We have also created a pass for our compiler which refactors the code into the form required by our opaque functions, i.e. instead of array accesses, the functions can only take scalars. In practice this means that the function takes a tuple of variables corresponding to every array access in a loop nest. The compiler has an OpenCL C backend and we use the LLVM clang front-end to generate LLVM IR, which is used as input for our TyTra-IR toolchain. The TyTra-IR compiler transforms the original LLVM IR into a pipelined datapath as explained in Sect. 6. Consequently, at the level of the opaque function the operation is always pipelined.
This is currently work in progress because the emitter from the map-and-fold based transformed Fortran code to TyTraCL is not yet finalized. As explained in [26], our current flow emits OpenCL host and kernel code suitable for GPU acceleration.
8.2 Transforming the SOR Kernel
The TyTra-CL version of the above program is very simple:

The corresponding AST is equally simple:

We can now apply a transformation where we for example split the vector into 4 parts and interpret this as 4 parallel lanes by using the Par variant of NDMap. We have expanded the AST as described before. The cost and performance for the actual kernel \(f_{sor}\) have been obtained from its IR representation using the TyTra-IR compiler.

We can generate many variants by changing the number of parts into which we split the vector and the variant for each part. However, as explained in Sect. 7, the cost model informs us that for splits higher than 4 we already hit the resource limits so the above transformation is the best candidate.
8.3 Comparison of TyTra-Generated Hyrbid Solution Against Two HLS Tools
As discussed earlier, our approach for generating a complete solution for FPGAs is to use a commercially available HLS tool for host-device API, as well as the generate the shell logic on the FPGA for interfacing with the DRAM and the host. The kernel is implemented using HDL generated by our back-end compiler. In this section, we compare this hybrid approach against baselines. Both the hybrid and the clean solutions are compared for two commercial HLS tools, Altera-OpenCL and Maxeler.
8.3.1 Experimental Setup
Altera (now Intel) OpenCL for FPGAs allows designers to program FPGAs using the OpenCL programming framework, effectively providing a “C-to-gates” route. It is an attractive framework to target for creating solutions in the TyTra flow, as it allows us to generate portable solutions that would also work with other FPGA-OpenCL tools like Xilinx’s Sdaccel, and eventually with truly heterogeneous platforms. Altera-OpenCL allows designers to integrate their custom HDL as library functions inside the C-based OpenCL framework, and this provides us with the opportunity to generate complete solutions based on our TyBEC-generated HDL dataflow (see Fig. 4).
The setup for the experiments using Altera-OCL+HDL flow is shown in Fig. 6.
A similar experimental setup was done for the Maxeler’s MaxJ [23] HLS design tool for FPGAs, which provides a Java meta-programming model for describing computation kernels and connecting data streams between them. Like Altera-OCL, Maxeler allows integration of custom HDL code into their HLS framework.
The CPU implementation (cpu) is compiled with gfortran -Ofast. One FPGA implementation is generated using the the HLS flow only (\(\textit{fpga-<HLS-tool-name>}\)), which incorporates pipeline parallelism automatically extracted by the HLS tool. Another FPGA implementation (fpga-tytra) is the design variant generated by the TyTra back-end compiler, based on a high-level type transformation that introduced parallelism (4\(\times \)PEs) in addition to pipeline parallelism. We collected performance results for both tools for different dimensions of the input arrays, i.e. im, jm, km, and also collected energy results for one of the solutions.
8.3.2 Performance Comparison
The performance comparison against Maxeler is shown in Fig. 7 (left). Note that fpga-maxJ could in principle be optimized manually to achieve a similar performance as fpga-tytra, but we deliberately use an unoptimized baseline for fpga-maxJ. Our contention is that by using our approach, one can obviate the need to carry out manual optimizations in an HLS tool like Maxeler. Hence our comparison is against an unoptimized HLS solution.
Apart from the smallest grid-size, fpga-tytra consistently outperforms fpga-maxJ as well as cpu, showing up to 3.9\(\times \) and 2.6\(\times \) improvement over fpga-maxJ and cpu respectively. In general, FPGA solutions tend to perform much better than CPU at large dimensions.
If we look at the (the fpga-tytra-est column) showing the performance predicted by our cost model, we can see they are not as accurate as the kernel-only estimates in Table 1. The introduction of the shell adds a degree of inaccuracy to the performance estimate, which in the worst case in this particular example is off by 2.35\(\times \). However, the use-case of finding the best variant from a search-space is still very much applicable as these results show.
Figure 8 shows the result of comparison against Altera-OpenCL (AOCL), using a 2D SOR kernel.Footnote 10 The Tytra solution (with an AOCL shell) yields an order of magnitude better performance than the AOCL-only solution on the same FPGA.
Both these performance comparison results clearly indicate that a straightforward implementation on an HLS tool will not be optimal and manual effort would be required; the TyTra flow can automate this.
8.3.3 Energy Comparison
For the energy figures, we used the actual power consumption of the host+device measured at the node’s power socket using a WattsUp power meter on the Maxeler desktop node. For a fair comparison, we noted the increase in power from the idle CPU power, for both CPU-only and CPU-FPGA solutions. As shown in Fig. 7, FPGAs very quickly overtake CPU-only solutions, and fpga-tytra solution shows up to 11\(\times \) and 2.9\(\times \) power-efficiency improvement over cpu and fpga-maxJ respectively. The energy comparison further demonstrates the utility of adopting FPGAs in general for scientific kernels, and specifically our approach of using type transformations for finding the best design variant.
8.3.4 Resource Utilization Comparison
Previous results show the optimized hybrid TyTra solution compared with baseline, unoptimized solutions using HLS tools. Here we compare what happens when we compare like-for-like variants, that is the same optimization using the two approaches, with the AOCL tool as the baseline. The results are shown in Fig. 9.Footnote 11 We also compare the effect of varying the array sizes for both cases, which effect the size of internal buffers for stencil data, and hence effect resource utilization.
We can see that the resource utilization is comparable for the baseline solution with one PE. However, when we optimize the design by replicating the PEs, then the AOCL-only solution—which implements the optimization by changing the number of compute-units in the OpenCL code—takes up much more resources than the AOCL-TyTra solution, especially in the utilization of BRAMs. A similar observation is made for the case when we fix the design to one PE, and change the size of data . In fact, the AOCL-only solution do not even synthesize in most cases as the available BRAM resources are exceeded. These results make a strong case for using our flow not just to generate or evaluate the variants, but also to implement them based on our generated HDL code.
9 Conclusion
FPGAs are increasingly being used in HPC for acceleration of scientific kernels. While the typical route to implementation is the use of high-level synthesis tools like Maxeler or OpenCL, such tools may not necessarily fully expose the parallelism in the FPGA in a straightforward manner. Hand-tuning designs to exploit the available FPGA resources on these HLS tools is possible but still requires considerable effort and expertise.
We have presented an original compilation flow that, starting from high-level program in a functional coordination language based on opaque, costable functions and higher-order functions, generates correct-by-construction design variants using type-driven program transformations, evaluates the generated variants using an analytical cost model on an intermediate description of the kernel, and emits the HDL code for the optimal variant.
We have introduced the theoretical framework of the vector type transformations and shown how program transformations in our TyTra-CL language can be automatically derived from the type transformations, with guaranteed correctness. We have explained compilation from TyTra-CL to TyTra-IR and the costing of the designs using the analytical cost model. The accuracy of the cost model was shown across three kernels: a kernel from the LES weather simulator, and two kernels from the Rodinia benchmark.
A case study based on the successive over-relaxation kernel from a real-world weather simulator was used to demonstrate the high-level type transformations. It was also used to give an illustration of a working solution based on HDL code generated from our compiler, shown to perform better than the baseline Maxeler HLS solution.
Our work presents a proof of concept for a solution which allows high level programming with a route from legacy Fortran code, and which will automatically converge on the best design variant from a single high-level description of the algorithm in a functional language through a combination of correct-by-construction program transformation and fast analytical cost models. Our future work focuses on completing the compiler toolchain, and in particular investigating the use of machine learning to explore the potentially very large search space of transformed programs.
Notes
The actual resource utilization figures are based on full synthesis, and actual cycle-counts are from RTL simulations. The design entry for these experiments is in Verilog RTL. The RTL is generated from TyTra-IR description using our back-end compiler.
This is purely an accident of history.
As opposed to the fpga-tytra or the fpga-maxj solution, we were unable to use on-chip buffers for stencil data in the fpga-aocl solution, as AOCL failed to synthesize within available resources (see Fig. 9). Hence the fpga-aocl solution accesses the main memory for every data-point in the stencil, which affects its performance.
Full synthesis results are used, apart from cases where design could not synthesize because required resources exceeded availability, in which case we used estimated resources emitted by AOCL.
References
Agron, J.: Domain-Specific Language for HW/SW Co-design for FPGAs, pp. 262–284. Springer, Berlin (2009). https://doi.org/10.1007/978-3-642-03034-5_13
Canis, A., Choi, J., Aldham, M., Zhang, V., Kammoona, A., Anderson, J.H., Brown, S., Czajkowski, T.: Legup: High-level synthesis for FPGA-based processor/accelerator systems. In: Proceedings of the 19th ACM/SIGDA International Symposium on FPGAs, FPGA’11, pp. 33–36. ACM, New York, NY, USA (2011)
Che, S., Boyer, M., Meng, J., Tarjan, D., Sheaffer, J., Lee, S.H., Skadron, K.: Rodinia: A benchmark suite for heterogeneous computing. In: IEEE International Symposium on Workload Characterization, 2009. IISWC 2009, pp. 44–54 (2009). https://doi.org/10.1109/IISWC.2009.5306797
Chris, L., Vikram, A.: The LLVM Instruction Set and Compilation Strategy. Technical Report UIUCDCS-R-2002-2292, CS Department, University of Illinois at Urbana-Champaign (2002)
Cole, M.: Algorithmic skeletons. In: Hammond, K., Michaelson, G. (eds.) Research Directions in Parallel Functional Programming, pp. 289–303. Springer, London (1999)
Cole, M.: Bringing skeletons out of the closet: a pragmatic manifesto for skeletal parallel programming. Parallel Comput. 30(3), 389–406 (2004). https://doi.org/10.1016/j.parco.2003.12.002
Czajkowski, T., Aydonat, U., Denisenko, D., Freeman, J., Kinsner, M., Neto, D., Wong, J., Yiannacouras, P., Singh, D.: From OpenCL to high-performance hardware on FPGAs. In: 22nd International Conference on Field Programmable Logic and Applications (FPL), 2012, pp. 531–534 (2012). https://doi.org/10.1109/FPL.2012.6339272
da Silva, B., Braeken, A., D’Hollander, E.H., Touhafi, A.: Performance modeling for FPGAs: extending the roofline model with high-level synthesis tools. Int. J. Reconfig. Comput. 2013, 7:7–7:7 (2013). https://doi.org/10.1155/2013/428078
Darlington, J., Field, A., Harrison, P., Kelly, P., Sharp, D., Wu, Q., While, R.: Parallel programming using skeleton functions. In: PARLE’93 Parallel Architectures and Languages Europe, pp. 146–160. Springer (1993)
Deng, L., Sobti, K., Zhang, Y., Chakrabarti, C.: Accurate area, time and power models for FPGA-based implementations. J. Signal Process. Syst. 63(1), 39–50 (2011)
Kaul, M., Vemuri, R., Govindarajan, S., Ouaiss, I.: An automated temporal partitioning and loop fission approach for FPGA based reconfigurable synthesis of DSP applications. In: Proceedings of the 36th Annual ACM/IEEE Design Automation Conference, DAC’99, pp. 616–622. ACM, New York, NY, USA (1999). https://doi.org/10.1145/309847.310010
Keinert, Jea: Systemcodesigner;an automatic esl synthesis approach by design space exploration and behavioral synthesis for streaming applications. ACM Trans. Des. Autom. Electron. Syst. 14(1), 1:1–1:23 (2009)
Kerr, A., Diamos, G., Yalamanchili, S.: Modeling GPU-CPU workloads and systems. In: Proceedings of the 3rd Workshop on General-Purpose Computation on Graphics Processing Units, GPGPU ’10, pp. 31–42. ACM, New York, NY, USA (2010). http://doi.acm.org.prx.library.gatech.edu/10.1145/1735688.1735696
Keutzer, K., Ravindran, K., Satish, N., Jin, Y.: An automated exploration framework for FPGA-based soft multiprocessor systems. In: Third IEEE/ACM/IFIP International Conference on Hardware/Software Codesign and System Synthesis, 2005. CODES+ISSS’05, pp. 273–278 (2005). https://doi.org/10.1145/1084834.1084903
Korinth, J., de la Chevallerie, D., Koch, A.: An open-source tool flow for the composition of reconfigurable hardware thread pool architectures. In: IEEE 23rd Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), 2015, pp. 195–198. IEEE (2015)
Kulkarni, C., Brebner, G., Schelle, G.: Mapping a domain specific language to a platform FPGA. In: Proceedings of the 41st Annual Design Automation Conference, DAC’04, pp. 924–927. ACM, New York, NY, USA (2004). https://doi.org/10.1145/996566.996811
Kulkarni, D., Najjar, W.A., Rinker, R., Kurdahi, F.J.: Compile-time area estimation for LUT-based FPGAs. ACM Trans. Des. Autom. Electron. Syst. (TODAES) 11(1), 104–122 (2006)
Mehri, H., Alizadeh, B.: Analytical performance model for FPGA-based reconfigurable computing. Microprocess. Microsyst. 39(8), 796–806 (2015). https://doi.org/10.1016/j.micpro.2015.09.009
Nabi, S.W., Vanderbauwhede, W.: Using type transformations to generate program variants for FPGA design space exploration. In: 2015 International Conference on ReConFigurable Computing and FPGAs (ReConFig), pp. 1–6 (2015). https://doi.org/10.1109/ReConFig.2015.7393365
Nabi, S.W., Vanderbauwhede, W.: A fast and accurate cost model for FPGA design space exploration in HPC applications. In: 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), pp. 114–123 (2016). https://doi.org/10.1109/IPDPSW.2016.155
Nakayama, H., Takemi, T., Nagai, H.: Large-eddy simulation of urban boundary-layer flows by generating turbulent inflows from mesoscale meteorological simulations. Atmos. Sci. Lett. 13(3), 180–186 (2012)
Park, J., Diniz, P.C., Shayee, K.R.S.: Performance and area modeling of complete FPGA designs in the presence of loop transformations. IEEE Trans. Comput. 53(11), 1420–1435 (2004). https://doi.org/10.1109/TC.2004.101
Pell, O., Averbukh, V.: Maximum performance computing with dataflow engines. Comput. Sci. Eng. 14(4), 98–103 (2012). https://doi.org/10.1109/MCSE.2012.78
Penczek, F., Herhut, S., Scholz, S.B., Shafarenko, A., Yang, J., Chen, C.Y., Bagherzadeh, N., Grelck, C.: Message driven programming with s-net: methodology and performance. In: 39th International Conference on Parallel Processing Workshops (ICPPW), 2010, pp. 405–412. IEEE (2010)
Segal, O., Colangelo, P., Nasiri, N., Qian, Z., Margala, M.: Sparkcl: A unified programming framework for accelerators on heterogeneous clusters. CoRR arXiv:abs/1505.01120 (2015)
Vanderbauwhede, W., Davidson, G.: Domain-specific acceleration and auto-parallelization of legacy scientific code in FORTRAN 77 using source-to-source compilation. Comput. Fluids. ArXiv preprint arXiv:1711.04471 (2017)
Williams, S., Waterman, A., Patterson, D.: Roofline: an insightful visual performance model for multicore architectures. Commun. ACM 52(4), 65–76 (2009). https://doi.org/10.1145/1498765.1498785
Xilinx: The Xilinx SDAccel Development Environment. http://www.xilinx.com/publications/prod_mktg/sdx/sdaccel-backgrounder.pdf (2014)
Acknowledgements
The authors acknowledge the support of the UK EPSRC for the TyTra project (EP/L00058X/1).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Vanderbauwhede, W., Nabi, S.W. & Urlea, C. Type-Driven Automated Program Transformations and Cost Modelling for Optimising Streaming Programs on FPGAs. Int J Parallel Prog 47, 114–136 (2019). https://doi.org/10.1007/s10766-018-0572-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10766-018-0572-z