Efficient Processing of Large Data Structures on GPUs: Enumeration Scheme Based Optimisation

Abstract

The purpose of this paper is to highlight the performance issues of the matrix transposition algorithms for large matrices, relating to the Translation Lookaside Buffer (TLB) cache. The existing optimisation techniques such as coalesced access and the use of shared memory, regardless of their necessity and benefits, are not sufficient enough to neutralise the problem. As the data problem size increases, these optimisations do not exploit data locality effectively enough to counteract the detrimental effects of TLB cache misses. We propose a new optimisation technique that counteracts the performance degradation of these algorithms and seamlessly complements current optimisations. Our optimisation is based on detailed analysis of enumeration schemes that can be applied to either individual matrix entries or blocks (sub-matrices). The key advantage of these enumeration schemes is that they do not incur matrix storage format conversion because they operate on canonical matrix layouts. In addition, several cache-efficient matrix transposition algorithms based on enumeration schemes are offered—an improved version of the in-place algorithm for square matrices, out-of-place algorithm for rectangular matrices and two 3D involutions. We demonstrate that the choice of the enumeration schemes and their parametrisation can have a direct and significant impact on the algorithm’s memory access pattern. Our in-place version of the algorithm delivers up to 100% performance improvement over the existing optimisation techniques. Meanwhile, for the out-of-place version we observe up to 300% performance gain over the NVidia’s algorithm. We also offer improved versions of two involution transpositions for the 3D matrices that can achieve performance increase up 300%. To the best of our knowledge, this is the first effective attempt to control the logical-to-physical block association through the design of enumeration schemes in the context of matrix transposition.

1 Introduction

Matrix transposition is one of the fundamental operations in linear algebra, and is used in many scientific and engineering applications [9]. Over the past few decades, many algorithms dedicated to matrix transposition were proposed [1, 8, 17, 30]. The majority of them have been dedicated to rectangular matrices and were based on a thorough mathematical analysis of permutation cycles [4].

As computer systems advanced, it was realised that the system architecture can significantly influence the performance of transposition algorithms. Over many years, existing algorithms were improved, and new ones were designed from the ground up to reflect new trends in a computer design [7]. The faster the systems became, the larger the matrices scientists and engineers wanted to work with. Sometimes, the size of the matrix was larger than the operational memory capacity, which led to the introduction of out-of-core algorithms [16]. Transposition algorithms also had difficulty running fast enough, even with faster CPUs available. With time, multi-CPU solutions were proposed to tackle the computational deficiencies of the existing solutions. However, with the advent of GPGPU technology, a new unexplored realm of massively parallel computing became available, offering both scalability and performance benefits. In many domains, GPU based algorithms successfully outperformed traditional single or multi CPU approaches. A new class of transposition algorithms were proposed to take advantage of this new technology. GPU versions of in-place algorithms for rectangular matrices were described in [3, 26] and the performance considerations of out-of-place algorithms were explained in [24]. In addition, based on the optimisations techniques described in [24], a new range of efficient 3D matrix transposition algorithms have been proposed in [14]. However, since the research on processing large data structures on GPUs is so scarce, we investigate whether the existing optimisations are adequate and if the new methods are required.

Recently, a new approach for transposing square matrices in parallel computing environments was proposed [10]. In our research, we focus on in-place and out-of-place transposition performed on square matrices. However, some of the presented concepts can also be applied to rectangular matrices, or even 3D matrices Our main goal is to design an algorithm that is both computational and resource efficient. We try to develop a solution that is independent of any specific hardware platform. Nevertheless, we decided to conduct our initial tests on CUDA capable devices.

The contributions of this paper are as follows:

• We present an extended version of the concept of mapping a rectangular grid of elements onto a triangular part of a matrix. This mapping is achieved using various enumeration schemes and can be applied to both cores [10] or blocks as we propose.

• We describe in detail how enumeration schemes can be used to mitigate performance problems associated with TLB cache misses, and how to control memory access pattern through them.

• We offer an improved version of a thread-wise algorithm that delivers stable performance and high throughput regardless of matrix size.

• We propose a modified version of NVIDIA’s out-of-place algorithm by applying an enumeration scheme that delivers sustained high throughput for large matrices.

• We demonstrate that the 3D matrix transposition presented in [14] is also susceptible to the TLB cache misses. An improved version of the involution transposition $T_{\textit{yxz}}$ is suggested.

The rest of the paper is organised as follows: Sect. 3 explains the general concept of mapping a rectangular grid of elements onto the entries of the triangular part of the matrix. We extend the analysis of this technique described in [10] and propose an improved version of the transposition algorithm. Section 4 describes some of general properties that enumeration schemes can feature. Detailed analysis of the triangular schemes is presented in Sects. 4.1 and 5. The rectangular schemes are briefly discussed in Sect. 6. Section 7 shows the results of the performance tests we conducted using our algorithm and existing approaches. Finally, conclusions are presented in Section 8.

2 Prior Art

Knowledge of complex multi-level memory hierarchies, together with exploiting the data locality (through tiling and block data layouts) provide the best strategy to design an efficient matrix transposition algorithm and overcome performance issues related to the sub-optimal memory access patterns.

In [31], various loop transformations are introduced that subdivide an iteration space into tiles or blocks. These blocks become units of work for any further parallel processing. As stated in [31], the iteration space does not have to be rectangular, which allowed for many other interesting space shapes such as triangular or trapezoidal.

Similarly, Kim et al. [15] explored the concept of tiling a little further and developed an efficient algorithm that can generate multi-level parametrised tiled loops.

Park et al. [23] demonstrated that tiling and block data layout techniques could reduce TLB misses. They concluded that these optimisation techniques deliver better TLB performance over the other methods. They also highlighted that as the data problem sizes become larger, the detrimental effect of TLB thrashing becomes more discernible. Their experiments were validated using a tiled version of matrix multiplication, LU decomposition, and Cholesky factorisation.

The recursive blocked data formats introduced by Gustavson et al. [12] allow for efficient utilisation of memory hierarchy. They proposed a hybrid technique that, at the block level, stores matrix entries in either row-major or column-major order. The size of a block is limited by the size of the cache and it was assumed that only a few of them will occupy the cache. The blocks are stored recursively, and variants for rectangular and triangular are described.

Another interesting cache oblivious algorithm was described by Bader and Zenger [2]. They argued that while Morton ordering can provide temporal locality during matrix multiplication, it may not be sufficient for the spatial locality. Instead, using the Peano curve, they subdivided the matrix recursively into 3-by-3 blocks. They demonstrated that their approach can completely avoid jumps in the address space. However, the utilisation of space filling curves as an element or block ordering scheme is limited to square matrices.

Performance tests conducted on various multi-core platforms and presented by Heinecke and Bader [13] confirmed that the space filling curves are computationally viable. In particular, they showed that the Peano-curve based matrix multiplication algorithm offers better scalability than the other parallel implementations and exhibit strong data locality properties. The majority of matrix transposition optimisation research studies dedicated to tiling, block data layouts and TLB performance were mainly focused on single or multi-CPU environments [5, 11, 29].

For instance, Chatterjee and Sen [5] proposed several in-place transposition algorithms for square matrices. They investigated various memory models and experimentally validated their performance. They demonstrated that by using a Morton layout their cache efficient transposition algorithm offered better performance than other canonical layouts. Thanks to two level tiling they were able to reduce the number of TLB misses, because virtual memory pages were holding sub-matrices instead of rows or columns.

The algorithms using block structures (tiles) and utilising element ordering based on space filling curves subdivide the matrices recursively into smaller matrices [2, 5, 13]. Usually, the recursion terminates when tile size matches architecture specific cache size [5]. In most cases, the order of the elements within a single tile is architecture dependent and typically row-major or column-major layouts are used. The use of Peano-curve or Morton order to enumerate blocks is restricted to certain matrix sizes. One way to overcome such a limitations is to normalise the size of a matrix with zero-padding [13].

Gustavson et al. [11] presented an efficient parallel algorithm for in-place transposition. They also described standard and blocked matrix storage conversion techniques and emphasised that blocked data layouts can reduce number of the TLB misses.

Recently, based on the work presented in [15], Wei and Mellor-Crummey [29] exploited data locality to avoid cache and TLB misses. Their framework for optimised parallel out-of-place tensor transposition achieved high throughput in single and multi-socket systems.

In massively parallel computational environments such as GPUs, the impact of the TLB cache is not yet well researched, especially when large data sets are being processed, i.e., during the matrix transposition. To date, there are few notable studies that explain the internal cache and memory structures on GPUs [28, 32]. However, these papers do not target TLB related issues which arise when large data structures are processed by the memory bound algorithms. Matrix transposition solutions presented in [3, 24, 26] include many GPU specific optimisations, yet they also do not consider the impact of the TLB on algorithm performance.

The in-place and out-of-place transposition of the 3D matrices described in [14] utilises the performance optimisations proposed in [24]. We will demonstrate that these optimisations are not sufficient to achieve high and stable throughput when large 3D matrices are transposed.

The data layout transformations on GPUs have been also proposed for structured grid applications operating on multidimensional dense arrays [25]. This work identifies a flattening function FF that defines a linearization of coordinates of elements in a grid. Depending on its definition different memory layouts can be achieved. In contrast, the pairing function ${\varPi }$ we introduce is used to translate element coordinates without changing the data physical layout. In other words, we manage the logical relation between the elements and the given data layout.

In addition, we realise that as the GPU’s global memory increases with new hardware, it is certain that many of the existing GPU-specific optimisations will not be sufficient to mitigate the detrimental effects that TLB thrashing incurs. NVIDIA’s plan to launch a 32GB GPU with Pascal architecture and the introduction of a technology called NVLink [19] that offers data transfers at much higher rate than the traditional PCI Express interconnect, will stress all the existing algorithms even more. Nevertheless, we suspect that once all the issues are overcome, the GPU based solutions will be favoured over their CPU counterparts.

3 Background

Matrix transposition is one of the simplest yet important algebraic operations that can be applied to matrices. When performed on a computer system, hardware specific limitations such as memory bandwidth or cache size are factors resulting in poor overall performance. In our research we try to tackle these problems and propose an algorithm that offers both stable and high performance regardless of the input matrix’s size. Although we primarily concentrate on the in-place (IP) transposition of square matrices performed in parallel computing environments, the idea presented below can be also be used to improve the out-of-place (OOP) transposition of rectangular matrices or even 3D matrices [14].

Usually the techniques described in [24] are extensively exploited to improve memory operations during the matrix transpose. Because the whole matrix occupies global memory, aligned and coalesced access are used to maximise read and write throughput. Otherwise, thread block accessing range of addresses can cause multiple load/store operations to be issued.

Shared memory has the benefit of lower latency and higher bandwidth than global memory. It can only be accessed by device code and depending on the GPU architecture it can offer up to 96KB of memory per Streaming Multiprocessor (SM). This size limit affects the number of thread blocks that can occupy any single SM. Poor allocation of shared memory resources can result in low occupancy or suboptimal pipe utilisation.

Shared memory is especially helpful during matrix transposition. Each thread block maps onto the relevant block of entries within a matrix. Threads within a block cooperatively read matrix entries row-wise and store them in shared memory (tile) column-wise. Once the whole block of entries is copied to shared memory, the same thread block reads it row-wise from the tile and stores in the destination location. Listing 1 presents the pseud-code for the out-ouf-place kernel. The index of the source and destination elements is based on the thread and block coordinates within a grid.

As was shown in [24] this approach delivers the best performance of the out-of-place transposition of square matrices. In order to transpose square matrix in place the above mentioned optimisation techniques still apply. However, minor modification of the kernel are required. During the in-place transposition, two tiles are maintained and exchanged by a single thread block. As before, the source and destination index of the matrix elements is obtained from the thread and block coordinates. For example, the Listing 2 shows a simplified version of the in-place transposition kernel. The if statement ensures that only blocks below or on the main diagonal participate in the transposition. The use of branching is not advised in CUDA parallel programming as it can cause thread divergence. However, since the if statement does only affect the execution path of all threads in a block, this does not introduce any branching at a single thread level. Nevertheless, its presence can have some impact on algorithm performance.

The above mentioned optimisations are regularly employed in memory-bound algorithms. So far they have been sufficient to improve performance of matrix transposition algorithms. But their limitations arise from the fact they were introduced to tackle specific performance issues. As the new generations of the GPUs feature an increased amount of global memory the ineffectiveness of these optimisations becomes more evident. Matrix transposition is good example of an algorithm that lacks both temporal and spatial locality [5]. When transposing large matrices the corresponding pairs of transposed elements can be located close to each other or far apart. This potentially leads to a situation where virtual memory pages are excessively used, causing TLB thrashing. We will discuss this issue furhter in the following section.

3.1 Problem Definition

Based on our tests, both of the presented kernels deliver high throughput. However, we observed that as the size of the matrix increases the performance of these solutions gradually deteriorates.

In Fig. 2, we can clearly see that for matrices of an order 24 and beyond the throughput starts to decline. Since we know that the access to global memory is optimised, there has to be another reason for this behaviour.

From the matrix transposition definition, the location of two entries situated at $x + my$ and $y + xm$ is swapped. We can realise that the larger the matrix is, the bigger the address difference between corresponding elements becomes.

Because there is usually one specific type of cache used during the virtual address translation, we suspected that the TLB cache was responsible for the performance degradation. Unfortunately, the TLB’s structure and size remains NVIDIA’s well-kept secret. TLB structures on GPUs can be more complex than their CPU counterparts [6]. Furthermore, on multi-core platforms, only a few threads access the main memory, while on GPUs there can be thousands of threads accessing the global memory [6]. The heuristic nature of cache eviction algorithms makes the TLB less predictable and harder to control programmatically.

There are only a few published works that focus on the TLB’s structure and size on GPUs [28, 32]. Through specially crafted micro-benchmarking, it is possible to reveal some of its properties such as size or type. However, it is more difficult to determine how it behaves when the data problem size is increased and the spatial locality is not maintained. Usually in this situation, the original logic needs to be revised and adjusted using smaller kernels [27]. Thus, the matrix is further divided into separate, independent grids—square regions. Each region becomes part of a super grid, spanning over the entire matrix. Figure 1 presents this concepts. Such an approach, although well studied [18] and commonly practised in heterogeneous computing environments, introduces strong interdependence between host and device code. Hence, we argue that it is more feasible to design efficient “pure” GPU algorithms without the need to employ hybrid solutions.

Fig. 1

Logical decomposition of matrix M into blocks and regions

Since CUDA does not allow natively creating super grids, the host code is responsible for splitting the matrix into regions and maintaining their respective sizes and indexes. In addition, the host code needs to supply the kernel with the region’s index so that it was possible to obtain the absolute thread block index within the matrix element’s space. The revised version of the region-based IP kernel and the fragment of the host application are presented in the Listings 3 and 4 below. The order of a region (r) is a multiple of block size b. This time the if statement ensures not only that the block is located below or on the main diagonal, but also that it remains within the matrix element’s space.

Figure 2 compares the performance of the original IP and OOP kernels with the super grid (SG) version of the IP kernel. It is evident that the multi-kernel approach can eliminate the effects of TLB thrashing. Specifically, the GPU kernel is invoked by the host application $\frac{n_r^2+n_r}{2}$ times, where . The smaller the region size, the lower the chance that the TLB misses will occur, but this also means that more smaller grids will need to be spawned by the host code. Larger region size decreases the number of kernels to run, but it also increases the risk that the TLB starts affecting performance. Lastly, the $n_r$ regions located on the main diagonal of the $M_r$ matrix are defined as a square grid comprised of r blocks. However, only $\frac{r^2+r}{2}$ of them participate in the transposition. The remaining idle blocks can be regarded as computational resource overhead that can have some impact on the kernels’ performance.

Fig. 2

Performance comparison of IP and OOP algorithms with Super Grid version of the IP algorithm

3.2 Transparent Block Reordering

Naturally, for square matrices, it would be simpler to define a triangular grid of blocks, but CUDA does not support such a concept. It is possible, however to do so at code level by mapping a rectangular grid of threads onto triangular part of the matrix [10]. They showed that the in-place transposition of the square matrix can be accomplished in a parallel environment using only $\frac{m^2-m}{2}$ threads. As opposed to “killing” the redundant blocks programmatically after the necessary resources have been allocated [14]. The algorithm was very flexible in terms how the size of grid could be selected. Its biggest flaw was scatter memory access, resulting in a serious performance degradation. The main principal of their method was to enumerate all the entries below the matrix main diagonal. Using a pairing function, an entry’s x and y coordinates are uniquely encoded into a natural number k and assigned to it. During the actual transposition, each thread obtains the k value from its coordinates within a block and a grid. Once the k is known, its value is decoded using the pairing function inverse and the x and y coordinates are obtained.

In order to maintain optimised access to global memory, we apply the idea presented in [10] at the block level, instead of single threads. As before, we divide a square matrix M of order m into (mainly) square sub-matrices of order b and let . Now, we create a new square matrix $M_b$, whose entries are sub-matrices of M. In general, we can encounter two situations.

• 1. b is a divisor of m. Then each sub-matrix is a square one of order b and there are $m_b^2$ such sub-matrices, which means that $M_b$ is of order $m_b$.

• 2. b is not a divisor of m. Then there are $m_b^2$ square sub-matrices of order b, one of order less than b and $2m_b$ non-square ones, which occupy the bottom and the right part of the matrix M. This means that $M_b$ is of order $m_b+1$.

In addition, the entries in the lower-triangular part of $M_b$ can be of 4 types:

• 1. those lying on the main diagonal and being square sub-matrices of M of order b—there are $m_b$ of them, called type $B_d$ (diagonal)

• 2. those situated under the main diagonal and being square sub-matrices of M of order b—there are $t=\frac{m_b(m_b-1)}{2}$ of them, called type $B_t$ (lower-triangular)

• 3. those lying on the main diagonal and being a square sub-matrix of M of order less than b—appears only if b is not a divisor of m, called type $B_c$ (corner)

• 4. those located under the main diagonal and being non-square sub-matrices of B—appear only when b is not a divisor of m, there are $m_b$ of them, called type $B_e$ (edge)

The idea is presented in Fig. 3.

Fig. 3

Matrix M and idea of $M_b$ with highlighted various entries types

As with the thread-wise algorithm, we can use decoding functions (which we describe below) to map individual sub-matrices $B_t$ onto corresponding blocks within a grid $G_t$. The mapping is achieved through finding an inverse of an enumeration scheme’s pairing function that encodes the entries of a matrix. The grid $G_t$ consists of t blocks, each containing $b^2$ cores. Another grid $G_d$ is required to handle the sub-matrices $B_d$ from the diagonal. This time we can apply a decoding function within a block to locate individual entries.

To describe decoding functions, we first introduce the notation which will be used throughout this section.

• 1. n denotes the order of a (sub-)matrix in question, N

• 2. x, y denotes the number of a column and row of N, respectively, where $x,y\in \{0,1, \ldots ,n-1\}$

• 3. $k_t=k_t(x,y)$ is a function assigning a unique natural number to each entry of N below the main diagonal (called an encoding function). So $k_t(x,y)\in \{0,1, \ldots ,\frac{n^2-n}{2}-1\}$ for all x, y such that $x<y$, or $k_t(x,y)\in \{0,1, \ldots ,\frac{n^2+n}{2}-1\}$ for all x, y such that $x<=y$.

• 4. $g_w$ is the width of a corresponding grid, G, and $g_h$ - its height

• 5. $c_i,c_j$ denotes the number of a column and a row of G (starting from 0), where $c_i\in \{0,1, \ldots ,g_w-1\},\ c_j\in \{0,1, \ldots ,g_h-1\}$

• 6. $k_r=k_r(c_i,c_j)$ is a function (called an encoding function) enumerating all elements of G row-by-row, from left to right, that is $k_r(c_i,c_j) = c_i + g_w \cdot c_j$

The idea is as follows: from the definitions of $k_t$ and $k_r$, it follows that both functions have exactly the same range. When the blocks from the main diagonal are included, the range is $R_{k_t}=R_{k_r}=\{0,1, \ldots ,\frac{n^2+n}{2}-1\}$. So, for a given n, we first choose $g_w$ and $g_h$ (where $k_r$ is given) and they satisfy the following equality:

$$\begin{aligned} \frac{n^2 + n}{2} = g_w \cdot g_h \end{aligned}$$

(1)

When the blocks from the main diagonal are excluded, the range is $R_{k_t}=R_{k_r}=\{0,1, \ldots ,\frac{n^2-n}{2}-1\}$ and the following equality needs to be satisfied:

$$\begin{aligned} \frac{n^2 - n}{2} = g_w \cdot g_h \end{aligned}$$

(2)

Next, $k_t$ is chosen using a predefined enumeration scheme. Some candidate schemes are described in Sect. 4. Now, if k is a value of $k_r$ (for given $c_i,c_j$) it is also the value for $k_t$ (for given x, y). The point is to recover x, y such that $k=k_t(x,y)$, which helps to find the inverse of $k_t$. Note however, that x and y are not independent—the formula for x can also involve y or vice-versa.

The important thing here is that this approach does not increase the number of cores needed. Indeed, as was mentioned above, for each sub-matrix below the main diagonal (type $B_t$ or $B_e$) we perform the actions using as many cores as entries. But for sub-matrices lying along the main diagonal (type $B_d$ or $B_c$), we only use as many cores as entries in the lower-triangular part of the matrix. That means that we use exactly as many cores as the entries in the lower-triangular part of the original matrix M—as in the naive (thread-wise) algorithm.

For completeness, Listing 5 presents the pseudo-code of a general scheme-based IP kernel.

The idea of enumerating individual blocks according to a predefined scheme can be also applied to rectangular matrices, as presented in Sect. 6.

3.3 Involution Transposition Optimisation

The optimisation technique described above can be also used to improve the 3D matrix transposition. For the purpose of our demonstration, we assume that these matrices are stored in memory row-wise and that each separate plane occupies contiguous block of memory. In principal, the involution transpositions can be reduced to the 2D transpositions [14]. For instance, transposition $T_{\textit{yxz}}$ can be regarded as z transpositions of the $\textit{xy}$ planes. Meanwhile, the involution transpositions $T_{\textit{zyx}}$ and $T_{\textit{xzy}}$ can be simplified as a transposition of matrix consisting of column-elements and row-elements respectively. Regardless of the involution transposition orientation, to achieve high and stable throughput yield, the two basic optimisation techniques are not sufficient and the same performance degradation can be observed for larger matrix dimensions. Even if the involution kernels are more complex than the 2D transpose, our optimisation technique can be applied seamlessly without changing the kernel’s logic. To illustrate this, Listing 6 presents the unoptimised version of the in-place involution transposition $T_{\textit{yxz}}$ of a 3D matrix M for which $\textit{xy}$ plane is a square. Here, the $T\_\textit{yxz}\_\textit{kernel}$ kernel invokes $\textit{transpose}\_3d\_\textit{yxz}$ device function for blocks located on and below the main diagonal. The other blocks although allocated are idle and eventually terminated. The actual logic responsible for the $T_{\textit{yxz}}$ transpose is defined within $\textit{transpose}\_3d\_\textit{yxz}$ function. Its actual implementation is not pertinent as we merely demonstrate how enumeration scheme based technique can be applied.

Listing 7 show optimised version of the involution transposition $T_{\textit{yxz}}$. We can note that the same $\textit{transpose}\_3d\_\textit{yxz}$ function is invoked as before. However, this time $\textit{blockIx}$ variable is passed to the device function. The $\textit{blockIx}$ variable holds the necessary information about the block’s logical mapping, obtained through the thread block coordinates flattening and k value decoding.

We mentioned before that the redundant thread blocks above the main diagonal can also have some impact on the algorithm’s performance. In situation where 3D matrices are transposed the impact of this effect is amplified as the matrix’s third dimension increases. While for the 2D square matrices just $\frac{n^2-n}{2}$ blocks are redundant, the unoptimised version of the 3D transposition defines a grid with $n\frac{n^2-n}{2}$ blocks that are unneeded when cubes are transposed. The other 3D matrix transposition types, such a rotation transposition, are more involving, yet it is still possible to optimise them as well.

4 Enumeration Schemes

This section provides a general overview of some enumeration schemes and explores their key properties. We focus only on schemes applied to the triangular part of a matrix. Schemes that can be applied to the entire matrix (e.g., in order to improve out-of-place algorithms) are presented in Sect. 6. In our analysis we assume that the entries below the main diagonal are enumerated. In order to enumerate entries in the upper triangular part of the matrix, coordinates of a particular entry need to be swapped.

Each scheme features a pairing function ${\varPi }$ and an inverse of ${\varPi }$. While ${\varPi }$ encodes each entry’s coordinates and uniquely generates a single natural number k, the inverse is used to find entry’s coordinates by decoding k. Although the pairing function is not directly used by our algorithm, we include its definition for some of the schemes. We do so because in many cases obtaining an inverse of ${\varPi }$ depends on the pairing function analysis results.

Since the pairing function generates unique values, we know that every enumeration scheme, regardless of its complexity, has got only one starting point ( location with value 0 assigned to it). The location of the starting point can be chosen arbitrarily, however, all the schemes we present have their starting points located in one of the three corners of the triangular part of the matrix, e.g., top-left (TL), bottom-left (BL) or bottom-right (BR) corner.

Once the starting point is selected, the remaining entries are enumerated according to a predefined traversal strategy. The key traversal directions (alignments) that any scheme can use are: along the x (horizontal), y (vertical) axis, or the main diagonal (diagonal). Although the enumeration along the anti-diagonal can be also defined, we do not describe in detail any scheme utilising such an alignment in this paper.

Depending on the scheme complexity, the traversal signature can utilise many different traversal alignments. Each scheme also features at least two traversal directions which we refer to as primary and secondary. The primary direction defines the alignment along which the individual entries are enumerated. The secondary direction determines the main path for subsequent enumeration iterations. Both the primary and/or the secondary directions can be reversed creating additional variants of the initial scheme. In Fig. 4a various traversal directions and orientations are shown. Thin arrows denote primary enumeration direction, while the bold arrows show secondary traversal direction.

Fig. 4

Example traversal orientations (a), traversal direction configurations (b) and enumeration scheme with multiple traversal directions (c)

The simplest schemes enumerate entries by moving along one of three orientations. Some of the advanced schemes can combine many traversal alignments together, resulting in a traversal pattern that changes enumeration direction during single pass (Fig. 4b).

The last group of schemes we explore arranges matrix entries into clusters. Within a single cluster we can still distinguish primary and secondary traversal directions. However, in order to move from one group to another, a third (tertiary) traversal direction is required. As before, by changing any of the three different directions we generate new schemes. Figure 4c presents an example enumeration scheme that organises entries into vertically aligned bands.

In general, the multitude of starting point locations and the fact that many traversal alignments can be combined together allow us to define many variants of the enumeration schemes. Since we know how many entries need to be enumerated, we can easily obtain a reversed version of any scheme through the k value adjustment. Thus, the location of the starting point, and the definition of a traversal layout are considered the two fundamental properties of any enumeration scheme.

We want to emphasise that in many cases functions defining the enumeration schemes also depend on the matrix order or other scheme parameters. For example, the band width defined in Sect. 5 is one such parameter. Since these parameters are constant within the given scheme we decided not to point out this dependence explicitly in the notation.

4.1 Basic Schemes

Basic schemes exhibit only primary and secondary traversal directions. Usually, throughout the entire enumeration process, both the primary and secondary directions remain unchanged. However, when a certain degree of divergence is applied only to the primary direction, new variants of the original scheme are created.

In the following subsections we present a formal definition of two fundamental enumeration schemes and some of their variants. The definition of basic scheme variants is obtained through transformations of the x and y axes or, as mentioned earlier, by changing the location of the starting point, for example, swapping x and y axes together without changing the enumeration order or shifting the entries along one of the axes towards the opposite edge of the matrix. We will demonstrate how individual schemes can be combined together using a technique that can be applied to more advanced schemes. We also provide a definition of a pairing function ${\varPi }$ and its inverse.

4.2 Basic Pairing Functions

Before we analyse the individual schemes we have to define the fundamental pairing function that will serve as a template for the other schemes.

Proposition 1

For any given square matrix M, a function

$$\begin{aligned} {\varPi }_{\textit{LR}}(x,y) = \frac{y^2-y}{2} + x \end{aligned}$$

(3)

enumerates all the entries below the main diagonal row-by-row, from left to right and

$$\begin{aligned} {\varPi }_{\textit{RL}}(x,y) = \frac{y^2+y}{2} - x - 1 \end{aligned}$$

(4)

enumerates row-by-row from right to left.

Proof

Observe first that below the main diagonal, numbers of entries in rows form an arithmetic sequence with difference 1. Therefore ${\varPi }_{\textit{LR}}(0,y)$ is the number of elements lying in all preceding rows. In other words it is the sum of the arithmetic sequence with difference 1, which is

$$\begin{aligned} {\varPi }_{\textit{LR}}(0,y)=\frac{y^2-y}{2} \end{aligned}$$

For a given y, ${\varPi }_{\textit{LR}}$ and x increases or decreases simultaneously, which gives the first formula.

To obtain (4) observe that now ${\varPi }_{\textit{RL}}(0,y)$ is one less than the number of elements in all rows including the y-th, which gives

$$\begin{aligned} {\varPi }_{\textit{RL}}(0,y)=\frac{y^2+y}{2}-1 \end{aligned}$$

For any given y, as x increases ${\varPi }_{\textit{RL}}$ decreases which gives the second formula and finishes the proof. $\square$

4.3 $V_1$ Scheme

The analysis presented in [10] includes a single enumeration scheme, which we refer to as $V_1$. $V_1$ offers the simplest mapping between the core’s coordinates and the matrix element’s location and it can be used as a base for many other schemes. $V_1$ can decode $k_t$ values, generated by the pairing function, and assigned to the elements below the main diagonal.

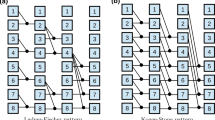
Starting at the (0,1)-entry and moving along the x axis towards the main diagonal, $V_1$ assigns values of the pairing function ${\varPi }$ to the elements in a row. Once the elements of one row are numbered, the same process continues in the next row. By Proposition 1, the pairing function in this scheme is given by formula (3) and shown in Fig. 5a.

Thus, $V_1$ can be described as a scheme with TL starting point in the lower triangular part of the matrix and its primary and secondary directions are: row- and column-wise, respectively.

Fig. 5

Enumeration layout of scheme $V_1$ (a) and its reversed version $V_{1R}$ (b)

From now on we shall denote the value $k_t(x,y)$ by k for short.

So we have

$$\begin{aligned} k = \frac{y^2-y}{2} + x \end{aligned}$$

From that we get

$$\begin{aligned} x = k - \frac{y^2-y}{2} \end{aligned}$$

(5)

Now, to obtain y we first denote

$$\begin{aligned} t := \frac{y^2-y}{2} \end{aligned}$$

Then

$$\begin{aligned} y^2-y-2t = 0\ \Longrightarrow \ y = \frac{\sqrt{8t+1}+1}{2} \end{aligned}$$

(6)

Moreover, by our assumptions of x and y we have

$$\begin{aligned} t \leqslant k=t+x < t + y \end{aligned}$$

(7)

From (6), (7) it follows that

$$\begin{aligned} y= & {} {\frac{\sqrt{8t+1}+1}{2}}\le {\frac{\sqrt{8k+1}+1}{2}} < {\frac{\sqrt{8\left( t+\frac{\sqrt{8t+1}+1}{2}\right) +1}+1}{2}} \\= & {} {\frac{\sqrt{(8t + 1) + 4\sqrt{8t+1} + 4} + 1}{2}} = {\frac{\sqrt{(\sqrt{8t+1} + 2)^2} + 1}{2}} = {\frac{\sqrt{8t+1}+3}{2}} \\= & {} y+1 \end{aligned}$$

Since y is natural we get by definition

(8)

4.4 $V_1$ Scheme: Reversed

When we invert $V_1$’s primary traversal direction while keeping the same starting point, we obtain new scheme—$V_{1R}$. As is the case with $V_1$, the $V_{1R}$ scheme first enumerates elements row-wise then moves to the next row ($y + 1$). The main difference between $V_1$ and $V_{1R}$ is that the latter moves “backwards” over the elements. Thus, by Proposition 1 the pairing function in this case is given by formula (4). Figure 5b shows the enumeration pattern of the $V_{1R}$ scheme.

(9)

(10)

5 Banded Schemes

Another group of schemes that can be used to enumerate the entries below the main diagonal, features a set of bands (of width w) laid out along the traversal direction. Within each band, single entries can be enumerated arbitrarily. For example in Fig. 6, row-wise enumeration is used for two different banded schemes. As was discussed in Sect. 4, introducing groups of entries requires specifying tertiary traversal direction, which determines the path between the bands.

Fig. 6

Example banded schemes

To simplify our analysis of banded schemes the following symbols are introduced:

• 1. $\mathfrak {S}^{+}(t), \mathfrak {S}^{-}(t)$ is a number of entries below the main diagonal in a square matrix of order t, including or excluding entries from the diagonal,

• 2. m is the order of the matrix,

• 3. w is a width of a band, while r denotes width of the shortest band,

• 4. $\beta$ denotes the number of bands,

• 5. i denotes the index of a band,

• 6. ${\varPi }_b$ denotes the pairing function of a banded scheme,

• 7. $\mathbb {B}_i$ is a set of consecutive values generated by ${\varPi }_b$ for the i-th band, and $B_i$ denotes its cardinality,

• 8. $b_i$ denotes the smallest element in the set $\mathbb {B}_i$,

• 9. $I_b(k)$ is a function used to obtain band’s index (i) from k,

In addition, based of the above mentioned definitions, we can define the main properties of banded schemes that will be referenced throughout this section.

• 1. $\mathfrak {S}^{+}(t) = \frac{t^2+t}{2}$, $\mathfrak {S}^{-}(t) = \frac{t^2-t}{2}$,

• 2. $m > 1, m \in \mathbb {N}$,

• 3. $w \in \{1,\ldots ,m-1\}, w \in \mathbb {N}$; if w is a divisor of $m-1$ then the triangular part of each band contains exactly the same number of entries: $\mathfrak {S}^{+}(w)$ and $r=w$; otherwise, $r = (m-1)\mod w$ and the shortest band contains $\mathfrak {S}^{+}(r)$ entries,

• 4. ,

• 5. $i\in \{0,\ldots ,\beta - 1\}$,

• 6. the range of ${\varPi }_b$ is $\bigcup _{i=0}^{\beta -1} \mathbb {B}_i$

• 7. $\mathbb {B}_i = \{b_i,\ldots ,b_{i+1}-1\}$ and $B_i = \vert \mathbb {B}_i\vert = b_{i+1} - b_i$

• 8. $\exists b_i \in \mathbb {B}_i, \forall q_i \in \mathbb {B}_i \backslash \{b_i\} : b_i < q_i$

• 9. $i = I_b(k), k \in \mathbb {B}_i$

5.1 $V_{1B}$ Scheme

The simplest form of a banded scheme labelled $V_{1B}$ is presented in Fig. 7. It divides the triangular part of a matrix into vertically oriented bands, indexed from left to right. Within each band, starting from the top-left corner, individual entries are enumerated row-wise, from left to right. Once all the entries in a band are numbered, the process starts over in the next adjacent band.

Fig. 7

Scheme $V_{1B}$ enumeration layout and two stages of its logical decomposition

We can obtain the inverse of the $V_{1B}$ pairing function by finding the number of all entries in a single band as well as the minimum value of an entry in a band.

Proposition 2

Number of entries in the i-th band of the width w is

$$\begin{aligned} B_i = w m - i w^2 - \mathfrak {S}^{+}(w)=w m - i w^2-\frac{w^2 + w}{2} \end{aligned}$$

(11)

and the minimum value k that the pairing function generates within i-th band is

$$\begin{aligned} b_i = i w m - \mathfrak {S}^{+}(i w) \end{aligned}$$

Proof

The proof is by induction on i, the number of a band. Since $B_0$ consists of first w columns we have

$$\begin{aligned} B_0= & {} (m-1)+(m-2)+ \cdots +(m-w) = w m - (1+2+\cdots + w) \\= & {} w m - 0\cdot w^2 - \frac{w^2 + w}{2} \end{aligned}$$

which means that the formula is valid for $i=0$. Suppose now it is valid for $i=l$. Then each column (there are w of them) within $B_{l+1}$ has w elements less than the corresponding column within $B_l$ which gives

$$\begin{aligned} B_{l+1} = B_l - w\cdot w = w m - (l+1)w^2 - \mathfrak {S}^{+}(w) \end{aligned}$$

so the formula is valid for $l+1$. By the induction principle, the formula is valid for every natural $i\geqslant 0$.

Using the formula for $B_i$ we can now obtain a minimum value of k that $V1_B$ generates for a particular band. For example, we can observe that

$$\begin{aligned} \min _{b_0}(k)= & {} 0 \\ \min _{b_1}(k)= & {} B_0 \\ \min _{b_2}(k)= & {} B_1 + B_0 \\&\dots&\end{aligned}$$

Therefore, in general, we get

$$\begin{aligned} \min _{b_i}(k) = B_0 + B_1 + \dots + B_{i-1} \end{aligned}$$

(12)

Thus, from (11) and (12), the minimum value o k in the i-th band is

$$\begin{aligned} b_i = \sum \limits _{j=0}^{i-1}B_j = i w m - \mathfrak {S}^{+}(iw) \end{aligned}$$

(13)

Which finishes the proof. $\square$

Having determined the number of entries in the i-th band, as well as the minimum value assigned to one of the entries comprised by the band, we can obtain the inverse of the scheme $V_{1B}$. From (12) we can conclude that within a single band, numbers generated by the ${\varPi }_{1B}$ satisfy the following system of inequalities.

$$\begin{aligned} b_i \leqslant k < b_{i+1} \end{aligned}$$

(14)

Proposition 3

The index i of a band of width w is

(15)

Proof

From (14), we obtain the following system of inequalities

$$\begin{aligned} iwm - \frac{i^2w^2 + iw}{2} \leqslant k < (i+1)wm - \frac{(i+1)^2w^2 + (i+1)w}{2} \end{aligned}$$

Solving the first inequality for i

$$\begin{aligned}&w^2 i^2 + (w-2wm)i + 2k \geqslant 0 \end{aligned}$$

(16)

$$\begin{aligned}&i_{1,2} = \frac{(2m-1) \mp \sqrt{ (2m-1)^2 - 8k} }{2w} \end{aligned}$$

(17)

$$\begin{aligned}&i \leqslant i_1 \text { and } i \geqslant i_2 \end{aligned}$$

(18)

Solving the second inequality and substituting t for $i+1$ we get

$$\begin{aligned}&w^2 t^2 + (w-2wm)t + 2k < 0 \end{aligned}$$

(19)

$$\begin{aligned}&i_1< t < i_2 \end{aligned}$$

(20)

$$\begin{aligned}&i_1 - 1< i < i_2 - 1 \end{aligned}$$

(21)

From (18) and (21), the common solution is

$$\begin{aligned} i_1 - 1 < i \leqslant i_1 \end{aligned}$$

(22)

Solving (22) gives us

$$\begin{aligned} i \leqslant i_1 < i + 1 \end{aligned}$$

(23)

Since i is natural, from the definition of the floor function we get

This completes the proof $\square$

Being able to obtain the index of a band from k allows us to determine the number of entries in that band. As a result, we can perform logical decomposition of a scheme as presented in Fig. 7. During the first stage, we normalise the values generated for each band so that each one is numbered from 0, as per the centrally position matrix in Fig. 7. We achieve this by subtracting the minimum value in a band $b_i$ from k, and we get $k_2$ as follows

$$\begin{aligned} k_2 = k - b_i \end{aligned}$$

(24)

Next, we separate the triangular and rectangular part of the band so that the numbers generated for each of these regions can be further normalised, as the right-most matrix in Fig. 7 depicts. We know that the triangular part of the band consists of $\mathfrak {S}^{+}(w)$ entries. Consequently, the numbering of entries located in the rectangular region is normalised as well, and achieved using the following formula

$$\begin{aligned} k_3 = k_2 - \mathfrak {S}^{+}(w) \end{aligned}$$

(25)

Since the shortest band does not have the rectangular region, its normalisation is limited to the triangular region.

We are now presented with two cases. When $k_2$ is less than $\mathfrak {S}^{+}(w)$, the inverse decodes the values assigned to the triangular regions. Otherwise, values assigned to entries occupying the rectangular region are decoded.

The definition of an inverse for the triangular region can be obtained from the $V_1$ inverse—(8), (5). However, since there are $\gamma$ bands in total, i-th region is shifted by iw entries along the y-axis. In general, the y coordinate for the entries located in the triangular part is defined as follows

(26)

Similarly, the rectangular part of the subsequent bands is also shifted by w entries along the y-axis against the the previous band. Besides that, each row contains w entries, hence in order to determine the relative value of its y coordinate we can use . In addition, considering the relative location between both regions, and taking into account the result of the second stage normalisation, we get

(27)

Thus, the $V_{1B}$ inverse to obtain the entry’s y coordinate is

$$\begin{aligned} y = {\left\{ \begin{array}{ll} y_1, &{}\quad \text {if }k_2 < \mathfrak {S}^{+}(w).\\ y_2, &{}\quad \text {if }k_2 \geqslant \mathfrak {S}^{+}(w). \end{array}\right. } \end{aligned}$$

(28)

As indicated earlier, the part of the $V_{1B}$ inverse that calculates the value of the x coordinate within the triangular region of the band can be obtained from (5). As before, the value of x needs to be adjusted with respect to the index of the band. However, the x is not only shifted by w positions along the x-axis, but it also depends on $y_1$ which is shifted as well.

The same horizontal shift by w entries applies to the consecutive bands in the rectangular region. Within each band, respective positions of the entries in a row can be calculated using the modulo operation. The final version of the $V_{1B}$ inverse for the x coordinate is presented below

$$\begin{aligned} x = {\left\{ \begin{array}{ll} k_2 - \mathfrak {S}^{-}(y_1 - i w) + i w,&{}\quad \text {if }k_2 < \mathfrak {S}^{+}(w).\\ k_3 \mod w + i w,&{}\quad \text {if }k_2 \geqslant \mathfrak {S}^{+}(w). \end{array}\right. } \end{aligned}$$

(29)

A closer look at the enumeration layout of the scheme presented in Fig. 7 allowed us to realise that the $V_{1B}$ can generate other schemes that depend on the w parameter. In particular, for terminal values of w, either 1 or $m-1$, we get schemes $V_2$ or $V_1$ respectively. Meaning that two basic schemes are just specific versions of the broader group of schemes that $V_{1B}$ can instantiate.

6 Rectangular Schemes

The schemes presented so far can only be applied to the triangular (upper or lower) part of the matrix. However, schemes that can enumerate all matrix entries can be also defined. In this section we present a banded scheme ($V_{1\textit{BF}}$) that enumerates rectangular matrices. Similar to triangular schemes, we introduce the following symbols:

• 1. m and n are the horizontal and vertical dimensions of the matrix,

• 2. w is the width of a band, while r denotes the width of the narrowest band when n is not a multiple of w,

• 3. $\beta$ denotes the number of bands,

• 4. i denotes the index of a band,

• 5. ${\varPi }_{\textit{BF}}$ denotes the pairing function of a banded scheme,

• 6. $\mathbb {B}_i$ is a set of consecutive values generated by ${\varPi }_{\textit{BF}}$ for the i-th band,

• 7. $b_i$ denotes the smallest element in the set $\mathbb {B}_i$,

• 8. $I_{\textit{BF}}(k)$ is a function used to obtain band’s index (i) from k,

Based of the above mentioned definitions, we can define the main properties of banded schemes that will be referenced throughout this section.

• 1. $m> 1, n > 1, m \in \mathbb {N}, n \in \mathbb {N}$,

• 2. $w \in \{1,\ldots ,m-1\}, w \in \mathbb {N}$; if w is a divisor of m then each band contains exactly the same number of entries: wn and $r=w$; otherwise, $r = m\mod w$ and the narrowest band contains rn entries,

• 3. ,

• 4. $i\in \{0,\ldots ,\beta - 1\}$,

• 5. the range of ${\varPi }_b$ is $\bigcup _{i=0}^{\beta -1} \mathbb {B}_i$

• 6. $\mathbb {B}_i = \{b_i,\ldots ,b_{i+1}-1\}$ and $\vert \mathbb {B}_i\vert = b_{i+1} - b_i$

• 7. $b_0 = 0, b_i = \sum _{k=0}^{i-1} B_k$

• 8. $i = I_{\textit{BF}}(k), k \in \mathbb {B}_i$

In order to find the inverse of the pairing function, we need to obtain band’s index i from k. We omit the proofs for $B_i$ and $b_i$, because they can be straightforwardly derived by following the steps presented in Sect. 5. The complete definition of the pairing function inverse is presented below. Meanwhile, Fig. 8 presents the enumeration layout of the rectangular banded scheme.

$$\begin{aligned} x= & {} {\left\{ \begin{array}{ll} (k - i w n) \mod w + i w , &{}\quad \text {if }r = 0\\ (k - i w n) \mod w + i w , &{}\quad \text {if }r \ne 0 \wedge i < \gamma - 1 \\ (k - i w n) \mod r + i w , &{}\quad \text {if }r \ne 0 \wedge i = \gamma - 1 . \end{array}\right. } \end{aligned}$$

(30)

(31)

Fig. 8

Rectangular scheme enumeration layout

7 Performance Evaluation

In order to compare the performance of our solution with the other algorithms, we prepared a series of test runs to measure their effective throughput. Each of the enumeration schemes mentioned in Sect. 4 was tested separately against the naive version of the in-place (IP) and NVIDIA’s out-of-place (NVI) algorithms. For completeness, we also included throughput measured for the thread-wise (TW) algorithm [10]. All algorithms were implemented using CUDA. In addition, each algorithm (except TW) was optimised using the same techniques described in [24]. This was to ensure that various well known hardware specific issues, such as non-coalesced access or shared memory bank conflicts, did not affect the test results and could be ruled out from the further analysis. We also include test results obtained for the original and optimised version of two involution transpositions of 3D matrices: $T_{\textit{yxz}}$ and $T_{\textit{zyx}}$ [14].

We carried out our tests on three different NVIDIA GPU architectures, known as Fermi [21] (GeForce GTX 580), Kepler [22] (GeForce Titan Black) and Maxwell [20] (GeForce Titan X). In order to compare original and banded version of the 3D transpositions, we used only Maxwell device as it had the largest global memory capacity among the chosen GPUs. We tested various configurations of the thread block sizes and present only some of the best results obtained. Depending on the thread block size, each individual thread was responsible for transposition of up to 32 elements.

Since each of the tested devices is configured with a different amount of global memory and because OOP algorithms require twice as much memory than IP algorithms, we divided our tests into three groups, one per device. We examined square matrices of order n, where n was a multiple of 1024. The largest order of a matrix we could transpose on a Maxwell device was $54 \times 2^{10}$, allowing us to transpose 12GB of raw data in-place. In terms of the 3D transposition $T_{\textit{yxz}}$, we selected narrow range of matrix dimensions for the x, y plane with $z=3$ and $z=2$ so that we could demonstrate stability of the banded version of the involution transposition. Similarly, the 3D transposition $T_{\textit{zyx}}$ was tested with $y=2$ and $y=3$, while keeping the range of x, z plane relatively narrow.

Fig. 9

Throughput comparison between various enumeration schemes and IP and OOP algorithms—measured on Fermi device using a block $32 \times 8$ threads

The following groups of graphs present the experimental results obtained for the three selected GPUs. Figures 9, 10 and 11 show the throughput measured on the individual devices for the tested schemes, against the results obtained for the IP and OOP algorithms. Figures 9, 10 and 11 present the results for the Fermi, Kepler and Maxwell devices respectively.

In addition, we prepared performance heat maps of the Super Grid (SG) and Banded algorithms obtained on the Maxwell device. For the in-place algorithms, each heat graph shows the performance fluctuations for different values of the w parameter. The heat maps of the out-of-place algorithms for rectangular matrices present the performance distribution by the range of matrix sizes collected by the NVIDIA’s and the Banded algorithm. The OOP results gathered for the Banded algorithm were measured for $w=8$ and follow the series of graph prepared for the IP algorithm.

In Fig. 9, we can see that only $V_{1B}$ scheme and SG offer relatively stable performance across matrix size range. The other schemes together with the IP and NVI algorithms exhibit gradual performance decrease above 24K mark. However, it still clear that banded scheme and SG outperform other methods. Comparing only the $V_{1B}$ to SG, it can be observed that the $V_{1B}$ kernel yields higher performance than SG.

In Fig. 10, we can see similar performance pattern for all tested schemes together with IP and OOP algorithms. Unlike Fermi device, the banded version of the OOP algorithm (OOPB) dominates first half of the tested matrix size. Nevertheless, the $V_{1B}$ and SG algorithms still deliver higher and stable throughput, regardless of matrix size. However, the $V_{1B}$ scheme clearly outperforms SG performance on Kepler device.

Fig. 10

Throughput comparison between various enumeration schemes and IP and OOP algorithms—measured on Kepler device using a block $32 \times 8$ threads

Fig. 11

Throughput comparison between tested enumeration schemes and IP and OOP algorithms—measured on Maxwell device using a block $32 \times 8$ threads

In Fig. 11, we can observe again that in spite of their complexity, $V_{1B}$ and OOPB outperform other algorithms. However, only the $V_{1B}$ and SG deliver similar stability, but the former yields the highest throughput. It is evident that banded approach improves both the IP and OOP algorithms. The other schemes together with IP and NVI algorithms continue to decline above 24K mark.

Fig. 12

Comparison of throughput heat maps obtained on Kepler device between Nvidia and Banded out-of-place algorithms

Fig. 13

Comparison of throughput heat maps obtained on Maxwell device between Nvidia and Banded out-of-place algorithms

Fig. 14

Throughput comparison between original and optimised version of the in-place involution transposition $T_{\textit{yxz}}$—measured on Maxwell device using various thread block sizes ($z=2,3,4$, $w=8$)

The heat maps in Figs. 12 and 13 present results collected on Kepler and Maxwell GPUs while testing two OOP algorithms for rectangular matrices. The first algorithm is the NVIDIA’s matrix_transpose kernel available with the CUDA SDK. It was tested against our version of the banded OOP algorithm, with a band of width $w = 8$. Due to global memory size limits, the “extremely” cold region in the top right corner represents 0 throughput. The region of the heat maps with throughput levels below 150 GB/s represents the performance decrease caused by TLB misses. Based on the maps obtained for the banded algorithm, we can confirm that this “seashore” effect is eliminated. It is evident that the performance of our algorithm remains relatively stable, regardless of the matrix dimensions. Apart from uniform stability, the banded algorithm also delivers higher throughput than the original NVIDIA’s kernel. Lastly, in Figs. 14 and 15, we can notice that similarly to 2D matrix transposition the performance of the original version of the 3D transposition algorithm decreases starting at the 24K mark. We can also see that the algorithm utilising the enumeration scheme based optimisation is not affected by the TLB cache misses and maintains its stability. Due to global memory capacity limitations we can only offer limited set of the results. Nevertheless, we can clearly show that our optimisation technique allows improving performance of the 3D transposition algorithm.

Fig. 15

Throughput comparison between original and optimised version of the in-place involution transposition $T_{\textit{zyx}}$—measured on Maxwell device using various thread block sizes ($y=2,3,4$, $w=8$)

8 Conclusion

This paper presents an improved version of two matrix transposition algorithms. We demonstrated that the original concept of mapping the matrix elements onto the computational cores can be extended and applied to segments. In addition, we showed that it was possible to control the algorithm’s performance by using different enumeration schemes. Through scheme design we were able to change the logical-to-physical block association and subsequently minimise the impact of the TLB misses. Furthermore, thanks to the parametrised version of the banded scheme it was possible to adapt our algorithm to three different CUDA architectures so that its performance is substantially improved. In fact, the banded version of our algorithm proved that it is possible to eliminate performance degradation caused by the TLB cache misses for both in-place and out-place algorithms, as well as the 3D transpositions we optimised. Although the Super Grid approach delivers similar throughput, it significantly increases the complexity of the overall solution and in turn results in GPU kernel’s deep dependence on the host code.

As expected, the experimental results confirmed that the additional computational effort required to decode scheme’s pairing function did not affect solution’s performance. This was mainly due to the memory-bound nature of the in-place and out-of-place transposition algorithms for square and rectangular matrices respectively. Moreover, even the 3D transpositions, in spite of their different memory access pattern, could benefit from the banded scheme based optimisation and deliver high and stable throughput. In fact, we were able to use exactly the same banded scheme $V_{1B}$ and apply it to both in-place 2D and 3D involution transposition $T_{\textit{yxz}}$. On the other hand, the other involution transposition $T_{\textit{zyx}}$ required slightly modified version of the $V_{1B}$. However, in general, the scheme based optimisation proved to be very flexible and seamlessly applicable and adjustable.

Encouraged by the results of the performance tests conducted on different NVIDIA GPUs, we plan to extend our research to explore the capabilities of the AMD devices. We also consider utilisation of the banded enumeration schemes to improve the performance of the in-place transposition of the rectangular matrices. Apart from the 2D transpositions, we also intend to study more the in-place 3D rotation transpositions and propose new enumeration schemes that could improve their performance.