1 Introduction

One class of methods for the precise measurement of the dynamic viscosity of Newtonian fluids involves the bulk flow of the material through a channel of well-defined geometry and makes use of measurements of the pressure differences necessary to drive the flow at a prescribed rate [1, 2]. Other methods measure the viscous torque on a solid body rotating continuously at a finite rate when immersed in the fluid, while others observe the decay of oscillations of a body of revolution suspended in the fluid from an elastic torsion wire [3, 4]. It is also possible to use the time of fall of solid bodies of a well-defined shape through the fluid under the influence of gravity [5, 6]. Most recently, it has been possible to use light scattering to determine the viscosity of liquids as described in Refs [7, 8]. None of these techniques lend themselves easily to the convenience of electrical measurement and for that reason have seldom been successful for applications at extremes of temperature. Equally, they have also never been adopted for routine use as on-line monitors of production processes. Two techniques that do yield directly to electrical measurements are the vibrating-wire technique, the subject of another paper in this Special Issue [9], and the Torsional Quartz-Crystal viscometer which is the subject of this paper.

The first ideas of making use of the motion of piezoelectric crystals to determine the viscosity of fluids arose from the work of electrical engineers on quartz among a range of other materials in the 1940s. W.P. Mason was a pioneer of this activity and his paper in The Transactions of the American Society of Mechanical Engineers [10] excited much interest from notable physicists and engineers. In subsequent papers, Mason and his co-workers [11, 12] developed the original idea but focused on studies of viscoelastic fluids which had not been fully explored but where the high frequencies of piezoelectric oscillations gave access to shear rates that exposed viscoelasticity in a wide range of materials. This was a direction that others followed [13,14,15] and continue to follow [16,17,18]. Indeed, there have been commercial realizations of quartz-crystal viscometers for a range of purposes including process monitoring and applications downhole in oil well drilling have been contemplated [19]. These developments led to the use of crystals of a variety of materials and different configurations to cover a wide frequency range and the original, right-cylindrical X-cut crystal, performing torsional oscillations was rather little exploited for the measurement of the viscosity of simple fluids which is the subject of this review.

There was a resurgence of interest in the torsional quartz-crystal viscometer in the 1960s when work began in NASA and then NIST (formerly NBS), as well as elsewhere, on the viscosity of cryogenic fluids including liquid helium, hydrogen, argon, and oxygen in gaseous and liquid phases that continued over the next two decades prompted by interest in rocket propulsion using liquid fuels [20,21,22,23,24,25,26,27]. The fact that electrical measurements were all that was required, was a particular advantage of the technique for operation at extremely high or low temperatures and high pressures. More recently the technique has been applied to the measurement of the viscosity of alternative refrigerants and of hydrocarbons in both gas and liquid phases by work at NIST, USA [28,29,30,31,32], at CALTECH, USA [33], in the University of Lisbon, Portugal [34] and at Helmut-Schmidt-Universitat/Universitat der Bundeswehr [35, 36] at pressures up to 100 MPa; again, the fact that only electrical measurements were necessary, made with readily attainable instrumentation, was particularly attractive. It is interesting that until recently, the theory of the experimental method was not entirely soundly based on a rigorous analysis of the solid and fluid mechanics of the quartz crystal and its surrounding fluid. Rather, it was based on the plausible assumption that, because the amplitude of the motion of the crystal was small and the penetration of the viscous disturbance into the fluid was small by comparison with the radius of the quartz cylinder, a model of a plane viscous wave propagation could be employed. Nonetheless, the simple working equation that emerged from the analysis proved remarkably effective and revealed that the technique could be made an absolute one, requiring no calibration and, to first order at any rate, needing information only about the mass of the quartz crystal and surface area, both easily determined. Generally, the uncertainty in the reported viscosity data for simple fluids was estimated at between 0.5 and 2% which was borne out by comparisons with data obtained from other, more precise sources. Given the long lifetime of the technique, it is not surprising that both its practical realization and its theory have been enhanced as abilities to refine crystal production, electrical measurements, and theory have advanced. It is therefore timely to review the application of the instrument in order to guide potential users on how to take the greatest advantage of this powerful, but under-exploited technique.

We begin with a summary of the latest theory of the method and then review how the instrument has been realised in practice. As implied by the remit for this Special Issue of the Journal we then concentrate on the conditions necessary to achieve satisfactory results and how the differences between the theoretical model of the experiment and the reality may be accounted for.

2 Theory

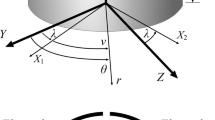
The summary of the theory of the instrument provided here draws heavily on the work by Richardson and Wakeham [37]. The torsional quartz-crystal viscometer consists of an X-cut right-circular cylinder of radius \(R\) and length \(L\) and of density \({\rho }_{\text{c}}\). The crystal is forced to undergo torsional oscillations at a (radian) frequency ω with angular amplitude \(\varepsilon\). The crystal is suspended by a mechanism which exerts no force upon it other than to oppose gravity and is immersed in an incompressible Newtonian fluid of viscosity \(\mu\) and density ρ.

A diagram of the quartz crystal is contained in Fig. 1, which also illustrates the coordinate system that has been employed to describe its motion and that indicates the positions of the four electrodes used to excite motion. To build a mathematical model of the crystal oscillations we employ a right-handed coordinate system. For a quartz crystal, rectangular coordinates {X,Y,Z} are conventionally used such that the X-direction is aligned along the binary axis of the crystal and the Z-direction is aligned along its trigonal axis. An X-cut quartz cylinder is one such that the X-direction is aligned with the axis of the cylinder. It is also more appropriate in the analysis to use a system of cylindrical polar coordinates {r,θ,z} with its origin at the center of the one end of the cylinder and the. z-direction aligned along its axis towards its other end. Thus z = X and it is convenient to let r = Y when θ = 0 so r = Z when \(\theta =\pi /2\).

Fig. 1
figure 1

The Torsional quartz-crystal resonator and its co-ordinate system

Full size image

To be clear, when the opposing quadrant electrodes are fed with an alternating current, the piezoelectric characteristics of quartz are such that to first order, and in the fundamental mode, each plane of the crystal perpendicular to the X-axis oscillates in its own plane so that the outer surface of the crystal rotates about the axis with an amplitude that is zero at the mid-plane (a node) of the crystal and a maximum at its ends. When the crystal is excited in this way in a vacuum, the resonant frequency and the width of the resonance are characteristic of the crystal alone, but when immersed in a fluid, the viscous dissipation and entrained mass, in a small layer of fluid (thickness, d) adjacent to the crystal, add both mass and damping to the crystal leading to a lowered resonant frequency and a broadened resonant peak.

The basic measurements required in the torsional quartz crystal viscometer are therefore those of the resonant frequency and bandwidth of the resonance in vacuo and of the same quantities when the crystal is immersed in the test fluid. Of course, it is also necessary to characterise the thermodynamic state of the fluid by measuring temperature and pressure.

Subject to a large number of conditions, established rigorously by Richardson and Wakeham [37], and set out later, two working equations that can be used for the evaluation of the viscosity of the fluid emerge from the theoretical analysis. We shall discuss the implications of the various conditions in the next section, but the basic working equations are:

$$\mu = {{\text{1/2 }\omega }_{1\text R}^{*}\left({M}_{\text c}/{S}_{\text c}\right)}^{2}[({B}_{1}^{*}/{\omega }_{1\text R}^{*})-1/2({B}_{0}^{*}/{\omega }_{0\text R}^{*}){]}^{2}/\rho$$
(1)

and

$$\mu = \left( {M_{\text c} /S_{\text c} } \right)^{2} ~\frac{{\omega _{{1\text R}}^{*} ~(\omega _{{0\text R}}^{*} ~{-}\omega _{{1\text R}}^{*} )^{2} \left( {1~{-}~1/2~\left( {B_{0}^{*} /\omega _{{0\text R}}^{*} } \right)} \right)^{2} }}{{2\rho \omega _{{0\text R}}^{*} }^{2}}$$
(2)

here, \({M}_{\text c}\text{ and }{S}_{\text{c}}\) are the mass and surface area of the crystal respectively, while \({B}_{1}^{*}\text{ and }{\omega }_{1\text{R}}^{*}\) are the bandwidth of the resonance curve and the angular frequency of resonance when the fluid is immersed in the fluid and \({B}_{0}^{*}\text{ and }{\omega }_{\text{0R}}^{*}\) are the corresponding quantities for the crystal in vacuo. The symbol \(\mu\) represents the dynamic viscosity of the fluid and \(\rho\) its density, both at the temperature and pressure of the measurement. We note that in common with most viscometers` the density of the fluid must be known to evaluate the viscosity itself.

For later use it is important to note that whereas the mass of the crystal is conserved under changes in pressure and temperature, the dimensions of the crystal respond to changes in both and, as a result, the surface area of the crystal, \({S}_{\text{c}}\), obviously changes. It is related to the length, \(L\) and its radius \(R\) by the equation:

$${S}_{\text{c}}= 2\pi R L \left(1 + \left(R/L\right)\right)$$
(3)

while

$${M}_{\text c}={\rho }_{\text c}\pi {R}^{2}L$$
(4)

The first term of Eq. 3 corresponds to the curved surface area of the cylinder while the second relates to the two circular ends.

Almost all work with the torsional quartz crystal viscometer has made use of Eq. 1 for the analysis of the electrical resonance data, even though it had not been given a rigorous foundation until recently. Equation 2 on the other hand, which requires only resonant frequency measurements, had not been derived until recently, and, as our subsequent error analysis will show, requires a higher level of precision in frequency measurements than was attainable in early work.

2.1 Conditions for the Validity of the Working Equations

The solid and fluid mechanics analysis upon which the two working equations are subject to a large number of conditions that must always be satisfied for valid measurements. Table 1 is taken, with minor changes from reference [37]. It expresses all the conditions that must be imposed on the design and operation of a torsional quartz-crystal viscometer in terms of inequalities for a series of dimensionless groups. In the table, they have been evaluated for a representative range of fluid properties for a fluid encompassing the gas phase of methane under atmospheric conditions to a liquid hydrocarbon with six carbon atoms at a pressure of 10 MPa. The crystal dimensions employed are those typical of practical instruments, with a crystal radius of between 2.5 mm and 5 mm and a length of about 50 mm. The origin of the various conditions is contained in the detailed analysis of Richardson and Wakeham [37], but is useful for a reader for us to provide some physical insight into the nature of each condition. In addition to the quantities already defined, we add the pressure, p, and the temperature, T, as well as:

Table 1 Typical and desired values of dimensionless groups for the quartz-crystal viscometer
Full size table

\({t}^{*}\), the time for decay of an initial transient in the oscillation after its initiation,

\(\lambda\), the thermal conductivity of the fluid,

\(c\), the speed of sound in the fluid,

\(e\), the ellipticity of the crystal cross-section,

\({l}_{\text{r}}\), a linear dimension characteristic of the roughness of the crystal surface,

\({L}^{*}\), a typical distance between the surface of the crystal and the walls of the vessel containing the fluid,

\(\Delta {T}^{*}\), an imposed or adventitious temperature difference in the system.

These conditions therefore dictate the dimensions of the crystal that can be employed and thus its resonant frequency, typically 35 kHz, or the size of the containing vessel. They do not prescribe how the electrical measurements of resonance shall be performed and that is considered after we have described the physical arrangements used to mount the crystal and operate it. First, we note that the twist of the crystal, that is the fraction of the circumference by which the surface moves should be very small, \(\varepsilon \ll 1\). The electric field applied to the quartz crystal must be small enough to make sure this is so. The theory then requires that the radial dimension of the region in which there are significant spatial variations of flow variables is much less than the axial dimension of the cylinder and that the twist on the cylinder varies weakly with axial position. This is ensured, provided εR ≪ L, so that the flow is planar and so that the velocity and pressure fields do not vary significantly with axial position. The fluid flow must also always be laminar which is ensured if \(\mathit{Re}\ll 1\text{ or}\sim 1\) (non-accelerating). The fractional thickness of the fluid layer perturbed by the oscillation,\(d\), is then certainly very small because \(d/R=\sqrt{\frac{\mu }{\rho \omega {R}^{2}}}\ll 1\). Furthermore, the sensor is always observed when all transients have decayed, so that \({t}^{*}\) is large enough. Finally, the crystal is supposed such that \(\frac{R}{L}\ll 1\text{ or} \sim 1\). These conditions ensure that the theory of the fluid flow around the crystal reflects reality. The remainder of the conditions considers practical effects associated with the practical realization of the instrument.

The condition associated with the Nahme number, \(\mathbf{N}\mathbf{a}\), must be small to be sure the temperature increase caused by viscous dissipation in the fluid is negligible, while that on the Mach number, \(\mathbf{M}\mathbf{a}\), expresses the fact that the fluid can be treated as incompressible. The theory of the instrument is based upon an exactly circular cylinder, impossible to attain in practice but analysis [37] shows that if the ellipticity is small, the theory is adequate. The remaining conditions then refer, in order, to the effect of the crystal roughness, the size of the fluid containment vessel, the limitations to small temperature and pressure non-uniformities owing to the dependencies of the fluid properties upon these state variables, the conditions to avoid perturbations from acoustic resonances in the fluid cavity. For our present purposes, as can be seen from Table 1, almost all of the conditions are rather easily satisfied by the typical dimensions of the crystals employed.

What emerges clearly from this analysis is that the condition which it is least easy to satisfy is that imposed by the roughness of the crystal surface; for a roughness of only 100 nm, the relevant dimensionless group is of order \(1{0}^{-1}\) which is smaller than unity but not very much smaller as formally required. It is worthwhile recording that there have, indeed, been deliberate attempts to empirically enhance the roughness of the surface of quartz crystals to make their characteristics separately sensitive to the density of the fluid and its viscosity [38, 39] but that is not within the scope of the present paper. Indeed, an examination of practical implementations of the Torsional Crystal Viscometer [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] shows that almost all instruments have fulfilled almost all of the conditions of Table 1, but that the concern with roughness has seldom been addressed.

3 Practical Considerations

Throughout the wide range of thermodynamic states that have been studied with the torsional quartz-crystal viscometer, (Temperatures from 4 to 500 K and pressures from 0 to 100 MPa), only three different configurations have been employed to provide the electrical drive to excite the torsional oscillations combined with two mechanisms to support the crystal.

3.1 Electrical Drive and Crystal Support

The mechanisms that have enjoyed the most frequent application are illustrated in Fig. 2a–c together with the two mechanisms of support. Figure 2a shows the approach employed by the various workers at NIST over a period of some 50 years [23, 28,29,30,31,32], and originally used in the work on liquid helium by Webeler [21, 22]. In this approach, the crystal is supported by two nylon threads resting in grooves at the midplane of the crystal which are tensioned by a spring to hold the crystal vertically inside an insulating cage which carries the four electrodes on its inside face. The field generated in the electrodes is then capacitively coupled to the crystal’s surface. The positioning of the supports at the nodal plane ensures minimal interference with the crystal motion. This method of suspension has the advantage that the surface roughness of the crystal is unaffected by any extraneous coatings. In recent work, Meier and colleagues [36, 40] have used the same basic idea but support the crystal with two thin glass plates in grooves at the nodal plane of the crystal. This has the advantage that it is much more certain that the crystal axis remains aligned with the axis of the electrodes.

Fig. 2
figure 2

Configurations of the quartz-crystal excitation and support. (a) Electrodes on a surrounding cage, nylon thread supports [32], (b) Electrodes plated on crystal surface, and phosphor-bronze wire supports [33, 34], adapted with permission from California Institute of Technology, USA. (c) Parallel wire electrodes scheme [40]

Full size image

An alternative approach was first employed by Collings and McLaughlin [27], Strumpf (1972) [33], and subsequently by Santos and Nieto de Castro [34] is contained in Fig. 2b. In that case, the electrodes are made of gold, directly plated onto the surface of the crystal in the four quadrants, with small spacings between them. This allows the attachment of four electrical leads at the nodal plane which are then attached to a cage around the crystal. These leads provide not only the electrical connections to the electrodes but also act as mechanical supports for the crystal. The assembly of this suspension is perhaps slightly easier than that with the spring suspension and could operate at higher temperatures in principle than with the nylon support, but that has not been tested. The disadvantage of this method of construction is that the roughness of the surface that matters to the fluid motion is that of the golden coating and not of the crystal itself. Given its method of deposition it would seem likely that the roughness could be greater, but there is no direct evidence available one way or the other.

The final means of exciting the crystal motion is shown in Fig. 2c and has recently been proposed by Junker and Meier [36]. In this case, the electrical field is provided by four vertical wires near the crystal and parallel to its axis. The idea for this configuration came from an analysis of the electrical field inside the quartz crystal for 6 different configurations of driving electrodes. It was observed in this study that the configurations in which the electric field was created by electrodes plated on the surface of the crystal the electric field in the crystal is very much higher than when the electrodes are separated from the crystal surface. Furthermore, when the plated electrodes each subtend an angle that approaches \(\pi /2\), the reversal of the potential on two electrodes in close proximity generates very intense electric fields in the vicinity which may promote distortions of the piezoelectric motion. For electrodes on the surface, it is therefore recommended to use plating that subtends an angle of \(\pi /4\) at the centre of the cylinder’s cross-section. When the electrodes are separate from the crystal it is again best not to allow them to occupy the complete quarter circle if a nearly uniform field is to be obtained. Junker and Meier [36] recommend that the use of four wire electrodes placed around the cylindrical crystal produces the optimal field for excitation of the desired piezoelectric mode.

It might be remarked here that the application of this wire configuration of electrodes has only been carried out by Meier and his colleagues [36, 40]. In other applications, the angular span of the electrodes has often exceeded the value of \(\pi /4\) recommended by Junker and Meier and there is no evidence that this has led to any deterioration in the behavior of the crystal oscillation. However, for future applications, the findings of Junker and Meier should be borne in mind.

It is a relatively simple matter to mount the crystal and electrode assembly in a fluid containment vessel appropriate to the temperatures and pressures that are to be studied because only electrical connections are required to pass through the envelope.

3.2 The Crystal Preparation

Quartz crystals can be grown in sizes much larger than are required for the cylindrical sample to make the sensor in the viscometer. The crystal can be cut accurately to align the X- axis with the longitudinal axis of the cylinder. In the form in which the crystals are grown, they contain small impurities, and they can be removed by a process known as sweeping or electrolysis [28, 41]. Generally, for operation at a temperature below 400 K, where most viscometers have been operated, it is not necessary to remove the impurities because the internal damping in the crystal remains small [28]. However, above 400 K in un-swept crystals, the internal damping, represented by the bandwidth of the crystal resonance in vacuo increases rapidly with increasing temperature [28]. For higher temperatures then it is necessary to use swept crystals (treated electrolytically at high temperatures to remove impurities) when the internal damping remains essentially independent of temperature at least up to 650 K, but possibly beyond [28, 41].

The crystal cylinders often have a small degree of non-circularity, the effect of which is usually negligible as shown in Sect. 2. Equally, it is often not exactly of uniform radius throughout its length, but this is a small defect that has no practical consequence. More important is the roughness of the crystal surface which, as Table 1 reveals, is the most difficult condition of the theory to satisfy practically with a large margin. There are very few reports of the surface roughness of the crystals that have been employed for viscometers, whether or not they have been coated with electrodes so that not much can be said about the past. Diller and Frederick [28] state that all the surfaces of their crystal were polished to an optical finish without being more precise. However, recent, unpublished work by Meier and his colleagues [40], has explored the roughness of the cylindrical surface with a confocal microscope, the examination revealed longitudinal surface oscillations with an amplitude less than 0.1 μm which is superimposed on a surface roughness of about 20 nm. The longitudinal fluctuations are not significant, but the surface roughness means that the group, \({l}_{\text{r}}\sqrt{\frac{\rho {\omega }_{0\text{R}}}{\mu }}\), of Table 1 has the values shown there, typically, for liquids, a little less than 0.1. Thus, the condition that the value of this group should be very much less than unity is barely satisfied. The consequences of this observation have not been explored at this time. However, it is plausible to assert, but no more than that, that there will be a small amount of fluid trapped in the roughness that moves with the surface, but which does not contribute to viscous damping of the motion. It is quite possible that the surface roughness is greater when the electrodes are on the surface but there are no measurements to prove or disprove that.

3.3 Dimensions of the Sensor

The dimensions of the sensor under ambient conditions are rather straightforwardly measured and they feature in both Eqs. 1 and 2 for the evaluation for the viscosity. The mass of the crystal sensor is typically 3–5 g and can easily be determined with an uncertainty of \(1 {\upmu g}\). Its length is usually around 50 mm and can readily be determined with an uncertainty of 5 nm, as can the diameter of the cylinder which is about 5 mm. This means that the uncertainty in the mass is about 1 ppm, while the uncertainty in the surface area is \(0.1\%\) under ambient conditions.

When the instrument is employed away from ambient conditions it is necessary to correct the surface area of the crystal to account for changes in its length and diameter caused by thermal expansion and compression at high pressures. For this purpose, one needs to make use of the thermal expansion and elastic properties of quartz which is not an isotropic solid. There have been a very large number of studies of the elastic properties of quartz and the most recent, by Wang and his colleagues [42] discusses the inconsistencies in the available data and attempts to resolve them. They have studied the elastic constants by Brillouin scattering at pressures up to 10GPa near ambient temperature and report pressure derivatives of them for moderate pressures such as are required in the viscometric study of liquids. The relevant elastic constants for quartz are designated [42] as \({c}_{11}\text{, }{c}_{12}\text{, } {c}_{13}\text{, }{c}_{14}, {c}_{33}\text{, } {c}_{44}\text{ and }{c}_{66}.\) In terms of these constants, the resonant frequency of the crystal for the fundamental mode of torsional oscillation is given by [37]:

$$\omega _{{0\text{R}}}^{*} ~ = \left( {{{2~\left( {c_{{44}} c_{{66}} {-}~c_{{14}} ^{2} } \right)} \mathord{\left/ {\vphantom {{2~\left( {c_{{44}} c_{{66}} {-}~c_{{14}} ^{2} } \right)} {\left( {\rho _{c} \left( {c_{{44}} + ~c_{{66}} } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\rho _{c} \left( {c_{{44}} + ~c_{{66}} } \right)} \right)}}} \right)^{{1/2}} \pi ~/~L,$$
(5)

In terms of the same elastic constants the bulk modulus of the crystal is:

$${K}_{0}= \left(\left({c}_{11}+ {c}_{12}\right) {c}_{33}-2 {{c}_{13}}^{2}\right)/ \left({c}_{11}+ {c}_{12}+ 2 {c}_{33}-4 {c}_{13}\right),$$
(6)

while the linear modulus for compression along the X-axis is:

$${K}_{\text{c}}= \left(\left({c}_{11}+ {c}_{12}\right) {c}_{33}- 2 {{c}_{13}}^{2}\right) / \left({c}_{11}+ {c}_{12}- 2 {c}_{13}\right),$$
(7)

and along the other two axes, it is:

$${K}_{\text{a}}= \left(\left({c}_{11}+ {c}_{12}\right) {c}_{33}- 2 {{c}_{13}}^{2}\right) / \left({c}_{33}- \, {c}_{13}\right)$$
(8)

Values for these elastic constants are given in the paper by Wang et al. [42] together with their pressure derivatives.

Laesecke et al.[32]. have given means of evaluating the effects of thermal expansion on the crystal dimensions. The equations in that reference have an obvious misprint corrected here.

Along the X-axis the fractional change of a length l by virtue of thermal expansion, \(\frac{\Delta {l}_{\text{T}}}{l}\), is given by:

$$1-\frac{\Delta {l}_{\text{T}}}{l}=0.998821-3.710\times 1{0}^{-7}T+1.8794\times 1{0}^{-8}{T}^{2}-1.2907\times 1{0}^{-11}{T}^{3}$$
(9)

in which the temperature is measured in Kelvin. Along the other two axes the fractional change is given by:

$$1-\frac{\Delta {l}_{\text{T}}}{l}=0.994799+2.9369\times 1{0}^{-5}T-5.9583\times 1{0}^{-8}{T}^{2}-6.80\times 1{0}^{-11}{T}^{3}$$
(10)

The change in dimension owing to pressure along the X-axis is given by:

$$\frac{\Delta {l}_{\text{P}}}{l}=\frac{P}{{K}_{\text{c}}}$$
(11)

where is \({K}_{\text{c}}\) given by Eq. 7 and P is the system pressure. Along the other two axes,

$$\frac{\Delta {l}_{\text{P}}}{l}=\frac{P}{{K}_{\text{a}}}$$
(12)

with \({K}_{\text{a}}\) given by Eq. 8.

These equations then permit the evaluation of the surface area \(S(T,P)\) for any temperature and pressure. At temperatures up to about 450 K the thermal expansion amounts to a maximum increase in the surface area of about 0.4%, whereas the compression to 100 MPa produces a decrease in the surface area of about 0.2%. These figures are sufficiently small that, if account of them is taken as indicated, and even though the surface area enters as the square in the working equations, the contribution to the final uncertainty in the viscosity is only a few parts in a thousand.

3.4 Measurement of the Resonance Characteristics

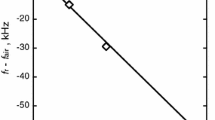
In general, the resonant characteristics of the quartz oscillator can be determined in any AC bridge supplied with a source of variable frequency and a means of balancing it. In practice, these measurements have been conducted by connecting the crystal electrodes into a wave impedance analyzer, such as the HP 4150A using, either the internal source of the analyzer or an external source of the AC signal. At any given thermodynamic state (T, P) a sweep of the oscillating frequency across the resonance from regions where there is no response enables automatic measurement of the conductance and reactance of the crystal. Typical response curves for both quantities in a fluid are shown in Fig. 3.

Fig. 3
figure 3

Measurements of the conductance, \(G(\omega )\) and reactance \(H(\omega )\) of a torsionally oscillating quartz crystal immersed in a fluid

Full size image

Laesecke et al. [32] have carried out studies of the effect of the drive voltage on the observed characteristics of the resonance. They observed that above a certain level of drive voltage, the characteristics are dependent upon the value of the drive voltage, and they recommend always to operate the instrument in regions where there is no discernible effect. This is especially important when making observations of the resonant frequency and bandwidth of the resonance in vacuo because the response of the unloaded crystal is much greater in the absence of the fluid. For these reasons, the best operational method is to drive the crystal with the smallest voltage that is consistent with the sensitivity of the available detector. If it is necessary to operate the bridge with a higher drive voltage then the advice from Laesecke et al. [32] is to operate the bridge at the same drive voltage in the fluid and out of it.

In order to obtain the characteristics of the resonance from conductance and reactance measurements such as are shown in Fig. 3, it is usual to fit the data to a complex Lorentzian function given by:

$$G(\omega )+iH(\omega )=\frac{A}{(\frac{{B}_{1}^{*}}{2})+i(\omega -{\omega }_{{1}{\text{R}}}^{*})}+({b}_{1}+i{b}_{2})+({h}_{1}+i{h}_{2})\omega$$
(13)

in which, \(G(\omega )\) is the conductance and \(H(\omega )\) the susceptance. In addition, \({B}_{1}^{*}\) is the bandwidth of the resonance, \({\omega }_{1\text{R}}^{*}\), the resonant frequency, \({b}_{1}\text{ and }{h}_{1}\) are the background conductance and susceptance respectively at zero frequency (far from resonance) and \({b}_{2}\text{ and }{h}_{2}\) are frequency coefficients for conductance and susceptance, respectively. The latter four terms allow for the inclusion of any drift in the baseline acceptance as the frequency scan progresses. Figure 3 shows just how well this function fits typical experimental data.

The requisite measured quantities determined from this fit are \({B}_{1}^{*}\text{ and }{\omega }_{1\text{R}}^{*}\). Similar measurements and fitting are carried out with the crystal in a vacuum to determine the quantities \({B}_{0}^{*}\text{ and }{\omega }_{\text{0R}}^{*}\). Laesecke et al. [32] report that a reproducibility of about 0.5% can be achieved in the determination of the bandwidth of the resonance, \({B}_{1}^{*}\) in this fashion. The uncertainty in the determination of the corresponding quantity \({B}_{0}^{*}\) in vacuo is much greater because the width of the resonance is much smaller. As we shall see below in the error analysis this is a problem only for the dilute gas regime where the resonance is still relatively narrow. For that reason, it is considered best to confine the use of this viscometer to the dense gaseous or liquid regions.

It should be pointed out here that Hafer et al. [31] have conducted free decay measurements on the oscillations of the torsional quartz-crystal excited initially at its resonant frequency and then allowed to oscillate without a drive until rest. In this way, they were able to observe the logarithmic decrement of the oscillations and thus deduce from it the bandwidth. The high frequency of the resonance means that exceedingly fast analogue/digital conversion was necessary, which proved problematic at the time. Thus, the measurement could not be performed with the same uncertainty as could be achieved with the forced oscillations.

3.5 Further Effects

The implementation of the experiment is so nearly coincident with the theoretical model that there are few other corrections to be made. This is because, as shown in Table 1, most of the conditions required for the applicability of the model are easily satisfied.

Three effects need to be considered. The first is automatically incorporated into the experimental scheme as outlined above. That is the fact that the support of the crystal, however it is achieved, introduces some small losses over and above those intrinsic to the crystal itself. Thus, the measurement of the bandwidth in vacuo does not measure only the internal losses but also those imposed externally. Since these remain the same when the fluid is present the measurement is of the quantity required rather than that owing to the crystal alone.

A second effect that might perturb the measurement would be stray reactance in the AC bridge system not nulled with the wave impedance analyzer. Fortunately, the application of the analysis of Wakeham and Richardson [37, 43, 44] shows that such a reactance would not affect the measurement of either the resonant frequency or the width of the resonance.

A final effect that has not been considered hitherto is the fact that the crystal is under pressure in the fluid when the measurement of the resonant frequency and width of the resonance are determined. This means that the effective parameters of the crystal with no viscous damping are not quite those at zero pressure, but, instead, those appropriate to a crystal free of the fluid but at the pressure and temperature of the measurement; we denote it by \({{\omega }{\prime}}_{0\text{R}}(P,T)\). The effect of temperature upon the quantity \({\omega }_{0\text{R}}^{*}\) is readily dealt with via direct measurement in vacuo. The effect of pressure must be evaluated via the elastic constants given earlier by making use of Eq. 5:

$$\frac{{{\omega }{\prime}}_{0\text{R}}(P,T)}{{{\omega }_{0\text{R}}^{*}}(0,T)}={\left[\frac{2({c}_{44}(P,T){c}_{66}(P,T)-{c}_{14}^{2}(P,T)}{\left\{{c}_{44}(P,T)+{c}_{66}(P,T)\right\}}\right]}^{1/2}\times {\left[\frac{2({c}_{44}(0,T){c}_{66}(0,T)-{c}_{14}^{2}(0,T)}{{\rho }_{\text{c}}(0,T)\left\{{c}_{44}(0,T)+{c}_{66}(0,T)\right\}}\right]}^{1/2}{ \frac{{\rho }_{\text{c}}(0,T)}{{\rho }_{\text{c}}(P,T)}}^{1/2}\frac{L(0,T)}{L(P,T)}$$
(14)

This allows the experimentally determined value of the in vacuo frequency to be corrected to higher pressures using the elastic constants of Wang et al. [42], correcting the crystal density through the bulk modulus of Eq. 6 and the length of the crystal using the linear compressibility of Eq. 7. For pressures up to 100MPa the correction to the resonant frequency in vacuo amounts to only 0.15%.

4 Uncertainty Analysis

4.1 Random Errors

For the purposes of uncertainty analysis and because, in general, \({B}_{1}\gg {B}_{0}\), the working equation for the derivation for the viscosity from the measurement of bandwidth can be written:

$$\mu \simeq \frac{{\omega }_{{1}{\text{R}}}^{*}}{2\rho }{\left(\frac{{M}_{\text{c}}}{{S}_{\text{c}}}\right)}^{2}{\left(\frac{{B}_{1}}{{\omega }_{\text{1R}}^{*}}\right)}^{2}$$
(15)

so that the fractional error in the derived viscosity is given by:

$${\left(\frac{\delta \mu }{\mu }\right)}^{2}=2{\left(\frac{\delta {M}_{\text{c}}}{{M}_{\text{c}}}\right)}^{2}+2{\left(\frac{\delta {S}_{\text{c}}}{{S}_{\text{c}}}\right)}^{2}+{\left(\frac{\delta \rho }{\rho }\right)}^{2}+{\left(\frac{\delta {\omega }_{1\text{R}}^{*}}{{\omega }_{1\text{R}}^{*}}\right)}^{2}+2{\left(\frac{\delta {B}_{1\text{R}}}{{B}_{1\text{R}}}\right)}^{2}$$
(16)

For the working equation relying only on measurements of the resonant frequency the corresponding fractional error is given by:

$${\left(\frac{\delta \mu }{\mu }\right)}^{2}=2{\left(\frac{\delta {M}_{\text{c}}}{{M}_{\text{c}}}\right)}^{2}+2{\left(\frac{\delta {S}_{\text{c}}}{{S}_{\text{c}}}\right)}^{2}+{\left(\frac{\delta \rho }{\rho }\right)}^{2}+{\left(\frac{\delta ({\omega }_{1\text{R}}^{*}-{\omega }_{0\text{R}}^{*})}{({\omega }_{1\text{R}}^{*}-{\omega }_{0\text{R}}^{*})}\right)}^{2}+2{\left(\frac{\delta {\omega }_{0\text{R}}^{*}}{{\omega }_{0\text{R}}^{*}}\right)}^{2}$$
(17)

We assume typical uncertainties in the frequency measurements of \(\delta \omega =2\pi \delta f\simeq 0.006\text{ rad/s}\), whereas \(\delta B\simeq 0.6\text{ rad/s}\). The density of the fluid can usually be known to within \(\pm 0.1\%\) while in a dense gas it may have an uncertainty of \(\pm 0.2\%\). In a liquid, \({B}_{1}\) is typically 240 rad/s while \({\omega }_{1\text{R}}^{*}\text{ and }{\omega }_{\text{0R}}^{*}\) are \(\sim\) 240,000 rad/s. The difference between \({\omega }_{1\text{R}}^{*}\text{ and }{\omega }_{\text{0R}}^{*}\) in a liquid is also typically 240 rad/s. In a gas, depending upon the density, the width of the resonance \({B}_{1}\) can be much smaller perhaps only a few rad/s. The overall uncertainty in the viscosity arising from these uncertainties and those discussed earlier means that the overall relative uncertainty in the measured viscosity can range from 0.005 to 0.02 with a 95% confidence limit depending on the density of the fluid.

It is worth noting that according to this analysis, roughly the same uncertainty results whether using the bandwidth equation or using resonant frequencies with the proviso, of course, that there are no unidentified systematic errors.

4.2 Comparison of the Working Equations

Wakeham and Richardson [43, 44] have carried out a preliminary analysis of the results of applying the two working equations to the experimental data for the viscosity obtained by three different groups [32, 34, 36, 40] with three different experimental arrangements. The experiments included non-polar liquids, non-polar gases, and polar liquids at pressures up to 100 MPa and temperatures from ambient to 400 K. Their results show a remarkable difference between the results for the two working equations which amounts to more than an order of magnitude in some cases. They have examined a large number of possible explanations for this discrepancy but were unable so far to find an explanation [44].

In these circumstances, one can only be guided by the fact that when the working Eq. 1, which is based upon the measurement of bandwidth is employed, the viscosity results obtained deviate by less than 2% from the consensus of values obtained by a wide range of other techniques [1,2,3,4,5,6,7]. This strongly suggests that this working equation is essentially correct and that there may be some unaccounted systematic effect that causes substantial errors when Eq. 2 is used to analyze the same data. For that reason, only Eq. 1 should be utilised for the analysis of measurement.

5 Conclusions

The torsional quartz crystal viscometer has been shown to be a robust instrument for the measurement of the viscosity of Newtonian fluids from temperatures as low as 4 K to 450 K and pressures from 0.1 to 100 MPa in the gas and liquid phase. Analysis of experimental results with a working equation based upon measurement of the bandwidth of a forced resonance yield results with an overall relative uncertainty in the measured viscosity between 0.005 and 0.02 with a 95% confidence limit depending on the density of the fluid. Still higher temperatures might be attained by using specially prepared swept quartz crystals. It must be emphasized that particular attention needs to be paid to minimising the surface roughness of the quartz crystal because the condition of the theory of the method which it is most difficult to satisfy relates to it.