Optical $n(p,\ T_{90})$ Measurement Suite 2: H$_2$O and D$_2$O

Abstract

A suite of measurements of refractive index $n(p,\ T_{90})$ is reported for gas phase ordinary water H$_2$O and heavy water D$_2$O. The methodology is optical refractive index gas metrology, operating at laser wavelength $633\ \text {nm}$ and covering the range $(293< T_{90} < 433)\ \text {K}$ and $p < 2\ \text {kPa}$. A key output of the work is the determination of molar polarizabilities $A_{\text {R}} = 3.7466(18) \cdot [1 + 1.5(6) \times 10^{-6} (T/\text {K} - 303) ]\ \text{cm}^3 \cdot \text{mol}^{-1}$ for ordinary water, and $A_{\text {R}} = 3.7135(18) \cdot [1 + 4.4(10) \times 10^{-6} (T/\text {K} - 303) ]\ \text{cm}^3 \cdot \text{mol}^{-1}$ for heavy water, with the numbers in parentheses expressing standard uncertainty. For heavy water, this work appears to be only the second gas phase measurement to date. For both ordinary and heavy water, this work agrees within $0.15\ \%$ with recent ab initio theoretical results for $A_{\text {R}}$, but the comparison is affected by imperfect knowledge of dispersion. For ordinary water, the close agreement between the present work and theory suggests problems at the $2\ \%$ level in the low density limit of the reference formulation for refractivity.

1 Introduction

Water is one of the most studied substances [1], but gas phase measurements of refractivity are rare. Consider the measurement challenge. A refractometer measures refractivity $n - 1$ as a change in refractive index n relative to the vacuum reference state $n = 1$. For liquid phase water, the refractive index $n \approx 1.33$, and the refractivity is $n - 1 \approx 0.33$. An accuracy target of $10^{-4} \cdot (n - 1)$ therefore requires an instrument capable of measuring with $3.3 \times 10^{-5}$ fractional uncertainty. The liquid phase accuracy requirement is satisfied with a hollow prism-type refractometer [2,3,4,5], assuming $10\ \upmu \text {rad}$ competence in angle metrology. By contrast, gas phase measurement is difficult for two compounding reasons. First, gas phase refractivity strongly depends on pressure, and meaningful measurement must be referenced to a known density. Therefore, gas pressure must be accurately measured, which (practically) bounds operation below water’s saturation pressure $p_{\text {s}} \approx 2.3\ \text {kPa}$, because pressure metrology is done at room temperature. Second, constraining operation to low pressure exacerbates the technical challenge because refractive index changes as a function of pressure $\frac{\text {d}n}{\text {d}p} \approx 2.3 \times 10^{-9}\ \text {Pa}^{-1}$ for water vapor. Consequently, the refractivity is very small. For example, at half the saturation pressure, the difference between gas $n \approx 1.0000023$ and vacuum $n = 1$ means that the original $10^{-4} \cdot (n - 1)$ target has become a $2.3 \times 10^{-10}$ fractional uncertainty requirement. So, a gas phase measurement is some $10^5$ times more challenging than liquid phase. Angle metrology (prisms and autocollimators) must be abandoned in favor of length metrology (cells and interferometers) [6]. To place the measurement challenge in context: an interferometer will have a gas pathlength approximately $0.1\ \text {m}$, and measuring $2.3 \times 10^{-10}$ fractional uncertainty requires accuracy in the length metrology of $23\ \text {pm}$—about one-eighth the diameter of the water [1] molecule!

Despite these ominous opening remarks, there is good reason to take up the gas phase measurement challenge. Water is a substance of central importance to science and industry, in fields diverse as thermodynamics, climatology, geophysics, and biochemistry. Measurements of thermophysical properties that help establish an accurate equation of state are a chief interest. The refractivity of water does not contribute to the equation of state, but the Lorentz–Lorenz equation links density to refractivity via the molar polarizability. This fact frames a fundamental motivation for the present work: gas phase measurement of optical refractivity extrapolated to zero density determines molar polarizability, without the complications known to the liquid phase interactions [7] or the molecule’s permanent dipole moment [8]. Experimental determination of polarizability bears on more critical thermophysical properties because of the growing importance of computational chemistry [1, 9]. For example, under extreme conditions where accurate thermophysical measurement are impractical, there is a growing consensus that calculation can supplement or replace measurement. Confidence in calculation is bolstered when there is agreement between measurement and calculation in fundamental aspects of the physical system. (This fact also motivates contemporaneous measurement of H$_2$O and D$_2$O by the same apparatus: comparison of ratios can be enlightening.)

Besides a benchmarking interest in the advance of ab initio calculation, the present work is also motivated by historical sensibility. One surprise is that a literature survey returned only one existing measurement for gas phase heavy water [10], dating to 1936. The situation for ordinary water is not much better. First, there are perhaps only four gas phase measurements, and consistency is no better than $2\ \%$ in refractivity [11, 12]. Second, the $n(p,\ T_{90})$ formulation adopted [13] by the International Association for the Properties of Water and Steam (IAPWS) has a molar polarizability that is surprisingly large and negative proportional to temperature, possibly driven by only one data source [14]. It is hoped that the present work ameliorates the historical record.

This article is the second part of a series reporting highly accurate $n(p,\ T_{90})$ measurements for gases of interest to thermodynamic metrology. The first article [15] reported work on helium, argon, and nitrogen, which have application to pressure and temperature standards [16]. This second article focuses on water, which has application to humidity standards [17, 18], an important topic for climate science metrology [19]. The opening remarks above explain why the water measurements are less accurate (and more challenging) than those in the first article. This second article begins by describing the measurements of ordinary water H$_2$O and heavy water D$_2$O, and concludes with discussion of their literature context. For the remainder of this article, the modifier “gas phase” will be dropped; later mention of literature data on liquid phase water will be so identified.

2 Method and Results

The apparatus was outlined in Refs. [12, 15]. However, compared to Ref. [15], measuring water required one change in configuration, now described.

2.1 Change in Apparatus, and Procedure

For water, since the gas supply manifold and the pressure indicator remain at room temperature, the operating pressure must remain below the saturation pressure. (At $293.15\ \text {K}$ the saturation pressures are $p_{\text {s}} \approx 2.3\ \text {kPa}$ for H$_2$O and $p_{\text {s}} \approx 2.0\ \text {kPa}$ for D$_2$O). Therefore, the barometric piston-gage used in Ref. [15] was replaced by two low pressure transducers. One transducer was based on the principle that strain applied to a quartz crystal changes the resonant frequency; the other transducer principle was that deformation to one electrode of a parallel plate capacitor changes the capacitance. One significance of this change in the pressure metrology is that calibration is required and drifts need to be handled. The calibration details are in App.  A. Another significance is that compared to Ref. [15], the relative precision of the measurements of $n - 1$ and p in water is reduced by a factor of 100 or more.

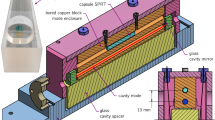
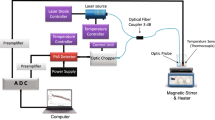
Apart from the change in pressure range and instrumentation, the procedure was similar to Ref. [15]. The $n(p,\ T_{90})$ data were sampled across nine isotherms $(293< T_{90} < 433)\ \text {K}$, with 100 triplets acquired at each isotherm. The $T_{90}$ was measured by a capsule type standard platinum resistance thermometer (cSPRT), which had been calibrated at the ITS-90 fixed points of water and indium. The pressure p was measured with the calibrated transducers. The refractivity $n - 1$ was measured with a Fabry–Perot (FP) cavity-based refractometer, readout by a frequency counter as a change in cavity resonance frequency between vacuum and gas. The change in resonance frequency was measured relative to an iodine-stabilized laser, which served as the fixed frequency reference. The two $n(p,\ T_{90})$ datasets are included in the supplemental material.

Ordinary water of grade “liquid chromatography, mass spectrometry” was used, and was specified to have evaporation residue less than 1 part in $10^7$, and cumulative trace elements less than 20 parts in $10^9$. Heavy water of grade “high purity” was used, and specified to have a deuterium enrichment of $99.91\ \%$. In each case, the water sample was syringe-transferred under argon to the evaporating vessel, which had been evacuated. The evaporating vessel was sealed, and then connected to the gas supply manifold feeding the refractometer apparatus. The evaporating vessel was a borosilicate glass bulb, which transitioned to a stainless steel flange. Room temperature remained at $(19.8 \pm 0.1)\ ^{\circ }\text {C}$ for all isotherms.

2.2 Polarizabilities of H$_2$O and D$_2$O

For a dilute gas, the Lorentz–Lorenz equation predicts that the molar polarizability

$$\begin{aligned} A_{\text {R}} = \lim \limits _{\rho \rightarrow 0} \frac{n^2-1}{n^2 + 2} \frac{1}{\rho }, \end{aligned}$$

(1)

should be approached in the limit of zero density, where $A_{\text {R}} \equiv \frac{4 \pi }{3} N_{\text {A}} (\alpha + \chi )$, with $N_{\text {A}}$ being Avogadro’s constant and $\alpha$ the electronic polarizability. For water, the magnetic susceptibility $\chi$ contributes [1] only about $1.5 \times 10^{-5} \cdot A_{\text {R}}$, and is irrelevant for the accuracy level of this work. At optical frequency ($474\ \text {THz}$), water’s strong dipole moment has no influence on (1). In practice, deducing $A_{\text {R}}$ comprises measurements of three quantities: refractivity $n - 1$, pressure p, and temperature $T_{90}$. The refractivity tells about the Lorentz–Lorenz quotient $(n^2 - 1)/(n^2 + 2)$. The pressure and temperature tell about the molar density $\rho = \frac{p}{Z R T}$, with the compressibility factor Z given by the reference equation of state [20, 21]; R is the gas constant. Strictly, (1) demands that the measured temperature $T_{90}$ be converted to thermodynamic temperature T using the consensus estimate [22,23,24]. However, the error $T - T_{90}$ is much smaller than the accuracy level of the present work.

The principle underlying the determination of $A_{\text {R}}$ is (1), but the refractometer employed in this work has an end-effect error that complicates the analysis. Details about the working-equation for the refractometer are in Ref. [15]. Here, is given just a simplistic explanation:

$$\begin{aligned} n - 1 = \frac{\Delta f + \kappa \Delta p}{ \nu \left( 1 - \kappa \Delta p \right) } + \frac{2 \epsilon _{\varphi }}{L}. \end{aligned}$$

(2)

The refractivity $n - 1 \approx \frac{\Delta {f}}{\nu }$ is mostly the measured change in (fractional) resonance frequency of the FP cavity between conditions of vacuum and gas. However, two corrections must be applied. The smaller is for the compressibility $\kappa$ of the cavity. The length of the cavity L decreases by a fractional amount $\kappa \Delta p$ when compressed by a change in the gas pressure $\Delta p$. The compressibility of the cavity was precisely characterized in Ref. [15], and the residual error resulting from imperfect knowledge was negligible for the present work.

The larger correction applied to $n - 1 \approx \frac{\Delta {f}}{\nu }$ is an end-effect $\epsilon _{\varphi }$ caused by the FP cavity mirrors having a moisture dependent reflection phase shift. A thin film coating is sensitive to humidity [25] because of its large internal surface area. Water condensing inside the thin film (by adsorption and capillary condensation) effectively increases the refractive index of the thin film [26, 27]. It is known that water adsorption in an optical filter shifts the peak reflectance to longer wavelength [28, 29]. What is less appreciated is the effect on the reflection phase shift. One can surmise [12] that the shift $\epsilon _{\varphi }$ of the reflecting surface inside a dielectric stack could be up to $70\ \text {nm}$ upon exposure to water. The present work employs ion beam sputtered coatings, so the effect of moisture on the reflection phase shift is reduced to only a few nanometers. Nevertheless, given the small change in optical pathlength $\Delta n L \approx 0.5\ \upmu \text {m}$ induced by low pressure water vapor, an $\epsilon _{\varphi }$ of a few nanometers represents a fractional error at the few percent level. As water vapor pressure increases, the reflecting surface moves farther into the dielectric stack by an amount $\epsilon _{\varphi }$, effectively increasing the cavity length—correcting (2) means $\epsilon _{\varphi }$ is signed negative. Knowledge about $\epsilon _{\varphi }$ is the most crucial aspect of this work. The final analysis deduces $\epsilon _{\varphi }$ via global optimization, as a parameterized correction factor needed to make (1) a constant value for each isotherm. The global optimization simultaneously identifies $A_{\text {R}}$ and $\epsilon _{\varphi }$, and this work employs (1) in the sense of multi-isotherm regression. Details are in App.  B, and the key concept is that $A_{\text {R}}$ is a free parameter (constant value) for each isotherm, but $\epsilon _{\varphi }$ is functionalized (nonlinear) in p and T by a physically motivated model for adsorption.

Here, the focus is on $A_{\text {R}}(T)$ and the optimized datasets. The subplots (a) and (b) of Fig. 1 show the $n(p,\ T_{90})$ datasets, graphed in terms of molar refraction and density. Several things can be appreciated from the ordinate on these two subplots. First, the measurement resolution is approximately $0.001\ \text{cm}^3 \cdot \text{mol}^{-1}$, or $0.03\ \%$. Second, the temperature dependence is difficult to detect with this resolution. Third, apparatus precision increases as temperature increases, because the dominating error $\epsilon _{\varphi } \propto \frac{p}{p_{\text {s}}}$ effectively decreases as temperature increases. However, as $\frac{p}{p_{\text {s}}} < 10^{-3}$, difficulties with the low pressure behavior of the adsorption model possibly come into play.

Fig. 1

Results for ordinary water are on left and heavy water are on right. Subplots (a) and (b): the $n(p,\ T_{90})$ datasets, converted to molar refraction and density. Errorbars span standard deviation on 10 repeats at each set pressure, and for most pressures and temperatures the errorbars are smaller than the markers. Subplots (c) and (d): molar polarizabilities derived from the $n(p,\ T_{90})$ datasets, plotted for each isotherm. Errorbars span statistical uncertainty in the global optimization. The shaded area about the linear fit covers combined standard uncertainty, as detailed in Table 1 and Fig. 2

The optimized $A_{\text {R}}(T)$ deduced from the data represented in Fig. 1(a) and (b) are graphed in subplots (c) and (d), with the convention $A_{\text {R}}(T) = A_{303} \cdot [1 + A_{\theta }(T/\text {K} - 303)]$. At the operating wavelength $\lambda = 632.9908(1)\ \text {nm}$, for H$_2$O the data are described by

$$\begin{aligned} A_{\text {R}} = 3.7466(18) \cdot [1 + 1.5(6) \times 10^{-6} (T/\text {K} - 303) ]\ \text{cm}^3 \cdot \text{mol}^{-1}, \end{aligned}$$

and for D$_2$O

$$\begin{aligned} A_{\text {R}} = 3.7135(18) \cdot [1 + 4.4(10) \times 10^{-6} (T/\text {K} - 303)]\ \text{cm}^3 \cdot \text{mol}^{-1}. \end{aligned}$$

These results are for a weighted linear fit to the nine datapoints (reduced isotherms) in Fig. 1(c) and (d), with the weighting inversely proportional to the square of the shaded areas. The numbers in parentheses denote standard uncertainty. The fixed value is described by the uncertainty budget listed in the next subsection; the temperature dependent part is given by statistical uncertainty of the linear fit. The relevance of the present results in the literature context will be discussed in Sect. 3. The reduced data of Fig. 1(c) and (d) are tabulated in the supplemental material.

2.3 Measurement Uncertainty $u(A_{\text {R}})$

An uncertainty budget for the determination of water polarizability $A_{\text {R}}$ at $303\ \text {K}$ is listed in Table 1. The budget is dominated by a single issue— adsorption of water into the thin film mirror coating—which has systematic and statistical entries. Throughout this article, the notation u(x) is used to denote the standard uncertainty of the quantity x. Unless otherwise stated, all uncertainties in this work are one standard uncertainty, corresponding to approximately a $68\ \%$ confidence level.

The dominant entry in Table 1 relates to error caused by a changing reflection phase shift from a thin film coated mirror when exposed to water vapor. In this work, the error is corrected by a global optimization of the data, together with an error model based on microporous adsorption. Therefore, correcting for the moisture dependent reflection phase shift has two uncertainty components: systematic (model error) and statistical (robustness error). A detailed discussion is given in App.  B, and here is a synopsis. Model error was evaluated by modifying the adsorption model to enforce Henry’s law behavior at low pressure. Effectively, the model based on potential theory is empirically modified to include kinetic theory characteristics at low pressure. When implemented in the global optimization, the modified model produced values of $A_{\text {R}}$ that fractionally differed from each other by $(0.3 \pm 0.9) \times 10^{-4}$ for H$_2$O and $(0.4 \pm 0.2) \times 10^{-4}$ for D$_2$O. Robustness error was evaluated by changing the optimization of $A_{\text {R}}$, from one that treated $A_{\text {R}}$ as a free parameter on each isotherm, to one that treated $A_{\text {R}}(T) = A_{303} \cdot [1 + A_{\theta }(T/\text {K} - 303)]$ as a (two parameter) linear function of temperature. Changing the optimization produced values of $A_{\text {R}}$ that fractionally differed from each other by $(0.2 \pm 0.3) \times 10^{-4}$ for H$_2$O and $(0.0 \pm 0.1) \times 10^{-4}$ for D$_2$O. The entry $\epsilon _{\varphi }$ in Table 1 combines the systematic and statistical contributions to error in cavity length caused by water adsorption.

Table 1 Relative standard uncertainty in the polarizability of water at $303\ \text {K}$. Details on the temperature dependencies are depicted in Fig. 2

In principle, fitting a refractivity isotherm in powers of pressure can determine $A_{\text {R}}$ without knowledge of density, and just rely on measured pressure and temperature. The reason $\rho = \frac{p}{Z R T}$ appears in Table 1, rather than just p and T, is because the approach to correct $\epsilon _{\varphi }$ assumes that nonlinearity in the relationship between pressure and refractivity is caused by an end-effect error. Ultimately, at the very low densities of the present work, the assumption is that the second density virial coefficients derived from the reference equations of state [20, 21] are exact. For ordinary water, measurements of the density virial coefficients were not used to construct the equation of state [21]. Nevertheless, there is good evidence [30] the equation of state produces a second density virial coefficient accurate within $2\ \%$, and is also consistent with recent ab initio calculation [31]. For heavy water, experimental data on the density virial coefficients are scarce, and the reference formulation [20] was constructed with input from ab initio calculation [31]. Again, evidence [31] supports the view that the equation of state produces a second density virial coefficient accurate within $2\ \%$ in the present temperature range. When calculating $\rho = \frac{p}{Z R T}$, the uncertainty of the compressibility factor is significant in $u(\rho )$ for $T < 320\ \text {K}$. Above $320\ \text {K}$, the contribution of pressure dominates at $1.1 \times 10^{-4} \cdot \rho$. Pressure was measured with two calibrated transducers. The calibration is detailed in App.  A, and the estimated uncertainty is about $114\ \text {mPa}$: the transducer with high precision drifts from its calibration, while the transducer with long-term stability has lower precision. Additionally, thermal transpiration (a thermomolecular pressure gradient) needs correction; as the temperature of the refractometer increases,  it generates a thermal gradient across the plumbing to the pressure transducers. At its worst case, operating with a $140\ \text {K}$ gradient at $200\ \text {Pa}$, the empirical correction [32] is $76 \ \text {mPa}$. Conservatively assuming that the water pressure gradients can be corrected within $10\ \%$, the error of the thermal transpiration correction is considerably smaller than the calibration uncertainty of the transducer. The contribution of gas temperature to density uncertainty is insignificant at $4.4 \times 10^{-6} \cdot \rho$. Temperature was measured by the cSPRT, which had been calibrated on ITS-90. Uncertainty in gas temperature is dominated by conversion of ITS-90 to thermodynamic temperature [22], rather than performance of the calibrated cSPRT.

Fig. 2

Temperature dependence for the main components contributing to the combined standard uncertainty of Table 1

Outgassing was noticeable as a drift in the density-corrected resonant frequency. The refractivity of the sealed sample was increasing from the pure substance value by $2.1 \times 10^{-10}\ \text {h}^{-1}$. Outgassing was corrected by extrapolating data to the time of filling using a linear fit to the density-corrected resonant frequency. In principle, this should have corrected the outgassing effect within $10\ \%$, for a total contribution below $10^{-5} \cdot A_{\text {R}}$. However, transients on $\epsilon _{\varphi }$ spoiled the correction, and required long wait times after a gas fill before acquiring the $n(p,\ T_{90})$ sample. The effect of outgassing on the final $A_{\text {R}}$ was evaluated by analyzing the data (linearly extrapolated) using three different wait times, $(0.5,\ 0.75,\ 1)\ \text {h}$. At low temperatures, the difference for $A_{\text {R}}$ between $0.75\ \text {h}$ and $1\ \text {h}$ wait times was four times larger than the assumption outgassing was corrected within $10\ \%$. Deviation in $A_{\text {R}}$ increased by a further factor of five for $0.5\ \text {h}$ versus $1\ \text {h}$ wait times. From this analysis it is clear that the estimate of outgassing is influenced by the time constant of adsorption. The entry in Table 1 uses half the range of disagreement between the two $A_{\text {R}}$ deduced for the $0.75\ \text {h}$ and $1\ \text {h}$ wait times.

Dimensional instability covers temporal drift and expansivity of the cavity length, as inferred by measurement of the vacuum resonance frequency. These effects were characterized in Fig. 2(c) and (d) of Ref. [15], and are highly reproducible. The temperature dependence of temporal drift is notable: drift rates (shrinking) increase with increasing temperature until reaching a maximum near $380\ \text {K}$, but then reverse trend—at $433\ \text {K}$ the temporal drift-rate is near zero, and cavity length is slightly increasing as a function of time. This phenomenon is not understood. The net effect is that dimensional instability is mostly proportional to operating temperature, but levels off as $T > 380\ \text {K}$; see Fig. 2. The entry $\frac{\text {d}L}{L}(t,T)$ is the baseline instability in dry gas. As mentioned elsewhere, transients on $\epsilon _{\varphi }$ significantly disturb cavity length, but this large influence on cavity instability is already accounted for in $u(\epsilon _{\varphi })$.

The D$_2$O used in the present work is $99.91\ \%$ pure, translating into about $0.18\ \%$ contamination by HDO, which differs in molar refraction from D$_2$O by $0.6\ \%$. Likewise, pure H$_2$O is contaminated by $0.03\ \%$ HDO. The entry “isotopologue” is a measurement bias, which more strongly affects $A_{\text {R}}$ for D$_2$O. Since water is a sticky system, the procedure of measuring ordinary water followed by heavy water could introduce slowly desorbed H$_2$O into the D$_2$O dataset. However, this problem is not realistic because between the two isotopologue measurement sequences, the pressure transducers were recalibrated in argon. There was a ten day separation between the two measurement sequences, in which the system was thoroughly purged, and then continuously pumped out at $160\ ^{\circ }\text {C}$. Furthermore, the procedure repeatedly used fresh gas—for each isotherm, every datapoint was acquired with a fresh fill of evaporated water, which was preceded by a vacuum pumpout.

Two entries contribute negligibly to $u(A_{\text {R}})$. The first negligible contributor is frequency metrology. The change in fractional frequency was measured relative to an iodine-stabilized laser, which provided a reference stable to $5\ \text {kHz}$ at $474\ \text {THz}$. The second negligible contributor is the compressibility of the cavity length. Without correction, the length change caused by compressibility $\Delta L = \kappa \Delta p$ represents a large fractional error $4.2 \times 10^{-3} \cdot A_{\text {R}}$. Compressibility was characterized within $1.4 \times 10^{-4} \cdot \kappa$ relative uncertainty in Ref. [15].

The final entry “statistical” in Table 1 was numerically provided by the diagonal elements of $\left( \chi ^2_{\nu } \cdot \mathcal {I}^{-1} \right) ^{1/2}$, with $\chi ^2_{\nu }$ being the reduced chi-square statistic (i.e., the residual sum of squares result of the global optimization divided by the degrees of freedom), and $\mathcal {I}$ is the information matrix (i.e., the negative-Hessian evaluated at the final-iteration estimate). This entry covers statistical regression on $A_{\text {R}}$. (The $\mathcal {I}$ with global optimization also provides statistical error on $\epsilon _{\varphi }$. The robustness error evaluated in this work is equivalent in magnitude to the $\mathcal {I}$ estimate.)

3 Discussion

Comparison of the present measurements with literature is hindered by the scarcity of gas phase data. Indeed, measurement of gas phase D$_2$O appears to have only one antecedent. Nevertheless, the discussion begins by drawing confidence on knowledge of molar polarizability from the agreement between the present measurements and ab initio calculation. After that, some commentary follows about an existing $2\ \%$ irregularity in the low density limit of the IAPWS reference formulation for refractivity. Finally, when faced with scarce gas phase data, comparing ratios $\text {H}_2\text {O} : \text {D}_2\text {O}$ for gas and liquid phases has some merit. Departures of liquid phase molar refraction from the molar polarizability [7] should mostly cancel in the ratio.

3.1 Literature Comparison of $A_{\text {R}}(T)$

For H$_2$O, the present measurements of molar polarizability $A_{\text {R}}(T)$ are mostly consistent with two older measurements and recent ab initio calculations.

Comparing to measurement: Schödel et al. [11] reported the specific refractivity $(n - 1)M/\rho$ with M the molar mass, which converts to $A_{\text {R}} = 3.737(2)\ \text{cm}^3 \cdot \text{mol}^{-1}$ at $\lambda = 632.991\ \text {nm}$ and $T_{90} = 293.15\ \text {K}$. The disagreement between the present measurements and Schödel et al. is 2.9 times larger than the mutual standard uncertainty. The comparison uses a $7.5 \times 10^{-4}$ relative uncertainty for Schödel et al., which they stated was dominated by the pressure transducer calibration [11]. Disagreement exceeding the mutual expanded uncertainty gives pause because the present work and that by Schödel et al. are both modern: precision interferometry in a well-controlled process, providing an absolute measurement of pure water, and discussion of measurement uncertainty. The present work also agrees with the much older work of Cuthbertson and Cuthbertson [6]. Their results were reported with a customary conversion factor (nominally based on the density of hydrogen), but the conversion factor is inconsistent at $0.11\ \%$ among separate publications—their value for a single dataset might be $A_{\text {R}} = 3.753\ \text{cm}^3 \cdot \text{mol}^{-1}$ [6] or $A_{\text {R}} = 3.748\ \text{cm}^3 \cdot \text{mol}^{-1}$ [10] at $140\ ^{\circ }\text {C}$ and interpolated to $\lambda = 633\ \text {nm}$. Cuthbertson and Cuthbertson do not have an uncertainty description, but they suggested their measurement was probably correct within $0.2\ \%$. Their challenging procedure entailed breaking liquid ampules inside a sealed evacuated cell, then heating the cell to elevate the saturation pressure while recording the change in optical pathlength. To remain state-of-the-art after more than 100 years is an awesome achievement. Finally, the present work agrees within mutual uncertainty of the provisional effort [12] using the same apparatus. The present work supersedes Ref. [12], with uncertainty in polarizability reduced by a factor of four: the present dataset is more comprehensive, the error analysis for water adsorption is more refined, and the pressure metrology has independent crosschecks.

Comparing to calculation: Garberglio et al. [33] estimated the first dielectric virial coefficient of water (isotropic, vibrationally averaged, fully quantum), comprising contributions from electronic polarizability and the dipole moment. For the former, their estimate used the polarizability surface of Lao et al. [34]. To compare with the present measurements at $474\ \text {THz}$, the tabulated results of Garberglio et al. were adjusted for the frequency dependence. The frequency adjustment used the dipole oscillator strength distributions of Zeiss and Meath [35]. For H$_2$O, this procedure produced $A_{\text {R}} = 3.752(9) \cdot [1 + 5.5(29) \times 10^{-6}(T/\text {K} - 303) ]\ \text{cm}^3 \cdot \text{mol}^{-1}$. For the temperature dependence, the present work agrees well with calculation, a result of some significance for reasons discussed in the next subsection. For the value of $A_{\text {R}}$ at $303\ \text {K}$, the present experimental work is consistent with the ab initio calculation, but the comparison is imperfect because the frequency adjusted value of Garberglio et al. [33] has some unquantified uncertainties. First, the polarizability surface of Lao et al. [34] has no stated uncertainty, and Garberglio et al. caution that their uncertainty budget for zero frequency polarizability is incomplete. Second, for the frequency dependence, Zeiss and Meath [35] have no explanation of uncertainty, but their work offers three sets of Cauchy coefficients formulated by different constructions of the distribution, from which one can surmise that flexibility in the dispersion correction to $474\ \text {THz}$ is on the order of $0.006\ \text{cm}^3 \cdot \text{mol}^{-1}$, or $1.4 \times 10^{-3} \cdot A_{\text {R}}$. On the one hand, this flexibility is surprisingly large—for neon and argon, dipole oscillator strength distributions [36] have successfully predicted dispersion within $2 \times 10^{-5} \cdot A_{\text {R}}$ [15, 37,38,39], and provisional results [15, 40] for nitrogen [41] are similarly accurate, albeit across a smaller frequency range. On the other hand, the high accuracy water measurements of Schödel et al. [11] includes three optical frequencies separated by $179\ \text {THz}$, which exhibit a disagreement range of $\pm 0.004\ \text{cm}^3 \cdot \text{mol}^{-1}$ from the average recommendation of Zeiss and Meath. Likewise, the older multiwavelength work of Cuthbertson and Cuthbertson [6] shows $\pm 0.003\ \text{cm}^3 \cdot \text{mol}^{-1}$ disagreement over a similar range (centered at higher frequency). For both comparison cases, the Cauchy coefficients from the dipole oscillator strength distributions predict a frequency dependence smaller than the measurements of Schödel et al. and Cuthbertson and Cuthbertson. Therefore, a rough uncertainty estimate of $0.006\ \text{cm}^3 \cdot \text{mol}^{-1}$ on dispersion from zero frequency to $474\ \text {THz}$ is reasonable, and the (limited) experimental evidence suggests that a frequency adjustment using Zeiss and Meath will produce an $A_{\text {R}}$ systematically small. In any case, the rough estimate of $0.006\ \text{cm}^3 \cdot \text{mol}^{-1}$ is added in quadrature with the tabulated uncertainties of Garberglio et al. to produce the $0.009\ \text{cm}^3 \cdot \text{mol}^{-1}$ stated above. So, even without knowledge of uncertainty in the polarizability surface, the rough estimate of dispersion error suggests the present work and that of Garberglio et al. are consistent within one-half of the mutual standard uncertainty.

(Aside: The aforementioned dispersion comparison between Zeiss and Meath [35] and either Schödel et al. [11] or Cuthbertson and Cuthbertson [6] was normalized, and describes frequency scaling only. The zero frequency polarizability of Zeiss and Meath is almost $0.07\ \text{cm}^3 \cdot \text{mol}^{-1}$ lower than experiment and ab initio calculation. Notably, this discrepancy in Zeiss and Meath originates in their decision to treat the Cuthbertson and Cuthbertson measurement as spuriously high. Zeiss and Meath constrained their zero frequency Cauchy term to a value of water vapor refractivity inferred from measurement of moist air [42]. Dismissing Cuthbertson and Cuthbertson has not proved durable for the dipole oscillator strength distributions of water, nor the original formulation for water vapor in the refractive index of air [43, 44].)

Finally, for D$_2$O there is only the older work of Cuthbertson and Cuthbertson [10], which converts to $A_{\text {R}} = 3.710(8)\ \text{cm}^3 \cdot \text{mol}^{-1}$ at $140\ ^{\circ }\text {C}$ and interpolated to $\lambda = 633\ \text {nm}$. As above, Cuthbertson and Cuthbertson have an informal accuracy statement of $0.2\ \%$, and disagreement between their result and the present work is at that level. For the calculation of D$_2$O, there are no dipole oscillator strength sums to adjust Garberglio et al. [33] for dispersion. Isotopologues should have a similar frequency dependence of polarizability, but a molecule with different bondlengths will exhibit finite differences. A theoretical insight [45] from hydrogen and deuterium shows a difference between the isotopes of less than $0.06\ \%$, when polarizability is adjusted from static to $633\ \text {nm}$. This difference is almost three times smaller than the present estimate of uncertainty from water’s Cauchy coefficients. Therefore, with the assumption that H$_2$O and D$_2$O have identical dispersion, the work of Garberglio et al. translates to $A_{\text {R}} = 3.721(9) \cdot [1 + 4.8(48) \times 10^{-6}(T/\text {K} - 303) ]\ \text{cm}^3 \cdot \text{mol}^{-1}$. Again, the agreement between the present work and ab initio calculation is excellent, though as discussed above, the comparison is imperfect because of the incomplete description of uncertainty (in the polarizability surface and dispersion).

3.2 Comment on the IAPWS Formulation

Qualitative discussion about the temperature dependence of molar refraction benefits from the visualization of literature data in Fig. 3, which also includes the $A_{\text {R}}(T)$ estimates mentioned in the previous subsection. The clustered areas signifying gas phase and liquid phase are selfevident. The offset in molar refraction between liquid- and gas phase is expected [7], but irrelevant to this discussion. The purpose of the figure is to frame discussion about $A_{\text {R}}(T)$ and the IAPWS formulation for the gas phase refractivity of ordinary water—the dotted line in Fig. 3(a).

Fig. 3

Survey of literature for refractivity measurements and calculation of (a) ordinary water and (b) heavy water, adjusted to $633\ \text {nm}$. The errorbars on Ref. [33] include a rough estimate of standard uncertainty in the frequency adjustment. The shaded area on this work covers standard uncertainty

Some observations can be made about ordinary water from Fig. 3(a). First, liquid phase measurements [3,4,5,6, 46, 47] appear mutually consistent, and the IAPWS formulation [13] is consistent with the source data; the consistency is within $0.02\ \%$ for the molar refraction. By contrast, gas phase data are irregular. The IAPWS formulation is inconsistent with the present work: $1.9\ \%$ in the absolute value of $A_{\text {R}}$ at $303\ \text {K}$, and a factor of 17 larger in magnitude (with contrary slope) for the temperature dependence. As mentioned in the previous subsection, the present work is consistent in $A_{\text {R}}$ within $0.25\ \%$ of other measurements [6, 11], and consistent within $0.14\ \%$ of dispersion adjusted [35] ab initio calculation [33].

Explaining the discrepancy between the IAPWS formulation and recent measurement and calculation is a matter of speculation. At the time the first version of IAPWS formulation was created, Schiebener et al. [48] warned that “measurements of the refractive index of water vapor [were] virtually nonexistent, with one exception, the work of Achtermann and Rögener [14].” The revised IAPWS formulation [13] had no additional source data besides Achtermann and Rögener for the gas phase. Four $A_{\text {R}}(T)$ from the Achtermann and Rögener dataset are plotted in Fig. 3(a), and show a strong (nonmonotonic) temperature trend. Beginning in the mid-1980s, Achtermann and collaborators pioneered several innovations in optical refractometry. One of their earliest works [49] foresaw a generation ahead into modern developments on the optical pressure scale [50]. After thirty years, their work on second refractivity virial coefficients [51, 52] is still state-of-the-art, and has proven consistent with highly accurate calculation [53]. Clearly, the work of Achtermann and collaborators makes an outstanding portfolio. For water, their apparatus used in Ref. [14] was an impressive feat of engineering: the entire apparatus was heated to $500\ \text {K}$, which elevated the saturation pressure well above $0.1\ \text {MPa}$. In principle, elevating water’s saturation pressure is desirable for measurement, because the higher gas pressures allowable have larger refractivity, thereby increasing the “signal-to-noise” ratio. However, increasing the operating temperature of an interferometer and a barometer might introduce systematic errors. (Achtermann and Rögener ingeniously used nitrogen as a standard of optical pressure at $0\ ^{\circ }\text {C}$, and transferred knowledge of mechanical pressure to a separate laser barometer external to the heated water apparatus. However, instead of using a differential pressure transducer to measure the gradient between permanently separated water and nitrogen systems, the two systems were equalized in pressure by toggling valves to a mixing chamber. Achtermann and Rögener claimed the mixing of water and nitrogen was a negligible influence on the results.) In any case, two statements seem true: (i) the gas phase ordinary water measurements of Achtermann and Rögener appear irregular, and (ii) a multiphase, multiwavelength formulation for the refractivity of water is complicated. Based on these statements, it is speculated that a reference formulation, relying on only one source of gas phase input data, may have created an irregular outcome.

At present, there is no reference formulation for the refractive index of D$_2$O, owing to the lack of data. Heavy water data plotted in Fig. 3(b) qualitatively follow the trend of ordinary water, with approximately $1.1\ \%$ separation between molar refraction in the liquid phase [3,4,5, 54] and gas phase [10, 33]. Next, by looking at ratios of H$_2$O to D$_2$O, a more quantitative analysis follows.

3.3 Ratio $\text {H}_2\text {O}:\text {D}_2\text {O}$

Comparison of $\text {H}_2\text {O}:\text {D}_2\text {O}$ ratios are listed in Table 2. The qualification for a listed ratio is that both isotopologues were measured in the same apparatus. Another preference is that both isotopologue measurements were performed contemporaneously; this appears mostly satisfied, apart from early works of Cuthbertson and Cuthbertson [6, 10] and Tilton and Taylor [55, 56]. Except for the gas phase work of Cuthbertson and Cuthbertson [6, 10], all other measurement literature [2,3,4,5, 55, 57,58,59] ratios are for liquid phase. Most ratios from the measurement literature were interpolated in wavelength to $633\ \text {nm}$ using source data; the exception is work from the Eisenberg group [57,58,59] which operated at $589\ \text {nm}$ and $546\ \text {nm}$. The ratio from ab initio calculation [33] is at zero frequency. References [3, 4, 33] and this work are reported at $303\ \text {K}$; other literature is usually at $20\ ^{\circ }\text {C}$ or $25\ ^{\circ }\text {C}$, but Cuthbertson and Cuthbertson operated at $140\ ^{\circ }\text {C}$. The ab initio calculation [33] predicts the influence of temperature on the ratio is only $-5.8 \times 10^{-8}\ \text {K}^{-1}$.

Table 2 Survey of molar refraction ratios $\text {H}_2\text {O} : \text {D}_2\text {O}$. For this work, the number in parentheses is the standard uncertainty of the ratio, dominated by statistical error in the measurement

The ratios are notably uniform. Historical measurements are mutually consistent within $0.07\ \%$. If the challenging, and temporally separated, gas phase procedure of Cuthbertson and Cuthbertson [6, 10] is omitted, together with the imprecise Rayleigh scattering technique [59], the consistency is within $0.03\ \%$. Agreement at $0.03\ \%$ evident in Table 2 is very encouraging, especially toward explaining some $2\ \%$ problems in Fig. 3(a), discussed in the previous subsection. Consistent measurement ratios between gas and liquid phases reinforce the view that problems are in the gas phase behavior of the IAPWS formulation for refractivity. It is unlikely that several independent gas phase measurements plus ab initio theory all share systematic errors of the same magnitude.

One attraction of ratio comparisons is the cancellation of systematic error, and a ratio could be significantly more precise than an absolute value. The ab initio calculation would have almost perfect cancellation of systematic error, but in the range $(250< T < 500)\ \text {K}$, the tabulated data of Ref. [33] has standard deviations from a linear fit of $0.04\ \%$ for H$_2$O and $0.06\ \%$ for D$_2$O, so knowledge of the calculated ratio is influenced by statistical effects. Likewise, for the present work, the two dominant contributors to the water measurements are statistical, and a ratio achieves no improvement in precision. Moreover, an exact ratio comparison between experiment and theory faces a number of challenges. First, an experimental ratio incurs systematic bias caused by isotopologue contamination, and in this work is expected to reduce the ratio by $0.01\ \%$. Second, and most importantly, a comparison between experiment and theory is limited by imperfect knowledge of dispersion. Using the hydrogen molecule [45] as a guide, one might expect an experimental ratio at $474\ \text {THz}$ to be $0.06\ \%$ larger than an ab initio ratio at zero frequency. So, the $0.04\ \%$ offset between the present work and Ref. [33] is nominally expected, but a more quantitative statement awaits improved knowledge of water dispersion.

4 Conclusion

Precise $n(p,\ T_{90})$ measurement suites for gas phase ordinary water H$_2$O and heavy water D$_2$O have been consecutively carried out in the same apparatus. Accurate measurements in the gas phase are rare, and measurement across a wide temperature range are rarer.

The work derives values for the temperature dependent polarizabilities. Comparison with the literature is good among experiment [6, 11], and excellent with ab initio calculation [33]. However, it is suggested that the IAPWS formulation of gas phase ordinary water overestimates the polarizability (refractivity) by $1.9\ \%$ at $303\ \text {K}$, and that the sign of the temperature dependence is inconsistent with the present experimental data. No explanation for this is offered, but a truism is that more data leads to better consensus.

Finally, refractive index gas metrology has been touted for humidity metrology [17, 18]. The embodiment is essentially a polarizing binary gas analyzer, which acts on the enormous molar refraction of water at microwave frequency. By contrast, what optical resonators lack in signal they overcome in sensitivity. For the water–nitrogen system, the analyte differs by $16\ \%$ ($0.7\ \text{cm}^3 \cdot \text{mol}^{-1}$) in molar refraction from the carrier gas, and the change in refractive index per mole is $3 \times 10^{-5}$ near ambient conditions. One should expect an optical refractive index hygrometer to determine a mole fraction of water vapor within $10^{-5}$ (or $0.4\ \%\text {RH}$), which would be competitive with the microwave approach. However, such projected performance will elude by an order of magnitude until mirror technology advances. In this context, water adsorption studies on crystalline coatings [60] and monolithic grating mirrors [61] would be especially interesting.

Appendices

Appendix A: Pressure Transducer Calibration

Before and after the water measurements, the pressure transducers were calibrated on the optical pressure scale [50]. The calibration consisted of running the apparatus in argon: optical pressure $p_{\text {ops}} = \frac{2 R T}{3 A_{\text {R}}} (n - 1) + \cdots$ was realized by measurement of argon refractivity $n - 1$ at known temperature T. The key parameter is the molar polarizability of argon $A_{\text {R}}$ [15], and R is the gas constant.

Fig. 4

Pressure transducer calibration. (a) The calibration function $\delta p = p_{\text {ops}} - p_{\text {dpt}}$ fits the difference between the optical pressure scale $p_{\text {ops}}$ and the pressure transducer indication $p_{\text {dpt}}$. Drift over time for each transducer is represented by the progressing fit lines. (b) Residuals from the respective fit to $\delta p$ for both transducers. The errorbars span standard deviation on five repeat measurements at each set pressure

The calibration results are plotted in Fig. 4(a), with $\delta p = p_{\text {ops}} - p_{\text {dpt}}$ the difference between the realization of optical pressure $p_{\text {ops}}$ versus the digital pressure transducer indication $p_{\text {dpt}}$. The calibration effectively sought functions describing $\delta p$ in argon to enable subsequent correction $p_{\text {ops}} = p_{\text {dpt}} + \delta p$ in water. For the quartz-based transducer, $\delta p$ was a linear function. For the diaphragm-based transducer, $\delta p$ required a quartic. Next, uncertainty in the calibrated pressure transducers is described.

Uncertainty of a calibrated pressure transducer is listed in Table 3. The budget has a systematic component from $u(p_{\text {ops}})$, combined with larger statistical components. The systematic component has $3.5\ \upmu \text {Pa} \cdot \text {Pa}^{-1}$ from uncertainty in the polarizability of argon [15], and $2.4\ \upmu \text {Pa} \cdot \text {Pa}^{-1}$ from uncertainty in the temperature of argon. The estimated temperature uncertainty includes realization of ITS-90 in a cSPRT calibrated by fixed points, and uncertainty in the correction from ITS-90 to thermodynamic temperature near $293\ \text {K}$ [23]. Statistical effects arise from irreproducibility of the pressure transducer, offset errors in the refractometer, and uncertainty in fitting $\delta p$. The three statistical components were assessed as follows. Irreproducibility of the pressure transducer was evaluated with short and long-term effects. The short term reproducibility was estimated by the standard deviation from a linear trend in the vacuum zero. More discussion about the vacuum zero data follows in App.  C below. The long-term reproducibility was evaluated by how much $\delta p$ varied between three argon calibrations, at the beginning, middle, and end of the H$_2$O and D$_2$O campaign. Irreproducibility in the pressure transducers holding a $\delta p$ calibration over time is depicted by the lines in Fig. 4(a). Offset error in the refractometer was also estimated by standard deviation from a linear trend on the vacuum zero. Offset error is caused by expansivity of the cavity and undetected changes in glass temperature. Errors in glass temperature were estimated to be $2\ \text {mK}$, and the thermal expansion coefficient of the cavity was $1 \times 10^{-8}\ \text {K}^{-1}$ at $293\ \text {K}$. Therefore, offset errors in the refractometer would be expected to contribute $10\ \text {mPa}$ uncertainty to the pressure transducer calibration, conforming with the entry in Table 3. Lastly, uncertainty in regression was evaluated by the standard deviation on residuals from the function fit to $\delta p$. Residuals from the first calibration (day zero) of $\delta p$ are shown in Fig. 4(b).

Table 3 Standard uncertainty in the quartz- and diaphragm-based pressure transducers at $1\ \text {kPa}$, after calibration on the optical pressure scale

Finally, three notes about the results for the pressure measuring technologies above. First, regarding complexity of the calibration function $\delta p$: the quartz-based transducer output was in nominal pressure units, so that the change in oscillator frequency as a function of pressure was preconditioned by the manufacturer; by contrast, the diaphragm-based transducer output was in volts, which was stated to be proportional to nominal pressure units within a $0.12\ \%$ tolerance. Second, regarding reproducibility of the vacuum zero: the range of the quartz-based transducer is 30 times larger than the diaphragm-based transducer. Third, the only “rough treatment” of the transducers between each water sequence was a purge with argon, flowing $33\ \text{mL} \cdot \text{s}^{-1}$ at $10\ \text {kPa}$: this purging was unlikely to have disrupted the transducer calibration $\delta p$.

Appendix B: Correcting Moisture Dependent Reflection Phase Shift

Data reduction simultaneously deduced $A_{\text {R}}$ and $\epsilon _{\varphi }$ by multivariate optimization. The key concept is that refractivity $n - 1 \approx \frac{3 p}{2 R T} A_{\text {R}}$ is linear in pressure and temperature, but the end-effect error $\epsilon _{\varphi } \propto \frac{p}{p_{\text {s}}}$ in the refractometer equation is nonlinear in pressure (and temperature, via the saturation pressure $p_{\text {s}}$). The validity of this analysis rests on four assumptions:

• 1. Molar refraction is constant on an isotherm. This assumption is valid within the ability to correct deviations from ideal gas behavior. By including the compressibility factor in the analysis, deviation from constant molar refraction then reduces to residual error in the reference equation of state plus small contribution from the refractivity virial coefficients. At the low pressures of this work, relative deviation from constant molar refraction is less than $10^{-4}$. [Not much is known about the second refractivity virial coefficient $B_{\text {R}}$ of water. Theoretical work for a simple water model found [62] the induction part (high frequency) of the dielectric virial coefficient to be approximately $50\ \text {cm}^6 \cdot \text {mol}^{-2}$ at ambient temperature. Schiebener et al. [48] inferred an experimental (optical) value an order of magnitude smaller. The relative contribution of the refractivity virial coefficient to nonideality is $\frac{B_{\text {R}}}{A_{\text {R}}}\frac{1}{B_{\rho }}$ smaller than the second density virial coefficient, which most likely takes a value between $1\ \%$ and $0.1\ \%$ and is smaller than the $2\ \%$ on $u(B_{\rho })$ [30, 31]. This work has assumed $B_{\text {R}} = 0$.]

• 2. Geometric cavity length is known as a function of pressure and temperature. This assumption is valid because compressibility and expansivity of the refractometer were precisely characterized in Ref. [15]. Since change of cavity length is proportional to pressure, an unknown compressibility would still produce constant molar refraction, but the constant value would be erroneous. Imperfect knowledge of compressibility causes less than $10^{-5} \cdot A_{\text {R}}$ error on the constant value.

• 3. Mirror reflection phase shift $\phi$ is negatively proportional to the amount of water adsorbed. This assumption was validated by a transfer matrix model of the mirror stack [63], which calculated $\phi (n_{\text {v}})$ as the refractive index of the layer voids $n_{\text {v}}$ was increased (by water adsorption). The model allowed the refractive index [64] of each layer $n_{\text {h,l}}^2 = \left[ (1 - d) n_{\text {v}}^2 + (1 + d) n_{\text {v}}^2 n_{\text {s}}^2 \right] / \left[ (1 + d) n_{\text {v}}^2 + (1 - d) n_{\text {s}}^2 \right]$ to change as a function of $n_{\text {v}}$, with $n_{\text {s}}$ the refractive index of the solid (thin film) and d the packing density (volume of solid divided by total volume of the layer including pores). This approach is approximate because it assumes every layer adsorbs the same amount of water, but it honors the important fact that $\delta n_{\text {v}}$ has a different relative effect on the high- and low-index layers. For this work, neither $\delta n_{\text {v}}$ nor d are independently known. However, $d = 0.9$ is reasonable for ion beam sputtering. Consequently, $\delta n_{\text {v}} \approx 0.011 \frac{p}{p_{\text {s}}}$ is constrained by $\delta \phi = -\delta L \frac{2 \pi }{\lambda }$ because $\delta L \equiv \epsilon _{\varphi }$ is known. (That is, the $\delta n_{\text {v}}$ input to the mirror model must produce a $\delta \phi$ consistent with the experimentally observed $\delta L$.) Given these inputs to the mirror model, the predicted nonlinearity $\phi (n_{\text {v}})$ was less than $\pm 70\ \upmu \text {rad}$. So, the relationship between the reflection phase shift and the amount of water adsorbed deviates from linear by about $0.2\ \%$. This deviation contributes error less than $3 \times 10^{-5} \cdot A_{\text {R}}$ at $293\ \text {K}$, and becomes smaller as temperature increases.

• 4. The amount of water adsorbed into the thin film follows a microporous adsorption model. For the water–silica system, there is good cause [65, 66] to employ a Dubinin-type potential model [67]. Since the reflection phase shift is negatively proportional to the amount of water adsorbed, displacements in the reflecting surface of the mirror follow the characteristic curve of adsorption. A physically motivated model for the end-effect (in length units) then takes the form

  $$\begin{aligned} \epsilon _{\varphi } = \gamma \exp \left[ - \left( \frac{RT}{\beta } \ln \frac{p_{\text {s}}}{p}\right) ^{\eta } \right] . \end{aligned}$$

  (B1)

  The three parameters $\gamma$, $\beta$, and $\eta$ are scalars that establish the characteristic curve, and all three are independent of temperature. The $\gamma$ is the maximum shift in mirror location when the thin film has fully adsorbed water; $\gamma$ is related to micropore volume, and the weak dependence on expansivity is ignored. The $\beta$ is proportional to the affinity coefficient. The $\eta$ relates to pore size distribution; an $\eta = 2$ corresponds to normally distributed pore size. [Strictly, (B1) should be in fugacity rather than pressure. This technicality slightly affects the parameters $\gamma$, $\beta$, and $\eta$, but has no affect on the final result for $A_{\text {R}}$.]

So, resting on the four assumptions above, the analysis minimizes the difference between the Lorentz–Lorenz quotient $(n^2 - 1)/(n^2 + 2)$ and the product of molar polarizability and density $A_{\text {R}} \rho$. In practice, the implementation numerically

$$\begin{aligned} \min _{A_{\text {R}}, \gamma , \beta , \eta } \left\{ \sum _{p, T}\left|(n - 1)\left[ \frac{2}{3} - \frac{1}{9}(n - 1) \right] - A_{\text {R}} \frac{p}{ZRT} \right|^2 \right\} , \end{aligned}$$

(B2)

with weighting applied to the $n - 1$ and p, inversely proportional to the square of their measurement uncertainty. On the left, the Lorentz–Lorenz quotient has been series expanded in refractivity $n - 1$, the thing that is measured. On the right, the compressibility factor Z has been used to convert measured $\frac{p}{T}$ to molar density. Note that $\epsilon _{\varphi }$ is part of (B2) via $n - 1$ and (2), and is governed by the $p,\ T$ water conditions, together with the optimized $\gamma$, $\beta$, and $\eta$ of (B1). So, for the 900-sample dataset, the optimization has 12 free parameters: nine $A_{\text {R}}$, one $\gamma$, one $\beta$, and one $\eta$. The $A_{\text {R}}$ result is the focus of the main text and is plotted in Fig. 1. The three parameters describing $\epsilon _{\varphi }$ are listed in Table 4.

Concerning uncertainty of $A_{\text {R}}$, the Sect. 2 offered an abridged description of the dominant uncertainty contributor, labeled “end-effect model $\epsilon _{\varphi }$” in Table 1. An in-depth discussion of that entry now follows. The $u(\epsilon _{\varphi })$ was evaluated as having two components: model error and robustness error. The model error is further split into two subcomponents: characteristic curve and cycle time. The first component of model error was evaluated by changing the characteristic curve of adsorption. Modeling adsorption is empirical, and dozens of models exist in literature; Ref. [68] surveys at least nine possibilities. The (B1) is of Dubinin-type [67] and based on potential theory. Compelling reasons for the Dubinin model are its adaptability (i.e., handling temperature dependence), its foundation on the principle of microporosity, and its proven suitability to water adsorption [65, 66]. However, one criticism of the Dubinin model is that it does not obey Henry’s law at low pressure. Linear behavior at low pressure may be enforced [69] by adding a limiting term to (B1), and weighting the two contributions to the adsorption by complimentary functions. The characteristic curve becomes a five parameter equation. When the analysis of (B2) is performed with the modified Dubinin model, the identified $\epsilon _{\varphi }$ differs as shown in Fig. 5(a). Deviation becomes most pronounced as temperature increases (i.e., as $\frac{p}{p_{\text {s}}}$ decreases). The feature is expected: Ref. [69] shows error appearing in the Dubinin model as $\frac{p}{p_{\text {s}}} < 10^{-2}$, and the present work samples ratios as small as $3.2 \times 10^{-4}$. The net difference between the two models is the first input to $u(\epsilon _{\varphi })$. In terms of the objective function (B2), the modified Dubinin model reduced $\chi ^2_{\nu }$ by $5.3\ \%$ for H$_2$O and $13.0\ \%$ for D$_2$O. This work favors (B1) to describe the adsorption characteristic because of its relative simplicity over the Henry’s law compliant modification.

Fig. 5

Evaluation of (a) model error and (b) robustness error for the ordinary water dataset. Model error reflects a change in the characteristic curve of adsorption underlying $\epsilon _{\varphi }$. Robustness error reflects a change in the optimization setup by linearly constraining $A_{\text {R}}(T)$. Results are plotted as the fractional contribution the end-effect error makes to a refractivity measurement

(Aside: attempts to fit the datasets to Toth or Unilan adsorption models [68] were unsuccessful. The suitability of those alternate models based on kinetic theory is questionable, because they describe adsorption of monolayers on a surface, rather than the filling of internal voids. Moreover, to describe the influence of water adsorption on the center wavelength of thin film optical filters, Brunsting et al. [29] searched 625 different empirical functions. They found the data were best described by a function with the essential characteristics of a Dubinin-type adsorption model.)

The other subcomponent of model error originates in cycle time, adsorption hysteresis, and the long time constant of desorption. (Strictly, this error is caused by imperfect experimental technique, rather than a shortcoming in the adsorption model.) The component is characterized in App.  C, by monitoring how the vacuum resonance frequency of the FP cavity changes during an isotherm. A gradual build-up of moisture occurs in the coating because of insufficient pumping time after a water measurement. The gradual build-up is removed by linear correction to the expected vacuum drift-rate. After linear correction there remains residual instability in cavity length. The root mean square deviation on the residuals from a linear fit is the second input to $u(\epsilon _{\varphi })$. Residual instability is the dominant contributor to $u(\epsilon _{\varphi })$ for the $293\ \text {K}$ and $303\ \text {K}$ isotherms, respectively, being 4.3 and 2.1 times larger than the other two components.

Table 4 Parameters for (B1) describing the change in reflection phase shift caused by water adsorption, for optimization by free $A_{\text {R}}$ or constrained $A_{\text {R}}(T)$. The numbers in parentheses are the estimate of statistical error

Robustness error refers to how $\epsilon _{\varphi }$ varies by a slight change in the implementation of (B2). The assumption that molar refraction is constant on an isotherm suggests $A_{\text {R}}$ should be a free parameter for each isotherm in (B2). However, the constant molar refraction assumption is also satisfied, within the precision of the present work, if polarizability follows $A_{\text {R}}(T) = A_{303} \cdot [1 + A_{\theta }(T/\text {K} - 303)]$. In this case, $A_{\text {R}}$ in (B2) would then be described for all isotherms by only two free parameters. These two implementations of (B2)—a free $A_{\text {R}}$ versus a constrained $A_{\text {R}}(T)$—the two implementations produced results for $A_{\text {R}}(T)$ which agree within $0.4 \times 10^{-4} \cdot A_{\text {R}}$. However, there are changes to the three parameters describing $\epsilon _{\varphi }$, as listed in Table 4, and the net difference in $\epsilon _{\varphi }$ is plotted in Fig. 5(b). No change was made to (B1) between free $A_{\text {R}}$ versus constrained $A_{\text {R}}(T)$. In terms of the objective function (B2), the constrained $A_{\text {R}}(T)$ implementation increased $\chi ^2_{\nu }$ by $6.6\ \%$ for H$_2$O and $28.8\ \%$ for D$_2$O. The net difference between the two optimizations is the third and final input to $u(\epsilon _{\varphi })$.

Appendix C: Vacuum Zero and Cavity Length Instability

Problems with the refractometer were observed during the water measurements. The origin of these problems was water adsorption into the thin film mirror coating, which shifted the location of the reflecting surface. These problems are directly tackled in App.  B. This appendix concerns a second-order effect of water adsorption, related to time constants and hysteresis.

These second-order problems are best depicted by comparing the vacuum zero readings in argon and water. In the App.  A, argon was used to calibrate the pressure transducers on the optical pressure scale. The sequence of vacuum zeros during that calibration procedure are shown in Fig. 6(a). The vacuum zero means the reading on the instrument when it was turbopumped below $10\ \text {mPa}$. For the conventional quartz and diaphragm transducers, the vacuum zero was in a pressure unit; for the refractometer, vacuum zero was the resonant frequency at vacuum, using the conversion constant $0.84\ \text{mPa} \cdot \text{kHz}$. There is nothing notable in Fig. 6(a): there are slow drifts in all instruments, and the data reflect the $10\ \text {mPa}$ reproducibility statements associated with Table 3 above.

Fig. 6

Vacuum zero readings during (a) argon and (b) heavy water measurement sequences at $293\ \text {K}$. Note the different vertical scales

The situation is remarkably different in water, shown in Fig. 6(b). For the pressure transducers, there is no significant difference in vacuum zero instability between argon and water. By contrast, stability in the vacuum zero of the cavity length degrades by about a factor of 100 between argon and water cycles. The trend on the “optical” vacuum zero of Fig. 6(b) represents a gradual build-up of adsorbed water inside the coating. This occurs because the $1.5\ \text {h}$ cycle is fast relative to long (and variable) time constants associated with water release. (A cycle had $1.2\ \text {h}$ in water and $0.3\ \text {h}$ for pumpdown.) When the pumpdown time is extended to $6\ \text {h}$, the increasing trend is diminished, but there remains fluctuation on the dry (true) cavity length, larger relative to argon. Reducing the effect of adsorption hysteresis by increasing cycle times would have extended the duration of the water measurement suite to several years. Features of a short cycle time are further emphasized:

• The $1.5\ \text {h}$ cycle employed in this work does not witness the full effect of adsorption on reflection phase shift. The pumpdown time was insufficient to release all water from the thin film coating.

• The $7.5\ \text {Pa}$ change on Fig. 6(b) corresponds to an increase of $2\ \text {nm}$ in cavity length at vacuum, sampled between exposures to $\frac{p}{p_{\text {s}}} \approx 0.87$ of water.

• A trend like that in Fig. 6(b) becomes undetectable at $353\ \text {K}$ and above; that is, the mirror instability caused by water build-up is smaller than the temporal and thermal drifts in the glass cavity.