1 Introduction

It is very common to consider diffusion coefficients of species in various applications to be constant. Although this is, naturally, the canonical choice, it can lead to profoundly misleading predictions, because diffusion coefficients may hugely vary with the species concentration over a range of two or more orders of magnitude [1,2,3,4,5,6]. Boltzmann and Matano [7, 8] proposed a method to determine varying coefficients in 1D diffusion processes in porous materials that has since become standard [9,10,11,12,13,14]. The application of this method is rather straightforward, even though care must be taken to do so properly [11]. However, a great disadvantage is that the key input data—space-time profiles of the species concentration in a sample—are measured in experiments that are very tedious and time consuming, given that diffusion is usually a very slow process in porous materials. Fluctuations in the profiles due to experimental errors could be occur.

As an alternative, in geophysical and soil science they frequently apply models that use pore size distribution curves to predict hydraulic conductivity, \(k_h\), of water or water permeability, \(K_w\), in unsaturated porous media. One of the earliest models for this purpose is due to Burdine [15] that was later improved by Mualem [16], implicitly including the ink-bottle effect [17]. This approach is very effective and convenient (measurements of pore curves are straightforward and rather short) and has been widely employed [18,19,20,21]. On the other hand, this approach has been applied to determine \(k_h\) or \(K_w\) for porous building materials on a much less frequent basis [22, 23]. Nevertheless, it could be applied also to obtain moisture diffusivity, because it is proportional to \(k_h\) through retention curves [24].

In this paper we elaborate on this pore-model approach. We first present a simple pore model based on the well-known Lucas-Washburn equation [25, 26]. Then we apply it to two samples of a ceramic brick whose moisture profiles as well as pore size distributions curves had already been measured. Thus, we determine a moisture content dependence of the moisture diffusivity from both the Boltzmann-Matano approach as well as our pore model and compare them. A comparison of diffusivities yielded by our pore model and by the Burdine and Mualem models is also provided.

2 Theoretical Background

2.1 The Boltzmann–Matano (BM) Method

The BM method [7, 8, 11] uses a 1D moisture profile w(x, t) to determine the moisture diffusivity \(\kappa (w)\) varying with w. Starting from the water mass balance equation in 1D,

$$\begin{aligned} \frac{\partial w}{\partial t} = \frac{\partial }{\partial x} \, \Big [ \kappa (w) \, \frac{\partial w}{\partial x} \Big ], \end{aligned}$$
(1)

the Boltzmann parameter

$$\begin{aligned} \eta = \frac{x}{\sqrt{t}} \end{aligned}$$
(2)

(for which \(\partial /\partial x = (1/\sqrt{t}) \, d/d\eta \) and \(\partial /\partial t = - (\eta /2t) \, d/d\eta \)) is used to rewrite Eq. 1 as an ordinary differential equation

$$\begin{aligned} \eta \, w'(\eta ) = - 2 [ \kappa (\eta ) \, w'(\eta ) ]', \end{aligned}$$
(3)

where the prime indicates a derivative with respect to \(\eta \) and \(\kappa (\eta ) = \kappa (w(\eta ))\). Integrating Eq. 3 from \(\eta \) to \(\infty \) yields

$$\begin{aligned} \int _\eta ^\infty \eta \, w'(\eta ) \, d\eta = - 2[ \kappa (\eta ) \, w'(\eta ) ]_\eta ^\infty = 2\kappa (\eta ) \, w'(\eta ). \end{aligned}$$
(4)

Hence, using the reduced water content \(W = w/w_{{{\,\textrm{sat}\,}}}\), the moisture diffusivity may be expressed as [11, 13]

$$\begin{aligned} \kappa _{\text {BM}}(\eta ) = \frac{I(\eta )}{2W'(\eta )} , \qquad I(\eta ) = \int _\eta ^\infty \eta \, W'(\eta ) \, d\eta = - \eta \, W(\eta ) - \int _\eta ^\infty W(\eta ) \, d\eta , \end{aligned}$$
(5)

where \(W'(\eta ) = dW(\eta )/d\eta \). The diffusivity \(\kappa _{\text {BM}}(W)\) varying with the moisture content follows from combining \(\kappa _{\text {BM}}(\eta )\) from Eq. 5 and \(W(\eta )\) calculated from the w(x, t) curve (which is obtained from 1D in-diffusion experiments).

2.2 Pore Models

Rather than from the moisture profiles, models were developed to determine \(\kappa \) from pore curves—the differential and cumulative pore size distribution f and F, respectively. The differential distribution f denotes the probability density of occurrence of pores of sizes between r and \(r + dr\) in a sample, while the cumulative distribution F denotes the probability of occurrence of pores of sizes larger than or equal to r. Thus, they are related as

$$\begin{aligned} F(r) = \int _r^{r_{\max }} f(r) \, dr, \qquad f(r) = - \frac{dF(r)}{dr} , \end{aligned}$$
(6)

where r is the pore radius, ranging between its minimal and maximal values \(r_{\min }\) and \(r_{\max }\), respectively. We shall consider two pore models in which the moisture diffusivity is expressed via the integral

$$\begin{aligned} J_n (r) = \frac{1}{r^n f(r)} \, \int _r^{r_{\max }} R^n f(R) \, dR \end{aligned}$$
(7)

with a suitable value of n.

  1. 1.

    The Burdine model uses the simplest approximation of cylindrical pores to express the moisture diffusivity as [15, 21, 27]

    $$\begin{aligned} \kappa _{\text {B}}(W) = \kappa _{{{\,\textrm{sat}\,}}} \; W^2 \, \frac{J_2 (F^{-1}(W))}{ J_2 (r_{\min }) } , \end{aligned}$$
    (8)

    where \(F^{-1}\) is the inverse function to F.

  2. 2.

    A more advanced model of Mualem takes into account the ink-bottle effect for pores [17]. In this model the expression for moisture diffusivity is given as [16, 21, 27]

    $$\begin{aligned} \kappa _{\text {M}}(W) = \kappa _{{{\,\textrm{sat}\,}}} \; \sqrt{W} \; \Big [ \frac{J_1 (F^{-1}(W))}{ J_1 (r_{\min }) } \Big ]^2 . \end{aligned}$$
    (9)

In both models the saturation diffusivity \(\kappa _{{{\,\textrm{sat}\,}}}\) is an unknown parameter and needs to be determined independently.

3 Experimental Data

We consider two samples of a fired ceramic brick already studied in [28, 29] for which both the pore size curves and moisture profiles had already been measured. This will enable us to compare the results obtained from pore models and from the BM method.

Their cumulative pore size distributions of the two samples had been measured by standard mercury porosimetry using a Pore Sizer 9310 (Micromeritics Instrument Corp.) and are plotted in Fig. 1. They have a simple, unimodal behavior with a single jump near the pore radius of \({5}{\upmu {m}}\). In fact, we observe that the brick samples are such that

  • \(10 \%\) of the smallest pores (i.e., \(F \ge 0.9\)) have sizes below \({0.7}{\upmu \hbox {m}}\) for sample 1 and below \({0.4}{\upmu \hbox {m}}\) for sample 2;

  • \(10 \%\) of the largest pores (i.e., \(F \le 0.1\)) have sizes above \({10.6}{\upmu \hbox {m}}\) for sample 1 and above \({9.9}{\upmu \hbox {m}}\) for sample 2;

  • \(80 \%\) of the pores (i.e., \(0.1 \le F \le 0.9\)) have sizes \({0.7}{\upmu \hbox {m}} \le r \le {10.6}{\upmu \hbox {m}}\) for sample 1 and \({0.4}{\upmu \hbox {m}} \le r \le {9.9}{\upmu \hbox {m}}\) for sample 2.

Fig. 1
figure 1

The cumulative pore size distribution curves for the two ceramic brick samples

Full size image

The moisture profiles had been measured by the capacitance technique [30] in water suction experiments. Samples of dimensions 20mm \(\times \)40mm \(\times \) 300mm had been placed in the horizontal position to eliminate the effect of gravity on the moisture transport, and the lateral sides of the samples had been water and vapor-proof insulated to establish 1D transport. A water container had been attached to one end of a sample with a good contact with the sample surface (through a viscous sponge), and a constant level of water had been maintained in the container (using a float chamber). A capacitance moisture meter with parallel plates of dimensions \({20\,\textrm{mm}} \times {40\,\textrm{mm}}\) had been used to measure the moisture profiles [30]. An adequate space averaging of results and reduction of the effect of inhomogeneities in the samples was achieved by placing the moisture meter readings \({5\,\textrm{mm}}\) apart. The moisture content curves, reduced to the saturation value, are plotted in Fig. 2. The difference between the moisture profiles at early and late stages reflects different behavior of water diffusion at the beginning of experiment (near the contact boundary of the samples) and at subsequent periods of experiment (deeper in the samples).

Fig. 2
figure 2

The reduced moisture profiles for the two ceramic brick samples at early stages of measurement (at time \({180\,\textrm{s}}\)) and at later stages (times longer than \({1200\,\textrm{s}}\))

Full size image

4 Results

4.1 A Novel Pore Model of Diffusivity

According to the Lucas-Washburn equation [25, 26], the distance traveled by a liquid penetrating into a cylindrical pore of radius r is \(d_0 = (C_0 r t)^{1/2}\). The constant \(C_0 = \sigma \cos \theta / 2 \mu \), where \(\sigma \) is its surface tension, \(\theta \) is the contact angle, and \(\mu \) is the dynamic viscosity of the liquid. We apply this relation to approximate the moisture profile W in a 1D flow of water through a porous material. However, instead of \(C_0\), we use a different constant, C (m·s−1), that may account for tortuosity, constrictivity, or other effects. Thus, the distance of water penetration into a pore of radius r will be taken as

$$\begin{aligned} d(r,t) = \sqrt{C r t} . \end{aligned}$$
(10)

A pore of diameter r contributes to W(x, t) only if the distance d(r, t) exceeds x; i.e., if \(d(r,t) \ge x\), or \(r \ge x^2/Ct = \eta ^2/C\) by Eqs. 2 and 10. Therefore,

$$\begin{aligned} W(\eta ) = \int _{r_\eta }^{r_{\max }} f(r) \, dr = F(r_\eta ), \qquad r_\eta = \frac{\eta ^2}{C} . \end{aligned}$$
(11)

This equation is the basis of our model and will be used to evaluate the moisture diffusivity \(\kappa \) (see Eqs. 19 and 20 below).

The value of constant C can be obtained as follows. At time t the water inflow into a sample via the pores of size r is \(\phi (r,t) = \rho _w w_{{{\,\textrm{sat}\,}}} f(r) \, d(r,t)\), and so the total water inflow is

$$\begin{aligned} \Phi (t) = \int _{r_{\min }}^{r_{\max }} \phi (r,t) \, dr = \rho _w w_{{{\,\textrm{sat}\,}}} \sqrt{C} \; \langle \sqrt{r} \rangle \, \sqrt{t} , \qquad \langle \sqrt{r} \rangle = \int _{r_{\min }}^{r_{\max }} \sqrt{r} \; f(r) \, dr. \end{aligned}$$
(12)

Since the inflow \(\Phi \) is proportional to the square root of time as \(A \, t^{1/2}\), where A is the water absorption coefficient, Eq. 12 yields

$$\begin{aligned} C = \frac{\kappa _0}{\langle \sqrt{r} \rangle ^2}, \qquad \kappa _0 = \Big ( \frac{A}{\rho _w w_{{{\,\textrm{sat}\,}}}} \Big )^2. \end{aligned}$$
(13)

Thus, C is expressed via A that is measured in 1D water absorption experiments in a rather straightforward way (contrary to the measurement of moisture profiles). If preferred, it is possible to express

$$\begin{aligned} \langle \sqrt{r} \rangle = \sqrt{r_{\min }} + \frac{1}{2} \, \beta _0, \qquad \beta _0 = \int _{r_{\min }}^{r_{\max }} \frac{F(r)}{\sqrt{r}} \, dr. \end{aligned}$$
(14)

via the F curve (rather than the f curve), where Eq. 6 and integration by parts were used. Note that \(\langle r^{1/2} \rangle \) is the average (over the distribution f) of a square root \(r^{1/2}\) of pore size.

The constant C can be obtained also from the moisture profile W. In fact, Eq. 11 yields

$$\begin{aligned} \beta _0 = \frac{2}{\sqrt{C}} \, A_W, \qquad A_W = \int _{\eta _{\min }}^{\eta _{\max }} W(\eta ) \, d\eta , \end{aligned}$$
(15)

where the integration limits \(\eta _{\max } = (Cr_{\max })^{1/2}\) and \(\eta _{\min } = (Cr_{\min })^{1/2}\) make \(A_W\) be dependent on C. Hence, the value C is such that \(2 A_W(C) / C^{1/2}\) is equal to \(\beta _0\) by Eq. 15. Note that \(A_W\) is equal to the area under the moisture profile W between the values \(\eta _{\max }\) and \(\eta _{\min }\) (which may be expected to be almost the whole area under the W curve).

Finally, let us determine the moisture diffusivity \(\kappa \). Equations (6) and (11) yield

$$\begin{aligned} \frac{dW(\eta )}{d\eta } = \frac{d F(r_\eta )}{d\eta } = \frac{2\eta }{C} \, \frac{dF(r_\eta )}{dr} = 2 \sqrt{\frac{r_\eta }{C}} \; \frac{dF(r_\eta )}{dr} = - 2 \sqrt{\frac{r_\eta }{C}} \; f(r_\eta ) \end{aligned}$$
(16)

and

$$\begin{aligned} I(\eta )&= 2 \int _\eta ^\infty r_\eta \, F'(r_\eta ) \, d\eta = \sqrt{C} \, \int _{r_\eta }^{r_{\max }} \sqrt{r} \, F'(r) \, dr \nonumber \\&= - \frac{\sqrt{C}}{2} \, \big [ 2\sqrt{r_\eta } \, F(r_\eta ) + \beta (r_\eta ) \big ] = - \sqrt{C} \; \alpha (r_\eta ), \end{aligned}$$
(17)

where

$$\begin{aligned} \alpha (r) = \int _r^{r_{\max }} \sqrt{R} \; f(R) \, dR, \qquad \beta (r) = \int _r^{r_{\max }} \frac{F(R)}{\sqrt{R}} \, dR \end{aligned}$$
(18)

Thus, Eq. 5 gives

$$\begin{aligned} \kappa (\eta ) = C \, \frac{ 2 F(r_\eta ) + \frac{ \beta (r_\eta ) }{ \sqrt{r_\eta } } }{ 8 \, |F'(r_\eta )| } = \frac{ \kappa _0 }{4 \, \langle \sqrt{r} \rangle ^2} \, J_{1/2} (r_\eta ), \end{aligned}$$
(19)

implying

$$\begin{aligned} \kappa (W) = C \, \frac{ 2W + \, \frac{\beta (F^{-1}(W))}{\sqrt{F^{-1}(W)}} }{ 8 \, |F'(F^{-1}(W))| } = \frac{ \kappa _0 }{4 \, \langle \sqrt{r} \rangle ^2} \, J_{1/2} (F^{-1}(W)) \end{aligned}$$
(20)

by Eq. 11. Contrary to the Burdine and Mualem models (see Eqs. 8 and 9), these formulas for \(\kappa \) contain no undetermined multiplicative parameter—values of the constants C and \(\kappa _0\) can be calculated from Eqs. 13 or 15.

Remark 4.1

According to the Krus-Künzel formula, the average diffusivity is estimated as \(\kappa _{\text {aver}} \approx (\pi /4) \kappa _0\) [31]. Our model yields

$$\begin{aligned} \kappa _{\text {aver}} = \int _0^1 \kappa (W) \, dW = \frac{\langle r \rangle }{2\langle \sqrt{r} \rangle ^2} \, \kappa _0, \end{aligned}$$
(21)

where \(\langle r \rangle \) is the average (over f) of the pore size r. In fact, we have

$$\begin{aligned} \kappa _{\text {aver}}&= - \int _0^\infty \kappa (\eta ) \, W'(\eta ) \, d\eta = - \frac{1}{2} \, \int _0^\infty I(\eta ) \, d\eta = - \frac{\sqrt{C}}{2} \, \int _0^\infty d\eta \int _{r_\eta }^{r_{\max }} \sqrt{r} \, F'(r) \, dr \nonumber \\&= \frac{\sqrt{C}}{2} \, \int _{r_{\min }}^{r_{\max }} dr \, \sqrt{r} \, f(r) \int _0^{\sqrt{Cr}} d\eta = \frac{C}{2} \, \int _{r_{\min }}^{r_{\max }} \, r \, f(r) \, dr = \frac{C}{2} \, \langle r \rangle . \end{aligned}$$
(22)

It now suffices to recall Eq. 13.

4.2 Application to the Ceramic Brick

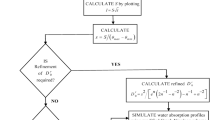
We begin by fitting the experimental data by simple functions for which the moisture diffusivity can be evaluated from Eq. 20. This analytical approach will also enable us to avoid problems related to the numerical determination [6].

The F pore curves are fitted with the complementary error function, \({{\,\textrm{erfc}\,}}\), modified by a cubic polynomial, \(P_3\), to achieve good fits near \(r_{\min }\),

$$\begin{aligned} F_{{\text {fit}}} (r) = P_3 (r) \, F_0 (r), \qquad F_0 (r) = \frac{ {{\,\textrm{erfc}\,}}\big ( a \log \frac{r}{r_0} \big ) }{ {{\,\textrm{erfc}\,}}\big ( a \log \frac{r_{\min }}{r_0} \big ) } , \quad P_3 (r) = 1 + \sum _{i=1}^3 b_i \log ^i \frac{r}{r_{\min }}, \end{aligned}$$
(23)

where a, \(r_0\), and \(b_i\) are five fitting parameters. Note that \(F_{{\text {fit}}} (r_{\min }) = 1\). In Fig. 3 the best fits to both F curves are plotted; the values of the fitting parameters are listed in Table 1. Both F curves are fitted with very good accuracy, the coefficients of determination \(R^2\) being 0.999914 and 0.999935.

Fig. 3
figure 3

The fits of F pore curves with theoretical curves from Eq. 23

Full size image
Table 1 Values of the fitting parameters in the best fits to the F pore curves
Full size table

We use \({{\,\textrm{erfc}\,}}\) modified by a cubic polynomial to fit also the moisture profiles,

$$\begin{aligned} W_{{\text {fit}}} (\eta ) = Q_3 (\eta ) \, \frac{ {{\,\textrm{erfc}\,}}[p(\eta - \eta _0)] }{ {{\,\textrm{erfc}\,}}(-p\eta _0) } , \qquad Q_3 (\eta ) = 1 + \sum _{i=1}^3 r_i \eta ^i, \end{aligned}$$
(24)

where p, \(\eta _0\), and \(r_i\) are five fitting parameters. For the early stage data the cubic polynomial is not actually needed to obtain a good fit, so we take \(r_i = 0\) for the early stage. The best fits to the moisture profiles are plotted in Fig. 4; the values of the fitting parameters are listed in Table 2. The moisture profiles are fitted with rather good accuracy, the corresponding \(R^2\) being 0.997748 and 0.998674 for the early and late stages of sample 1, and 0.994892 and 0.997414 for the early and late stages of sample 2.

Fig. 4
figure 4

The fits of W profiles with theoretical curves from Eq. 24

Full size image
Table 2 Values of the fitting parameters in the best fits to the W profiles
Full size table

Using the fits \(F_{{\text {fit}}}\) to the pore curves, we evaluate \(\beta _0\) from the second equality in Eq. 14, yielding \({4.26}\times 10^{-3}{\hbox {m}^{1/2}}\) for sample 1 and \({4.13}\times 10^{-3}{\hbox {m}^{1/2}}\) for sample 2. Then, with the help of the fits \(W_{{\text {fit}}}\) to the moisture profiles, the values of constant C are calculated from Eq. 15. We get 1.04 m·s−1 and 0.56 m·s−1 for the early and late stages of sample 1, and 1.18 m·s−1 and 0.88 m·s−1 for the early and late stages of sample 2. We may now assess whether the moisture profile \(F_{{\text {fit}}} (\eta ^2/C)\) predicted by our pore model (see Eq. 11) is in good agreement with the actual data from Fig. 2. This is shown in Fig. 5. While for the early data the agreement is quite good, for the late stage data the predicted moisture profiles are less steep in the central parts (near \(W=1/2\)). For example, at \(\eta _0\) both fits \(F_{{\text {fit}}} (\eta ^2/C)\) and \(W_{\text {fit}}(\eta )\) to late stage data have almost the same values (between 0.35 and 0.38) for both samples. However, the slopes of \(F_{{\text {fit}}} (\eta ^2/C)\) for the two samples are 2.8 and 3.6 times smaller than the slopes of \(W_{\text {fit}}(\eta )\). The corresponding \(R^2\) are 0.992 and 0.979 for the early and late stages of sample 1, and 0.992 and 0.975 for the early and late stages of sample 2.

Fig. 5
figure 5

A comparison of the moisture profiles predicted by the model (the curves) with the measured data from Fig. 2

Full size image

Using Eq. 5, it is possible to determine the moisture diffusivities \(\kappa _{\text {BM}}\) by the BM method from the fits \(W_{\text {fit}}\) to the moisture profiles. These can be compared to the diffusivities \(\kappa \) predicted by our model from Eq. 20. The resulting dependences on W are plotted in Fig. 6. First, it is observed that the diffusivities for which cubic polynomials were used in \(F_{{\text {fit}}} (\eta ^2/C)\) and \(W_{\text {fit}}(\eta )\) have non-monotonous behavior when W is above 0.8. The same effect was observed in previous studies (see [11], for example). Second, very good agreement between our \(\kappa \) and \(\kappa _{\text {BM}}\) occurs for early stages. On the other hand, for late stages our \(\kappa \) is about three to four times higher than \(\kappa _{\text {BM}}\) on an average between \(W = 0.1\) and \(W = 0.8\). Since the data from late stages are considered to be more representative (while the early data could be prone to inaccuracy) [11], we conclude that our model overestimates the diffusivity. The reason is as follows. As a general rule, it is the slope of a moisture profile at its center that determines the values of \(\kappa \) [6]. In our case, this slope is given by parameter p in \(W_{{\text {fit}}}\), whereas our pore-model predicts the slope \(2a/(c r_0)^{1/2}\) by Eqs. 11 and 23. According to Tables 1 and 2, both these slopes have similar values for early stages but they differ for late stages. Thus, the diffusivity predicted by our pore model at late stages is higher than \(\kappa _{\text {BM}}\) due to the above-given fact that \(F_{{\text {fit}}} (\eta ^2/C)\) are about three to four times less steep than the measured moisture profiles at late stages (see Fig. 4). It will be a matter of future research to analyze whether this discrepancy can be remedied. There could be inaccuracies contained in both approaches (in our pore model as well as in the measured profiles) and it will be necessary to assess them in detail. One source for refinement may be corrections to the measured pore curves which would lead to steeper slopes in F, such as the study [32] in which corrections due to shielding effects in mercury porosimetry were taken into account.

Fig. 6
figure 6

The moisture diffusivity \(\kappa \) for the early and late stages as predicted by our model and the BM method for (a) sample 1 and (b) sample 2. The ratio of \(\kappa \) predicted by our model to \(\kappa _{{\text {BM}}}\) from the BM method for W between 0.1 and 0.8 and for (c) sample 1 and (d) sample 2

Full size image

Note that the moisture diffusivity \(\kappa \) in Fig. 6 strongly varies with the relative moisture content W, over one or two orders of magnitude. This fact is a property of \(\kappa \) in porous media, resulting from the diffusional behavior of moisture in a porous matrix (it has nothing to do with changes in temperature or other external parameters). Such strong variations in \(\kappa \) have been observed in various applications [11, 13, 14] where the assumption of a constant \(\kappa \) would have yielded rather erroneous predictions. This is true also for our study: if we considered that \(\kappa \) was constant, then Eq. 3 would lead to the solution \(W(\eta ) = {{\,\textrm{erfc}\,}}( \eta / 2 \sqrt{\kappa })\) that would not fit the moisture profiles data in Fig. 2 with good inaccuracy. To make fits accurate, \(\kappa \) must notably change with W.

Finally, let us compare the diffusivity relative, \(\kappa _{\text {rel}}\), to its value corresponding to the radius \(r_0\) from Table 1 as it is predicted by our model (Eq. 19) with those predicted by the Burdine and Mualem models (Eqs. 8 and 9). The main difference between these three cases is that the results are expressed via different integrals, namely, \(J_{1/2}\), \(J_2\), and \(J_1\), respectively. The comparison is plotted in Fig. 7. Our \(\kappa _{\text {rel}}\) is less increasing than the Mualem and Burdine relative diffusivities. All three \(\kappa _{\text {rel}}\) intersect at \(W_0\) corresponding to the chosen reference pore radius \(r_0\) (this is \(W_0 = 0.35\) for sample 1 and \(W_0 = 0.39\) for sample 2). For W between 0.1 and \(W_0\) the relative diffusivities yielded by the Mualem and Burdine models are up to 3 and 15 times, respectively, smaller than our \(\kappa _{\text {rel}}\). On the other hand, for W between \(W_0\) and 0.8 the relative diffusivities yielded by the Mualem and Burdine models are both higher than our \(\kappa _{\text {rel}}\), by up to 12 to 13 times.

Fig. 7
figure 7

A comparison of the relative moisture diffusivity given by our, the Burdine (B), and the Mualem (M) models for the early and late stages and for both samples

Full size image

4.3 An Expression for the Diffusivity

For function \(F_{{\text {fit}}} (r) = P_3 (r) \, F_0 (r)\) (see Eq. 23) with which we fitted the F curve data it is possible to explicitly evaluate the diffusivity, \(\kappa _{{\text {fit}}} (\eta )\), using Eq. 19. Since the resulting formula for \(\kappa _{{\text {fit}}}\) is rather complex, let us present its simplification that is based on the observation that the \(b_i\) coefficients have small values (see Table 1). Namely, let us take all \(b_i\) to be equal to zero. Then the polynomial \(P_3 = 1\) and \(F_{{\text {fit}}} = F_0\). Using Eq. 19 for the F pore curve equal to \(F_0\), we get the diffusivity

$$\begin{aligned} \kappa _{\text {appr}}(\eta ) = \frac{\sqrt{\pi }\; C \, r_0}{8a} \, e^{(z_\eta + 1/4a)^2} \, \varphi (z_\eta ) \end{aligned}$$
(25)

with

$$\begin{aligned} \varphi (z)&= {{\,\textrm{erfc}\,}}\Big ( z - \frac{1}{4a} \Big ) - {{\,\textrm{erfc}\,}}\Big ( z_{\max } - \frac{1}{4a} \Big ) + e^{z_{\max }/(2a) - 1/(4a)^2} {{\,\textrm{erfc}\,}}z_{\max } \nonumber \\&\approx {{\,\textrm{erfc}\,}}\Big ( z - \frac{1}{4a} \Big ), \end{aligned}$$
(26)

where \(z = a \ln (r/r_0)\), \(z_\eta = a \ln (r_\eta /r_0)\), and \(z_{\max } = a \ln (r_{\max }/r_0)\). We may solve \(W = F_0(z_\eta )\) for z and obtain the W dependence of the diffusivity as

$$\begin{aligned} \kappa _{\text {appr}}(W) = \frac{\sqrt{\pi }\; C \, r_0}{8a} \, e^{({{\,\textrm{IE}\,}}_W + 1/4a)^2} \, \varphi ({{\,\textrm{IE}\,}}_W) \end{aligned}$$
(27)

with \({{\,\textrm{IE}\,}}_W = {{\,\textrm{ierfc}\,}}(W {{\,\textrm{erfc}\,}}z_{\min })\), where \(z_{\min } = a \ln (r_{\min }/r_0)\) and \({{\,\textrm{ierfc}\,}}\) is the inverse to \({{\,\textrm{erfc}\,}}\). Near \(W = 1/2\) we may use a linear approximation

$$\begin{aligned} \kappa _{\text {appr}}(W) \approx \frac{\sqrt{\pi }\; C \, r_0}{8a} \, \Big \{ e^{1/(4a)^2} \, {{\,\textrm{erfc}\,}}\Big (- \frac{1}{4a} \Big ) \, \Big [ 1 - \frac{\sqrt{\pi }}{4a} \, (2W - 1) \Big ] + (2W - 1) \Big \} \end{aligned}$$
(28)

Fig. 8 shows the comparison of the approximate diffusivity \(\kappa _{\text {appr}}\) from Eq. 27 with the diffusivity \(\kappa _{{\text {fit}}}\) plotted in Fig. 6(a) and (b). Agreement between them is rather good, the best occurring near \(W = 0.35\).

Fig. 8
figure 8

The approximate diffusivity \(\kappa _{\text {appr}}\) from Eq. 27 relative to the diffusivity \(\kappa _{{\text {fit}}}\) from Fig. 6a and b. The early and late stages yield almost identical results, so only late stages are plotted for either sample

Full size image

5 Conclusions

A dependence of the moisture diffusivity \(\kappa \) on the moisture content W was determined from a novel pore model based on the Lucas-Washburn equation. The expression for \(\kappa (W)\) contains (a) the standard diffusivity \(\kappa _0\) that is often used to estimate \(\kappa \) from the water absorption coefficient A, (b) the mean value (over the pore distribution f) of the square root of pore radius, and (c) the integral \(J_{1/2}\). There are no undetermined multiplicative parameters as in the Burdine and Mualem models in which the formulas for the diffusivity use the integrals \(J_2\) and \(J_1\), respectively.

Experimental data on the cumulative pore curve F and moisture profiles W for two brick samples were fitted with high accuracy by polynomially modified error functions. These were then used to calculate \(\kappa \) from our pore model and the BM method. It turned out that our pore-model predicted \(\kappa \) that was in very good agreement with \(\kappa _{\text {BM}}\) only for early stage data in the moisture profiles. For late stage data our \(\kappa \) was three to four times higher. Relative diffusivity resulting from our pore model is less increasing than those yielded by the Burdine and Mualem models. We also presented an approximate formula that explicitly showed the W dependence of the diffusivity.

It could be concluded that our model has a potential to become an efficient tool in the prediction of moisture diffusivity of porous materials. To this end, however, it will be necessary to perform further investigation with the emphasis on its testing for a wide range of porous materials and possible subsequent improvements in (a) the pore model itself, and/or (b) measured pore curves by adopting appropriate corrections (for example, due to shielding [32]). Both of these could influence the results for \(\kappa \) in a significant way. Comparisons with results yielded by other methods than that of Boltzmann and Matano will also be beneficial.