1 Introduction

Viscosity is a very important thermophysical property in several fields of metal processing, like the fluid flow behaviour, kinetics of the metallurgic process, and others. Despite this fact, the industry still needs new data for several molten materials, like salts, metals, and alloys, as the available data frequently shows large discrepancies [1], and the effect of “impurities” is difficult to model. This may be attributed to technical difficulties in measuring the viscosity at high temperatures (high-temperature measurement and control, materials reactivity between the samples and containers) and the necessity to account for a variety of phenomena that generally do not influence the measurements at low temperatures [2]. This task is both challenging for the experimentalist (also time-consuming) and for the theoretical interpretation.

Although there are many methods to measure the viscosity of fluids [3,4,5,6], temperature is a key parameter in selecting state-of-the-art instruments (absolute measurements), due to physical, chemical (reactivity of samples with atmosphere and viscometer components), and material constraints.

Among the several methods available for measuring high-temperature viscosity, the most suitable for molten salts, metals, and alloys are [2,3,4, 7]:

  • the capillary viscometers;

  • the oscillating-body (plate, cup, or sphere) method;

  • the rotational method (cone and plate, cylinder).

Any type of oscillating body viscometer consists of an axially symmetric body suspended from an elastic stand, usually a metal wire, through which torsional oscillations can be induced in the body, immersed or filled with liquid. The fluid viscosity is obtained from the measured decrement of the oscillations and their period. Once an oscillation in the body is induced, the fluid drag will cause a logarithmic decrement of the amplitude of oscillation and an increase in the period of oscillation, relative to vacuum. These parameters depend on the viscosity and density of the fluid, as well as other factors, like the liquid level in the cell, the straightness of the wire suspension, and the non-existence of non-planar oscillations, among others. In principle, if the viscometer is well designed for the desired range of temperatures and viscosity/density of the melts, the only measurements that are necessary, besides pressure and temperature (and composition, in mixtures), are mass and time, which can be obtained with high accuracy. This is an absolute method, so it is not necessary to make any calibration with fluids of known viscosity.

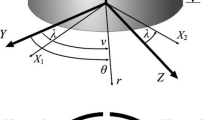
The most extensive method used for high-temperature molten salts and metals is the oscillating cup method, which has been used extensively by the authors, after the first developments for molten salts by Torklep et al. [8], Abe et al. [9] and Ejima et al. [10], metals by Tippelskirch et al. [11] and Grouvel et al. [12] and molten semiconductors by Nakamura et al. [13]. Figure 1 shows schematically the cup filled with the liquid used by these authors.

Fig. 1
figure 1

Scheme of the oscillating cup, filled with the liquid. The lid is expanded for clearness

Full size image

This method has an additional advantage, as it can be used at temperatures close to room temperature [14, 15], and for higher temperatures, if the temperature control of the furnaces is accurate. In this case, it is essential to ensure an appropriate furnace design, selection of insulation materials, and radiative shields, adequate to the cup dimension.

As discussed before [5], experimental methods used for transport properties determination can be classified as absolute and relative. For viscosity, for state-of-art instruments, absolute methods are a must, as the measured value has to be defined precisely in terms of the measured quantities, like mass, length, and time, which must be related by a working equation, and a well-defined model of the experimental measurement. Furthermore, the quality of the working equation (i.e., the rigor in describing and designing the instrument and the measurement) and its departures from all the idealizations involved, as well as the uncertainty of the principal measurement parameters, must be subjected to an unambiguous assessment, governed by the international accepted metrology traceability directives/standards.

This statement is conceptually identical to the definition of primary methods by CCQM/BIPM, in 1995, later slightly revised in 1998 [16, 17], citing “A primary method of measurement is a method having the highest metrological qualities, the operation of which can be completely described and understood, for which a complete uncertainty statement can be written down in terms of SI units”. No reference to a standard of the quantity being measured is accepted. However, this definition applied to viscosity measurements is impossible to apply to its full extent. As the viscosity of a fluid is a measure of its tendency to dissipate energy when it is perturbed from equilibrium by a force field, which distorts the fluid at a given rate, it depends on temperature, pressure, and composition. The dissipative mechanism of shear creates, inevitably, local temperature gradients, which can alter slightly the reference thermodynamic state to which the measurement is assigned, from the initial, unperturbed, equilibrium state. As it is impossible to measure local shear stresses, the measuring methods must be based on some integral effect, amenable to accurate measurements, from which, by averaging, the reference state is obtained. The rates of shear must be small enough to maintain a near-equilibrium state and hydrodynamic stability. Disregarding one or more of these restrictions can be responsible for severe errors of measurement, a fact that has not been acknowledged by many previous publications.

Until now, there is no primary method at present for the measurement of the viscosity of liquids, because the absolute methods developed so far, to achieve high accuracy, involve the use of instrumental parameters obtained through calibration. However, the analysis of such methods [3,4,5, 18] (designated as relative or secondary) shows a large range of departure levels from the accepted definition of a primary method. Therefore, it was chosen by Nieto de Castro et al. [5] designate as “quasi-primary” any method for which a physically sound working equation, relating the viscosity to the experimental-measured parameters, is available, but where the values of some of these parameters must be obtained by an independent calibration with a known standard. Among the existing methods of viscosity measurement, we can consider as “quasi-primary” the oscillating body (disk, cup, or sphere). In the oscillating disk viscometer, the disk’s edge effect must be calibrated, in the oscillating cup it is necessary to guarantee that the cup is at least 95 % filled with the liquid to make the meniscus effect negligible (see below), while in the oscillating sphere, a large correction for the effect of air damping must be estimated.

Finally, we need to state that to obtain the dynamic viscosity of a fluid using any of these methods, density values are required. The uncertainty of these data reflects directly on the viscosity uncertainty. For the measurements at high temperatures, this is an additional problem, as it is difficult to obtain density data with uncertainties smaller than 2 %.

It is the objective of the current paper to serve as a resource for workers who use or want to use oscillating-cup viscometry for the measurements of dynamic viscosity of fluids at high temperatures, or in judging the results obtained by others when comparing data with their own.

2 Theory of the Method

2.1 Basic Equations

The theory of the oscillating body viscometer, according to the revisions of Kestin and Wakeham [19] and Nieuwoudt and Shankland [20], after the original works of Kestin and Newell [21] and Beckwitt and Newell [22], can be formulated through the equation that describes the body movement, Eq. 1:

$$I{\omega }_{0}^{2}\left[\frac{{{\text{d}}}^{2}\alpha \left(\tau \right)}{{\text{d}}{\tau }^{2}}+2{\Delta }_{0}\frac{{\text{d}}\alpha \left(\tau \right)}{{\text{d}}\tau }+{\left(1+{\Delta }_{0}\right)}^{2}\alpha \left(\tau \right)\right]=M\left(\tau \right),$$
(1)

where α(τ) is the angular displacement of the body from the equilibrium, ω0 = 2π/T0 is the natural angular frequency of oscillation in vacuum, with T0 the corresponding period of oscillation. τ = ω0·t is the dimensionless time elapsed since the start of the oscillation, I the moment of inertia of the suspension oscillating system (body, suspension, fixing mechanisms). M(τ) is the frictional moment (or torque) exerted by the fluid (induced in the body that rotates about the symmetrical axis) and Δ0 is the logarithmic decrement of the oscillation in vacuum [no fluid, no friction, M(τ) = 0], in radian units. Equation 1 must be solved subjected to the initial conditions for the movement of the body, which are given by Eq. 2:

$$\alpha \left(\tau \right)={\alpha }_{0} {\text{and}} \frac{{\text{d}}\alpha \left(\tau \right)}{{\text{d}}\tau }=0 , {\text{for}} \tau =0.$$
(2)

The movement in the fluid, originating from the viscous drag in the body (external or internal) can be described by its angular velocity, Ω. In a cylindrical polar system, with coordinates r, ϕ, and z, it obeys the differential Eq. 3:

$$\frac{\partial\Omega }{\partial \tau }=\nu \left[\frac{{\partial }^{2}\Omega }{\partial {r}^{2}}+\frac{3}{r}\frac{\partial \omega }{\partial r}+\frac{{\partial }^{2}\Omega }{\partial {z}^{2}}\right],$$
(3)

where ν is the kinematic viscosity of the fluid, ν = η/ρ, η is the dynamic viscosity of the fluid, and ρ its density.

The fluid has to be initially in rest and have no slip in contact with the body (continuity). Therefore, it has to obey the boundary conditions given by Eq. 4:

$$\Omega \left(r,z,0\right)=0,$$
(4)
$$\Omega \left(r,z,t\right)= \frac{{\text{d}}\alpha }{{\text{d}}t} ,\mathrm{ in\, the\, body\, surface}.$$

The torque M(τ) is related with the fluid movement through Eq. 5:

$$M\left(\tau \right)=-\varrho \upsilon \underset{A}{\overset{}{\iint }}{r}^{2}\left(\frac{\partial\Omega }{\partial \mathbf{n}}\right){\text{d}}\sigma ,$$
(5)

where A is the area of the oscillating body in contact with the fluid (wet surface), n is the normal to the surface and dσ is the area element.

Applying Laplace transform to Eq. 1, the solution is given by Eq. 6:

$$\alpha \left(\tau \right)=\frac{{\alpha }_{0}}{2\pi i}{\int }_{C}{\text{d}}s {e}^{s\tau }\left[\frac{1}{s}-\frac{1+{\Delta }_{0}^{2}}{s\left[{\left(s+{\Delta }_{0}\right)}^{2}+1+D\left(s\right)\right]}\right],$$
(6)

where α0 is the initial angular displacement and s is the conjugated variable of τ. In this equation D(s) is given by, Eq. 7:

$$D\left(s\right)= \frac{s\widetilde{M}\left(s\right)}{I{\omega }_{0}^{2}\left[s\alpha \left(s\right)-{\alpha }_{0}\right]},$$
(7)

where \(\widetilde{M}\left(s\right)\) is the Laplace transform of M(τ).

In order to calculate the integral of Eq. 6 it is necessary to solve the characteristic equation, Eq. 8:

$${\left(s+{\Delta }_{0}\right)}^{2}+1+D\left(s\right)=0.$$
(8)

Which, apart from the initial transient movements of the oscillating body (about 2 periods of oscillation), has roots associated to the long-time movement, s, given by Eq. 9:

$$s=\left(-\Delta \pm i\right)\frac{{T}_{0}}{T}.$$
(9)

In this Eq. 9 Δ is the logarithmic decrement of the oscillation amplitude of the body in contact with the fluid. The oscillation has the form of a damped harmonic oscillation, Eq. 10:

$$\alpha \left(t\right)={\alpha }_{0}{e}^{-2\pi \Delta t/T}{\text{sin}}\left(\frac{2\pi t}{T}\right).$$
(10)

If the logarithmic decrement Δ and the period T are determined from the motion of the body in an experiment, and knowing these values for vacuum, Δ0, and T0, they can be introduced in the characteristic equation, Eq. 8. As the expression for the torque D(s) contains the viscosity and the density of the fluid, the characteristic equation can then be inverted to obtain the fluid viscosity, and only the Laplace-transformed form of D(s) has to be obtained, not being necessary to solve the equations of motion.

The torque exerted by the fluid on the body can be calculated from the fluid flow near the oscillating body, using the linearized Navier–Stokes equations for an incompressible fluid [23], assuming that the fluid's interaction with the wall induces a no-slip boundary condition (zero velocity at the wall). This flow along the surface of the body creates a thin layer of fluid near a bounding surface, designated by the boundary layer. This boundary layer has a natural length scale, the boundary layer thickness, defined as, Eq. 11:

$$\delta ={\left(\eta {T}_{0}/2\pi \rho \right)}^{1/2}.$$
(11)

This discussion is valid for any oscillating body, depending on its application to the expressions for D(s). Here we only review the expressions for the oscillating cup.

The characteristic function can be an exact solution, obtained by Kestin and Newell [21], or an approximate solution derived by Beckwitt and Newell [22]. The latter is, Eq. 12:

$$D\left(s\right)={s}^{2}\frac{{I}^{\prime}}{I}\left(\frac{4}{{s}^{1/2}{\zeta }_{0}}-\frac{6}{s{\zeta }_{0}^{2}}+\frac{3}{2{{s}^{3/2}\zeta }_{0}^{3}}+\frac{3}{2{s}^{2}{\zeta }_{0}^{4}}+\frac{1}{{s}^{1/2}{z}_{0}}-\frac{16}{\pi s{\zeta }_{0}{z}_{0}}-\frac{9}{{s}^{3/2}{\zeta }_{0}{z}_{0}}-\frac{8}{{s}^{2}{\zeta }_{0}{z}_{0}}-\frac{{\text{exp}}\left[-2{s}^{1/2}{z}_{0}\right]}{2{s}^{1/2}{z}_{0}}\right),$$
(12)

where \({\zeta }_{0}=R/\delta\) and \({z}_{0}=h/\delta\) are the dimensionless quantities for the inner radius of the cup, R, and the height of the fluid in the cup, h. This equation is applicable when \({\zeta }_{0}\gg 1\) and \({z}_{0}\gg 1\), i.e., when \(R\gg \delta\) and \(h\gg \delta\). I′ is the inertia moment of the fluid inside the cup, given by Eq. 13:

$${I}^{\prime}=\frac{1}{2}\pi \rho h{R}^{4}.$$
(13)

The exponential term in Eq. 12 is negligible for \({z}_{0}>10\). From this general equation, Brockner et al. [24] developed working equations from the general solution of Eq. 12, for the oscillating cup viscometer, for what is conventionally called large cups [20], when \({\zeta }_{0}\gg 1\) and \({z}_{0}\gg 1\). Solutions exist for small cups (h < δ; R > δ) and intermediate cups. The operational zones for all three zones were sketched in Fig. 2.3 of Reference [20]. However, here we recommend, if possible, to obtain better accuracy (and smaller uncertainty) the use of large cups.

As s is a complex variable, Eq. 12 when solved for s, will have two parts, a solution with the imaginary part of D(s) and another with its real part. The real part is less utilised for the measurement of viscosity as a term appearing (1 − θ2) ≈ 2 (1 − θ), can have a larger uncertainty, as \({T}_{0 }\sim T\) and therefore (1 − θ2) ≈ 0. The solution for the imaginary part is given by Eq. 14,

$$\frac{\pi \rho h{R}^{4}}{2I}\left[A\left(p-\Delta q\right){x}^{-1}-B{x}^{-2}+Cq{x}^{-3}\right]=2\left(\Delta -\frac{{\Delta }_{0}}{\theta }\right),$$
(14)

where

$$A=4+\frac{R}{h};\quad B=6+\left(\frac{16}{\pi }\right)\left(\frac{R}{h}\right);\quad C=1.5+9\left(\frac{R}{h}\right);\quad D=1.5-\left(\frac{8}{\pi }\right)\left(\frac{R}{h}\right),$$
(15)
$$\theta =\frac{{T}_{0}}{T};p=\frac{1}{{\left[2\left(\Delta +{\left(1+{\Delta }^{2}\right)}^{1/2}\right)\right]}^{1/2}} ;q=\frac{1}{2p},$$
$$x=R{\left(\frac{2\pi \rho }{\eta T}\right)}^{1/2}.$$

Equation 14 can be solved numerically for the value of x, with an error smaller than 0.1 %, when R/h > 1 and \({z}_{0}>10\), otherwise the exact solutions of Kestin and Newell [21] must be used.

The working equation for the calculation of viscosity is then Eq. 16:

$$\eta =\frac{2\pi \rho {R}^{2}}{T{x}^{2}}.$$
(16)

2.2 Applicability Requirements

The application of Eq. 16 to the determination of the viscosity of high-temperature molten materials is based on the following assumptions:

  1. (1)

    Linearized Navier–Stokes equations for an incompressible fluid are strictly applicable when the motion of the fluid is unidimensional, i.e., the fluid should move only in the direction perpendicular to the axis of oscillation. Any wagging that would create secondary flows, must be avoided.

  2. (2)

    The liquid is Newtonian and no convective or secondary flows are present.

  3. (3)

    Oscillations must be small, to be considered harmonic. This is also imposed by the behaviour of the suspension wire, as its material has to be elastic (obeying Hooke’s law).

  4. (4)

    The effect of the pressure above the liquid, caused by its the vapor phase, in the torque induced in the mechanical system is negligible. Applications for high vapour pressure molten materials should be reanalyzed, and therefore, measurements near the boiling point of the materials are not recommended.

  5. (5)

    The cup is fully filled with liquid, and we can use the concept of the large cup, i.e., when \({\zeta }_{0}\gg 1\) and \({z}_{0}\gg 1\). Otherwise, the designated meniscus effect, dependent on the surface tension of the liquid, affects the oscillation scheme, overestimating the calculated values of viscosity.

2.3 Additional Requirements for Quality Measurements

In addition, the following points are recommended to be followed to perform quality measurements, with low uncertainty:

  1. (6)

    Geometrical measurements of cup and suspension systems known with low uncertainty. In addition, and for large temperature measurements, the moment of inertia, the radius of the cup, and the period of oscillation in the vacuum must be corrected for the temperature, using the isobaric thermal expansion coefficient of the cup material.

  2. (7)

    The elastic modulus of the torsion wire must be monitored with care, as aging and high-temperature cycles can affect its torsional characteristics, and therefore its elastic modulus and applied torque to the system.

  3. (8)

    The torsion wire must be vertical, straight.

  4. (9)

    The logarithmic decrement of the planar oscillation must be measured experimentally with low uncertainty.

  5. (10)

    Because the viscosity is a strong function of temperature for molten materials at high temperatures, accurate temperature measurement is vital.

These requirements, added to some experimental limitations that appear in the design of oscillating-cup viscometers, namely for high temperatures will be discussed in the next section, calling attention to the factors that affect drastically the uncertainty of the measurements.

3 The Physical Realization of an Oscillating Cup Viscometer

An oscillating cup viscometer is composed of four fundamental systems: an oscillating system (including the suspension system and oscillations initiator), a furnace (heating system) with measurement thermometers, a vacuum system (or in alternative measurements can be made under a controlled gas atmosphere) and a system to detect oscillations.

The oscillating system, including the cup, must be designed to fulfill the working equation of the method, Eq. 16. However, it is convenient here to discuss some design considerations, consistent with the model equations, as there are alternatives/choices of each application, and to describe some operational constraints or limitations, which condition the quality of the results to be obtained.

3.1 Design Considerations

3.1.1 CONSIDERATION 1: The Torsion Wire

This torsion wire has mechanical exigencies, as it needs to be straight, and made of a metal with elastic modulus suitable for the materials to be measured (suspension obeys Hooke’s law). Its dimensions (diameter and length) must be adequate to the weight of the cup and suspension rods/disks/mirrors. Several wires have been used, for instance, Pt92/W8 wire with 0.5 mm of diameter and a length of 603 mm, material chosen by Nunes et al. [26], Torklep and Oye [8], Abe et al. [9], Sato et al. [25] due to its low internal friction and stable elastic behaviour, as suggested by Kestin and Mozynsky [27] and used by several groups, also for oscillating-disk viscometers. However, depending on the molten material studied, other wires, like Pt87/Rh13, with a higher elastic modulus have been used [28] to improve the accuracy of the logarithm decrement determination (see below) or pure W [14, 29], in its appropriate temperature regions.

3.1.2 CONSIDERATION 2: The Oscillation Initiator

This initiator can be manual or electrically driven. This last version is better, as it can improve the reproducibility of the oscillations for repeating measurements. However, as referred to above, the working equation is valid only after some transient oscillations (2 to 3), and the effect can be minimized. Only the experience with the system chosen can select the best initial amplitude, to obtain a good reproducibility of the generated damped oscillation.

3.1.3 CONSIDERATION 3: The Cup

The cup design requires a careful study of the material's chemical compatibility between the metal of the cup and the molten material (salt, metal, semiconductor,…). This fact is mostly important at high temperatures, where the corrosion kinetics play an important role. In addition, considerations about the wettability of the melt in the cup have to be considered, namely the surface tension of the melt (see meniscus effect below). Nevertheless, the most important mechanical characteristics of the cup to be known are its geometric measurements (height, internal and diameter, bottom thickness) dimensions of the cup top, and material density. This affects immediately the working equation (R), the validity of the solutions (h, ζ0 and z0), and the inertia moments (I and I′). For instance, an error of 0.06 % in R can contribute to an uncertainty of 0.17 % for the viscosity.

3.1.4 CONSIDERATION 4: Vacuum/Gas Atmosphere

The use of Eq. 16 requires the determination of T and Δ in the fluid, and their values in vacuum, T0 and Δ0, where no damping exists. The working equation, through the root x, is very sensitive to the ratio θ and the difference Δ − Δ0. As these values are always very similar, an error in the “vacuum values” caused by the presence of a low-pressure gas (air for non-oxidized samples, argon or nitrogen) outside the cup, which introduces a non-zero damping, has to be considered. This fact has been analyzed by Nieuwoudt et al. [30]. These authors showed that the ratio between the period in vacuum T0 (ideal) and the period in the gas, Tg would be of the order of the ratio \({\left(\frac{{\rho }_{g}}{\overline{\rho }}\right)}^{2}\), while the difference between the logarithmic decrement in the gas, Δg and that in a vacuum, Δ0 would also be of the order of \({\left(\frac{{\rho }_{g}}{\overline{\rho }}\right)}^{2}\), where \(\overline{\rho }\) is the density of the cup material. Using the density of air and SS 316 at room temperature and atmospheric pressure, 1.293 kg·m−3 and 7980 kg·m−3, we have O(1.293/7980)2 ≈ O(2.6 × 10−8). For a typical system [26], and a run for molten NaNO3 at 700.76 K, T0 ≈ 1.6622 s and Δ0 ≈ 2.10562 × 10−4 and the error will be smaller than 0.007 % in the period and 0.012 % in the logarithmic decrement, much smaller than the experimental uncertainty of these parameters determination (0.03 % and 0.9 %) [28]. It can be concluded, therefore, that we do not need to use determinations in vacuum for most of the applications, and air or inert gas atmospheres can be used.

3.2 Operational Constraints

3.2.1 CONSTRAINT 1: Oscillating Period and Logarithmic Decrement

The measurement of the body oscillation dynamic characteristics is the heart of the operation of oscillating body viscometers. In all cases, the measurement is performed by observing the angular displacement, in the plane of the torsional oscillation. As shown above, in Eq. 10, the motion of the pendulum is adequately described by a damped harmonic motion. For the majority of instruments so far developed, a light source, generally a Ne–He low-power laser, is pointed to a plane mirror, part of the oscillating system of the viscometer. This light is deflected (changing its path with the oscillation) and the “time of flight” can be detected by two or more photodetectors, linked to a timer counter. Two slightly different processes have been used. Kestin and Khalifa [31] described a technique where one photodetector is placed in the resting position of the oscillating system, at the distance of 2 m, and the other photodetector is placed in a fixed angular position, which does not need to be measured. Times of flight of the beam in both detectors are measured, triggering the timer/counter. Abe et al. [8] used a similar technique, placing the second detector in a position about 15 cm from the zero-oscillation point. The period was determined by the passage of the laser beam in the central point detector, and the logarithmic decrement was determined by the increment of successive time intervals of passage in the photodetectors. The equation for the logarithmic decrement is Eq. 17:

$$\Delta =\frac{1}{2\pi }\frac{{\text{ln}}\left[{\text{sin}}\left(2\pi {t}_{i+n}/T\right)/{\text{sin}}\left(2\pi {t}_{i}/T\right)\right]}{n+\left({t}_{i+n}-{t}_{i}\right)/T},$$
(17)

where ti is the time interval at an arbitrary moment, and ti+n is the time interval n periods after. This procedure can be observed graphically in Fig. 2.

Fig. 2
figure 2

Damped oscillation. Adapted from [9]

Full size image

The relative standard uncertainty for the determination of the period and the decrement was estimated to be ur(T) = 0.00003 and ur(Δ) = 0.003. This technique was used by Nagashima’s group in Keio, Japan, and Sato et al. [28] for molten salts, and also by Kakimoto and Hibiya [32] for molten semiconductors.

Ohta et al. [33] showed that it is not necessary to measure physically the period using a photodetector placed at the zero-oscillation position. They used two detectors placed at fixed angular displacements, α1* and α2*, and determined the passing times of the laser beam in these two positions. The logarithmic decrement is obtained using a curve-fitting process to the equation that describes the harmonic movement of the damped oscillation, Eq. 10. This technique was further used by Torklep and Oye [8] and Berstad et al. [34] for water, and Wang and Overfelt [35] for molten alloys. In our group in Lisbon, we have applied it to molten salts [26, 36,37,38] and molten alloys [15, 39, 40], with relative standard uncertainty for the period determination and decrement was estimated to be ur(T) = 0.00018 and ur(Δ) = 0.0017.

The non-planarity of the oscillation (wagging, bouncing) can be easily detected experimentally, as the periods will not be reproducible, and the uncertainty of the logarithmic decrements is 10 to 50 times bigger. As a recommendation, the photodetectors have to be optically clean, with a target area and a sensitivity that is compatible with the angular speed of the oscillation.

There are more recent possibilities, including the use of a laser profilometer increasing space and time resolution, to properly describe θ(t) [41, 42]. As these authors report, the use of 3-D profilometers could give direct access to accurate characterization of secondary oscillations, with additional information about the rotating unbalance.

3.2.2 CONSTRAINT 2: The Liquid Level in the Cup

One of the controversies arising from this method is the so-called “meniscus effect”. In fact, for the determination of the fluid viscosity, we need to know the height of liquid inside the cup, h, and check if the cup is fulfilled with the melt, i.e., if the liquid height is H, the internal cup height. As the working equation was developed for large cups, its use requires that the cup is filled (or, as filled as possible, namely h/H > 0.95, as reported below). If this is not the case, the solutions for short cups and intermediate cups (see Sect. 2) have to be used.

There are two ways of filling the cup, one for liquids around room temperature, like water or Galinstan, or as solids, used for materials for which the melting temperature is above room temperature, which are placed in the cup at room temperature, the whole being heated with the increase of temperature in the furnace above the melting point.

In the first case, the complete filling can be checked by weighing the fluid and using the known values for the density and cup dimensions. But, due to the surface tension of the liquid, this can never be exact, because of the formation of a meniscus that is a function of the contact angle between the liquid and solid surface of the cup. In the second case, knowing the volume variation of the material on melting, and the thermal expansion of both (the melt and the cell), it is possible to calculate the amount of solid to introduce in the volume of the cup, to fill the cup completely. However, when conducting research for new materials, like new alloys and semiconductors, for which thermodynamic data is scarce or non-available, property estimation methods for density, thermal expansion, and melting volume variation have to be used.

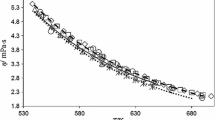
This problem was fully discussed in the publication by Nunes et al. [43], which evaluated the influence of the meniscus of liquid in the determination of viscosity by the oscillating cup method, using water at 298.15 K for several heights of water inside the cup. The height of the cup used was H = 7.4 cm and the radius was 8.590 ± 0.005 mm. Measurements were performed for 5 heights of the liquid inside the cup, h = 2.83 cm, 4.05 cm, 5.17 cm, 6.98 cm, and 7.40 cm (filled cup). For each height a set of 7 to 9 measurements were performed for temperatures around 298.15 K, and corrected to this nominal temperature, using Berstad et al. [34] data for the viscosity of water. The mean values and the root mean square deviation of the measurements for the empty cup where Δ0 = (2.105 ± 0.03) × 10−4 and T0 = 1.6007 ± 0.0003 s. Table 1 and Fig. 2 display the results obtained for the viscosity of water at 298.15 K, for each height of liquid in the cell, h, and the deviations from Marsh [44] data, including the error bars associated with the standard deviation of the replicate measurements.

Table 1 Measured viscosity of water at 298.15 K as a function of fluid height, h
Full size table

These results show how important is the use of a cup completely filled with the liquid. Figure 3 shows that the measured value converges to the recommended value as the height of fluid increases, η (298.15 K) = 0.8904 mPa·s. As reported in [39], if h <  < H the wettability of the cup is very important. If the liquid wets the solid surface of the cup the calculated height of the liquid is lower than the ‘true’ value and the value of the viscosity derived from the measurement will be higher than the true value. This is the case for water in steel where the contact angle is about 70° to 90°, depending on temperature and surface finishing. A condition of non-wettability (like mercury) will decrease this problem.

Fig. 3
figure 3

Viscosity of water at 298.15 K and 0.1 MPa, as a function of the fluid height inside the cup. The dashed horizontal line indicates the recommended value (error bars in viscosity are given by the uncertainty of Table 1)

Full size image

Any reported data on the viscosity of molten materials should demonstrate that the cup is almost completely filled (h/H > 0.95), otherwise, the values might be at least 5 % to 10 % greater than the true values, as previously found when a comparison of data from different laboratories is made.

3.2.3 CONSTRAINT 3: Temperature Measurement and Control in the Vertical Tubular Furnace

Using the oscillating-cup viscometer at high temperatures, one has to consider the temperature measurement and control very carefully, as in any property measurement in these temperature ranges. Although thermometry is highly developed for temperatures up to 1800 K, several types of thermometers can be used, from thermocouples to metal resistance thermometers, from infrared to optical pyrometers. In any case, the problem is to measure the temperature of a molten material, inside the closed cup, in normal oscillation. Contact thermometers and contactless systems can be used, but the key decision is the uncertainty of the temperature measurement. Viscosity is extremely sensitive to temperature, and for instance for a molten salt, like NaNO3, at 600 K, an error of 1 K corresponds to an error of 0.53 % in viscosity, while that of 5 K originates an error of 2.7 % [37], while for a molten alloy, like the Al–Zn alloy II [41], the effect is similar (at 700 K 0.46 % for 1 K uncertainty and 2.33 % for 5 K). As an example, in the instrument developed by Nunes et al. [26], shown schematically in Fig. 4a, the temperature could be measured with type K thermocouples, calibrated up to the silver point, with an uncertainty of 0.1 K to 0.5 K, or a PT100 (better uncertainty up 900 K), held in axial direction just beneath the bottom of the cup, inside a metal finger, at about 1.5 mm from it (see Fig. 4b). However, the thermocouple is not inside the cup, and its temperature TTC is different from the melt temperature, inside the cup, TM. This difference depends on the distance of the temperature sensor to the bottom of the cup and the furnace stability/control. The following methodology is suggested:

  1. (a)

    Study very well the profile of the furnace (with appropriate insulation), controlled by a very sensitive PDI controller, in the temperature range to be used, as a function of the height in the tube, namely in the region above and below (at least 5 cm) and around the cup (usually with 10 cm height) and infer on the fluctuations within the expected duration of an experimental point determination.

  2. (b)

    Make a blank measurement with the cell open to the atmosphere, suspended in the same position in the tubular furnace, by immersing a second calibrated temperature sensor in the melt. The temperature of the furnace is then scanned in the temperature interval used for the viscosity measurements, in steps of 50 K to 100 K, and the temperatures measured by both temperature sensors can be recorded as a function of the temperature of the outside probe, TTC. In the furnace of the referred instrument [28], a systematic positive temperature difference was found, increasing with temperature, as expected. This systematic difference can then be applied to the measured temperature TTC in each experimental point, to obtain the melt temperature, TM. As referred, this difference can be minimized by using the discussion above related to furnace control in the region around the cup.

  3. (c)

    Obtain data points for both increasing and decreasing temperatures, to observe any possible hysteresis of the system, which will influence the uncertainty of the measurements.

Fig. 4
figure 4

(a) High-temperature oscillating cup viscometer [28]. (1) Oscillating initiator; (2) Pt92/W8 wire; (3) mirror and inertial disk; (4) window for laser beam; (5) molybdenum cup suspension bar; (6) tube with radiation shields; (7) ceramic and steel tubes; (8) furnace; (9) molybdenum cylindrical cup; (10) thermocouple assembly. (b) Detail of the position of the cup and thermometer in the furnace

Full size image

3.3 Expected Contributions for the Overall Uncertainty

When reporting experimental data, it is fundamental to estimate its uncertainty. Most of the experimental effects mentioned can be quantified to access this value. The total uncertainty can be calculated from the root-mean-square deviations of the different contributions and reported as global uncertainty [expanded at 95 % confidence level (k = 2)], as suggested in the ISO_GUM guides. An example of this estimation can be seen in Table 2, where data was taken from our previous work with NaNO3 [37].

Table 2 Uncertainty analysis for the oscillating-cup viscosity measurements [39]
Full size table

4 Final Comments

In the current work, the solutions for the oscillating-cup viscometer based on the theory developed by Kestin and co-workers [21, 22], have been used. However, other equations were also used in the past to determine the viscosity with this technique, in an absolute way. Not pretending to review all those previously employed, we would like to refer to the equations developed by Roscoe [45] and Roscoe and Brainbridge [46], which proved to be very accurate, leading to results that agree with Kestin and colleagues [21, 22] solutions within their mutual uncertainty, below 0.1 %. However, they have been used incorrectly by several authors, and readers are directed to Ferriss and Quested [47]. Recently Zhu et al. [40] have developed an oscillating-cup viscometer for molten materials. These authors claim that using the Shvidkovskiy equation [48], with Roscoe corrections [45, 46], obtained data for water with deviations up to 2.5 %, although claiming a global relative uncertainty Ur(η) = 0.021, probably too optimistic, as no discussion about the meniscus effect and temperature control and measurement was performed, and the mass uncertainty can be made 10 times smaller than what is quoted.

The application of Shvidkovskiy equation [48] for the measurement of molten metals at very high temperatures (2135 K) has been recently tested by Patouillet and Delacroix [42], who also developed a new oscillating-cup viscometer. They used a new acquisition method of the oscillatory motion, a boron nitride crucible, a steel wire, as well as an accurate temperature measurement that is corrected to compensate for variations in tungsten emissivity. The authors claim a global relative uncertainty Ur(η) = 0.03.

The problem of the convective or secondary measurements, when present, have been discussed in [20] and recently reviewed by Elyukhina [49], who presented a review on high-temperature measurement viscometry, and extended the application of the oscillating-cup viscometer to non-Newtonian fluids, like Bingham plastics and viscoelastic/pseudoplastic fluids. Several effects on the type of oscillations have to be dealt and the equations of motion have to be solved numerically. Elyukhina and Vikhanski [50] have shown by numerical calculations (CFD) that the effect of the secondary flows on the decrement and period of the oscillations scales as the square of the amplitude of oscillations, α0. The secondary flow consists of a stationary circulation and a periodic component whose period is half of the period of the primary oscillations. Knowing the functional form of the non-linear term one can filter it out from the experimental data. Following these authors, using the proposed numerical procedure one can work with higher amplitudes of the oscillations and stronger fluid-crucible coupling, and extend the application of this technique t non-Newtonian fluids.

5 Conclusions

This paper lays the necessary and sufficient conditions for instruments based on the oscillating-cup, to obtain high-quality measurements. This method uses a complete working equation, with very accurate solutions. If the suspension/oscillating system is designed to minimize deviations to the mathematical model, like small oscillations perpendicular to the vertical axis of the cup suspension, the cell is at least 95 % filled with the molten material, and a correct temperature control and temperature measurement of the melt temperature is made, the oscillating-cup viscometers can be trusted as the best instruments for medium to high temperatures. Several considerations regarding the instrument design have been identified, as well as several operational constraints that require a correct approach when making the measurements, to obtain excellent results. If all these points are followed in the design and operation of the instrument, results in global uncertainties Ur(η) between 0.02 and 0.04 are possible to obtain. Otherwise, if they are neglected, erroneous measurements can be made, making comparisons and quality assessment difficult. It was written to be a resource for workers who use or want to use oscillating-cup viscometry for the measurements of dynamic viscosity at high temperatures, or in judging the results obtained by others when comparing data with their own.